微纳米流体力学主要关注大约100 μm~1 nm范围内的流动。该尺度范围的流动具有显著的表面、界面作用(如静电力、范德华力等)以及雷诺数小于1(黏性相比惯性起主导作用)等特征。微纳米流体力学长期以来关注连续性假设的适用性以及滑移边界条件两个科学问题。
对于连续性假设适用性问题, 经过近年来的研究, 学界有了一定共识。一般认为, 当流动的空间和时间尺度比"分子"动力学尺度大一个量级以上, 即可采用连续性假设[1]。对于纯水的流动, 流动尺度L应远大于液体黏性长度lv(~0.5 nm), 流动时间尺度τh远大于微观液体分子运动的时间尺度τσ(τσ~1 ps)。上述观点得到了一系列实验和分子动力学模拟结果的支持[2-5]。
相比连续性假设问题, 界面滑移的理论描述、大小及影响因素, 至今仍存在较多争议。研究中常采用的滑移理论模型是Navier[6]于1823年提出的线性滑移边界条件模型:
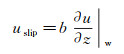 (1)
(1)
式中, uslip为滑移速度, u为流场速度, b为滑移长度(定义为液体速度分布线性延长至0的点到界面的距离), 下标"w"表示əu/əz为壁面处的剪切率(图 1)。式(1)是一个唯象的描述性方程, 虽然方便使用, 但并未考虑液固界面处应力连续的问题[7-8]。
早期的滑移实验结果非常分散, 滑移长度的测量值分布于10 nm~10 μm范围[9-12]。测量结果的影响因素被认为与壁面粗糙度、亲疏水性、流体黏度、表面电荷密度等属性相关[2-3, 13-14]。近年来, 随着实验技术的发展, 光滑壁面的滑移长度测量结果逐渐集中于1~20 nm范围[2, 5, 15-16]。一般而言, 光滑亲水壁面的滑移长度接近0, 而光滑疏水壁面的滑移长度会大一些, 能达到10 nm量级。
然而, 随着微纳尺度流动研究的推进, 液固界面滑移的研究也面临新的挑战。一方面, 当流动的特征尺度减小至纳米量级(比如单个纳米管中的流动), 滑移就成为非常重要的影响因素[17-18], 如何更准确地测量及建立完整的理论描述, 都是亟需解决的问题。另一方面, 微纳流动与生物医学深入交叉, 涉及的流体不再是简单牛顿流体, 复杂的流体结构使得界面附近的流动特性更为复杂, 这就可能引入了新的滑移机制, 从而引起了广泛的研究兴趣[19-21]。
本文将综述近年来微纳米流体力学领域中液固界面滑移研究的新进展, 着重介绍纳米尺度流动中滑移研究的新结果, 以及从简单流体扩展到复杂非牛顿流体的研究过程中, 滑移实验研究的新的测量结果以及理论描述方法。关于复杂流体滑移的进展, 主要介绍法国Charlaix教授课题组采用表面力仪(Surface Force Apparatus, SFA)测量高分子电解液取得的一系列新的实验结果[7, 21-23]。
1 液固界面滑移的理论模型及测量方法近十年来, 一系列综述文章对液固界面滑移的理论模型及实验测量方法进行了比较详细的介绍[1-3, 24-26]。限于篇幅, 本节仅简单介绍光滑液固界面滑移的一些常用理论模型及实验测量方法。
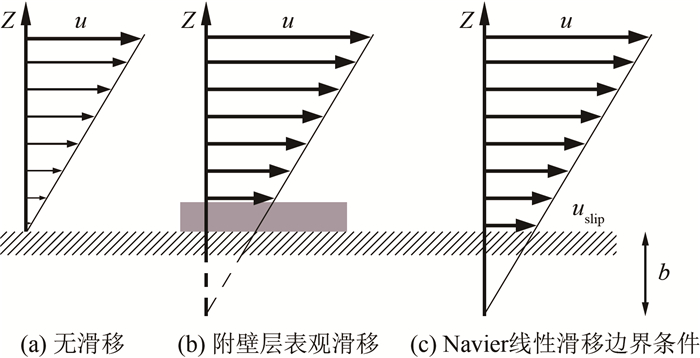
1.1 理论模型给出适当的边界条件对于描述液固界面附近的流动有着重要的物理意义。长期以来, 人们普遍采用的边界条件是唯象性的无滑移边界条件[3, 25](图 1(a)), 即认为紧靠固体表面的液体的流动速度与固体表面的速度一致。此外, 还有两种不同的边界条件被提出:
一为附壁层边界条件[3, 25, 27](图 1(b)), 认为有一层很薄的液体紧密附着于固体表面, 液体在此薄层(即附壁层)上发生滑移, 附壁层的厚度与液固两相分子相互作用、液体流动结构等因素相关。在血液、石油、高分子溶液这一类复杂流体的近壁流动中, 往往基于图 1(b)的模型, 认为体相流体在附壁层上发生表观滑移。
一为式(1)提及的Navier线性滑移边界条件模型[3, 25](图 1(c)), 该模型定义了滑移速度uslip和滑移长度b, 两者成线性比例关系, 比例系数为壁面剪切率。如果在界面上剪切应力连续, 则固体表面的剪切应力应等于液体表面的剪切应力。依据Brillouin[28]于1907年提出的液固界面剪切应力表达式:
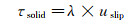 (2)
(2)
又由牛顿流体剪切应力公式:
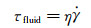 (3)
(3)
联立式(1)、(2)和(3), 就能得到滑移长度b的表达式:
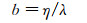 (4)
(4)
在式(2)~(4)中, λ为壁面对流体的阻力系数, η为流体黏度, 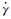
要从分子角度描述液固界面的滑移, 可以从Green-Kubo关系出发[29-30]。Green-Kubo关系通过相关函数来描述阻力系数λ, 再将λ代入式(4)得到滑移长度b。以Green-Kubo关系求λ如下式所示:
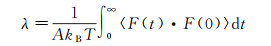 (5)
(5)
式中, A为液固界面的面积, kB为玻尔兹曼常量, T为温度, F为液固两相分子间作用力, "〈 〉"表示系综平均。
Green-Kubo关系一个成功的应用是它可以解释表面亲疏水性对滑移的影响。若把式(5)的积分简化为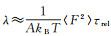
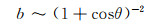 (6)
(6)
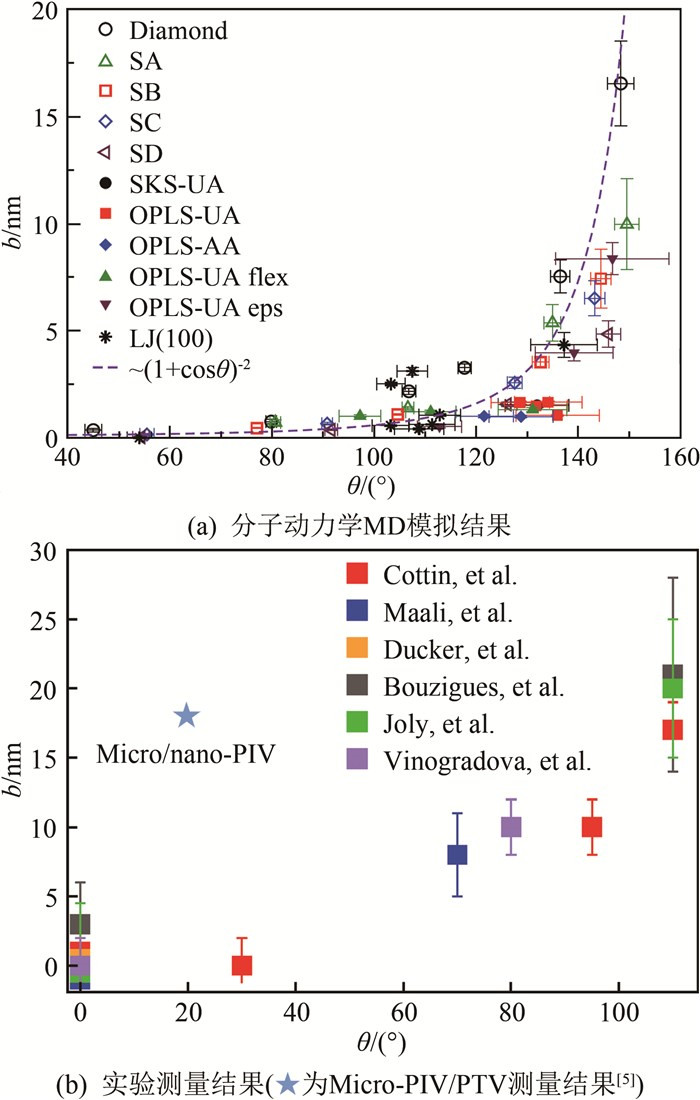
式(6)可以很好地解释分子动力学MD模拟结果(图 2), 且趋势上也和实验结果符合[2, 15]。
总的来说, Green-Kubo关系以及MD模拟结果对水在光滑壁面的滑移长度测量结果给予了理论支持, 使研究者对光滑液固界面滑移长度的量级形成如下共识:其值基本上从0.1 nm到10 nm, 亲水表面基本没有滑移, 疏水表面滑移更大一些。
1.2 测量方法常用的测量滑移的实验方法可以分为3类:压力-流量关系测量、速度分布测量、表面力测量。
1.2.1 压力-流量(p-Q)关系测量压力p驱动流体流经微纳尺度流道, 流体流量Q可表示为两部分:Q=Q0+Qslip, 即采用无滑移边界条件时, Q等于经典Poiseuille公式描述的流量Q0与滑移导致的流量增加Qslip之和。比如, 对于半径r、长度L的微圆管, 实验测得的流量可表示为[32-33]:
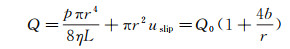 (7)
(7)
由于Q~r4, p-Q测量结果的不确定度受到管径r的测量不确定度的严重制约。早期大量的直接在纳米管道或其阵列中通过p-Q关系测量得到的滑移结果分散性非常大[34-36], 其可靠性也受到较多质疑。尽管如此, 近年仍有大量此类实验[17-18, 37-38], 希望通过改进实验技术, 能够真正实现对单根纳米管内流动的精确测量。
1.2.2 速度分布测量通过速度分布来测量滑移的理论依据即为Navier线性滑移边界条件模型。通常测量速度的方法为粒子示踪测速, 即Micro-PTV、Nano-PTV等, 相关测量结果可参阅文献的综述。需要注意的是, 在微纳尺度近壁流动中, 使用粒子示踪测速往往会受到壁面与粒子的相互作用、双电层、物镜景深等因素的影响[5, 39-41], 以示踪粒子速度来表征流体速度往往需作修正, 给出测量结果也需谨慎。目前, 近壁区域粒子示踪测速得到的滑移长度结果通常比表面力测量等方法得到的结果略大, 如图 2(b)中郑旭等[5]采用Micro-PTV测量近壁1 μm范围内的速度分布而得到的滑移长度(以蓝色"★"表示)。
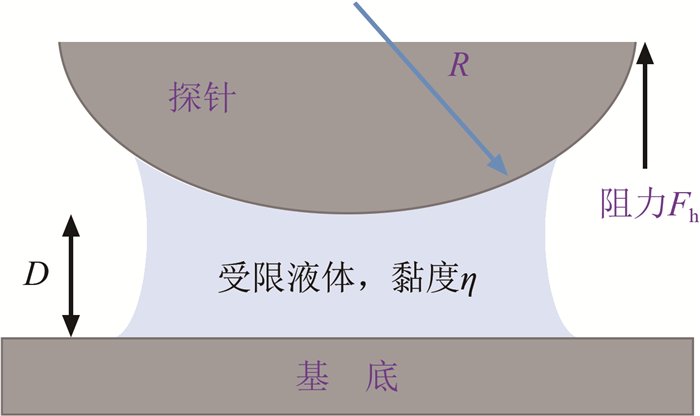
1.2.3 表面力测量使用表面力仪或原子力显微镜(Atomic Force Microscope, AFM)进行测量, 其原理[21-22]如图 3所示。当一个球形(或圆柱形)探针以一定速度u向下挤压液体, 接近平板基底时, 探针受到的水动力学阻力Fh可以表示为[3, 42]:
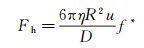 (8)
(8)
|
| 图 3 表面力仪测量滑移原理示意图 Fig.3 Schematic diagram of measuring slip by surface force apparatus |
式中, D为两物体间距, R为小球曲率半径, f*为表征滑移的参数。当f*=1时, 式(8)为无滑移时的Taylor解; 当f*<1时, 存在滑移, 阻力变小。f*与滑移长度b有如下关系:
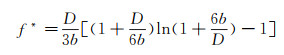 (9)
(9)
两物体间距D可以达到1 nm左右, 这提供了粒子示踪测速技术无法达到的纳米尺度的探测能力。在此基础上, 可以在探针下压过程中施加振动, 从而动态测量非牛顿流体的黏弹性响应以及界面滑移, 相关内容将在第3节中详细介绍。
2 简单流体滑移的新进展简单流体滑移的最新研究成果主要集中于两个重要方面:一是对单根纳米管内流动的测量, 希望给出滑移增强纳米管道流动的确定性结论; 二是液固界面双电层对滑移影响的研究, 这是因为在微纳流控应用中, 双电层及界面静电作用是不可避免的影响因素。
2.1 单根纳米管内的流动测量相比早期实验中使用的纳米管阵列[34-36], 对单根纳米管内的流动进行测量, 可以避免管径尺寸不确定度大及流体泄漏等缺点, 但对单根纳米管进行实验操控面临巨大的技术挑战。Bocquet教授课题组[17-18]在这个方面开展了突出的工作, 如图 4所示。
如图 4(a)所示, Bocquet教授课题组提出了基于扫描隧道显微镜TEM的操控系统[17-18], 可以在TEM系统观测下协助定位, 并对单根纳米管进行切割、粘接等操作。密封后的管路系统(图 4(b))可施加压力、电压、浓度差等产生流动, 继而可测量流经纳米管的流量。需要指出的是:目前通过电信号、浓度信号等间接测量纳米管输运流体流量的方法, 往往受限于纳米尺度壁面附近电场、浓度场分布不均等问题, 反推流量的精度也因此而受限于所使用的物理模型的适用性。针对该问题, 基于柔性腔体的变形直接测量不可压缩液体流量的方法[38]值得借鉴; 而Bocquet教授课题组则发展了基于Landau-Squire射流的方法(图 4(c)), 通过测量纳米管出口的流场分布间接测量管口的流速及管道的流量。有意思的是, 其对比实验显示(图 4(d)):在碳纳米管(CNT)中, 滑移长度b随管径减小而增大(b可达300 nm甚至更大); 而在氮化硼纳米管(BNNT)中, 滑移长度为0。这个结果显示了液固分子相互作用的巨大影响。当纳米管内双电层交叠时, 通过压力驱动盐溶液流过此类纳米管, 可实现机械能向电能的转化。Bocquet教授课题组发现:当滑移长度达到50~100 nm时, 可以通过滑移减小机械能损耗, 从而大幅提高能量转化效率[17, 43]。
2.2 双电层的影响在微纳流动中, 液固界面带电导致水溶液在界面附近形成双电层[44]。一般固壁表面带负电, 则双电层内溶液带等量的正电荷, 以保持电中性。在组成结构上, 一部分正电荷由于静电吸引或物理吸附, 与固壁表面紧密结合, 构成Stern层; 其余正电荷则分布在溶液中, 构成扩散层(Diffuse layer)。在扩散层中, 电荷分布由静电力及扩散主导, 满足指数型Boltzmann分布。双电层厚度一般为1~100 nm量级(由德拜长度lD表征), 因此, 对于微米量级以下的流动, 双电层的影响是显而易见的:在液固界面上, 表面电荷对双电层内离子等流动输运起主要作用, 也对界面附近的滑移有重要影响。
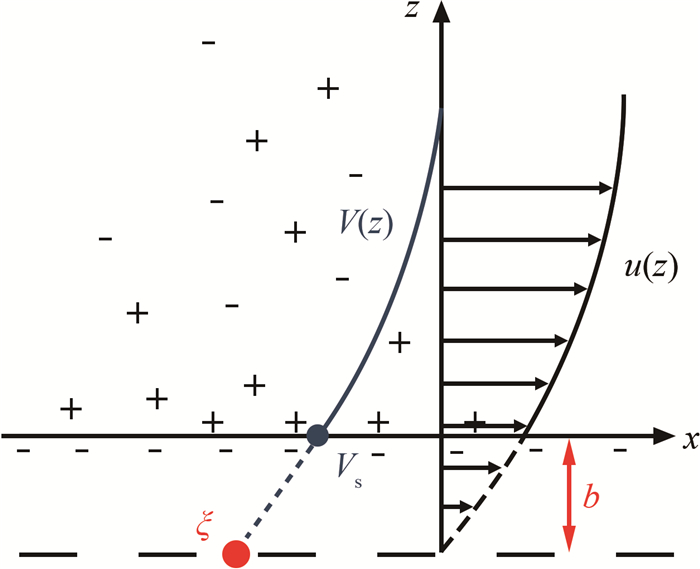
理论上描述图 5所示的双电层流动, 需联立引入静电力的Stokes方程(10)及Poisson方程(11)[13, 44]:
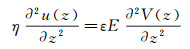 (10)
(10)
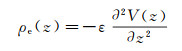 (11)
(11)
其中, V(z)为电势分布, 在界面处V=Vs(Vs为表面电势), E为电场强度, ε为介电常数, ρe为电荷密度。由于远离壁面时电势梯度为0, 且流动速度达到稳定的电渗速度ueo, 对式(10)积分可得:
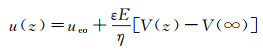 (12)
(12)
由电渗速度可定义zeta电势ζ:ueo=-εζE/η。ζ与电动现象密切相关, 其电势的定义位置基于滑移位面。无滑移时, 流体分子及电荷在Stern层表面处的速度为0, ζ=Vs; 若存在滑移, 将滑移边界条件式(1)代入式(12), 可得液固界面的滑移速度:uslip=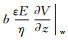
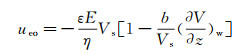 (13)
(13)
这相当于通过滑移放大了zeta电势, 得到zeta电势变化与滑移长度的关系(式(14)), 这一关系在一些实验中得到了验证[13, 45]。
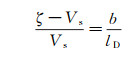 (14)
(14)
对高分子溶液、乳状液等复杂流体的滑移研究也有很长的历史, 相关的影响因素包括高分子的排空效应、剪切稀化、浸润性等[19-20, 27, 46-47]。由于复杂流体存在复杂且非均匀的微观结构, 往往需要采用介观的方法在不同尺度范围内认识并描述其流动[21, 48]。本节着重介绍采用动态表面力方法(Dynamic Surface Force Apparatus, DSFA)来测量高分子电解液在光滑液固界面上的滑移(详见文献)。该方法不仅能得到滑移的结果, 还可以揭示界面附近复杂流体的结构以及流体黏弹性等物理信息[22-23, 49]。
3.1 动态表面力测量动态表面力方法发展自前述表面力仪, 同样是使用一个球形探针以一定速度挤压流体向基底运动(图 6(a))。不同之处在于, 在探针下行过程中, 同时对探针施加一定的周期性振动(图 6(b)), 比如余弦型振动h0cos(ωt)(h0和ω分别为振动的振幅和频率)。实验过程中, 控制探针挤压流体的下行速度u和振动的振幅、频率, 同时独立测量探针与基底的间距D以及基底受力F。
由于复杂流体具有黏弹性, 谐振的探针的受力响应可分为稳态和动态两部分(图 6(b))。稳态部分Fstat可由Derjaguin给出的公式近似求出[50]:
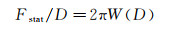 (15)
(15)
式中, W(D)为受限于探针与基底之间的高分子溶液自由能。
动态部分Fdyn则较为复杂, 需要区分弹性和黏性的影响。简而言之, 若有一个正弦波应变γ(t)=γ0sin(ωt), 则弹性应力(以E表示弹性模量)可表示为σ(t)=Eγ(t)=Eγ0sin(ωt); 黏性应力可表示为:σ(t)=ηdγ(t)/dt=ηγ0sin(ωt+π/2)。弹性应力正好和该应变同相位, 而黏性应力则有一个π/2的相位差。实际测得的响应是弹性和黏性响应的叠加。习惯上常用复数表示黏弹性响应, 弹性是实部, 黏性是虚部。若以润滑理论考虑复杂流体受挤压的流动, 可以推导出系统的复阻抗[7, 21]:
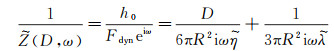 (16)
(16)
需要强调的是, 以上推导过程中, 边界条件并非采用Navier的简单线性模型(式(1)), 而是基于Brillouin的应力平衡。将式(2)、(3)联立:
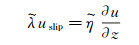 (17)
(17)
上式左侧为固壁对流体的阻力, 右侧为壁面剪切应力。由于采用了复数的表示方式, 阻力系数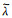
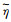
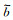
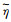
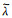
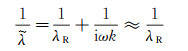 (18)
(18)
λR即为我们熟悉的实阻力系数, k为界面刚度。
对于非柔性壁面, 其阻力系数仅与流体黏度有关, 与k无关, 因此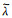
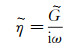 (19)
(19)
式中, 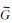
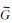
将式(18)、(19)代入式(16), 得到1/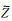
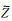
在实验测量中, 分别得到复阻抗的实部和虚部随间距D的变化, 就可以分别定量得到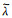
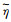
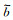
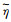
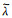
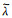
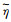
动态表面力方法测量的复阻抗1/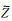
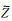

|
| 图 7 动态表面力仪测量高分子电解液在光滑液固界面上的滑移的实验结果 Fig.7 The experimental results of the slip of polyelectrolyte solution on smooth liquid-solid surface measured by DSFA |
依据式(16), 1/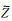
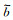
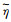
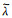
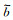
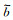
在接近液固界面时, 动态表面力方法测量的结果还能提供更丰富的信息。从图 7(a)的子图可以看到, 阻抗曲线在距离壁面200 nm的范围开始偏离远场的趋势。Charlaix教授课题组[7, 21]在远场和近场曲线的结合上进行了分析, 结合界面附近高分子排空效应导致的排空层(Depletion layer)、双电层静电作用, 并引入双流体表观滑移模型, 对此时的滑移及界面流体结构作了介观的解释。
图 7(b)采用双对数图来显示远场向近场的过渡, 流动区域可分为三个部分:
其一, 即图 7(b)右侧的远场区域, 前文已作介绍, 可以用一个宏观角度的表观滑移进行描述, 认为体相溶液在近壁区的排空层上作滑移长度为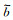
其二, 即图 7(b)左侧的距离界面约20 nm以内的近场区域。测量点的实部相对而言为小量, 可以忽略; 而虚部基本符合绿色虚线表示的纯黏性流体无滑移的趋势, 没有弹性的贡献。这意味着当球和基底接近至20 nm左右时, 其间隙内相当于只有纯水, 是高聚物的耗散层; 而且从微观角度看, 该区域内流动的壁面滑移接近零。
其三, 前两者之间的过渡区。在过渡区, 耗散层的存在对黏性和弹性的曲线都会有影响。为定量地描述其影响, 可以拟合得到耗散层厚度大约接近30 nm(耗散层厚度与高聚物排空效应、双电层静电作用有关)。如图 7(c)所示, 排空层的厚度近似与2lD+ξ相当(ξ为高分子结构的特征尺度)。
上述复杂流体的滑移结果, 不但丰富了我们对纳米尺度界面流动的认识, 对纳流控应用也有重要的意义。比如, 通过压力驱动电解质溶液流经纳米管道的纳流控能量器件[51-53], 实质是机械能做功用于输运双电层中的净电荷。而高分子电解液中发现的较大的滑移, 对于在纳米流道中强化输运、提高能量转化效率有着重要的意义。
4 结论本文综述了从简单流体扩展到复杂流体的研究过程中, 液固界面滑移实验研究取得的进展。对于水在光滑壁面上的滑移, 测量结果与理论分析逐渐趋于一致, 一般滑移长度在0.1~10 nm量级, 疏水表面的滑移长度大于亲水表面; 而在纳米管道的实验测量中, 发现滑移长度可达10~100 nm量级, 且滑移长度随管径增大而逐渐减小, 显然受到了固壁分子与水分子相互作用的限制影响。
复杂流体的滑移是一个介观的问题。从宏观来看, 存在体相溶液在界面附近附壁层上的表观滑移; 从微观来看, 存在耗散层。综合来看, 可以用双流体模型来描述整体流动, 微观流动结构的尺寸由高分子特征结构及双电层厚度共同决定。复杂流体存在复杂的流动结构及黏弹性效应, 给微纳流动及界面流动引入了更多的、丰富多彩的物理问题, 值得进一步深入探索。
从实验测量技术方面考虑, 测量精度一直是滑移实验研究的一大瓶颈。流体力学常采用的速度测量方法, 受限于光学分辨率极限(约200~300 nm), 难以获得100 nm以内的流动信息。针对此问题, 一方面, 随着超分辨技术的发展[54-55], 在显微观测上有了突破光学分辨率极限的技术可能; 另一方面, 正如本文介绍的表面力测量方法, 还可以通过其他物理方法对界面附近的流动进行直接或间接测量, 比如, 参考石英共振[56]或Bessel光束显微测量[57]。在提高空间分辨率的同时, 实验测量中时间分辨率的提高也值得进行研究。
在实际应用中, 发生滑移的情况不仅限于理想的液固界面, 对液气界面[58]或移动三相接触线[59]的处理也需要引入滑移。因此, 对滑移机理的研究有助于理解介观尺度的各种现象。目前, 滑移的模型仅回答了如何从宏观流体力学描述滑移边界条件, 而滑移的微观机理——不仅涉及流体本身的属性、流动剪切, 还涉及界面粗糙度、分子相互作用等——仍然是需要长期研究的复杂问题。
| [1] |
李战华, 郑旭. 微纳米尺度流动实验研究的问题与进展[J]. 实验流体力学, 2014, 28(3): 1-11. LI Z H, ZHENG X. The problems and progress in the experimental study of micro/nano-scale flow[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(3): 1-11. |
| [2] |
BOCQUET L, CHARLAIX E. Nanofluidics, from bulk to interfaces[J]. Chemical Society Reviews, 2010, 39(3): 1073-1095. DOI:10.1039/B909366B |
| [3] |
NETO C, EVANS D R, BONACCURSO E, et al. Boundary slip in Newtonian liquids:a review of experimental studies[J]. Reports on Progress in Physics, 2005, 68(12): 2859-2897. DOI:10.1088/0034-4885/68/12/R05 |
| [4] |
CUI H H, SILBER-LI Z H, ZHU S N. Flow characteristics of liquids in microtubes driven by a high pressure[J]. Physics of Fluids, 2004, 16(5): 1803-1810. DOI:10.1063/1.1691457 |
| [5] |
ZHENG X, KONG G P, SILBER-LI Z H. The influence of nano-particles tracers on the slip length measurements by microPTV[J]. Acta Mechanica Sinica, 2013, 29(3): 411-419. DOI:10.1007/s10409-013-0027-0 |
| [6] |
NAVIER C L M H. Mémoire sur les lois du movement des fluids[J]. Mémoires de l'Académie Royale des Sciences de l'Institut de France, 1823, 6: 389-440. |
| [7] |
CROSS B, BARRAUD C, PICARD C, et al. Wall slip of complex fluids:interfacial friction versus slip length[J]. Physical Review Fluids, 2018(3): 062001. |
| [8] |
郑旭.光滑及带微结构表面的液体滑移实验研究[D].北京: 中国科学院研究生院, 2009. http://d.g.wanfangdata.com.cn/Thesis_Y1629688.aspx
|
| [9] |
TRETHEWAY D C, MEINHART C D. A generating mechanism for apparent fluid slip in hydrophobic microchannels[J]. Physics of Fluids, 2004, 16(5): 1509-1515. DOI:10.1063/1.1669400 |
| [10] |
COTTIN-BIZONNE C, CROSS B, STEINBERGER A, et al. Boundary slip on smooth hydrophobic surfaces:intrinsic effects and possible artifacts[J]. Physical Review Letters, 2005, 94(5): 056102. DOI:10.1103/PhysRevLett.94.056102 |
| [11] |
HUANG P, GUASTO J S, BREUER K S. Direct measurement of slip velocities using three-dimensional total internal reflection velocimetry[J]. Journal of Fluid Mechanics, 566: 447-464. DOI:10.1017/S0022112006002229 |
| [12] |
CHOI C H, KIM C J. Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface[J]. Physical Review Letters, 2006, 96(6): 066001. DOI:10.1103/PhysRevLett.96.066001 |
| [13] |
AUDRY M-C, PIEDNOIR A, JOSEPH P. Amplification of electro-osmotic flows by wall slippage:direct measurements on OTS-surfaces[J]. Faraday Discussions, 2010, 146: 113-124. DOI:10.1039/b927158a |
| [14] |
SCHAEFFEL D, YORDANOV S, SCHMELZEISEN M, et al. Hydrodynamic boundary condition of water on hydrophobic surfaces[J]. Physical Review E, 2013, 87(5): 051001. DOI:10.1103/PhysRevE.87.051001 |
| [15] |
KANNAM S K, TODD B, HANSEN J S. How fast does water flow in carbon nanotubes?[J]. The Journal of Chemical Physics, 2013, 138(9): 094701. DOI:10.1063/1.4793396 |
| [16] |
LI Z Z, D'ERAMO L, LEE C, et al. Near-wall nanovelocimetry based on total internal reflection fluorescence with continuous tracking[J]. Journal of Fluid Mechanics, 2015, 766: 147-171. DOI:10.1017/jfm.2015.12 |
| [17] |
SIRIA A, PONCHARAL P, BIANCE A L, et al. Giant osmotic energy conversion measured in a single transmembrane boron nitride nanotube[J]. Nature, 2013, 494(7438): 455-458. DOI:10.1038/nature11876 |
| [18] |
SECCHI E, MARBACH S, NIGUÈS A, et al. Massive radius-dependent flow slippage in single carbon nanotubes[J]. Nature, 2016, 537(7619): 210-213. DOI:10.1038/nature19315 |
| [19] |
CUENCA A, BODIGUEL H. Submicron flow of polymer solutions:slippage reduction due to confinement[J]. Physical Review Letters, 2013, 110(10): 108304. DOI:10.1103/PhysRevLett.110.108304 |
| [20] |
BÄUMCHEN O, JACOBS K. Slip effects in polymer thin films[J]. Journal of Physics:Condensed Matter, 2010, 22(3): 033102. DOI:10.1088/0953-8984/22/3/033102 |
| [21] |
BARRAUD C, CROSS B, PICARD C, et al. Large slippage and depletion layer at the polyelectrolyte/solid interface[J]. Soft Matter, 2019, 15: 6308-6317. DOI:10.1039/C9SM00910H |
| [22] |
GARCIA L, BARRAUD C, PICARD C, et al. A micro-nano-rheometer for the mechanics of soft matter at interfaces[J]. Review of Scientific Instruments, 2016, 87(11): 113906. DOI:10.1063/1.4967713 |
| [23] |
LEROY S, STEINBERGER A, COTTIN-BIZONNE C, et al. Hydrodynamic interaction between a spherical particle and an elastic surface:a gentle probe for soft thin films[J]. Physical Review Letters, 2012, 108(26): 264501. DOI:10.1103/PhysRevLett.108.264501 |
| [24] |
LEE T, CHARRAULT E, NETO C. Interfacial slip on rough, patterned and soft surfaces:a review of experiments and simulations[J]. Advances in Colloid and Interface Science, 2014, 210: 21-38. DOI:10.1016/j.cis.2014.02.015 |
| [25] |
LAUGA E, BRENNER M P, STONE H A. Microfluidics: the no-slip boundary condition[M]//Tropea C, Yarin A L, Foss J F. Springer handbook of experimental fluid mechanics. Berlin, Heidelberg: Springer, 2006: 1219-1240.
|
| [26] |
JING D L, BHUSHAN B. The coupling of surface charge and boundary slip at the solid-liquid interface and their combined effect on fluid drag:a review[J]. Journal of Colloid and Interface Science, 2015, 454: 152-179. DOI:10.1016/j.jcis.2015.05.015 |
| [27] |
BARNES H A. A review of the slip (wall depletion) of polymer solutions, emulsions and particle suspensions in viscositmers:its cause, character, and cure[J]. Journal of Non-Newtonian Fluid Mechanics, 1995, 56(3): 221-251. DOI:10.1016/0377-0257(94)01282-M |
| [28] |
BRILLOUIN M. Leçons sur la viscositédes liquides et des gaz[M]. Paris: Gauthier-Villars, 1907.
|
| [29] |
BOCQUET L, BARRAT J L. Hydrodynamic boundary conditions, correlation functions, and Kubo relations for confined fluids[J]. Physical Review E, 1994, 49(4): 3079-3092. DOI:10.1103/PhysRevE.49.3079 |
| [30] |
HUANG D M, SENDNER C, HORINEK D, et al. Water slippage versus contact angle:a quasiuniversal relationship[J]. Physical Review Letters, 2008, 101(22): 226101. DOI:10.1103/PhysRevLett.101.226101 |
| [31] |
LUAN B Q, ZHOU R H. Wettability and friction of water on a MoS2 nanosheet[J]. Applied Physics Letters, 2016, 108(13): 131601. DOI:10.1063/1.4944840 |
| [32] |
CHOI C H, WESTIN K J A, BREUER K S. Apparent slip flows in hydrophilic and hydrophobic microchannels[J]. Physics of Fluids, 2003, 15(10): 2897-2902. DOI:10.1063/1.1605425 |
| [33] |
李战华, 吴健康, 胡国庆, 等. 微流控芯片中的流体流动[M]. 北京: 科学出版社, 2012.
|
| [34] |
MAJUMDER M, CHOPRA N, ANDREWS R, et al. Nanoscale hydrodynamics:enhanced flow in carbon nanotubes[J]. Nature, 2005, 438(7064): 44. DOI:10.1038/438044a |
| [35] |
HOLT J K, PARK H G, WANG Y M, et al. Fast mass transport through sub-2-nanometer carbon nanotubes[J]. Science, 2006, 312(5776): 1034-1037. DOI:10.1126/science.1126298 |
| [36] |
WHITBY M, CAGONON L, TAHANOU M. Enhanced fluid flow through nanoscale carbon pipes[J]. Nano Letters, 2008, 8(9): 2632-2637. DOI:10.1021/nl080705f |
| [37] |
QIN X C, YUAN Q Z, ZHAO Y P, et al. Measurement of the rate of water translocation through carbon nanotubes[J]. Nano Letters, 2011, 11(5): 2173-2177. DOI:10.1021/nl200843g |
| [38] |
SHARMA P, MOTTE J F, FOURNEL F, et al. A direct sensor to measure minute liquid flow rates[J]. Nano Letters, 2018, 18(9): 5726-5730. DOI:10.1021/acs.nanolett.8b02332 |
| [39] |
JOSEPH P, TABELING P. Direct measurement of the apparent slip length[J]. Physical Review E, 2005, 71(3 Pt 2A): 035303. |
| [40] |
LAUGA E. Apparent slip due to the motion of suspended particles in flows of electrolyte solutions[J]. Langmuir, 2004, 20: 8924-8930. DOI:10.1021/la049464r |
| [41] |
ZHENG X, SHI F, SILBER-LI Z H. Study on the statistical intensity distribution (SID) of fluorescent nanoparticles in TIRFM measurement[J]. Microfluidics and Nanofluidics, 2018, 22: 127. DOI:10.1007/s10404-018-2145-2 |
| [42] |
VINOGRADOVA O I. Drainage of a thin liquid film confined between hydrophobic surfaces[J]. Langmuir, 1995, 11(6): 2213-2220. DOI:10.1021/la00006a059 |
| [43] |
MARBACH S, BOCQUET L. Osmosis, from molecular insights to large-scale applications[J]. Chemical Society Reviews, 2019, 48(100): 3102-3144. |
| [44] |
SCHOCH R B, HAN J Y, RENAUD P. Transport phenomena in nanofluidics[J]. Review of Modern Physics, 2008, 80(3): 839-883. DOI:10.1103/RevModPhys.80.839 |
| [45] |
SILKINA E, ASMOLOV E S, VINOGRADOVA O I. Electro-osmotic flow in hydrophobic nanochannels[J]. Physical Chemistry Chemical Physics, 2019, 21(41): 23036-23043. DOI:10.1039/C9CP04259H |
| [46] |
DE GENNES P G. Polymer solutions near an interface. adsorption and depletion layers[J]. Macromolecules, 1981, 14(6): 1637-1644. DOI:10.1021/ma50007a007 |
| [47] |
THOMPSON P A, TROIAN S M. A general boundary condition for liquid flows at solid surfaces[J]. Nature, 1997, 389(6649): 360-362. DOI:10.1038/38686 |
| [48] |
GRAHAM M D. Fluid dynamics of dissolved polymer molecules in confined geometries[J]. Annual Review of Fluid Mechanics, 2011, 43(1): 273-298. DOI:10.1146/annurev-fluid-121108-145523 |
| [49] |
LAINÉA, JUBIN L, CANALE L, et al. MicroMegascope based dynamic surface force apparatus[J]. Nanotechnology, 2019, 30: 195502. DOI:10.1088/1361-6528/ab02ba |
| [50] |
CHURAEV N V, DERJAGUIN B V, MULLER V M. Surface forces[M]. New York: Springer US, 1987.
|
| [51] |
DAIGUJI H. Ion transport in nanofluidic channels[J]. Chemical Society Reviews, 2010, 39(3): 901-911. |
| [52] |
CHENG C, JIANG G P, SIMON G P, et al. Low-voltage electrostatic modulation of ion diffusion through layered graphene-based nanoporous membranes[J]. Nature Nanotechnology, 2018, 13(8): 685-690. DOI:10.1038/s41565-018-0181-4 |
| [53] |
ZHANG H C, TIAN Y, JIANG L. Fundamental studies and practical applications of bio-inspired smart solid-state nanopores and nanochannels[J]. Nano Today, 2016, 11(1): 61-81. |
| [54] |
BETZIG E. Nobel Lecture:Single molecules, cells, and super-resolution optics[J]. Reviews of Modern Physics, 2015, 87(4): 1153-1168. DOI:10.1103/RevModPhys.87.1153 |
| [55] |
HELL S W. Nobel lecture:Nanoscopy with freely propagating light[J]. Reviews of Modern Physics, 2015, 87(4): 1169-1181. DOI:10.1103/RevModPhys.87.1169 |
| [56] |
SHU J J, TEO J B M, CHAN W K. Fluid velocity slip and temperature jump at a solid surface[J]. Applied Mechanics Reviews, 2017, 69(2): 020801. DOI:10.1115/1.4036191 |
| [57] |
SNOEYINK C, WERELEY S. A novel 3D3C particle tracking method suitable for microfluidic flow measurements[J]. Experiments in Fluids, 2013, 54(1): 1453. DOI:10.1007/s00348-012-1453-7 |
| [58] |
MAALI A, BOISGARD R, CHRAIBI H, et al. Viscoelastic drag forces and crossover from no-slip to slip boundary conditions for flow near air-water interfaces[J]. Physical Review Letters, 2017, 118(8): 084501. DOI:10.1103/PhysRevLett.118.084501 |
| [59] |
VARAGNOLO S, FERRARO D, FANTINEL P, et al. Stick-slip sliding of water drops on chemically heterogeneous surfaces[J]. Physical Review Letters, 2013, 111(6): 066101. DOI:10.1103/PhysRevLett.111.066101 |