2. 清华大学 工程力学系, 北京 100084
2. Department of Engineering Mechanics, Tsinghua University, Beijing 100084, China
当超疏水表面浸入水中时, 表面上的微结构会捕捉空气, 并在微结构间形成气-水界面[1-2]。在流动剪切、压强或其他扰动因素的作用下, 气-水界面会失稳并塌陷, 因此气-水界面的寿命和相关影响因子是人们关注和研究的对象[3-4]。在流动中, 超疏水表面气-水界面的状态与流动的静压、对流效应、实验时间及表面微观结构特性等因素相关[5]。Lee和Kim[6]发现, 具有复合结构的表面可以使得气-水界面更加稳定, 他们认为这是二级结构给气-水界面提供了更多钉扎点的原因。Jones等[7]使用结晶和低温聚集粒子束铣技术冻结气-水界面并通过扫描电镜观测, 以比较微米一级结构表面和具有纳米/亚微米二级结构表面的气-水界面情况, 结果发现:在相同实验条件下, 只有微米一级结构的表面气-水界面消失, 而具有复合结构(纳米或亚微米二级结构)的表面存在气-水界面。Tuteja等[8]对表面微结构的几何形貌进行了更进一步的研究。他们发现, 在表面上加工出具有内凹特性的微结构后, 对于很多表面能较低的液体(如酒精等, 在传统超疏水表面上容易发生浸润)也能表现出不浸润的特性。这说明内凹的几何形貌有助于增强微结构间气-水界面的稳定性。随后, Liu和Kim[9]设计并加工出一种具有二次凹陷特征的"蘑菇状"表面, 由亲水的硅片直接刻蚀加工得到, 却具有不可思议的超全疏特性, 即使是表面能极低的聚四氟乙烯液体也无法浸润表面。
众所周知, 微流动系统因表面效应增强而具有很大的流动阻力, 因此如何减小微通道的表面阻力是研究者一直致力解决的问题。Ou等[10]在槽深为76~254 μm的一系列微槽道中测量了具有不同表面结构的超疏水表面的阻力特性, 发现在层流中超疏水表面压降减小量最高可达40%。他们通过激光共聚焦技术监测发现, 超疏水表面上方存在一层气膜, 形成气-水界面。气-水界面的存在可大大降低界面剪切力, 引入滑移速度, 从而实现减阻。随后, 研究者展开了一系列实验对超疏水表面在槽道中的层流减阻特性进行了验证和测量。Joseph等[11]在微槽道中引入碳纳米管森林状结构形成超疏水表面, 并使用粒子图像测速(Particle Image Velocimetry, PIV)技术进行测量, 证实当微结构上方界面为Cassie状态(微结构间存在气-水界面)时, 边界存在数微米量级的速度滑移; 而当液体润湿进微结构, 界面转变为Wenzel状态(微结构间不存在气-水界面)后, 速度滑移则会消失。Choi等[12]制备了具有纳米光栅结构(230 nm间距, 500 nm深)的超疏水表面并在微槽道中实现了20%~30%的最大减阻。Byun等[13]制备了具有不同亲疏水特性的微槽道, 并使用PIV测量槽道内的速度剖面, 发现亲水表面上没有速度滑移, 而超疏水表面上存在速度滑移, 对应滑移长度为2 μm左右。此外, 他们发现, 对于具有展向沟槽结构的超疏水侧壁, 其气-水界面存在一定的不稳定性。Hao等[14]在微槽道侧壁加工出具有交错展向沟槽的微结构, 使得侧壁具有较好的疏水性能。通过测量压降和使用Micro-PIV技术测量内部流场, 发现减阻可达10%~30%, 对应速度滑移达到槽道中心速度的8%。
在实际工程应用中(例如油路运输、水路运输等), 涉及到的往往是宏观尺度的槽道流动问题。因此, 针对宏观尺度槽道的超疏水表面减阻研究十分必要。在宏观尺度下, 壁面效应相对来说没有微槽道中那么明显, 因此, 超疏水表面的减阻率和微槽道的相比可能会偏小, 测量也面临着更大的挑战。同时, 宏观流动往往流速较高, 达到湍流状态, 因此还需研究流动转捩和高雷诺数下的相关阻力特性。Woolford等[15]在水力直径为8.2 mm、宽深比为8.9的扁平槽道中进行实验, 将超疏水表面置于槽道下壁面, 通过测量压降计算阻力特性, 实验雷诺数从4800到10000。实验发现, 超疏水表面减阻效果和其表面微结构形貌高度相关, 具有流向沟槽结构的超疏水表面可以减阻11%, 而具有展向沟槽结构的超疏水表面反而会增阻6.5%。类似的, Daniello等[16]在水力直径为13.1 mm、宽深比为4.8的槽道中测量了具有流向沟槽结构的超疏水表面, 与Woolford等的结果不同, 他们发现, 减阻开始于一个临界雷诺数(ReDH=2500), 即在层流时表面并不减阻, 在湍流状态下减阻率最大可达50%。
一系列研究表明, 超疏水表面在槽道减阻中的效果和其表面上方气膜的状态密切相关。具有微纳二级复合结构的超疏水表面憎水性能更为优异, 具有更好的自清洁性能[17]。对于减阻来说, 这种复合结构有助于增强超疏水表面气-水界面的稳定性, 从而延长其减阻效果[18]。然而, 关于二级复合结构对减阻的影响效果还需要更多的研究支持。同时, 在一些理论研究中, 具有相同固体面积分数(固体面积分数φs=表观固体面积/表面积)的超疏水表面被认为具有相似的减阻效果[19]。在实际实验中, 一些具有相同固体面积分数但是结构形状或尺寸不同的超疏水表面减阻效果可能差距甚大, 这是由于不同结构使得其上方气-水界面稳定性和曲率产生变化所致。为更好地探究这些问题, 本文将针对不同类型的超疏水表面进行槽道流动的测量, 并同时观测表面的气膜情况, 研究复合结构和结构尺寸对表面气-水界面稳定性和减阻的影响。
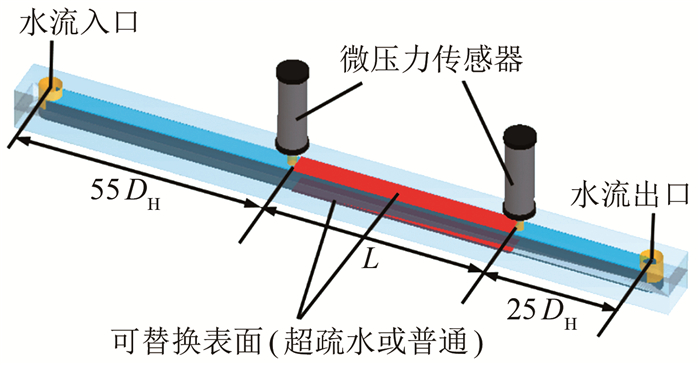
1 槽道减阻实验的设备与方案在槽道减阻实验中, 槽道的具体布置如图 1所示。槽道全长450 mm, 截面形状为矩形, 展向宽度为10 mm, 高度为2 mm, 对应等效水力直径为DH=4 A/P=3.33 mm, 其中A为槽道截面积, P为槽道截面周长。图 1中红色区域设计为可替换表面, 根据实验需求, 可安装各种类型的超疏水表面和作为对照的普通表面, 这样不同表面的测量可保证均在相同槽道中进行, 共享同一系统误差。如图 1所示, 可替换表面设置在槽道中后段, 为保证测量区域流动充分发展, 前后均预留了进出口过渡距离, 分别设为55 DH和25 DH。为测量流经表面的压降, 在替换表面的前后边界处安装了微压力传感器(CGYL-202, 量程0~30 kPa, 精度0.03 kPa, 测量频率1000 Hz), 2个微压力传感器距离L=140 mm。槽道由微型磁驱动齿轮泵(MG1018A-ZWX-40/24)驱动注入水流, 通过调节微泵可控制水速, 实验雷诺数Re为700~4700 (Re=umDH/ν, 其中um为槽道内截面上平均流速, ν为运动黏性系数)。在槽道出口处使用精细测力天平(G & G T5000, 精度1 g)和秒表测量质量流量, 记为Qm。实验槽道为长矩形槽道, 在槽道上下表面分别安装超疏水或普通表面(图中红色框标识), 并测量流经表面的压降, 记为Δp。
|
| 图 1 实验槽道示意图 Fig.1 Schematic of the experimental channel |
本实验中共使用了3种类型表面, 分别为:普通表面(光滑硅片表面)、规则微米一级结构表面和规则复合结构表面。其中规则结构为微柱阵列结构, 微柱具有3种几何尺寸, 进行了自组装疏水处理(OTS); 复合结构为在此基础上涂覆纳米二氧化硅粒子二级结构。表面的尺寸特征和接触角特性如表 1所示, 不同超疏水表面类型用表中字母和数字表示, 其中数字代表微柱的边长, "+nano"表示添加了纳米粒子结构, 为复合结构表面。
| 表面类型 | 微柱边长w/μm | 微柱间距s/μm | 微柱高度h/μm | 固体面积分数 | 静态接触角/(°) |
| 普通Si | -- | -- | -- | 1.000 | 67.4±2.0 |
| OTS16 | 16 | 16 | 30 | 0.250 | 143.0±1.2 |
| OTS16+nano | 16 | 16 | 30 | 0.144 | 150.2±1.2 |
| OTS8 | 8 | 8 | 30 | 0.250 | 143.2±0.2 |
| OTS8+nano | 8 | 8 | 30 | 0.144 | 148.3±1.5 |
| OTS4 | 4 | 4 | 30 | 0.250 | 145.0±1.6 |
| OTS4+nano | 4 | 4 | 30 | 0.144 | 147.9±1.5 |
此外, 为观测超疏水表面气膜的状态, 将超疏水表面设置在槽道测量段的下表面, 槽道测量段上表面为透明观察窗, 可在实验中实时观测表面气膜情况。超疏水表面上方的气膜可通过气-水界面不同的反射率进行观测, 如图 2所示。不同的界面材质会有不同的反射效果, 表面上方存在气膜的区域呈现银色, 而没有气膜的区域呈暗色。采用MATLAB图像灰度过滤算法监测并统计表面上方的气膜区域(即银色反光区域), 可算出对应表面的气膜损耗面积比例β。在实验中, 所有超疏水表面上方均有气膜, 但存在一定比例损耗, 气膜损耗面积比例越大, 意味着从统计上来看, 表面的超疏水性能越差。如图 2所示, "OTS16"超疏水表面上方气膜损耗面积最大, 达到52%;"OTS4"和"OTS4+nano"超疏水表面气膜损耗面积非常小, 小于1%, 这意味着实验中在这2种表面上方的气膜基本上没有损耗。可以看出, 具有同样一级微结构的表面, 添加纳米粒子后, 表面上方气膜的稳定性得到了提升, 气膜的损耗面积减小了。

|
| 图 2 实验中超疏水表面上方的气膜状态 Fig.2 Statuses of air plastron on SH surfaces during measurement |
根据达西-韦斯巴赫(Darcy-Weisbach)公式, 通过测量流经表面的压降Δp和对应的质量流量Qm, 槽道中的阻力系数f可计算为:
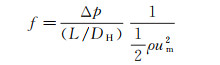 (1)
(1)
式中, L为2个压力测量点间距, L = 140 mm; um=Qm/ρA为槽道内截面平均流速, ρ为水的密度。
由早期工程研究可知, 在充分发展的规则槽道流动中, 槽道内部的阻力系数f可由经验公式进行计算[20]:
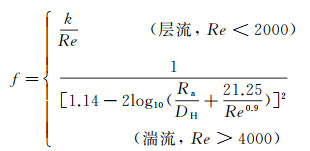 (2)
(2)
其中Ra为表面粗糙度(对于带微结构表面, 表面粗糙度为微结构高度的一半), k为无量纲系数:
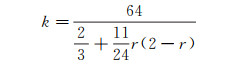 (3)
(3)
其中r为截面比例系数。本实验中r=0.2, 代入计算得k=77.0。
在本实验中, 利用所测数据, 阻力系数f可由式(1)算出。对于普通光滑表面情况, 由测得数据算出的阻力系数f0分布和由经验公式(2)算出的阻力系数曲线较为相符(图 3)。对于超疏水表面情况, 由测得数据算出的阻力系数fs分布和经验公式算出的阻力系数曲线形式相同, 但需要加一个比例系数c修正, 表示为fs=cf0。由于超疏水表面上气-水界面的存在, 对应局部区域剪切力近似为零, 因此超疏水表面上的阻力因子小于普通表面, 即有c < 1。通过曲线拟合的方法, 对于不同超疏水表面的数据可以得到不同的c。据此, 减阻率DR可定义为:
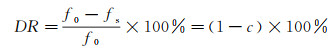 (4)
(4)
|
| 图 3 阻力系数f随雷诺数Re的分布 Fig.3 Friction factor f for smooth and SH surfaces |
根据实验测量结果, 使用式(1)计算表面摩擦系数, 并用式(4)计算对应的减阻率。实验时, 针对每种表面情况均测量3次, 每次测量均在表面干燥后进行(保证初始时表面均未失效), 并包含Re由小变大和由大变小的测量(为排除泵的滞留效应)。
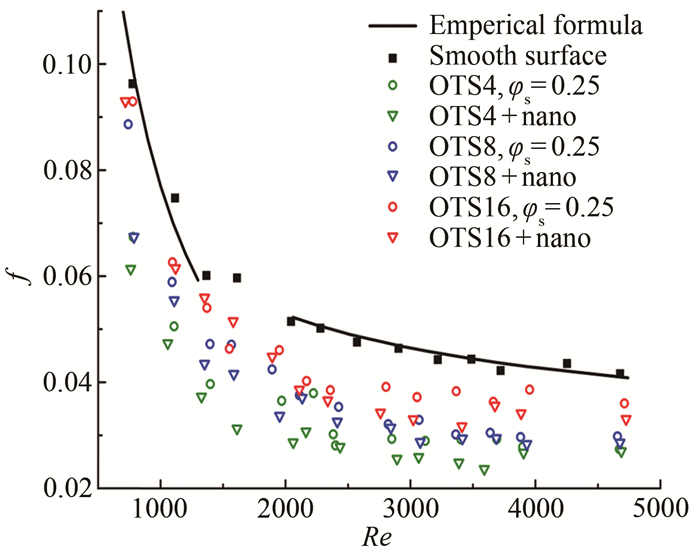
图 3所示为实验中各种表面上方的阻力系数f随雷诺数Re的变化。
在图 3中, 黑色实线为使用经验公式(2)计算出的阻力系数结果, 黑色实心方块是普通表面的实验结果平均值。可以看出, 普通表面的实验结果和经验值十分接近, 这验证了本实验装置的可靠性。空心的标记点表示超疏水表面的结果, 其中空心圆圈表示规则微米一级结构表面, 空心倒三角表示规则复合结构表面。颜色表示不同的微柱间距(边长和间距相等), 绿色、蓝色、红色分别表示微柱间距为4、8和16 μm的超疏水表面。
从图 3可以看出, 对于超疏水表面, 其上方的阻力系数f在实验雷诺数范围内(700 < Re < 4700)均小于普通表面上方的阻力系数, 这表明本实验中所有的超疏水表面均具有减阻效果。使用式(4)可以计算出具体的减阻率, 其中系数c可由图 3结果拟合得到。对于结构间距最大(16 μm)的OTS16表面, 由于其上气膜状态十分不稳定, 在一些实验中气膜损耗, 造成表面减阻性能下降。
表 2为各超疏水表面在层流和湍流状态下的减阻率。
| 超疏水表面 | 减阻率DR(层流) | 减阻率DR(湍流) |
| OTS16 | (13.1±4.7)% | (14.4±11.2)% |
| OTS16+nano | (14.3±6.0)% | (23.5±6.5)% |
| OTS8 | (14.6±2.9)% | (29.1±1.4)% |
| OTS8+nano | (27.3±1.6)% | (31.2±1.9)% |
| OTS4 | (29.7±1.6)% | (34.7±8.8)% |
| OTS4+nano | (37.2±3.0)% | (38.6±4.5)% |
表 2表明, 实验采用的所有超疏水表面在层流和湍流下均具有一定的减阻效果, 最大减阻率达到(38.6 ±4.5)%, 对应表面为"OTS4+nano"表面。
实验中, 超疏水表面OTS16, OTS8和OTS4具有相同的固体面积分数φs和相同的槽道内截面平均流速um, 但是对应减阻率并不相同, 减阻率DR随微柱尺寸(边长和间距)增大而减小, 这一现象是由于界面曲率和不稳定性的影响导致的。在相同的固体分数下, 微柱的尺寸(边长和间距)越大, 气-水界面弯曲效应越强, 稳定性越差, 对应表面减阻效果越弱。在本实验中, 对于各种超疏水表面, 湍流减阻效果均优于层流减阻效果。这一结果与Lu等[21]的实验结果类似。在Zhang等[22]的超疏水表面外流减阻研究中发现, 对于湍流流动, 减阻是界面速度滑移和涡结构改变共同作用的结果, 因此减阻效果比层流状态下更为优异。此外, 复合结构表面("+nano"表面)上方的气膜面积比微米一级结构表面的气膜面积大(见图 2), 这说明增添纳米粒子增强了气-水界面的稳定性, 进而也提高了流动的减阻率。
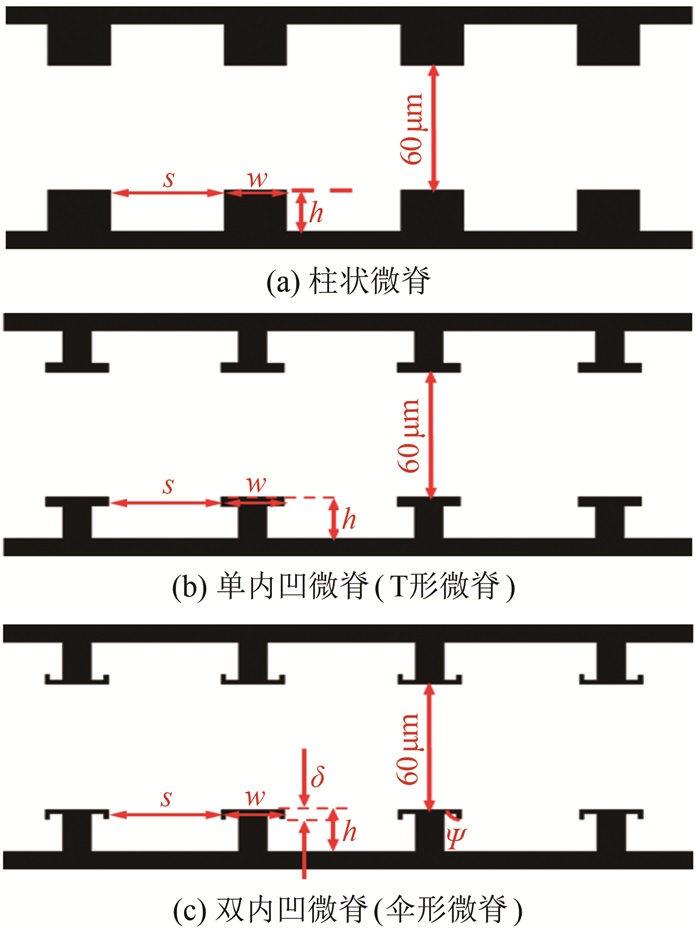
3 表面微结构形状对气-水界面稳定性影响的研究为了研究表面微结构形状对流动的影响, 制作了不同形状的微脊结构。通过硅微刻蚀, 在硅片上刻蚀了60 μm宽、50 μm深、28 000 μm长的微槽, 并在其侧壁加工了微脊结构, 使用玻璃键合封闭槽道的上表面。设计加工了3类微脊结构, 分别为:普通柱状微脊、单内凹微脊(T形微脊)和双内凹微脊(伞形微脊)(图 4)。
|
| 图 4 微槽道内3类微脊结构 Fig.4 Schematic diagrams of three types of micro-ridge structures |
如图 4所示, 3类微脊结构的基本尺寸相同, s=40 μm, w=20 μm, h=20 μm, 对于内凹型结构, 内凹面高度δ=5 μm。本实验测得流动静止条件下气-水界面与壁面的夹角为(50±3)°, 即壁面的本征接触角。由此可知, 加工壁面为亲水表面。
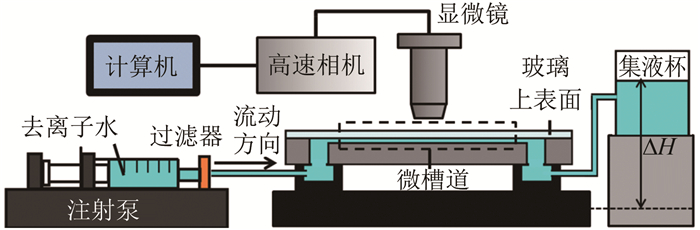
图 5所示为微槽道内气-水界面稳定性研究实验装置。流动由注射泵推动, 从左向右(图示箭头方向)流经微槽道, 最后流入集液杯中。集液杯应放置在高于微槽道水平面的位置, 以保证微槽道内流动正常进行, 实验中选取ΔH= 100 mm。在微槽道上方, 使用竖立式显微镜系统(OLYMPUS, BX51, 目镜2×, 物镜20×)观测槽内流体流动情况, 并使用高速相机(FASTCAM Mini UX100, Photron)拍摄入流界面。因为入流过程时间很短(30 ms内流经整个观测区域), 界面变化快, 因此需要将高速相机调至高帧频状态, 并于合适的时机进行触发。本实验高速相机帧频为4000帧/s。
|
| 图 5 微槽道流动显示装置 Fig.5 Micro-channel flow visualization device |
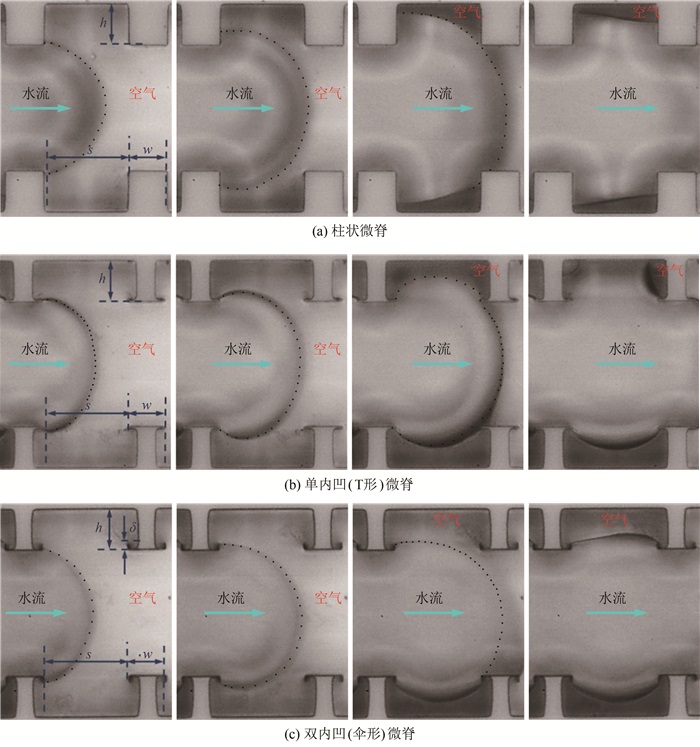
3种侧壁类型的微槽道入流情况如图 6所示, 图中用点划线将气-水界面描绘出来。图 6(a)~(c)分别表示柱状微脊结构、单内凹微脊结构和双内凹微脊结构。图中流体从左往右流动, 相邻2幅图时间间隔为0.75 ms。
|
| 图 6 3种微槽道侧壁类型的入流情况 Fig.6 Formation processes of the air-water interfaces for three types of micro-ridge structures |
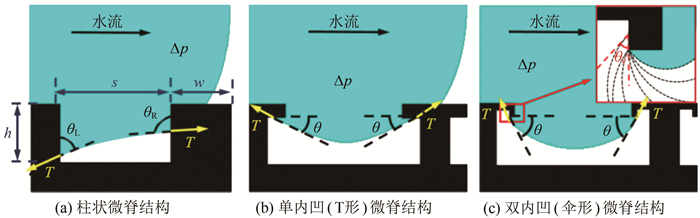
从图 6(a)可以看出, 对于柱状微脊结构, 当水流入时, 结构间的气-水界面会沿着竖直的侧壁下滑, 结构间气体会逐渐耗散, 对应气-水界面逐渐消失。相比柱状微脊结构, 单内凹(T形)结构在初始时可以捕捉气-水界面(图 6(b)), 但具有一定随机性:气-水界面一开始在结构内凹面钉扎, 但会很快坍塌, 导致界面消失。双内凹(伞形)结构则表现出优异的性能(图 6(c)), 即使表面是亲水的, 仍然可以较好地捕捉气-水界面。图 7给出了3种表面上方的气-水界面情况示意图, 在图 7(a)情况下, 壁面对流体的表面张力(图中的矢量T)会指向微结构内, 使得液面不断侵入微结构间, 即使槽道内部流动没有驱动压差(Δp=0), 界面上也无法达到力平衡。对于单内凹(T形)微脊结构(图 7(b)), 气-水界面会停留在结构的内凹里侧。此时, 虽然液体和固壁的本征接触角小于90°, 但由于固壁的角度改变(翻转180°), 使得壁面对液体的力指向流道内部, 从而能够与Δp相抗衡。对于双内凹(伞形)微脊结构(图 7(c)), 气-水界面能够较好地存在于微结构间。气-水界面的发展可以分为2个阶段。在第一阶段, 气-水界面会悬挂在双内凹结构的内凹小平台上, 这时界面的状态及发展与单内凹结构类似。当Δp增加到第一临界压差Δpc1, 界面开始移动, 最终钉扎在结构第二拐角处。随着槽道压差增大, 界面在拐角处的变化如图 7(c)右上角放大图中虚线所示。随着压差的增大, 界面会不断向结构内侵入。在这个过程中, 存在气-水界面切线与水平方向夹角等于90°的时刻, 此时气-水界面悬挂在壁面第二拐角上, 壁面对界面的张力完全用来与槽道压差相抗衡, 表面张力的效能发挥到最大, 因此具有较好的气-水界面稳定性。
|
| 图 7 3种结构上方的气-水界面情况及力平衡关系示意 Fig.7 Schematic diagrams illustrating the air-water interface for three types of micro-ridge structures and force balance |
根据第2节的实验结果可以推测, 伞形结构持有气体的能力最强, 有可能带来明显的减阻效果, 需要后续实验予以验证。
4 结论具有相同固体面积分数、不同微结构尺寸的超疏水表面的扁平矩形槽道, 在层流和湍流下均具有一定的减阻效果, 最大减阻率在具有最小结构间距的微纳二级结构表面上实现, 为(38.6±4.5)%。实验中发现:减阻率和气-水界面的稳定性与微结构层级、微结构尺寸、槽道流态和微结构形貌均有一定关系:
(1) 复合结构可以显著提升减阻效果, 这是由于增加纳米二级结构减小了原有表面的固体面积分数, 并提高了气-水界面的稳定性。
(2) 相同的固体面积分数表面不一定具有相同的减阻效果, 减阻率还和表面结构尺度相关。结构间距越小, 表面气-水界面越稳定, 对应减阻率越高。
(3) 在本实验研究中, 湍流减阻效果优于层流减阻效果。
(4) 利用双内凹(伞形)微脊结构, 在微槽道中使用亲水材料也可以有效捕捉气体, 形成稳定的气-水界面, 从而实现超疏水性能, 减小流动阻力。
| [1] |
RASTEGARI A, AKHAVAN R. The common mechanism of turbulent skin-friction drag reduction with superhydrophobic longitudinal microgrooves and riblets[J]. Journal of Fluid Mechanics, 2018, 838: 68-104. DOI:10.1017/jfm.2017.865 |
| [2] |
RAAYAI-ARDAKANI S, MCKINLEY G H. Drag reduction using wrinkled surfaces in high Reynolds number laminar boundary layer flows[J]. Physics of Fluids, 2017, 29(9): 093605. DOI:10.1063/1.4995566 |
| [3] |
ROTHSTEIN J P. Slip on superhydrophobic surfaces[J]. Annual Review of Fluid Mechanics, 2010, 42(42): 89-109. |
| [4] |
HEMEDA A A, GAD-EL-HAK M, TAFRESHI H V. Effects of hierarchical features on longevity of submerged superhydrophobic surfaces with parallel grooves[J]. Physics of Fluids, 2014, 26(8): 082103. DOI:10.1063/1.4891363 |
| [5] |
吕鹏宇, 薛亚辉, 段慧玲. 超疏水材料表面液气界面的稳定性及演化规律[J]. 力学进展, 2016, 46(1): 179-225. LYU P Y, XUE Y H, DUAN H L. Stability and evolution of liquid-gas interfaces on superhydrophobic surfaces[J]. Advances in Mechanics, 2016, 46(1): 179-225. |
| [6] |
LEE C, KIM C J. Maximizing the giant liquid slip on superhydrophobic microstructures by nanostructuring their sidewalls[J]. Langmuir, 2009, 25(21): 12812-12818. DOI:10.1021/la901824d |
| [7] |
JONES P R, HAO X Q, CRUZ-CHU E R, et al. Sustaining dry surfaces under water[J]. Scientific Reports, 2015, 5(1): 12311. DOI:10.1038/srep12311 |
| [8] |
TUTEJA A, CHOI W, MABRY J M, et al. Robust omniphobic surfaces[J]. Proceedings of the National Academy of Sciences of the United States of America, 2008, 105(47): 18200-18205. DOI:10.1073/pnas.0804872105 |
| [9] |
LIU T L, KIM C J. Turning a surface superrepellent even to completelywetting liquids[J]. Science, 2014, 346(6213): 1096-1100. DOI:10.1126/science.1254787 |
| [10] |
OU J, PEROT B, ROTHSTEIN J P. Laminar drag reduction in microchannels using ultrahydrophobic surfaces[J]. Physics of Fluids, 2004, 16(12): 4635-4643. DOI:10.1063/1.1812011 |
| [11] |
JOSEPH P, COTTIN-BIZONNE C, BENOIT J M, et al. Slippage of water past superhydrophobic carbon nanotube forests in microchannels[J]. Physical Review Letters, 2006, 97(15): 156104. DOI:10.1103/PhysRevLett.97.156104 |
| [12] |
CHOI C H, ULMANELLA U, KIM J, et al. Effective slip and friction reduction in nanograted superhydrophobic microchannels[J]. Physics of Fluids, 2006, 18(8): 087105. DOI:10.1063/1.2337669 |
| [13] |
BYUN D, KIM J, KO H S, et al. Direct measurement of slip flows in superhydrophobic microchannels with transverse grooves[J]. Physics of Fluids, 2008, 20(11): 113601. DOI:10.1063/1.3026609 |
| [14] |
HAO P F, WONG C, YAO Z H, et al. Laminar drag reduction in hydrophobic microchannels[J]. Chemical Engineering & Technology, 2009, 32(6): 912-918. |
| [15] |
WOOLFORD B, PRINCE J, MAYNES D, et al. Particle image velocimetry characterization of turbulent channel flow with rib patterned superhydrophobic walls[J]. Physics of Fluids, 2009, 21(8): 085106. DOI:10.1063/1.3213607 |
| [16] |
DANIELLO R J, WATERHOUSE N E, ROTHSTEIN J P. Drag reduction in turbulent flows over superhydrophobic surfaces[J]. Physics of Fluids, 2009, 21(8): 085103. DOI:10.1063/1.3207885 |
| [17] |
SU Y W, JI B H, HUANG Y G, et al. Nature's design of hierarchical superhydrophobic surfaces of a water strider for low adhesion and low-energy dissipation[J]. Langmuir, 2010, 26(24): 18926-18937. DOI:10.1021/la103442b |
| [18] |
BHUSHAN B, KOCH K, JUNG Y C. Biomimetic hierarchical structure for self-cleaning[J]. Applied Physics Letters, 2008, 93(9): 093101. DOI:10.1063/1.2976635 |
| [19] |
SBRAGAGLIA M, PROSPERETTI A. A note on the effective slip properties for microchannel flows with ultrahydrophobic surfaces[J]. Physics of Fluids, 2007, 19(4): 043603. DOI:10.1063/1.2716438 |
| [20] |
BLEVINS R D. Applied Fluid Dynamics Handbook[M]. New York: Van Nostrand Reinhold, 1984.
|
| [21] |
LU S, YAO Z H, HAO P F, et al. Drag reduction in ultra hydrophobic channels with micro-nano structured surfaces[J]. Science China-Physics Mechanics & Astronomy, 2010, 53(7): 1298-1305. |
| [22] |
ZHANG J X, TIAN H P, YAO Z H, et al. Evolutions of hairpin vortexes over a super hydrophobic surface in turbulent boundary layer flow[J]. Physics of Fluids, 2016, 28(9): 095106. DOI:10.1063/1.4962513 |



