2. 香港科技大学 物理系, 香港
2. Department of Physics, The Hong Kong University of Science and Technology, Hong Kong, China
生命系统中的力学问题与人类生命健康密切相关, 已经成为近年来力学、物理学、生命科学和医学等学科所关注的交叉学科热点问题。生命系统中的力学问题涉及丰富的复杂流体和微纳尺度流动现象, 是流体力学致力解决的重要科学问题之一。针对活细胞、细胞组件等生命物质的力学性质表征, 研究其与外界(力学、化学、生物等)环境的相互作用及其在不同生命活动和状态下的动态变化, 是生物力学及其交叉研究的重要内容[1-5]。
对生命物质进行力学测量, 其挑战在于生命物质力学性质的独特性以及流体介质的复杂性。一方面, 活细胞等生命物质弹性模量非常小(千帕量级), 还具有黏弹性、多孔弹性、界面黏附性、各向异性等复杂的力学属性[4-7]; 另一方面, 活细胞和组织的形态与力学性质会因生命活动和健康状态发生动态改变, 并受到微环境中的力学、化学和生物等因素的影响[8-10]; 此外, 生命系统中的流体介质(如细胞液、血液、组织液等)以及生物实验中使用的细胞培养液多为复杂流体, 内含大量的多糖、蛋白质等生物大分子, 在此类流体介质中进行力学测量, 既要克服流体的阻尼, 又要考虑与生物大分子的相互作用。因此, 发展高精度的生物力学实验测量方法与技术, 是该研究领域亟待解决的关键问题。
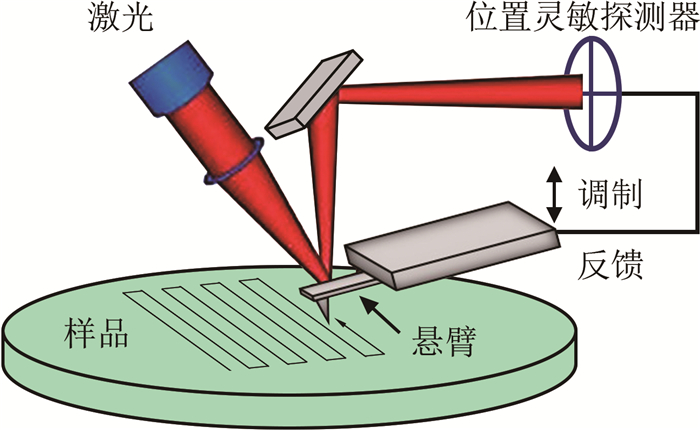
目前, 已利用微管、光镊、磁镊、原子力显微镜等发展了多种实验技术对各类生命物质的力学性质进行测定[11-22]。其中, 原子力显微镜技术(Atomic Force Microscopy, AFM)是近年发展起来的一种表面探测技术。其核心是一根微米尺度的悬臂, 悬臂的探针尖端与样品表面发生相互作用而产生形变, 该形变通过激光的反射被放大和检测, 如图 1所示。原子力显微镜具备纳米级高分辨率, 被广泛应用于纳米材料表面形貌、样品和探针之间各种相互作用力(如范德华力[23]、电磁力[24]、光力[25-27]、毛细力[28-31]等)的测量; 还被应用于软材料力学性质[31-32]的测量, 并进而被应用于测量生命物质的力学特性[33-36]。常规原子力显微镜技术一般用于空气或真空中的精密测量, 但在生物力学实验的液体环境中, 由于液体阻尼(黏滞力)对悬臂的影响, 需要对探针的选取和测量条件作进一步考量。
|
| 图 1 原子力显微镜示意图 Fig.1 A schematic of an AFM |
本文旨在从微纳尺度力学角度厘清液体环境中原子力显微镜的生物力学实验方法, 综述本课题组在相关领域的研究进展(此前, 国内研究者已分别从力学-生物学-化学耦合[37]、连续介质力学[38]、生物力学到力学生物学的进展[39]等角度对生物力学的交叉领域进行了较为全面的综述, 本文不再赘述)。首先介绍原子力显微镜力学测量的基本原理, 分析不同测量模式的力学灵敏度和优缺点; 然后介绍原子力显微镜常用的生物力学实验方法, 包括探针的制备与修饰、生物样品的准备和实验条件等; 最后通过原子力显微镜在不同尺度生命物质力学测量中的应用, 阐明原子力显微镜系统作为微纳尺度力学的实验平台为多尺度生物力学问题研究开辟了一条新的道路。
1 原子力显微镜力学测量原理在气体或液体中, 原子力显微镜悬臂的运动可以由朗之万(Langevin)方程[27, 29]精确描述:
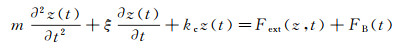 (1)
(1)
式中, z(t)为t时刻悬臂尖端的纵向位移; 等式左侧第一项代表惯性力, m为探针的等效质量; 第二项代表流体作用于悬臂的黏滞力, ξ为黏滞系数; 第三项代表悬臂弯曲导致的弹性力, kc为悬臂的弹性系数; Fext(z, t)代表作用于悬臂的外力, FB(t)为流体热扰动导致的随机布朗力。根据悬臂的驱动形式, 原子力显微镜的力学测量模式可分为静态模式和动态模式两大类。
1.1 静态模式静态模式(又称接触模式)是指原子力显微镜工作时不主动对悬臂施加额外的驱动力。作用于悬臂尖端的力可用胡克定律简单地描述:
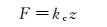 (2)
(2)
在静态模式下, 力灵敏度Fmin由悬臂纵向位移z的不确定度zmin决定。在布朗力FB的作用下, zmin=(kBT/kc)1/2, 因此[40]:
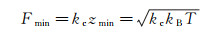 (3)
(3)
其中, kBT为布朗运动热噪声的能量(kB为玻尔兹曼常数, T为实验室温度)。通常, 原子力显微镜在静态模式下的力灵敏度Fmin可达10 pN量级, 为准确测量生命物质的力学性质提供了保障。
静态模式是原子力显微镜最基本的测量模式, 通过控制探针以恒定速度v接近和远离样品, 可以测量得到探针与样品之间的力-位置曲线、力-时间曲线等, 被广泛应用于单分子拉伸[17, 41]以及单细胞和组织的力压痕、力弛豫等实验[8, 34-35]。
1.2 动态模式与静态模式相比, 动态模式具有额外的周期性驱动力Fext=F0cos(ωt), 使悬臂以驱动频率ω作周期性振荡。通常Fext≫ FB, 式(1)的稳态解为:
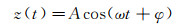 (4)
(4)
式中, A为悬臂尖端的振幅, 与驱动力振幅F0成正比, φ为悬臂末端位移z相对于驱动力Fext的相位:
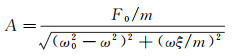 (5)
(5)
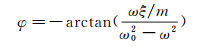 (6)
(6)
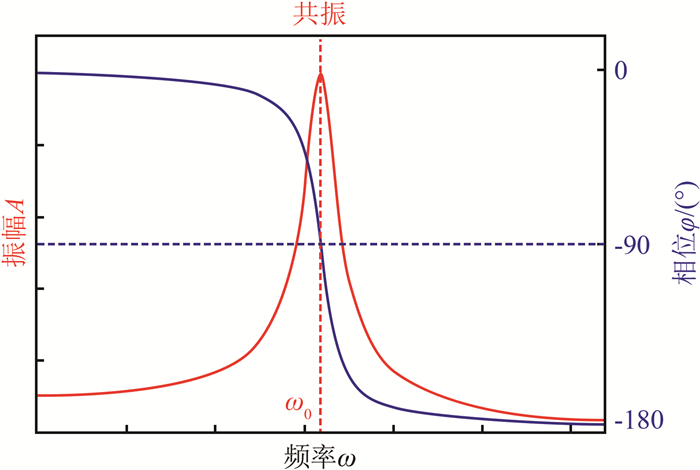
图 2展示了典型的振幅A和相位φ随驱动频率ω变化的曲线。当驱动频率ω为系统的共振频率ω0=(kc/m)1/2时, 振幅A=F0/(ξω0), 相位φ=-90°。
|
| 图 2 振幅A和相位φ在共振频率附近随驱动频率ω的变化 Fig.2 The amplitude A and phase φ as a function of driving frequency ω near resonance ω0 |
不同于静态模式的力灵敏度受到布朗运动热噪声的限制, 在动态模式下, 原子力显微镜的力灵敏度可进一步提高。原子力显微镜在动态模式下利用锁相技术跟踪驱动频率ω或相位φ, 仅检测驱动频率ω附近带宽为ΔB范围内的信号, 从而消除其他频率的背景噪声。因此, 动态模式的力灵敏度大小为[42]:
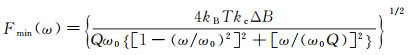 (7)
(7)
式中, Q=(ω0m)/ξ为悬臂的品质因数, Fmin随Q的增大而减小, 从而力灵敏度越高。在空气中, Fmin可达0.1 pN量级。
基于不同的反馈参数, 动态模式的原子力显微镜有两种基本调制模式:调幅(Amplitude Modulation)和调频(Frequency Modulation)[43]。调幅的动态模式也称为"轻敲模式", 是以一个固定频率ω驱动悬臂振动, 测量式(5)和(6)中的振幅A和相位φ, 被广泛应用于测量样品表面的形貌等。调频的动态模式则通过锁相环路使相位φ保持于-90°, 测量解耦的共振频率ω0和系统阻尼ξ。在调频模式下, 当探针接触样品时, 系统的新共振频率ω' 0= 1/2包含了样品弹性的信息ks, 而阻尼ξ包含了样品黏性或耗散力的信息。因此, 调频模式可被用于测量样品表面的黏弹性等力学属性。
在液体中, 动态模式的定量力学测量具有一定局限性。一方面, 由于液体的黏滞系数ξ相比空气大两个数量级左右, 使得悬臂的品质因数Q小两个数量级(通常Q < 10), 这导致力灵敏度大幅下降; 另一方面, 悬臂的周期性振动会引发周围液体的流动, 与壁面产生复杂的相互作用。例如, 当探针与生物样品的距离在微纳尺度时, 由于受到流体介质黏滞力与生物软表面黏弹力的共同影响, 探针与样品间的液体流动极为复杂(详见3.4节)[32, 36]。因此, 在液体中对生物样品力学性质的定量测量, 大多数采用静态模式, 或者采用特殊类型的原子力显微镜探针(如较小尺寸的探针、长针型探针等), 以减小探针在液体中的阻尼[36, 44]。
2 原子力显微镜生物力学实验方法如图 3(a)所示, 原子力显微镜探针悬臂的长度通常为100~200 μm, 末端有一个微米尺度的锥型尖端, 尖端的最小曲率为10 nm量级, 以提供纳米级的空间分辨率。但对于生物样品(如活细胞), 一方面, 锋利的尖端容易刺破细胞膜, 对细胞造成损伤; 另一方面, 生物介质和细胞表面的生物大分子极易吸附于探针表面, 产生极强的黏附性并造成空间分辨率的降低。因此, 在使用原子力显微镜进行生物力学实验前, 要根据实验对象对探针尖端形状及表面进行适当修饰。另外, 原子力显微镜的生物力学实验对生物样品的制备和实验条件也有一定的特殊要求, 本节对具体的实验条件和方法给出建议。
2.1 特殊形状探针的制备将一个直径为微米尺度的球形颗粒粘接于悬臂末端, 即为胶体探针(这里"胶体"泛指纳米至微米尺度的球形颗粒, 与颗粒材质无关), 如图 3(b)所示(直径d约26 μm的玻璃球附着于悬臂末端)。作为一种改良的特殊形状的探针, 胶体探针广泛应用于软物质及生命物质的力学性质测量[23, 33-45]。与锥形尖端探针相比, 胶体探针增大了尖端曲率半径, 减小了作用于细胞表面局部的压强; 增大了探针与细胞的接触面积, 可对接触面积范围内的细胞力学性质的不均匀性进行平均; 球形的几何结构为使用Hertz等力学模型刻画力压痕实验的结果时提供了便利(详见3.1节)。
长针型原子力显微镜探针为另一种新开发的特殊形状的探针[32, 36], 其悬臂末端粘接了一根细长的玻璃纤维, 直径d的范围为0.5~5.0 μm, 长度L的范围为100~500 μm, 玻璃纤维末端可加工为针尖状, 尖端半径R为50~500 nm, 如图 3(c)所示(图中玻璃纤维长180 μm, 直径d约2.5 μm; 小图为针尖放大图, 针尖半径R~200 nm)。以长针型探针进行原子力显微镜实验时, 只需把长针尖端浸入液体, 悬臂则处于空气中。这样的设计使得作用于长针尖端的阻尼比完全浸入液体时大为减小。在动态模式下, 系统的品质因数Q约为10~50, 提高了在液体中测量的力灵敏度。
以上两种特殊形状的探针, 通常在实验室中基于普通商业探针组装得到。胶体探针的微球通常选择表面粗糙度较小的玻璃球, 其优点是便于清洗和进行化学修饰。组装探针时, 在高倍数体式显微镜下, 利用三维微操纵系统, 先在悬臂末端点涂一滴直径10 μm左右的胶水滴, 再将微球与胶水滴接触粘接。如操作时间较长, 可使用紫外固化胶水。长针型探针组装与胶体探针组装类似。其中, 微米尺度的玻璃纤维是以毛细管拉制仪将直径1 mm的玻璃棒拉制而成, 再以煅针仪将其末端加工成针尖状。为确保实验时玻璃纤维垂直于液体水平面, 要根据探针悬臂与水平面的角度调整玻璃纤维与悬臂的角度进行组装。
2.2 探针表面的化学修饰在生物力学实验中, 为减弱蛋白质等生物大分子对探针表面的黏附, 可对探针表面进行适当的化学修饰, 比如在探针表面附着一层Poly(L-Lysine)-graft-Poly(Ethylene Glycol)高分子(PLL-g-PEG)。该分子的PLL端可吸附于玻璃和金属氧化层表面, 暴露在外的PEG端可以极大减弱蛋白质对表面的吸附。实验前, 将探针在等离子清洗器中清洗15 min后, 浸入0.5 mg/mL的PLL-g-PEG溶液中约2 h, 即可完成镀膜。为确保较好的实验效果, 建议每次实验前重新镀膜。
2.3 生物样品的准备和实验条件原子力显微镜在进行生物样品成像和力学测量时, 首先要将被测量的样品"固定"在基底上。以活细胞为例, 除了部分表皮细胞可直接牢固地吸附于盖玻片等基底上, 大部分的活细胞对基底的吸附并不牢固。因此, 实验前需要将基底镀上一层化学或生物膜, 如Poly-D-Lysine、Poly-L-Lysine、胶原蛋白、ECL(entactin-collagen Ⅳ-laminin)等, 再将活细胞栽种于处理后的基底上。
由于生命物质对外界环境(如温度、酸碱度、培养液成分等)极为敏感, 在原子力显微镜实验中, 应尽量将生物样品保持于最适宜的生命环境。例如, 大部分哺乳动物的活细胞, 应在37 ℃、5%二氧化碳浓度、该类细胞的细胞培养液中进行实验, 以确保活细胞的良好生命状态。若实验持续时间较短, 也可选用磷酸盐缓冲液(PBS)代替培养液作为介质。PBS的优点是不含有易吸附于探针表面的蛋白质等大分子, 缺点是缺乏细胞所需的营养物质, 长时间的实验会使细胞处于饥饿状态, 进而影响其力学性质。
以上不同材质的基底和测量条件都会对细胞骨架的形成及其力学性质产生影响。因此, 生物力学的实验结果需指明选用的基底和采用的各种实验条件, 并在相同条件下进行各组生物对照实验。
3 多尺度生物系统中的力学测量原子力显微镜技术在生物力学测量中的一大优势是可覆盖从十纳米至百微米尺度的介观系统, 实现从单分子到单细胞的局部与整体, 以及组织等不同生命物质的力学研究, 具有一定的普适性。本节将以单细胞的力学测量为例, 介绍原子力显微镜在研究细胞弹性模量中的重要应用, 进而推广到对相分离蛋白质液滴、生物组织的力学测量, 最后介绍一种基于微纳尺度流动所研发的活细胞表面黏弹性成像技术。
3.1 单细胞的力学测量利用原子力显微镜结合胶体探针的测量技术, 通过力压痕实验测量单细胞的弹性模量E(主要由细胞骨架中的肌动蛋白丝所形成的网络结构所决定), 是目前最普遍的单细胞尺度力学实验方法。2007年, 研究者利用该方法发现癌变细胞的弹性模量E远小于正常细胞[46]。其后的诸多研究发现, 细胞弹性模量E的大小与其生命活动、健康状态密切相关[1-5]。因此, 力学测量提供了一种潜在的单细胞尺度疾病与健康诊断的新方法。
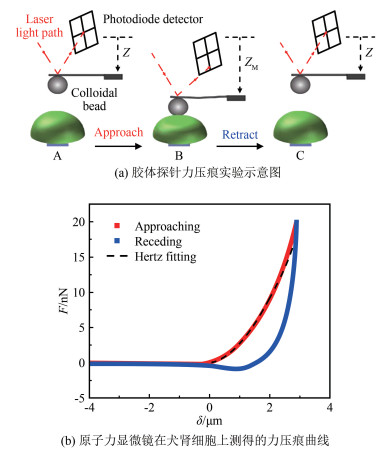
力压痕实验的基本方法如图 4(a)所示。在静态模式下, 胶体探针在细胞上方以恒定速度v向下运动, 接触细胞表面后, 继续按压使其发生形变δ, 同时探针感受到细胞的反作用力F(从A至B所示); 当原子力显微镜测量到的F达到预设的最大压入力FM时, 探针反向以恒定速度v撤回(从B至C所示)。
|
| 图 4 胶体探针力压痕实验 Fig.4 The force-indentation experiment with a colloidal probe |
图 4(b)展示了原子力显微镜在犬肾细胞(MDCK Ⅱ)上测得的力压痕曲线。其中, 红、蓝曲线分别为压入过程和撤回过程中的力F随压入深度(细胞形变)δ的变化, 可见红、蓝曲线并不完全重合, 存在力的迟滞(Hysteresis)现象。
对力压痕实验结果的定量分析, 通常采用Hertz模型[47]。当探针尖端为球形时:
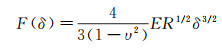 (8)
(8)
其中, υ为泊松系数(活细胞通常采用不可压缩的假设, υ=0.5), R=1/(1/R1+1/R2)为系统的有效半径, R1和R2分别为胶体探针和被测细胞的半径。如图 4(b)所示, 虚线为Hertz模型对按压曲线的拟合, Hertz模型可以很好地描述胶体探针按压细胞过程中的力F随压入深度δ的变化曲线。通过式(8)的拟合, 可以测定单细胞的弹性模量E。通常活细胞的E在1~100 kPa范围内。
Hertz模型在描述活细胞的力压痕曲线时具有一定的局限性。首先, Hertz模型的前提假设为各向同性的纯弹性材料, 且在应变较小的情况下成立; 而对活细胞而言, 以上假设通常并不满足, 所测定的E为单细胞表观的弹性模量。其次, Hertz模型并不能解释压入和撤回曲线的力迟滞现象。力迟滞现象的产生, 是因为活细胞属于具有黏弹性的软物质(以聚合物、胶体和许多生命物质为代表的软物质, 表现出不同于刚性材料的力学特性, 兼具液体的黏性和固体的弹性。由于黏弹性的存在, 软物质的形变落后于应力变化, 呈现出力迟滞现象或松弛现象)。对于活细胞, 其黏性来源于细胞形变过程中细胞骨架、细胞质、生物大分子之间相对运动的能量耗散。最后, 由于细胞的黏弹性, 使得力压痕曲线以及通过Hertz模型所测得的弹性模量E具有速度依赖性, 即E随探针按压速度v的增大而增大, 且呈近似指数的依赖关系(E~vα)[48]。由此可见, Hertz模型并不能全面描述活细胞的力学性质; 而其他的接触力学模型, 如JKR模型(Johnson-Kendall-Roberts model)、DMT模型(Derjaguin-Müller-Toporov model)等, 虽在Hertz模型的基础上进一步考虑了探针与细胞之间的黏附性, 但仍不适用于描述细胞的黏弹性。从力学角度在实验和理论两个方面揭示细胞的本构关系与黏弹特性, 仍是当前单细胞力学的核心科学问题。
3.2 液-液相分离液滴的力学测量液-液相分离与相变本是物理学概念, 如油与水的液-液相分离、气态水蒸气-液态水-固态冰的相变等。近十年来, 生物学家发现细胞中存在相分离和相变现象[49-50]。在原本相对均一的环境中, 某些蛋白质或核酸分子通过多价相互作用(生物大分子间有多个结合位点), 形成无膜的细胞结构, 例如核内的核仁、着丝粒、核孔复合物以及胞质中的应激颗粒、神经颗粒等。相分离不仅是生物体内一种极为普遍的功能调控方式, 更具有重要的生物学功能, 例如介导细胞特定区域的信号传导、赋予生物体应对胁迫环境的能力等[35]。相分离所形成的细胞结构通常呈现出液态或胶体态的特征, 它们的物理性质(表面张力、黏度、弹性等)是判断和区分相分离的重要依据。另外, 相分离结构的物理性质及其随时间的演化也与其生物功能密切相关。因此, 对相分离液滴力学性质的表征至关重要。
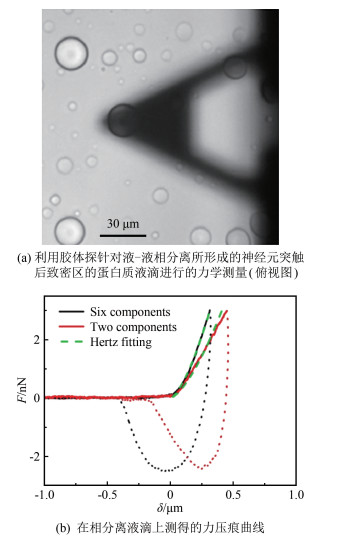
图 5(a)所示为利用胶体探针对液-液相分离所形成的神经元突触后致密区的蛋白质液滴(图中小圆圈)所进行的力学测量, 其力压痕实验结果如图 5(b)所示。图中, 压入曲线为实线, 撤回曲线为虚线; 黑色、红色分别代表由构成神经元突触后致密区的主要6种和2种蛋白质组分所重构的蛋白质液滴的测量结果; 绿色虚线为Hertz模型与压入曲线的拟合。首先, 从压入和撤回过程的力曲线迟滞可判断相分离液滴呈现软物质的黏弹性; 其次, 撤回曲线经历了很长的负值段, 表明界面具有极强的黏附性。
实验发现相分离液滴的力学性质与其内部蛋白质的构成和功能密切相关。图 5(b)中黑色曲线所代表的6种组分重构的蛋白质液滴, 相比红色曲线所代表的2种组分重构的液滴, 其发生相变的临界蛋白质浓度更低, 但弹性模量更大。由Hertz模型测得的弹性模量分别为3.5 kPa(6种组分)、2.5 kPa(2种组分)。这是由于相分离液滴中6种蛋白质通过多价相互作用相结合, 一部分形成蛋白质支架, 另一部分附着于支架上, 形成具有生物功能的整体。由于真实突触中的蛋白质种类更多, 多价相互作用更强, 因此, 神经元突触后致密区的力学性质会更接近于凝胶、玻璃化材料。
在实验中, 我们还发现相分离液滴的老化、随时间变硬的趋势[35], 对应着人在衰老过程中, 一部分与脑疾病相关的蛋白质或多肽会发生纤维化。这一力学研究成果将有助于对神经突触的形成及调节机制的研究, 也将有助于阐明一系列因突触蛋白编码基因突变引起的脑疾病的病理机制, 最终或可以帮助精神障碍的早期诊断与治疗。
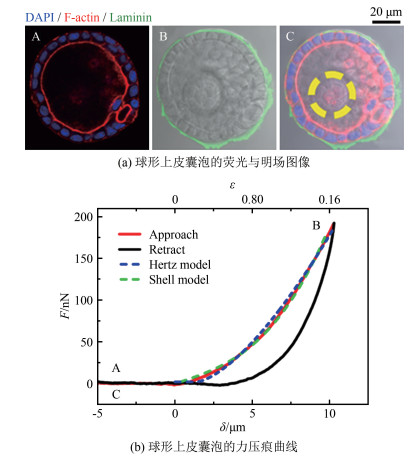
3.3 球形上皮囊泡组织的力学测量由形态相似、功能相同的多个细胞组成的生命结构即为组织。其中, 球形上皮囊泡是构成肺、肾脏等器官的一种重要组织, 如图 6(a)所示, 它由单层细胞构成球形的外壳, 内腔由组织液填充(图中, 蓝、红、绿色分别表示细胞核、F-肌动蛋白、层粘连蛋白, 黄色虚线圆表示与基底结合的区域)。在压力驱动下, 球形上皮囊泡会产生较大形变, 其力学测量与机理研究对认识肺泡、肾小球等结构的生理功能和工作原理具有重要意义。
图 6(a)所示为通过生物工程手段在体外形成的球形上皮囊泡[34]。图 6(b)为通过原子力显微镜结合胶体探针的测量技术得到的球形上皮囊泡的力压痕曲线(图中虚线为压入曲线与Hertz模型、球壳模型的拟合)。以Hertz模型拟合按压过程的力曲线, 可以得到该球形囊泡的表观弹性模量约为0.58 kPa。然而, 由于该组织存在内腔结构, Hertz模型并不能真实地描述该生物结构的力学性质, 而应采用描述球壳型结构的力学模型, 如:
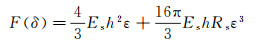 (9)
(9)
等式右边第一项、第二项分别代表球壳弯曲和拉伸对弹性力的贡献。其中, Es为球壳的弹性模量, h为球壳厚度, Rs为球壳半径, ε=δ/(2Rs)为球壳的应变。通过式(9)拟合得到的弹性模量Es=8.2 kPa, 略大于该类上皮细胞单细胞的弹性模量5~7 kPa。
上皮细胞的一大特征是呈现出明显的极性, 即上皮细胞的两端在结构(如图 6(a)所示)和功能上具有明显的差别。朝向有腔结构的一面, 称为游离面; 与游离面相对的另一面称为基底面。上皮细胞极性的建立和维持, 对其力学性质有重要的影响。例如, 尚未生长成熟的上皮组织或紊乱的实心囊肿, 由于上皮细胞的极性无法建立, 其弹性模量大幅度减小[34]。
与单细胞和相分离蛋白质液滴类似, 球形上皮囊泡的力曲线也呈现出迟滞现象。由此可见, 对于不同尺度的生命物质, 从亚细胞结构到单细胞, 再到组织, 软物质的黏弹性是生命物质中最具代表性的力学特性。对传统软物质力学性质的研究是揭示生命软物质力学性质的基础。
3.4 细胞表面的黏弹性成像以上实验结果, 皆系利用原子力显微镜结合胶体探针的测量技术, 基于材料各向同性的力学假设, 将研究对象整体的力学性质进行表征。然而, 许多生命物质存在力学的各向异性以及微观的力学不均一性, 因此亟需一种力学手段, 在光学成像的基础上, 对活细胞等生命物质实现更小尺度的力学成像。
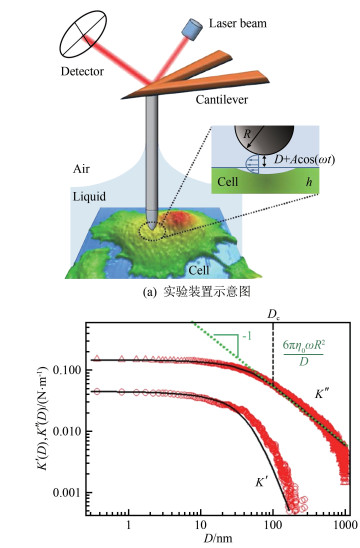
利用原子力显微镜结合长针型探针的测量技术(下文简称"长针式原子力显微镜"), 可以在扫描单细胞形貌的同时, 实现细胞表面黏弹性分布等多个物理量的测量[36]。如图 7(a)所示, 在扫描细胞形貌的过程中, 长针式探针在靠近细胞表面处作周期性振荡, 在此驱动下, 流体周期性地被排出和回流至探针与细胞表面的间隙之中。图 7(a)中的放大图显示了探针尖端和细胞表面间隙区域的液体流动的几何结构。通过该微纳尺度的流动和流固耦合效应, 可以定量测量下方固壁(即细胞)的力学性质。由水的润滑方程和表述软物质的线性黏弹性理论[51], 可以解出力的反馈函数K* (D) =Fh/A随探针与细胞表面距离D的变化关系(Fh为作用于探针尖端的水动力, A为探针驱动的振幅)。由于细胞具有黏弹性, K* (D)通常为复数, 实部K'(D)代表弹性响应, 虚部K″(D)代表黏性响应。
如图 7(b)所示, 在长针型探针靠近细胞表面的过程中, 可测得活细胞表面某位置的K'(D)和K″(D)。图中, 红色数据为调频模式下的测量结果, 红色圆圈代表K'(D), 红色三角形代表K″(D); 绿色虚线表示适用于刚性基底雷诺阻尼的变化规律, 黑色虚线表示特征转变距离Dc=100 nm, 黑色实线为数值计算结果与实验数据的拟合。
由图 7(b)可见, 在此微纳尺度流动体系中, 黏性响应K″(D)占主导地位。当D大于某一特征尺度Dc时, K″(D)服从雷诺阻尼的变化关系K″(D)=6πη0ωR/D, 其中η0为液体黏度, ω为驱动频率, R为探针尖端半径[52]; 当D<Dc时, 在水动力Fh作用下, 细胞表面产生较为明显的形变(~A), K'(D)与K″(D)趋于饱和。K'(D)与K″(D)在D→0的饱和值以及特征转变距离Dc共同决定了下表面细胞的弹性模量E和黏度η。基于图 7(b), 可进而得到在该位置细胞的弹性模量E=58 kPa和黏度η=1.19×10-2 Pa·s。
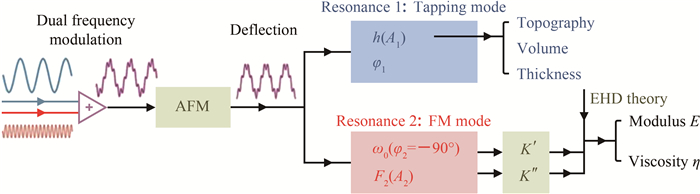
由于细胞并不是理想的各向均一性材料, 在其不同位置进行测量时, 力的反馈K* (D)和黏弹性信息各异。为此, 我们设计了在探针扫描细胞形貌的同时对每个位置的力学性质进行测量的力学成像方法, 如图 8所示。在悬臂的两个共振频率同时驱动探针运动, 其中, 在第一个共振频率作调幅的轻敲模式, 扫描每一点的高度, 进而得到活细胞的形貌、厚度和体积信息; 在第二个共振频率作调频的共振模式, 通过前述方法, 测量每一点的黏弹性信息, 由此可以实现对细胞表面的形貌、黏弹性等多个物理量的同时测量。
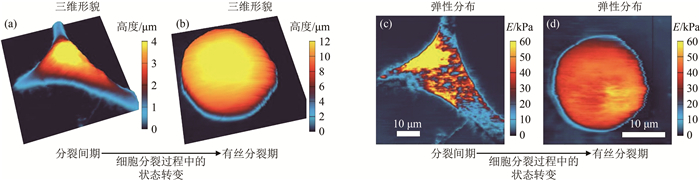
图 9(a)和(c)为采用长针式原子力显微镜测量得到的一个HeLa细胞的形貌与弹性分布图。如图 9(c)所示, 单细胞表面的弹性模量数值在较大范围内(20~80 kPa)连续变化, 且呈现出不均一的分布。前述的水动力学方法在细胞表层的力学探测深度为几百纳米, 该区域的弹性模量主要由靠近细胞膜内侧的肌动蛋白层所主导。因此, 相对于力压痕实验测量得到的单细胞表观的弹性模量E, 细胞表面的弹性模量约大一个数量级。
实验发现, 细胞表层弹性模量的分布与细胞的状态密切相关。例如, 当细胞由分裂间期(图 9(a)和(c))进入有丝分裂期时(图 9(b)和(d)), 细胞形态由平铺状变为近似球状, 同时弹性模量由不均一状态变为均一状态。力学性质对于处于分裂期的母细胞至关重要, 转变为均一状态, 有利于在分裂过程中将内部染色体和细胞质等组件均匀分裂至两个子细胞中去。此外, 实验还发现:处于迁移过程中的细胞的弹性模量呈极性分布, 弹性模量在朝向迁移方向的前部远大于后部[36]。
4 结论与展望本文介绍了原子力显微镜技术的力学测量原理及其在生物力学研究中的实验方法, 综述了该技术在从亚细胞结构到组织的多尺度力学研究中的具体应用, 强调了液体的流动和生命物质的黏弹性对测量结果的影响。作为一个较为通用且有效的微纳尺度力学实验工具, 原子力显微镜技术已被越来越多地应用于生物力学领域, 并在此交叉学科的实验研究中发挥着重要作用。
在创新实验技术的推动下, 研究者对细胞整体力学性质和局部力学行为的认识愈来愈清楚。但由于生命系统的复杂性, 对生命物质力学性质的研究仍处于探索阶段, 仍有许多力学问题亟需解决。
首先, 由Hertz等纯弹性力学模型测得的弹性模量E依赖于测量速度等实验条件, 无法完善地描述具有黏弹性的生命物质, 亟待发展更为完善的接触力学模型以揭示生命物质的本构关系。
其次, 在不同生命状态、细胞癌变迁移的过程中, 可能涉及多个物理量的动态转变。但与弹性模量E相比, 目前对生命物质的其他力学性质(如表面张力系数、黏度系数等)的研究仍然较少。
最后, 虽然原子力显微镜在生物力学的体外实验(in vitro)中应用广泛, 但在体内实验(in vivo)中的应用存在极大的困难。
综上, 生物力学领域亟需新实验技术的不断涌现, 通过多种力学测试方法的对比研究和多个物理量的同时测量, 帮助跨学科的研究者更为全面地认识和了解复杂生命物质的力学性质, 进一步探究力学性质的转变与人类重大疾病的关联, 挖掘力学检测在医药应用中的潜在价值。
| [1] |
INGBER D E. Tensegrity:The architectural basis of cellular mechanotransduction[J]. Annual Review of Physiology, 1997, 59(1): 575-599. DOI:10.1146/annurev.physiol.59.1.575 |
| [2] |
VOGEL V, SHEETZ M. Local force and geometry sensing regulate cell functions[J]. Nature Reviews Molecular Cell Biology, 2006, 7(4): 265-275. |
| [3] |
JANMEY P A, MCCULLOCH C A. Cell Mechanics:Integrat-ing cell responses to mechanical stimuli[J]. Annual Review of Biomedical Engineering, 2007, 9(1): 1-34. DOI:10.1146/annurev.bioeng.9.060906.151927 |
| [4] |
KASZA K E, ROWAT A C, LIU J, et al. The cell as a material[J]. Current Opinion in Cell Biology, 2007, 19(1): 101-107. DOI:10.1016/j.ceb.2006.12.002 |
| [5] |
MOEENDARBARY E, HARRIS A R. Cell mechanics:principles, practices, and prospects[J]. Wiley Interdisciplinary Reviews:Systems Biology and Medicine, 2014, 6(5): 371-388. DOI:10.1002/wsbm.1275 |
| [6] |
FLETCHER D A, MULLINS R D. Cell mechanics and the cytoskeleton[J]. Nature, 2010, 463(7280): 485-492. DOI:10.1038/nature08908 |
| [7] |
CHEN D T, WEEKS E R, CROCKER J C, et al. Rheological microscopy:local mechanical properties from microrheology[J]. Physical Review Letters, 2003, 90(10): 108301. DOI:10.1103/PhysRevLett.90.108301 |
| [8] |
LEKKA M, LAIDLER P, GIL D, et al. Elasticity of normal and cancerous human bladder cells studied by scanning force microscopy[J]. European Biophysics Journal, 1999, 28(4): 312-316. |
| [9] |
NAGAYAMA M, HAGA H, KAWABATA K. Drastic change of local stiffness distribution correlating to cell migration in living fibroblasts[J]. Cell Motility and the Cytoskeleton, 2001, 50(4): 173-179. DOI:10.1002/cm.10008 |
| [10] |
GIRARD P P, CAVALCANTI-ADAM E A, KEMKEMER R, et al. Cellular chemomechanics at interfaces:sensing, integra-tion and response[J]. Soft Matter, 2007, 3(3): 307. DOI:10.1039/b614008d |
| [11] |
HOCHMUTH R M. Micropipette aspiration of living cells[J]. Journal of Biomechanics, 2000, 33(1): 15-22. |
| [12] |
SÁNCHEZ D, JOHNSON N, LI Chao, et al. Noncontact measurement of the local mechanical properties of living cells using pressure applied via a pipette[J]. Biophysical Journal, 2008, 95(6): 3017-3027. |
| [13] |
MOEENDARBARY E, VALON L, FRITZSCHE M, et al. The cytoplasm of living cells behaves as a poroelastic material[J]. Nature Materials, 2013, 12(3): 253-261. DOI:10.1038/nmat3517 |
| [14] |
AMBLARD F, MAGGS A C, YURKE B, et al. Subdiffusion and anomalous local viscoelasticity in actin networks[J]. Physical Review Letters, 1996, 77(21): 4470-4473. DOI:10.1103/PhysRevLett.77.4470 |
| [15] |
DAI J W, SHEETZ M P. Mechanical properties of neuronal growth cone membranes studied by tether formation with laser optical tweezers[J]. Biophysical Journal, 1995, 68(3): 988-996. |
| [16] |
HOFFMAN B D, MASSIERA G, VAN CITTERS K M, et al. The consensus mechanics of cultured mammalian cells[J]. Proceedings of the National Academy of Sciences of the United States of America, 2006, 103(27): 10259-10264. DOI:10.1073/pnas.0510348103 |
| [17] |
MVLLER D J, DUFRÊNE Y F. Atomic force microscopy:a nanoscopic window on the cell surface[J]. Trends in Cell Biology, 2011, 21(8): 461-469. DOI:10.1016/j.tcb.2011.04.008 |
| [18] |
SOKOLOV I, DOKUKIN M E, GUZ N V. Method for quantitative measurements of the elastic modulus of biological cells in AFM indentation experiments[J]. Methods, 2013, 60(2): 202-213. |
| [19] |
STEWART M P, HELENIUS J, TOYODA Y, et al. Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding[J]. Nature, 2011, 469(7329): 226-230. DOI:10.1038/nature09642 |
| [20] |
FISCHER-FRIEDRICH E, TOYODA Y, CATTIN C J, et al. Rheology of the active cell cortex in mitosis[J]. Biophysical Journal, 2016, 111(3): 589-600. |
| [21] |
MATZKE R, JACOBSON K, RADMACHER M. Direct, high-resolution measurement of furrow stiffening during division of adherent cells[J]. Nature Cell Biology, 2001, 3(6): 607-610. DOI:10.1038/35078583 |
| [22] |
STEWART M P, TOYODA Y, HYMAN A A, et al. Force probing cell shape changes to molecular resolution[J]. Trends in Biochemical Sciences, 2011, 36(8): 444-450. DOI:10.1016/j.tibs.2011.05.001 |
| [23] |
CAPPELLA B, DIETLER G. Force-distance curves by atomic force microscopy[J]. Surface Science Reports, 1999, 34(1-3): 1-104. DOI:10.1016/S0167-5729(99)00003-5 |
| [24] |
WANG Y J, XU Z L, SHENG P, et al. Electric-field-induced forces between two surfaces filled with an insulating liquid:the role of adsorbed water[J]. The European Physical Journal Applied Physics, 2014, 66(3): 31301. DOI:10.1051/epjap/2014130388 |
| [25] |
KOHOUTEK J, DEY D, BONAKDAR A, et al. Opto-mechanical force mapping of deep subwavelength plasmonic modes[J]. Nano Letters, 2011, 11(8): 3378-3382. DOI:10.1021/nl201780y |
| [26] |
MA D K, GARRETT J L, MUNDAY J N. Quantitative measurement of radiation pressure on a microcantilever in ambient environment[J]. Applied Physics Letters, 2015, 106(9): 091107. DOI:10.1063/1.4914003 |
| [27] |
GUAN D S, HANG Z H, MARCET Z, et al. Direct measurement of optical force induced by near-field plasmonic cavity using dynamic mode AFM[J]. Scientific Reports, 2015, 5: 16216. DOI:10.1038/srep16216 |
| [28] |
WANG Y J, GUO S, CHEN H Y, et al. Understanding contact angle hysteresis on an ambient solid surface[J]. Physical Review E, 2016, 93(5): 052802. DOI:10.1103/PhysRevE.93.052802 |
| [29] |
XIONG X, GUO S, XU Z, et al. Development of an atomic-force-microscope-based hanging-fiber rheometer for interfacial microrheology[J]. Physical Review E, 2009, 80(6 Pt 1): 061604. |
| [30] |
GUAN D S, WANG Y J, CHARLAIX E, et al. Asymmetric and speed-dependent capillary force hysteresis and relaxation of a suddenly stopped moving contact line[J]. Physical Review Letters, 2016, 116(6): 066102. DOI:10.1103/PhysRevLett.116.066102 |
| [31] |
GUAN D S, WANG Y J, CHARLAIX E, et al. Simultaneous observation of asymmetric speed-dependent capillary force hysteresis and slow relaxation of a suddenly stopped moving contact line[J]. Physical Review E, 2016, 94(4): 042802. DOI:10.1103/PhysRevE.94.042802 |
| [32] |
GUAN D S, BARRAUD C, CHARLAIX E, et al. Noncontact viscoelastic measurement of polymer thin films in a liquid medium using long-needle atomic force microscopy[J]. Langmuir, 2017, 33: 1385-1390. DOI:10.1021/acs.langmuir.6b04066 |
| [33] |
SHU Y W, CHAN H N, GUAN D S, et al. A simple fabricated thickness-based stiffness gradient for cell studies[J]. Science Bulletin, 2017, 62(3): 222-228. DOI:10.1016/j.scib.2016.12.012 |
| [34] |
SHEN Y S, GUAN D S, SERIEN D, et al. Mechanical characterization of microengineered epithelial cysts by using atomic force microscopy[J]. Biophysical Journal, 2017, 112(2): 398-409. |
| [35] |
ZENG M L, CHEN X D, GUAN D S, et al. Reconstituted postsynaptic density as a molecular platform for understanding synapse formation and plasticity[J]. Cell, 2018, 174(5): 1172-1187. DOI:10.1016/j.cell.2018.06.047 |
| [36] |
GUAN D S, CHARLAIX E, QI R Z, et al. Noncontact viscoelastic imaging of living cells using a long-needle atomic force microscope with dual-frequency modulation[J]. Physical Review Applied, 2017, 8(4): 044010. DOI:10.1103/PhysRevApplied.8.044010 |
| [37] |
龙勉. 细胞-分子层次的多尺度力学-化学-生物学耦合[J]. 医用生物力学, 2016, 31(4): 327-332. LONG M. Multiscale mechano-chemo-biological coupling at cellular and molecular levels[J]. Journal of Medical Biomech-anics, 2016, 31(4): 327-332. |
| [38] |
陈恩惠, 杨锦鸿, 李栋, 等. 软物质中的理性连续介质力学基础[J]. 物理学报, 2016, 65(18): 79-100. CHEN E H, YANG J H, LI D, et al. On the theoretical basis of rational continuum mechanics in softmatter[J]. Acta Physica Sinica, 2016, 65(18): 79-100. |
| [39] |
姜宗来. 从生物力学到力学生物学的进展[J]. 力学进展, 2017, 47(1): 309-332. JIANG Z L. Advance from biomechanics to mechanobiology[J]. Advances In Mechanics, 2017, 47(1): 309-332. |
| [40] |
BUTT H J, JASCHKE M. Calculation of thermal noise in atomic force microscopy[J]. Nanotechnology, 1999, 6(1): 1. |
| [41] |
JANSHOFF A, NEITZERT M, OBERDÖRFER Y, et al. Force spectroscopy of molecular systems-single molecule spectroscopy of polymers and biomolecules[J]. Angewandte Chemie (International Edition), 2000, 39(18): 3212-3237. |
| [42] |
LI M, TANG H X, ROUKES M L. Ultra-sensitive NEMS-based cantilevers for sensing, scanned probe and very high-frequency applications[J]. Nature Nanotechnology, 2007, 2(2): 114-120. DOI:10.1038/nnano.2006.208 |
| [43] |
GARCÍA R, RUBÉN P. Dynamic atomic force microscopy methods[J]. Surface Science Reports, 2002, 47(6-8): 197-301. DOI:10.1016/S0167-5729(02)00077-8 |
| [44] |
WALTERS D A, CLEVELAND J P, THOMSON N H, et al. Short cantilevers for atomic force microscopy[J]. Review of Scientific Instruments, 1996, 67(10): 3583-3590. DOI:10.1063/1.1147177 |
| [45] |
BUTT H, CAPPELLA B, KAPPL M. Force measurements with the atomic force microscope:Technique, interpretation and applications[J]. Surface Science Reports, 2005, 59(1): 1-152. |
| [46] |
CROSS S E, JIN Y S, RAO J Y, et al. Nanomechanical analysis of cells from cancer patients[J]. Nature Nanotechnology, 2007, 2(12): 780-783. DOI:10.1038/nnano.2007.388 |
| [47] |
HERTZ H. On the contact of elastic solids[J]. Journal für die Reine und Angewandte Mathematik, 1882, 92: 156-171. |
| [48] |
KOLLMANNSBERGER P, FABRY B. Linear and nonlinear rheology of living cells[J]. Annual Review of Materials Re-search, 2011, 41(1): 75-97. DOI:10.1146/annurev-matsci-062910-100351 |
| [49] |
BRANGWYNNE C P, ECKMANN C R, COURSON D S, et al. Germline P granules are liquid droplets that localize by controlled dissolution/condensation[J]. Science, 2009, 324(5935): 1729-1732. DOI:10.1126/science.1172046 |
| [50] |
BANANI S F, LEE H O, HYMAN A A, et al. Biomolecular condensates:organizers of cellular biochemistry[J]. Nature Reviews Molecular Cell Biology, 2017, 18(5): 285-298. DOI:10.1038/nrm.2017.7 |
| [51] |
LEROY S, CHARLAIX E. Hydrodynamic interactions for the measurement of thin film elastic properties[J]. Journal of Fluid Mechanical, 2011, 674: 389-407. DOI:10.1017/S0022112010006555 |
| [52] |
BRENNER H. The slow motion of a sphere through a viscous fluid towards a plane surface[J]. Chemical Engineering Science, 1961, 16: 241-251. |