微纳米尺度的液滴、胶囊及颗粒在科学研究与工程实际中具有重要应用, 涉及了生物制药、医学、材料学、分析化学、食品科学等学科[1]。特别地, 具有壳-核结构的复合微纳胶囊能够将一种物质包裹于另一种物质中, 实现更为丰富的结构和功能。毛细流动聚焦(Capillary flow focusing, 简称"流动聚焦")作为一种典型的利用毛细流动中的射流不稳定性来实现微流控的方法, 已被广泛应用于微液滴及胶囊的制备[2-4]。流动聚焦的原理为:一种流体从毛细管流出, 经过毛细管下方的小孔被外部另一种流体所聚焦并在管孔之间形成流体锥形。在一定条件下, 锥形顶端产生微射流进入小孔下游自由空间并最终破碎成液滴[5]。当使用同轴毛细管替代单层毛细管后, 可进一步形成同轴流动聚焦(Coaxial flow focusing), 此时两相不相溶流体从同轴毛细管流出, 经过小孔聚焦形成同轴锥-射流结构并生成复合微液滴[6-7]。近年来, 又有多种复杂结构的毛细管被引入到流动聚焦中, 并成功制备了具有丰富几何结构的复合液滴[8-11]。
单轴流动聚焦几何结构简单且最易实现, 目前已得到广泛研究。1998年, Gañán-Calvo[12]最早利用高速气体驱动液体实现了液-气流动聚焦, 并基于无黏流动和忽略表面张力假设给出了小孔出口处射流直径的理论预测。后续研究考虑了流体黏性和表面张力的影响, 对射流直径的理论推导进行了一阶和二阶修正[13-14]。进一步实验发现, 当液体流量和驱动气体压差变化时, 锥-射流结构存在丰富的流动模态[15-17], 多种模态间的转换均可通过量纲分析或线性不稳定性理论进行预测[16, 18-19]。与液-气流动聚焦对应的为外部液体驱动内部气体的气-液流动聚焦。实验发现这种流体组合下无法在小孔下游形成射流, 微气泡均是在锥形顶端即小孔出口处产生[20-21]。当两相流体均为液体时, 则形成液-液流动聚焦。研究者对液-液流动聚焦中的流动模态及模态转换也已开展了一定的研究[22-24]。事实上, 液-液流动聚焦更多地是与二维微管道或玻璃毛细管流动相结合[25-28], 此时液滴将在受固壁约束的有限空间内生成。微通道构型下的流动聚焦研究可参考一系列综述文献[29-33], 其在流体流速、液滴尺寸及产率、介质选取、几何结构影响上均与开放式的流动聚焦有显著不同[34]。在应用方面, 流动聚焦技术已成功制备了不同材料的单分散性微颗粒, 具有良好的可控性与重复性[35-36]。
与单轴流动聚焦相同, 同轴流动聚焦的提出最早也可追溯至1998年[12]。实验中, 通过高速气体驱动形成了"内水外油"的同轴射流并最终破碎为复合液滴。其后相关的实验研究既关注了聚焦小孔上游的同轴锥形结构[37], 也展示了不同内外射流流量情况下同轴射流及复合液滴的形态[38]。针对液体驱动下的同轴流动聚焦, 穆恺[7, 39]探讨了复合锥-射流的流动模态及模态转换, 并针对射流模态下两层界面破碎的耦合规律及物理机理开展了研究。与单轴情况类似, 通过与微通道流动结合, 在玻璃毛细管和二维微管道中也成功实现了同轴流动聚焦[40-42]。近年来, 同轴流动聚焦已被成功应用于制备可控几何结构及壳核材料, 以及具有一定功能的单分散性复合微胶囊[43-46]。
尽管流动聚焦技术有能力制备单分散性良好的微液滴, 但在可控液滴制备上仍有明显的局限性, 例如:液滴粒径通常分布于一定范围; 射流破碎的非线性效应导致普遍存在卫星液滴; 液滴粒径和产率难以精确控制等。鉴于此, 通过对流动系统施加外部主动激励来控制液滴生成, 在应用上具有重大意义。对流动施加外部激励有多种方式, 包括电场力控制、离心力控制、调控流体流量以及实时改变流体黏度、界面张力、浸润性等[30]。其中, 调控流量作为一种不引入额外作用力、可控性强且容易实施的方式被广泛采用。目前, 对流量激励下射流破碎的研究主要针对液-液环境下的微流控器件[47-50], 由于受流速限制, 可控生成液滴的频率范围较低(通常为1 Hz量级), 而流动聚焦中射流的高频破碎(102~106 Hz量级)给失稳主动控制带来了挑战。近年来, 作者所在团队针对这种高速、高频条件下激励的施加与标定方式以及流动失稳的机理开展了研究, 对频率、振幅、扰动相等多种因素对液滴生成的影响进行了一定的探讨[51-52]。
基于团队近年来的研究工作, 本文详细介绍流动聚焦的核心装置、实验平台及图像拍摄方法, 探讨参数对锥形及射流的影响规律, 并对引入外部激励后射流的破碎状态进行研究。
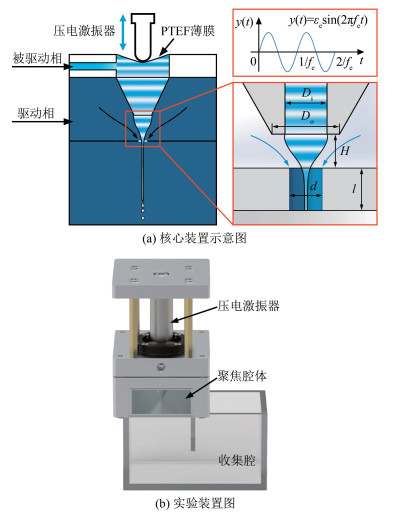
1 实验方法 1.1 实验平台根据几何结构, 常见的流动聚焦核心装置可分为吹气式和吸气式两种类型(图 1)。吹气式核心装置(图 1(a))聚焦孔上游的腔体以有机玻璃板粘接而成, 其前后板为观察窗, 左右侧板分别开有输入驱动气体的吹气孔(靠近气腔顶端)以及连接压力表的测压孔(靠近气腔底端); 腔体顶部中心开一圆孔, 可将毛细管以橡胶塞固定于其中并与圆孔保持同轴, 这种设计也便于调整毛细管的几何结构(单轴、同轴、三轴等)和尺寸。实验中, 驱动气体经连接于吹气孔的输气管进入气腔, 在聚焦孔对毛细管流出的流体(内、外层流量分别为Qin和Qout)进行聚焦, 调节气体流量可控制驱动压差Δpg(可通过连接于测压孔的压力表准确测量)。为制备更小粒径的微液滴, 通常还需对管孔间的流体锥形或聚焦孔下游的射流施加额外电场。因此, 在腔体底板下部紧贴一块带孔金属圆片(以螺丝固定), 在射流下游放置另一块金属圆片。实验中, 通过调整高压电源正负极的连接位置, 可分别对流体锥形、射流或整个锥-射流区域施加电场力。

|
| 图 1 流动聚焦核心装置示意图及实物图 Fig.1 Sketches and real pictures of the devices in flow focusing experiments |
吹气式核心装置多用于射流观测及微液滴接收, 而在对聚焦孔上游流体锥形的研究中, 吸气式核心装置(图 1(b))更具独到优势。吸气式装置的特点是将毛细管与聚焦腔体分离(通常是将毛细管位置固定, 而将聚焦腔体放置于精密位移台上)。聚焦腔体同样以有机玻璃板粘接而成, 侧板上开有连接真空泵的吸气孔、连接负压表的测压孔以及排出废液的排液孔; 腔体顶部开一圆孔, 其上紧贴一块电极板和一块玻璃片(都开有圆孔)。实验中, 对腔体吸气使之内部形成负压, 外部空气通过聚焦孔对流体形成聚焦。与吹气式装置相比, 吸气式装置的主要优势有:无需透过观察窗就能直接观测流体锥形, 避免了图像失真; 通过调节精密位移台、更换毛细管及聚焦孔玻璃片, 可对诸多几何参数(管孔距离、同轴度、聚焦孔直径、毛细管直径等)进行调节。两类装置相辅相成, 为广泛开展锥-射流结构演化和液滴生成特性研究提供了实验基础。
图 2以吹气式核心装置为例展示了流动聚焦实验平台。毛细管流出的被聚焦相流体流量由外部的微量注射泵准确提供; 压缩空气由储气罐经过输气管道进入聚焦腔体; 外部电场由高压直流电源提供; 射流破碎生成的液滴由核心装置正下方的收集器接收。实验中, 射流与液滴的尺度通常为微米量级, 需通过显微镜进行观测。由于射流通常处于高频破碎的非定常状态, 普通拍摄方法很难捕捉到清晰无重影的射流破碎图像, 通常采用的拍摄方式有2种:其一, 采用高速相机在强光源下进行拍摄, 可以捕捉到完整的扰动发展及射流破碎过程, 但为达到足够快的拍摄速度, 往往会牺牲一定的图像空间分辨率; 其二, 采用普通CCD相机结合脉冲式频闪光源进行拍摄, 可获得高空间分辨率图像, 但受拍摄速度限制, 无法获取完整的射流破碎过程。值得一提的是, 采用频闪光源时, 为避免出现全部为暗场的图片, 需将频闪光源触发频率设置为相机快门速度的倍数, 例如, 当CCD相机快门速度设置为0.02 s时, 频闪光源触发频率需设置为3000, 6000或12 000 Hz等。

|
| 图 2 流动聚焦实验平台示意图 Fig.2 Sketch of the flow focusing experimental platform |
为有效控制高速、高频状态下的射流破碎, 近年来, 作者所在团队提出了基于外部激励主动控制流动聚焦的液滴生成实验方法[51], 其核心装置如图 3所示。该装置将聚焦腔体与毛细管进行了集成, 在毛细管尾端开孔并安装弹性薄膜, 以压电激振器激振薄膜, 对被聚焦相流体流量实现周期性扰动。施加扰动的频率、振幅以及波形(正弦形、方波等)均可由波形发生器和扰动放大器准确调控。与传统激振的扰动施加方式(激振连接毛细管与注射器之间的软管)[47-50]相比, 该方式不仅可避免扰动在毛细管下游的衰减, 也便于将激振器上下振荡的位移与施加于流体流量的扰动幅值进行标定。
在实验中, 发现拍摄光路对获得的图像有重大影响。对于单层界面(液-气界面), 直接以透射光照明并在核心装置另一侧进行拍摄(如图 2所示), 即可获得清晰的锥-射流界面; 而对于复合界面(液-液及液-气双层界面), 情况则复杂得多。以同轴流体锥形为例对拍摄光路进行介绍:当采用透射光拍摄时(光源与相机异侧), 光线在经过两层锥形界面时发生明显折射甚至全反射, 很难观测到清晰的内层锥形界面(图 4(a)); 当光源与相机同侧时, 入射至内层锥形界面的光线被部分反射进入相机, 可以观测到清晰的内层锥形, 但图像整体背景比较暗淡(图 4(b))。因此, 在实验中采用透射光与反射光结合的照明方式, 反射光源主要用于照亮内层锥形界面, 透射光源主要用于照亮外层锥形界面并使锥形外部背景光强分布均匀。图 4(c)展示了相应的实验结果, 表明采用该照明方式可以获得清晰的双层锥形界面轮廓。关于光路折射对拍摄图像的影响, 将在2.3节作定量分析。

|
| 图 4 不同照明方式下拍摄的同轴流体锥形 Fig.4 The images of coaxial liquid cone under different illumination conditions |
在流动聚焦中, 毛细管口形成稳定的锥形, 是在聚焦孔下游形成射流并高通量制备微液滴的前提条件。本节以同轴带电流动聚焦为例, 探讨各参数对同轴锥形形态及稳定性的影响规律。实验中, 外层流体为食用油, 内层流体为牛奶, 核心装置为吸气式结构(图 1(b)), 电压施加于锥形区域。同轴毛细管尺寸固定, 其中, 内毛细管内外径分别为D1i=0.52 mm, D1o=0.81 mm, 外毛细管内外径分别为D2i=1.10 mm, D2o=1.48 mm。
图 5展示了装置几何参数对流体锥形的影响(图 5各图从左至右, 几何参数逐渐变大)。几何参数主要通过改变聚焦孔附近驱动气体的流场来对锥形的形态及稳定性产生影响。图 5(a)展示了管孔距离H的影响, 当H较小时, 驱动气体在毛细管和聚焦孔之间具有较高的流速, 锥形会在驱动气体的轴向剪切及径向汇聚作用下呈现"内凹"; 随着H逐渐增大, 在远离聚焦孔的区域, 由于剪切作用减弱, 锥形会在表面张力作用下向外鼓起, 呈现"外凸"; 当H持续增大时, 驱动气体对同轴锥形的剪切作用越来越小, 最终因无法提供足够的驱动力而导致锥形失稳, 在管孔之间不断振荡。

|
| 图 5 结构参数对同轴流体锥形形态及稳定性的影响(流动控制参数:Qin=1mL/h, Qout=60 mL/h, Δpg=60 kPa, U=1 kV) Fig.5 Effect of geometry parameters on the profiles and instabilities of the coaxial liquid cone (the flow parameters are fixed at Qin=1 mL/h, Qout=60 mL/h, Δpg=60 kPa and U=1 kV) |
聚焦孔直径d对锥形形态的影响与H相反, 如图 5(b)所示, 随着d的增大, 驱动气体高速流动和汇聚的区域会逐渐增大并且向上游毛细管处延伸, 导致锥形逐渐由d较小时的"下部汇聚、上部凸起"的形状逐渐过渡到"整体汇聚内凹"的形状。另外, d的改变对锥形稳定性几乎没有影响, 这是由于在驱动压差一定时, 聚焦孔处气体平均流速保持不变(Δpg≈1/(2ρgvg2), 其中, vg、ρg分别表示驱动气体的平均流速和密度), 使得驱动气体对锥形的剪切作用也始终维持恒定。
图 5(c)展示了管孔之间的同轴度L对锥形的影响。可以看到, L会显著影响锥形的形态。当毛细管与聚焦孔不同轴时(L≠0), 锥形不再是对称形状; 当L增大到一定程度, 由于毛细管远离了驱动气体的高速流动区域, 锥形将无法获得足够的剪切力而呈现失稳振荡状态。
同样, 研究了流动控制参数对流体锥形的形态及稳定性的影响, 实验结果如图 6所示。

|
| 图 6 流动控制参数对同轴流体锥形形态及稳定性的影响 Fig.6 Effect of flow parameters on the profiles and instabilities of the coaxial liquid cone |
图 6(a)展示了内层流量Qin对锥形的影响。当Qin减小时, 内锥形逐渐向内收缩, 锥形顶端射流直径逐渐变细。由于Qin比外层流量Qout小很多, Qin的减小对外锥形的影响不大。当Qin小于某临界值时, 内锥形将发生失稳并处于振荡状态, 这是由于此时内层流体的动能密度(~1/(2ρinvin2), ρin、vin分别表示内层流体的密度和平均流速)无法突破界面张力而引起的势垒(~σ/Ri, σ为表面张力系数, Ri为聚焦孔处的内射流半径)所导致[19]。图 6(b)展示了外层流量Qout的影响。随着Qout的减小, 锥形顶端射流逐渐变细; 当Qout小于某临界值时, 锥形将发生失稳。
驱动压差Δpg的影响如图 6(c)所示。与流量的影响类似, 在一定内外流体流量情况下, 存在一个临界气压差Δpg, min, 当Δpg<Δpg, min时, 由于外部驱动力不足, 同轴锥形将不能保持稳定; 而在稳定锥形的情况下(Δpg>Δpg, min), 随着Δpg增大, 锥形形态不会有明显变化, 但是锥形顶端射流直径逐渐变细, 这也符合参数Δpg对射流直径dj影响的理论预测(dj~Δpg-1/4)[12]。
电压U对锥形的影响如图 6(d)所示。可以看出, 额外施加电场力对锥形的稳定性有明显促进作用, 随着电压的增加, 可使同轴锥形由失稳状态逐渐过渡至稳定状态。
结合对图 5和6的分析可以看出, 同轴锥形的形态主要受几何参数(管孔距离H、聚焦孔直径d、同轴度L)的影响, 而同轴锥形的稳定性主要受H、L和诸多控制参数(液体流量Qin和Qout)、驱动压差Δpg和电压U的共同影响。实验中, 为在较宽的流量和压差范围内获得稳定的锥形, 通常会保持管孔完全同轴(L=0)并设置几何参数H、d和外毛细管内径D2i近似相等。
2.2 流动参数对射流的影响本节将在稳定锥形的前提下研究参数对射流失稳的影响规律。实验全部采用吹气式核心装置。当锥形处于稳定状态时, 几何参数不会对聚焦孔下游射流的演化产生明显影响[53]。实验中, 主要研究流动参数对聚焦孔下游射流的影响规律。以单轴带电流动聚焦为例(对应图 1中U1=0.8 kV, U2=10 kV), 图 7给出了驱动压差Δpg变化时射流破碎及液滴生成的规律, 图中箭头方向代表Δpg逐渐增大。
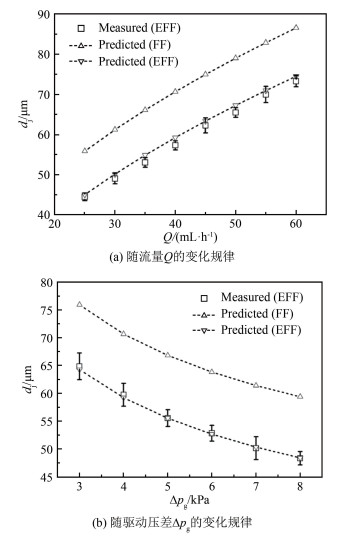
从图 7可以看到, Δpg对射流直径dj、界面扰动波长λ及生成液滴粒径均有显著影响。图 8定量给出了射流直径dj随被聚焦相流量Q及驱动压差Δpg的变化规律。
当不考虑外加电场时, 射流直径的理论预测值dFF为[12]:
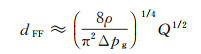 (1)
(1)
其中, ρ为液体射流密度。将理论预测值(图 8中的FF线)与实验值对比可以看出, 施加电场后, 射流直径相对于不加电场时会明显减小。参考相关研究工作[55], 可以通过修正给出带电流动聚焦中射流直径的尺度率为[54]:
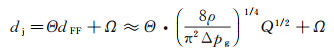 (2)
(2)
式中的Θ和Ω可通过实验结果拟合得到。根据实验结果, 选取Θ=0.96和Ω=-8.6 μm, 可以看到拟合结果(图 8中的EFF线)与实验值吻合很好。
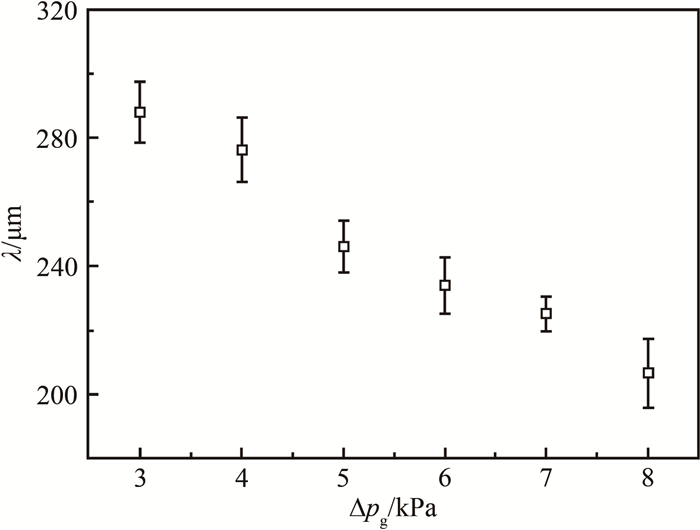
图 9给出了扰动波长λ随Δpg的变化规律。可以看出, Δpg的增大会显著减小界面扰动波长λ。扰动波长可以通过线性时间不稳定性理论进行定量分析[56-60]。
|
| 图 9 Δpg对界面扰动波长λ的影响 Fig.9 The effect of Δpg on the perturbation wavelength λ of the jet interface |
除了考虑单层射流, 还进一步研究了流动参数对同轴射流破碎的影响。由于同轴射流存在两层射流界面, 界面间的耦合对射流破碎有重要作用。耦合作用的强弱与两层界面的间距密切相关, 而界面间距则由射流的流量比rQ直接决定(rQ=Qin/(Qin+Qout)), 内外射流直径比κ定量满足[39]:κ≈ 1/2。
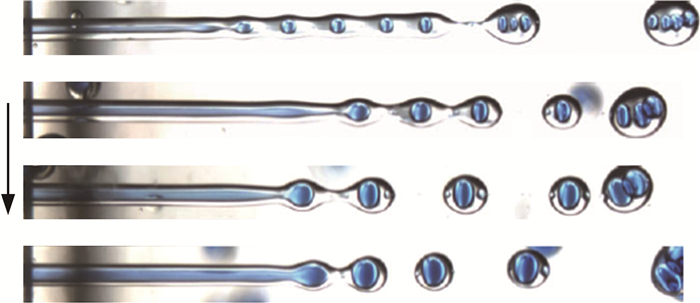
从图 10可以看出(图中箭头为rQ增大方向), 当rQ较小时, 两层射流界面近似独立地发生破碎, 此时同轴射流可近似为两条单射流进行分析; 而随着rQ增大, 两层界面的耦合作用逐渐增强, 内外射流界面同步发生破碎。rQ较小和较大时, 射流破碎的耦合可分别定义为"弱耦合"和"强耦合"状态[61]。
|
| 图 10 同轴射流在不同rQ下破碎时的界面耦合规律 Fig.10 The interface coupling of the coaxial liquid jets under different rQ |
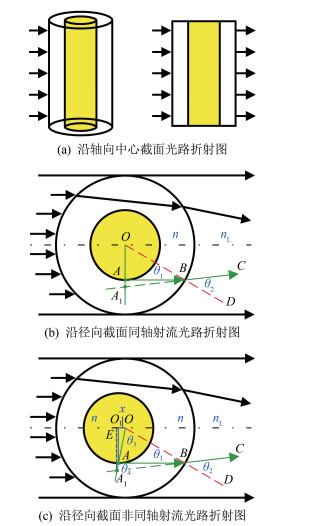
需要说明的是, 由于同轴流动聚焦存在着两层界面, 外层界面上光线折射引发的透镜效应会使观察到的内层锥形和射流界面发生失真。当平行光垂直入射至同轴射流界面时, 由于射流近似为圆柱形, 在射流轴向, 光线不会发生偏折(图 11(a)), 故观测到的内射流轴向尺度(射流长度、扰动波长等)不会发生失真; 而在射流径向, 光线因折射而向内部汇聚, 导致内射流径向尺度(射流直径、内液滴粒径等)失真。因此, 基于光路折射关系提出对射流径向透镜效应的修正方法。
|
| 图 11 平行光通过射流界面后的折射规律 Fig.11 Refraction of the parallel light after crossing the jet interfaces |
当内外射流严格同轴时, 如图 11(b)所示, O为圆心, 内界面上A点发出的光线AB经外界面折射后沿BC传播, BC的反向延长线A1即为A点的成像位置, ∠ABO和∠DBC分别以θ1和θ2表示。由光的折射定律可知:
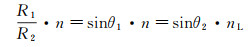 (3)
(3)
式中, n和nL分别为外射流和驱动流体折射率, R1和R2为内外射流半径, 进一步通过几何关系可以得到:
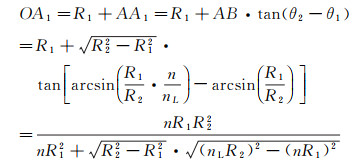 (4)
(4)
OA1和R2均可通过实验采集得到(图 11中, OA1和OA分别表示图像界面与真实界面), 代入式(4), 即可得到实际的内射流半径R1。进一步考虑两种特殊情况:第一种情况是外射流和驱动流体折射率完全一致(n=nL), 此时根据式(4)可得OA1=R1, 即观察到的内射流半径即为实际值; 第二种情况是R2≫R1, 可得OA1=n/nL×R1, 此式通常用于粗略估计内射流半径。
值得一提的是, 在某些制备特殊结构微纳胶囊的流动聚焦实验中[9-11], 内外射流往往处于非同轴的情况(图 11(c)), 这就使透镜效应修正变得较为复杂。这里仅讨论假设内外射流折射率相同的情况, 此假设对于常规的由水和硅油两相组成的同轴射流近似成立(折射率:水1.33, 硅油约1.40)。在图 11(c)中, 内外射流的圆心分别为O1和O, 偏心度O1O=x; BC与AO反向延长线的交点A1为内界面上点A的成像位置, 通过A1向OO1作一垂线并与其交于E; ∠ABO、∠DBC、∠AOB和∠OA1B分别以θ1, θ2, θ3和θ4表示。由折射定律和几何关系可得:
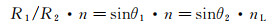 (5)
(5)
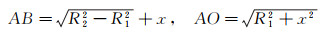 (6)
(6)
结合正弦定理:
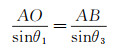 (7)
(7)
可进一步得到:
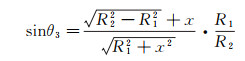 (8)
(8)
再通过相似三角形关系:
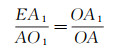 (9)
(9)
最终得到透镜效应修正公式为:
 (10)
(10)
式中, EA1和R2均可通过实验测量获得, 内外射流的偏心度x则可以根据聚焦孔上游复合毛细管的几何结构近似得出, 代入以上公式就可得到实际的内射流半径R1。
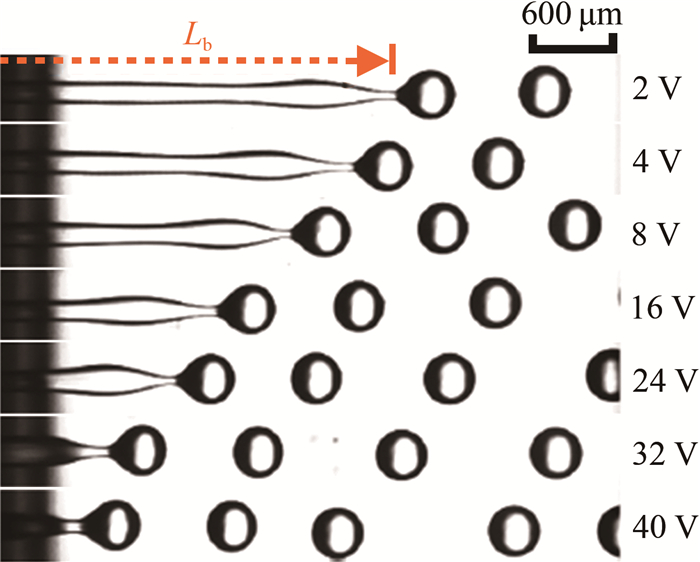
2.4 外部激励对射流破碎的影响最后, 对外部激励作用下的射流破碎开展讨论。实验中, 被聚焦相和聚焦相流体均选择为液体, 流量分别为Q1和Q2。从图 12可以看出, 施加外部激励可以大大提高生成液滴粒径的均匀性并抑制卫星液滴的出现。
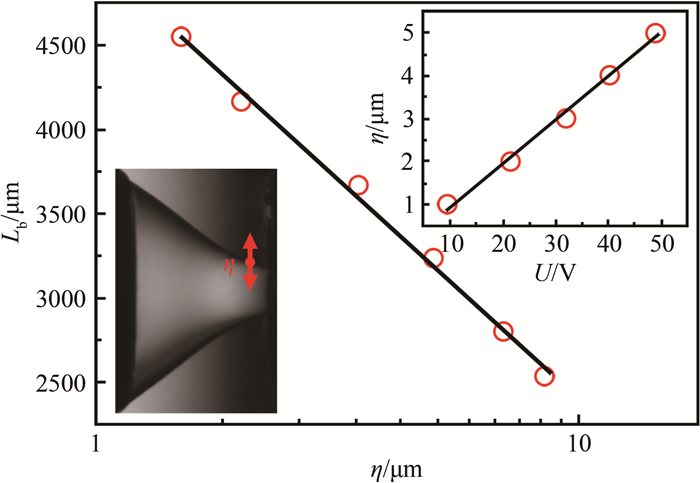
通过调整激励电压U, 还可以对射流破碎长度Lb进行调控。图 13定量给出了Lb随上游锥形在聚焦孔处界面的脉动振幅η的变化规律, η直接反映了电压U的大小, 二者近似呈线性关系(如图 13中的小图所示)。锥形在聚焦孔处的脉动振幅η可视为射流的初始扰动振幅, 该扰动随着射流向下游的发展而不断放大, 并最终引发射流破碎。
根据线性不稳定性理论[56], 射流破碎时间tb与初始扰动振幅η满足关系式β·tb=ln(R/η), 其中β为扰动增长率, R为射流半径。推导可得射流长度的理论预测值为:
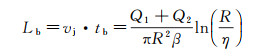 (11)
(11)
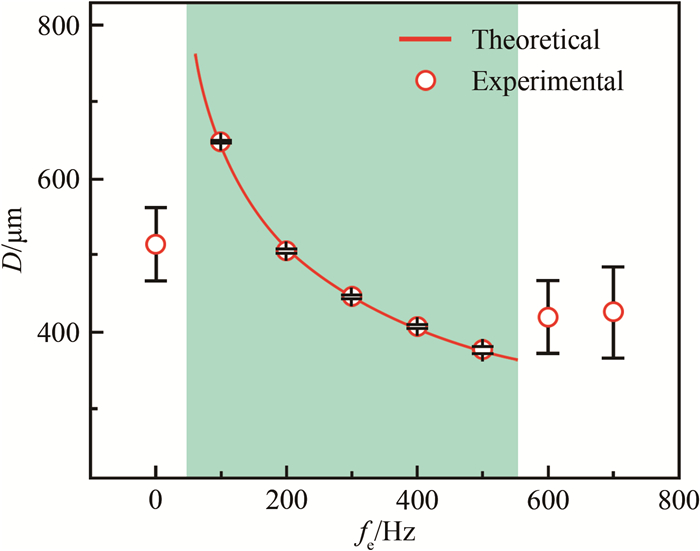
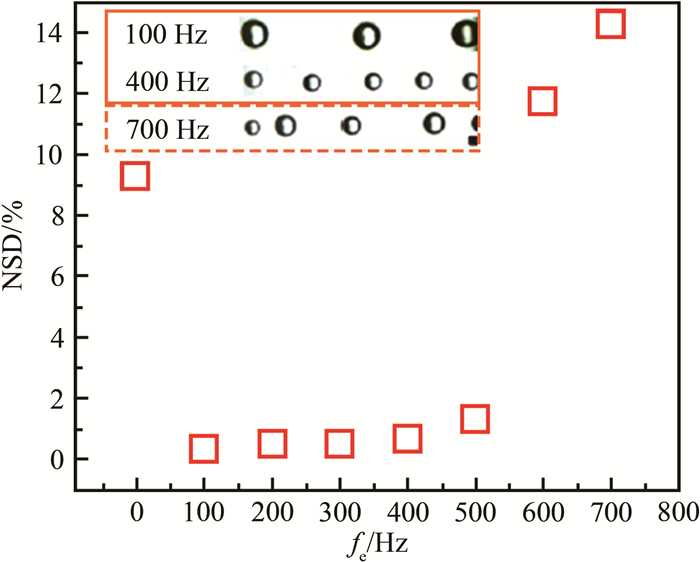
式中, vj为射流平均速度。可以看出, Lb与-lnη近似成正比, 与图 13的实验结果反映的关系完全一致。图 14进一步展示了生成液滴粒径D随激励频率fe的变化规律, 可以看出, 在涵盖射流自由破碎固有频率(约200 Hz)的一定频率范围内(约50~550 Hz), 与外部激励同步, 射流破碎生成粒径均匀的液滴(液滴粒径标准差NSD如图 15所示), 改变激励频率还可对液滴粒径和生成频率进行主动控制(如图 15中的小图所示); 而在该频率范围以外, 外部激励不再对生成液滴的粒径和单分散性产生明显影响。
3 结论本文回顾了毛细流动聚焦的实验方法, 介绍了实验平台及图像采集方法, 探讨了各参数对流动聚焦初期流体锥形收缩与后期射流失稳破碎的影响规律, 主要结论如下:
(1) 流动聚焦核心装置包括吸气式和吹气式两种。吸气式装置主要用于直接观测流体锥形的收缩, 而吹气式装置主要用于观测和研究射流失稳。
(2) 采用高速摄影或频闪摄影技术可以分别获得高时间分辨率和高空间分辨率的锥-射流运动图像。对于同轴界面, 采取透射光与反射光结合的方式可以拍摄得到清晰的内外两层界面。
(3) 装置的几何参数和流动控制参数对流体锥形的形态及不稳定性具有重要影响。在稳定锥形的情况下, 流动参数还将对射流直径、扰动波长以及复合射流的界面耦合产生影响。对于同轴射流, 外界面的透镜效应会引发内界面变形失真, 基于光的折射定律可对透镜效应进行修正。
(4) 在流动聚焦核心装置上施加外部激励可对射流的破碎进行主动调控。射流长度将随激励振幅的增大而减小, 且射流可在一定频率范围内破碎生成均匀粒径的液滴。
| [1] |
GAÑÁN-CALVO A M, MONTANERO J M, MARTÍN-BANDERAS L, et al. Building functional materials for health care and pharmacy from microfluidic principles and flow focusing[J]. Advanced Drug Delivery Reviews, 2013, 65(11-12): 1447-1469. DOI:10.1016/j.addr.2013.08.003 |
| [2] |
BARRERO A, LOSCERTALES I G. Micro-and nanoparticles via capillary flows[J]. Annual Review of Fluid Mechanics, 2007, 39: 89-106. DOI:10.1146/annurev.fluid.39.050905.110245 |
| [3] |
MONTANERO J M, GAÑÁN-CALVO A M. Dripping, jetting and tip streaming[R]. arXiv: 1909.02073.2019.
|
| [4] |
司廷, 李广滨, 尹协振. 流动聚焦及射流不稳定性[J]. 力学进展, 2017, 47: 201706. SI T, LI G B, YIN X Z. Flow focusing and jet instability[J]. Advances in Mechanics, 2017, 47: 201706. DOI:10.6052/1000-0992-16-026 |
| [5] |
司廷.流动聚焦的实验和理论研究[D].合肥: 中国科学技术大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10358-2009110996.htm
|
| [6] |
李广滨.复合流动聚焦的实验和理论研究[D].合肥: 中国科学技术大学, 2016. http://d.wanfangdata.com.cn/Thesis/Y3021236
|
| [7] |
穆恺.液驱流动聚焦中界面失稳及耦合研究[D].合肥: 中国科学技术大学, 2018. https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CDFD&dbname=CDFD&filename=1018096839.nh
|
| [8] |
SI T, FENG H X, LUO X S, et al. Formation of steady compound cone-jet modes and multilayered droplets in a tri-axial capillary flow focusing device[J]. Microfluid and Nanofluidics, 2015, 18: 967-977. DOI:10.1007/s10404-014-1486-8 |
| [9] |
SI T, YIN C S, GAO P, et al. Steady cone-jet mode in compound-fluidic electro-flow focusing for fabricating multicompart-ment microcapsules[J]. Applied Physics Letters, 2016, 108: 021601. DOI:10.1063/1.4939632 |
| [10] |
WU Q, YANG C Y, LIU G L, et al. Multiplex coaxial flow focusing for producing multicompartment janus microcapsules with tunable material compositions and structural characteristics[J]. Lab on a Chip, 2017, 17(18): 3168-3175. DOI:10.1039/C7LC00769H |
| [11] |
WU Q, YANG C Y, YANG J X, et al. Photopolymerization of complex emulsions with irregular shapes fabricated by multiplex coaxial flow focusing[J]. Applied Physics Letters, 2018, 112(7): 071601. DOI:10.1063/1.5018207 |
| [12] |
GAÑÁN-CALVO A M. Generation of steady liquid microthreads and micron-sized monodisperse sprays in gas streams[J]. Physical Review Letters, 1998, 80(2): 285. DOI:10.1103/PhysRevLett.80.285 |
| [13] |
ROSELL-LLOMPART J, GAÑÁN-CALVO A M. Turbulence in pneumatic flow focusing and flow blurring regimes[J]. Physical Review E, 2008, 77(2): 036321. |
| [14] |
HERRADA M A, GAÑÁN-CALVO A M, OJEDA-MONGE A, et al. Liquid flow focused by a gas:jetting, dripping, and recirculation[J]. Physical Review E, 2008, 78(2): 036323. |
| [15] |
GAÑÁN-CALVO A M, BARRERO A. A novel pneumatic technique to generate steady capillary microjets[J]. Journal of Aerosol Science, 1999, 30(1): 117-125. DOI:10.1016/S0021-8502(98)00029-9 |
| [16] |
SI T, LI F, YIN X Y, et al. Modes in flow focusing and instability of coaxial liquid-gas jets[J]. Journal of Fluid Mechanics, 2009, 629: 1-23. DOI:10.1017/S0022112009006211 |
| [17] |
SI T, LI F, YIN X Y, et al. Spatial instability of coflowing liquid-gas jets in capillary flow focusing[J]. Physics of Fluids, 2010, 22(11): 112105. DOI:10.1063/1.3490066 |
| [18] |
VEGA E J, MONTANERO J M, HERRADA M A, et al. Global and local instability of flow focusing:The influence of the geometry[J]. Physics of Fluids, 2010, 22: 064105. DOI:10.1063/1.3450321 |
| [19] |
GAÑÁN-CALVO A M, MONTANERO J M. Revision of capillary cone-jet physics:electrospray and flow focusing[J]. Physical Review E, 2009, 79(2): 066305. |
| [20] |
GAÑÁN-CALVO A M, GORDILLO J M. Perfectly monodisperse microbubbling by capillary flow focusing[J]. Physical Review Letters, 2002, 87(1): 274501. |
| [21] |
GAÑÁN-CALVO A M. Perfectly monodisperse microbubbling by capillary flow focusing:An alternate physical description and universal scaling[J]. Physical Review E, 2004, 69(2): 027301. DOI:10.1103/PhysRevE.69.027301 |
| [22] |
GAÑÁN-CALVO A M, RIESCO-CHUECA P. Jetting-dripping transition of a liquid jet in a lower viscosity co-flowing immiscible liquid:the minimum flow rate in flow focusing[J]. Journal of Fluid Mechanics, 2006, 553: 75-84. DOI:10.1017/S0022112006009013 |
| [23] |
MU K, DING H, SI T. Instability analysis of the cone-jet flow in liquid-driven flow focusing[J]. Microfluidics and Nanofluidics, 2018, 22(12): 138. DOI:10.1007/s10404-018-2158-x |
| [24] |
MU K, SI T, DING H. Nonlinear dynamics and manipulation of dripping in capillary flow focusing[J]. Science China Physics, Mechanics and Astronomy, 2019, 62(12): 124713. DOI:10.1007/s11433-019-9444-8 |
| [25] |
ANNA S L, BONTOUX N, STONE H A. Formation of diepersions using "flow-focusing" in microchannels[J]. Applied Physics Letters, 2003, 82(3): 364-366. DOI:10.1063/1.1537519 |
| [26] |
刘赵淼, 杨洋. 几何构型对流动聚焦生成微液滴的影响[J]. 力学学报, 2016, 48(4): 867-876. LIU Z M, YANG Y. Influence of geometry configurations on the microdroplets in flow focusing microfluidics[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(4): 867-876. |
| [27] |
ZHU P A, KONG T T, KANG Z X, et al. Tip-multi-breaking in capillary microfluidic devices[J]. Scientific Reports, 2015, 5: 11102. DOI:10.1038/srep11102 |
| [28] |
CORDERO M L, GALLAIRE F, BAROUD C N. Quantitative analysis of the dripping and jetting regimes in co-flowing capillary jets[J]. Physics of Fluids, 2010, 23(9): 094111. |
| [29] |
李战华, 郑旭. 微纳米尺度流动实验研究的问题与进展[J]. 实验流体力学, 2014, 28(3): 1-11. LI Z H, ZHENG X. The problems and progress in the experimental study of micro/nano-scaleflow[J]. Journal of Experiments in Fluid Mechnics, 2014, 28(3): 1-11. |
| [30] |
ZHU P A, WANG L Q. Passive and active droplet generation with microfluidics:a review[J]. Lab on a Chip, 2016, 17(1): 34-75. |
| [31] |
ANNA S L. Droplets and bubbles in microfluidic devices[J]. Annual Review of Fluid Mechanics, 2016, 48(1): 285-309. DOI:10.1146/annurev-fluid-122414-034425 |
| [32] |
陈晓东, 胡国庆. 微流控器件中的多相流动[J]. 力学进展, 2015, 45: 201503. CHEN X D, HU G Q. Multiphase flow in microfluidic devices[J]. Advances in Mechanics, 2015, 45: 201503. DOI:10.6052/1000-0992-14-063 |
| [33] |
刘赵淼, 杨洋, 杜宇, 等. 微流控液滴技术及其应用的研究进展[J]. 分析化学, 2017, 45(2): 282-296. LIU Z M, YANG Y, DU Y, et al. Advances in droplet-based microfluidics technology and its applications[J]. Chinese Journal of Analytical Chemistry, 2017, 45(2): 282-296. |
| [34] |
杨超宇, 吴强, 徐晓嵘, 等. 制备复合液滴的微尺度流动方法[J]. 气体物理, 2018, 3(4): 13-23. YANG C Y, WU Q, XU R X, et al. Advacens on microfluidic methods for producing compound droplets[J]. Physics of gases, 2018, 3(4): 13-23. |
| [35] |
MARTÍN-BANDERAS L, FLORES-MOSQUERA M, RIESCO-CHUECA P. Flow focusing:a versatile technology to produce size-controlled and specific morphology microparticles[J]. Small, 2005, 1(7): 688-692. DOI:10.1002/smll.200500087 |
| [36] |
MARTIN-BANDERAS L, Rodríguez-Gil A, CEBOLLA A, et al. Towards high-throughput production of uniformly encoded microparticles[J]. Advanced Materials, 2006, 18(5): 559-564. DOI:10.1002/adma.200501976 |
| [37] |
GAÑÁN-CALVO A M, GONZÁLEZ-PRIETO R, RIESCO-CHUECA P, et al. Focusing capillary jets close to the continuum limit[J]. Nature Physics, 2007, 3(10): 737-742. DOI:10.1038/nphys710 |
| [38] |
HERRADA M A, MONTANERO J M, FERRERA C, et al. Analysis of the dripping-jetting transition in compound capillary jets[J]. Journal of Fluid Mechanics, 2010, 649: 523-536. DOI:10.1017/S0022112010000443 |
| [39] |
MU K, DING H, SI T. Experimental and numerical investigations on interface coupling of coaxial liquid jets in co-flow-focusing[J]. Physics of Fluid, 2020, 32(4): 042103. DOI:10.1063/5.0002102 |
| [40] |
UTADA A S, LORENCEAU E, LINK D R, et al. Monodisperse double emulsions generated from a microcapillary device[J]. Science, 2005, 308(5721): 537-541. DOI:10.1126/science.1109164 |
| [41] |
NIE Z H, XU S Q, SEO M S, et al. Polymer particles with various shapes and morphologies produced in continuous microfluidic reactors[J]. Journal of the American Chemical Society, 2005, 127(22): 8058-8063. DOI:10.1021/ja042494w |
| [42] |
PANG Y, DU Y, WANG J, et al. Generation of single/double Janus emulsion droplets in co-flowing microtube[J]. International Journal of Multiphase Flow, 2019, 113: 199-207. DOI:10.1016/j.ijmultiphaseflow.2019.01.011 |
| [43] |
SI T, LI G B, WU Q, et al. Optical droplet vaporization of nanoparticle-loaded stimuli-responsive microbubbles[J]. Applied Physics Letters, 2016, 108(12): 111109. |
| [44] |
ZHU Z Q, SI T, XU R X. Microencapsulation of indocyanine green for potential applications in image-guided drug delivery[J]. Lab on a Chip, 2015, 15(3): 646-649. |
| [45] |
XU J S, YUAN S, TIAN J L, et al. Ultrasound mediated delivery of oxygen and lll12 loaded stimuli responsive microdroplets for the treatment of hypoxic cancer cells[J]. Scientific Reports, 2017, 7: 44908. DOI:10.1038/srep44908 |
| [46] |
ZHU Z Q, WU Q, HAN S Y, et al. Rapid production of single-and multi-compartment polymeric microcapsules in a facile 3D microfluidic process for magnetic separation and synergistic delivery[J]. Sensor and Actuator B:Chemical, 2018, 275: 190-198. DOI:10.1016/j.snb.2018.08.044 |
| [47] |
ZHU P A, TANG X, WANG L Q. Droplet generation in co-flow microfluidic channels with vibration[J]. Microfluidics and Nanofluidics, 2016, 20(3): 47. DOI:10.1007/s10404-016-1717-2 |
| [48] |
SAURET A, SHUM H C. Forced generation of simple and double emulsions in all-aqueous systems[J]. Applied Physics Letters, 2012, 100(15): 154106. DOI:10.1063/1.3702434 |
| [49] |
SAURET A, SPANDAGOS C, SHUM H C. Fluctuation-induced dynamics of multiphase liquid jets with ultra-low interfacial tension[J]. Lab on a Chip, 2012, 12(18): 3380-3386. DOI:10.1039/c2lc40524e |
| [50] |
SHUM H C, VARNELL J, WEITZ D A. Microfluidic fabrication of water-in-water (w/w) jets and emulsions[J]. Biomicrofluidic, 2012, 6(1): 012808. DOI:10.1063/1.3670365 |
| [51] |
YANG C Y, QIAO R, MU K, et al. Manipulation of jet breakup length and droplet size in axisymmetric flow focusing upon actuation[J]. Physics of Fluids, 2019, 31(9): 091702. DOI:10.1063/1.5122761 |
| [52] |
MU K, SI T, LI E Q, et al. Numerical study on droplet generation in axisymmetric flow focusing upon actuation[J]. Physics of Fluids, 2018, 30: 012111. DOI:10.1063/1.5009601 |
| [53] |
MONTANERO J M, REBOLLO-MUÑOZ N, HERRADA M A, et al. Global stability of the focusing effect of fluid jet flows[J]. Physical Review E, 2011, 83(2): 036309. |
| [54] |
LI G B, LUO X S, SI T, et al. Temporal instability of coflowing liquid-gas jets under an electric field[J]. Physics of Fluids, 2014, 26(5): 054101. DOI:10.1063/1.4875109 |
| [55] |
GAÑÁN-CALVO A M, LÓPEZ-HERRERA J M, RIESCO-CHUECA P. The combination of electrospray and flow focusing[J]. Journal of Fluid Mechanics, 2006, 566: 421-445. DOI:10.1017/S0022112006002102 |
| [56] |
EGGERS J, VILLERMAUX E. Physics of liquid jets[J]. Reports on Progress in Physics, 2008, 71(3): 036601. DOI:10.1088/0034-4885/71/3/036601 |
| [57] |
LIN S P, REITZ R D. Drop and spray formation from a liquid jet[J]. Annual Review of Fluid Mechanics, 1998, 30(1): 85-105. DOI:10.1146/annurev.fluid.30.1.85 |
| [58] |
LIN S P. Breakup of liquid sheets and jets[M]. Cambridge: Cambridge University Press, 2003.
|
| [59] |
LASHERAS J C, HOPFINGER E J. Liquid jet instability and atomization in a coaxial gas stream[J]. Annual Review of Fluid Mechanics, 2000, 32: 275-308. DOI:10.1146/annurev.fluid.32.1.275 |
| [60] |
李帅兵, 司廷. 射流破碎的不稳定性分析方法[J]. 空气动力学学报, 2019, 37(3): 356-372. LI S B, SI T. Advances on linear instability analysis method of jet breakup[J]. Acta Aerodynamica Sinica, 2019, 37(3): 356-372. DOI:10.7638/kqdlxxb-2018.0153 |
| [61] |
司廷, 李广滨, 罗喜胜, 等. 同轴流动聚焦中射流不稳定性研究[J]. 气体物理, 2017, 2(1): 30-38. SI T, LI G B, LUO X S, et al. Theoretical investigation on flow instability of liquid jets in co-flow focusing[J]. Physics of Gases, 2017, 2(1): 30-38. |