随着检测器件微型化和集成化的发展以及多学科交叉研究的需求, 能够在微米尺度上对微小体积流体实现精准操控的微流控技术(Microfluidics)应运而生, 并快速发展起来。相对于传统宏观尺度的操控方法, 微流控技术可以将生化实验室功能集成到一个数厘米尺寸的芯片上, 具有低消耗、低成本、高通量、高效率等优点[1], 软光刻加工技术的简易化和高速流动显示设备的普及化更是进一步推动了其在各个相关领域的推广和应用。目前, 微流控技术已经在生物制药、医学介导治疗、化妆品乳化制备、微尺度相变换热、材料合成等领域的科学研究和工程应用中发挥出难以替代的作用[2-4]。
液滴是微流控系统中的一种重要载体, 通过将目标试剂离散到连续相液体中以实现对微小体积液体的包裹, 液滴界面的密封作用从理论上避免了各个单元之间的互相干扰, 从而得到了大量可操控的独立单元。此外, 液滴体系的比表面积得到增大, 在传质传热等方面表现出显著优势[5-8]。微流控液滴制备法不仅可以提供传统乳化法难以达到的单分散性, 基于微流控系统中过程参数的调节, 还可以实现对液滴自身形貌、尺寸、结构等性能指标以及液滴移动、融合、分裂、捕获、混合等行为的精准控制[3-4]。上述液滴多相流动的诸多优点与可变形的相界面密不可分, 而相界面的存在也将非线性动力学特性引入流动系统, 使得多相流动的相关物理机制更加复杂[9-11]。因此, 结合相界面的形变规律, 分析液滴多相流中的界面受力变化, 是深入认识复杂多相流动背后主导物理机制的有效途径, 也是微流控芯片中各个功能模块能够精准实现和系统集成的基础。对于液滴多相流动现象, 通道壁面起到的作用往往也需要被考虑进来, 当液滴运动受到通道壁面所形成空间的限制时, 液滴的界面变形以及液体与固壁之间的动态浸润效应依赖于通道结构参数和液体流动条件, 并对液滴运动行为产生直接影响[12-14]。
以粒子分选运动为代表的惯性微流控是微流控技术的另一个重要研究内容。由于粒子和循环肿瘤细胞具有相似的球形结构, 其运动行为和受力状况也类似, 二者的操控规律具有相互借鉴意义[15-17]。相对于细胞分选研究, 粒子分选无需细胞培养等前期步骤, 方便获取材料以及定量控制粒径、形状、密度等变量, 可以从更大的参数范围内探究靶向目标的高效分选方法[18]。作为微流控细胞分选研究的一种重要手段, 粒子分选已经逐渐发展成为继流式细胞分选、免疫磁珠分选之后的新一代被动式物理分选技术。此外, 虽然粒子惯性迁移所对应的流动仍然处于层流范围(Re<2300), 然而惯性力的作用已经无法被忽略, 粒子最终达到的平衡状态也受到通道结构和流动条件等系统参数的耦合影响[19]。深入研究粒子惯性迁移的相关运动行为并建立不同条件下的受力模型, 有助于进一步丰富微尺度下复杂流体的流动机制, 为细胞分选和肿瘤疾病早期诊断等应用提供更加详实的理论基础。
本文将对课题组近期在微尺度多相流动方面的研究进行综述, 主要包括微通道中的液滴运动特性和微凹槽内的粒子分选运动特性2个方面。
1 微通道中的液滴运动特性对于尺寸与通道特征长度相近的液滴, 通道结构的变化直接影响液滴在微通道中的运动行为[20]。在常用的微通道系统中, 分岔结构和交汇结构是组成通道网络的基本单元, 因此, 本节先分别对具有典型结构变化的分岔处和交汇处的液滴运动特性进行分析, 再对通道网络中的液滴运动特性进行研究。
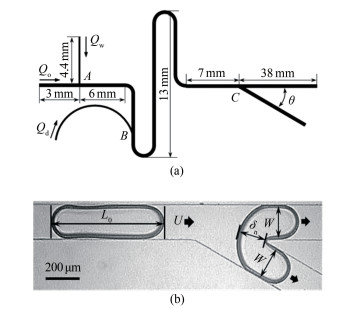
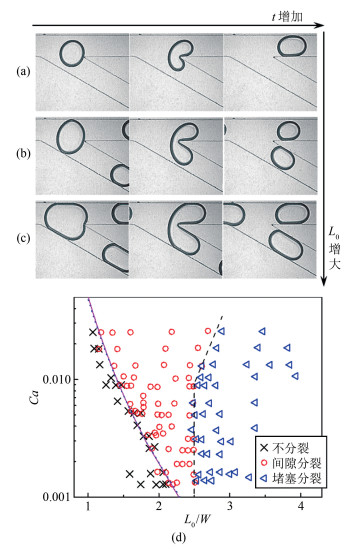
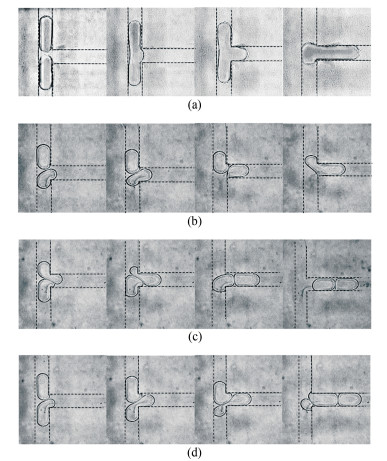
1.1 分岔结构处的液滴运动特性对于一个支路与主通道夹角为θ的分岔结构(如图 1(a)所示), 液滴从左侧流入, 在分岔处C点形成2个新的前端界面并逐渐被拉伸(图 1(b)), 液滴界面的变形程度增加使得液滴处于不稳定状态。为降低因变形而增加的界面能, 液滴会保持完整流入某一支路或分裂成子液滴并分别流入2个支路, 以达到更加稳定的状态。以θ=30°为例, 在相同的流速下, 随着液滴初始长度L0的增加, 液滴在分岔处的运动行为呈现从不分裂(图 2(a))到分裂的转变; 根据分裂过程中液滴与通道侧壁面之间是否存在间隙, 又可将液滴分裂细分成间隙分裂(Breakup with gaps)和堵塞分裂(Breakup with obstruction)2种模式, 分别如图 2 (b)和(c)所示。以无量纲液滴长度L0/W(W为通道宽度)和毛细数Ca(Ca=μcUd/γ, 式中μc为连续相的黏度, Ud为液滴运动速度, γ为液液两相间的界面张力系数)为坐标轴建立如图 2(d)所示的运动行为分布图, 液滴的3种行为模式各自分布在明显不同的区域[21]。值得一提的是, 液滴在不对称分岔结构中的行为模式分布特性与对称分岔结构中的结果非常相似, 下面就行为模式的转变条件进行对比分析。
Link等[23]最早在对称T形分岔通道的研究中提出了受限液滴分裂的临界条件:当液滴长度延伸到大于其截面周长时, 液滴会在Rayleigh-Plateau不稳定性的作用下发生分裂。此后, Leshansky等[24]进一步考虑了液滴与通道之间的间隙流动, 重新提出一种分裂临界毛细数与无量纲液滴长度的关系式:L0/W =χCa-0.21, 其中, χ为无量纲的比例系数。在此基础上, Fu等[25]和Chen等[26]发现当微流动系统的参数范围扩大时, 更加一般化的关系式L0/W=κCaζ能更好地实现对分裂临界的预测, 其中, κ和ζ均为无量纲的比例系数。利用上述2种幂函数表达式对实验结果进行拟合, 分别如图 2(d)中的实线和点线所示, 可以发现2种函数表达式都和文献的实验所划分的液滴分裂临界条件比较吻合。该结果表明离散化单元(包括液滴和气泡)的分裂具有比较相似的内在规律, 且现有用于预测分裂的理论不仅适用于对称结构, 也同样适用于不对称的分岔结构, 而不同研究中拟合参数的差异可能与通道的结构尺寸和流体的物性参数有关[27]。对于图 2实验中选用的"去离子水-葵花籽油"的流体系统, 拟合得到的系数分别为:χ=0.5350, κ=0.5216, ζ=-0.2146。
如图 2(d)中虚线所示, 可以发现液滴分裂时堵塞的临界条件包含2个阶段:当毛细数Ca < 0.010时, 堵塞分裂的临界条件是不受毛细数影响的固定液滴长度, 维持在L0/W≈2.5;当Ca>0.010时, 临界液滴长度随着毛细数的增大而增大。作为对比, Jullien等[28]针对对称T形结构得到的临界液滴长度在其研究的毛细数范围内都固定不变, 并且指出液滴在分裂过程中是否堵塞侧壁面实质上是一个几何限制条件, 当液滴长度足够长时, 液滴在延伸过程中就可以始终接触通道侧壁面而不出现间隙; 然而能够实现堵塞分裂的具体临界值还受到两相黏度比和通道宽度比的影响[26, 28]。不对称分岔结构中不同的堵塞临界条件源于两支路中的流动差异, 当毛细数较小时, 两支路的流动差异还不明显, 因此堵塞的临界条件同对称分裂的规律相似, 也是一个不随毛细数变化的临界液滴长度。但是随着毛细数的增加, 支路中存留子液滴的流阻差别增加, 两支路的流动差异加剧[29-30], 导致液滴在分流较少的一侧容易出现间隙, 最终呈现出临界液滴长度逐渐增加的现象。
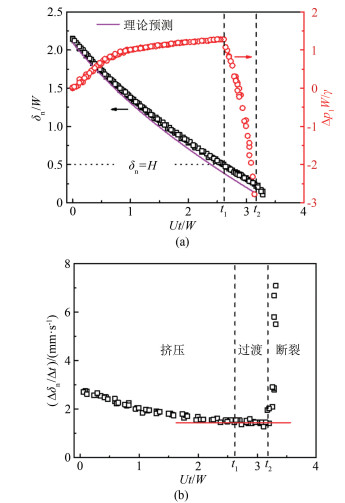
液滴的分裂过程也是液滴颈部在分岔处的断裂过程, 因此液滴颈部的形变过程可以反映分裂的动力学特性。如图 1(b)所示, 将液滴尾部界面与分岔点之间的最短距离定义为液滴颈部宽度δn。对于微通道中的液滴断裂过程, 液滴主要受到3个力:沿程压差力、黏性剪切应力和界面张力(毛细压差力)。其中, 界面张力是阻碍液滴变形的作用力。为了反映液滴颈缩过程的受力变化, 借助杨-拉普拉斯(Young-Laplace)公式计算液滴前后界面的毛细压差, Δp=γ(1/R1+1/R2), 其中, R1、R2为液滴界面在水平和竖直2个方向的曲率半径。由于毛细压差的计算公式在静止条件下才严格成立, 因此, 下文的毛细压差计算仅考虑较低毛细数的流动条件。图 3(a)中右侧所示为上支路的毛细压差Δp1, 通过γ/W进行了无量纲化[31]。
对于堵塞分裂模式(图 2(c)), 无量纲液滴颈部宽度δn/W在无量纲断裂周期Ut/W(液滴从全部流入分岔结构到刚刚断开定义为1个断裂周期, t=0为液滴完全流入分岔结构的时刻, U=Q/(WH)为主通道内的平均流速, Q为主通道内的体积流量, H为通道深度)内的变化过程如图 3(a)所示(对应的流动条件为:Ca=6.4×10-3, L0/W=3.4)。根据液滴颈缩速度Δδn/Δt的变化规律可以将分裂过程划分成3个阶段:挤压阶段、过渡阶段和断裂阶段, 如图 3(b)所示。在挤压阶段, 通道内的绝大部分流通面积被液滴堵塞, 仅留下矩形截面与液滴界面形成的边角可流过连续相(低毛细数下, 液膜厚度远小于边角尺寸, 流过液膜的连续相可以被忽略[12]), 使得液滴上游的压力逐渐积累, 而边角流对液滴界面施加的黏性剪切应力相对较小, 此时液滴上下游的沿程压差力是驱动液滴移动和颈缩的主导作用力, 并且可以通过液滴前后端毛细压差之和来估算得到(图 3(a))。另外, 颈缩速度逐渐减慢, 原因是持续增加的界面张力阻碍液滴变形。当颈部宽度等于通道高度(δn=H)时, 液滴前后端的压差达到最大值; 此后, 液滴尾部界面的毛细压差随着颈部宽度的减小而快速增大, 导致液滴前后端的毛细压差之和急剧下降。过渡阶段的典型特点是液滴颈部不再接触通道上下壁面, 而是在空间上呈三维方式减小, 此时的颈缩速度也基本保持稳定不变(如图 3(b)中红线所示)。当液滴尾部界面由向外凸扩转变为向内凹陷时, 界面张力诱发液滴的快速断裂, 最大颈缩速度达到前两个阶段的2倍以上。结合液滴前后端的毛细压差变化规律, 颈部断裂发生在压差为负值的范围, 因此连续相会在反向压差力的驱动下回流, 从而触发液滴颈部的快速断裂[31]。
对于间隙分裂模式(图 2(b)), 由于连续相流动不能一直被液滴堵塞, 从间隙流过的连续相起到的作用不能再被忽略, 导致沿程压差力、黏性剪切应力和界面张力在液滴分裂过程中的影响比重发生变化。在液滴流入分岔处的初始阶段, 液滴与通道侧壁面的间隙还没有打开, 此时的运动特性与堵塞模式下接近。随着液滴向支路下游延伸, 液滴与侧壁面的间隙逐渐变宽, 更大比例的连续相从液滴两旁流过。液滴前后端的压差和间隙中连续相施加的黏性剪切应力与间隙宽度Wgutter的比例关系分别为Δp~(Wgutter)-3, τ ~ (Wgutter)-2, 可知压差力和黏性剪切应力都随着间隙宽度增加而减小[32]。另一方面, 液滴变形导致阻碍运动的界面张力增加, 液滴颈缩速度逐渐减小。液滴长度和毛细数都和间隙流动直接相关, 因此会对颈缩过程产生明显影响。而在堵塞模式下, 液滴长度和毛细数的影响几乎可以被忽略, 液滴颈缩过程仅依赖于通道分岔处的几何结构参数[22]。
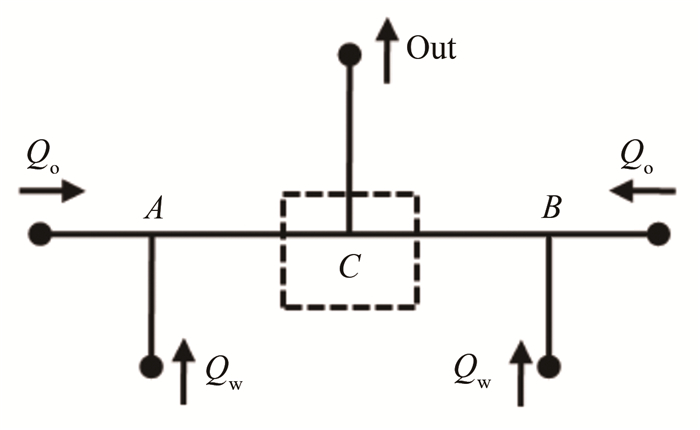
1.2 交汇结构处的液滴运动特性为了研究液滴的碰撞特性, 采用如图 4所示的微通道交汇结构, 利用T形通道实现液滴生成以及尺寸调节。为了实现等大小液滴碰撞, 2个T形通道的尺寸和流动条件在实验中都保持相同。在通道的引导下, 一对液滴在通道交汇处相遇并表现出4种不同的运动行为:直接融合、滑动后融合、不融合和分裂, 分别如图 5(a)~(d)所示。对于直接融合, 两液滴几乎不发生可观察到的形变, 液滴的接触位置处快速形成液桥, 然后瞬间融合; 由于T形通道结构的限制, 融合后的液滴也变形为T形(图 5(a))。实验发现只有当两相流量较低时, 直接融合才能发生。相比而言, 液滴间融合多为滑动后融合这种形式(图 5(b)), 上游的两液滴在交汇处相遇, 液滴间接触面积随着流动逐渐增大, 而两液滴间的连续相液膜阻碍融合发生。根据液膜排液理论, 当液滴间液膜的最小厚度降低到分子间作用力主导的范围时, 范德华吸引力会诱导液膜的破裂[33-34]。由于液膜厚度还未达到失稳临界, 液滴相互滑动且界面形变明显; 因受到挤压, 位于前面的液滴先进入交汇处的下游通道, 液膜厚度随排液过程持续减小直至液滴融合。
当两相流量增大时, 液滴运动速度加快导致其在交汇处的停留时间变短, 如果液膜排液过程不能完成, 融合就不会发生, 两液滴前后相连进入下游通道(图 5(c))。当液滴长度比较大时, 两液滴会因滑动过程中的相互挤压而发生分裂, 位于前面的液滴在滑动过程中被拉长, 并在界面形变达到一定临界值后分裂成两段(图 5(d))[35]。
液滴挤压过程中, 液膜中的毛细压力驱动液体排出, 而碰撞速度和连续相液体黏度等参数决定的黏性力阻碍排液, 因此表征毛细压力和黏性力相对大小的毛细数可以用来衡量排液结果[38]。实验发现液滴融合存在临界毛细数, 且通道交汇处结构和两相液体黏度比都会影响临界值的大小[36-37], 临界毛细数与黏度比的幂函数关系Ca*~λμ-0.75也与Wang等[39]得到的结果相吻合。对于交汇碰撞的微液滴来说, 融合临界毛细数大都低于0.02, 表明低速碰撞有利于液滴融合。
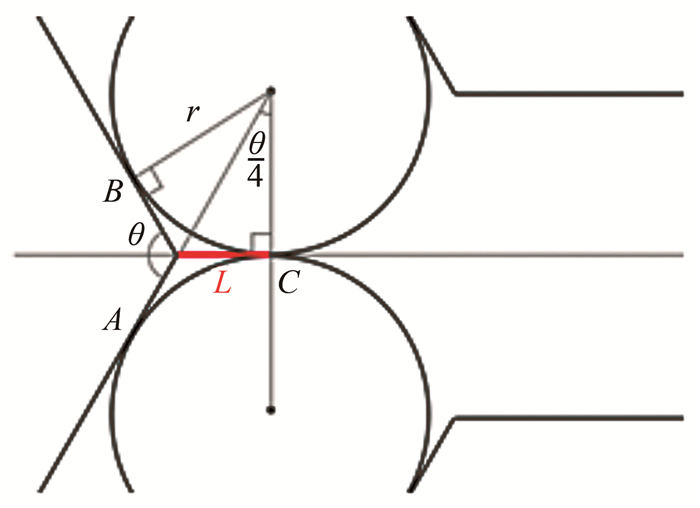
液滴在通道交汇处碰撞时, 通道交汇点与两液滴之间的空间仍然被连续相液体占据。由于连续相液体间隔其中, 液滴间因剪切应力和局部压力而减慢了液体排出速度。而随着通道夹角减小, 液滴能更早地相互接触, 因此交汇角度影响液滴融合过程。为了对此进行说明, 绘制了如图 6所示的液滴碰撞示意图, 此处将液滴形状简化为标准圆形, 忽略了挤压下的界面形变。两液滴接触点到通道交叉点的距离L与通道夹角存在比例关系L=rsin(θ/4), 在实验研究的夹角范围内(30°≤θ≤180°), L随通道交汇角度减小而减小。在交汇角度较大的微通道内, ABC部分存留的连续相液体更多, 其持续施加的剪切应力会使液滴界面拉向两侧, 减缓排液过程。当交汇角度较小时, 液滴从接触到流入下游通道的距离较长, 延长了液滴相互接触的时间, 从而给液膜排液过程提供了较长的时间。
通过对比图 5(a)和(b)中的2种融合方式, 发现二者存在比较突出的差别, 即图 5(b)中2个液滴的不同步性(到达汇合通道中轴线的时刻不同)。事实上, 液滴与汇合通道中轴线的距离差严重限制着其碰撞效率, 只有把距离差限定在一定范围内, 液滴才会发生碰撞[38]。当2个液滴与汇合通道中轴线的距离存在差异时, 液滴间更容易发生相互滑动。由于连续相被包裹在液滴间而无法被立即排出, 两液滴只能依次流入下游汇合通道。位于前面的液滴在汇合通道中的加速运动触发了液滴间的相互分离, 为液滴间界面形变提供一种新的可能。实验发现在分离阶段液滴间会形成一种锥形结构[40], 根据拉普拉斯压差理论可知, 这种形态会在接触位置形成局部低压区, 诱发液膜破裂和液滴快速融合[41]。此时的融合方式已经发生转变, 该融合方式与Borrell等[42]提出的解压融合(Decompressing coalescence)非常相似, 当一对液滴存在初始错位偏移时, 液滴在碰撞过程中会发生相对旋转, 并且随着偏移的增加, 液滴更容易发生解压融合。
通过显微粒子图像测速(Micro-Particle Image Velocimetry, Micro-PIV)技术拍摄的液滴内部流场可以发现, 2种融合方式对应的排液过程也存在差别。当液滴逐渐靠近并发生碰撞时, 通道内连续相的流动路径被液滴堵塞, 导致液滴上游的压力增加, 将液滴靠近下游通道的界面挤出交汇腔。液滴靠近通道壁面处和液滴间接触区域都发生界面变形, 而液滴间接触位置的速度最大, 超过液滴单独流动时最大速度的几倍, 且速度方向垂直于液滴互相挤压方向, 表明挤压时液滴间排液占主导。对于直接融合方式, 液滴在挤压后快速融合, 流场在很短时间内就恢复至均匀状态, 并且在融合的整个过程中, 流场基本都表现出对称性。对于滑动后融合方式, 液滴在挤压后相互旋转且中间界面持续保持接触, 最大速度分布在先进入下游通道的液滴中靠近交界面的位置, 而另一个液滴由于运动路径被堵塞而急剧减速, 液滴交界面两侧的速度差可以达到接近一个量级, 表明液膜间存在流动。在黏性剪切流动和壁面结构限制下, 后流入下游通道的液滴内部出现旋转涡, 旋转方向与液滴的先后顺序相关。
为了缓解液滴运动的不同步性对碰撞效率的限制, 可以在汇合通道中增加一个横截面突扩的矩形槽[43-44]。当液滴流入突扩矩形槽后, 液滴界面与通道侧壁面之间形成间隙, 使得一部分连续相从两侧绕过液滴流走, 实现液滴流速降低以等待与后续液滴碰撞。对于一个固定尺寸的矩形槽, 两相流量比对液滴的融合结果具有显著影响, 随着流量比增加, 液滴运动行为先从不融合转变为2个液滴融合, 再到3个液滴融合。相对而言, 研究范围内的毛细数对矩形槽内的液滴运动行为没有明显的影响[45]。由于两相流量比同时调节了液滴的尺寸和间距, 因此, 液滴尺寸、间距和流速等参数对液滴运动行为的作用规律需要在后续工作中进一步研究。然而可以确定的是, 增加矩形槽后液滴的融合效率得到大幅提高, 在文献的整个实验范围内, 融合效率都保持在50%~92%, 远远高于未加矩形槽时的融合效率范围15%~50%。
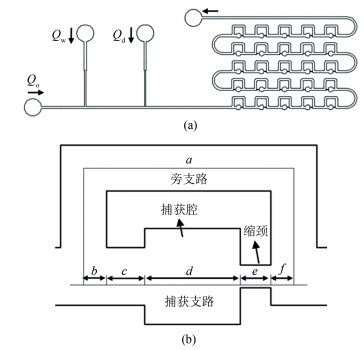
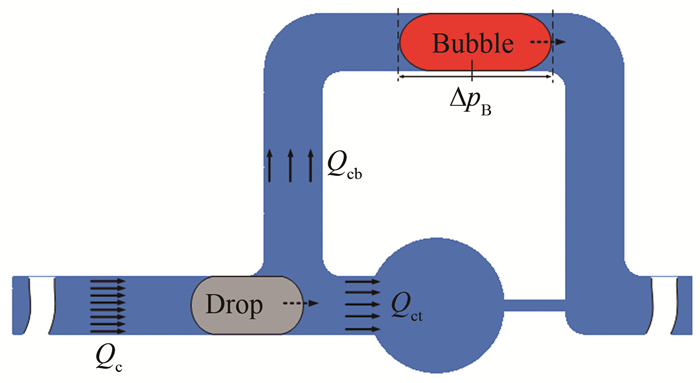
1.3 微通道网络中的液滴运动特性图 7(a)所示为多个液滴捕获单元组成的微通道网络示意图, 其中, 每个捕获单元的放大结构如图 7(b)所示, 包括2条流通路径:一条是液滴直接流走的旁支路, 另一条是实现液滴停留的捕获支路。捕获支路的典型特点是在捕获腔的下游设置宽度较小的缩颈, 液滴一旦流入捕获腔后, 只有当流动施加的压差大于液滴流入缩颈需要克服的拉普拉斯压差时, 液滴才会被挤出。如果在分岔处可以保持完整而不发生分裂, 液滴在进行路径选择时会流入流速较大的支路, 由于2条路径的压降相等(相当于电路中的并联关系), 也可以认为是流入流阻较小的支路[46]。理论上, 可以根据矩形管道中层流流动的流阻公式来计算每条路径的总流阻[47]。对于深宽比H/W小于1的矩形通道, 单相液体流动的流阻公式为:
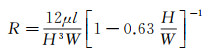 (1)
(1)
其中, R为流阻, l为通道长度, μ为液体黏度, 以此公式来确定液滴运动路径的优先级。而实际上, 该理论计算只是考虑了单相液体流动时的流阻, 当液滴流过时, 两相界面引入的流阻变化可能会导致设计的路径选择规律失效。再进一步, 对于具有多个分岔结构和交汇结构的微通道网络来说, 液滴不再是作为独立的个体进行运动, 在分岔处或交汇处进行路径选择时容易受到相近液滴的干扰, 液滴的完整性也可能会被破坏, 其运动行为更加复杂[48]。
图 8所示为一串均匀排布液滴在捕获阵列中的运动行为, 为了方便后续描述, 对前4个液滴进行着色和编号处理。由于该捕获单元中捕获支路的流阻小于旁支路的流阻, 可以观察到液滴1在分岔处选择流入捕获支路, 并且在整个流动过程中都稳定停留在第一个捕获腔内。当液滴1将捕获支路堵塞后, 该路径的流阻显著增加, 后续液滴只能从旁支路流向下游。在第二个捕获单元处, 液滴2同样直接流入捕获腔, 然而液滴3和液滴4在流经旁支路时发生了融合; 紧接着, 融合后的长液滴在下一个捕获腔的分岔处分裂成2个子液滴, 由1.1节的理论可知这是由于融合后的液滴运动达到了分裂的临界条件。总体来看, 对于实验中设计的25个捕获单元, 理想的液滴捕获发生了15次, 其他10次对应液滴的融合、分裂等行为, 这种"融合-分裂"循环不仅导致液滴尺寸的不均匀, 也造成液滴间物质的交换和污染[50-51]。
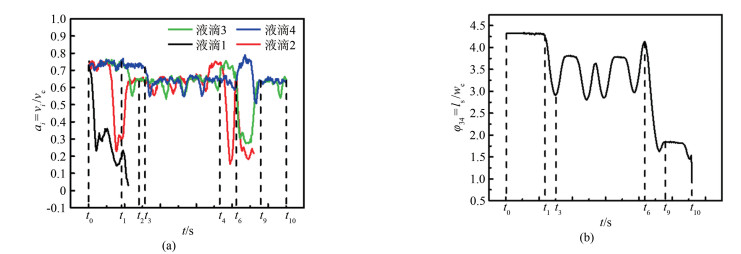
为了揭示液滴出现不同运动行为的原因, 通过追踪液滴运动路径得到每个液滴质心的时域变化情况, 如图 9所示[49]。其中, 图 9(a)的纵坐标为液滴无量纲速度, vc为主通道中的连续相平均流速; 图 9(b)的纵坐标为"液滴3-液滴4"无量纲间距, ls为液滴间距, wc为主通道宽度。从表面上看, 液滴2的捕获过程是对前一个捕获过程的重复, 但是"液滴2-液滴3"的间距在16.2 s时明显低于初始间距, 其中一个重要原因是液滴2与通道侧壁面之间的间隙流动(详见1.1节的间隙分裂过程), 液滴间最小距离低于通道宽度, 其运动行为互相干扰。"液滴2-液滴3"间距的降低对后续液滴运动也存在影响, 事实上后面液滴的融合就是源于此。由于液滴2增加了捕获支路的瞬时流阻, 液滴3只能流向旁支路并且同样增加了旁支路的瞬时流阻, 而液滴2被捕获后并不能立刻堵塞缩颈(18.27 s), 捕获腔内存在的间隙可供连续相流通, 此时捕获支路成为流阻较小的一侧, 因此"液滴3-液滴4"中间的连续相从捕获支路流走, 并同时推动液滴2逐渐向缩颈运动。当缩颈被液滴2堵塞后, 后续液滴又重新开始从旁支路流走, 此时"液滴3-液滴4"间距ls/wc已经降低到难以在图示放大倍率下被清楚识别(19.40 s), 从而导致了后续运动中融合和分裂的不理想结果。
由上述分析可知, 液滴间距对其运动行为的稳定性至关重要, 下面分别从结构参数和流动条件两方面对稳定性的改善进行讨论。从结构的角度来说, 图 8所示通道在单相流动下的优先级是捕获支路先于旁支路, 根据流阻计算方法, 可以通过调节通道的结构参数来反转2条路径的优先级, 然而液滴运动时的融合和分裂等不理想运动行为仍然存在。由液滴追踪分析可知, 不理想运动行为的产生根本上是液滴间距在运动中实时变化导致的, 对于矩形截面通道中的液滴运动, 拐角处和扩张处的通道横截面变化为连续相泄漏打开新的路径, 液滴间距的变化无法避免[50, 52]。从流动的角度来说, 如果可以将液滴参数控制在特定范围, 使得液滴间距在运动中无论怎样变化也不会产生互相干扰, 那么液滴运动的稳定性也可以得到改善。然而满足上述要求的两相流量条件受到很大限制, 且具体的流量范围还依赖于通道的结构参数, 难以得到比较普适的规律, 在实际操作中的指导作用比较有限。
液滴不稳定行为的起源是间距降低所导致的液滴融合, 既然液滴间距的变化无法避免, 那么引入不与液滴相融的气相有望成为一种解决办法, 如图 10所示。实验发现, 当液滴在气泡的引导下运动时, 液滴可以被非常规律地捕获, 且满足稳定运动对应的两相流量范围扩大到无气泡时的2倍以上。除了气泡和液滴不融合的特点外, 2种离散相的流阻差异也起到关键作用。根据Parthiban等[53]的研究, 当液滴内外相液体的黏度比远低于1时, 液滴的运动特性与气泡非常接近, 黏性耗散项引起的压差可被忽略, 单个液滴或气泡造成的压差可表示为Δp~(2γ/H)Ca2/3。如果假定压差表达式中液滴和气泡的比例系数是相等的, 相同流动条件下二者造成的流阻比约等于界面张力系数之比的1/3次幂, 则对于实验中气-油和水-油间的界面张力系数, 气泡的流阻约为液滴的1.25倍。在气泡引导下, 路径选择时2条路径的阻力差异更加明显, 从而实现了更加稳定的液滴捕获。
2 微凹槽内的粒子分选运动特性凹槽结构具有诱发流动分离和形成涡胞的特性, 利用涡胞结构进行颗粒/细胞分选是惯性微流控技术研究的重点和热点, 因此对凹槽内粒子的运动特性进行深入研究有助于更好地理解和运用微凹槽分选特性, 为循环肿瘤细胞分选提供理论指导[54]。本节先对微凹槽内的涡胞流动特性进行分析, 再对粒子的运动特性进行研究。
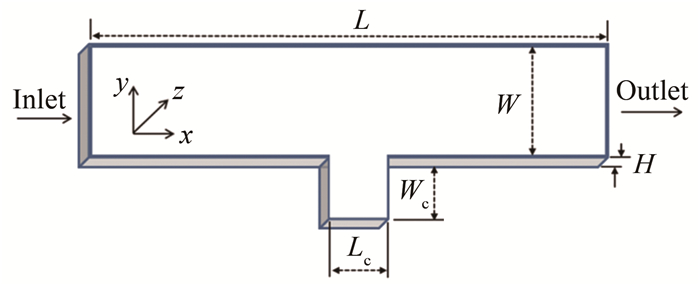
2.1 微凹槽内的涡胞流动特性如图 11所示为含有微凹槽的通道结构示意图, 凹槽的宽度Lc和高度Wc通过微通道的统一深度H进行无量纲化, 将凹槽尺寸定义为:无量纲宽度δ=Lc/H, 无量纲高度ε=Wc/H, 高宽比λ=Wc/Lc。为了研究不同条件下凹槽内的涡胞流动特性, 利用Micro-PIV进行流场可视化拍摄。
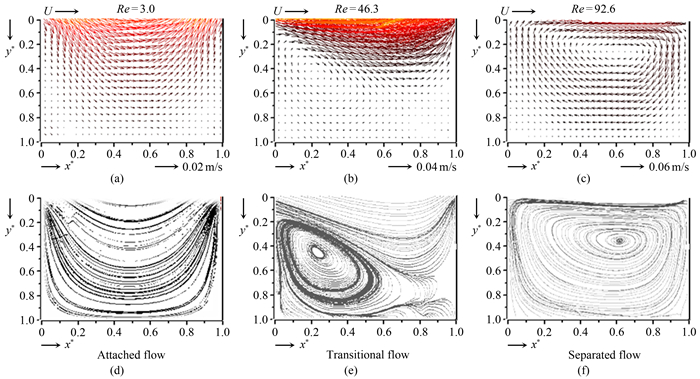
通过改变入口流量可调节入口雷诺数Re(Re=ρUDH/μ, 式中ρ、U、μ分别为液体的密度、平均流速和黏度, DH=2WH/(W+H)为主通道的水力直径)。随着入口雷诺数Re增加, 凹槽内依次出现3种流动形态:附着流、过渡流和分离流[55], 分别如图 12(a)~(c)所示。当雷诺数Re=3时, 微凹槽内的流动本质上和主通道内的层流一样, 可以看作主通道内流动的一部分, 定义为附着流(图 12(d))。当雷诺数增大至Re=46.3时, 微凹槽内的流动转变为过渡流, 此时微凹槽内的流场既包含了附着流, 同时也包含了分离流, 凹槽的左下角出现反向流动(图 12(e))。随着雷诺数继续增大至Re=92.6, 微凹槽内的流动最终转变为分离流, 凹槽内的流场完全被一个独立的单涡结构覆盖(图 12(f))。
凹槽内涡旋结构的演变与入口雷诺数密切相关。当主通道内的液体进入凹槽时, 由于通道截面尺寸突然增大, 液体内部压力发生改变从而形成逆压梯度, 其大小与入口雷诺数正相关。主通道内液体通过黏性力的作用带动凹槽内的液体随之一起运动, 由于黏性耗散作用, 凹槽内流动速度和剪切应力在横向方向上急剧减小, 越靠近凹槽底部液体流速越慢, 流动的剪切应力越小。随着入口雷诺数增大至过渡流的范围, 凹槽底部的流动速度会减小为零甚至为负, 从而产生边界层分离现象并表现出层流涡结构。此时凹槽内的涡旋结构刚开始出现, 位置分布在凹槽入口处且尺寸很小, 凹槽内的附着流仍占据主导地位。随着雷诺数进一步增大, 层流涡逐渐发展并抑制凹槽内附着流的发展, 最终覆盖了整个凹槽, 使得凹槽内的流场由过渡流转变为分离流。不同于宏观条件下凹槽内会出现边角涡结构, 微尺度下凹槽内只有一个层流涡, 涡旋的分布范围随Re的增大而增大; 此外, 涡心位置随着雷诺数增大先向凹槽后壁面移动, 再逐渐达到稳定状态[56]。值得注意的是, 主通道宽度对涡心位置也有影响。当主通道宽度由H增加到2H时, 虽然涡心位置随雷诺数的变化规律仍然保持一致, 但相同尺寸凹槽内的涡心位置发生变化, 最终达到的稳定状态也存在差别。
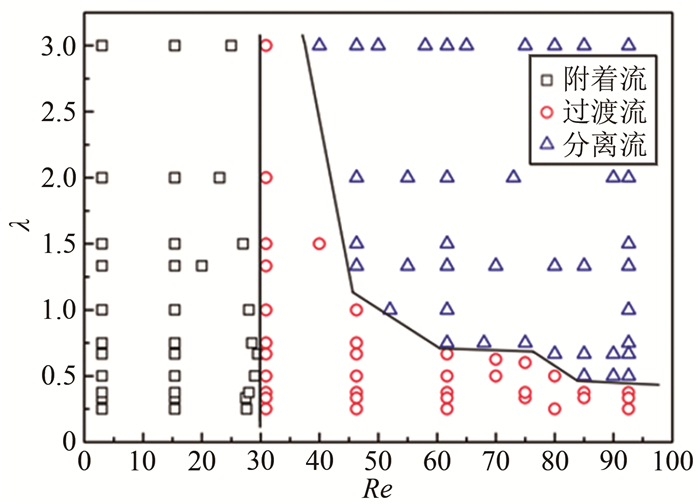
凹槽的尺寸参数对其内部的流动特性也有重要影响。当仅改变凹槽宽度或高度中的一个尺寸时, 凹槽内的流场结构会发生相应改变。当凹槽宽度增大时, 凹槽内层流涡的横向尺寸变大, 但附着流的作用范围也同时增大, 导致凹槽内涡心的相对位置会逐渐向凹槽的前壁面移动。另外, 凹槽底部壁面剪切应力随着宽度增大而增大, 主通道流动对凹槽内流动的影响也增强, 使得凹槽中附着流的作用越来越明显。当附着流能够达到凹槽底面时, 层流涡会在凹槽底面出现附着点, 底面剪切应力分布曲线发生改变。当凹槽高度增大时, 凹槽中的层流涡尺寸也增大, 层流涡对附着流的抑制作用逐渐增强, 直至附着流消失。另外, 随着凹槽高度增大, 凹槽底面剪切应力减小, 底部的流动变得缓慢。综合考虑凹槽宽度和高度对流动的影响, 可以绘制如图 13所示的流动形态分布相图。可以发现附着流只与雷诺数有关, 附着流向过渡流转变的临界雷诺数不受凹槽高宽比λ影响; 但过渡流向分离流转变的临界雷诺数与高宽比密切相关, 过渡流易发生在Re较小(30 < Re < 40)的流动条件下或者λ较小(λ < 0.6)的微凹槽中, 而分离流易出现在Re较大(Re>40)的流动条件下或者λ较大(λ>0.6)的微凹槽中。
2.2 微凹槽的粒子分选行为粒子分选是指从非均一粒子溶液中捕获性质均一的目标粒子的一种技术, 一般以粒子的直径或者密度作为分选和隔离的选取原则。其中, 粒子的运动分析是实现对粒子精确操控的基础。微凹槽是一种常用于粒子操控的结构, 凹槽中的层流涡结构可以实现不同直径粒子的惯性聚焦运动, 也可以将目标粒子引入凹槽随层流涡一起在凹槽中旋转, 从而实现粒子的隔离。
利用微凹槽将粒子捕获的过程可以分为3个阶段:粒子进入凹槽前的惯性聚焦阶段、粒子被凹槽捕获的捕获阶段、粒子进入凹槽后的运动阶段。目前探究微凹槽粒子捕获机理的研究以惯性聚焦为主, 认为粒子在矩形微通道中随液体运动时会在惯性升力的作用下聚焦在特定的平衡位置, 称为粒子"偏移理论"。事实上, 惯性升力由一对平衡力组成, 包括驱动粒子靠近壁面的剪切梯度升力FS和驱使粒子远离壁面的壁面诱导升力FW。二者的表达式分别为FS=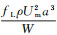
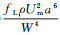
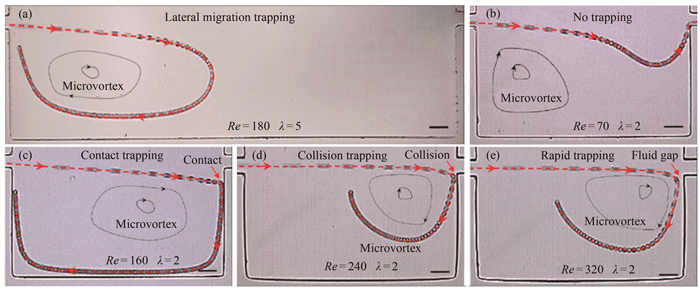
除了偏移捕获方式之外, 微凹槽还存在其他捕获方式, 实验发现对于特定深宽比的凹槽结构和入口流动条件, 捕获凹槽的后壁面与粒子发生碰撞、接触等多种作用关系, 将其统称为后壁面作用捕获。根据粒子捕获瞬间运动形式的不同, 进一步将后壁面作用捕获细分为接触捕获、碰撞捕获和分离捕获, 分别如图 14(c)~(e)所示。根据2.1节的分析可知, 当雷诺数较低时, 凹槽内处于过渡流状态, 粒子跟随液体进入凹槽并向内侧偏移但无法储存在凹槽内, 最后随附着流状态的液体流出凹槽(图 14(b))。当Re在90~240范围内时, 凹槽内流动处于低强度的分离流, 即凹槽内形成独立涡胞结构但涡流强度相对较低, 粒子进入凹槽后直接和下游壁面发生接触, 在近壁效应作用下, 粒子跟随液体沿凹槽内壁低速旋转一周, 然后再进入凹槽内中心涡流, 该方式定义为接触捕获。当Re增加到240~320时, 粒子进入凹槽后在剪切梯度升力FS作用下向凹槽内侧迁移, 但凹槽宽度较窄且横向偏移距离较短, 粒子无法依靠自身转向实现捕获, 而是与凹槽后壁面发生碰撞。发生碰撞后的粒子速度急剧降低, 粒子更容易跟随液体进入凹槽而实现捕获, 该方式定义为碰撞捕获。随着Re继续增加到320~375, 凹槽内形成充分发展的高速分离流, 由于凹槽出口处液体速度梯度较大, 粒子在冲向后壁面时难以穿越高速区域带, 从而直接跟随高速转向的液体进入凹槽。由于粒子与凹槽后壁面间存在空隙, 该方式称为分离捕获[58]。
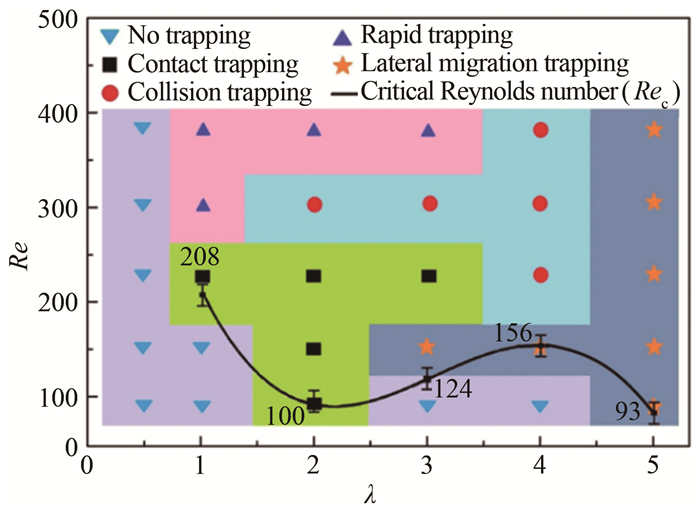
为了进一步分析微凹槽的粒子捕获能力及影响因素, 实验以凹槽深宽比和雷诺数为研究变量, 探究粒子捕获类型以及临界雷诺数的变化规律。其中, 捕获凹槽的深宽比分别为λ=0.5, 1.0, 2.0, 3.0, 4.0和5.0, 雷诺数变化范围为Re=0~400, 实验结果如图 15所示。当λ=0.5时, 凹槽无法实现粒子捕获行为, 虽然较小的凹槽更容易形成涡胞结构, 但凹槽宽度较窄导致粒子纵向偏移时间和距离有限, 粒子经过凹槽的减速效果不明显, 难以偏移进入凹槽内。当λ=5时, 在任意捕获速度范围内, 粒子都可实现偏移捕获; 无论是低速过渡流还是高速分离流状态, 较大深宽比的凹槽内液体减速效果都比较明显, 粒子具备充足的纵向偏移时间和偏移距离, 容易实现粒子捕获。当凹槽深宽比处于1<λ < 5时, 随着Re增加, 凹槽后壁面对腔内流场结构产生影响, 进而改变粒子进入凹槽的运动方式, 粒子捕获先后呈现接触捕获、碰撞捕获和分离捕获3种方式。
通过染色实验对主通道和凹槽内液体的物质交换形式进行了研究, 如图 16所示。在低Re条件下(Re=80), 凹槽内涡流与主通道内液体之间的边界线相对模糊, 染料以分子扩散形式进入捕获凹槽, 表明主通道液体和凹槽内液体速度差较小, 凹槽内还未形成独立的涡胞结构, 该流场结构无法实现粒子捕获。当Re=80~160时, 主通道与凹槽内液体的色差比较明显且分界线清晰, 如图 16(b)所示, 主通道染色液体只有小部分进入腔内, 表明凹槽内已经形成独立的涡胞结构, 凹槽内外液体的速度差较大, 边界线附近较高的速度梯度导致染料无法跨越分界线进入槽内, 因此形成主通道颜色较深而凹槽内颜色较浅的现象。该流场结构使得凹槽内涡胞强度小且速度低, 凹槽内近壁面形成较低的速度梯度带, 导致接触捕获过程中粒子绕近壁面旋转一周的低速流动。当流速继续增大到Re=160~240范围时, 主通道和凹槽内液体的颜色接近, 表明凹槽内流速随主通道流速增加, 二者之间速度差减小, 主通道液体流入凹槽后又流出。由图 16(c)还可以发现凹槽中心位置的颜色相对较浅, 表明该位置为涡心低速区域, 主通道液体和凹槽内液体的分界线逐渐消失, 粒子跟随主通道液体直接冲击凹槽后壁面, 呈现碰撞类型的捕获行为。当Re>240时, 主通道液体直接流入凹槽内使其中液体颜色变浓, 主通道流域与凹槽内液体分界线完全消失, 液体速度梯度最大区域出现在后壁面处, 粒子进入凹槽而无法穿越高速度梯度的后壁面区域, 在此之前就发生减速转向, 实现分离捕获。
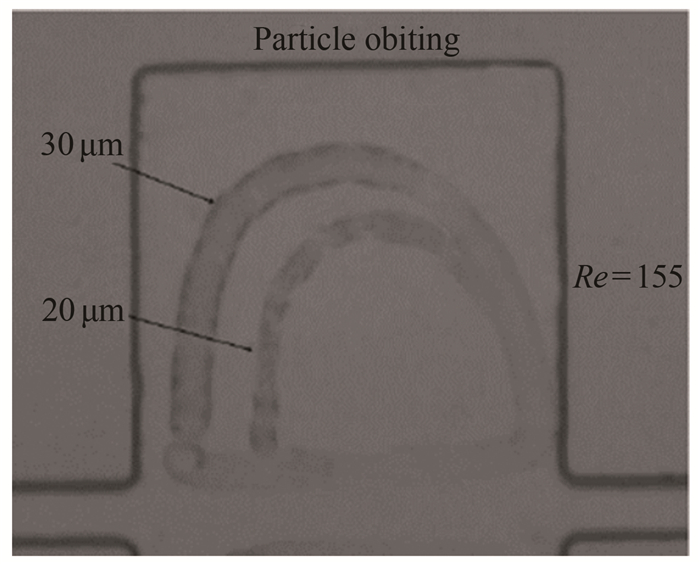
2.3 微凹槽内的粒子轨道运动对于适宜的凹槽尺寸和流动条件, 粒子会被微凹槽内的层流涡捕获, 从而形成特定的粒子轨道。如图 17所示为相同凹槽和流动条件(Re=178)下的粒子运动轨道, 可以看出单个粒子在微凹槽中存在一个稳定的运动轨道, 且粒子的运动轨迹与层流涡的流线类似[59]。小粒径的运动轨道更靠近涡心位置, 随着粒径增大, 粒子运动轨道的覆盖区域也随之增大, 但相同流动条件下的粒子运动轨道呈现相似形状, 图中为半月型的闭合轨道[60]。此外, 由于图 17中的粒子轨道是多张等时间间隔的图片叠加所得到的, 粒子位置的不均匀分布表明粒子在轨道上的运动速度随位置发生变化, 靠近凹槽出口处粒子速度较大, 在靠近后壁面拐角处达到最大, 而凹槽底面的粒子速度较小。此外, 当一个凹槽内同时捕获2种尺寸(粒子直径a=20和35 μm)的粒子时, 同样是大粒径的粒子运动轨道在小粒径的外侧, 如图 18所示。
需要说明的是, 上述结果是单个或2个粒子在凹槽内的运动轨道, 实验中进入凹槽内的粒子越多, 粒子之间的相互作用也越明显, 从而影响凹槽内粒子轨道的分布, 本节内容重点关注单个粒子在凹槽内的运动。
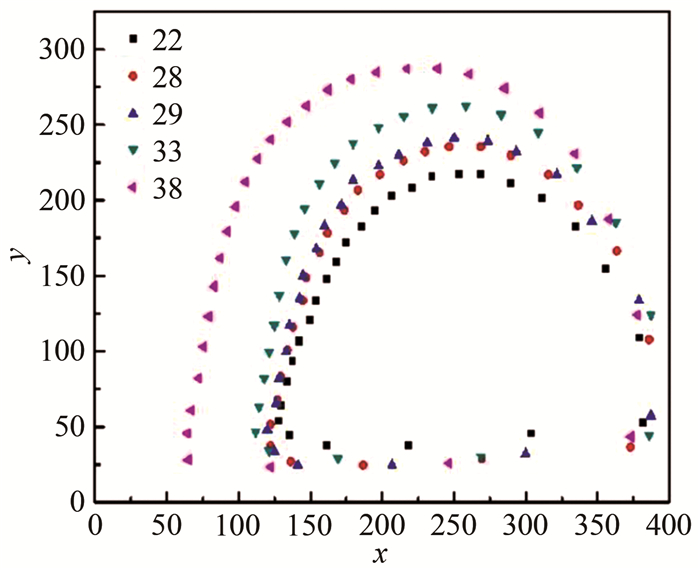
由凹槽内流场特性的影响因素可知, 入口雷诺数显著影响凹槽内涡胞结构等特性, 结合粒子轨道与层流涡流线的相似性可推测, 不同雷诺数下凹槽内的粒子运动轨道也会发生变化。图 19所示为粒径a=20 μm的粒子在不同运动时刻的图像叠加结果, 可以发现随着Re的增大, 粒子轨道也相应增大, 计算得到的轨道覆盖面积也单调增加[61]。相对而言, Re=89的流动条件无法让小粒径a=10 μm的粒子在凹槽中形成运动轨道, 即粒子在横截面上移动的位移不足以进入凹槽中的层流涡, 最终粒子随主通道内的流体流出凹槽。当Re>111后, a=10 μm的粒子同样可以在凹槽中形成固定的轨道, 并且轨道覆盖面积随Re的变化规律同a=20 μm粒子相似。
微尺度受限空间中, 液滴和粒子的运动特性与通道几何结构、流体物性参数和流动条件等密切相关。对于微尺度液滴多相流动, 界面形变规律直接反映了受力状况, 也决定了液滴的最终运动行为。液滴在分岔处的分裂过程可以根据界面变形状况划分成不同阶段, 各个阶段中沿程压差力、黏性剪切应力和界面张力起到的作用都会发生变化, 导致不同的颈缩规律。液滴分裂的临界条件可以表示成液滴长度和运动速度的函数关系L0/W=κCaζ(见第1.1节), 反映了分裂临界条件对液滴初始参数的依赖性。液滴在交汇处的碰撞过程同样伴随着复杂的界面变形, 当液滴形变程度超过一定界限后会发生相似的液滴分裂行为。液滴碰撞后的排液过程对其融合至关重要, 而通道交汇处的不同局部结构导致不同的排液速度, 表现为各不相同的临界毛细数。液滴融合的临界毛细数大都分布在Ca*<0.02的范围, 且与两相液体的黏度比存在幂函数关系Ca*~λμ-0.75(见第1.2节)。此外, 液滴运动的不同步性也会影响液滴间的排液过程, 导致直接融合和滑动后融合2种不同的融合方式。通过增加突扩矩形槽可以显著改善运动不同步性所限制的碰撞效率, 液滴融合率可以提高到90%以上。液滴在通道网络中运动时改变所在通道的流动阻力, 借助液滴间的互相作用关系可以实现对液滴运动路径的控制, 然而液滴在路径选择的同时也伴随着界面形变, 一旦变形程度达到上述的分裂或融合临界条件后, 液滴会发生相应的运动行为, 导致液滴路径选择的规律被破坏。当采用流阻较大的气泡来引导液滴运动时, 液滴在通道网络中的捕获性能得到显著提升, 液滴能够稳定运动的流量范围也得到扩大。
随着入口雷诺数Re的增加, 微凹槽中的液体流动形态从附着流逐渐转变为分离流, 而凹槽中形成独立涡胞结构的临界雷诺数Re*与凹槽的高宽比λ等直接相关。当粒子从直通道流过凹槽时, 流动的平衡状态被打破, 如果粒子的惯性迁移量可以达到被凹槽内涡胞结构所捕获的条件, 粒子就会在流动的引导下流向凹槽。在特定的凹槽结构和流动条件下, 粒子会与凹槽后壁面发生接触、碰撞或分离等直接作用, 为粒子捕获提供了新的控制方式。通过对比还可以发现, 粒子被捕获的临界条件与凹槽内分离流的分布范围存在明显差异, 表明粒子自身的尺寸效应会对连续相流动产生影响。粒子的尺寸效应还体现在粒子被捕获后在凹槽内的轨道运动, 当少量粒子在凹槽内运动时, 不同粒径的粒子会在各自不同的轨道中周期运动, 凹槽捕获性能对控制对象尺寸的敏感性也符合惯性微流控的典型特点。
微通道中的多相液体系统或含有粒子的复杂液体系统存在丰富多样的流动现象, 认识不同现象对应的参数范围及流动规律对其应用至关重要。微通道中的流动通常涉及多参数耦合和非线性等复杂效应, 使得流动规律及背后的物理机制比较复杂, 现有研究从微通道中的分岔、交汇等一些常用结构入手, 开展了比较有针对性的流动机理方面的研究工作, 然而这些前期研究仍然存在很多不足之处, 需要在后续工作中进一步完善。首先, 前期研究重点针对比较简单的和规则的通道模型, 而相关工程应用往往都是比较复杂的或集成的通道结构, 前期研究结果的适用性需要得到验证。其次, 现有研究大都考虑少数液滴或粒子同时存在的流动现象, 较少涉及液滴或粒子之间的相互作用, 大量液滴或粒子同时运动的规律和机理需要得到揭示。最后, 将流动规律的理论研究与工程实际的具体需求相结合也是未来的发展方向, 通过力学、化学、生物、物理等多个学科的交叉与合作, 以逐步建立完善的理论体系和工程技术。
| [1] |
林炳承. 微纳流控芯片实验室[M]. 北京: 科学出版社, 2013.
|
| [2] |
李战华, 吴健康, 胡国庆, 等. 微流控芯片中的流体流动[M]. 北京: 科学出版社, 2012. LI Z H, WU J K, HU G Q, et al. Fluid flow in microfluidic chips[M]. Beijing: Science Press, 2012. |
| [3] |
陈晓东, 胡国庆. 微流控器件中的多相流动[J]. 力学进展, 2015, 45: 201503. CHEN X D, HU G Q. Multiphase flow in microfluidic devices[J]. Advances in Mechanics, 2015, 45: 201503. DOI:10.6052/1000-0992-14-063 |
| [4] |
司廷, 李广滨, 尹协振. 流动聚焦及射流不稳定性[J]. 力学进展, 2017, 47: 201706. SI T, LI G B, YIN X Z. Flow focusing and jet instability[J]. Advances in Mechanics, 2017, 47: 201706. DOI:10.6052/1000-0992-16-026 |
| [5] |
LIN X, BAO F, TU C, et al. Dynamics of bubble formation in highly viscous liquid in co-flowing microfluidic device[J]. Microfluidics and Nanofluidics, 2019, 23(5): 74. DOI:10.1007/s10404-019-2221-2 |
| [6] |
PANG Y, KIM H, LIU Z, et al. A soft microchannel decreases polydispersity of droplet generation[J]. Lab on a Chip, 2014, 14(20): 4029-4034. DOI:10.1039/C4LC00871E |
| [7] |
PANG Y, DU Y, WANG J, et al. Generation of single/double Janus emulsion droplets in co-flowing microtube[J]. International Journal of Multiphase Flow, 2019, 113: 199-207. DOI:10.1016/j.ijmultiphaseflow.2019.01.011 |
| [8] |
LIU Z M, LI M, PANG Y, et al. Flow characteristics inside droplets moving in a curved microchannel with rectangular section[J]. Physics of Fluids, 2019, 31(2): 022004. DOI:10.1063/1.5080373 |
| [9] |
FUERSTMAN M J, GARSTECKI P, WHITESIDES G M. Coding/decoding and reversibility of droplet trains in microfluidic networks[J]. Science, 2007, 315(5813): 828. DOI:10.1126/science.1134514 |
| [10] |
PANG Y, WANG X, LIU Z M. Study of droplet flow in a T-shape microchannel with bottom wall fluctuation[J]. Acta Mechanica Sinica, 2018, 34(4): 632-643. DOI:10.1007/s10409-018-0750-7 |
| [11] |
LIU Z, ZHANG L, PANG Y, et al. Micro-PIV investigation of the internal flow transitions inside droplets traveling in a rectangular microchannel[J]. Microfluidics and Nanofluidics, 2017, 21(12): 180. DOI:10.1007/s10404-017-2019-z |
| [12] |
BAROUD C N, GALLAIRE F, DANGLA R. Dynamics of microfluidic droplets[J]. Lab on a Chip, 2010, 10(16): 2032-2045. DOI:10.1039/c001191f |
| [13] |
SEEMANN R, BRINKMANN M, PFOHL T, et al. Droplet based microfluidics[J]. Rep Prog Phys, 2012, 75(1): 016601. DOI:10.1088/0034-4885/75/1/016601 |
| [14] |
LIU Z, ZHAO J, PANG Y, et al. Generation of droplets in the T-junction with a constriction microchannel[J]. Microfluidics and Nanofluidics, 2018, 22(11): 124. DOI:10.1007/s10404-018-2144-3 |
| [15] |
MUINELO-ROMAY L, VIEITO M, ABALO A, et al. Evaluation of circulating tumor cells and related events as prognostic factors and surrogate biomarkers in advanced NSCLC patients receiving first-line systemic treatment[J]. Cancers, 2014, 6(1): 153-165. DOI:10.3390/cancers6010153 |
| [16] |
LIU C, HU G, JIANG X, et al. Inertial focusing of spherical particles in rectangular microchannels over a wide range of Reynolds numbers[J]. Lab on a Chip, 2015, 15(4): 1168-1177. DOI:10.1039/C4LC01216J |
| [17] |
REN Y, LIU X, LIU W, et al. Flexible particle flow-focusing in microchannel driven by droplet-directed induced-charge electroosmosis[J]. Electrophoresis, 2018, 39(4): 597-607. DOI:10.1002/elps.201700305 |
| [18] |
TONER M, IRIMIA D. Blood-on-a-chip[J]. Annu Rev Biomed Eng, 2005, 7: 77-103. DOI:10.1146/annurev.bioeng.7.011205.135108 |
| [19] |
DI CARLO D. Inertial microfluidics[J]. Lab on a Chip, 2009, 9(21): 3038-3046. DOI:10.1039/b912547g |
| [20] |
WANG J, YU D. Asymmetry of flow fields and asymmetric breakup of a droplet[J]. Microfluidics and Nanofluidics, 2014, 18(4): 709-715. |
| [21] |
WANG X, LIU Z M, PANG Y. Droplet breakup in an asymmetric bifurcation with two angled branches[J]. Chemical Engineering Science, 2018, 188: 11-17. DOI:10.1016/j.ces.2018.05.003 |
| [22] |
WANG X, LIU Z M, PANG Y. Breakup dynamics of droplets in an asymmetric bifurcation by μPIV and theoretical investigations[J]. Chemical Engineering Science, 2019, 197: 258-268. DOI:10.1016/j.ces.2018.12.030 |
| [23] |
LINK D R, ANNA S L, WEITZ D A, et al. Geometrically mediated breakup of drops in microfluidic devices[J]. Phys Rev Lett, 2004, 92(5): 054503. DOI:10.1103/PhysRevLett.92.054503 |
| [24] |
LESHANSKY A M, PISMEN L M. Breakup of drops in a microfluidic T junction[J]. Physics of Fluids, 2009, 21(2): 023303. DOI:10.1063/1.3078515 |
| [25] |
FU T, MA Y, FUNFSCHILLING D, et al. Dynamics of bubble breakup in a microfluidic T-junction divergence[J]. Chemical Engineering Science, 2011, 66(18): 4184-4195. DOI:10.1016/j.ces.2011.06.003 |
| [26] |
CHEN Y, DENG Z. Hydrodynamics of a droplet passing through a microfluidic T-junction[J]. Journal of Fluid Mechanics, 2017, 819: 401-434. DOI:10.1017/jfm.2017.181 |
| [27] |
CHEN B, LI G, WANG W, et al. 3D numerical simulation of droplet passive breakup in a micro-channel T-junction using the Volume-of-Fluid method[J]. Applied Thermal Engineering, 2015, 88: 94-101. DOI:10.1016/j.applthermaleng.2014.11.084 |
| [28] |
JULLIEN M C, TSANG MUI CHING M J, COHEN C, et al. Droplet breakup in microfluidic T-junctions at small capillary numbers[J]. Physics of Fluids, 2009, 21(7): 072001. DOI:10.1063/1.3170983 |
| [29] |
SAMIE M, SALARI A, SHAFII M B. Breakup of microdroplets in asymmetric T junctions[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2013, 87(5): 053003. DOI:10.1103/PhysRevE.87.053003 |
| [30] |
YAMADA M, DOI S, MAENAKA H, et al. Hydrodynamic control of droplet division in bifurcating microchannel and its application to particle synthesis[J]. J Colloid Interface Sci, 2008, 321(2): 401-407. DOI:10.1016/j.jcis.2008.01.036 |
| [31] |
VAN STEIJN V, KLEIJN C R, KREUTZER M T. Flows around confined bubbles and their importance in triggering pinch-off[J]. Phys Rev Lett, 2009, 103(21): 214501. DOI:10.1103/PhysRevLett.103.214501 |
| [32] |
SUN X, ZHU C, FU T, et al. Dynamics of droplet breakup and formation of satellite droplets in a microfluidic T-junction[J]. Chemical Engineering Science, 2018, 188: 158-169. DOI:10.1016/j.ces.2018.05.027 |
| [33] |
CHESTERS A K. The modelling of coalescence processes in fluid-liquid dispersions:a review of current understanding[J]. Chemical Engineering Research and Design, 1991, 69: 259-270. |
| [34] |
SHEN F, LI Y, LI MU Z, et al. Advances in Micro-droplets coalescence using microfluidics[J]. Chinese Journal of Analytical Chemistry, 2015, 43(12): 1942-1954. DOI:10.1016/S1872-2040(15)60886-6 |
| [35] |
GAI Y, KHOR J W, TANG S K Y. Confinement and viscosity ratio effect on droplet break-up in a concentrated emulsion flowing through a narrow constriction[J]. Lab on a Chip, 2016, 16(16): 3058-3064. DOI:10.1039/C6LC00478D |
| [36] |
LIU Z M, WANG X, CAO R T, et al. Droplet coalescence at microchannel intersection chambers with different shapes[J]. Soft Matter, 2016, 12(26): 5797-5807. DOI:10.1039/C6SM01158F |
| [37] |
LIU Z M, CAO R T, PANG Y, et al. The influence of channel intersection angle on droplets coalescence process[J]. Experiments in Fluids, 2015, 56(2): 24. DOI:10.1007/s00348-015-1901-2 |
| [38] |
CHRISTOPHER G F, BERGSTEIN J, END N B, et al. Coalescence and splitting of confined droplets at microfluidic junctions[J]. Lab on a Chip, 2009, 9(8): 1102-1109. DOI:10.1039/b813062k |
| [39] |
WANG K, LU Y, YANG L, et al. Microdroplet coalescences at microchannel junctions with different collision angles[J]. AIChE Journal, 2013, 59(2): 643-649. DOI:10.1002/aic.13825 |
| [40] |
WANG X, LIU Z, PANG Y. Collision characteristics of droplet pairs with the presence of arriving distance differences[J]. Journal of Industrial and Engineering Chemistry, 2019, 69: 225-232. DOI:10.1016/j.jiec.2018.09.017 |
| [41] |
RISTENPART W D, BIRD J C, BELMONTE A, et al. Non-coalescence of oppositely charged drops[J]. Nature, 2009, 461(7262): 377-380. DOI:10.1038/nature08294 |
| [42] |
BORRELL M, YOON Y, LEAL L G. Experimental analysis of the coalescence process via head-on collisions in a time-dependent flow[J]. Physics of Fluids, 2004, 16(11): 3945-3954. DOI:10.1063/1.1795291 |
| [43] |
SHEN F, LI Y, LIU Z, et al. Study of flow behaviors of droplet merging and splitting in microchannels using Micro-PIV measurement[J]. Microfluidics and Nanofluidics, 2017, 21(4): 66. DOI:10.1007/s10404-017-1902-y |
| [44] |
WANG X, LIU Z, PANG Y. Concentration gradient generation methods based on microfluidic systems[J]. RSC Advances, 2017, 7(48): 29966-29984. DOI:10.1039/C7RA04494A |
| [45] |
SHEN F, LI Y, WANG G, et al. Mechanisms of rectangular groove-induced multiple-microdroplet coalescences[J]. Acta Mechanica Sinica, 2017, 33(3): 585-594. DOI:10.1007/s10409-016-0623-x |
| [46] |
OH K W, LEE K, AHN B, et al. Design of pressure-driven microfluidic networks using electric circuit analogy[J]. Lab on a Chip, 2012, 12(3): 515-545. DOI:10.1039/C2LC20799K |
| [47] |
BRUUS H. Theoretical Microfluidics[M]. New York: Oxford University Press, 2008.
|
| [48] |
BITHI S S, VANAPALLI S A. Collective dynamics of non-coalescing and coalescing droplets in microfluidic parking networks[J]. Soft Matter, 2015, 11(25): 5122-5132. DOI:10.1039/C5SM01077B |
| [49] |
ZHANG L, LIU Z, PANG Y, et al. Trapping a moving droplet train by bubble guidance in microfluidic networks[J]. RSC Advances, 2018, 8(16): 8787-8794. DOI:10.1039/C7RA13507F |
| [50] |
BITHI S S, WANG W S, SUN M, et al. Coalescing drops in microfluidic parking networks:A multifunctional platform for drop-based microfluidics[J]. Biomicrofluidics, 2014, 8(3): 034118. DOI:10.1063/1.4885079 |
| [51] |
WEN H, YU Y, ZHU G, et al. A droplet microchip with substance exchange capability for the developmental study of C. elegans[J]. Lab on a Chip, 2015, 15(8): 1905-1911. DOI:10.1039/C4LC01377H |
| [52] |
BITHI S S, NEKOUEI M, VANAPALLI S A. Bistability in the hydrodynamic resistance of a drop trapped at a microcavity junction[J]. Microfluidics and Nanofluidics, 2017, 21(11): 164. DOI:10.1007/s10404-017-2006-4 |
| [53] |
PARTHIBAN P, KHAN S A. Bistability in droplet traffic at asymmetric microfluidic junctions[J]. Biomicrofluidics, 2013, 7(4): 44123. DOI:10.1063/1.4819276 |
| [54] |
JIANG M, QIAN S, LIU Z. Fully resolved simulation of single-particle dynamics in a microcavity[J]. Microfluidics and Nanofluidics, 2018, 22(12): 144. DOI:10.1007/s10404-018-2166-x |
| [55] |
SHEN F, XIAO P, LIU Z. Microparticle image velocimetry (μPIV) study of microcavity flow at low Reynolds number[J]. Microfluidics and Nanofluidics, 2015, 19(2): 403-417. DOI:10.1007/s10404-015-1575-3 |
| [56] |
SHEN F, XU M, ZHOU B, et al. Effects of geometry factors on microvortices evolution in confined square microcavities[J]. Microfluidics and Nanofluidics, 2018, 22(4): 36. DOI:10.1007/s10404-018-2056-2 |
| [57] |
HUR S C, MACH A J, DI CARLO D. High-throughput size-based rare cell enrichment using microscale vortices[J]. Biomicrofluidics, 2011, 5(2): 22206. DOI:10.1063/1.3576780 |
| [58] |
SHEN F, XUE S, XU M, et al. Experimental study of single-particle trapping mechanisms into microcavities using microfluidics[J]. Physics of Fluids, 2019, 31(4): 042002. DOI:10.1063/1.5081918 |
| [59] |
HADDADI H, DI CARLO D. Inertial flow of a dilute suspension over cavities in a microchannel[J]. Journal of Fluid Mechanics, 2016, 811: 436-467. |
| [60] |
SHEN F, XU M, WANG Z, et al. Single-particle trapping, orbiting, and rotating in a microcavity using microfluidics[J]. Applied Physics Express, 2017, 10(9): 097301. DOI:10.7567/APEX.10.097301 |
| [61] |
SHEN F, XUE S, ZHOU B, et al. Evolution of single-particle recirculating orbits within a hydrodynamic microvortex[J]. Journal of Micromechanics and Microengineering, 2018, 28(8): 085018. DOI:10.1088/1361-6439/aac02d |