压电天平是利用压电材料的正压电效应来进行测量的天平,主要用于脉冲风洞中的气动力测量试验[1-2]。常用的压电天平有3种:一种以美国康奈尔航空试验室(GAL)早期研制的压电天平为代表,直接采用无弹性压电元件组合测量气动特性[3];一种是中国空气动力研究与发展中心(CARDC)研制的具有弹性元件的梁式微应变压电天平;一种是直接采用压电型力传感器进行气动特性测量的压电天平[4]。
梁式微应变压电天平采用粘贴在天平力敏梁上的压电陶瓷片来感受力敏梁的变形,从而达到在风洞中测量模型所受气动力的目的。由于压电陶瓷材料具有很高的频响和较大的压电常数,天平的刚度可以做得较高,从而提高了天平的频响范围,可用于激波风洞等脉冲风洞的测力试验。
但在激波风洞的有效试验时间内(一般为毫秒量级,在几毫秒至几十毫秒之间),模型、天平和支撑系统在风洞启动时受到的冲击振动得不到完全阻尼,天平输出的是多种频率的振动信号和有效试验信号的叠加信号,必须采用惯性补偿方法去除振动信号,以得到有效的试验信号。能否有效地去除振动信号,是制约风洞试验数据质量的一个重要因素。在惯性补偿设计中,一般采用加速度计进行惯性补偿:通过合理设计加速度计的安装位置,使得加速度计仅感受惯性振动信号;在试验前,通过动态校准试验获得惯性补偿系数[2-8]。
目前,有限元分析方法已广泛应用于模拟求解真实的工程问题,尤其是在各种结构和传感器的设计中[9-10]。在风洞天平设计领域,有限元分析方法被用于评估天平敏感梁微应变和结构变形均匀性以预估天平的性能[11-16]。ANSYS力电耦合的有限元分析方法在压电型传感器、俘能器、驱动器[17-21]等设计中具有较多应用。在压电天平设计领域,ANSYS有限元分析方法基本上是用于结构分析,采用力电耦合方法评估天平整体性能的研究工作则少有报道[22-25]。
在本文研究中,将压电天平结构本体和压电陶瓷片作为一个整体,分别对压电天平结构本体和压电陶瓷片进行建模,采用力电耦合的求解方法,直接得到各种载荷作用下天平各分量压电陶瓷片上的输出开路电压,可以更直观地评估压电天平性能;同时对加速度计的输出进行评估,可以直接检验加速度计惯性补偿的效果。
1 有限元分析的基本理论有限元分析方法的核心思想是将被分析物体(连续的求解域)离散为有限个单元,每个相邻单元通过单元间的公共界面或边界面彼此连接。对每一个单元建立方程,集合为一组联立代数方程组,可得到整个物体的解答。有限元法可以解决结构分析、热传导、流体力学的流场分析、电磁场分析等问题[10]。
在本文研究中,主要使用了ANSYS软件中的结构分析和压电分析模块。
1.1 力电耦合动力学模型在压电结构的本构关系中,除弹性变形关系外,还存在力电耦合作用和介电作用。通常其本构关系可用如下2个压电方程(压电弹性方程、电荷方程)描述:
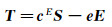 (1)
(1)
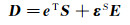 (2)
(2)
式中各变量的定义为:T为压电应力矩阵;D为压电输出电位移矢量;S为压电应变矩阵;E为电场强度矢量;cE为结构弹性矩阵;e为压电应力常数矩阵;εS为常应变下的压电材料介电常数矩阵。
上述2个方程用于描述压电结构的逆压电效应和正压电效应。正压电效应可用于设计各类传感器。本文的压电天平传感器仅外载荷已知,需要同时求解整体结构的力学响应和电响应,因此需要联立2个压电方程进行求解。
利用ANSYS有限元分析软件的前处理功能,完成几何建模、单元类型定义、材料属性定义、网格划分、耦合节点处理以及载荷施加,可以在软件后台获得如下形式的压电天平整体结构的动力学方程:
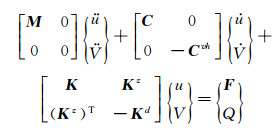 (3)
(3)
其中,u和V分别为整体结构的位移响应和输出电势响应,M、C、K分别为结构的质量阵、阻尼阵和刚度阵,F为结构载荷矢量,Kz、Kd分别为压电耦合矩阵和压电介电系数矩阵,Q为压电结构电极面上的输出电荷量, Cvh为压电介电阻尼矩阵,其影响通常可忽略。若考虑压电陶瓷片开环输出情况,式(3)可改写为:
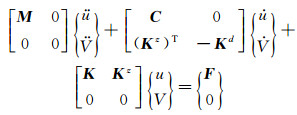 (4)
(4)
模态特征是机械结构的固有振动特性,每个模态具有特定的固有频率、阻尼比和模态振型。对于压电结构,主要针对其弹性振动特性进行模态分析。由式(3)可得线性自由振动方程:
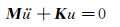 (5)
(5)
对压电结构进行模态分析,即求解式(4)的特征值问题,即:
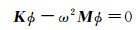 (6)
(6)
其中,φ为模态振型矩阵,ω为模态频率。
1.3 静力学分析模型静力分析用于计算结构在固定不变的载荷下的响应,是ANSYS默认的分析类型。该分析不考虑结构的惯性和阻尼影响,即忽略式(3)中所有惯性项和阻尼项的作用,适用于求解惯性和阻尼对结构响应的影响不重要的问题。
1.4 瞬态动力学分析模型动力学分析用于求解随时间变化的载荷对结构或部件的影响。与静力分析不同,动力学分析需考虑随时间变化的力载荷及其对阻尼和惯性的影响。
本文的瞬态动力学分析用于求解天平在瞬态载荷冲击条件下的响应。在动力学分析中必须考虑阻尼项,否则不能获得收敛的振动响应结果。本文采用Rayleigh阻尼的施加方式,即首先假设结构的前两阶模态阻尼系数为ξ1=ξ2=0.08%,然后以下式计算Rayleigh阻尼比例系数:
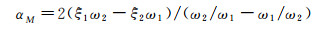 (7)
(7)
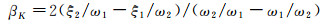 (8)
(8)
则最终的阻尼矩阵C为:
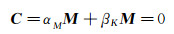 (9)
(9)
本文设计的压电天平是一台三分量梁式微应变天平。天平力敏梁的横截面为矩形,通过压电陶瓷片极性的组合实现分量间的抗干扰特性。当气动力作用于模型,天平力敏梁发生变形,粘贴其上的压电陶瓷片输出电荷,电荷量与力敏梁变形程度相关,通过检测电荷量即可测量作用于模型的气动力。天平前端通过锥段与模型连接,后端通过锥面配合、双头螺母拉紧的方式与模型支杆连接。
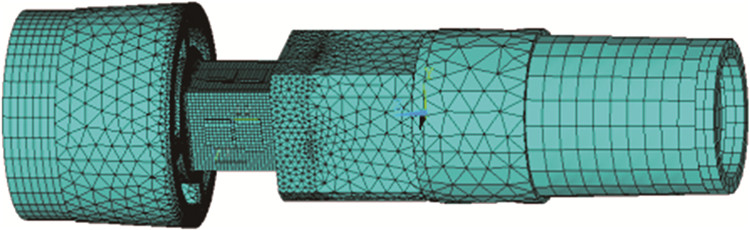
3 天平结构的有限元分析 3.1 有限元模型在有限元建模时,压电陶瓷片采用正压型的PZT-5,天平本体采用00Ni18Co8Mo5TiAl材料(性能参数见表 1。表中,c为弹性刚度矩阵元;E、ρ、μ分别为弹性模量、密度、泊松比;ε为介电常数;e为压电应力常数)。采用SOLID5压电耦合单元模拟压电陶瓷片(压电陶瓷片上会出现力场和压电场耦合,而SOLID5单元具有三维磁场、热场、电场、压电场和结构场分析能力,并能在各场之间实现有限的耦合);采用SOLID45单元模拟天平本体。建立的压电天平有限元模型如图 1所示。
|
| 图 1 压电天平的有限元模型 Fig.1 Finite element model |
| Parameter | 00Ni18Co8Mo5TiAl | PZT-5 |
| c11、c22/GPa | - | 115.65 |
| c12/GPa | - | 64.89 |
| c13、c23/GPa | - | 62.29 |
| c33/GPa | - | 92.98 |
| c44、c55/GPa | - | 17.86 |
| c66/GPa | - | 17.86 |
| E/GPa | 207 | - |
| ρ/(kg·m-3) | 7850 | 8640 |
| μ | 0.3 | - |
| ε11、ε22/(nF·m-1) | - | 8.93 |
| ε33/(nF·m-1) | - | 6.92 |
| e13、e23/(C·m-2) | - | -12.31 |
| e33/(C·m-2) | - | 20.76 |
| e52、e61/(C·m-2) | - | 17.04 |
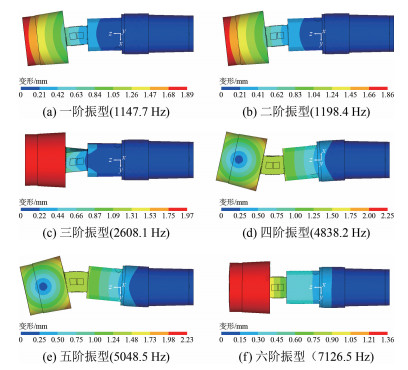
模态分析的主要目的是获得天平的各阶振动频率和振型,以判断其是否满足激波风洞测量的需求。本文主要计算了压电天平的前6阶固有频率和相应的振型(如图 2所示),可以看出:压电天平的一阶和二阶振型分别为天平支杆沿侧向和法向的摆动(力敏梁的宽度和高度分别为20和22 mm,因此一阶和二阶振动频率有少许差异);三阶振型为天平支杆沿轴线的滚转运动;四阶和五阶振型为天平支杆沿法向和侧向的弯曲摆动;六阶振型为天平支杆沿轴向的伸缩运动。
|
| 图 2 压电天平前6阶振型 Fig.2 The first six modal shapes of piezoelectric balance |
模态分析结果表明:压电天平的频响相对较高,前两阶振动频率均超过1 kHz,可以满足激波风洞测力试验的需求。
3.3 静力分析压电天平的灵敏度、线性度、抗干扰能力是其设计的关键,以ANSYS软件进行静力分析的方法能够获得上述性能指标,从而很好地评估天平设计的合理性。静力分析的目的就是为了获得天平输出与施加载荷之间的关系。本文在不同加载条件下计算了天平各分量的电压输出情况,评估天平各分量的主灵敏度系数和干扰灵敏度系数。
采用类似天平单元校准的方案,即一次只施加一个载荷,得到天平各分量的输出,取主分量电势输出为Vz,其他干扰分量电势输出为Vgi,则主灵敏度系数εz可以定义为主分量输出电势Vz和外加载荷Fz的比值,而干扰灵敏度系数εgi是其他分量输出电势Vgi和外加载荷Fz的比值:
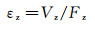 (10)
(10)
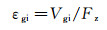 (11)
(11)
在静力分析的加载中,为了实现在天平力矩中心加载,在模型中应用附加质量和局部刚度化处理。在天平的力矩中心生成一个节点,设置为质量单元,质量为1×10-12 kg,将该节点与天平前端连接锥面上的节点通过局部刚度化进行耦合处理,再将该节点作为加载点分别进行力、力矩以及综合加载。这样处理的好处是:在进行法向力加载时,可以避免引入附加的俯仰力矩干扰,从而得到更为准确的主灵敏度系数和干扰灵敏度系数计算结果。
3.3.2 天平各分量灵敏度分析在轴向力加载中,分别进行了10、100、200、350和500 N的加载。从各加载条件下天平各分量输出电压(表 2)可见,轴向力分量VA的主灵敏度系数较大,轴向力加载对其他2个分量(VN为法向力分量,VMz为俯仰力矩分量)的干扰很小。
| Axial force/N | VA/V | VN/V | VMz/V |
| 10 | -0.204 | 5.00×10-5 | 1.00×10-4 |
| 100 | -2.04 | 5.00×10-4 | 1.00×10-3 |
| 200 | -4.08 | 1.00×10-3 | 2.10×10-3 |
| 350 | -7.13 | 1.70×10-3 | 3.70×10-3 |
| 500 | -10.20 | 2.50×10-3 | 5.30×10-3 |
| Sensitivity | -2.04×10-2 | 4.96×10-6 | 1.07×10-5 |
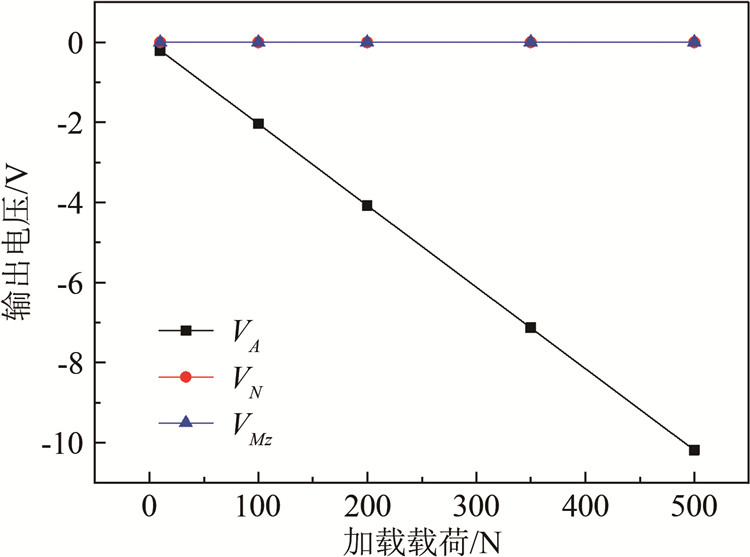
轴向力加载时各分量的输出电压随加载载荷的变化如图 3所示,可见压电天平结构响应的线性特性显著。采用类似方法对法向力和俯仰力矩的测量灵敏度进行评估,结果表明:天平整体的结构响应线性特性显著。
|
| 图 3 各分量输出电压随加载载荷的变化 Fig.3 The balance output voltage with different axial force loads |
综合加载用于评估天平整体性能。在综合加载验证中,在加载点同时施加350 N的轴向力、150 N的法向力和1 N·m的俯仰力矩。从各分量输出电压(表 3)可以看出,综合加载的输出为各分量单独加载的输出之和,这也说明采用单独加载的方案能够实现天平灵敏度的评估。
| Load mode | VA/V | VN/V | VMz/V |
| Axial force | -7.13 | 1.70×10-3 | 3.70×10-3 |
| Normal force | -1.00×10-4 | 9.47 | -0.913 |
| Pitching moment | -2.70×10-3 | -1.40×10-3 | 5.10 |
| Sum above | -7.14 | 9.47 | 4.19 |
| Composite load | -7.14 | 9.47 | 4.19 |
在实际使用中,压电天平测量得到的是压电片上的电荷输出量,而不是电压输出量。为实现与真实校准结果的对比分析,本文将ANSYS评估得到的天平的电压灵敏度系数通过下式转变为电荷灵敏度系数[3]:
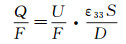 (12)
(12)
其中,ε33为PZT压电陶瓷的Z向介电常数,Q为电荷输出量,U为电压输出值,F为力载荷,S为压电陶瓷片的面积,D为压电陶瓷片的厚度。
从静力分析得到的天平的电荷灵敏度系数(表 4)可以看出:压电天平各分量具有较高的主灵敏度系数和较小的干扰灵敏度系数,天平具有较强的抗干扰能力。
| Component | VA/mV | VN/mV | VMz/mV |
| Axial force | -14.10 | 3.361×10-3 | 7.315×10-3 |
| Normal force | -4.152×10-4 | 43.69 | -4.211 |
| Pitching moment | -1.799 | -0.9688 | 3.529×103 |
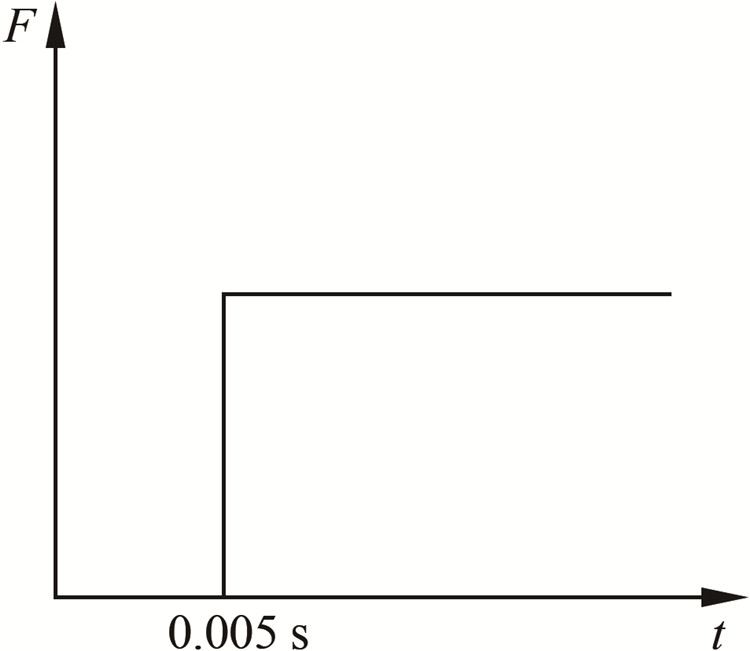
对压电天平进行了瞬态加载过程的模拟,以研究其动力学特性。动力学分析的加载过程分为2个阶段:前0.005 s为载荷为0的阶段;从0.005 s开始施加阶跃载荷,模拟突然加载的过程,考察天平对阶跃载荷的响应特性,时间间隔为0.0001 s。加载曲线如图 4所示。
|
| 图 4 动力学分析加载过程 Fig.4 Load process in transient analysis |
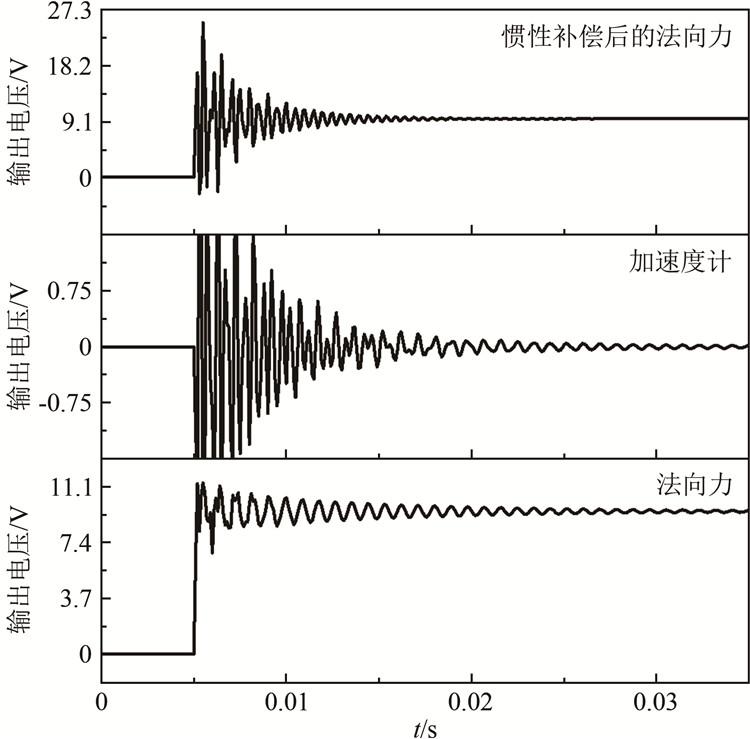
动力学分析为综合模拟,加载的载荷为轴向力350 N、法向力150 N、俯仰力矩1 N·m。计算加载过程中天平各分量的电压输出情况。在动力学分析中,对加速度计的输出特性也进行了模拟,图 5为使用加速度计惯性补偿前后的天平法向力的输出电压曲线。
|
| 图 5 法向力输出补偿结果 Fig.5 The compensation results of normal force output |
动力学分析的结果表明:进行惯性补偿后,天平输出信号平直段的信号大小与静力分析的结果一致。法向力分量和俯仰力矩分量的补偿效果类似,而轴向力分量的频响较高,这也与试验结果一致。风洞试验中,对于法向力分量和俯仰力矩分量,在风洞有效试验时间内,天平一阶振动得不到完全阻尼,天平输出的是多种频率的振动信号和有效试验信号的叠加信号,必须使用加速度计对振动信号进行补偿,才能在试验中得到可靠的气动力数据。从图 5可以看出,使用加速度计可以对振动信号进行补偿,但在补偿过程中,又将加速度计的高频振动信号引入了试验信号中。在实际使用中,需要采用滤波方法滤除加速度计的高频振动信号,再对试验信号进行补偿。
4 天平校准和风洞试验结果分析 4.1 天平校准结果压电天平制作完成后,采用单分量校准的方式进行了静态校准,即保持其他分量为常量,每次只校准一个分量。压电天平静态校准结果见表 5。
| Component | VA/mV | VN/mV | VMz/mV |
| Axial force | -12.46 | 0.5898 | 1.089 |
| Normal force | -5.816×10-2 | 38.37 | 3.397 |
| Pitching moment | -50.23 | -1.349 | 3.11×103 |
对比表 4和表 5,可以看出:对于天平各分量的主灵敏度系数,天平校准结果比ANSYS模拟结果小12%左右。其主要原因是:在ANSYS模拟时,考虑的是一种理想状态,压电陶瓷片厚度采用名义值0.5 mm,但其实际厚度与名义值存在差异;另外,也未考虑压电片陶瓷片与力敏梁之间环氧树脂胶层的影响(因其厚度无法测量),从而造成天平校准得到的主灵敏度系数小于模拟得到的结果。
但天平的干扰灵敏度系数均远大于模拟得到的结果,某些分量间的干扰灵敏度系数存在量级差别。其主要原因是:(1)配对使用的压电陶瓷片的性能不完全一致,各分量间的干扰不能通过压电陶瓷片的极性选择完全抵消;(2)加工和校准天平时,力敏梁的结构对称性和天平安装位置存在误差。但在实际校准中,天平的干扰灵敏度系数是小量,因此,使用ANSYS有限元分析软件预估压电天平的性能是有效的。
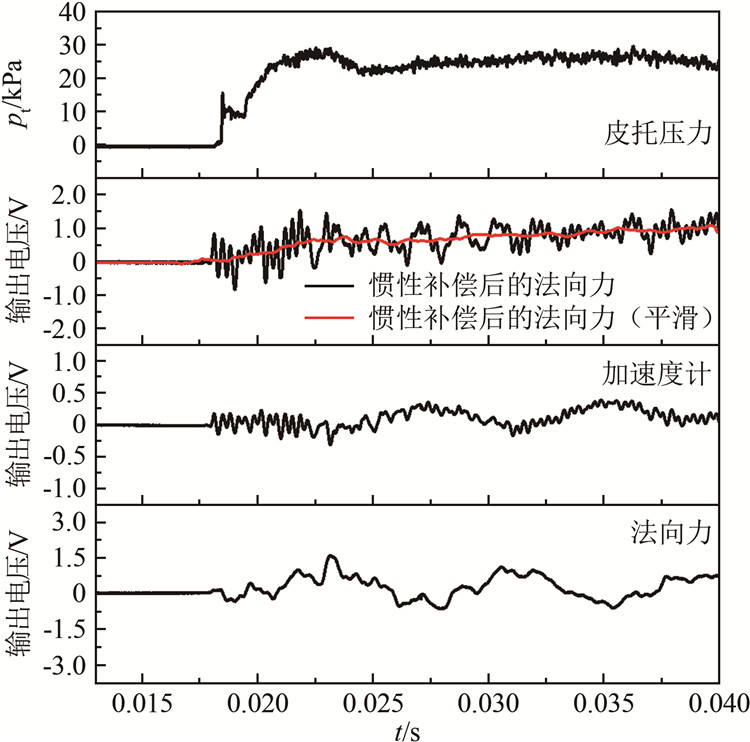
4.2 风洞试验结果为了检验天平的性能,在0.6 m激波风洞上进行了APOLLO模型测力验证试验。图 6为天平法向力、加速度计、惯性补偿后的法向力以及皮托压力输出曲线。从图中可以看出:使用加速计进行补偿后,可以明显去除法向力输出信号中的低频分量,这与模拟结果一致。经过加速度计补偿后的法向力输出曲线与皮托压力输出曲线有很好的跟随性。在风洞试验中,加速度计的一阶振动频率与模拟结果不一致,这主要是因为连接支杆的存在以及模型质量的影响,导致系统振动频率降低。
|
| 图 6 法向力试验输出信号 Fig.6 The normal force output in shock tunnel experiment |
利用ANSYS力电耦合的有限元分析方法,对一台三分量压电天平的性能进行了评估,并与天平实际校准结果进行了对比,得到如下结论:
(1) 静力学分析的结果表明,设计的三分量压电天平具有较好的线性特征,天平的主灵敏度系数较高,抗分量间干扰的效果较好。
(2) 模态分析的结果表明,天平的频响较高,通过加速度计对天平的一阶振动干扰进行补偿后,可以满足激波风洞毫秒级测力试验需求。
(3) 瞬态动力学过程分析能够评估压电天平的动态特性以及加速度计惯性补偿方案的有效性。
本文将ANSYS应用于压电天平设计,可以在设计阶段评估天平性能,达到为天平设计服务的目的。
| [1] |
贺德馨.风洞天平[M].北京: 国防工业出版社, 2001.
|
| [2] |
唐志共.高超声速气动力试验[M].北京: 国防工业出版社, 2004.
|
| [3] |
DURYEA G R, MARTIN J F. An improved piezoelectric balance for aerodynamic force measurements[J]. IEEE Transactions and Aerospace and Electronic Systems, 1968. |
| [4] |
MARINEAU E C. Force measurements in hypervelocity flows with an acceleration compensated piezoelelctric balance[J]. Journal of Spacecraft and Rockets, 2011, 48(4): 697-700. DOI:10.2514/1.A32047 |
| [5] |
SMOLINSKI G. Proof of concept for testing acceleration compensation force balance techniques in short duration flows with a CEV capsule[R]. AIAA-2007-1010, 2007.
|
| [6] |
孟宝清, 韩桂来, 姜宗林. 结构振动对大型激波风洞气动力测量的干扰[J]. 力学学报, 2016, 48(1): 102-110. MENG B Q, HAN G L, JIANG Z L. Theoretical investigation on aerodynamic force measurement interfered by structural vibrations in large shock tunnel[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(1): 102-110. |
| [7] |
MARNEAU E C, MACLEAN M, MUNDY E P, et al. Force measurements in hypervelocity flows with an acceleration compensated strain gauge balance[J]. Journal of Spacecraft and Rockets, 2012, 49(3): 474-482. DOI:10.2514/1.A32041 |
| [8] |
吕金洲, 张小庆, 陈光雄, 等. 基于惯性补偿的脉冲风洞测力天平瞬态研究[J]. 振动与冲击, 2018, 37(2): 216-222. LYU J Z, ZHANG X Q, CHEN G X, et al. Transient simulation for dynamic output of force measuring balance in an impulse combustion wind tunnel based on inertia compensation[J]. Journal of Vibration and Shock, 2018, 37(2): 216-222. |
| [9] |
谢龙汉, 刘新让, 刘文超. ANSYS结构及动力学分析[M].北京: 电子工业出版社, 2012.
|
| [10] |
黄亮.压电式四维力传感器的有限元仿真分析和设计[D].重庆: 重庆大学, 2008. HUANG L. Finite element simulation analysis and design of a four-axis piezoelectric force sensor[D]. Chongqing: Chongqing University, 2008. |
| [11] |
郑芳, 武家騊. ANSYS在风洞天平设计中的应用[J]. 流体力学实验与测量, 2004, 18(1): 80-83. ZHENG F, WU J T. Application of ANSYS method to the design of wind tunnel balance[J]. Experiments and Measure-ments in Fluid Mechanics, 2004, 18(1): 80-83. DOI:10.3969/j.issn.1672-9897.2004.01.018 |
| [12] |
张世雄.杆式应变天平结构分析与优化设计[D].北京: 北京理工大学, 2016. ZHANG S X. Structure analysis and optimization design for sting strain balance[D]. Beijing: Beijing Institute of Technology, 2016. |
| [13] |
WANG Y H, LIU W, XIE B, et al. Research on a micro-rolling-moment six-component strain gauge balance of composite structure[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(3): 76-79, 98. |
| [14] |
史玉杰, 黄勇, 田正波. 小展弦比飞翼布局高速标模测力天平研制[J]. 实验流体力学, 2015, 29(5): 50-54. SHI Y J, HUANG Y, TIAN Z B. Strain gauge balance development for force test on small aspect ratio flying wing high speed standard model[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(5): 50-54. |
| [15] |
胡国风. 应变天平矩形截面元件扭转应变计算准度分析[J]. 实验流体力学, 2012, 26(6): 75-78. HU G F. Accuracy analysis of the torsion strain calculation of a balance with rectangular cross-section[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(6): 75-78. DOI:10.3969/j.issn.1672-9897.2012.06.016 |
| [16] |
汪运鹏, 刘云峰, 苑朝凯, 等. 长试验时间激波风洞测力技术研究[J]. 力学学报, 2016, 48(3): 545-556. WANG Y P, LIU Y F, YUAN C K, et al. Study on force measurement in long-test duration shock tunnel[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(3): 545-556. |
| [17] |
LYU H Y, QIN L, LIU J. Principle research on a single mass six-degree-of-freedom accelerometer with six groups of piezoelectric sensing elements[J]. IEEE Sensors Journal, 2015, 15(6): 3301-3310. DOI:10.1109/JSEN.2014.2387829 |
| [18] |
汪泽浩.一种基于压电陶瓷晶体的振动能量回收装置的研究[D].杭州: 浙江大学, 2015. WANG Z H. A study on vibration energy recovery device based on piezoelectric ceramic crystal[D]. Hangzhou: Zhejiang University, 2015. |
| [19] |
OOI B L, GILBERT J M, AZIZ A R A, et al. Analytical and finite-element study of optimal strain distribution in various beam shapes for energy harvesting applications[J]. Acta Mechanica Sinica, 2016, 32(4): 670-683. DOI:10.1007/s10409-016-0557-3 |
| [20] |
刘月.周期性强冲击振动环境下d15模式压电俘能器研究[D].大连: 大连理工大学, 2017. LIU Y. Study of d15 mode piezoelectric energy harvesting under periodic strong impact vibration[D]. Dalian: Dalian university of technology, 2017. |
| [21] |
ZHU X J, ZHAO M, GAO Z Y, et al. Analysis of active vibration control for piezoelectric intelligent structures by ANSYS and MATLAB[C]//Proc of the 2010 International Conference on Computer Application and System Modeling (ICCASM 2010). 2010.
|
| [22] |
王飞.五维力杆式压电天平的研制[D].大连: 大连理工大学, 2015. WANG F. Development of five components stick-piezoelectric wind tunnel balance[D]. Dalian: Dalian University of Techno-logy, 2015. |
| [23] |
戴星, 汤世友. 基于压电效应的三分量动态天平的研制[J]. 河南科技, 2014(1): 60-61. DAI X, TANG S Y. The development of three component dynamic balance based on piezoelectric effect[J]. Journal of Henan Science and Technology, 2014(1): 60-61. |
| [24] |
李盼, 杨睿, 任宗金, 等. 全动舵面载荷测量的压电天平设计与误差分析[J]. 哈尔滨工业大学学报, 2018, 50(1): 181-185. LI P, YANG R, REN Z J, et al. Design and error analysis of a piezoelectric balance for the measurement of aerodynamic loads on all-movable rudder[J]. Journal of Harbin Institute of Technology, 2018, 50(1): 181-185. |
| [25] |
赵荣娟, 吕治国, 黄军, 等. 基于压电敏感元件的摩阻天平设计[J]. 空气动力学学报, 2018, 36(4): 555-560. ZHAO R J, LYU Z G, HUANG J, et al. Design of skin friction balance based on piezoelectric ceramics[J]. Acta Aerodynamica Sinica, 2018, 36(4): 555-560. DOI:10.7638/kqdlxxb-2016.0112 |



