在超精细粉末制备过程中,其表面晶格被破坏,表面活性大大增强,因而表现出良好的物理化学性质,被广泛应用于化工、材料等诸多领域,其制备工艺也得到了深入研究。气流磨具有颗粒自研磨无污染、损耗低、粉体尺寸均匀、适用于热敏感材料等优点,被业内普遍关注[1-2];但也存在效率低、能耗大等缺点[3],应用受到限制。随着绿色化学的兴起,如何进一步提高气流磨研磨效果并拓展其应用,成为超精细粉末制备行业的关注焦点[4-5]。
气流磨的原理是利用高速气流对颗粒进行加速,实现颗粒之间、颗粒与固壁之间的碰撞,从而达到研磨的目的,其核心是气固两相流和气动布局设计问题[6-7]。本文基于对传统气流磨流动特点的分析,提出一种中心引射式环状超声速气流磨布局方案,通过理论估算确定其核心部件“环状喷管”的外形及工作参数,并通过数值模拟及铁粉循环碰撞试验对设计加工的超声速靶式气流磨进行了方案验证。
1 典型气流磨中的流动特征在气流磨中,颗粒被高速气流裹挟,得到极高的动能,并通过高速碰撞实现动能到化学能的转换,因此,提高颗粒动能、实现高速碰撞是气流磨的设计核心。提高颗粒动能,最直接的方法是提高气流速度,即以超声速气流携带颗粒;实现高速碰撞,则需使颗粒充分加速并维持碰撞速度,并避免激波等减速因素。
工业领域的气流磨主要有旋流式、流化床式和靶式3大类[3]。大量的数值研究[8-10]表明:在旋流式、流化床式气流磨的旋流流场中难以获得超声速气流;而在靶式气流磨中,即使使用了Laval喷管,由于碰撞室中存在复杂的激波结构,超声速气流难以维持,也无法实现超声速碰撞。
Dogbe等[12]的研究表明:颗粒的碰撞动能和体积浓度是气流磨气动设计的关键。由于颗粒从壁面进入并分散于高速气流中,颗粒体积浓度较低,运动轨迹高度分散,其碰撞概率难以预测[11]。为提高颗粒碰撞概率,通常需增加颗粒在碰撞室中的滞留时间,这样就只能采用一种旋流流场,导致气流速度降低,使整个设计陷入两难境地。
2 超声速靶式气流磨的理论设计 2.1 工作原理通过上节分析可知,气流磨设计有3个关键问题:如何得到一个超声速流场;如何维持颗粒动能;如何提高碰撞概率。基于此,本文提出了一种中心引射式环状超声速靶式气流磨方案。如图 1所示,该气流磨由中心加料管、环状收缩扩张喷管、加速段、碰撞室和靶头5个部分组成。其工作原理为:

|
| 图 1 环状超声速靶式气流磨示意图 Fig.1 The schematic of the annular supersonic target jet mill |
自气源入口g引入高压气流,经环状收缩扩张喷管b加速至超声速状态,在引射截面h处达到压力最小值,从而在加料管a中形成顺流向的压降。该压降将自加料管入口f吸入的颗粒输送到下游的引射截面h,在该截面形成外圈的超声速气流对管道中心的亚声速气流的引射。携带颗粒的亚声速气流在加速段c中持续加速,使颗粒达到超声速并获得极高的动能。由于在加速段中径向速度较小,颗粒在管道中心维持颗粒束状态i并进入锥状碰撞室d,以极高动能准确碰撞于靶头, 实现粉碎。在出口j对粉碎产物进行回收、分级,并将大颗粒再次输送至加料管入口f作循环粉碎。
2.2 参数计算环状收缩扩张喷管和中心加料管是整个气流磨的核心气动部件,需作深入计算分析。假定环状收缩扩张喷管中的流动满足变截面等熵流假设、加料管中的流动为一维绝热摩擦管流, 在给定来流总温和总压、喷管工作马赫数以及环境参数的基础上,可以对喷管和加料管中的流动进行理论估算:
(1) 环状收缩扩张喷管中的变截面等熵流
 (1)
(1)
 (2)
(2)
式中,A、Athr分别为环状喷管出口截面积、环状喉道截面积;Ma为设计马赫数;γ为空气比热比(取γ=1.4);p0、T0为上游高压气源的总压、总温,p、T为喷管出口的静压、静温。
(2) 加料管中的绝热摩擦管流
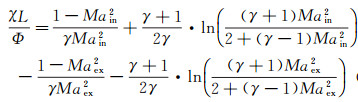 (3)
(3)
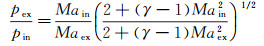 (4)
(4)
 (5)
(5)
式中,χ为壁面平均摩擦系数,可以由Moody图进行估算[13];L和Φ为几何长度和直径,在式(3)中表示加料管长度和直径;下标“in”和“ex”分别为各个部件对应的上游入口和下游出口处的参数,这里假定引射截面(h截面)处压力均匀。
给定气流磨几何参数,基于上述关系式可计算得到相关参数(见表 1)。表 1中,β为壁面倾角,
| 几何参数 | 热力学参数 | 动力学参数 | |
| 环状喷管 | Athr=15.7 mm2 Aex=66.5 mm2 |
p0=1.5 MPa T0=300 K pex=40.8 kPa Tex=107 K |
Ma=3.0 uex=622 m/s  =0.055 kg/s =0.055 kg/s |
| 加料管 | A=7.07 mm2 L=0.1 m |
patm=0.1 MPa Tatm=300 K |
uex=317 m/s =0.0013 kg/s =0.0013 kg/s |
| 加速段 | L=0.4 m Φin=10.02 mm Φex=14.00 mm |
||
| 碰撞室 | β=3° | pout=0.1 MPa T0,out=300 K |
|
| 靶头 | Φ=4.00 mm | ||
| 壁面 | χ=0.03 |
气流磨是一个复杂的循环系统(本文设计的中心引射式环状超声速靶式气流磨是其核心部件,此外还包括高压气源、颗粒分级器、颗粒回收系统、下游引风机以及气力输运管路等,在第4节具体阐述),对整个循环系统进行数值模拟极其困难,需要对颗粒循环研磨过程(颗粒分级器拦截的大尺度颗粒会被气力输运至加料管,再次进入气流磨循环研磨)进行简化。假定相同粒径的颗粒每次循环过程都保持一致,并假定颗粒为球形,因此,仅需模拟不同粒径的颗粒在气流磨中的一次加速与碰撞过程。
3.1 数值方法气流磨涉及的流动属于典型的气固两相流,且固相体积浓度小于5%,因此,采用多相流中的离散相(Discrete phase model, DPM)模型对颗粒与气体的相互作用进行模拟,通过模拟颗粒的运动速度和运动轨迹来评价气流磨的碰撞研磨效果。DPM模型是一种典型的模拟体积浓度小于10%的多相流模型,以欧拉观点的Navier-Stokes方程描述流体相,以拉格朗日观点的牛顿定律描述颗粒相,两项之间以曳力模型实现动量交换。
气相控制方程为雷诺平均的可压缩Navier-Stokes方程,并采用k-ε湍流模型来考虑湍流对多相流的影响:
 (6)
(6)
式中,ρ、p、h、u分别为气相的密度、压力、总焓和速度,g、μ、μT分别为重力加速度矢量、粘性系数和涡粘系数,Fgp为颗粒相与气相的相互作用力,σh为湍流模式对应的普朗特数(σh=0.9),t为时间。
颗粒相控制方程为拉格朗日观点下的牛顿第二运动定律,即:
 (7)
(7)
式中,
方程离散采用基于密度求解器的有限体积法,时间上采用隐式格式求解。考虑到气流磨的对称性,数值模拟采用轴对称定常模型。考虑径向和流向上的流动,忽略周向流动,因此仅需求解气流磨对称面上的流动方程。整个计算域按照理论计算结果(表 1)并采用四边形进行离散,网格量为34 130,大多数网格集中于壁面剪切区和中心引射区。气流磨加料口和高压气源入口均采用压力入口条件,碰撞室出口采用压力出口条件,所有壁面均假定为无滑移壁面。相关气相流动参数见表 1。
假定参与循环碰撞的颗粒为不同粒径(1、5、10、15、20和25 μm)的球形颗粒(模拟铁粉颗粒,ρp=7800 kg/m3)。每次模拟同一粒径的1000个球形颗粒从加料口以40 m/s的初速度均匀注入流场,采用DPM模型跟踪计算其速度和轨迹,并评价其碰撞动能和碰撞概率。
3.2 模拟结果 3.2.1 基本流场图 2给出了无颗粒注入时的基本流场。图 2(a)为喷管附近的流场,可见在喷管出口处就已获得环状超声速气流,引射截面外环的超声速气流对中心气流有明显引射作用,加料管内的气流速度已接近声速;图 2(c)为加速段内的流场,可见引射中心气流被逐步加速至超声速;图 2(b)为碰撞室内的流场,可见在加速段出口处速度剖面比较均匀,速度达到530 m/s,超声速气流在靶头上形成弓形激波结构。图 2表明在整个装置中建立了超声速流场。

|
| 图 2 装置中速度场的数值模拟结果 Fig.2 The velocity field in the jet mill by numerical simulation |
图 3和4为不同粒径颗粒的两相流模拟结果。图 3给出了粒径分别为1、5、10、15、20和25 μm的颗粒沿轴向的加速过程。粒径为1 μm的颗粒与气流完全跟随,而粒径较大的颗粒则对流场速度变化有时间迟豫,但总体而言,颗粒在加速段中都得到了足够加速(速度约为440~530 m/s)并获得充分的动能。靶头前的弓形激波会使气流突然减速,导致跟随性较好的小颗粒减速,而大颗粒则因惯性可以轻松穿透激波并碰撞靶头,如图 3中的放大图所示。图 4给出了粒径为1和25 μm的颗粒运动轨迹,颗粒的运动轨迹汇聚于流道中心,形成一股超声速颗粒束,在碰撞室中与靶头的碰撞概率很高。第一次碰撞都为超声速碰撞(速度约为500 m/s),部分颗粒还会发生第二次、第三次碰撞。

|
| 图 3 不同粒径的颗粒的轴向速度在中轴线上的加速过程 Fig.3 The accelerating process of the streamwise velocity of particles with different diameters along the axis |

|
| 图 4 采用DPM两相流模拟的不同粒径颗粒的运动轨迹 Fig.4 The motion trajectories of particles with different diameters numerically simulated by the discrete phases model |
为进一步验证设计方案、评估颗粒粉碎效果,制造了如图 5所示的气流磨。除图 1所示的气流磨核心部件外,还配置了高压气源、颗粒分级器、颗粒回收系统、下游引风机以及气力输运管路等(相关参数见表 1)。其工作过程为:从漏斗加入物料,先后打开引风机和高压气源,此时超声速流场就会在加速段和碰撞室中建立,将颗粒引射进入流场实现超声速碰撞。粉碎产物经分级器分离后,大颗粒再次进行循环粉碎,而小颗粒则被回收。

|
| 图 5 超声速气流磨 Fig.5 The supersonic jet mill |
在不含颗粒的超声速流场验证试验中,以中轴线上的超声速皮托管直接测量当地的波后总静压,并按照激波公式换算流场马赫数,来流总温由高压气源参数给出。表 2为不同来流总压下的测量结果。在试验给定总压范围内流场都是超声速流场,而在设计工况p0=1.5 MPa下,碰撞室入口的马赫数已经达到2.77。
| p0 /MPa | p/MPa | Ma | v/(m·s-1) | Kinetic energy/(J·g-1) |
| 0.5 | 0.091 | 1.77 | 481 | 115 |
| 1.0 | 0.082 | 2.29 | 555 | 154 |
| 1.5 | 0.058 | 2.77 | 604 | 182 |
| 2.0 | 0.053 | 3.02 | 623 | 194 |
为研究颗粒的碰撞能量,在气流磨中开展了铁粉碰撞粉碎试验。分别采用了圆柱型和圆盘型靶头,靶头和颗粒都采用相同的铁材料(高铬钢GCr5)。试验开始时,加入200 g平均粒径为60 μm的铁粉颗粒,进行90 min气流粉碎试验。图 6对比了试验前后的靶头形状,两种靶头的中心都被侵蚀出一个凹坑,表明颗粒在实验中获得了足够动能,聚集于流道中心并与靶头实现了聚焦式碰撞。

|
| 图 6 铁粉粉碎试验中靶头的侵蚀效果 Fig.6 The targets' erosion photographs of the iron particle size-reduction tests |
为进一步验证研磨效果,在电镜下仔细观察了粉碎前后的铁粉颗粒微观形貌,并对颗粒进行了粒径分析。由图 7(a)颗粒微观形貌电镜照片对比可以看出,细化后的颗粒表面不再光滑,其晶格被显著破坏,从而使表面化学性能得到有效改善。图 7(b)为粉碎前后铁粉颗粒的粒径分布,经过超声速碰撞,铁粉颗粒明显细化(统计粒径见表 3),d50自64.3 μm降低至7.8 μm。从铁粉的微观形貌和粒径分析可以推断:铁粉在碰撞时具有很大的动能,这也证实了铁粉颗粒从超声速气流中获得了很大的动能。

|
| 图 7 铁粉颗粒碰撞试验结果 Fig.7 The results of the iron particles size-reduction test |
| d10/μm | d50/μm | d90/μm | |
| Before | 28.2 | 64.3 | 150.8 |
| After | 2.6 | 7.8 | 29.9 |
基于对传统气流磨流动特征的研究,设计制造了一种新型超声速靶式气流磨。在新型气流磨中,采用环状超声速流动引射加速颗粒流,使颗粒最终达到超声速状态并获得极大动能,聚集于流动中心形成颗粒束,从而极大提升颗粒与靶头的碰撞概率。数值模拟结果表明:颗粒能够精准碰撞流场中心的靶头,实现超声速碰撞,碰撞速度可达500 m/s。铁粉颗粒的碰撞粉碎试验表明:在碰撞过程中,颗粒巨大的动能对靶头产生了显著的侵蚀效果。这说明新型气流磨可以使颗粒获得极大动能以及很高的碰撞效率。
| [1] |
BERTHIAUX H, DODDS J. Modelling fine grinding in a fluidized bed opposed jet mill: Part I: Batch grinding kinetics[J]. Powder Technology, 1999, 106(1-2): 78-87. DOI:10.1016/S0032-5910(99)00049-2 |
| [2] |
MIDOUX N, HOŠEK P, PAILLERES L, et al. Micronization of pharmaceutical substances in a spiral jet mill[J]. Powder Technology, 1999, 104(2): 113-120. DOI:10.1016/S0032-5910(99)00052-2 |
| [3] |
HIROAKI M, KO H, HIDETO Y. Powder technology handbook[M]. 3rd ed. Boca Raton: CRC Press, 2006.
|
| [4] |
TASIRIN S M, GELDART D. Experimental investigation on fluidized bed jet grinding[J]. Powder Technology, 1999, 105(1-3): 337-341. DOI:10.1016/S0032-5910(99)00156-4 |
| [5] |
NAKACH M, AUTHELIN J R, CHAMAYOU A, et al. Comparison of various milling technologies for grinding pharmaceutical powders[J]. International Journal of Mineral Processing, 2004, 74. |
| [6] |
CHAMAYOU A, DODDS J A. Air jet milling[M]//Salman A D, Ghadiri M, Hounslow M J. Handbook of Powder Technology: vol 12. Amsterdam: Elsevier, 2007: 421-435.
|
| [7] |
GHAMBARI M, SHAIBANI M E, ESHRAGHI N. Produc-tion of grey cast iron powder via target jet milling[J]. Powder Technology, 2012, 221: 318-324. DOI:10.1016/j.powtec.2012.01.020 |
| [8] |
LEVY A, KALMAN H. Numerical study of particle motion in jet milling[J]. Particulate Science and Technology, 2007, 25(2): 197-204. DOI:10.1080/02726350701257618 |
| [9] |
RAJESWARI M S R, AZIZLI K A M, HASHIM S F S. CFD simulation and experimental analysis of flow dynamics and grinding performance of opposed fluidized bed air jet mill[J]. International Journal of Mineral Processing, 2011, 98(1-2): 94-105. DOI:10.1016/j.minpro.2010.10.012 |
| [10] |
RODNIANSKI V, KRAKAUER N, DARWESH K, et al. Aerodynamic classification in a spiral jet mill[J]. Powder Technology, 2013, 243: 110-119. DOI:10.1016/j.powtec.2013.03.018 |
| [11] |
ESKIN D, VOROPAYEV S, VASILKOV O. Simulation of jet milling[J]. Powder Technology, 1999, 105(1-3): 257-265. DOI:10.1016/S0032-5910(99)00146-1 |
| [12] |
DOGBE S, GHADIRI M, HASSANPOUR A, et al. Fluid-particle energy transfer in spiral jet mill[J]. Powders and Grains, 2017, 140: 09040. |
| [13] |
WHITE F M. Fluid mechanics[M]. 4th ed. New York: McGraw-Hill Press, 2005.
|
| [14] |
SAFFMAN P G. The lift on a small sphere in a slow shear flow[J]. Journal of Fluid Mechanics, 1965, 22(2): 385-400. DOI:10.1017/S0022112065000824 |
| [15] |
WU W J, GIESE R F J, VAN OSS C J. Change in surface properties of solids caused by grinding[J]. Powder Technology, 1996, 89(2): 129-132. DOI:10.1016/S0032-5910(96)03158-0 |
| [16] |
XIAO Z L, CHEN Q Y, YIN Z L, et al. Calorimetric investigation of mechanically activated storage energy mechanism of sphalerite and pyrite[J]. Thermochimica Acta, 2005, 436(1-2): 10-14. DOI:10.1016/j.tca.2005.06.042 |
| [17] |
CROWE C T. Review-numerical models for dilute gas-particle flows[J]. Journal of Fluids Engineering, 1982, 104(3): 297-303. DOI:10.1115/1.3241835 |
| [18] |
ZHOU L X. Theory and numerical modeling of turbulent gas-particles flows and combustion[M]. Beijing: Science press and Florida: CRC press, 1993.
|



