2. 同济大学 上海地面交通工具风洞中心, 上海 201804;
3. 北京民用飞机技术研究中心, 北京 102211
2. Shanghai Automotive Wind Tunnel Center, Tongji University, Shanghai 201804, China;
3. Beijing Aeronautical Science &Technology Research Institute, Beijing 102211, China
方背Ahmed模型[1]是一种典型的类似于商用车的三维钝体模型, 气流在模型后缘发生分离, 形成回流区, 会导致背部压力较低, 带来较大的气动阻力和燃油消耗。对于方背Ahmed模型, 大约70%以上的阻力来自于背部负压的贡献[1-2], 因此充分理解其尾迹结构对于商用车辆减阻具有重要的科研价值。研究表明, 方背Ahmed模型尾迹区典型的定常流动特征为气流在后背的边缘发生分离, 形成涡流环, 涡流环是尾流区域内总压损失的主要部分[3-4]。为了更好地实现主被动控制减阻, 学者们对方背Ahmed模型的非定常尾迹进行了研究。研究表明Ahmed模型非定常尾迹中主要存在由全局振荡引起的垂向和侧向的涡脱落, 同时还伴随有回流区在流向方向和垂向方向上周期性的伸长和缩短(抽吸)[5-9]。近年来, Grandemange等[10-11]对1/4方背Ahmed模型研究发现其尾迹区呈现双稳态特性, 该特性包含2种确定且彼此关于垂直中截面对称的稳定流动结构, 并且这2种稳定状态之间的随机转换是长时间尺度的。
尽管关于方背Ahmed模型的尾迹研究已有一些工作, 但仍然没有充分理解其非定常特性, 尤其是双稳态特征与涡脱落以及回流区抽吸的关系。同时, 之前的研究未充分考虑到方背Ahmed模型尾迹的三维特性。为此, 本文通过测压、粒子图像测速(PIV)以及热线测量等实验手段, 对方背Ahmed模型的非定场尾迹进行精细测量和统计分析, 重点探究方背Ahmed模型的非定常流动结构的相互影响以及其三维流动特性, 为商用车的主被动减阻提供理论基础。
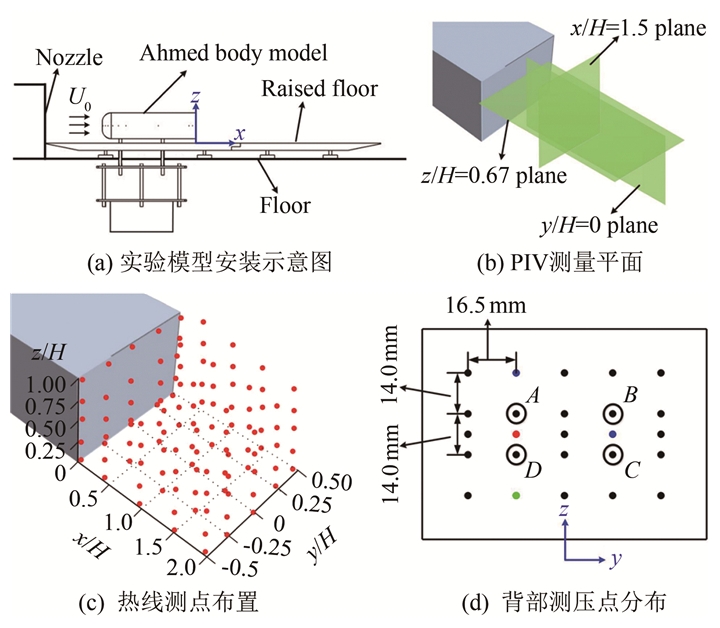
1 实验设置本实验在上海地面交通工具风洞中心1/15缩比的模型风洞中进行, 该风洞为3/4开口式回流风洞, 风洞实验段尺寸为1 m(长)×0.432 m(宽)×0.288 m(高), 实验段轴向静压梯度小于0.005 Pa/m, 来流的湍流度小于0.5%。实验模型为1/4缩比的方背Ahmed模型, 模型长度L=0.261 m, 宽度W=0.097 m, 高度H=0.072 m, 离地间隙为C=0.0125 m, 实验的阻塞比为5.8%, 远小于开口式风洞中的10%~ 12%的阻塞度限制, 因此其阻塞效应可以忽略。模型安装位置如图 1(a)所示。为了减少风洞地面剪切层的影响, 在风洞地板上方另外加设一块地板。实验时自由来流速度为U0=20 m/s, 雷诺数为Re=U0H/v= 9.2×104(U0为来流速度, H为模型高度, v为运动黏度)。
|
| 图 1 实验设置 Fig.1 Experimental setup |
在模型背部布置25个测压孔, 如图 1(d)所示。测压时通过1 mm的不锈钢管和测压软管将测压孔与传感器相连, 从而对模型表面测压孔位置进行压力测量, 测压采样频率为50 Hz, 采样总时间为600 s。利用粒子图像测速技术(PIV)测量模型尾部区域的速度分布, 包括3个测量平面:水平中截面z/H=0.67、垂直中截面y/H=0以及x/H=1.5平面, 如图 1(b), PIV采样频率为1.25 Hz, 实验中每个平面样本数量为1000帧。利用热线风速仪测量了尾迹区内116个点的速度, 采样点的布置如图 1(c)所示, 采样频率为2 kHz, 采样时间为60 s。
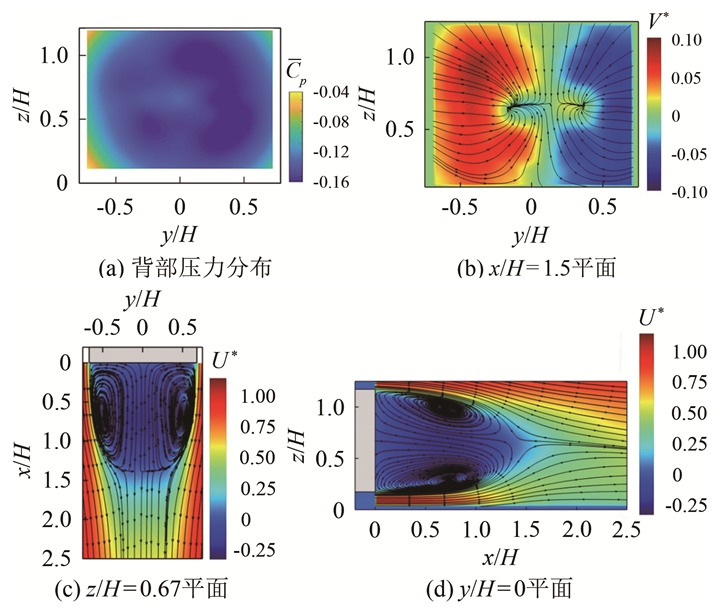
2 时均流场图 2展示了压力以及3个PIV测量平面的时均流场, 速度利用自由来流速度进行无量纲化。从压力的时均图可以看出, 存在一个涡环结构, 涡流环区域内总压损失, 引起压差阻力。而水平方向及垂直方向上的时均场与前人研究基本一致, 即水平方向上左右涡结构基本对称, 垂直方向上(由于地面效应的存在)上下涡结构呈现不对称性。从图 2(b), 即x/H=1.5平面的时均场也可以看出, 尾迹区左右基本对称。
|
| 图 2 时均流场 Fig.2 Time-averaged flow field |
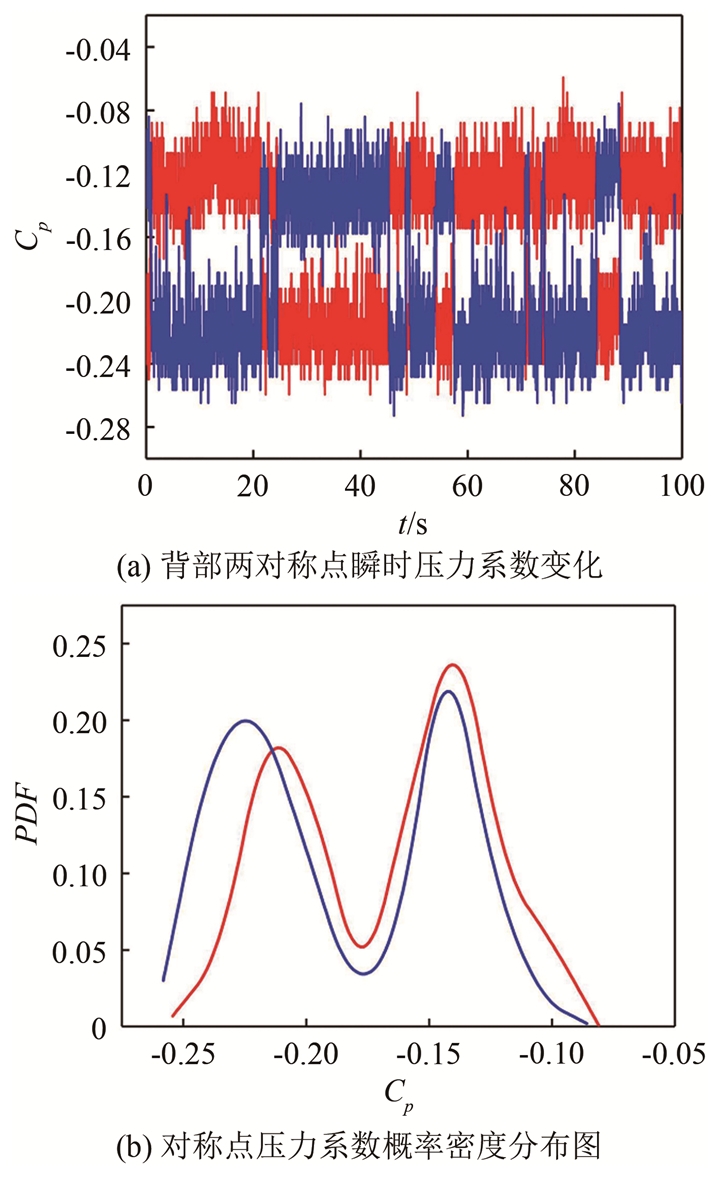
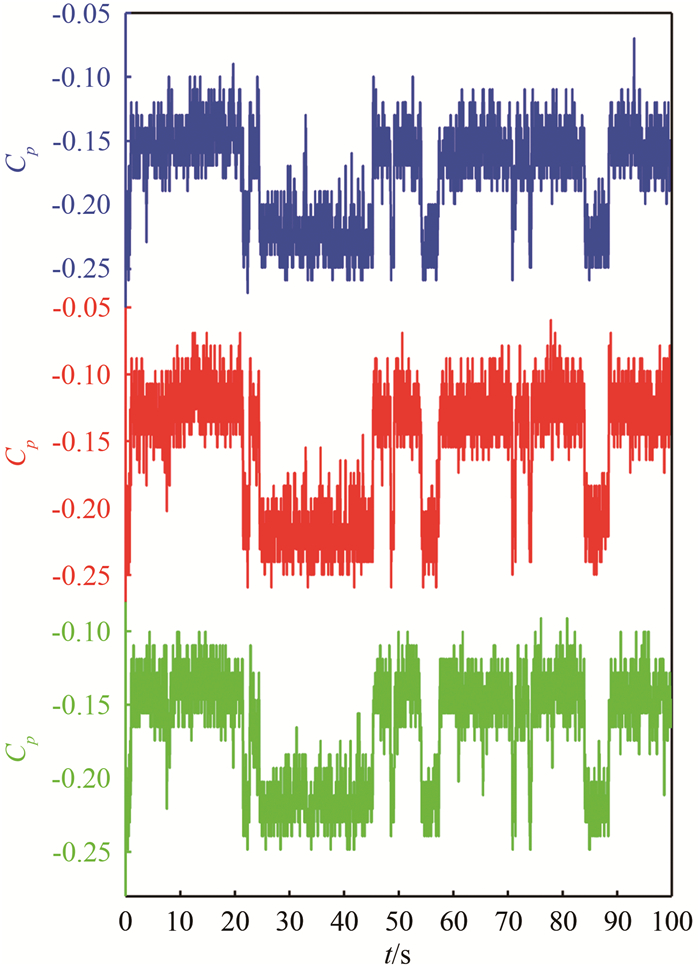
图 3(a)展示了100 s内背部水平中截线上两对称位置测压点(见图 1(d))的压力系数Cp随时间的变化。可以观察到左右测点的压力系数Cp均能在某一特定值稳定维持一段时间, 约为10 s, 随后转换到另一特定值, 这2个特定的稳定状态被称为双稳态。左右测点的压力系数的概率密度分布会呈现出2个明显的峰值, 如图 3(b)所示。而对于垂直方向上的3个压力测点(见图 1(d)), 如图 4所示, 压力系数Cp随时间的变化是同相位的, 不存在水平方向上反相位变化的情况。
|
| 图 3 背部两对称点压力测量结果 Fig.3 Pressure result of two symmetrical points on the back |
|
| 图 4 背部垂直方向测点瞬时压力系数变化 Fig.4 Instantaneous Cp of three pressure taps in the vertical direction on the back |
在模型背部选择4个测压点A、B(y/H=±0.23, z/H=0.77), C、D(y/H=±0.23, z/H=0.57), 如图 1(d)所示, 将水平方向和垂直方向压力梯度定义为:
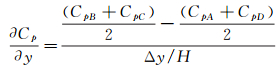 (1)
(1)
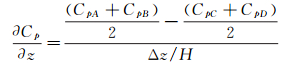 (2)
(2)
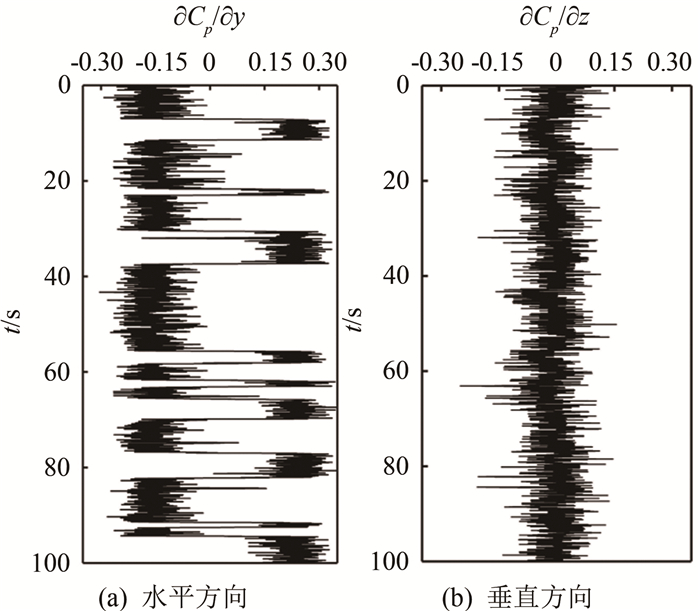
则可以得出如图 5所示的压力梯度随时间的变化。明显可以看出, 在100 s时间内, 水平方向的压力梯度与图 5(a)所示的瞬时压力变化趋势相同, 即在某一偏离零点的特定值稳定维持一段时间后转换为另一特定值, 2特定值分别对应于双稳态的2个状态, 本文将水平方向的压力梯度小于0定义为状态L, 水平方向压力梯度大于0定义为状态R, 水平方向压力梯度等于0定义为二者之间的转换状态。而图 5(b)中垂直方向的压力梯度则一直在零点附近小范围波动, 不存在转换状态, 即不存在双稳态特性。
|
| 图 5 压力梯度随时间的变化 Fig.5 Variation of pressure gradient over time |
方背体尾迹区的双稳态现象是一种长时间尺度的流动特性, 即会在状态L或状态R稳定维持一段时间, 再随机转换为另一状态。并且双稳态流动特性满足马尔可夫链(Markov)性质[2], 即:
(1) t+1时刻系统状态的概率分布只与t时刻的状态有关, 与t时刻以前的状态无关;
(2) 从t时刻到t+l时刻的状态转移与t的值无关。
将全部采样时间600 s内水平方向的压力梯度以1 Hz的频率滤波, 并以其正负作为指标区分状态R和状态L。为了展示其统计学特性, 计算2个状态出现的概率与它们之间的转换概率, 定义转换概率P转换=P(St≠St-1), 则:
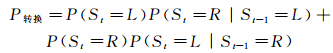 (3)
(3)
并且计算2种稳定状态的平均维持时间。结果表明状态L和状态R 2个稳定状态出现的概率分别为0.417和0.583, 存在差异主要是由于双稳态现象的出现对模型偏航角极其敏感, 如果模型与自由来流存在一定偏航角, 会导致某一种状态出现较多甚至可能出现锁定在某一个状态的情况, 而真实实验中自由来流方向很难保证完全平行于模型。根据式(3)可以得到2种稳定状态的转换概率为0.149。经过1 Hz滤波后计算得到2种稳定状态的平均维持时间为Tphase=6.76 s, 这也进一步说明了双稳态现象是一种长时间尺度的流动特征。
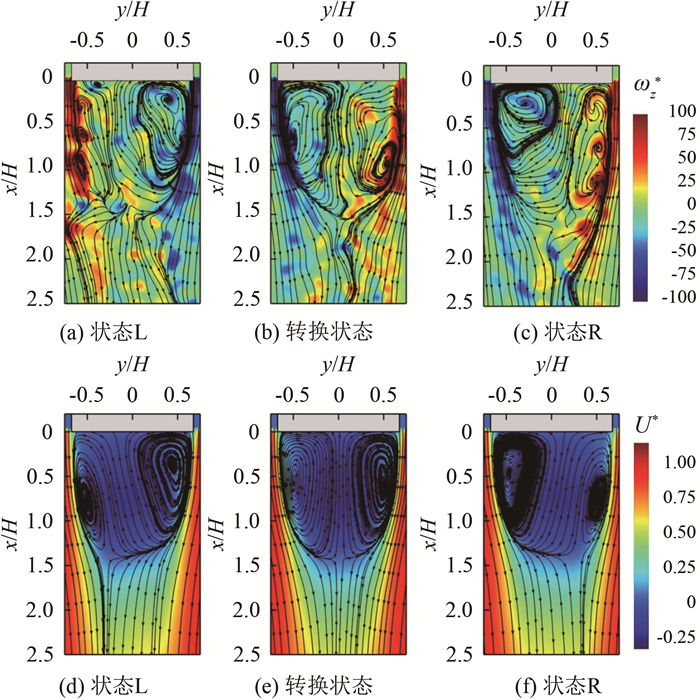
3.2 PIV瞬时流场图 6(a)、(b)和(c)显示了水平中截面z/H=0.67处3个具有代表性的瞬时时刻的涡量场和流线, (a)、(b)和(c)分别代表状态L、转换状态及状态R。当状态L出现时, 气流在背部分离, 右侧(y > 0)的剪切层向内卷积, 形成回流区内的大涡结构, 在另一侧则出现小尺度的涡脱落。大涡结构的出现会导致模型背部右侧出现较低的负压区。当状态R出现时, 情况正好相反, 大涡结构出现在回流区的左侧(y < 0), 而离散的涡结构从右侧脱落出来。转换状态时回流区内的涡结构基本是左右对称的, 几乎观察不到离散的涡脱落结构。当状态L、R出现时, 大涡结构的涡核中心距离模型背部很近, 对背压的影响很大, 会在大涡的同侧形成很低的负压区; 而在转换状态时, 回流区内对称涡结构的涡核中心距离模型背部较远, 所以对背压的影响很小, 此时背部压力往往比状态L、R更高, 由此带来的压差阻力也相对较小。此外, 当处于L、R状态时, 此时回流区在流向和展向方向上处于伸长状态, 回流区较大; 而当处于转换状态时, 回流区收缩, 这表明双稳态和回流区的抽吸现象是相互耦合的。
|
| 图 6 尾迹区横截面z/H=0.67处的瞬时涡量场及流线:(a)、(b)和(c)及条件平均速度场和流线:(d)、(e)和(f) Fig.6 Instantaneous vorticity field and streamline at the z/H=0.67 plane of the wake region: (a), (b), (c); and conditional average velocity field and streamline: (d), (e), (f) |
对该平面流场按不同状态进行条件平均, 结果如图 6(d)、(e)和(f)所示。可以更直观地观察到状态L、R出现时尾迹区结构的对称性被打破, 涡结构与背部的距离与在瞬时场中观察到的类似, 即状态L、R出现时, 大涡的涡核中心距离背部很近, 而处于转换状态时, 对称涡结构经平均后涡核中心距离背部较远; 并且能更清晰地观察到双稳态现象与回流区抽吸现象之间的关系。
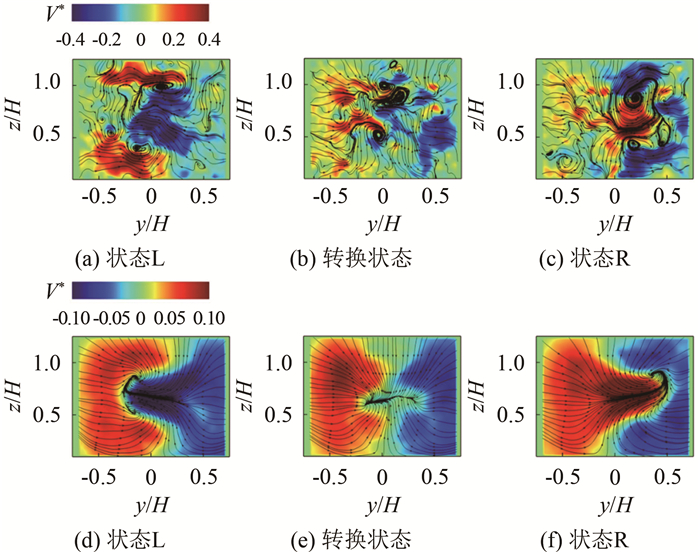
图 7通过x平面的瞬时流场和条件平均的结果展现了方背Ahmed模型尾迹的流动特征。从瞬时流场中y方向速度云图可以看出, (a)、(c)对应的瞬时流场中, y方向速度明显存在左右不对称的现象, 根据z/H=0.67平面流场分析可以知道, 这种不对称的现象主要是由于水平方向上左右涡结构的不对称造成的, 进一步根据不同状态进行条件平均可以得到(d)、(e)、(f)所示的条件平均流场, 更加清晰地表现出y方向速度的不对称性, 同时, 通过流线图也可以看出左右涡结构的不对称性。
|
| 图 7 尾迹区横截面x/H=1.5处的瞬时速度场及流线:(a), (b)和(c)及条件平均速度场和流线:(d), (e)和(f) Fig.7 Instantaneous velocity field and streamline at the x/H=1.5 plane of the wake region: (a), (b), (c); and conditional average velocity field and streamline: (d), (e), (f) |
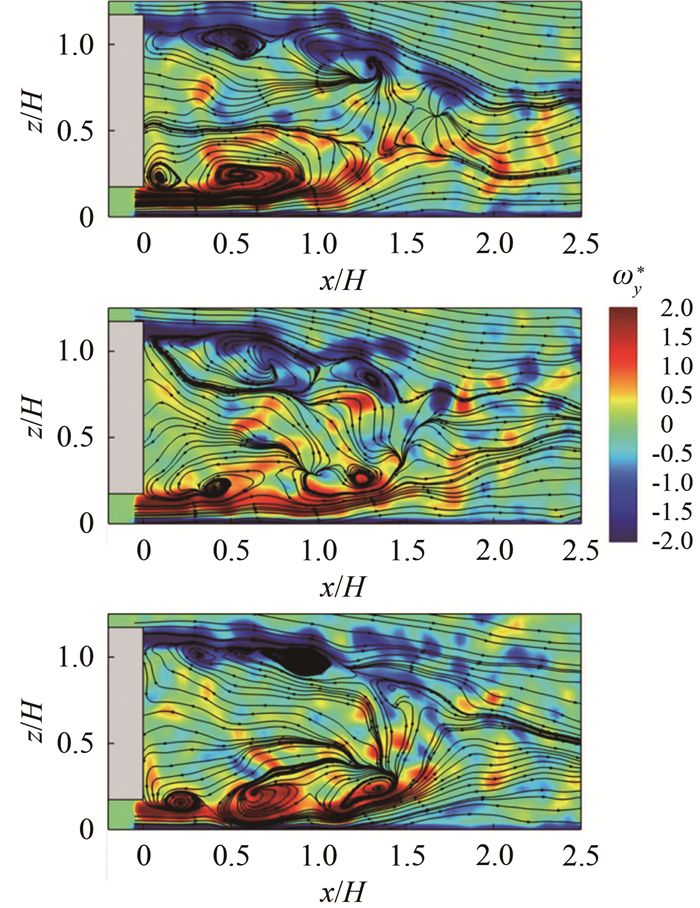
图 8展示了3个瞬时时刻纵截面y/H=0处的涡量场和流线, 与水平中截面不同的是, 在垂直中截面上不存在明显的大涡结构, 只能观察到上下两侧由尾迹振荡引起的离散的涡脱落, 故而在垂直方向上不存在双稳态特性。
|
| 图 8 尾迹区纵截面y/H=0处3个不同的瞬时时刻的涡量场和流线图 Fig.8 Three different instantaneous vorticity field and streamline of the y/H=0 plane in the wake region |
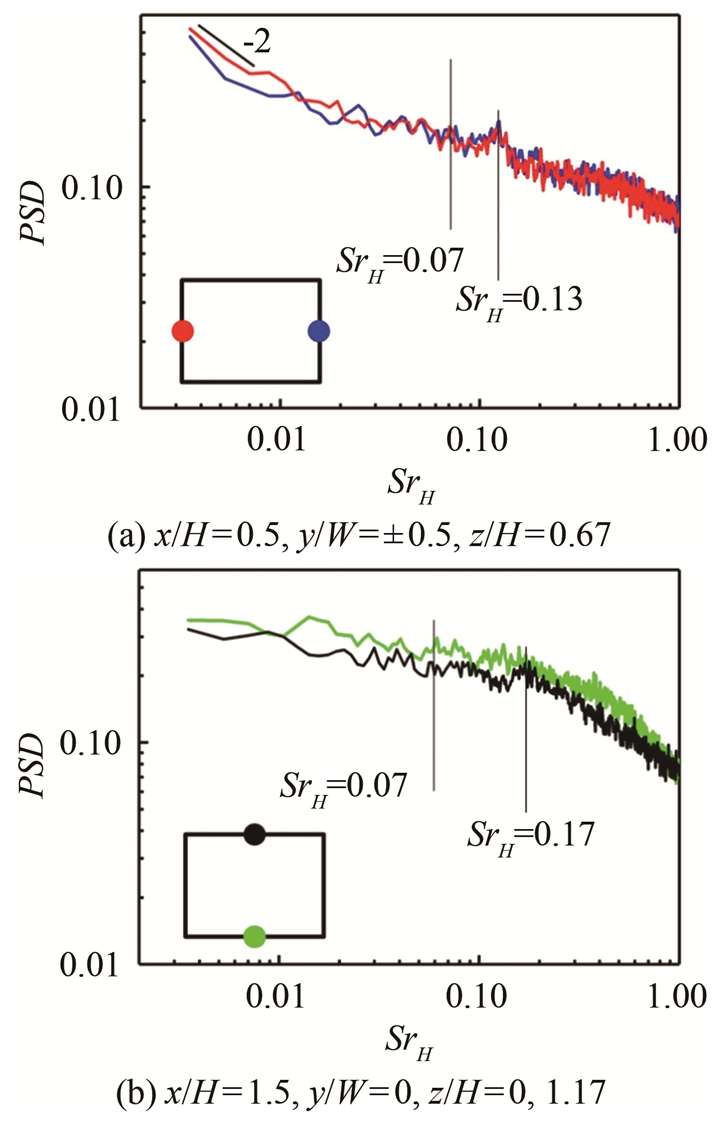
对热线测量的116个点的速度信号进行功率谱(PSD)分析, 并定义以模型高度H为特征长度的斯特劳哈尔数SrH=fH/U0, 选取其中具有代表性的4个点, x/H=0.5平面上水平对称的2测点和x/H=1.5平面上垂直对称的2测点进行分析, 如图 9所示。图 9(a)中水平方向上的2个测点结果显示, 存在一个SrH=0.13的峰值, 该频率对应于水平方向上的涡脱落频率, 水平方向上的涡脱落如图 6中瞬时场所示; 另外也存在一个低频峰值SrH=0.07, 该峰值频率在垂直方向上的2测点的频谱分析可以看出, 这一频率对应于周期性的抽吸现象, 这和文献的研究一致。同时, 水平方向上2测点的频谱图中, 在低频段, 幂律分布满足-2次幂分布, 该分布对应于方背体模型非定常尾迹中双稳态的现象[12]。垂直方向上的2个测点结果显示存在一个SrH =0.17的峰值, 对应于该方向上的涡脱落现象的脱落频率; 垂直方向上的涡脱落如图 8中的瞬时时场所示。
|
| 图 9 热线对称测点频谱图 Fig.9 Hot-wire symmetric point spectrum |
本文通过实验研究了方背Ahmed模型尾迹的非定常特性, 主要包括背部压力测量、空间流场的PIV测量以及空间点速度的热线测量, 可以得到以下结论:
(1) 方背Ahmed模型后缘气流发生分离, 向内卷积形成涡结构, 在水平方向上表现出双稳态现象, 即左右涡结构呈现长时间尺度的随机不对称现象, 这是一种低频的非定常流动结构, 其频谱特性满足-2次幂的幂律分布;
(2) 方背Ahmed模型尾迹的非定常流动主要包括双稳态现象、尾迹全局振荡引起的侧向和垂向的涡脱落现象以及回流区在流向和垂向上的周期性抽吸现象, 水平和垂直方向上的涡脱落频率分别为SrH =0.13和SrH =0.17, 回流区的周期性抽吸频率为SrH =0.07;
(3) 尾迹区内的3种非定常流动相互耦合, 双稳态现象出现时, 左右涡结构不对称, 大涡结构出现的另一侧会出现离散的涡脱落的现象, 同时回流区处于抽吸的伸长状态。此外, 大涡结构一侧, 涡核中心距离模型背部很近, 对背压的影响较大; 而在转换状态时, 回流区内对称涡结构的涡核中心距离模型背部较远, 对背压的影响较小。
| [1] |
Ahmed S R, Ramm G, Faltin G. Some salient features of the time-averaged ground vehicle wake[R]. SAE Technical Paper 840300, 1984.
|
| [2] |
Volpe R, Devinant P, Kourta A. Experimental characterization of the unsteady natural wake of the full-scale square back Ahmed body: flow bi-stability and spectral analysis[J]. Experiments in Fluids, 2015, 56(5): 99. DOI:10.1007/s00348-015-1972-0 |
| [3] |
Rouméas M, Gilliéron P, Kourta A. Analysis and control of the near-wake flow over a square-back geometry[J]. Computers & Fluids, 2009, 38(1): 60-70. |
| [4] |
Lucas J M, Cadot O, Herbert V, et al. A numerical investigation of the asymmetric wake mode of a squareback Ahmed body-effect of a base cavity[J]. Journal of Fluid Mechanics, 2017, 831: 675-697. DOI:10.1017/jfm.2017.654 |
| [5] |
Choi H, Lee J, Park H. Aerodynamics of heavy vehicles[J]. Annual Review of Fluid Mechanics, 2014, 46(1): 441-468. DOI:10.1146/annurev-fluid-011212-140616 |
| [6] |
Duell E G, George A R. Experimental study of a ground vehicle body unsteady near wake[R]. SAE Technical Paper 1999-01-0812, 1999.
|
| [7] |
Khalighi B, Zhang S, Koromilas C, et al. Experimental and computational study of unsteady wake flow behind a bluff body with a drag reduction device[R]. SAE Technical Paper 2001-01B-207, 2001.
|
| [8] |
McArthur D, Burton D, Thompson M, et al. On the near wake of a simplified heavy vehicle[J]. Journal of Fluids and Structures, 2016, 66: 293-314. DOI:10.1016/j.jfluidstructs.2016.07.011 |
| [9] |
崔文诗, 杨志刚, 王国俊, 等. 不同后倾角三维车辆的尾迹非定常流动分析[J]. 吉林大学学报(工学版), 2017, 47(3): 717-724. Cui W S, Yang Z G, Wang G J, et al. Unsteady flow analysis for wakes of three-dimensional vehicles with different rear slant angles[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(3): 717-724. |
| [10] |
Grandemange M, Gohlke M, Cadot O. Turbulent wake past a three-dimensional blunt body. Part 1. Global modes and bi-stability[J]. Journal of Fluid Mechanics, 2013, 722(5): 51-84. |
| [11] |
Grandemange M, Gohlke M, Cadot O. Bi-stability in the turbulent wake past parallelepiped bodies with various aspect ratios and wall effects[J]. Physics of Fluids, 2013, 25(9): 095103. DOI:10.1063/1.4820372 |
| [12] |
Grandemange M. Analysis and control of three-dimensional turbulent wakes: from axisymmetric bodies to road vehicles[D]. Paris: Ecole Polytechnique, 2013.
|



