2. 西南交通大学 风工程四川省重点实验室, 成都 610031;
3. 电子科技大学 自动化工程学院, 成都 611731
2. Key Laboratory for Wind Engineering of Sichuan Province, Southwest Jiaotong University, Chengdu 610031, China;
3. School of Automation Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China
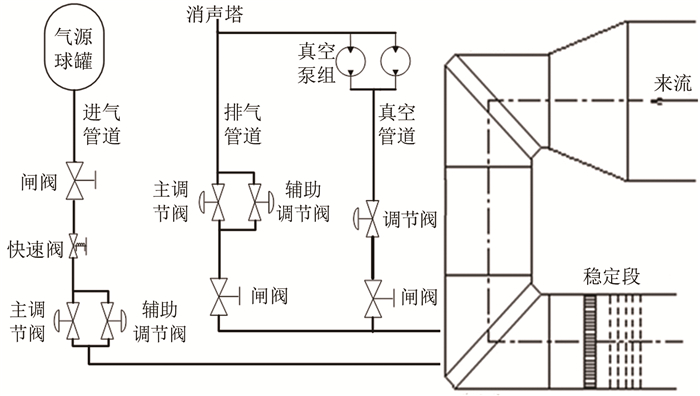
连续式风洞通过压缩机连续运转驱动风洞回路气体流动, 进而提供建立风洞流场所需要的运行压比, 按马赫数(Ma)运行范围可分成低速风洞、跨声速风洞和超声速风洞。对连续式跨声速风洞而言, 总压调节精度高、稳定速度快对保证试验数据精准度和提高试验效率具有重要作用, 尤其是对大型风洞而言, 其试验效率直接和巨大的经济效益相关。连续式跨声速风洞总压调节按照压力范围可分成负压工况(部分风洞无负压工况)、常压工况和增压工况。以中国空气动力研究与发展中心0.6 m连续式跨声速风洞为例, 其马赫数范围Ma=0.2~1.6, 压力范围20~250 kPa(绝对压力), 压力调节系统的结构布局见图 1。
|
| 图 1 压力调节系统结构 Fig.1 The structure of the pressure regulating system |
暂冲式风洞压力控制主要通过控制风洞进气主、辅调压阀等来实现[1-5], 而连续式跨声速风洞主要通过对进排气系统和抽真空系统的阀门/泵组合控制来实现不同的运行压力控制需求, 且总压调节受马赫数调节手段影响较大[3, 6-7]。目前, 国内连续式跨声速风洞数量较少, 西北工业大学NF-6风洞为国内首座连续式跨声速风洞[8-9], 而后陆续有中国空气动力研究与发展中心及中国航空工业空气动力研究院的0.6 m连续式风洞, 国内外公开文献资料中关于连续式风洞总压控制方法的描述较少[10-13], 而对马赫数控制以及风洞特性的描述更多[3, 6-9, 13-18]。美国NTF风洞(Ma 0.2~1.2)实现了0.005 atm (506 Pa)的总压波动控制, 但相关文献对流场参数的耦合以及总压的控制方法描述较少[7, 11, 15]。欧洲ETW风洞(Ma 0.15~1.3)总压范围为125~450 kPa, 控制精度为0.2%[13, 17], 但相关文献对总压控制方法和算法未做具体描述。文献[19]对0.6 m连续式风洞总压的控制策略进行了描述, 但对总压的影响因素和各调节手段的对应关系未做深入研究。
本文通过分析连续式跨声速风洞压力调节系统的特点以及多种流场调节手段下压力耦合特性, 建立总压控制精度和主要调节手段性能的对应关系, 以此选取性价比最优的阀门组合调节方式, 并通过分段变参数模糊PID算法和流量补偿算法进行总压控制, 以提高控制精度和稳定速度。
1 压力调节系统特性分析连续式跨声速风洞压力调节系统一般具有以下特性:
(1) 运行工况多, 包括常压、增压、负压3种不同工况, 且试验过程中需要连续变总压。
(2) 风洞用于压力调节的阀门/泵数量多, 不同的压力工况涉及多种不同的阀门/泵组合控制方式。
(3) 风洞配置了压缩机气密封系统, 导致有部分气体泄漏至洞体回路中, 对总压调节有较大影响, 尤其是当压力工况为常压或负压时, 影响明显。
(4) 相比暂冲式风洞, 连续式跨声速风洞对总压控制精度要求高, 但快速性要求低, 同时对调压阀的要求稍低, 配置稍差。
(5) 风洞运行过程中除调节总压外, 还需频繁地改变试验条件, 包括模型姿态角度、二喉道型面、压缩机转速、驻室抽气流量等, 这些对总压均有较大影响, 总压波动又导致Ma波动, 从来带了总压和Ma的严重耦合。
综上所述, 连续式跨声速风洞调节手段多, 工况多, 总压控制方法需要具备很强的适应性, 且总压调节必须和Ma的控制协调进行。
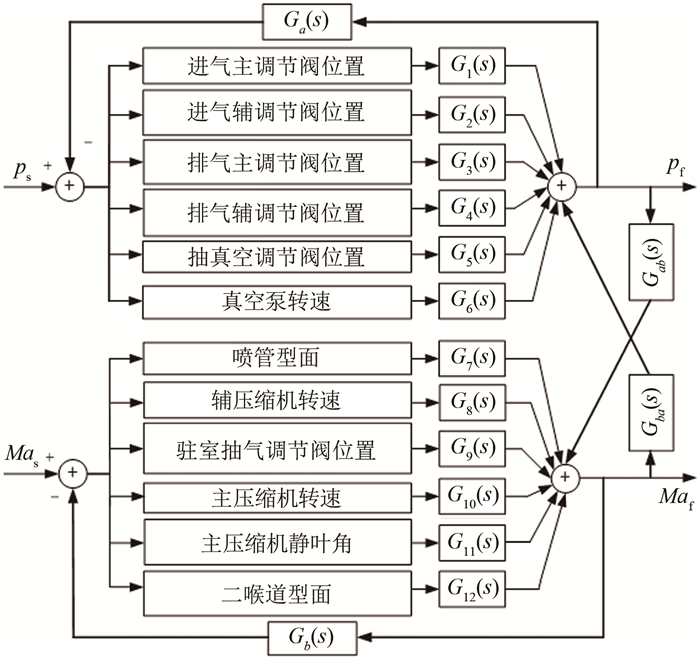
2 总压影响因素分析 2.1 风洞各调节手段对总压的影响Ma和总压为连续式跨声速风洞的主要流场参数。Ma调节手段包括主压缩机转速、静叶角、喷管型面、辅压缩机转速、驻室抽气流量、二喉道型面, 且Ma还受模型姿态角影响; 而总压调节手段包括真空泵转速、抽真空调节阀开度、进气主调节阀开度、进气辅调节阀开度、排气主调节阀开度、排气辅调节阀开度, 同时总压还受气源压力和压缩机系统漏气量影响。总压和Ma各调节手段相互影响, 耦合严重(见图 2), 致使调节难度大, 调节时间长。
|
| 图 2 总压、马赫数各调节手段的耦合关系 Fig.2 The coupling relation of adjusting means for total pressure and Mach number |
图 2中ps为总压控制目标, pf为总压反馈值, Mas为马赫数控制目标, Maf为马赫数反馈值, Ga(s)为总压传递函数, Gb(s)为马赫数传递函数, Gab(s)为总压对Ma的影响函数, Gba(s)为马赫数对总压的影响函数, G1(s)~G12(s)为对应调节手段的传递函数。为提高流场指标控制精度和试验效率, 需要对Ma和总压进行解耦, 但难度较大, 工程应用少, 实践中主要是结合总压和Ma耦合关系, 通过技术手段减少总压和Ma的耦合来实现。
2.2 总压控制与调节阀特性的关系如图 2所示, 总压的影响因素较多, 为减少控制难度, 真空泵采用软启动器启动, 按照额定转速运行, 这样, 不同工况下总压控制主要通过调节对应管路的调节阀来实现。为保证总压控制精度和速度, 需首先建立总压和调节阀特性之间的关系。
考虑到风洞内压力的波动由风洞内的气体质量变化引起, 假定某种工况下压力控制目标为ps, 风洞容积为V, 稳定段当前气流温度为T, 则假定当改变试验状态(比如变迎角或变二喉道型面)时, 压力波动量为p, 考虑到风洞目标压力较低, 且稳定段为常温, 根据理想气体状态方程得到:
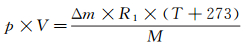 (1)
(1)
其中, p为压力波动量, Pa; Δm为气体质量增量, g; V为风洞容积, m3; T为气流温度, ℃; R1为气体状态常数, R1=8.314 J/(mol×K); M为气体摩尔质量, 空气为29 g/mol。
由于风洞换热器一直工作, 在压力波动的较短时间内, 可认为气流温度T基本不变, 假定从压力开始波动至压力回到设定值ps的时间为t(单位s), 可算出若需重新稳定至ps所需灌入风洞内的气体质量增量Δm。
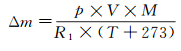 (2)
(2)
而风洞内气体密度和压力有很大关系, 在上述的压力波动过程中(在较短的控制时间t内), 总压的波动相对较小(在控制目标ps附近波动), 对密度的影响较小。风洞内气体是通过干燥气源充入的, 可认为是干燥空气, 结合空气在不同温度, 不同压力下的密度公式, 可得出风洞内气体密度:
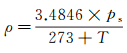 (3)
(3)
其中, ρ为空气密度, g/m3; ps为目标压力, Pa。
由式(2)和(3), 可得到上述调节过程中风洞内对应体积的增量ΔV:
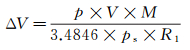 (4)
(4)
将调节时间t带入式(4), 得到该时间内体积流量的增量ΔQV为:
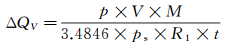 (5)
(5)
为便于压力调节, 当调节阀小开度调节时应平稳缓和, 大开度时应灵敏有效, 调节阀多采用等百分比特性曲线, 理想情况下其体积流量和阀门开度之间满足下式:
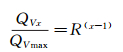 (6)
(6)
其中, QVx为开度为x时的体积流量, QVmax为流经阀门的最大体积流量, m3/s; R为阀门的可调比, 为流经阀门的最大流量和最小流量的比值, 受阀芯结构设计及加工方面的限制, 无法保证太小的最小流量; x为阀门开度(用百分比表示)。
在压力调节过程中, 风洞体积流量的增加由调节阀位置开度变化来实现, 假定初始平衡状态下, 阀门开度为x1, 经过上述调节过程后达到新的平衡状态, 此时阀门开度为xn, 可认为阀门调节过程中为匀速运动(阀门实际调节过程为往复运动, 但对多数电动执行器而言, 除加减速阶段外, 可认为中间速度恒定), 假定在t时间内经过n个调节位置, 则n和t应满足下式:
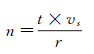 (7)
(7)
其中, t为调节时间, s; n为t时间内调节阀可识别出的阀门位置的数量; vs为阀门平均调节速度; r为阀门分辨率。
基于式(6)和(7), 上述调节过程中体积流量的增量用控制程序可表示为:
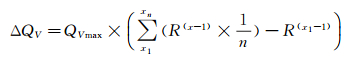 (8)
(8)
式(5)和(8)是等价的, 并令
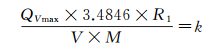 (9)
(9)
得到:
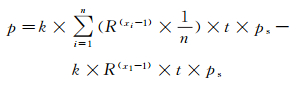 (10)
(10)
将式(10)用积分形式可表示为:
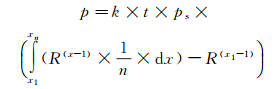 (11)
(11)
由此得到压力波动和调节阀开度的对应关系。
考虑到调节阀初始位置x1和开度变化量无相关性, 对式(11)两边求导, 可得到压力波动的变化量和调节阀开度变化量之间的关系:
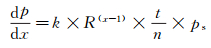 (12)
(12)
将控制目标压力也考虑进来, 并结合式(7), 可得到压力调节精度和调节阀特性的关系:
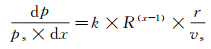 (13)
(13)
由式(13)可以得到以下几条结论, 以进气调节阀为例, 在同一气源压力下:
(1) 风洞容积越大, 总压控制精度越高;
(2) 阀门速度越快, 阀门分辨率越高, 总压控制精度越高;
(3) 阀门最大流量越小, 总压控制精度越高。
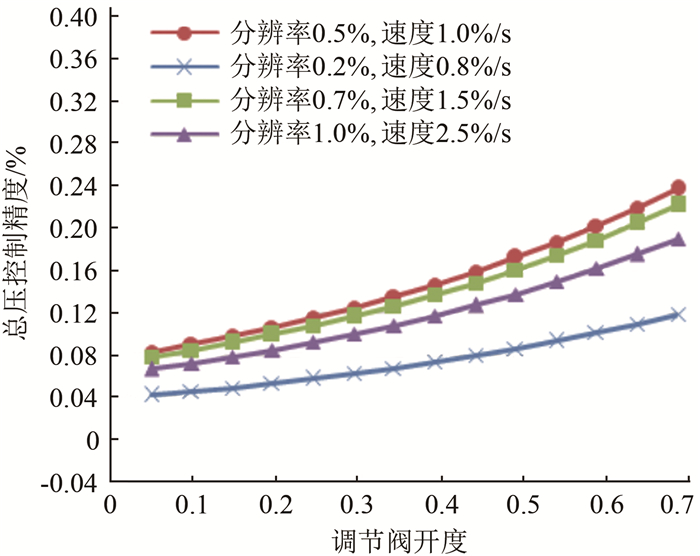
结合0.6 m风洞实际数据(风洞容积260 m3), 在某工况下可以得到调节阀不同性能参数和总压控制精度之间的关系曲线(见图 3)。阀门在实际运行时受工作特性影响, 其实际可调比很低, 一般均在10以下[20]。
|
| 图 3 调节阀特性和总压精度关系曲线 Fig.3 The relation between total pressure precision and regulating valve properties |
可以看出, 当阀门形式和可调比一定时, 总压精度和调节阀特性有直接关系, 以"分辨率0.5%, 速度1%/s(每秒开度为全行程的1%)"曲线为例, 压力趋稳后, 只有在开度60%以下调节时才能满足0.2%的总压控制要求, 而若要求更高的控制精度, 则必须要求更好的调节阀性能。但在调节阀选择时不能一味的要求精度(分辨率)和速度, 精度(分辨率)越高/速度越快, 制造难度越大, 成本越高, 且运行速度过快易导致阀门机构产生超调抖动。
3 多阀门组合控制策略由总压控制精度和调节阀特性之间的关系可知, 要保证总压控制精度, 调节阀的速度应足够快, 且分辨率(精度)应较高, 但连续式风洞调节阀很多, 若每台调节阀均采用高配置, 工程耗费较大, 因此需要对阀门进行分类设计, 其中用于压力闭环调节的阀门采用高精度、高速度, 而用于预置调节的阀门可适当降低性能指标。
根据风洞阀门配置情况, 以增压状态为例, 稳态状态下实施压力调节一般具有3种方式:第一种为固定排气阀开度, 调节进气阀实施压力调节; 第二种为固定进气阀开度, 调节排气阀实施压力调节; 第三种为进排气调节阀同时调节。但为减少相互干扰, 在同一时刻应尽量以某一种调节手段为主。
结合上述分析的风洞压力变化规律, 为保证较好的调节效果, 并减少气源消耗量, 确定阀门组合控制策略为:
(1) 常压工况时, 考虑到压缩机气密封系统往洞体漏气, 进气阀关闭, 利用排气主、辅调节阀进行总压闭环控制;
(2) 负压工况时, 预置进气阀开度, 真空泵额定转速运行, 调节抽真空调节阀进行总压闭环控制;
(3) 增压工况时, 预置进气调节阀开度, 通过调节主、辅排气调节阀进行总压闭环控制;
(4) 常压增压工况调节过程中, 排气主调阀进行初步调节, 待压力趋稳后由排气辅调节阀精确调节, 压力较长时间稳定在0.01%以下时排气主、辅调节阀均退出闭环, 以减少阀门磨损。
(5) 当改变Ma阶梯时, 压缩机转速变化较大, 压力波动也较大, 对参与调节的阀门调节过程中的积分值进行限制。同时在Ma控制算法设计时, 变Ma采用多阶梯逐次升/降速转速的控制方式(以某一个转速增量为阶梯, 转速到位且等待阀门有效动作后, 再调转速)。
(6) 当定Ma阶梯变总压时, 采用流量补偿算法根据不同目标压力以及压力偏差调整进气阀开度来开环调节, 实现快速补气, 并通过调节排气调节阀或抽真空调节阀进行压力精确控制。
4 总压控制算法 4.1 分段变参数模糊PID算法考虑到PID算法具有结构简单、稳定性好等优点, 但也存在自适应能力相对较差的缺点, 而模糊PID不需要精确模型, 参数可自由调整, 对不确定性系统有较好的适应性[21], 因此采用模糊PID算法作为压力控制的核心算法。模糊PID控制算法先计算被控量的误差e和误差变化率ec, 并将其作为模糊控制器的输入, 通过模糊化、模糊推理、解模糊得到Kp(比例系数)、Ki(积分系数)和Kd(微分系数)的修正量, 并在控制过程中实时调整PID控制参数。
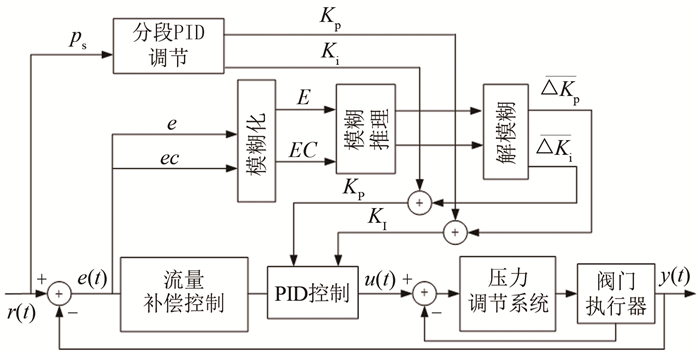
由于连续式跨声速风洞压力工况较多, 不同的压力区间下风洞的总压特性不同, 比如增压工况下, 由于压差增大, 风洞排气调节阀开度增大后排气阀流量增大, 总压下降明显, 若阀门动作速度过慢, 阀门的调节速度将跟不上压力变化的速度, 而此时若仍使用常压时的控制参数为基准, 即使通过模糊PID进行变参数控制, 也将导致控制算法适应性差。因此, 采用分段变参数加模糊PID相结合的方式, 即在模糊PID的基础上, 考虑不同目标总压带来的影响, 首先在几种典型总压目标下, 初步调试确定一组适合当前总压目标的PID控制参数作为基准值, 尔后由模糊算法结合压力目标和调节阀特性进行变参数控制, 其原理框图见图 4(控制参数Kd取值较小, 只采用同一种参数, 故图中未画出)。
|
| 图 4 总压控制框图 Fig.4 Block diagram of total pressure control |
压力控制算法采用外环压力闭环, 内环阀位监测的控制方式, 即只有当调节阀位置接近上一次目标位置时才给出下一个目标位置。
压力控制系统将目标压力、给定压力和实际压力的误差e和误差的变化率ec作为模糊控制器的输入, PID控制器的控制参数Kp、Ki的修正量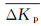
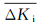

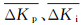
| E | EC | ||||
| NM | NS | 0 | PS | PM | |
| NB | PB/NB | PB/NM | PB/NM | PB/NS | PS/0 |
| NM | PB/NB | PB/NM | PB/NS | PB/NS | 0/0 |
| NS | PM/NM | PM/NS | PS/NS | 0/0 | NS/PS |
| 0P | PS/NS | PS/NS | 0/0 | NS/PS | NM/PM |
| 0N | NP/PS | PS/NS | 0/0 | NS/PS | PM/PS |
| PS | NS/NS | 0/0 | NS/PS | NS/PS | PM/PS |
| PM | 0/0 | NS/PS | NM/PS | NM/PM | PB/NB |
| PB | PS/0 | NM/PS | NM/PM | NM/PM | PB/NB |
参数选取的基本原则为:偏差大时选取较大的ΔKp、较小的ΔKi, 偏差适中时选取较小的ΔKp、适中的ΔKi, 偏差小时选取较大的ΔKp、较大的ΔKi。
根据压力目标进行分段, 能更准确地获取适合当前压力工况的基准参数值范围(可将其拟合处理后再作为模糊控制的输入), 而模糊PID对参数调整时只在当前基准参数上较小幅度修正, 进而避免了控制参数大幅变化带来的振荡, 增强了算法适应性。
4.2 流量补偿算法风洞调压过程中, 当压力欠压或变压力阶梯时, 需通过开启进气阀对风洞进行补气, 常压或25 kPa以下负压工况下补气结束后直接关闭进气阀, 而增压或高压力负压工况下若关闭进气阀, 仅依靠排气(抽真空)阀进行总压闭环, 可能会导致用于调节的排气(抽真空)阀的平均开度较小(大), 易陷入调节死区, 严重影响调节效果, 因此趋于稳态时需要一直通过开启进气阀进行流量补偿, 以确保排气(抽真空)阀处于合理的调节区间。流量补偿的具体过程为:当压力偏差较大时, 进气大阀根据偏差大小采用阶梯补气的方式, 偏差越大进气阀开度越大; 当压力偏差较小, 调节过程趋稳后进气大阀关闭, 进气小阀以一定的进气量往风洞充气。趋稳后进气小阀预置开度与气源压力pas和目标压力ps满足下列函数关系:
 (14)
(14)
负压小于25 kPa, 以及常压小于105 kPa时进气阀全关, 依靠压缩机气密封漏气进行欠压时的流量补偿。
5 试验验证为验证控制方法的可行性, 并测试算法性能, 在0.6 m连续式跨声速风洞上进行了验证, 设计了一套风洞总压控制系统, 对变流场参数、变模型姿态角等不同工况均进行了调试。控制系统以PLC 315-2PN/DP为核心, 通过对多台调节阀的调节实现总压控制, 其中排气主调节阀(DN150)精度0.5%、速度1.4%/s, 排气辅调节阀(DN50, 口径小, 可调流量范围小)精度0.2%、速度3%/s, 抽真空调节阀(DN250)精度0.5%、速度0.7%/s, 其他调节阀精度1.0%、速度1.3%/s。
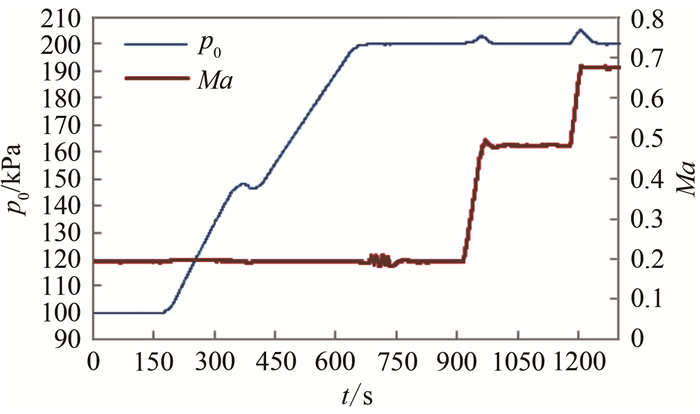
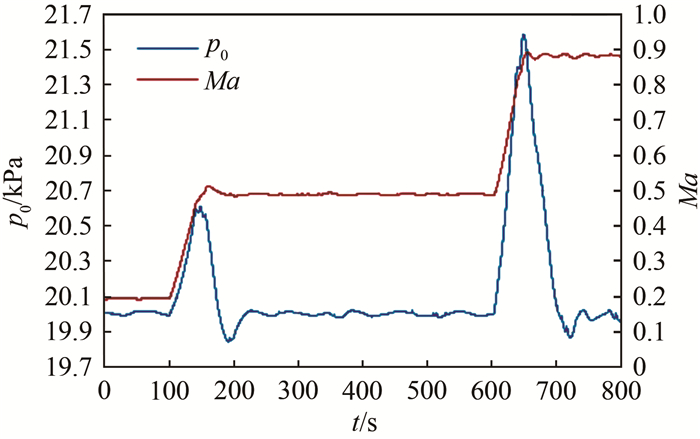
图 5为常压和增压工况下试验结果, 图 6为负压工况下试验结果, 图中p0为稳定段总压。由图 5和6可知, 常压和增压工况总压控制精度优于0.1%, 负压工况总压控制精度优于0.2%。改变Ma阶梯时, 尤其是跨越式大阶梯改变Ma阶梯时, 如图 5中Ma由0.2变至0.5, 图 6中Ma由0.5变至0.9时, 总压调节过程出现一个较大的尖峰, 这是由于大幅增加压缩机转速导致总压迅速上升, 而该风洞排气管路的泄压能力有限, 加上排气主调节阀的执行速度仍较慢, 来不及泄压。在上述工况中, 改变相邻Ma阶梯时, 总压首次稳定的平均时间为80 s(未考虑Ma极曲线时间)。
|
| 图 5 常压增压下变马赫数调试结果 Fig.5 Debugging result of changing Mach number under normal pressure and pressurization condition |
|
| 图 6 20 kPa变马赫数调试结果 Fig.6 Debugging result of changing Mach number at 20 kPa |
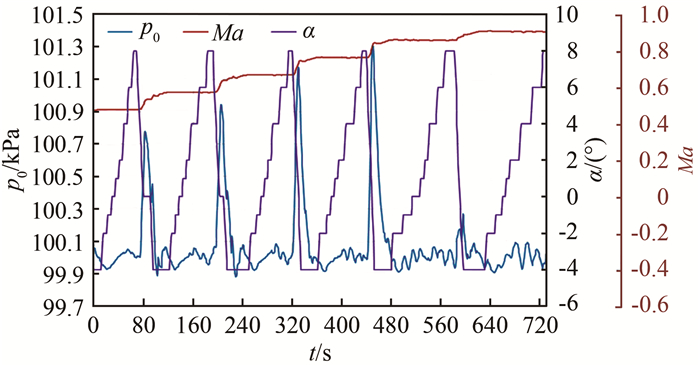
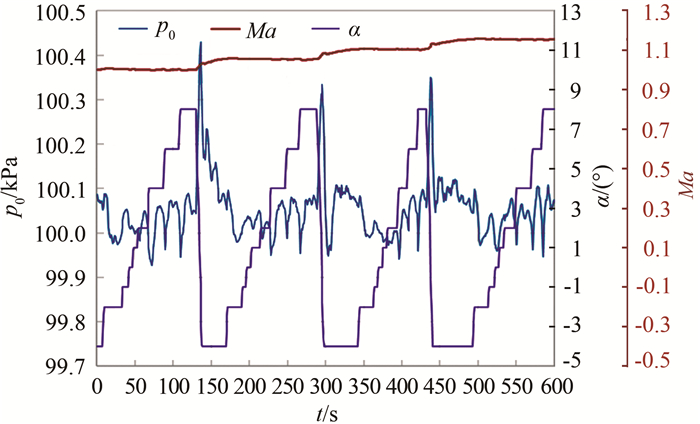
以常压工况为例, 图 7和8为保证Ma极曲线时间为前提的调试结果(设计指标为5 min一条极曲线), 其中图 7为采用压缩机转速精调Ma的数据, 图 8为采用中心体精调Ma的数据, 图中α为迎角。
|
| 图 7 常压下变转速调节马赫数的调试结果 Fig.7 The result of changing compressor speed to adjust Mach number under normal pressure condition |
|
| 图 8 常压下变中心体调节马赫数的调试结果 Fig.8 The result of changing center body to adjust Mach number under normal pressure condition |
图 7和8中马赫数极曲线时间9个迎角阶梯均远小于5 min, 改变相邻马赫数阶梯时, 总压首次稳定的平均时间为40 s, 总压控制精度优于0.1%(从第一个迎角阶梯到位且流场稳定后开始, 到完成所有迎角阶梯结束为一个流场参数采样周期), 达到国军标先进指标。
采用主压缩机转速及二喉道调节Ma时, 一般具有以下趋势:转速升高, Ma升高, 总压上升; 中心体张开, Ma下降; 调节片(一般仅预置调节)伸出, Ma下降。定Ma状态, 低Ma小迎角变化时总压波动小, 高Ma大迎角变化时总压波动大。另外, 从图 7和8可以看出, 采用中心体闭环Ma的方式带来的总压波动幅值相比采用转速闭环Ma的方式要小。
在上述的调试过程中, 若降低控制时间要求, 随着系统逐步趋稳, 总压控制精度将更高。
6 结论经过试验验证, 可以得出下列结论:
(1) 利用本文提出的总压控制方法能够满足0.6 m连续式跨声速风洞总压精度指标要求(该风洞常压增压下总压设计指标为0.2%), 并为保证总压和Ma极曲线时间提供了支撑;
(2) 建立的总压控制精度和调节阀特性之间的关系可为连续式跨声速风洞调节阀的设计选型提供参考。
(3) 本文探讨的风洞总压控制方法可为其他连续式跨声速风洞的压力控制提供参考。
| [1] |
高川, 周波, 蒋婧妍, 等. 基于Labview的大型超声速风洞总压测控系统设计与应用[J]. 测控技术, 2014, 33(8): 84-87. Gao C, Zhou B, Jiang J Y, et al. Design and implementation of total pressure measurement and control system of large-scare supersonic wind tunnel based on Labview[J]. Measurement & Control Technology, 2014, 33(8): 84-87. DOI:10.3969/j.issn.1000-8829.2014.08.022 |
| [2] |
褚卫华, 汤更生, 王帆. 2m×2m超声速风洞流场控制策略研究与实现[J]. 实验流体力学, 2012, 26(5): 98-102. Chu W H, Tang G S, Wang F. Research and realization on the control strategies of the 2m×2m supersonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(5): 98-102. DOI:10.3969/j.issn.1672-9897.2012.05.021 |
| [3] |
易家宁.风洞马赫数的控制策略与控制方法研究[D].沈阳: 东北大学, 2014. Yi J N. Research on control strategy and control method of Mach number for wind tunnel[D]. Shenyang: Northeastern University, 2014. |
| [4] |
杨海滨, 张伟, 罗承友, 等. 模糊控制在风洞主气流压力自动调节系统中的应用[J]. 兵工自动化, 2015, 34(4): 39-42. Yang H B, Zhang W, Luo C Y, et al. Application of fuzzy control in wind tunnel main airflow pressure auto-adjust system[J]. Ordnance Industry Automation, 2015, 34(4): 39-42. |
| [5] |
王博文, 黄叙辉, 秦建华, 等. 遗传算法在跨超声速风洞总压控制中的应用[J]. 计算机测量与控制, 2017, 25(11): 74-77. Wang B W, Huang X H, Qin J H, et al. Application of genetic algorithms in total pressure control system of transonic and supersonic wind tunnel[J]. Computer Measurement and Control, 2017, 25(11): 74-77. |
| [6] |
Nguyen N, Ardema M. Adjoint method and predictive control for 1-D flow in NASA Ames 11-Foot Transonic Wind Tunnel[R]. AIAA 2006-1433, 2006.
|
| [7] |
Chan D T, Balakrishna S, Walker E L, et al. Mach stability improvements using an existing second throat capability at the National Transonic Facility (Invited)[R]. AIAA 2015-0622, 2015.
|
| [8] |
张永双, 陈旦, 陈娇. NF-6连续式跨声速风洞马赫数控制方式比较与研究[J]. 实验流体力学, 2013, 27(2): 95-99. Zhang Y S, Chen D, Chen J. Comparison and research on the Mach number control methods for the NF-6 continuous transonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(2): 95-99. DOI:10.3969/j.issn.1672-9897.2013.02.019 |
| [9] |
郝礼书, 乔志德, 张永双, 等. NF-6风洞马赫数闭环控制系统设计研究[J]. 实验流体力学, 2010, 24(4): 85-88. Hao L S, Qiao Z D, Zhang Y S, et al. Design research on the Mach number closed-loop control system in the NF-6 wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(4): 85-88. DOI:10.3969/j.issn.1672-9897.2010.04.019 |
| [10] |
田昊, 云长江, 彭毅. 增量PID算法在某风洞压力控制中的应用改进[J]. 计算机测量与控制, 2016, 24(3): 64-66. Tian H, Yun C J, Peng Y. Improving application of increment PID adjust method for pressure control in wind tunnel[J]. Computer Measurement and Control, 2016, 24(3): 64-66. |
| [11] |
Balakrishna S, Kilgore W A, Thibodeaux J J. Control of large cryogenic tunnels[R]. AIAA-92-3930, 1992.
|
| [12] |
熊波, 周恩民, 程松, 等. 0. 6m连续式风洞调试运行关键技术研究[J]. 实验流体力学, 2016, 30(4): 81-86. Xiong B, Zhou E M, Cheng S, et al. Research on key technologies of debugging and operating in 0.6 m×0.6 m continuous transonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(4): 81-86. |
| [13] |
Gobert J L. ETW control system: design and first results[R]. AIAA-94-2514, 1994.
|
| [14] |
廖达雄, 陈吉明, 彭强, 等. 连续式跨声速风洞设计关键技术[J]. 实验流体力学, 2011, 25(4): 74-78. Liao D X, Chen J M, Peng Q, et al. Key design techniques of the low noise continuous transonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(4): 74-78. DOI:10.3969/j.issn.1672-9897.2011.04.014 |
| [15] |
Paryz R W. Subsonic transonic Applied refinements By Using Key Strategies-STARBUKS in the NASA Langley Research Center National Transonic Facility[R]. AIAA 2014-1481, 2014.
|
| [16] |
连晓飞.基于遗传算法优化BP网络的风洞马赫数控制研究[D].沈阳: 东北大学, 2011. Lian X F. Wind tunnel Mach number control based on genetic algorithm optimized BP-Neural network[D]. Shenyang: Northeastern University, 2011. |
| [17] |
Schulz M, Quest J. New techniques for operation in cryogenic windtunnels[R]. AIAA 2007-749, 2007.
|
| [18] |
Jackson F M. Progress update on the AEDC PWT sustainment program[R]. AIAA 2004-2500, 2004.
|
| [19] |
黎壮声, 杨鹏程, 陈旦, 等. 0. 6m连续式跨声速风洞总压控制策略设计[J]. 实验流体力学, 2016, 30(4): 87-92. Li Z S, Yang P C, Chen D, et al. The design of total pressure control strategy for 0. 6m continuous transonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(4): 87-92. |
| [20] |
明赐东. 调节阀计算选型使用[M]. 成都: 成都科技大学出版社, 1999. Ming C D. Calculation and selection of regulating valve[M]. Chendu: Chengdu University of Science and Technology Press, 1999. |
| [21] |
张强, 魏建华, 时文卓. 采用软溢流模糊PID控制器的液压垫压边力控制[J]. 浙江大学学报(工学版), 2017, 51(6): 1143-1152. Zhang Q, Wei J H, Shi W Z. Blank holder force control of hydraulic cushion with soft relief fuzzy PID controller[J]. Journal of Zhejiang University(Engineering Science), 2017, 51(6): 1143-1152. |



