2. 中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000;
3. 中国空气动力研究与发展中心 超高速空气动力研究所, 四川 绵阳 621000
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China;
3. Hypervelocity Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China
扩压器在超/高超声速风洞中的主要作用是对试验段来流气体减速、增压, 使得风洞在较低的压比(前室总压和扩压器后静压之比)下能够正常运行。在这种压力恢复作用下, 扩压器出口静压可以远高于喷管出口下游静压, 降低风洞运行的压比要求, 大大减少抽气系统的费用; 对于暂冲式风洞, 还可以延长风洞运行时间, 提高风洞运行效率。可见, 扩压器是超/高超声速风洞的关键部件之一, 其扩压效率的好坏, 直接关系到风洞运行的经济性[1]。
超/高超声速风洞通常采用"收缩段-等直段-扩张段"的扩压器结构, 其中, 收缩段可以对试验段超声速来流收缩减速; 等直段也称为第二喉道段, 该部分通过产生一系列激波串结构和边界层的粘性作用对气流进一步减速直至亚声速流动; 扩张段与风洞其他部件如冷却器等相连, 对亚声速气流也有一定的减速作用。研究表明, 对于常规超/高超声速风洞, 这种形式的扩压器能否达到较好的扩压效果, 关键在于第二喉道截面面积和长度的选取。
然而, 高超声速低密度风洞中, 在稀薄气体效应作用下, 扩压器内往往存在更加复杂的激波和边界层相互干扰形成的流场结构, 对扩压器的性能造成较严重的影响。且由于低密度风洞采用自由射流形式的试验段结构, 喷管和扩压器通过箱体进行连接, 使得从喷管出来的气流可以继续向外膨胀, 并在核心区外边界形成高超声速引射流动, 为了让这股射流能够顺利通过扩压器进入真空系统而不会对试验段均匀气流产生影响, 需要适当加大扩压器等直段尺寸, 这使得扩压器对试验段超声速来流的收缩减速增压作用存在不利因素。因此, 对于高超声速低密度风洞这样具有大跨度运行范围的风洞而言, 设计什么形式的扩压器成为一直困扰着风洞设计者的重大难题[2]。
本文采用CFD/DSMC分区耦合计算方法, 研究了高超声速低密度风洞中喷管、试验段、扩压器等的流场结构和流动机理, 根据计算结果的分析, 提出了一种能有效提高低密度风洞中扩压器实际使用效率的带中心锥型扩压器结构(国外超声速风洞中有类似结构, 如美国16S风洞, 但在高超声速风洞中未见报道)。为进一步验证带中心锥型扩压器在高超声速低密度风洞中应用的可行性, 设计了一套简易装置, 并在高超声速低密度风洞上开展了相关试验研究, 为改进高超声速低密度风洞现有扩压器结构、提高设备试验能力提供参考。
1 带中心锥型扩压器结构的提出低密度风洞是开展高超声速飞行器高马赫数过渡流区气动问题研究的主要地面试验设备, 其设计的关键问题在于需要同时模拟高空大气参数(低密度、低压力)和较快的飞行速度(高马赫数), 这就要求具备较低前室总压的同时要有较高的启动压比(前室总压/真空压力)。根据一维等熵流理论和正激波关系式, 理想启动压比和试验段马赫数的关系[3]:
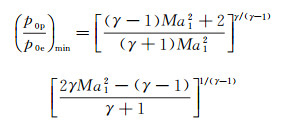 (1)
(1)
其中, p0p为前室总压, p0e为真空压力, Ma1为试验段马赫数。
根据(1)式可知, Ma为5、10、15和20时, 理想启动压比分别约为16、328、2275和9279, 随着模拟马赫数增加, 要求的启动压比急剧增加。实际上, 在稀薄流动强粘性效应的作用下, 高超声速低密度风洞实际启动压比远比理想值高。为了获得足够长的有效试验时间, 往往需要很高的真空度, 马赫数越高, 真空度要求越高。因此, 起着压力恢复作用的扩压器设计就成为提高高超声速低密度风洞试验设备性能的关键技术之一[4-5]。
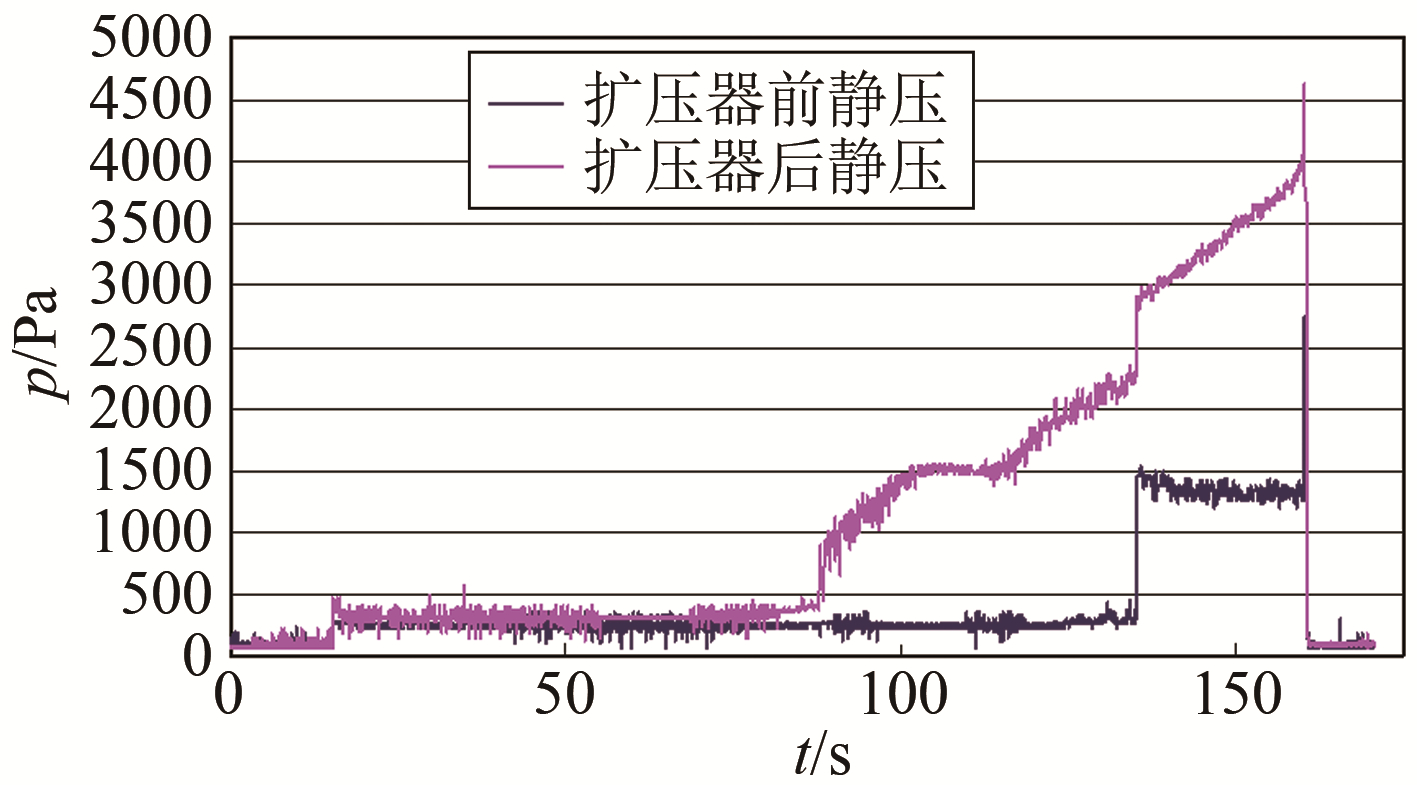
然而, 现有"收缩段-等直段-扩张段"结构形式的扩压器几乎没有起到压力恢复作用。图 1为高超声速低密度风洞上测得的扩压器前后静压随时间变化的典型曲线图。可以看出, 该风洞所采用的扩压器基本没有起到扩压作用, 只是在试验的后期, 由于扩压器有足够的长度, 适当延缓了由于逆压梯度的增大而形成的激波结构进入试验段破坏流场的时间。
|
| 图 1 低密度风洞扩压器前后静压典型变化图 Fig.1 Typical variation of static pressure before and after diffuser in low density wind tunnel |
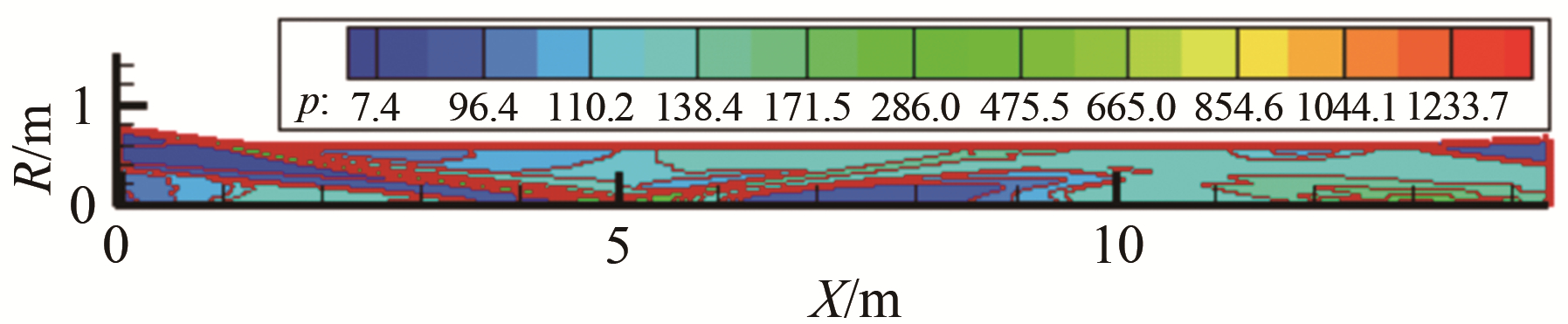
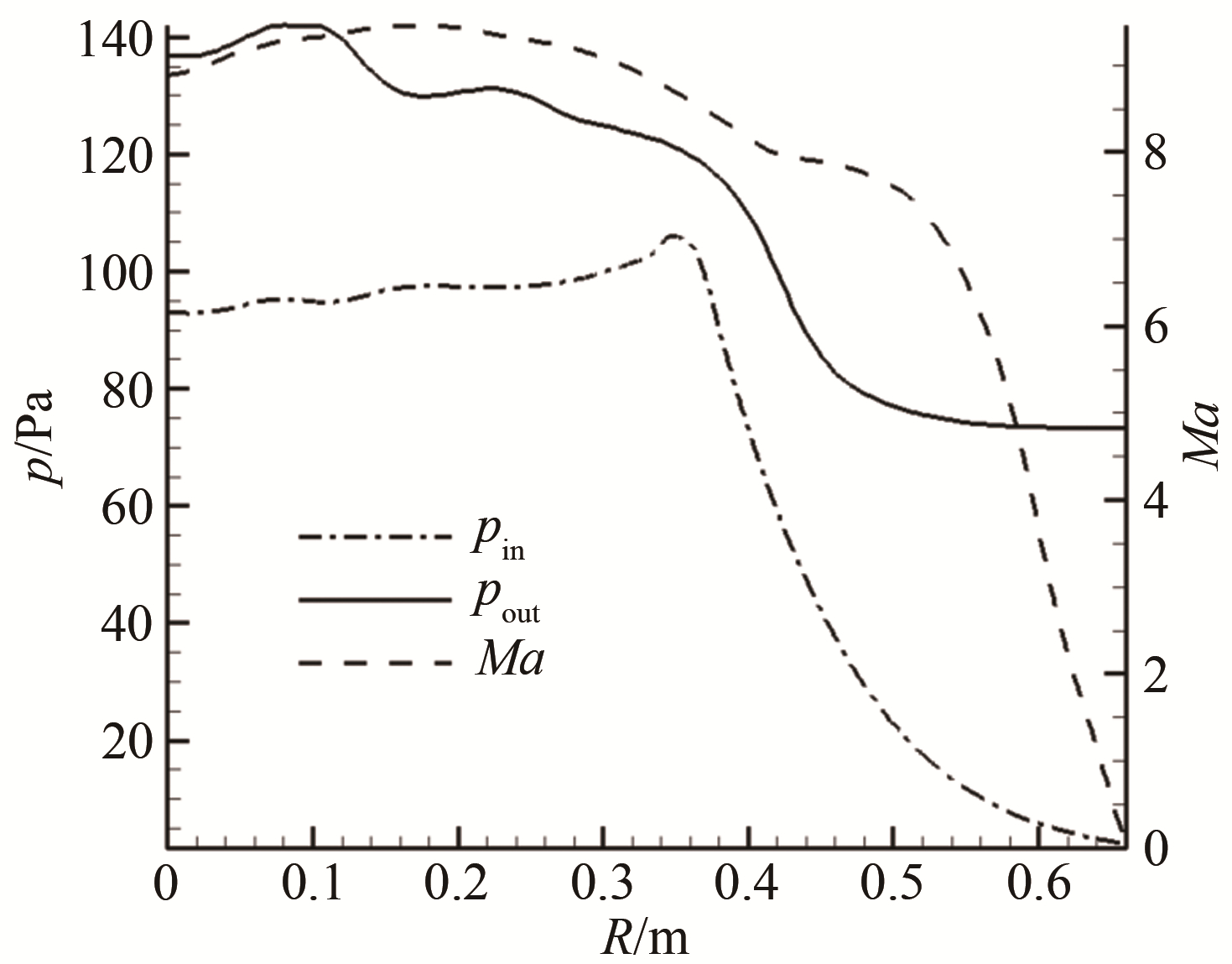
图 2为采用CFD/DSMC分区耦合计算方法模拟得到的低密度风洞扩压器内典型压力分布云图, 图 3为对应的扩压器入口径向压力、出口径向压力和马赫数分布。同样可以得出现有扩压器结构扩压作用不明显的结论, 初步分析认为导致这一问题的原因为:
|
| 图 2 低密度风洞常规扩压器内典型压力分布云图 Fig.2 Typical static pressure distribution of conventional diffuser in low density wind tunnel |
|
| 图 3 常规扩压器入口/出口径向压力和马赫数分布 Fig.3 Radial pressure and Mach number distribution at inlet and outlet of conventional diffuser |
(1) 试验气流核心区尺寸相对于扩压器收缩段小得多, 现有扩压器没有起到对主气流的变截面收缩作用;
(2) 边界层的粘性效应对扩压器中气流的减速增压作用不明显;
(3) 试验段来流马赫数很高, 而形成的斜激波较弱, 没有在扩压器内形成有效的激波串结构对试验段气体减速增压[6]。
能否在扩压器内设计一种装置, 对试验段核心区来流减速增压, 并使之与扩压器内壁面相互作用形成有效激波串, 从而达到扩压作用?这就是本文带中心锥新型扩压器结构设计思想的来源。
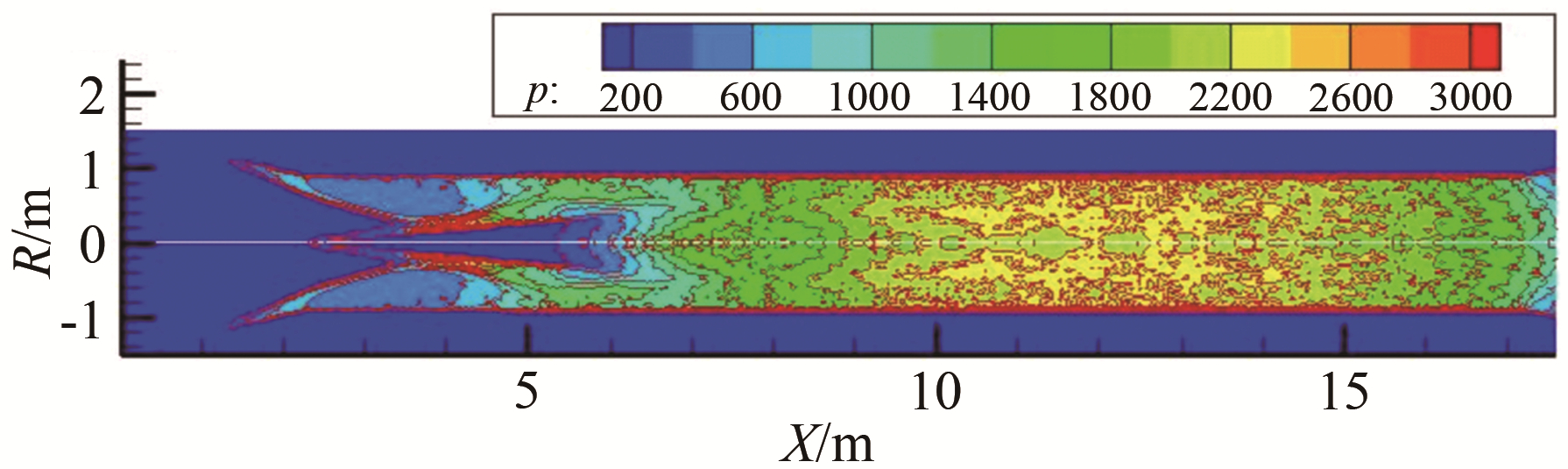
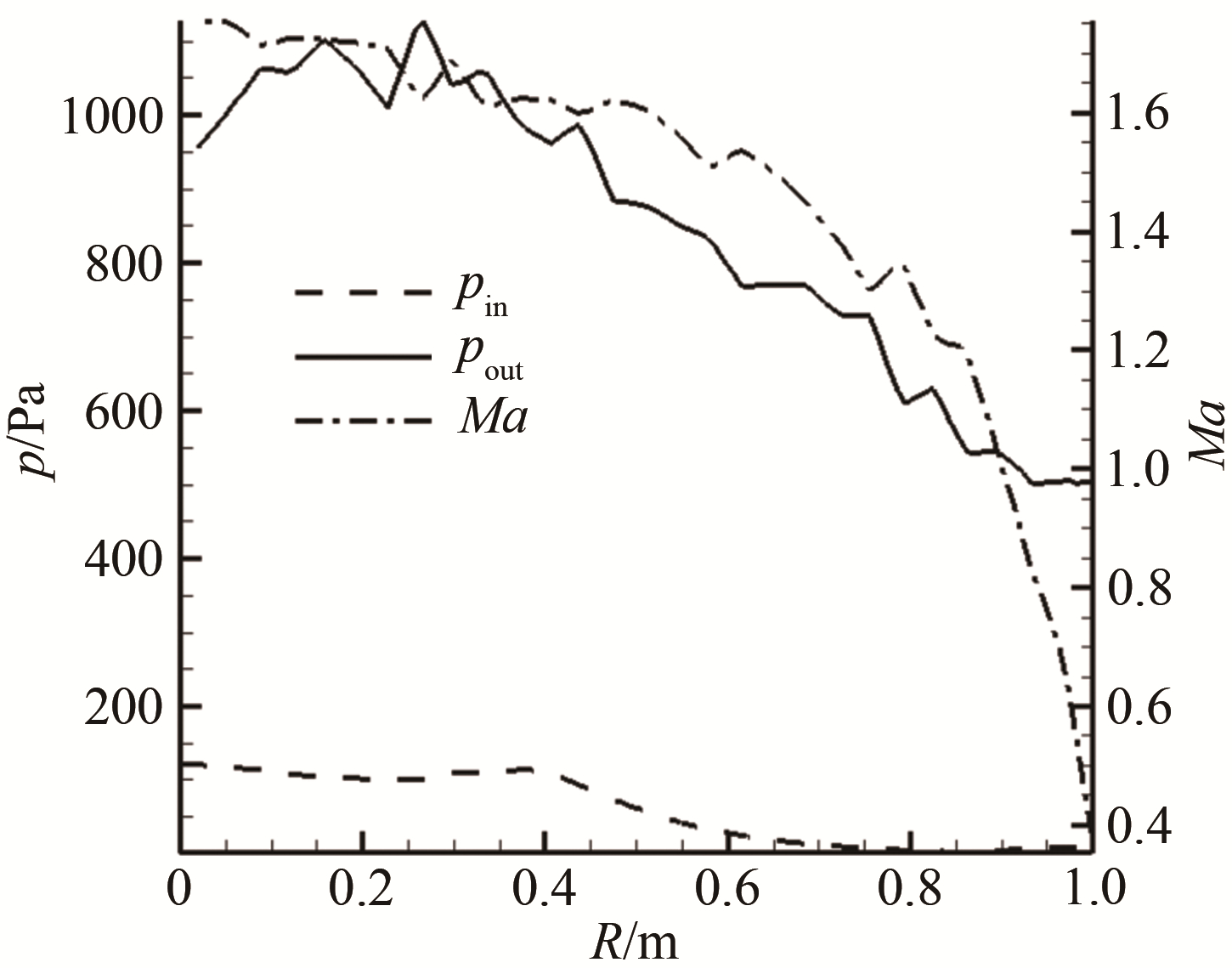
初步的计算(如图 4和5所示)分析表明, 该结构在高超声速低密度风洞中具有较高的扩压性能。为验证该类型扩压器的实际效率, 本文设计了一套简易装置, 并在高超声速低密度风洞中开展试验验证。
|
| 图 4 低密度风洞带中心锥型扩压器内典型压力分布云图 Fig.4 Typical static pressure distribution of central-type diffuser in low density wind tunnel |
|
| 图 5 带中心锥型扩压器入口/出口径向压力和马赫数分布 Fig.5 Radial pressure and Mach number distribution at inlet and outlet of central-type diffuser |
试验在Φ300 mm高超声速低密度风洞上进行(见图 6)。该风洞模拟高度范围为30~94 km, 可以在同一座风洞上实现连续流、滑移流和过渡流试验的模拟。风洞由气源系统、加热器、前室、喷管、试验段、扩压段、冷却器、真空系统和测试系统等部分组成。该风洞目前配备有型面喷管8套, 喷管出口马赫数为5、6、7、8、9、10、11和12;锥形喷管3套, 喷管出口马赫数为12、16和24, 所有喷管出口直径均为Φ300 mm。根据不同的状态可分别选用石墨电阻加热器或储热式加热器进行加热, 试验气体介质为氮气。

|
| 图 6 Φ300 mm高超声速低密度风洞 Fig.6 Φ300 mm hypersonic low-density wind tunnel |
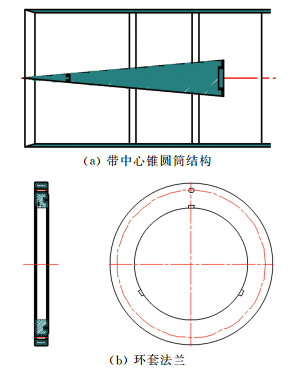
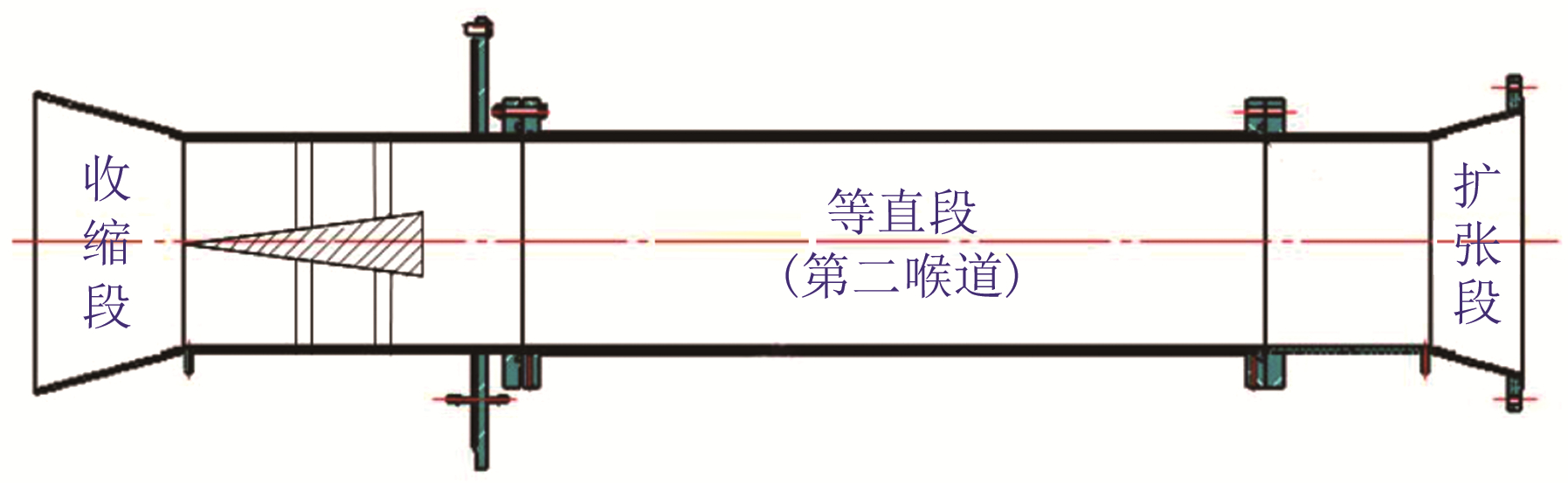
为不破坏现有风洞设备, 加工了一个环套法兰和圆筒, 并在圆筒内焊接中心锥, 带中心锥型扩压器套筒结构如图 7所示, 其中, 环套法兰安装在现有扩压器的收缩段和等直段连接处, 圆筒通过卡槽用螺钉紧固在环套法兰上。在现有扩压器中安装该套筒后, 中心锥顶点位于原扩压器等直段入口平面内, 其轴线与原扩压器轴线重合, 中心锥底部直径100 mm(扩压器等直段直径为400 mm, 远大于理想第二喉道面积, 而中心锥最大截面仅为等直段面积的6.25%, 第二喉道面积变化带来的影响可忽略), 半锥角为5°, 如图 8所示。另外, 试验时采用的试验段模型为底部直径100 mm、半锥角15°的钝锥模型。
|
| 图 7 带中心锥型扩压器套筒结构示意图 Fig.7 Sleeve structure of central diffuser |
|
| 图 8 中心锥安装在原扩压器中的位置示意图 Fig.8 Position of center cone installed in diffuser |
前室总压用CYG19(0~6 MPa)型压阻传感器测量; 当地大气压用数字式无汞气压计测量; 试验段、扩压器前后端、冷却器前后压力采用ZDZ电阻真空计和20 kPa绝对压力传感器测量。前室总温使用镍铬-镍硅热电偶测量。利用32通道数采系统进行数据采集处理。
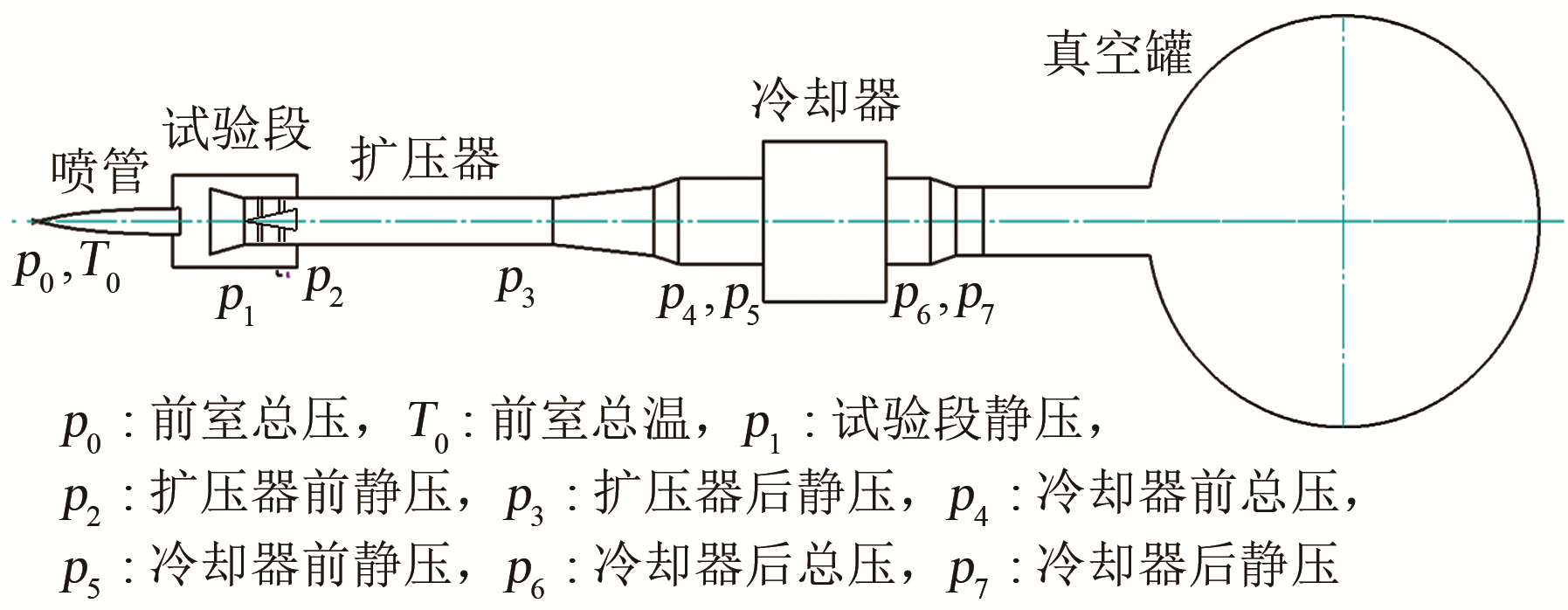
3 试验与结果分析 3.1 试验状态及测量点分布本文主要通过开展带中心锥型扩压器扩压性能试验分析, 研究中心锥在高超声速低密度风洞中的可行性问题。为完成相应的试验研究内容, 设计的2个试验状态分别为:M8喷管, 总温450 K, 总压1.5 MPa; M16喷管, 总温923 K, 总压1.0 MPa。该试验需对试验气体加热, 不同状态采用不同的加热方式。其中, 对于M8喷管采用储热式加热器加热, 对于M16喷管采用石墨电阻加热器加热。试验段抽真空至需要的启动压力后即开始试验。试验过程中需要对前室总温、总压, 试验段静压, 扩压器前后静压, 冷却器前后总压和静压进行测量, 试验测量点分布如图 9所示。
|
| 图 9 试验测量点分布示意图 Fig.9 Distribution of test measurement points |
为了考查有无中心锥对试验时间的影响, 定义稳定(有效)运行时间为试验段静压保持恒定的时间, 记t1s为依据经验计算得到的稳定运行时间, t2s为试验实际测得的稳定运行时间。表 1列出了M16喷管相同试验参数、不同试验条件下的稳定运行时间。可以看出, 带中心锥型扩压器对试验段气流稳定有积极作用, 能大幅度延长试验有效运行时间(在本次试验中, 相比于无中心锥而言平均延长了100 s左右), 这对高超声速飞行器地面试验精细化测量有很大帮助。
| 车次号 | 试验条件 | 总温/K | 总压/MPa | 启动前真空压力/Pa | t1s /s | t2s /s |
| 1 | 无模型无中心锥 | 936 | 1.15 | 49.5 | 232 | 179 |
| 2 | 无模型无中心锥 | 939 | 1.16 | 78.0 | 193 | 172 |
| 3 | 有模型无中心锥 | 931 | 1.17 | 41.6 | 243 | 177 |
| 4 | 有模型无中心锥 | 930 | 1.16 | 64.0 | 212 | 208 |
| 5 | 无模型有中心锥 | 935 | 1.19 | 56.4 | 225 | 260 |
| 6 | 无模型有中心锥 | 925 | 1.16 | 30.0 | 257 | 283 |
| 7 | 有模型有中心锥 | 920 | 1.17 | 41.6 | 241 | 275 |
| 8 | 有模型有中心锥 | 915 | 1.18 | 22.2 | 265 | 341 |
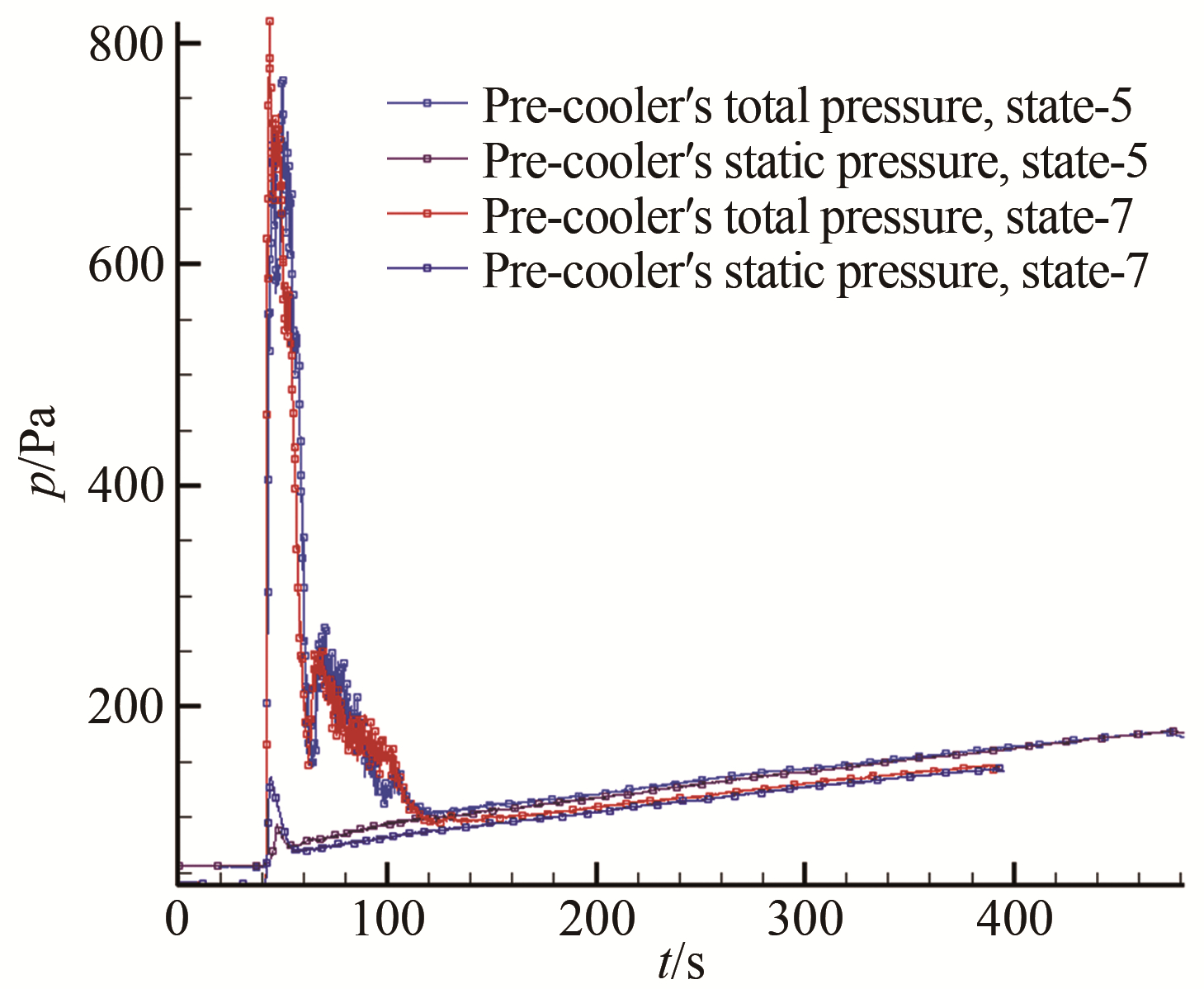
另外, 在无中心锥情况下, 试验稳定运行时间要小于经验计算结果, 而在有中心锥情况下, 试验稳定运行时间要大于经验计算结果。经分析, 这是因为中心锥对试验段气流产生了有效的压缩作用, 在扩压器内形成了显著的激波串结构, 扩压能力得到提高, 使得真空破坏压力增大, 真空泵抽气效率提升, 从而运行时间延长。表 1结果还表明, 在M16喷管下试验段有无模型存在对稳定运行时间影响不大, 这是因为试验气流流量较小, 稀薄度较高, 而模型尺寸又比较小, 其对扩压性能的影响未能体现。图 10也可以得到相同结论, 有无模型时冷却器前压力相差只有5 Pa左右, 其他测点情况类似。
|
| 图 10 车次5和车次7冷却器前总压与静压对比 Fig.10 Comparison of total pressure and static pressure at pre-cooler of test 5 and 7 |
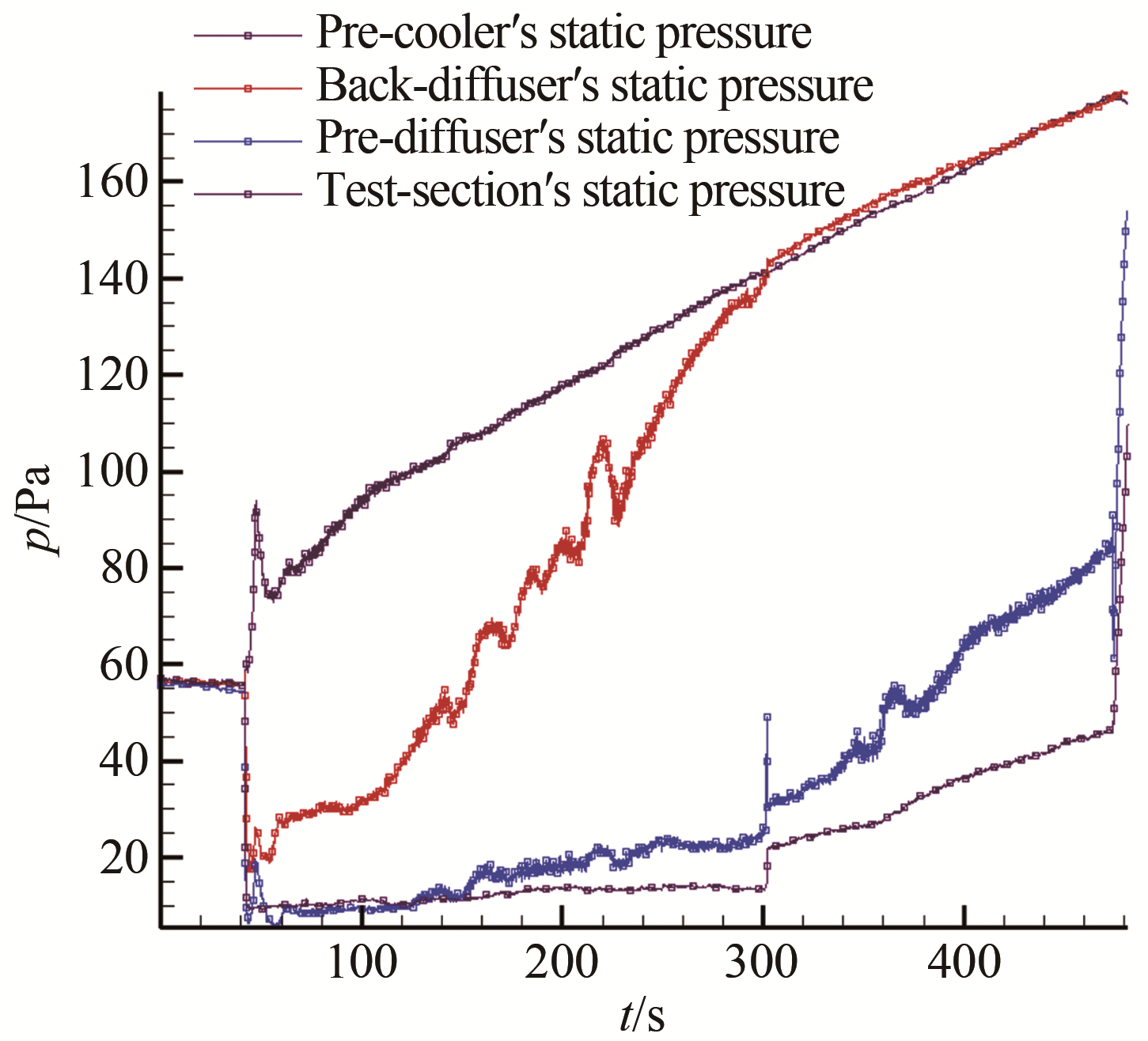
图 11是M16喷管带中心锥时的试验段、扩压器入口和出口及冷却器入口4个测点的静压随时间变化情况, 反映了试验过程中不同部段压力变化趋势。图中试验段压力在开车后至300 s左右保持稳定状态, 300 s之后由于扩压器无法继续维持随真空压力增大而增大的逆压梯度, 试验段的稳定气流遭到破坏, 使得试验段静压产生跳跃。在扩压器内部, 后端的压力要远大于前端的压力值, 且随时间变化更为剧烈, 呈波动式上升的过程, 这是因为经过中心锥后扩压器内形成的激波串结构随着真空压力的变化而变化, 直至马赫数降低至无法继续维持该结构形成亚声速流动。这一点也可以从试验后期扩压器后端静压和冷却器前静压重合看出。另外, 图 11中, 在稳定运行时间段内, 冷却器前的静压始终远大于扩压器后端静压, 这是因为扩压器扩张段和冷却器之间过渡段的波纹管对超声速气流的阻尼作用造成的。
|
| 图 11 车次5冷却器前、扩压器前后及试验段静压变化 Fig.11 Variation of static pressure at pre-cooler, back-diffuser, pre-diffuser and test section of test 5 |
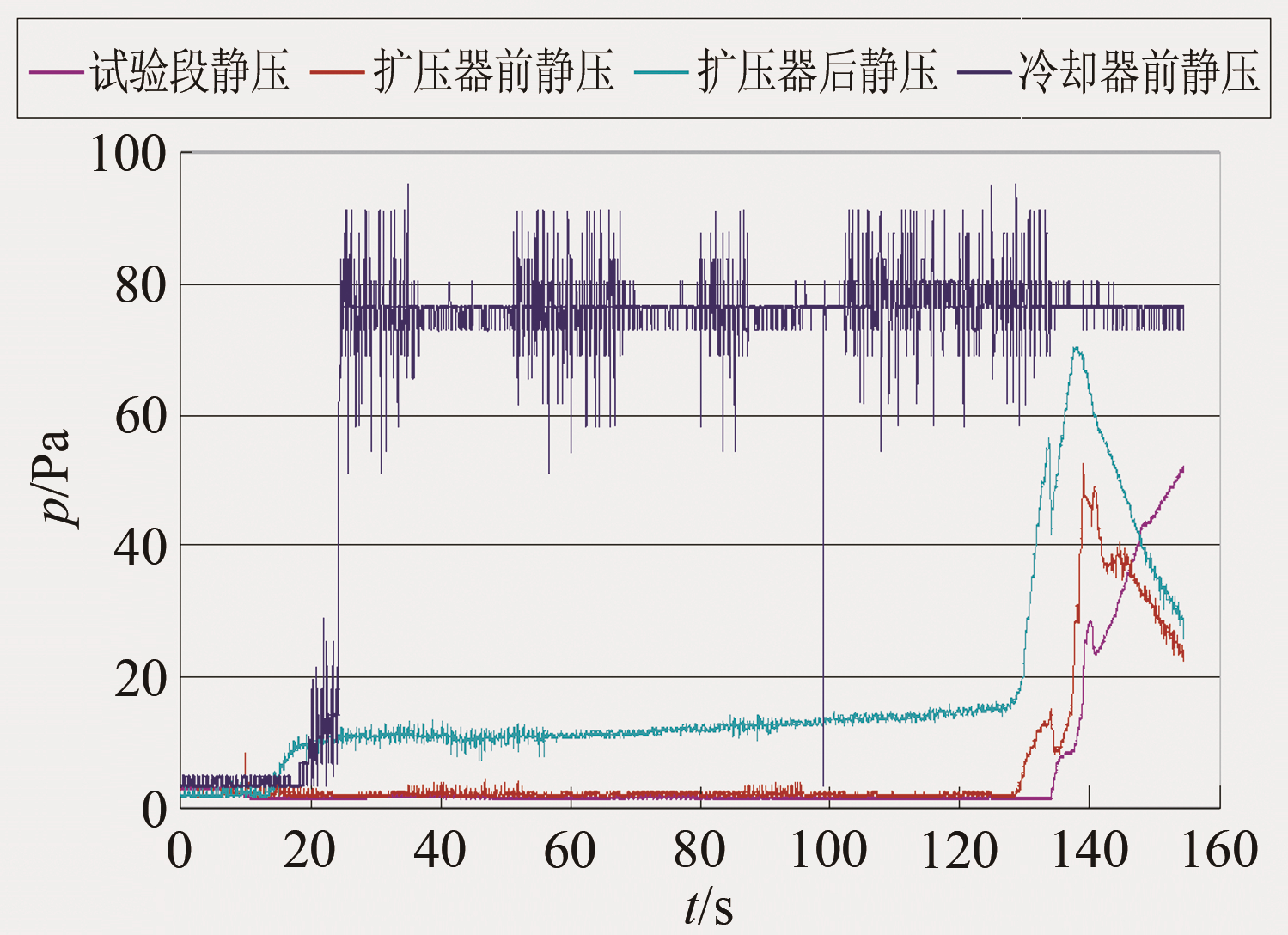
图 12是与车次5相同试验状态下, 无中心锥时的试验段、扩压器入口和出口及冷却器入口的静压随时间变化情况。将图 11和12相比较可以看出, 显然带中心锥时扩压性能有显著提高, 运行时间大幅度延长, 而无中心锥时, 扩压器内基本没有形成有效的激波串结构, 无法维持较大的逆压梯度, 仅能靠真空罐的容积来保证试验有效运行时间。
|
| 图 12 无中心锥冷却器前、扩压器前后及试验段静压变化 Fig.12 Variation of static pressure at pre-cooler, back-diffuser, pre-diffuser and test section without center cone |
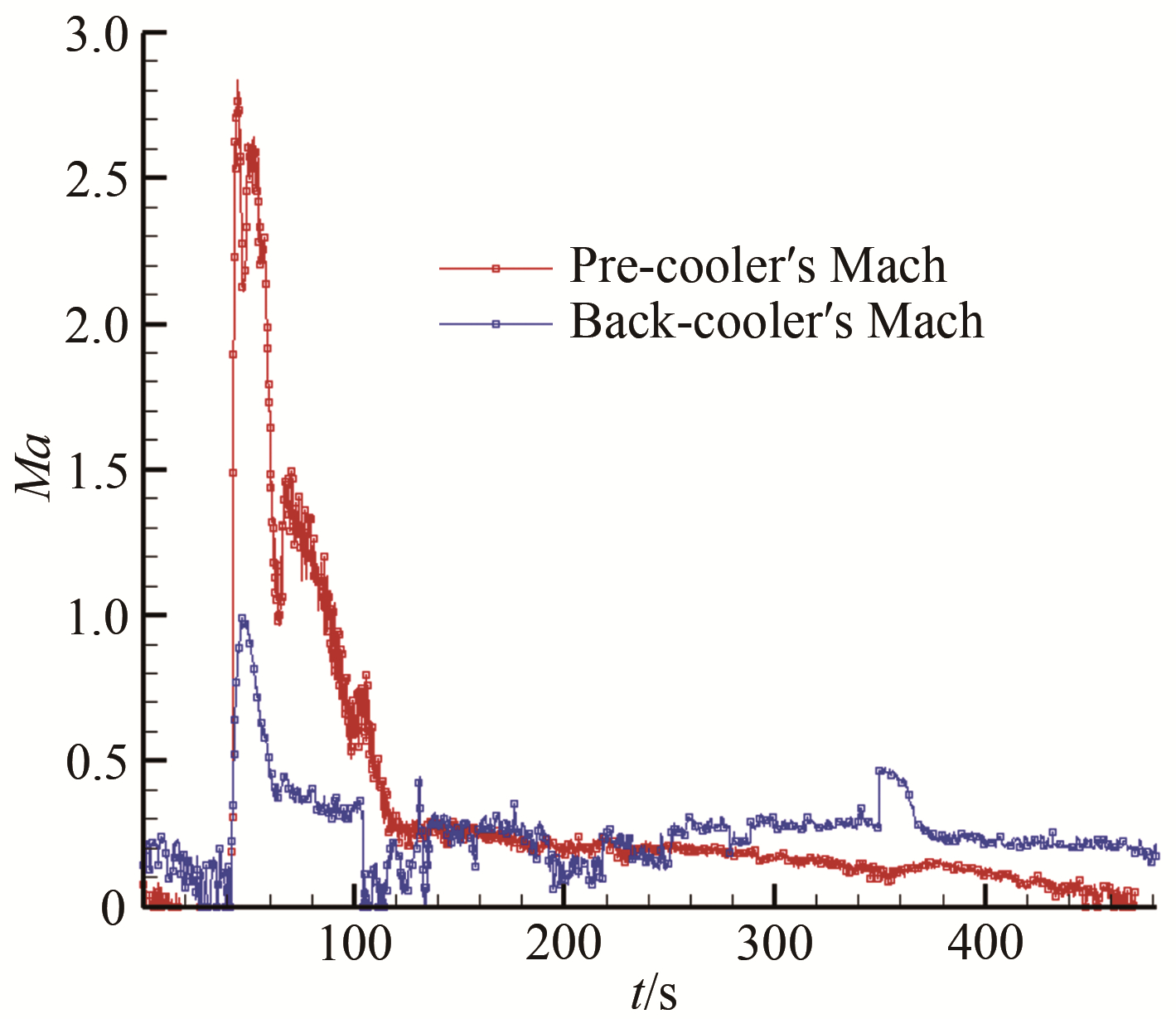
图 13是根据冷却器前后总压与静压估算得到的中心线上马赫数变化情况, 数值上和真实情况有差别, 仅反映总体变化趋势。可以看出, 气流经过中心锥扩压器后, 马赫数降低但仍然是超声速流动, 随着真空压力的增大, 马赫数进一步降低, 约在开车后50 s降至亚声速, 冷却器换热设计可以按照低速流动计算。
|
| 图 13 车次5冷却器前后中心线上马赫数变化情况 Fig.13 Variation of Mach number at center of pre- and back-cooler of test 5 |
为便于说明, 分别选择有无模型、有无中心锥4个不同试验条件下的典型车次进行分析, 试验状态如表 2所示。为消除前室压力波动的影响, 分析过程中以同一车次测得的试验段静压进行了无量纲处理。
| 车次号 | 试验条件 | 总温/K | 总压/MPa | 启动前真空压力/Pa |
| 24 | 有模型, 有中心锥 | 498 | 1.63 | 671 |
| 26 | 无模型, 有中心锥 | 482 | 1.69 | 670 |
| 27 | 无模型, 无中心锥 | 489 | 1.65 | 389 |
| 30 | 有模型, 无中心锥 | 485 | 1.52 | 726 |
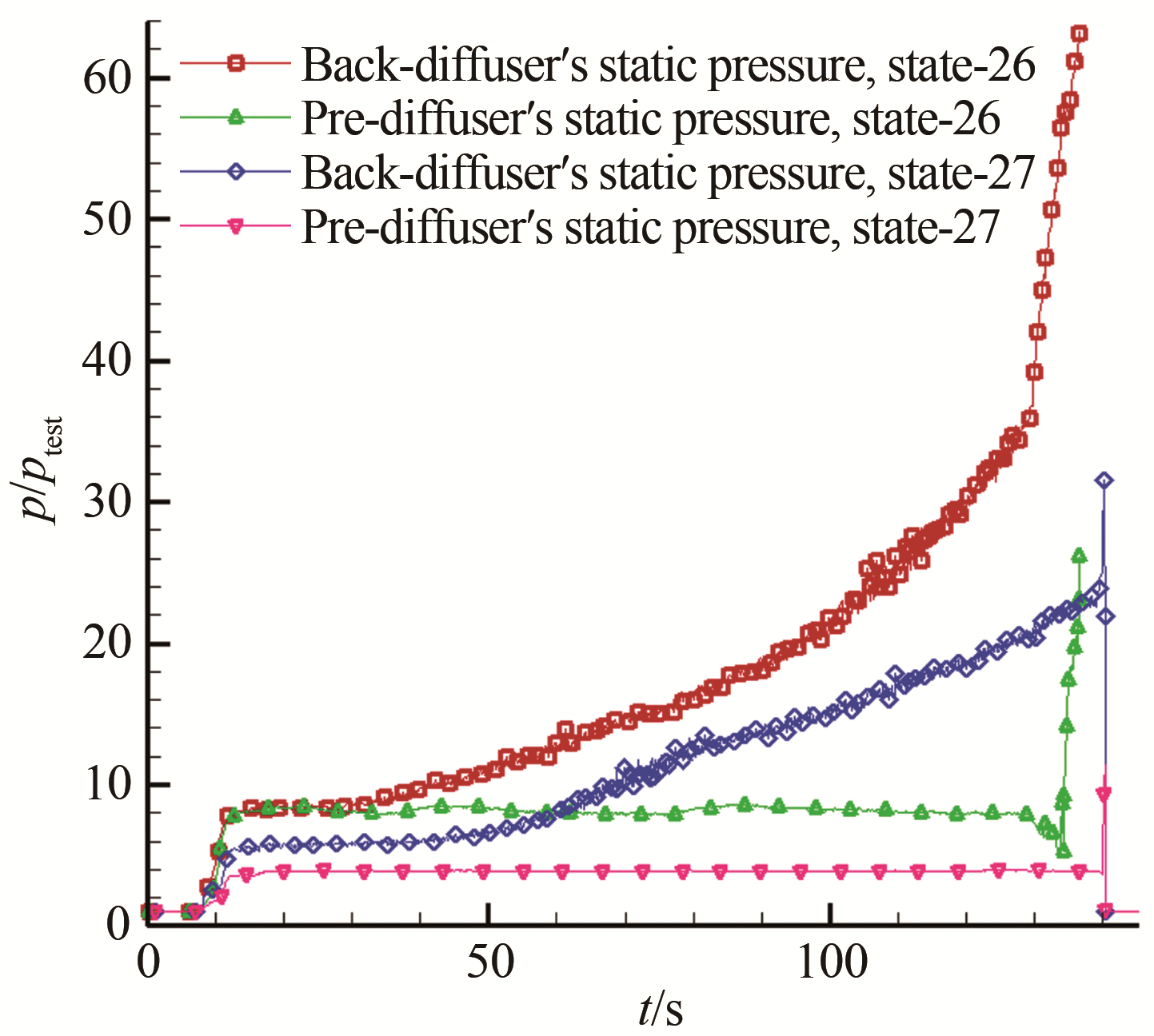
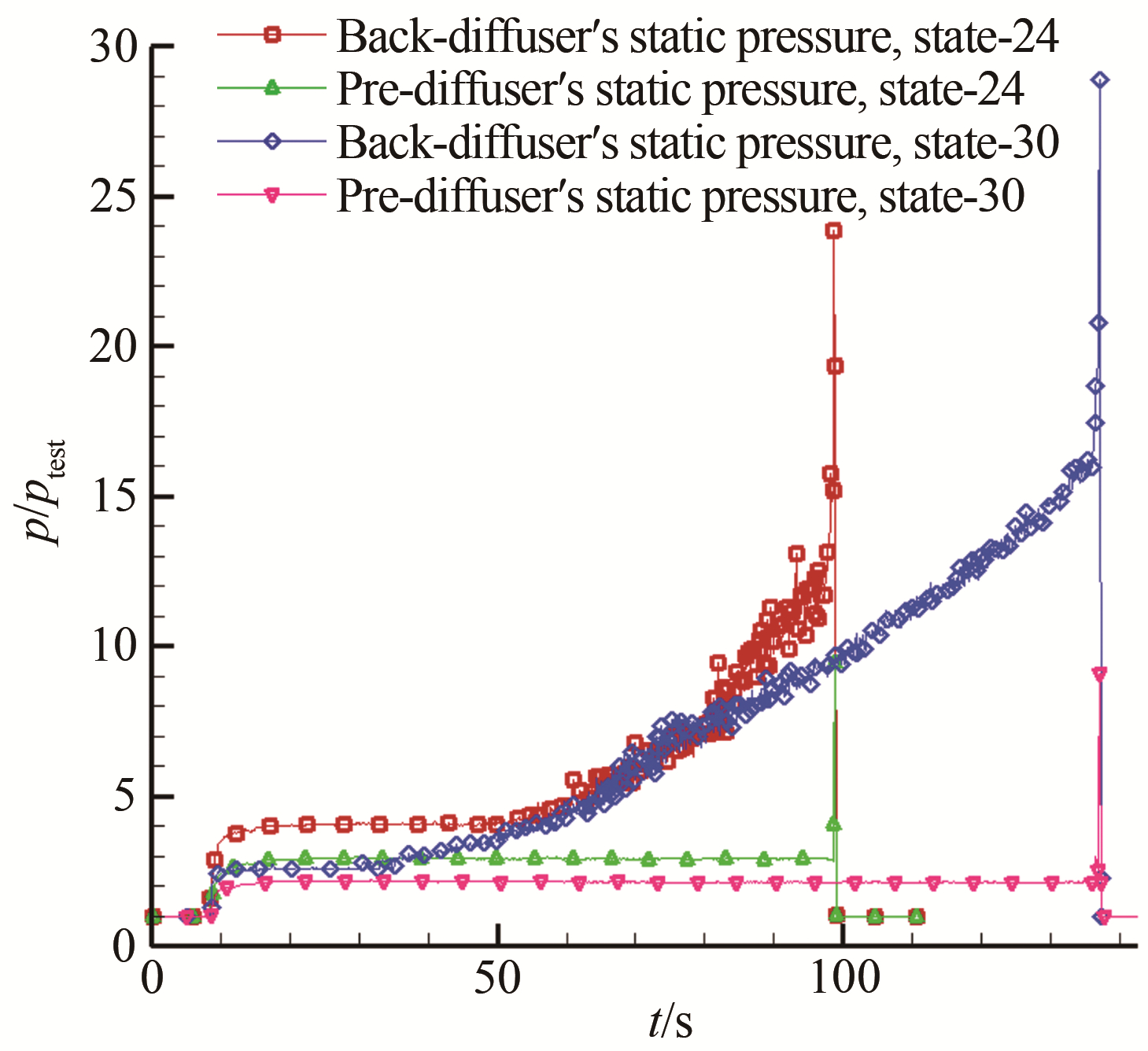
图 14为通过考察扩压器前后端静压变化分析试验段无模型时有无中心锥对扩压器扩压性能的影响, 图 15考察的是试验段有模型时有无中心锥对扩压器扩压性能的影响。对比分析可以看出, 有中心锥时扩压能力是无中心锥的1.5~2.0倍, 说明该中心锥结构不仅能够在M16喷管小流量状态下大幅度提升扩压性能, 而且在M8喷管大流量状态下也能较好地提升扩压器的扩压性能。
|
| 图 14 车次26和车次27扩压器前后静压变化对比(没有模型时中心锥的影响) Fig.14 Comparison of static pressure at pre- and back-diffuser of test 26 and 27(effect of center cone without test model) |
|
| 图 15 车次24和车次30扩压器前后静压变化对比(有模型时中心锥的影响) Fig.15 Comparison of static pressure at pre- and back-diffuer of test 24 and 30(effect of center cone with test model) |
从图 14和15考察试验段试验模型对扩压器扩压性能的影响, 可以发现:在M8喷管(大流量)情况下, 模型的存在对整个流动有很大影响, 且对扩压器的扩压能力有减弱作用。这是因为低密度风洞采用自由射流形式的试验段, 气流经过模型后迅速膨胀, 反而不利于激波串结构的形成, 而中心锥在扩压器中相对小的空间内能更好地对来流气体进行减速压缩, 因此, 中心锥不是简单的等同于试验模型。
4 结论在Φ300 mm高超声速低密度风洞上开展了M16小流量稀薄状态和M8大流量近连续流状态下带中心锥型扩压器结构扩压性能的研究。结果表明:
(1) 带中心锥结构的扩压器扩压性能更优, 能大幅度提高有效运行时间;
(2) 带中心锥结构的扩压器在本文试验运行参数范围内, 无论是小流量的M16状态还是大流量的M8状态, 均有较好的扩压性能;
(3) 试验段模型在小流量情况下对扩压器效率影响不大, 在大流量情况下对扩压器效率有减弱作用。
可见, 带中心锥结构的扩压器具有较好的扩压性能, 有效提高了风洞试验能力, 为高超声速风洞扩压器设计提供了一条新的思路。
| [1] |
Matsuo K, Miyazato Y, Kim H. Shock train and pseudo-shock phenomena in internal gas flows[J]. Progress in Aerospace Sciences, 1999, 35(1): 33-100. DOI:10.1016/S0376-0421(98)00011-6 |
| [2] |
童华, 孙启志, 张绍武. 高超声速风洞扩压器试验研究与分析[J]. 实验流体力学, 2014, 28(3): 78-81, 103. Tong H, Sun Q Z, Zhang S W. Investigation and analyse on the diffuser of hypersonic wind tunnel[J]. Jounal of Experiments in Fluid Mechanics, 2014, 28(3): 78-81, 103. |
| [3] |
博普A, 戈因K L.高速风洞试验[M].邓振瀛, 译.北京: 科学出版社, 1980.
|
| [4] |
Neumann E P, Lustwerk F. Supersonic diffusers for wind tunnls[J]. J Appl Mech, 1949, 16(2): 195-202. |
| [5] |
Neumann E P, Lustwerk F. High efficiency supersonic diffusers[J]. J Aeronaut Sci, 1951, 18(6): 369-374. DOI:10.2514/8.1975 |
| [6] |
李桦, 范晓樯, 丁猛. 超声速扩压器中激波串结构的数值模拟[J]. 国防科技大学学报, 2002, 24: 18-21. Li H, Fan X Q, Ding M. Numerical simulation of the shock train structure in the supersonic diffuser[J]. Journal of National University of Defense Technology, 2002, 24: 18-21. |



