荷电微射流雾化技术可获得大量粒度细小、单分散性好、可控性强、沉积率高的荷电微液滴[1]。与荷电液滴的产生、输运、沉积、分析、控制等相关的成果已在工农业生产中得到了广泛应用[2-3]。纳米制造技术、生物医药技术的迅猛发展, 使荷电微射流雾化被推广到微纳米薄膜/颗粒制备、微多相混合、微胶囊封装、微动力推进、微型燃烧等多学科领域[4-7], 显示了巨大的应用价值。
荷电微射流雾化及其应用过程中伴随着复杂的荷电多相流动, 其耦合场下的电流体动力学特性还存在较多的研究盲点。精确捕捉和描述荷电微射流雾化的显微演变形貌特征, 探讨影响雾化模式转变及射流不稳性的关键控制参数, 是揭示雾化机理的重要前提, 也是荷电流体雾化领域普遍关心的难点问题。Basset[8]最早研究了电场中的射流行为, 发现电场可以使轴对称的长波稳定, 同时使短波不稳定。随后, Zeleny[9]研究了电场作用下荷电射流的稳定性。Taylor[10-11]在电场中无粘射流稳定性的理论分析及实验研究方面取得了开拓性进展, 在小扰动近似下计算了varicose模态和kink模态的增长率。Turnbull[12]研究了射流在轴向电场和径向电场共同作用下的轴对称稳定性, 结果表明:径向电场对长波起稳定作用, 而短波的稳定主要受轴向电场的影响。González等[13]将射流稳定性拓展到周期电场下的情形, 研究了径向交流电场对导电粘性射流稳定性的影响, 发现射流的自然频率和交流电场的频率发生参量谐振, 导致射流在稳定区域内失稳。Lòpez-Herrera等[14]对低电导率液体射流在径向电场作用下的轴对称不稳定性进行了分析, 认为相对电松弛时间和介电常数对射流径向扰动增长率及最不稳定波长的影响不可忽略。李芳等[15]研究了径向电场和轴向电场作用下同轴射流的无粘稳定性, 发现粘性有使同轴射流所有不稳定模态趋于稳定的作用。王晓英等[16]数值分析了针-板电极荷电液体的射流不稳定性, 获得了液体物性、射流半径及电场强度等参数对荷电液体射流的轴对称模型和非轴对称模型的影响。甘云华等[17]建立了静电喷雾二维轴对称模型, 获得了锥射流模式下的乙醇静电喷雾形态、空间电场分布以及液滴速度场分布。纵观此类研究, 多半是基于理论分析与数值模拟方法, 模型往往得不到有效的验证。
近十年来, 随着现代流场测试技术的迅速发展, 应用于荷电微射流不稳定性分析的可视化测量成为当前电雾化的电流体动力学机理研究取得突破的必要手段。本文借助可视化实验手段精确捕捉无水乙醇荷电微射流雾化的显微演变行为, 探讨微射流的破碎形式对雾化特性的影响规律, 同时结合小尺度PIV技术获取荷电微射流不稳定雾化的流场信息, 分析锥射流及多股射流模式的射流不稳定性特征, 为判定荷电微射流的稳定雾化形态提供测量依据。
1 实验装置及方法图 1为荷电微射流可视化实验装置示意图。实验选用的毛细管内径为250 μm, 外径为500 μm。介质雾化流量用微流量注射泵精确控制在50 μL/min。负高压静电发生器(0~20 kV)的高压负极与毛细管尖端相连接, 正极与板状电极(紫铜材质)相连并接地, 组成负高压静电发生系统。板状电极放置于毛细管口端面正下方1.3 cm处, 形成针-板荷电形式的高压电场区域, 并以聚四氟乙烯材料将关键结合部位绝缘。借助二维滑动导轨精确微调荷电液滴在高速摄像机拍摄区域的位置, 方便荷电雾化微液滴拍摄区域的选取与定位。借助Phantom V1611高速摄像机(满幅分辨率1280 pixel×800 pixel下的拍摄频率为16 600帧/s), 配合NAVITAR 12×显微变焦镜头, 对荷电无水乙醇的微射流雾化行为进行显微拍摄, 获得亚毫秒级至微秒级时间内荷电微射流的过渡演变特征。以LED冷光源作为拍摄背光, 放置于相机正对面。为防止静电累积, 测量设备均接地进行保护。

|
| 图 1 无水乙醇荷电雾化的可视化实验装置 Fig.1 Apparatus of charged ethanol atomization |
对于低粘性的流体介质, 微通道静电雾化过程中毛细管口雾化模式的过渡演变是毛细力与静电力共同作用的结果, 可以借助电邦德数BoE加以描述[18]:
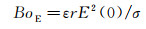 (1)
(1)
式中, ε和σ分别为空气的介电常数与液体固有表面张力, r为毛细管外半径, E(0)为毛细管口处的电场强度。对于实验采用的针-板形式的电场形态, E(0)表示为[19]:
 (2)
(2)
式中, U为荷电电压, h为板状电极表面到毛细管口端面的垂直距离。由式(1)和(2)可得:
 (3)
(3)
电邦德数BoE与电压U的平方成正比, 且受毛细微通道尺寸、极间距及液体固有表面张力的影响, 较单一的电压参数能更准确地表征射流模式及其过渡演变行为。需要指出的是, 若介质的奥内佐格数(Ohnesorge number)Oh≥0.1, 粘性对荷电液滴雾化形态的影响明显[20], 此时仅借助电邦德数分析荷电液滴形成及射流转变行为没有太大意义; 而当Oh<0.1, 介质的粘性对流体变形及破碎的影响可以忽略[21], 故实验选用无水乙醇这类低粘性流体。在低粘性前提下, 相关研究已验证电导率对荷电液滴的脉动变形影响可以忽略[22]。可认为电邦德数是一个非常重要的无量纲数, 对于研究荷电液滴形成及射流转变行为有重要意义。
荷电微射流形成及演化过程中, 静电力与毛细力比值的变化对雾化模式的影响非常显著。纯依赖电驱动的静电雾化, 其工作原理就是从毛细管口脱落液滴的荷电破碎过程, 可以通过Rayleigh极限进行解释, 即液滴带电后, 电荷会由于库仑斥力作用分布于液滴表面, 当表面电荷量达到一定程度, 液滴界面将变得极不稳定, 进而破碎为更细小的微液滴。需要指出的是, 带电液滴雾化为离散性液滴群, 导致流体表面能及动能的增加, 由能量守恒定律可知, BoE增大恰恰意味着能量输入的增加, 流体更容易生成具有更大流体表面能及动能的液滴群, 而静电雾化从滴状模式到多股射流模式的流态演变也正是这类荷电液滴群形成及输运的体现。
2.1 无水乙醇微射流的显微雾化形态图 2为随BoE增长而变化的无水乙醇微射流的显微雾化形态。粘性射流的色散模型表明, 粘性可有效抑制射流径向扰动的增长[23]。无水乙醇液体的粘性较低, 其荷电射流雾化特征表现为非轴对称性的色散关系, 射流径向扰动较强, 这有助于射流进一步破碎为更细小的微液滴。通过测量可以发现, 无水乙醇的射流微液滴尺寸一般在20 μm左右, 甚至能形成纳米级喷射; 粘性较高的生物柴油的荷电雾化液滴尺寸一般在100 μm左右[24], 这验证了无水乙醇的扰动增长率远远高于生物柴油。荷电微射流从进入纺锤模式(BoE=2.35)到最终形成多股射流模式(BoE=17.30), 射流的径向不稳定性扰动几乎占据了整个雾化区间。从图中可以看出, 在射流雾化的显微演变过程中, 随着BoE的增加, 射流末端的径向不稳定扰动有一个先增加后减小的趋势, 尤其当BoE=5.80时, 锥射流模式的不稳定性表现得尤为突出, 且在该区间未观察到稳定的射流雾化形态。

|
| 图 2 不同BoE下无水乙醇荷电微射流雾化形态 Fig.2 Morphology of the micro-jet at different Bond numbers |
值得一提的是, 实验中发现了多股射流模式的稳定雾化形态, 其雾化区间极短(13.30≤BoE≤13.60)。通过记录的图片可以看出, 该区间内各股射流都保持极低的径向扰动增长率, 射流雾化极其稳定, 射流破碎子液滴具有良好的单分散性, 由此打破了以往认为只有微流量锥射流才存在稳定雾化区间的传统观念[25]。这表明雾化射流流量的增加虽然打破了锥射流雾化模式的稳定区间, 但却可以在多股射流模式下发现其稳定雾化区间。这意味着通过参数的有效控制可实现较大流量范围内的射流稳定雾化, 从而在工业应用中大大提高微/纳颗粒制备及喷涂等环节的生产效率。
2.2 射流偏离度定义射流偏离度为aj, 表征单股射流偏离毛细管轴心的角度, 以直接反映荷电微射流的径向扰动情况。图 3为BoE影响下射流偏离度aj及其不确定性脉动值。从图中可以看出, 随着BoE增大, 无水乙醇的荷电微射流雾化先后经历了纺锤模式(区间①)、锥射流模式(区间②)及多股射流模式(区间③、④、⑤); aj则出现了先增大后减小的趋势, 且在区间④内(即13.30≤BoE≤13.60区间)保持了极大值aj=45.8°, 此时为荷电微射流的稳定多股射流模式, 多股射流的雾化形态保持一致且呈轴对称分布状态。对于非轴对称色散模型, 可以通过射流偏离度aj的变化情况间接反应射流的扰动增长率, 进而对射流的不稳定性特征加以判定。当BoE≤2.35时, aj保持0°不变, 表明此时射流扰动增长率较小以至于射流末端的库仑分裂过程稳定。当2.35≤BoE<9.41时(锥射流模式区间), aj的不确定性值的变化范围越来越大, 在BoE为3.55、5.80、9.41时, aj的不确定性范围分别为[-1,1.5]、[-1.8,2.6]及[-5.6,4.3], 这意味着随着BoE的增大, 此区间内的射流扰动增长率逐渐增大, 射流不稳定性增强。当9.41≤BoE<17.30时(多股射流模式区间), aj的不确定性范围先逐渐收缩至0而后又不断增大, 表明射流扰动增长率随着BoE的增大经历了先衰减后增长的过程, 且在13.30≤BoE≤13.60区间内射流扰动增长率极小。当BoE=17.30时, aj的不确定性脉动值为[-2.8,0.7], 这种不确定性的增加意味着荷电射流重新进入了一个不稳定的多股射流形态。在荷电微射流的多领域应用中, 类似BoE=13.60的工况是最理想的雾化模式, 获取其雾化规律信息, 有利于制定稳定雾化调控方法并指导工程实践。

|
| 图 3 不同BoE下无水乙醇微射流偏离轴心的角度变化 Fig.3 Deviation of the micro-jet at different Bond numbers |
图 4给出了微射流雾化区域的选取原则。通过从宏观到微观的3幅图片对比, 可以明确所测试目标流场的区域范围。其中, 图 4(a)为普通单反相机拍摄的微射流稳定多股射流形态的宏观图片(BoE=13.60); 图 4(b)为高速摄像拍摄的显微图像, 主要用于观察射流界面的演变形态特征, 分析射流过渡行为; 图 4(c)代表任意一对称射流破碎段的PIV图像, 主要用于获取射流末端破碎段雾化信息, 包括荷电子液滴群的速度分布、流线、湍动能等。在不同实验工况下, 对图 4(b)和(c)代表的射流雾化图像进行精确捕捉, 将PIV后处理的微液滴群速度场信息与高速摄像拍摄的微射流显微演变形态进行对比分析, 获得BoE影响下的荷电微射流雾化特性, 进而获取荷电微射流雾化模式的不稳定性信息。

|
| 图 4 微射流雾化区域的选择 Fig.4 The choice of micro-jet area |
无水乙醇的静电雾化微液滴粒度均在亚微米级, 是非常合适的示踪粒子。实验中, 以分辨率为2048 pixel×2048 pixel的CCD相机进行拍摄。在图像后处理中, 判读区窗口设置为64 pixel×64 pixel。在PIV捕捉的流场区域, 微液滴浓度的空间分布存在差异, 判读区内的微液滴数大都在20个左右; 而在射流边界区域, 由于判读区内液滴数目偏少, 在后处理中应以向量修正剔除错误矢量信息。一般地, 对于尺寸大小为N=64 pixel的判读区, 根据Nyquist采样定律, 计算所得位移不超过N/2, 此时, 误差大约为1/(64/2)≈3.13%;同时, 在后处理中运用三点高斯的亚像素拟合, 使计算结果精度提高至±0.1 pixel精度(即亚像素精度), PIV后处理误差降低至0.3%。
精确测量微射流雾化速度场, 有助于截取参数影响下射流雾化的动态流场信息并表征微射流的不稳定性特征。图 5为不同BoE下荷电微射流雾化的PIV图像、速度矢量图及流线图。可以看出, 随着BoE的增大, 荷电射流雾化速度场发生了显著变化:

|
| 图 5 不同BoE下的微射流雾化PIV图像、速度矢量图及流线图 Fig.5 PIV images, velocity vector and flow diagrams of the micro-jet at different Bond numbers |
当BoE较小时(图 5(a)), 射流速度基本沿着轴线方向向下, 射流核心区在轴心处, 且具有较好的轴对称性; 此时, 射流末端的径向扰动较小, 射流破碎相对稳定, 但考虑到此时的雾化模式为纺锤模式, 射流破碎是不连续的, 具有一定的周期性, 射流破碎在整个射流演变过程中是不稳定的。
当BoE=5.80时, 射流核心区偏离轴心, 速度方向偏离轴向, 射流的径向扰动明显增强, 射流速度分布沿射流核心区缺乏对称性, 且此时射流整体速度大小较纺锤模式有明显下降, 这表明荷电微射流的稳定性在急剧减弱。
当BoE=9.41时, 荷电微射流处于多股射流雾化模式, 射流核心区速度有明显回升, 但多股射流之间的速度分布差异性较大, 彼此的雾化结构缺乏对称性, 这导致整体的荷电微射流是一个不稳定的雾化状态。
当BoE=13.60时, 多股射流的速度分布沿毛细管轴向具有良好的轴对称性, 且各股射流的雾化区域都有一个沿其射流核心区的准对称结构, 此时射流核心区的速度达到了前所未有的峰值, 射流速度趋近于沿射流核心的轴向方向, 这意味着单股射流的径向扰动极小, 可认定为多股射流的稳定雾化形态。
雾化流场中的流线直接反映了某一时刻子液滴群的流动变化趋势, 是对流场特性最直接的描述。图 5中给出了不同BoE下荷电微射流破碎段的流线图。对于单股锥射流来说, 图 5(d)中射流破碎段的径向扰动较小, 其流线的轴对称性比图 5(b)和(c)更好, 流线相对平滑, 射流破碎形式较为稳定。多股射流模式中任意单股射流的雾化形态决定着整体射流雾化的稳定性。对比图 5(c)和(d)可以发现, 前者的单股射流流线之间的差异明显, 射流边界处的流线较为紊乱, 缺乏射流结构的对称性, 这是不稳定多股射流形态的典型特征(主要是受毛细管口半月面表面波的扰动所致); 随着BoE增大, 毛细管口半月面的电场强度逐渐增大, 其界面不稳定性逐渐增加, 荷电微射流在半月面上的扰动加剧, 使得射流破碎段雾化结构极不稳定。而后者的单股射流流线无论是平滑度还是对称性都非常好, 且没有明显的涡结构, 表明此时的射流雾化状态十分稳定, 属于多股射流模式的稳定雾化形态。
3 结论基于时空分辨率较高的高速摄像及小尺度PIV技术, 对无水乙醇荷电微射流雾化模式的演变行为及射流不稳定性进行了可视化研究, 主要结论如下:
(1) 无水乙醇的荷电微射流表现为非轴对称的色散关系。随着BoE增大, 射流的径向扰动贯穿于整个雾化模式区间, 锥射流模式下的不稳定性表现得尤为突出, 而多股射流模式下存在极稳定的雾化区间。
(2) 射流偏离度的不确定性映射了射流的不稳定性。随着BoE的增大, 射流偏离度在整个雾化模式区间呈现"先增大后减小"的趋势, 且在BoE=13.60时出现极大值。
(3) 在锥射流模式下, 射流偏离度的不确定性逐渐增大, 过渡到多股射流模式后, 不确定性逐渐降低(BoE=13.60时降低为0), 表明多股射流模式存在稳定的雾化区间。此后, 射流偏离度的不确定性又逐渐增大, 荷电微射流进入新的不稳定雾化阶段。
(4) 纺锤模式下, 射流速度基本沿着轴线向下, 射流末端的径向扰动较小; 锥射流模式下, 径向扰动明显增强, 射流速度明显回落; 多股射流模式下, 射流核心区速度明显回升, 但不同BoE下多股射流之间的速度分布差异较大。
(5) 多数情况下, 射流边界处的流线较为紊乱, 缺乏对称性; 仅在13.30≤BoE≤13.60的极小区间内, 射流核心区的速度达到峰值, 射流速度趋近于沿射流核心的轴向方向, 这意味着单股射流的径向扰动极小, 此时为多股射流的稳定雾化形态。
| [1] |
Brown N A, Zhu Y Q, German G K, et al. Electrospray deposit structure of nanoparticle suspensions[J]. Journal of Electrostatics, 2017, 90: 67-73. DOI:10.1016/j.elstat.2017.09.004 |
| [2] |
贾卫东, 李成, 薛飞, 等. 背负式静电喷雾器设计与试验[J]. 高电压技术, 2012, 38(5): 1078-1083. Jia W D, Li C, Xue F, et al. Design and experiment of knapsack electrostatic sprayer[J]. High Voltage Engineering, 2012, 38(5): 1078-1083. |
| [3] |
郑捷庆, 张军, 钟晓龙. 乳化柴油静电雾化的试验研究[J]. 实验流体力学, 2012, 26(6): 44-47. Zheng J Q, Zhang J, Zhong X L. Experimental investigation on electrostatic atomization characteristics of emulsified diesel[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(6): 44-47. DOI:10.3969/j.issn.1672-9897.2012.06.010 |
| [4] |
Roncallo S, Painter J D, Ritchie S A, et al. Evaluation of different deposition conditions on thin films deposited by electrostatic spray deposition using a uniformity test[J]. Thin Solid Films, 2010, 518(17): 4821-4827. DOI:10.1016/j.tsf.2010.01.061 |
| [5] |
Bock N, Dargaville T R, Woodruff M A. Electrospraying of polymers with therapeutic molecules: State of the art[J]. Progress in Polymer Science, 2012, 37(11): 1510-1551. DOI:10.1016/j.progpolymsci.2012.03.002 |
| [6] |
Varea A, Monereo O, Xuriguera E, et al. Electrospray as a suitable technique for manufacturing carbon-based devices[J]. Journal of Physics D: Applied Physics, 2017, 50(31): 315301. DOI:10.1088/1361-6463/aa798b |
| [7] |
Luo C J, Loh S, Stride E, et al. Electrospraying and electrospinning of chocolate suspensions[J]. Food and Biopro-cess Technology, 2012, 5(6): 2285-2300. DOI:10.1007/s11947-011-0534-6 |
| [8] |
Basset A B. Waves and jets in a viscous liquid[J]. American Journal of Mathematics, 1894, 16(1): 93-110. DOI:10.2307/2369834 |
| [9] |
Zeleny J. On the conditions of instability of liquid drops, with applications to the electrical discharge from liquid point[J]. Physical Review, 1914, 69(3): 71-83. |
| [10] |
Taylor G I, McEwan A D. The stability of a horizontal fluid interface in a vertical electric field[J]. Journal of Fluid Mechanics, 1965, 22(1): 1-15. |
| [11] |
Taylor G. Electrically driven jets[J]. Proceedings of the Royal Society of London, 1969, 313(1515): 453-475. DOI:10.1098/rspa.1969.0205 |
| [12] |
Turnbull R J. Finite conductivity effects on electrostatically sprayed liquid jets[J]. IEEE Transactions on industry applications IA, 1996, 32(4): 837-843. DOI:10.1109/28.511689 |
| [13] |
González H, García F J, Castellanos A. Stability analysis of conducting jets under ac radial electric fields for arbitrary viscosity[J]. Physics of Fluids, 2003, 15(2): 395-407. DOI:10.1063/1.1529659 |
| [14] |
Lòpez-Herrera J M, Riesco-Chuaca P, Gañán-Calvo A M. Linear stability analysis of axisymmetric perturbations in imperfectly conducting liquid jets[J]. Physics of Fluids, 2005, 17(3): 034106. DOI:10.1063/1.1863285 |
| [15] |
Li F, Yin X Y, Yin X Z. Instability analysis of an inner-driving coaxial jet inside a coaxial electrode for the non-equipotential case[J]. Journal of Electrostatics, 2008, 66(1-2): 58-70. DOI:10.1016/j.elstat.2007.08.001 |
| [16] |
王晓英, 王军锋. 荷电黏性液体射流线性不稳定性分析[J]. 排灌机械工程学报, 2012, 30(2): 225-230. Wang X Y, Wang J F. Linear stability analysis for charged viscid liquid jets[J]. Journal of Drainage and Irrigation Machi-nery Engineering, 2012, 30(2): 225-230. DOI:10.3969/j.issn.1674-8530.2012.02.020 |
| [17] |
甘云华, 张夏, 罗智斌. 微尺度锥射流雾化模拟分析[J]. 高电压技术, 2015, 41(12): 4000-4007. Gan Y H, Zhang X, Luo Z B. Numerical analysis on micro-scale cone-jet spraying[J]. High Voltage Engineering, 2015, 41(12): 4000-4007. |
| [18] |
Reznik S N, Yarin A L, Theron A, et al. Transient and steady shapes of droplets attached to a surface in a strong electric field[J]. Journal of Fluid Mechanics, 2004, 516: 349-377. DOI:10.1017/S0022112004000679 |
| [19] |
Coelho R, Debeau J. Properties of the tip-plane configuration[J]. Journal of Physics D: Applied Physics, 1971, 4(9): 1266. DOI:10.1088/0022-3727/4/9/305 |
| [20] |
Jaworek A, Machowski W, Krupa A, et al. Viscosity effect on EHD spraying using AC superimposed on DC electric field[C]//Proc of the 2000 IEEE Industry Applications Conference. 2000. https://www.researchgate.net/publication/3873043_Viscosity_effect_on_EHD_spraying_using_AC_superimposed_on_DC_electric_field
|
| [21] |
Guildenbecher D R, López-Rivera C, Sojka P E. Secondary atomization[J]. Experiments in Fluids, 2009, 46(3): 371-402. DOI:10.1007/s00348-008-0593-2 |
| [22] |
霍元平, 王军锋, 毛文龙, 等. 荷电液滴脉动变形特性的实验研究[J]. 工程热物理学报, 2013, 34(1): 99-102. Huo Y P, Wang J F, Mao W L, et al. Experimental study on oscillation and deformation of charged droplet[J]. Journal of Engineering Thermophysics, 2013, 34(1): 99-102. |
| [23] |
汪朝晖, 廖振方. 针板电极荷电液体射流不稳定性分析[J]. 农业机械学报, 2009, 40(8): 86-91. Wang Z H, Liao Z F. Analysis of instability for charged liquid jets with the needle-plate electrodes[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(8): 86-91. |
| [24] |
霍元平, 王军锋, 左子文, 等. 荷电液滴雾化演变过程的可视化研究[J]. 工程热物理学报, 2014, 35(8): 1559-1562. Huo Y P, Wang J F, Zuo Z W, et al. Visualization on the evolution of electrostatic atomization from capillary channel[J]. Journal of Engineering Thermophysics, 2014, 35(8): 1559-1562. |
| [25] |
Kim H H, Kim J H, Ogata A. Time-resolved high-speed camera observation of electrospray[J]. Journal of Aerosol Science, 2011, 42(4): 249-263. DOI:10.1016/j.jaerosci.2011.01.007 |



