传统飞行器的大气数据(主要指飞行马赫数、迎角、侧滑角以及自由来流静压等),一般通过探出飞行器的传感装置进行测量,例如以皮托管测量来流总压,以迎角传感器测量迎角等。但对高超声速飞行器而言,严酷的气动加热环境使得传感装置不可探出;同时,由于高性能飞行器对隐身性能的需求,传统的飞行参数测量系统已满足不了实际的飞控需求[1]。
针对上述问题,一种更经济、技术上可行的方法便是嵌入式大气数据传感系统(Flush Air Data Sensing System, FADS)。FADS系统是基于飞行器表面压力测量的一类方法,已针对飞机及航天飞行器进行了广泛研究。NASA的研究报告表明,机载FADS系统已应用于航天飞机[2-3]及X-33空天飞行器[4]的返回过程;在有人控制飞行器F-14[5]及KC-135[6]的飞行测试中也验证了FADS技术的可靠性,证实了该技术在各类飞行器上应用的可行性。
国外相关研究表明,FADS系统已成功应用于多种前身呈钝体的飞行器[7-9]。但对于尖锥前体飞行器,由于尖锥半径较小(1.0 mm左右),无法像钝头体一样在钝头表面配置多个测压孔以获得足够数量的表面压力(钝头体FADS系统的解算至少需要5个不同位置的压力),仅能配置总压孔测得来流总压。因此,若采用钝头体理论研究尖锥前体飞行器FADS系统,其精度及可靠性尚需进行系统论证。
作为一种非线性建模预测手段,人工神经网络技术在自适应性、模糊推理能力及自学习能力等方面具有优势,非常适用于解决非线性问题。国外已成功实现基于神经网络技术的FADS系统。Crowther等[10]通过风洞试验测试了位于战斗机机身的FADS系统测压孔配置方案;Calia等[11]利用神经网络算法计算了M-346喷气训练机的静压和马赫数,以风洞试验和飞行试验数据训练、测试神经网络;Rohloff等[12]基于神经网络技术建立了位于F-18头部的FADS系统的风速计算方法。Samy等[13]将基于神经网络算法的FADS系统用于小型无人飞行器中,建立了不同速度下的飞行参数误差分布。王鹏等[14]建立了尖楔前体飞行器用FADS系统的神经网络算法,并考核了算法精度。研究表明,FADS系统之所以选用神经网络算法,是因为该算法能够处理大批量的风洞试验及飞行试验数据而无需建立头部气动模型。
此前,针对FADS系统的神经网络算法已经证实了系统的精度以及在配备昂贵装备的大型、快速飞行器中的有效性,但关于神经网络方法用于尖锥前体飞行器的分析和研究工作较少。
为此,针对尖锥前体飞行器用FADS系统的特点,本文建立了基于径向基函数(Radial Basis Function, RBF)的人工神经网络模型,以代替FADS系统的气动模型,使FADS系统的解算不再依赖传统的气动模型(输入量仍需依靠气动模型确定,解算方法则完全替代气动模型的算法)。鉴于神经网络本身的容错功能, 即使各层中个别单元出现错误,也不会导致灾难性后果。因此,无论是从模型的可行性还是适用性来看,尖锥前体飞行器FADS系统的神经网络算法都是一种较好的选择,同时为人工神经网络建模技术在尖锥前体飞行器用FADS系统中的进一步发展提供参考。
1 FADS系统模型钝头机体用FADS系统的模型较简单,根据表面压力来反推飞行参数。该模型需满足:(1)适用于较大的马赫数范围;(2)足够简单,通过简化模型描述复杂的流场问题。为此,FADS系统的压力模型将势流理论(适用于亚声速条件)与修正的牛顿流理论(适用于超声速条件)通过形压系数ε结合起来。形压系数ε综合考虑了气动外形、测试条件及系统因素等影响,可将其视为马赫数Ma、当地迎角αe及当地侧滑角βe的函数,可通过风洞试验或CFD计算得到:
 (1)
(1)
FADS系统的理论模型[1]为:
 (2)
(2)
式中,pi为第i个测压孔的表面压力,q为动压,p∞为自由来流静压,θi为第i个测压孔处的来流入射角(该位置的法线方向与来流方向的夹角),由式(3)确定:
 (3)
(3)
式中,φi、λi为第i个测压点的圆周角和圆锥角,其定义如图 1所示。
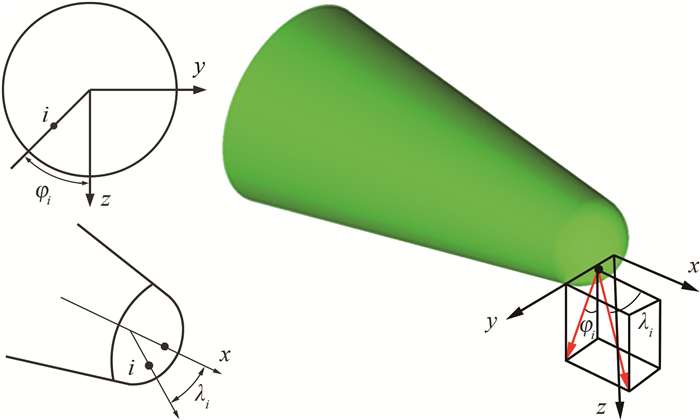
|
| 图 1 测压孔圆周角及圆锥角 Fig.1 Clock angle and cone angle definitions for pressure port i |
钝头机体用FADS系统的校准方法主要是针对上洗角、侧洗角及形压系数校准,综合反映系统因素对FADS系统的影响,作者已在文献[15-16]中详细论证,本文不再详述。
2 典型尖锥外形测压孔配置典型的尖锥外形测压孔配置如图 2所示(共13个测压孔,测压孔直径0.50 mm,孔深1.50 mm)。尖锥前缘半径仅为1.65 mm,因此在该位置仅配置驻点测压孔0,测压孔1~4、5~8、9~12则分别位于不同的尖锥前体截面上。其中,测压孔2、6、10位于迎风面,测压孔4、8、12位于背风面,测压孔1、3、5、7、9、11位于尖锥侧缘。测压孔位置信息见表 1。
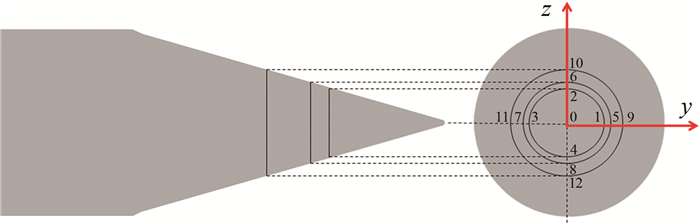
|
| 图 2 FADS系统测压孔配置 Fig.2 Pressure ports configuration for FADS system |
| 测压孔编号 | 圆周角φi /(°) | 圆锥角λi/(°) |
| 0 | 0 | 0 |
| 1、5、9 | 0 | 74 |
| 2、6、10 | 90 | 74 |
| 3、7、11 | 180 | 74 |
| 4、8、12 | 270 | 74 |
在中国航天空气动力技术研究院FD-06风洞中进行1:1.5缩比模型风洞试验。试验马赫数2.27、2.51、3.01;迎角范围-8°~8°,间隔1°;侧滑角范围-4°~4°,间隔1°。FD-06风洞是一座半回流暂冲式亚、跨、超声速风洞,试验段长1.575 m,横截面尺寸0.6 m×0.6 m,试验马赫数0.40~4.45,迎角范围-15°~15°(加预偏拐接头后可达0°~30°)。超声速试验时,可通过更换二元喷管块来改变马赫数(1.53~4.45)。
选用8400扫描阀测量各测压孔表面压力值。该扫描阀最多可同时测量1024个测压点,最大采样速度50 kHz,量程±0.2 MPa,压力扫描阀精度±0.05% FS,压力校准单元精度±0.01% FS,连接检测装置后的精度为0.3% FS。为提高测压管路稳定速度、减小压力滞后的影响,测压模块置于模型内部。
模型支杆设计充分考虑了刚度影响,能有效抑制模型振动。模型等直段有水平刻线,在风洞中可微调滚转角和侧滑角。根据超声速流场特点,改变模型在风洞中位置,以保证模型在所有试验迎角范围内都不受入口台阶波的影响。
该FADS系统对试验精度要求较高,需进行流场标校,根据标校结果进一步确定模型位置(通过改变支杆长度),以选择流场最稳定的区域进行试验。
速度场校测:加工长度为400 mm的延长杆,用于对试验段入口-100~400 mm范围内的流场进行校测,校测间隔为25 mm。
模型安装及校正:(1)迎角和滚转角方向安装:根据平均气流偏斜角调整0°迎角,利用象限仪调整迎角,利用左右刻线调整滚转角,确保安装误差都在0.05°以内;模型名义迎角根据试验要求迎角确定,试验完成后,提供各迎角下的弹性角估算值作为参考。(2)侧滑方向安装修正:设计加工侧滑角专用测量仪,提高侧滑角安装精度。在获得横向气流偏斜角的基础上,对比模型水平面上测压点的差值,计算出实际侧滑角,进一步校正模型侧滑角开展试验,确保安装误差在0.05°以内。图 3为FD-06风洞及模型示意图。
|
| 图 3 FD-06风洞及模型示意图 Fig.3 FD-06 wind tunnel and model |
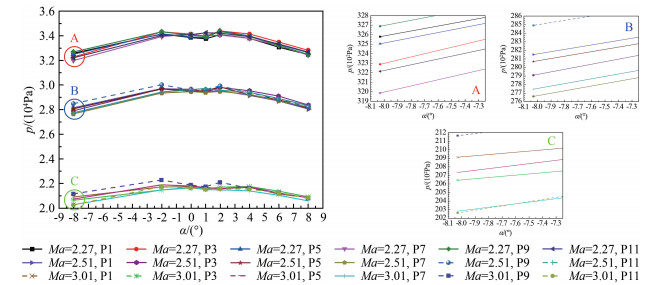
对测压孔1~12的试验数据进行了分析,如图 4和5所示(P1~P12分别代表测压孔1~12)。可以看出,测压孔2、6、10(位于迎风面)和4、8、12(位于背风面)的压力随迎角变化显著,且测压孔2、6、10及4、8、12的压力变化趋势基本一致,与尖锥外形规律相吻合。测压孔1、5、9与3、7、11位于尖锥侧缘,根据压力分布规律,在无侧滑角的情形下,具有相同圆锥角的测压孔的压力应一致,可以看出风洞试验数据吻合较好,最大偏差在5%以内。因此,本文实际选取的FADS系统的测压孔为0、1、2、3、4,共5个测压孔。
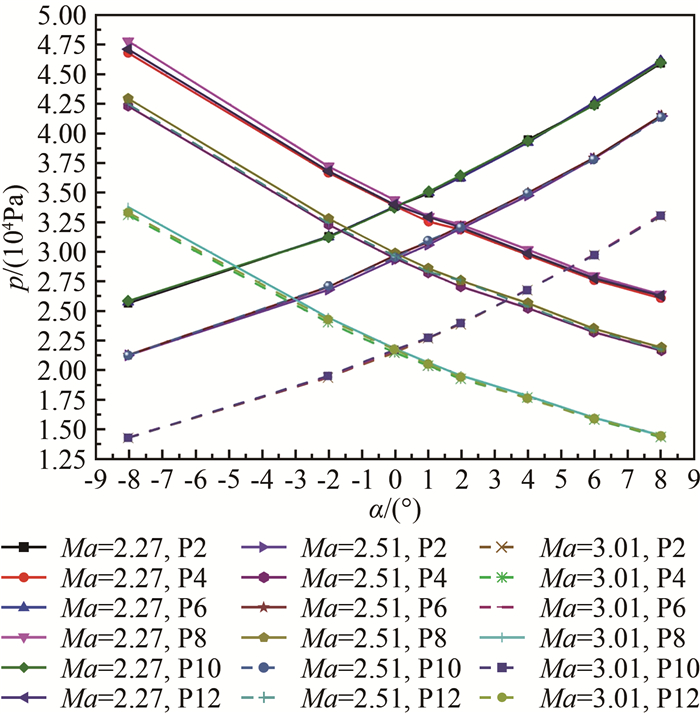
|
| 图 4 测压孔2、4、6、8、10、12的风洞试验数据 Fig.4 Wind tunnel test data for pressure ports 2, 4, 6, 8, 10, 12 |
|
| 图 5 测压孔1、3、5、7、9、11的风洞试验数据 Fig.5 Wind tunnel test data for pressure ports 1, 3, 5, 7, 9, 11 |
针对尖锥外形,采用CFD方法对特定状态进行验证(计算条件与风洞试验条件一致),并与风洞试验数据进行比较,以验证试验数据的有效性。计算格式采用Roe的FDS格式(因其具有较高的黏性分辨率且收敛性较好);物理流动模型为无湍流模型的薄层假设;时间离散采用LU-SGS方法;计算边界条件为:远场采用外插边界条件,物面采用无滑移的绝热壁面条件;网格为点对点多块结构网格,如图 6所示。

|
| 图 6 计算网格 Fig.6 Computational grid |
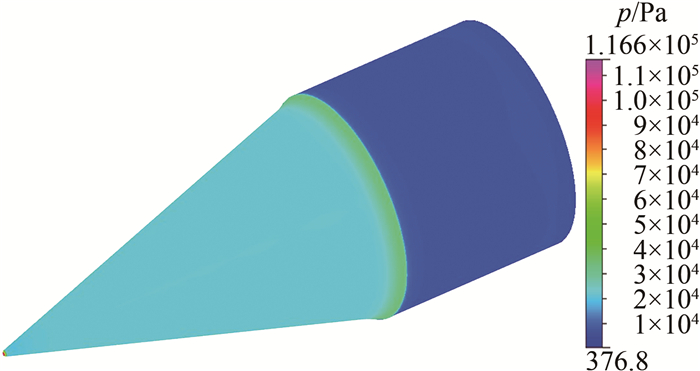
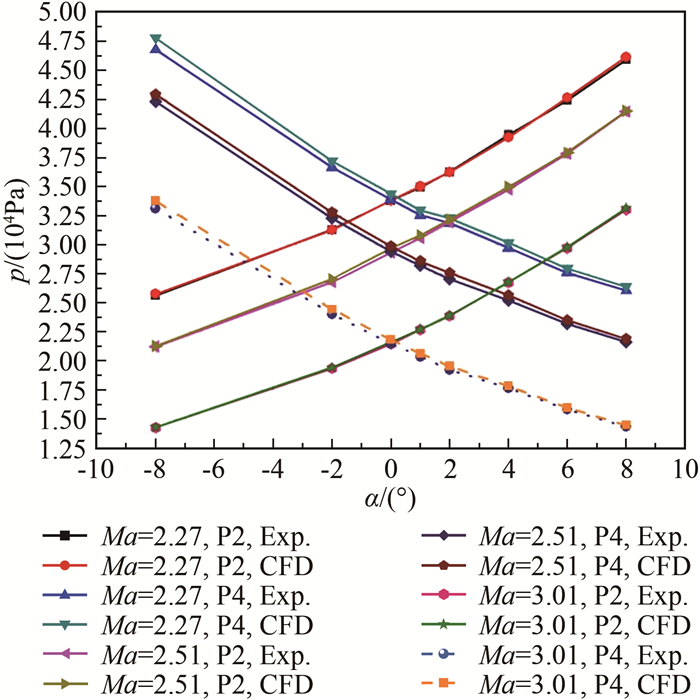
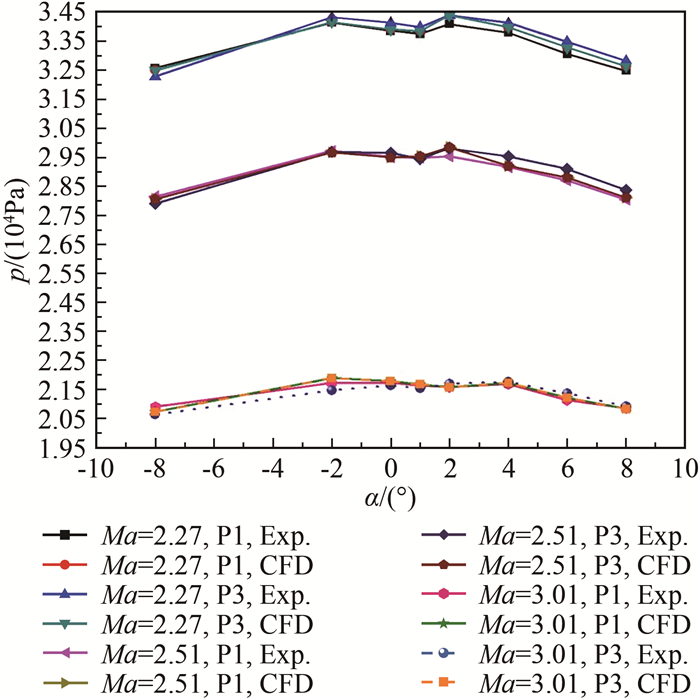
选取典型风洞试验状态进行计算,在Ma=3.01、迎角0°条件下得到壁面压力和流场分布(压力分布),如图 7和8所示。测压孔2、4与1、3的压力计算与试验结果对比如图 9、10所示。可以看出,迎风面测压孔2、背风面测压孔4的计算与试验结果吻合较好(测压孔4略有偏差);位于侧缘的测压孔1和3的计算与试验结果略有偏差(但小于5%)。试验与计算数据吻合较好,本文选取风洞试验数据作为FADS系统的测压输入。
|
| 图 7 Ma=3.01时壁面压力分布云图 Fig.7 Wall pressure distribution for Ma=3.01 |

|
| 图 8 流场结构(压力云图) Fig.8 Flow distribution (pressure contours) |
|
| 图 9 测压孔2、4的风洞试验与CFD结果对比 Fig.9 Pressure comparisons between wind tunnel test and CFD results for ports 2 and 4 |
|
| 图 10 测压孔1、3的风洞试验与CFD结果对比 Fig.10 Pressure comparisons between wind tunnel test and CFD results for ports 1 and 3 |
根据尖锥前体飞行器FADS系统的特点及人工神经网络建模技术的非线性建模能力,本节基于RBF神经网络建模技术,建立了FADS系统的解算模型。RBF网络算法以径向基函数作为隐含层单元的“基”,构成隐含层空间,并对输入矢量进行转换,将低维模式输入量转换至高维空间内,使低维空间内的线性不可分问题在高维空间内线性可分。采用的径向基函数为高斯函数。RBF神经网络是一种具有单个隐含层的三层前馈型局部逼近神经网络,具有收敛速度快、逼近性能好、不存在局部极小等优点。本文采用的是Li等[17]发展的RBF神经网络算法。
典型的含有N个神经元的单隐含层单输出的RBF神经网络模型为:
 (4)
(4)
式中,ψi(x)为隐含层第i个节点的基函数,
|
| 图 11 单隐含层的RBF神经网络模型 Fig.11 RBF neural network model with single hidden layer |
传统的径向基函数-高斯函数的中心向量及标准化常数(高斯函数的中心及宽度)是固定的,因此训练算法仅用于训练RBF网络的连接权值。但固定了隐含层节点基函数的中心及宽度,会使网络结构增大、训练时间增加,而且确定合理的隐含层节点个数及对应的中心和宽度非常困难[13]。为解决这些问题,Li等[17]发展了传统的RBF神经网络。对于单输出的神经网络而言,设定初始隐含层节点个数为0,仅当以下3个条件满足时增加隐含层的节点个数:
 (5)
(5)
 (6)
(6)
 (7)
(7)
式中,sr为输出目标值yr与估计值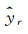
 (8)
(8)
式中,γ为衰减常数(0<γ<1);δmin、δmax分别为χ3的初始值、最终值。误差限χ1、χ2用于确保样本数据的训练精度,χ3用于检验当前的隐含层节点与输入向量的距离是否足够小,以保证至少有一个隐含层节点对输入敏感。
该RBF网络结构优势显著:(1)当训练条件不满足式(5)~(7)的3个条件时,算法仅对最活跃的神经元进行训练,加速迭代。(2)该结构可自动移除训练过程中对网络结构影响最小的神经元,简化网络结构。本节采用梯度回归算法训练所建立的神经网络,定义为:
 (9)
(9)
式中,ξ为训练参数向量,由高斯函数的中心、宽度及权值组成,η为学习率,r表示第r次迭代。E为均方差函数,定义为:
 (10)
(10)
实际每次迭代中,训练参数按式(9)所述的沿梯度相反的方向调整,使得均方差最小,直至收敛。在优化的目标函数中添加权值和阈值的调整项,可以改善神经网络训练过程中的过拟合问题。只需得到输入压力后,将这些值作为输入量输入到神经网络中,通过上述算法即可得到所需的输出参数。值得注意的是,本文训练过程中将输入和输出都进行了归一化处理,因此,实际使用中也需对相关数据作相应处理。
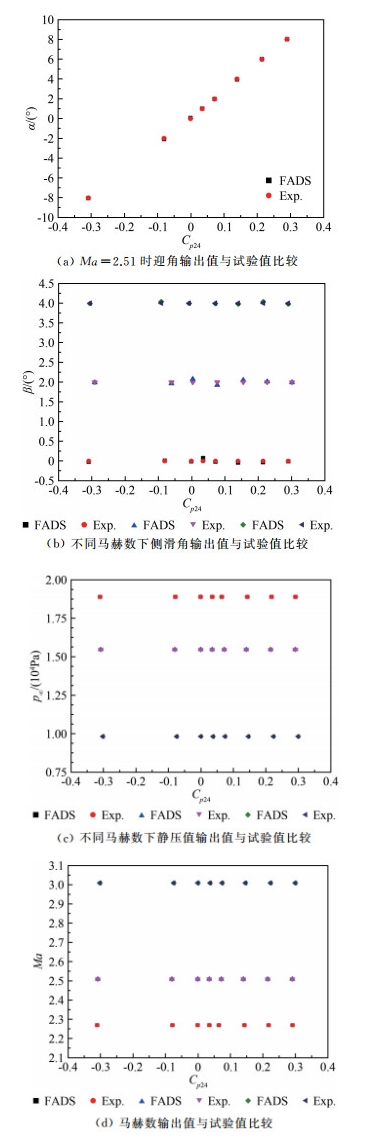
6 结果分析利用第5节建立的基于RBF的神经网络模型,将测压点0~5的压力数据作为输入参数,经过一系列训练,建立了迎角、侧滑角、马赫数及来流静压的神经网络,并将经该网络得到的飞行参数测试输出与风洞试验数值进行比较,如图 12(a)~(d)所示(图中Cp24表示测压孔2和4的压力系数差)。图 12(a)为Ma=2.51时网络测试输出与试验的比较,图 12(b)~(d)为不同马赫数下网络测试输出的侧滑角、静压及马赫数与试验的比较,均吻合较好,证实了神经网络算法在尖锥前体飞行器FADS系统中应用的有效性。
|
| 图 12 飞行参数输出值与试验值比较 Fig.12 Comparisons of flight parameters between neural network outputs and wind tunnel test |
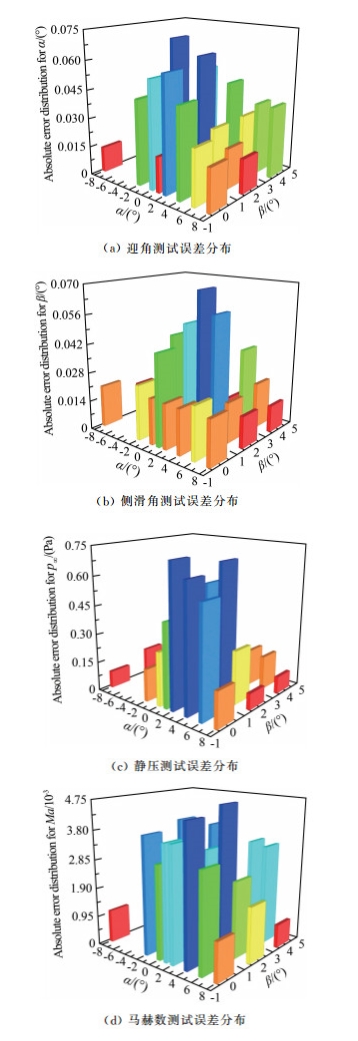
基于建立的迎角、侧滑角、马赫数及来流静压的神经网络,经针对各个飞行参数的网络结构得到的迎角、侧滑角、马赫数及来流静压的误差分布如图 13(a)~(d) 所示。可以看出,基于RBF的人工神经网络算法解算精度较好,迎角、侧滑角、静压及马赫数的测试误差输出(绝对值)分别小于0.1°、0.1°、50.0 Pa和0.01。因此,无论是从测试的飞行参数与风洞试验值的比较来看,还是从飞行参数总体测试误差分布来看,均表明基于神经网络算法的FADS系统解算精度较好。
|
| 图 13 输出飞行参数误差分布 Fig.13 Error distribution for flight parameters |
基于RBF神经网络建模技术建立了FADS系统模型,经测试,精度较好,可以得到与风洞试验相吻合的数据;同时全局误差分布较小,完全可以满足FADS系统的精度需求。作为一种代替气动模型的建模方法,神经网络算法在FADS系统中的应用前景广阔。
本文基于风洞试验数据对构建的网络进行训练及测试,受试验状态所限,数据点数不多。下一步将扩展飞行器的飞行包络,对神经网络算法在尖锥前体飞行器FADS系统中的应用进行更为系统的研究。
| [1] |
Ellsworth J C, Whitmore S A. Simulation of a flush air-data system for transatmospheric vehicles[J]. Journal of Spacecraft and Rockets, 2008, 45(4): 716-732. DOI:10.2514/1.33541 |
| [2] |
Siemers P M III, Wolf H, Henry M. Shuttle Entry Air Data System (SEADS)-flight verification of an advanced air data system concept[R]. AIAA-88-2014, 2014.
|
| [3] |
Larson T J, Siemers P M III. Use of nose cap and fuselage pressure orifices for determination of air data for Space Shuttle Orbiter below supersonic speeds[R]. NASA TR-1643, 1980.
|
| [4] |
Whitmore S A, Cobleigh B R, Haering E A Jr. Design and calibration of the X-33 Flush Airdata Sensing (FADS) system[R]. NASA/TM-1998-206540, 1998.
|
| [5] |
Larson T J, Whitmore S A, Ehernberger L J, et al. Qualitative evaluation of a flush air data system at transonic speeds and high angles of attack[R]. NASA TP-2716, 1987.
|
| [6] |
Larson T J, Siemers P M III. Subsonic tests of an all-flush-pressure-orifice air data system[R]. NASA TP-1871, 1981.
|
| [7] |
Terry L J, Timothy R M, Siemers P M III. Wind-tunnel investigation of a flush airdata system at Mach numbers from 0.7 to 1.4[R]. NASA TM-101697, 1990.
|
| [8] |
Westhelle C H. X-38 backup Air Data System(AeroDAD)[R]. AIAA 2002-0007, 2002.
|
| [9] |
Ellsworth J C, Whitmore S A. Reentry air data system for a sub-orbital spacecraft based on X-34 design[R]. AIAA 2007-1200, 2007.
|
| [10] |
Crowther W J, Lamont P J. A neural network approach to the calibration of a flush air data system[J]. The Aeronautical Journal, 2011, 105(1044): 85-95. |
| [11] |
Calia A, Denti E, Galatolo R, et al. Air data computation using neural networks[J]. Journal of Aircraft, 2008, 45(6): 2078-2083. DOI:10.2514/1.37334 |
| [12] |
Rohloff T J, Whitmore S A, Catton I. Fault-tolerant neural network algorithm for flush air data sensing[J]. Journal of Aircraft, 1999, 36(3): 541-549. DOI:10.2514/2.2489 |
| [13] |
Samy I, Postlethwaite I, Gu D W. Neural-network-based flush air data sensing system demonstrated on a mini air vehicle[J]. Journal of Aircraft, 2010, 47(1): 18-31. DOI:10.2514/1.44157 |
| [14] |
王鹏, 胡远思, 金鑫. 尖楔前体飞行器FADS系统驻点压力对神经网络算法精度的影响[J]. 宇航学报, 2016, 37(9): 1072-1079. Wang P, Hu Y S, Jin X. Effect of stagnation pressure on the neural network algorithm accuracy for the FADS system applied to the vehicle with sharp wedged fore-bodies[J]. Journal of Astronautics, 2016, 37(9): 1072-1079. DOI:10.3873/j.issn.1000-1328.2016.09.006 |
| [15] |
王鹏, 金鑫, 张卫民, 等. 钝头机体用FADS系统的校准[J]. 实验流体力学, 2016, 30(2): 97-102. Wang P, Jin X, Zhang W M. Calibration for the FADS system applied to the vehicle with blunt fore-bodies[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(2): 97-102. |
| [16] |
王鹏, 金鑫, 张卫民. FADS系统测压孔配置对攻角校准的影响[J]. 战术导弹技术, 2013(2): 51-55. Wang P, Jin X, Zhang W M. The effect of configuration of pressure ports on calibration for angle of attack in FADS system[J]. Tactical Missile Technology, 2013(2): 51-55. |
| [17] |
Li Y, Sundararajan N, Saratchandran P. Analysis of minimal radial basis function network algorithm for real-time identifi-cation of nonlinear dynamic systems[J]. IEE Proceedings-Control Theory and Applications, 2000, 147(4): 476-484. DOI:10.1049/ip-cta:20000549 |



