2. 昆明理工大学 民航与航空学院, 昆明 650504
2. Faculty of Civil Aviation and Aeronautics, Kunming University of Science and Technology, Kunming 650504, China
为了实现更经济、有效的高超声速飞行,一些基于爆轰的推进方式相继被提出,如脉冲爆轰发动机、斜爆轰发动机、旋转爆轰发动机等。在超声速流动环境中组织有效的燃烧,从而提供充足的动力,是这些推进系统共同的研究热点和难点之一[1-2]。其中,可燃气体经气动压缩处理(压缩波、激波、压缩构型等)后发生点火以及燃烧的发展和传播过程倍受关注。已有研究表明,燃料的点火过程和燃烧特性受流场的影响涉及到诸多因素[3],而实际工程中的点火和燃烧现象更是复杂多变。因此,发展并采用合适的研究方法来解析这种复杂现象中的关键机理是相关研究的迫切需求。
运动激波诱导点火是研究点火和燃烧特性的一种重要方法。其中,平面激波诱导点火因实验上较容易实现且激波压缩后的状态相对明确而被广泛应用[4-9]。但采用平面入射激波诱导点火难以构造多样的点火环境(温度梯度、组分浓度梯度、点火延迟时间梯度等)。此外,为产生足够强的平面激波,常采用平面反射激波诱导点火,此时反射激波与入射激波波后边界层的相互作用会对点火形成干扰[10-11],破坏了该方法构造点火环境的简洁性。与此相对,汇聚激波诱导点火则可构造多样的点火环境。Gelfand等详细讨论了平面激波进入抛物形、圆弧形、楔形等不同形状凹腔内汇聚点火的现象[12-13],王春、滕宏辉、何立明等也开展了大量研究[14-15]。需要指出的是,上述激波汇聚过程往往伴随复杂的激波反射、干涉等现象,这给有效评估点火环境以及分析点火发生与燃烧传播的动力学机理带来不确定性。
近年来,作者实验室将一种采用激波动力学方法反设计获得的圆柱面汇聚激波技术[16]应用于激波诱导点火研究[17]。这种经设计的柱面汇聚激波在光滑连续的不断增强过程中,在流场中诱导产生空间连续的准一维的梯度场(无复杂的激波干扰现象),并实现了梯度场中预混可燃气体的点火与燃烧波传播。该研究发现:自点火诱导的初始燃烧波其传播速度远大于当地CJ(Chapman-Jouguet)爆轰波的速度;这种超高速的燃烧波事实上是一种化学反应“相波”,即各质点自发化学演变过程中某一阶段的时空分布,或依据相关研究称之为“自发反应波”(spontaneous reaction wave/spontaneous auto-ignition wave)。根据Zeldovich的理论[18],这种自发反应波在减速转变为爆轰波的过程中一般不形成解耦的激波和燃烧波面结构,这有别于一般的DDT方式和直接起爆方式。
本文作为上述研究的延续,采用实验与数值模拟相结合的方法,对这种汇聚激波诱导预混可燃气体点火现象作进一步的研究,着重关注点火建立的爆轰波在后续传播中遭遇“相波”所导致的特殊现象。
1 研究方法 1.1 实验方法图 1为本研究所采用的激波管实验平台示意图。驱动段和被驱动段为等截面方管,长度分别为2.5 m、1.5 m,内截面大小为40 mm×70 mm。图 2显示了实验段内流道构型以及观察窗口的位置,与实验段末端相连的是等截面方管的泄压段,长度为2.5 m,内截面大小为40 mm×70 mm。激波管平台运行时,驱动段充入高压驱动气体,被驱动段、实验段及泄压段内充入预混可燃气体;首先采用电控破膜产生强度较弱的平面激波,不足以直接起爆;平面激波在等截面管道运动一段距离, 达到较理想状态后进入实验段,并与依据激波动力学反设计的内流道型线(红色实线)相互作用,从而连续光滑地转变为圆弧激波;圆弧激波在楔形段内维持相似波面形态进一步缓慢汇聚增强,并诱导发生点火。采用曝光时间为1 μs、拍摄频率超过250000 fps的高速纹影系统对观察窗内流场进行观测,捕捉流场的演变过程。

|
| 图 1 实验平台示意图 Fig.1 Schematic of experimental plat form |

|
| 图 2 实验段示意图 Fig.2 Schematic of the test section |
图 3为相同构型的汇聚角度为8°的数值计算域。内流道沿轴向分成3部分:平直段、弧形过渡段(500.0 mm < x < 657.5 mm)、楔形段。数值计算域的坐标原点为x=0,4 mm出口坐标为x=1054.2 mm,汇聚中心为x=1082.8 mm(即图 3中r=0处)。

|
| 图 3 汇聚角度8°数值计算域 Fig.3 Computational zone for an 8° convergent channel |
本文对以上构型内流动开展变截面准一维无粘数值模拟。控制方程为带化学反应的欧拉方程。计算采用基于非均匀网格的MUSCL格式,其中数值通量的计算采用HLLC格式。化学反应采用Oran的氢-空气基元反应模型[19]。反应源项采用分裂步法解耦处理,其中解耦后的源项常微分方程组采用VODE程序包[20]求解。上述数值模拟方法及程序的适用性和准确性已在Yang[17]及Shi[21]等的研究中得到验证。
计算采用非均匀网格,在出口前400 mm的收缩段内共布网格约1600个,其中最大网格尺度0.5 mm(左),最小网格尺度0.1 mm(右)。当自点火发生时,汇聚激波波面与着火点距离约29 mm,该距离内网格数不少于200个。这一网格尺度可保证点火过程的正确模拟。
2 结果与讨论本文考察两种不同配比的预混气体,如表 1所示。通过调配气体组分使A、B两种不同配比混合气体的声速保持一致,从而当入射平面激波强度一致时,冷态流场和燃烧流场具有可比性。
| Label | A | B |
| Component | 27.27%H2+72.73 %N2 | 28.38%H2+6.76%O2+64.86%N2 |
| Reactive | No | Yes |
| Molar mass/(g·mol-1) | 20.9 | 20.9 |
| Specific heat ratio | 1.4 | 1.4 |
| Sound speed at room temperature/(m·s-1) | 407.4 | 407.4 |
首先选取不可反应混合气体A研究点火环境的特性。图 4为冷态流动纹影实验结果。

|
| 图 4 圆弧激波汇聚过程冷态流动纹影实验结果(气体A、初始压力4.00 kPa、入射平面激波马赫数3.15) Fig.4 Schlieren pictures of the nonreactive shock converging process |
选定激波到达过渡段起始位置为t=0时刻,圆弧激波在楔形段汇聚过程中没有出现激波反射、相干等现象,流场中无明显间断(t=0.296~0.392 ms);激波到达出口后形成膨胀扇(t=0.392 ms),而后经历足够长时间(约80 μs),由于气流壅塞形成反射激波往上游传播。需要指出,圆弧激波汇聚增强的过程中,理论上必然扫过预混气体的着火点,这一过程发生在反射激波形成前,因此点火环境基本不会受到反射激波与边界层相互作用的干扰。
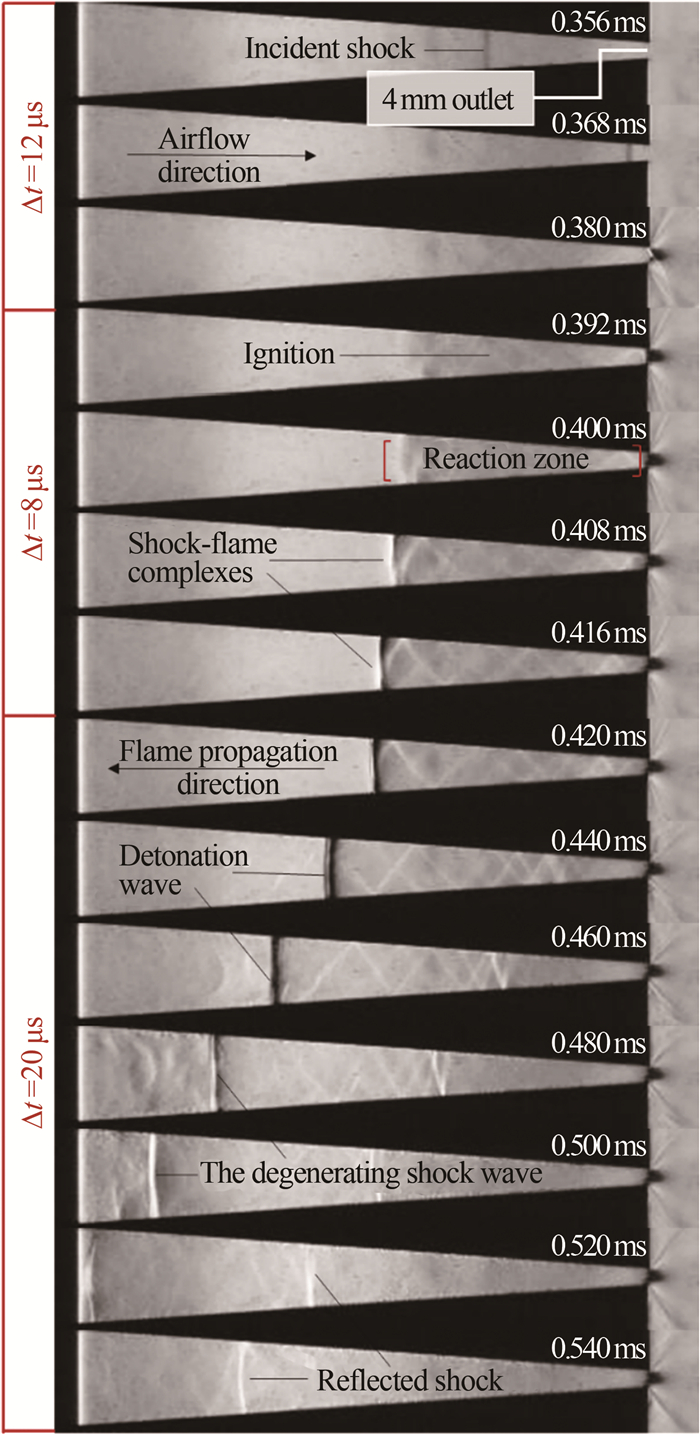
为了评估上述点火环境的有效性以及对自点火的基本物理现象有个清晰的认识,考察了与冷态实验相同入射平面激波马赫数和初始压力下气体B的点火及燃烧传播过程。图 5是气体B燃烧流场的典型纹影实验结果,其中,t=0.392~0.416 ms为燃烧传播初期的精细刻画。
|
| 图 5 圆弧汇聚激波诱导自点火纹影实验结果(气体B、初始压力4.00 kPa、入射平面激波马赫数3.15) Fig.5 Schlieren pictures of self-ignition induced by imploding arc-shaped shock wave |
圆弧激波在汇聚过程中维持相似波面稳定前行(t=0.356~0.368 ms);汇聚增强到一定程度后,波后流场中发生自点火(t=0.380~0.392 ms),反应区向上游和下游分别扩张。红框内纹影结果显示初始燃烧波传播阶段并未形成间断特征明显的激波,而后压缩波累积,激波逐渐凸显(t=0.408 ms),在激波后深黑色区域逐渐增加表明化学反应强度增强(t=0.408~0.416 ms)。往上游扩张的燃烧波面先形成激波-火焰复合结构(t=0.416 ms),然后激波和火焰形成相对稳定的强耦合,演变为自持传播的爆轰波(t=0.420 ms)。可以看到,纹影图中波面的深黑色区域逐渐追赶上激波的浅色区域,表明反应导致的流场密度降低趋势陡峭,此时反应较剧烈。同时,出口附近壅塞堆积产生反射激波,跟随左行爆轰传播。随后,自持传播的爆轰波在传播一定距离后逐渐弱化为激波(t=0.480~0.500 ms),纹影图中显示为燃烧波面逐渐由黑色变淡,直至仅剩下跨激波密度跃升所致的浅色区域,表明此时紧随激波的化学反应正逐渐减弱,而在激波的上游也逐渐凸显出新的燃烧波面。
上述点火及燃烧传播发生在反射激波前,不同于反射激波汇聚点火,上述自点火的发生不受反射激波扰动,体现了圆弧汇聚激波构造点火环境的简洁性。
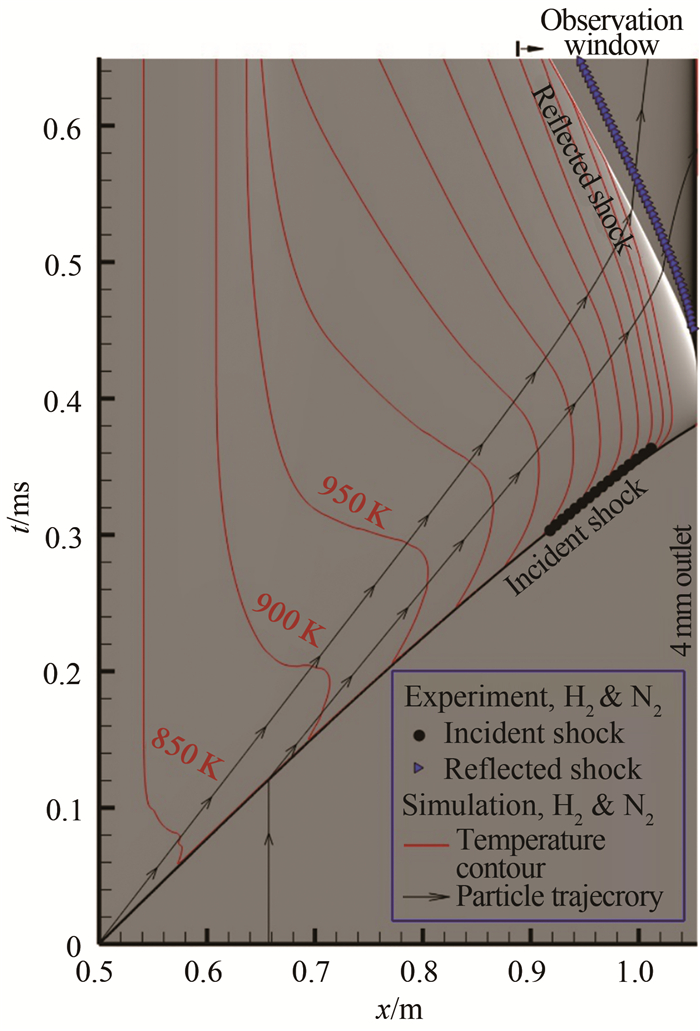
2.2 圆弧汇聚激波诱导的点火环境为了对冷态实验现象进行讨论分析,开展了与冷态实验相同工况下的准一维数值模拟。从图 6中密度梯度的x-t图与实验中各激波位置的对比结果来看,无论是入射激波还是反射激波,实验测得的轨迹虽稍滞后于数值结果(实验中粘性、壁面传热以及观察窗玻璃与内楔的间隙等均倾向削弱反射激波强度),但在流动特征上两者定性一致。
|
| 图 6 实验和数值纹影中入射激波和反射激波轨迹及温度等值分布(气体B、初始压力4.00 kPa、入射平面激波马赫数3.15) Fig.6 Experimental and numerical trajectories of incident shock and reflected shock and x-t diagram of the temperature contour distribution |
图 6中的等值线是相应的准一维流动x-t图的温度分布。结果表明,由于激波强度逐渐增强,波后气体温度连续升高,且紧随激波面位置的等值线越来越密集(ΔT=50 K)。汇聚激波作用于静止气体使其获得沿激波运动方向的诱导速度,对于某一特定流体质点(如带箭头流动迹线所示,两质点分别位于过渡段的首尾),由于波后的非定常运动导致其不断往高温区运动。温度的连续升高,导致各流体质点的反应诱导时间也在不断缩小。
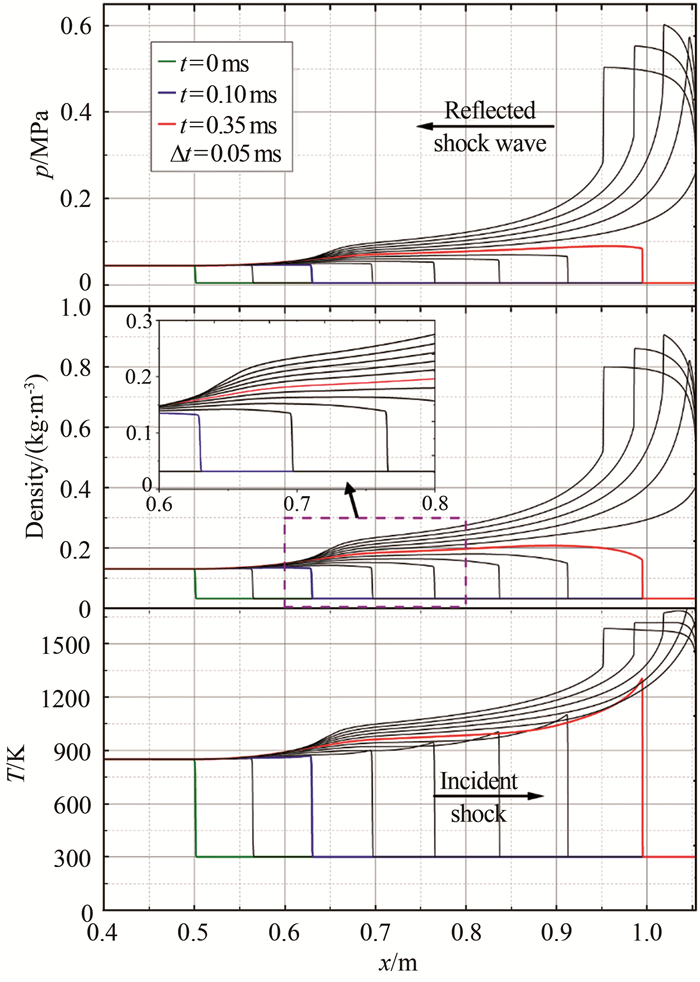
图 7为t=0~0.60 ms时段沿程压力、密度及温度分布。入射激波往下游运动时,在激波波面处,压力、密度、温度均陡然上升,且随着激波强度的增强,各激波波面处的参数值连续上升。同时可以看到,入射激波所诱导的温度峰值位于激波波面处;而由于波后运动的非定常性,压力、密度峰值均不在激波面位置,而是在波后一定距离处。在大约t=0.38 ms时,入射激波到达高度为4 mm的出口,气流壅塞导致压力、密度、温度峰值连续攀升,在反射激波形成后,各峰值往上游前传且逐步下降。
|
| 图 7 空间压力、密度、温度分布的演变过程 Fig.7 Evolution processes of spatial pressure、density and temperature distribution |
进一步分析沿程温度分布,认为该点火环境由3部分构成。入射激波在平直段运动时(如t=0 ms),其波后温度处处均匀;当激波进入弧线过渡段,激波强度连续增强,其波后温度场存在梯度(如t=0.10 ms);汇聚激波在过渡段末完成向圆弧激波的转变,而后在楔形管道内进一步汇聚增强,此时所诱导的温度分布呈现中间平缓、头部尖锐的趋势(如t=0.35 ms)。温度沿程分布表明:在汇聚管道内,圆弧激波诱导的温度梯度沿轴向具有复杂关系,且由于流体质点的运动使得温度梯度存在非定常性。这区别于已有理论和数值模拟研究中人为给定的定常线性温度梯度环境[22-23]。
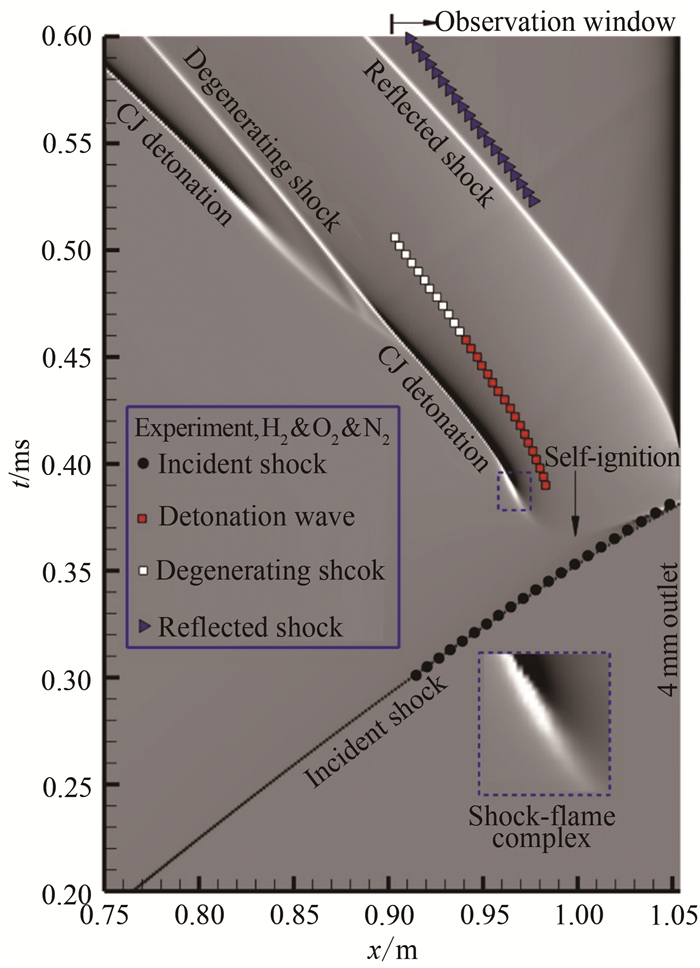
2.3 典型现象的分析借助数值模拟可以对上述点火环境中自点火及点火之后往上游传播燃烧波的发展过程进行详细刻画。图 8表示燃烧流场中激波、燃烧波传播轨迹实验和数值纹影之间的比较。圆点为实验中入射激波的位置,方形深色点为爆轰波的位置,方形浅色点为弱化激波的位置,三角形点为反射激波的位置;对于数值纹影中燃烧波的发展演变过程,浅色区域反映了激波压缩所致的流场密度上升趋势,深色区域反映了燃烧所致的流场密度下降趋势。对比结果表明,尽管实验与数值纹影结果中激波和燃烧波的传播有一定差异,但在波系结构和流动特征上两者定性一致。
|
| 图 8 实验和数值纹影中激波和燃烧波轨迹(气体B、初始压力4.00 kPa、入射平面激波马赫数3.15) Fig.8 Experimental and numerical trajectories of shock waves and combustion waves |
进一步考察数值纹影中燃烧波的发展演变过程。图 8表明,自点火发生于入射激波后某一点,初始传播阶段并未形成激波和燃烧波面结构;随着反应区的扩张速度降低,浅色区域的激波逐渐形成,同时波后的化学反应加强,导致深色区域也逐渐增加,两者互为促进,共同构成激波-火焰复合结构(如图 8中放大图所示);化学反应的逐步增强推动深色区域的反应面与浅色区域的激波强耦合在一起,发展为向上游自持传播的爆轰波;与实验现象一致,爆轰波传播一定距离后开始慢慢解耦,逐渐弱化为激波,同时波面上游凸显出速度较快的燃烧波面。数值纹影预测到实验观察窗口以外的现象,可以看出,新的燃烧波面处化学反应强度较弱,随着气动过程和化学反应的耦合增强,又再次形成激波-火焰复合结构,此后,反应面和激波重新强耦合演变为新的爆轰波。
从数值结果进一步分析这种独特现象的具体流场特性,图 9为流场压力、密度、温度及化学反应中间产物(自由基OH)的沿程分布。
|
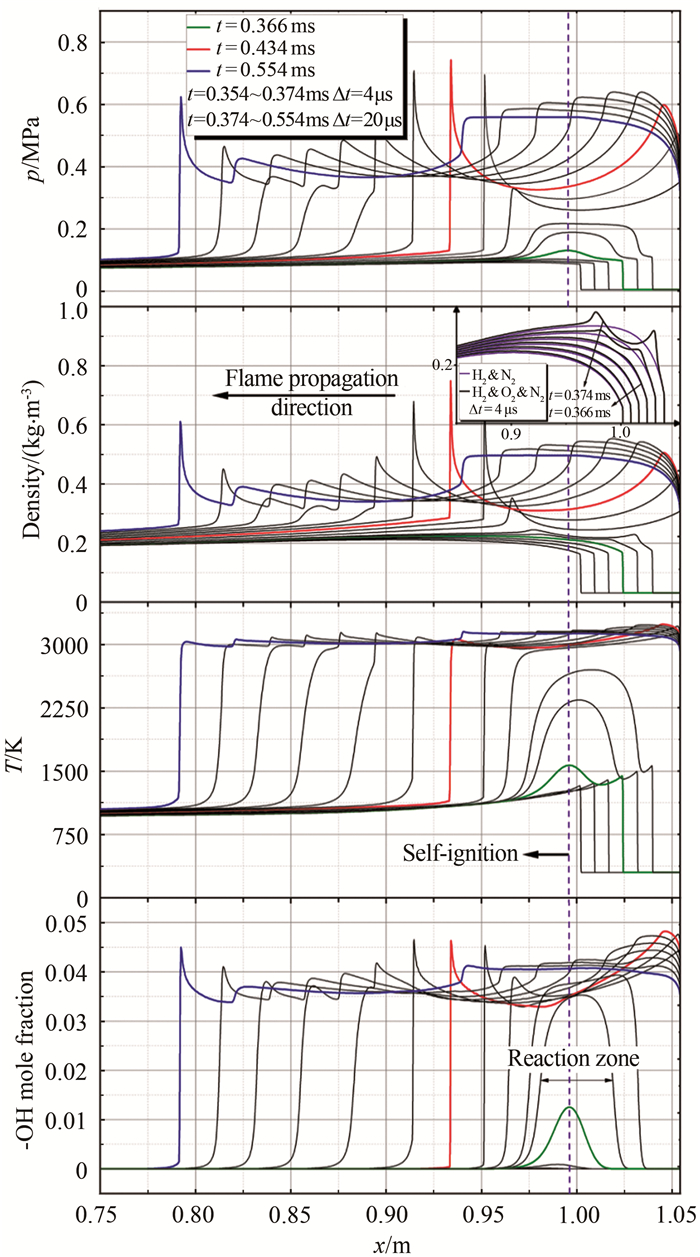
| 图 9 空间压力、密度、温度、自由基OH分布演变过程 Fig.9 Evolution process of spatial pressure、density and temperature free radical OH distribution |
自由基OH的分布一定程度上表征了反应区,自点火(约t=0.366 ms)后自由基OH含量迅速增加,并向上下游蔓延。初期燃烧时,高温反应区内呈现出压力均匀上升的特征;而从沿程密度分布来看(t=0.366~0.370 ms),燃烧流场(B气体)与冷态流场(A气体)的空间密度分布基本没有差别,说明初期燃烧近似等容燃烧过程,气体动力学过程被有效地“关闭”。直到t=0.374 ms,流场中密度才出现明显的强间断,此时,激波-火焰复合结构逐渐形成,这也解释了图 5实验纹影中初期燃烧没有形成激波的原因。随后,左行压缩波迅速累积为激波并与燃烧耦合传播(t=0.434 ms)。从各参数峰值形状来看,随后从间断波面处凸出新的燃烧波面,波面平缓并越过激波波面,后面的间断燃烧波面逐渐弱化为在燃烧产物中传播的激波,且激波强度进一步衰减。此后,燃烧波面处的各参数峰值逐渐变得尖锐,预示激波和燃烧耦合的爆轰波再次形成(t=0.554 ms)。
为了分析这一现象产生的机理,基于Zeldovich的自发传播机制[18],从考虑纯粹的化学反应过程的角度,对圆弧汇聚激波所诱导的非定常点火环境中的“自发反应波”[22-23]进行数值计算。Zeldovich指出当预混可燃气体沿空间位置x的点火敏感性——点火时间ti——连续变化时,继最小ti点发生点火后,速度为usp的“自发反应波”出现,并在点火时间ti较长的相邻位置通过因果无关的连续自燃而“传播”,其中:
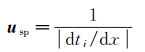 (1)
(1)
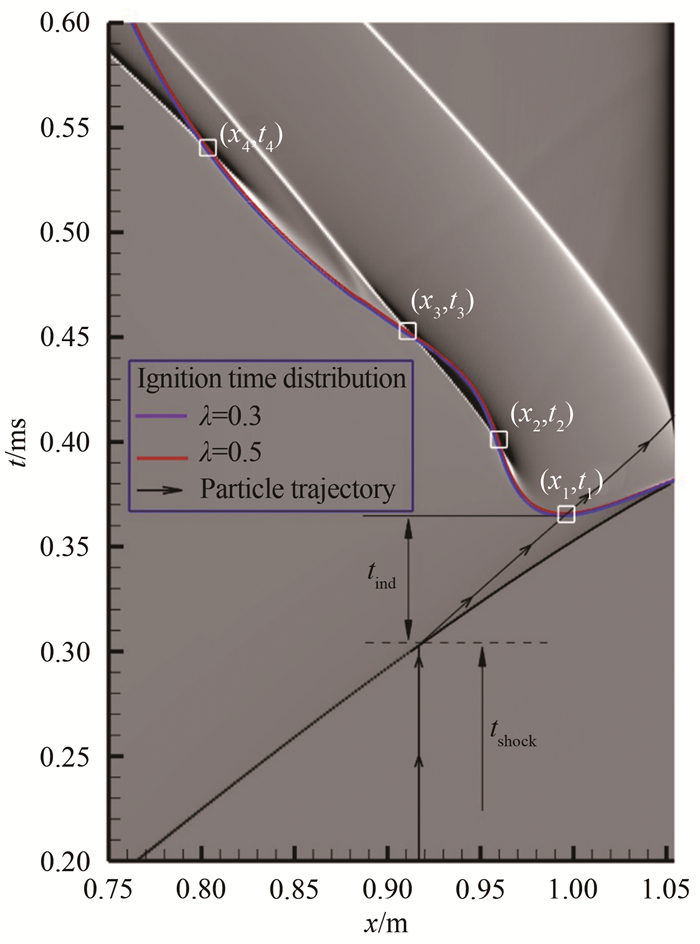
由图 10中质点轨迹可知,在圆弧汇聚激波所诱导的特定点火环境中,预混气体的点火时间ti包括两部分:激波到达时间tshock和激波预处理状态下的反应诱导时间tind,其中反应诱导时间是通过追踪各质点轨迹计算绝热燃烧直到放热反应速率达到最大值来获得。然后可以确定计算所得点火时间ti的轨迹,也即上述“自发反应波”的路径。更具体的,如果定义化学反应过程的进度为λ(λ=0:反应开始,λ=1:反应完全),则这种“自发反应波”实际上是流场中各点的λ取某一相同进度值时所处时空点的集合,其本质上是一种化学反应“相波”。区别于一般的动力学波(压缩波、稀疏波、激波),所谓化学反应“相波”的发展并非由前后介质分子间质量、动量和能量的传递所驱动,而是仅仅取决于当地介质自发的反应进程。从这个意义上,ZND爆轰波可视作前导激波波后的燃烧反应相波。图 10显示了以上描述的“相波”(选取λ=0.3、0.5)与实际燃烧波传播轨迹的比较。对于该算例富氢的情况,有:
|
| 图 10 “相波”和数值纹影中燃烧波传播轨迹的对比 Fig.10 Comparison of trajectories of "spontaneous reaction wave" and detonation wave |
 (2)
(2)
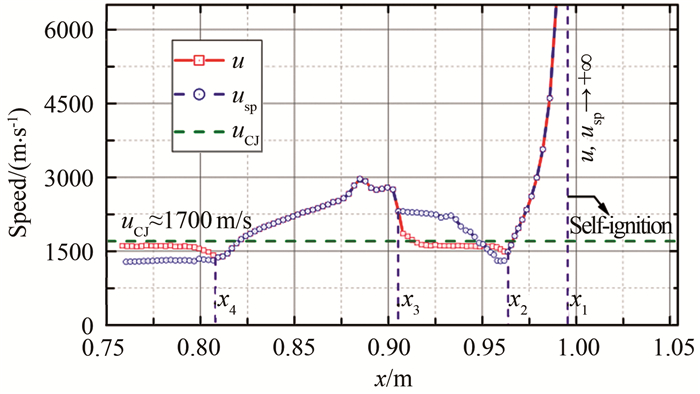
图 11展示了图 10中“相波”速度usp与数值纹影中实际燃烧波速度u(均相对流体质点)对比结果。结合图 10、11可知,对于往上游传播的燃烧波,在初始着火点(x1, t1),“相波”速度远超CJ速度,实验和数值结果均显示初期传播未形成激波,燃烧波后流动呈现一定的弱爆轰波特征。随着反应区迅速扩张,“相波”速度急剧衰减,反应区内压缩波逐渐形成,燃烧波转变为激波和火焰的复合结构,初期燃烧近似在等容环境中进行(t1~t2),基本未受到气动过程的影响,因此燃烧波轨迹与“相波”轨迹基本重合。当“相波”速度衰减至CJ速度以下时,左行压缩波累积形成激波,气动过程与化学反应过程强耦合导致能量释放和燃烧释热,激波-火焰复合结构加速演变为自持传播的CJ爆轰波(t=t2),使得实际燃烧波的速度超过“相波”的速度,因此“相波”滞后于实际燃烧波轨迹,此后,燃烧波速度维持在CJ速度附近(t2~t3)。
|
| 图 11 流动系统中“相波”与实际燃烧波速度对比 Fig.11 Comparison of speeds of "spontaneous reaction wave" and detonation wave |
从图 10可以看出,该工况下,由于上游特定的点火环境,梯度场中的“相波”的轨迹超过CJ爆轰波,成为新的燃烧波前。由于“相波”迅速扩张并消耗爆轰波前反应物,爆轰波失去化学反应的加持逐渐弱化为在反应产物中传播的激波(t3~t4),此时,燃烧波以“相波”的速度传播,数值纹影中燃烧波轨迹与“相波”轨迹再次重合。而后,“相波”的速度减小至CJ速度以下,再次滞后于CJ爆轰波(t4~),深黑色区域反应面和浅色区域激波又重新耦合, 象征爆轰波再次形成,演变为新的燃烧波前。
3 结论本文采用激波管实验和准一维数值模拟的方法,获得主要结论如下:
(1) 圆弧汇聚激波所诱导的非定常梯度环境由入射激波在不同形态下所诱导的3个梯度区共同构成,该环境为自点火、“自发反应波”的传播以及爆轰波的形成研究提供了独特的条件。
(2) 在圆弧汇聚激波所诱导的非定常梯度环境下,“自发反应波”在爆轰起始过程中起着关键作用。从自点火出现至激波-火焰复合结构(准爆轰复合体)形成,一个近似等容爆炸过程出现,自圆弧激波后某处形成往上游传播的、无激波耦合的反应面,初期传播速度远超CJ爆轰波速,呈现一定的弱爆轰波特征,其本质是“自发反应波”。
(3) 这种“自发反应波”与爆轰传播过程也存在着紧密联系。在本文条件下,自点火后实现了“相波”赶超爆轰波的过程,分析认为梯度环境中的“相波”速度usp与CJ爆轰波速的竞争关系主导了这一过程的出现。
| [1] |
Liu Y, Wang L, Xiao B G, et al. Hysteresis phenomenon of the oblique detonation wave[J]. Combustion and Flame, 2018, 192: 170-179. DOI:10.1016/j.combustflame.2018.02.010 |
| [2] |
Yao S B, Liu M, Wang J P. Numerical investigation of spontaneous formation of multiple detonation wave fronts in rotating detonation engine[J]. Combustion Science and Techno-logy, 2015, 187(12): 1867-1878. DOI:10.1080/00102202.2015.1067202 |
| [3] |
Lee J H S. The detonation phenomenon[M]. Camridge: Cambridge University Press, 2008.
|
| [4] |
Hanson R K, Davidson D F. Recent advances in laser absorption and shock tube methods for studies of combustion chemistry[J]. Progress in Energy and Combustion Science, 2014, 44(5): 103-114. |
| [5] |
Kéromnès A, Metcalfe W K, Heufer K A, et al. An experi-mental and detailed chemical kinetic modeling study of hydrogen and syngas mixture oxidation at elevated pressures[J]. Combustion and Flame, 2013, 160(6): 995-1011. DOI:10.1016/j.combustflame.2013.01.001 |
| [6] |
Hashemi H, Christensen J M, Gersen S, et al. Hydrogen oxidation at high pressure and intermediate temperatures:Experiments and kinetic modeling[J]. Proceedings of the Combustion Institute, 2015, 35(1): 553-560. DOI:10.1016/j.proci.2014.05.101 |
| [7] |
Koroglu B, Pryor O M, Lopez J, et al. Shock tube ignition delay times and methane time-histories measurements during excess CO2 diluted oxy-methane combustion[J]. Combustion and flame, 2016, 164: 152-163. DOI:10.1016/j.combustflame.2015.11.011 |
| [8] |
Boeck L R, Mével R, Sattelmayer T. Models for shock-induced ignition evaluated by detailed chemical kinetics for hydrogen/air in the context of deflagration-to-detonation transition[J]. Journal of Loss Prevention in the Process Industries, 2017, 49: 731-738. DOI:10.1016/j.jlp.2017.04.018 |
| [9] |
Chatelain K, Mével R, Menon S, et al. Ignition and chemical kinetics of acrolein-oxygen-argon mixtures behind reflected shock waves[J]. Fuel, 2014, 135: 498-508. DOI:10.1016/j.fuel.2014.07.004 |
| [10] |
Yamashita H, Kasahara J, Sugiyama Y, et al. Visualization study of ignition modes behind bifurcated-reflected shock waves[J]. Combustion and Flame, 2012, 159(9): 2954-2966. DOI:10.1016/j.combustflame.2012.05.009 |
| [11] |
Grogan K P, Ihme M. Regimes describing shock boundary layer interaction and ignition in shock tubes[J]. Proceedings of the Combustion Institute, 2017, 36(2): 2927-2935. DOI:10.1016/j.proci.2016.06.078 |
| [12] |
Gelfand B E, Khomik S V, Bartenev A M, et al. Detonation and deflagration initiation at the focusing of shock waves in combustible gaseous mixture[J]. Shock Waves, 2000, 10(3): 197-204. DOI:10.1007/s001930050007 |
| [13] |
Bartenev A M, Khomik S V, Gelfand B E, et al. Effect of reflection type on detonation initiation at shock-wave focusing[J]. Shock Waves, 2000, 10(3): 205-215. DOI:10.1007/s001930050008 |
| [14] |
滕宏辉, 王春, 邓博, 等. 可燃气体中激波聚焦的点火特性[J]. 力学学报, 2007, 39(2): 171-180. Teng H H, Wang C, Deng B, et al. Ignition characteristics of the shock wave focusing in combustive gases[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(2): 171-180. DOI:10.3321/j.issn:0459-1879.2007.02.005 |
| [15] |
何立明, 荣康, 曾昊, 等. 激波聚焦及起爆爆震波的研究进展[J]. 推进技术, 2015, 36(10): 1441-1458. He L M, Rong K, Zeng H, et al. Advances in shock wave focusing and induced detonation initiation[J]. Journal of Propulsion Technology, 2015, 36(10): 1441-1458. |
| [16] |
Zhai Z G, Liu C L, Qin F H, et al. Generation of cylindrical converging shock waves based on shock dynamics theory[J]. Physics of Fluids, 2010, 22(4): 041701. DOI:10.1063/1.3392603 |
| [17] |
Yang J T, Zhu Y J, Yang J M. Self-ignition induced by cylindrically imploding shock adapting to a convergent channel[J]. Physics of Fluids, 2017, 29(3): 031702. DOI:10.1063/1.4979135 |
| [18] |
Zel'Dovich Y B, Librovich V B, Makhviladze G M, et al. On the onset of detonation in a nonuniformly heated gas[J]. Journal of Applied Mechanics and Technical Physics, 1970, 11(2): 264-270. |
| [19] |
Oran E S, Weber J W Jr, Stefaniw E I, et al. A numerical study of a two-dimensional H2-O2-Ar detonation using a detailed chemical reaction model[J]. Combustion and Flame, 1998, 113(1-2): 147-163. DOI:10.1016/S0010-2180(97)00218-6 |
| [20] |
Brown P N, Byrne G D, Hindmarsh A C. VODE:a variable coefficient ODE solver[J]. SIAM Journal of Scientific and Statistical Computing, 1989, 10(5): 1038-1051. DOI:10.1137/0910062 |
| [21] |
Shi X F, Zhu Y J, Yang J M, et al. Mach stem deformation in pseudo-steady shock wave reflections[J]. Journal of Fluid Mechanics, 2019, 861: 407-421. DOI:10.1017/jfm.2018.920 |
| [22] |
Kapila A K, Schwendeman D W, Quirk J J, et al. Mechanisms of detonation formation due to a temperature gradient[J]. Combustion Theory and Modelling, 2002, 6(4): 553-594. DOI:10.1088/1364-7830/6/4/302 |
| [23] |
Kassoy D R. The Zeldovich spontaneous reaction wave propa-gation concept in the fast/modest heating limits[J]. Journal of Fluid Mechanics, 2016, 791: 439-463. DOI:10.1017/jfm.2015.756 |



