内转式进气道具有捕获流量大、压缩效率高及浸润面积小等优势[1],是高超声速飞行器设计中极具潜力的进气方案之一。然而,由于内转式进气道内部的三维流动更加复杂,目前对其流场结构、流动规律和作用机理等方面的认识,不如传统的二元进气道成熟。在内转式进气道流动问题中,轴对称内收缩几何约束所引起的激波汇聚效应尤为突出。
轴对称内收缩激波在向轴心汇聚的过程中,强度不断增大,最终超出von Neumann边界[2],在轴线上发生马赫反射,以马赫盘的形式,终结理想的中心汇聚过程,很多学者均论证了这种马赫反射的必然性[3]。这不仅引起流场中热力学参数的剧烈变化,而且带来总压损失增加和抗反压能力削弱等不利影响。现有的内转式进气道,在轴对称基准流场设计时,往往采用在轴线设置中心体的方法[4-5],规避汇聚中心的马赫反射,进而提升流场品质。但这种规避问题的做法,给进气道的创新设计带来约束。此外,即便在进气道中避免了汇聚中心的问题,在下游多采用近圆形截面的隔离段[6-7]内部,由于其近轴对称的几何特性,流场中同样存在汇聚效应,激波的反射、相交以及透射等相互作用,也表现出与二元构型的显著差异。因此,开展近轴对称内收缩流场中的激波相互作用研究,在促进三维激波汇聚干扰问题的解决和工程实际应用方面,都具有较高的价值。
对于理想的轴对称内收缩流场,已有许多研究工作。Mölder[8]较早地对轴对称内锥形入射激波在接近轴线时会变陡的现象,进行了相对详细的刻画。随后,Hornung[9-10]在非定常锥形内聚运动激波的数值模拟过程中,也发现了类似的现象。最近,Filippi[11]考察了轴对称弯曲内壁面对入射激波弯曲的影响。Mölder[12-14]从一般的弯曲激波出发,建立了弯曲激波理论,为分析弯曲入射激波问题提供了强有力的支撑。这些丰富的成果,增进了人们对轴对称内收缩流场的认识。然而在实际流动中,飞行姿态改变、吞入前体边界层等因素带来的非均匀来流,很容易使流场偏离轴对称状态。一旦理想的轴对称内收缩条件被打破,流场中是否存在与以往认识不同的激波干扰特性和规律,是值得关注的焦点。
本文针对实际工程应用中的三维内转式进气道复杂曲面激波干扰问题,简化提炼出不同来流迎角下的内收缩直锥流场,用以高效揭示小幅偏离轴对称状态时流场中的激波汇聚效应及其干扰机理。采用激波风洞实验观测结合数值模拟的方法,分别考察了轴对称和近轴对称流场中激波汇聚增强效应与激波干扰的差异,以期为内转式进气道中的激波干扰问题研究提供有价值的参考。
1 实验及计算方法 1.1 实验设备、模型和方法实验在中国科学技术大学的KDJB330反射型激波风洞中进行[15-17],来流名义马赫数Ma∞=6,静压p∞=900 Pa,静温T∞=110 K, 实验时间约为20 ms。
采用前缘压缩角度为θ的内收缩直锥模型,其对称面结构如图 1所示。模型入口半径R=100 mm,轴向长度L=100 mm。以模型入口的轴心为原点,取模型轴线方向为x方向,法向为y方向,展向为z方向。选取前缘角度θ=10°和12°的两种典型构型,考察不同强度初始入射激波对下游激波干扰的影响;并通过调整模型轴线与来流的相对角度,得到α=0°、2°和5°的3个典型来流迎角,探究轴对称和近轴对称流场中的激波演化规律。

|
| 图 1 实验模型对称面结构示意图 Fig.1 Schematic of the experimental model |
采用如图 2所示的Z字形纹影光路,拍摄模型出口流场的纹影。考虑到纹影显示的是沿光程的累积效果,难以直观分辨流场中的三维波系结构,借助平面激光散射(PLS)方法[18-19],拍摄了汇聚中心上游横截面的瞬时流场结构,所采用的实验光路如图 3所示。在来流有迎角α的实验中,平面激光与来流方向保持垂直,因此激光所在平面与模型轴线(x方向)成大小为α的角度。

|
| 图 2 纹影拍摄光路 Fig.2 Optical path of the schlieren method |

|
| 图 3 PLS光路 Fig.3 Optical path of the PLS method |
考虑到计算条件和实验环境的一致性,采用粘性计算,但本文主要关注远离壁面处的定常激波干扰结构,粘性和边界层效应对主要波系结构的影响较小[11]且非主要矛盾。利用基于有限体积法的Fluent软件[20]求解N-S方程,数值通量采用AUSM格式计算[17, 21]。经过考核,该方法对于激波干扰问题较为可靠。为提高计算效率,轴对称工况(α=0°)采用二维/轴对称计算,仅对偏离轴对称的工况进行三维计算。2种工况均采用结构化网格。远场来流边界条件设置与风洞来流条件保持一致。计算中,监测各方程残差以及对称面上入射激波后和三波点位置处的马赫数、压力等指标,待残差收敛且各项参数稳定后,认为流场收敛。
2 结果与分析 2.1 轴对称流场首先以前缘角度θ=10°的构型为例,简要说明作为参照的轴对称(α=0°)流场的基本特征。图 4对比了轴对称构型的对称面(z=0)和二维平面流场的数值纹影(计算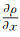

|
| 图 4 θ=10°构型的轴对称和二维流场数值纹影对比 Fig.4 Numerical schlieren comparison of the axisymmetric and planar flow field for the θ=10° configuration |
图 5给出θ=10°轴对称构型在马赫盘上游x/L =1.63及2.35截面上的PLS图像,中心较暗区域为来流,而入射激波(IS)的波后流场较为明亮[18-19],两区域的分界即为入射激波面与平面激光的截交线。为便于直观对比,在图 5中用虚线叠加了圆形。可以看出,x截面上的入射激波呈逐渐收缩的圆形,表明流场呈现理想的轴对称性,并且向中心汇聚。

|
| 图 5 θ=10°构型轴对称流场x/L=1.63和2.35截面散射图像 Fig.5 PLS images on the sections of x/L=1.63 and 2.35 for the θ=10° configuration |
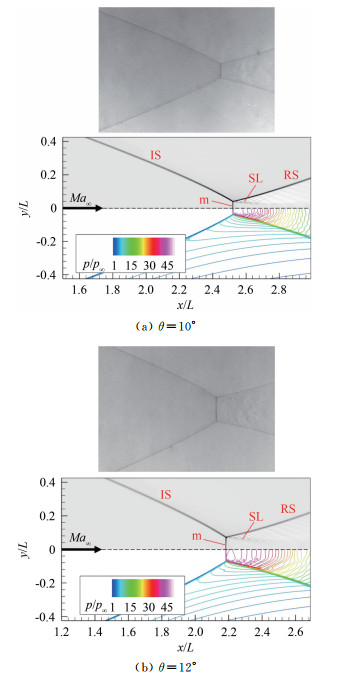
不同前缘角度θ下,轴对称流场中的激波干扰结构类似。图 6给出了前缘角度分别为θ=10°和12°两个构型的实验纹影和数值计算结果(压力p采用来流静压p∞进行无量纲化)。由纹影原理可知,实验纹影显示的是轴对称激波面在纵向平面的脊线。从图 6可以看出,两种构型的入射激波(IS)均在轴线上汇聚为强激波,并发生马赫反射,形成马赫盘(m)、反射激波(RS)和剪切层(SL)。2种构型流场中的马赫盘均近似为正激波,其波后为亚声速区,静压约为42p∞。随着前缘角度θ增加,流场结构的主要差异在于,马赫盘(m)的高度增大,并且位置更加靠近上游。θ=10°时,马赫盘位于x/L=2.52附近;θ=12°时,马赫盘位于x/L=2.18附近。
|
| 图 6 θ=10°和12°两种构型的轴对称流场实验纹影(竖直刀口)及数值结果(纹影和压力等值线) Fig.6 Experimental schlieren images (vertical knife edge) and numerical results (schlieren and pressure contours) of the axisymmetric flow fields for the θ=10° and 12° configurations |
在来流有迎角时,流场偏离轴对称状态,呈现出三维特性。在这种近轴对称情况下,即使迎角相同,不同前缘角度构型产生的激波干扰也有所差异。分别以前缘角度θ=10°和12°构型为例,分析不同迎角下的激波干扰特征及其演化规律。
2.2.1 前缘角度θ=10°图 7(a)和(b)分别给出了前缘角度θ=10°构型在来流迎角α=2°时的实验纹影和数值模拟的对称面(z=0)纹影。在该迎角下,入射激波小幅偏离轴对称形态,前缘处迎风侧初始入射激波(IS1)的强度略大于背风侧(IS2)。由于迎风侧受到的压缩强于背风侧,在相同流向位置处IS1的激波角大于IS2,在接近轴线时,IS1仍然受到向轴心汇聚作用的影响,其强度进一步增大,曲率变化明显。最终,IS1越过轴线仍然与IS2发生马赫反射,在x/L=2.55附近形成马赫盘(m)、反射激波(RS1和RS2)和剪切层(SL)。然而,此时马赫盘的高度与轴对称流场(见图 6(a))相比,已经明显变小,并且偏向背风侧。

|
| 图 7 θ=10°构型在α=2°时的纹影(竖直刀口) Fig.7 Schlieren images (vertical knife edge) for the θ=10° configuration at α=2° |
借助数值模拟,计算x截面上的密度梯度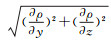
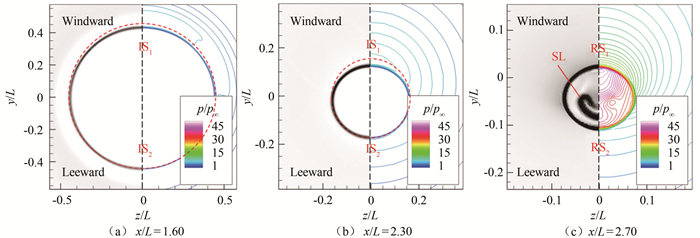
|
| 图 8 θ=10°构型在α=2°时x/L=1.60、2.30和2.70截面的流场图像 Fig.8 Flow features on the sections of x/L=1.60, 2.30 and 2.70 for the θ=10° configuration at α=2° |
增大来流迎角至α=5°时,实验纹影如图 9(a)所示。此时,前缘处迎风侧入射激波(IS1)的初始强度进一步增加,背风侧入射激波(IS2)的初始强度进一步减弱,两者的差异更加突出。受到向轴心汇聚作用的影响,IS1的强度比IS2增大得更快,IS1向轴心的弯曲更加明显。最终,IS1越过轴线与IS2干扰。值得注意的是,从实验纹影上看,在该来流迎角下,汇聚中心并没有出现马赫盘,而是表现为规则反射,形成反射激波RS1和RS2。在规则反射点上游出现了新的激波S′,如图 9(a)中局部放大纹影所示,并且激波S′似乎能够“穿过”规则反射点。然而,在图 9(b)数值模拟的对称面上(z=0),入射激波IS1与IS2位于x/L=2.57的规则反射点R附近,并没有出现激波S′。类比实验中的纹影原理,将数值模拟得到的三维流场沿光程进行积分[17],得到的数值纹影如图 9(c)所示。从图 9(c)中可以看到与图 9(a)的实验纹影类似的激波S′。这表明激波S′是由三维激波结构在实验纹影光路中的累积效果造成的。

|
| 图 9 θ=10°构型在α=5°时的纹影 Fig.9 Schlieren images for the θ=10° configuration at α=5° |
进一步地,通过图 10所示x截面的流场结构,分析这种三维激波结构的形成及演化过程。为便于直观对比,在图 10中用虚线叠加了圆形。在上游距离入射激波IS1与IS2规则反射点R较远的x/L=1.60截面上(见图 10(a)),IS1和IS2虽然仍为光滑连接的弧形,但前缘不对称压缩引起的IS1和IS2曲率的差异比α=2°时(见图 8(a))更加显著。入射激波在向下游发展的过程中,由于迎风侧的汇聚增强更快,IS1在对称面上的曲率迅速增大;而背风侧的汇聚缓慢,IS2在对称面上的曲率变化不明显。因此,在接近规则反射点R的x/L=2.44截面上(见图 10(b)),迎风侧入射激波IS1呈现扁平状,其曲率半径大于背风侧入射激波IS2。从该截面上可以清晰地看到,IS1与IS2不再光滑连接,而是出现Kink结构,并且在Kink位置产生新的反射激波RS′和剪切层SL,使得背风侧的低压气流能够与迎风侧的高压气流相匹配。图 10(c)给出了该截面附近的平面激光散射图像,可以看出,实验图像较好地展示了这种Kink结构。

|
| 图 10 θ=10°构型α=5°时x/L=1.60、2.44、2.52、2.57、2.68和2.76截面的流场图像 Fig.10 Flow features on the sections of x/L=1.60, 2.44, 2.52, 2.57, 2.68 and 2.76 for the θ=10° configuration at α=5° |
入射激波IS1与IS2沿流向继续向轴线汇聚增强,同时IS1与IS2连接处的Kink也在向对称面(z=0)靠近。在x/L=2.52截面上(见图 10(d)),剪切层(SL)进一步发展,在反射激波RS2′(即x/L=2.44截面上的反射激波RS′)的内侧出现明显的反射激波RS1′,三者均与Kink连接。紧接着,在x/L=2.57截面(见图 10(e))上,入射激波IS1与IS2在对称面(z=0)相交,此时Kink位于IS1与IS2交线的末端。
入射激波IS1与IS2直接相交之后,下游随即出现反射激波RS1和RS2,与此前已经存在的反射激波RS1′和RS2′进一步发生干扰,产生更加复杂的激波结构。在x/L=2.68截面上(见图 10(f)),迎风侧激波RS1和RS1′以及背风侧激波RS2和RS2′分别通过两个Kink点连接,而这两个Kink点通过展向反射激波RSs连接。此时自上游x/L=2.52截面(见图 10(d))产生的剪切层SL已经脱离Kink点,与反射激波RSs干扰。在流场中心被激波包围的区域,气流仍为超声速,并且经过入射和反射激波的多次压缩,中心区域的静压比迎角α=2°时(见图 8(c))马赫盘后的静压更高,可以达到约47p∞。然而,在向下游继续发展的过程中,气流由汇聚中心发散,这一高压状态难以为继。随着激波面向外扩张,其强度迅速减弱,反射激波RS1、RS2与RSs的连接也逐渐光滑,相应的RS1′和RS2′迅速减弱(见图 10(g))并最终消失。通过对图 10三维激波结构演化过程的分析可知,图 9(a)实验纹影中的激波S′即为反射激波RS2′的脊线。
实验和数值模拟结果表明,在来流迎角α由2°增加至5°的过程中,迎风侧入射激波IS1和背风侧入射激波IS2在对称面上的反射类型从马赫反射转变为规则反射。可见,近轴对称流场能够打破原有的因为向轴心汇聚而必然发生马赫反射现象的规律。进一步地,借助数值模拟,图 11(a)和(b)分别给出了迎角α=3°和4°时流场对称面的数值纹影。对比α=2°时的对称面流场(见图 7(b))可以看出,随着来流迎角增大,入射激波IS1和IS2干扰形成的马赫盘(m)的高度逐渐减小。α=4°时,马赫盘完全消失,IS1和IS2在对称面上发生规则反射。换言之,在迎角α=3°和4°之间,流场小幅度偏离轴对称的情况下,就发生了激波反射类型的转变。

|
| 图 11 θ=10°构型在α=3°和4°时流场对称面的数值纹影 Fig.11 Numerical schlieren images on the symmetry plane for the θ=10° configuration at α=3° and 4° |
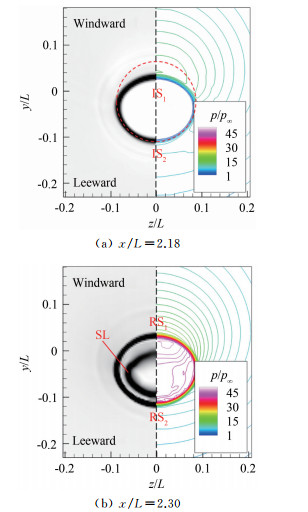
增大模型的前缘角度至θ=12°,图 12(a)和(b)分别给出了来流迎角α=2°时的实验纹影和数值模拟的对称面(z=0)纹影。与θ=10°构型类似,迎风侧的初始入射激波(IS1)强于背风侧(IS2),并且IS1向轴心的汇聚增强更快,使得IS1与IS2发生干扰的位置偏向背风侧。IS1与IS2在x/L=2.21附近发生马赫反射,仍以马赫盘(m)的形式终结汇聚过程。但与θ=12°的轴对称流场(见图 6(b))相比,此时马赫盘的高度变小。从图 13(a)马赫盘上游的x/L=2.18截面和图 13(b)马赫盘下游的x/L=2.30截面上的数值纹影和压力等值线可以看出,入射激波和反射激波均光滑连接,没有出现Kink结构,马赫盘后的局部压力与轴对称流场(见图 6(b))中马赫盘后压力相当。

|
| 图 12 θ=12°构型在α=2°时的纹影 Fig.12 Schlieren images for the θ=12° configuration at α=2° |
|
| 图 13 θ=12°构型α=2°时x/L=2.18和2.30截面的流场图像 Fig.13 Flow features on the sections of x/L=2.18 and 2.30 for the θ=12° configuration at α=2° |
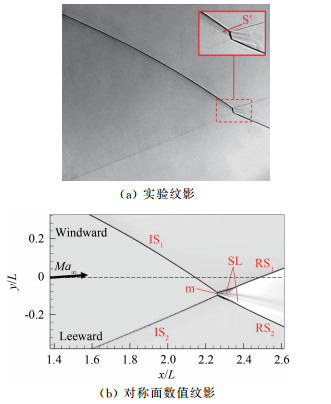
如图 14所示,来流迎角增大到α=5°时,入射激波IS1与IS2仍然发生马赫反射,在x/L=2.26附近形成马赫盘(m),但马赫盘的高度进一步减小。从图 14(a)实验纹影的局部放大图中可以看出,在马赫盘附近存在由三维激波结构在实验纹影光路上的累积而形成的激波S′,其产生机制与θ=10°构型(见图 10)类似。
|
| 图 14 θ=12°构型在α=5°时的纹影 Fig.14 Schlieren images for the θ=12° configuration at α=5° |
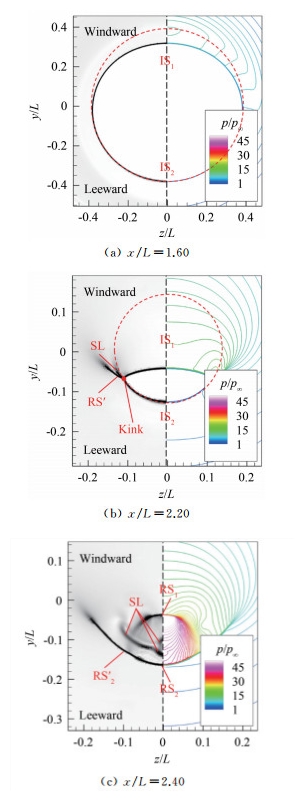
通过图 15给出的3个典型x截面的数值纹影可以看出,在最上游的x/L=1.60截面(见图 15(a)),IS1与IS2光滑连接;在x/L=2.20截面上(见图 15(b)),迎风侧和背风侧入射激波的形态差异已经凸显,IS1相较于IS2更加扁平,并且在IS1与IS2的连接处出现Kink结构。在Kink处形成反射激波RS′,即实验纹影(见图 14(a))中的激波S′。在马赫盘下游的x/L=2.40截面上(见图 15(c)),反射激波RS1和RS2连接处仍然存在Kink,直至更下游的位置Kink才逐渐消失。迎角α=5°时,马赫盘后的静压与α=2°时(见图 13(b))马赫盘后的静压相当。
|
| 图 15 θ=12°构型α=5°时x/L=1.60、2.20和2.40截面的流场图像 Fig.15 Flow features on the sections of x/L=1.60, 2.20 and 2.40 for the θ=12° configuration at α=5° |
对比图 12和14可以看出,随着来流迎角增大,马赫盘的高度呈现递减的趋势。借助数值模拟,继续逐步增大来流迎角,图 16给出了α=6°时流场对称面上的数值纹影。此时IS1与IS2在对称面上不再发生马赫反射,而是发生规则反射。可见,对于θ=12°的构型,增大来流迎角同样能够使得流场对称面上的激波反射类型从马赫反射转变为规则反射。这也表明,对于前缘角度θ较大的内收缩直锥构型,在流场更大程度偏离轴对称的情况下,才能打破原有的因为向轴心汇聚而发生马赫反射的规律,转变为规则反射。

|
| 图 16 θ=12°构型在α=6°时流场对称面的数值纹影 Fig.16 Numerical schlieren image on the symmetry plane for the θ=12° configuration at α=6° |
采用激波风洞实验结合数值模拟,分析了不同来流迎角下内收缩直锥流场中的激波干扰现象,主要得到了以下结论:
(1) 轴对称内收缩直锥的几何约束使得前缘入射激波在向下游发展的过程中,持续向轴线汇聚增强,最终均会发生马赫反射,以马赫盘的形式终结入射激波的汇聚过程。当内收缩直锥前缘角度增加时,马赫盘的高度增大,并且向上游移动。
(2) 来流有迎角时,迎风侧入射激波沿流向的汇聚增强比背风侧更快,使得激波干扰位置偏离几何轴线。迎角较大时,流场的三维激波结构更加复杂,在迎风侧和背风侧激波的展向连接处,出现Kink结构,并产生新的反射激波。
(3) 增大来流迎角,马赫盘的尺度范围逐渐减小,最终能够打破内收缩直锥流场向轴心汇聚而发生马赫反射的规律,使得迎风侧和背风侧激波在对称面上发生规则反射。没有马赫盘的限制,入射激波能够继续汇聚增强,规则反射点后的压力会高于轴对称流场中马赫盘后的压力。对于前缘角度较大的内收缩直锥,在更大的迎角下才会发生规则反射。
致谢: 感谢国家自然科学基金项目11872356,11772325,11621202对本文研究工作的支持。| [1] |
You Y C. An overview of the advantages and concerns of hypersonic inward turning inlets[R]. AIAA 2011-2269, 2011.
|
| [2] |
Ben-Dor G. Shock wave reflection phenomena[M]. New York: Springer, 2007.
|
| [3] |
Timofeev E, Mölder S, P Voinovich, et al. Shock wave reflections in axisymmetric flow[C]//Proc of the 23rd International Symposium on Shock Waves. 2001.
|
| [4] |
李永洲.马赫数分布可控的高超声速内收缩进气道及其一体化设计研究[D].南京: 南京航空航天大学, 2014. Li Y Z. Investigation of hypersonic inward turning inlet with controlled Mach number distribution and its integrated design[D]. Nanjing: Nanjing University of Aeronautics and Astronau-tics, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10287-1015951706.htm |
| [5] |
尤延铖, 梁德旺. 内乘波式进气道内收缩基本流场研究[J]. 空气动力学学报, 2008, 26(2): 203-207. You Y C, Liang D W. Investigation of internal compression flow field for internal waverider-derived inlet[J]. Acta Aerodynamica Sinica, 2008, 26(2): 203-207. DOI:10.3969/j.issn.0258-1825.2008.02.012 |
| [6] |
王卫星, 李博, 郭荣伟. 不同反压下椭圆形隔离段流场特征与气动性能[J]. 航空动力学报, 2010(3): 647-653. Wang W X, Li B, Guo R W. Flow characteristic and aerodynamic performance in elliptic shape isolator at different back pressures[J]. Journal of Aerospace Power, 2010(3): 647-653. |
| [7] |
何粲.双模态超燃冲压发动机隔离段流动特性研究[D].绵阳: 中国空气动力研究与发展中心, 2015. He C.Investigation of flow characteristics in the dual-mode scramjet isolator[D]. Mianyang: China Aerodynamics Research and Development Center, 2015. |
| [8] |
Mölder S. Internal, axisymmetric, conical flow[J]. AIAA Journal, 1967, 5(7): 1252-1255. DOI:10.2514/3.4179 |
| [9] |
Hornung H G. Oblique shock reflection from an axis of symmetry[J]. Journal of Fluid Mechanics, 2000, 409: 1-12. DOI:10.1017/S0022112099007831 |
| [10] |
Hornung H G, Schwendeman D W. Oblique shock reflection from an axis of symmetry:shock dynamics and relation to the Guderley singularity[J]. Journal of Fluid Mechanics, 2001, 438: 231-245. DOI:10.1017/S0022112001004360 |
| [11] |
Filippi A A. Supersonic flow fields resulting from axisymmetric internal surface curvature[J]. Journal of Fluid Mechanics, 2017, 831: 271-288. DOI:10.1017/jfm.2017.643 |
| [12] |
Mölder S. Curved aerodynamic shock waves[D]. Montreal: McGill University, 2012.
|
| [13] |
Mölder S. Curved shock theory[J]. Shock Waves, 2016, 26(4): 337-353. DOI:10.1007/s00193-015-0589-9 |
| [14] |
Mölder S. Flow behind concave shock waves[J]. Shock Waves, 2017, 27(1-4): 1-10. |
| [15] |
Li Z F, Gao W Z, Jiang H L, et al. Unsteady behaviors of a hypersonic inlet caused by throttling in shock tunnel[J]. AIAA Journal, 2013, 51(10): 2458-2492. |
| [16] |
李祝飞, 高文智, 李鹏, 等. 一种进气道自起动特性检测方法[J]. 实验流体力学, 2013, 27(2): 14-18. Li Z F, Gao W Z, Li P, et al. A test method for inlet self-starting ability detection[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(2): 14-18. DOI:10.3969/j.issn.1672-9897.2013.02.003 |
| [17] |
张恩来, 李祝飞, 李一鸣, 等. 斜激波入射V形钝前缘溢流口激波干扰研究[J]. 实验流体力学, 2018, 32(3): 50-57. Zhang E L, Li Z F, Li Y M, et al. Investigation on the shock interactions between an incident shock and a plate with V-shaped blunt leading edge[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(3): 50-57. |
| [18] |
李一鸣, 李祝飞, 杨基明, 等. 典型高超声速内转式进气道激光散射流场显示[J]. 航空学报, 2017, 38(12): 138-149. Li Y M, Li Z F, Yang J M, et al. Flow visualization of a typical inward-turning inlet using laser scatting[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(12): 138-149. |
| [19] |
Miles R B, Lempert W R, Forkey J N. Laser rayleigh scattering[J]. Measurement Science and Technology, 2001, 12(5). |
| [20] |
肖丰收.若干典型高超声速激波干扰流动特性研究[D].合肥: 中国科学技术大学, 2016. Xiao F S. Research on flow characteristics of Some typical hypersonic shock wave interactions[D]. Hefei: University of Science and Technology of China, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10358-1016319976.htm |
| [21] |
阎超, 涂正光, 于晓红, 等. 激波碰撞干扰流动非定常效应的数值研究[J]. 北京航空航天大学学报, 2003, 29(3): 214-217. Yan C, Tu Z G, Yu X H. Numerical research on unsteady effect of shock-shock interference flow[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(3): 214-217. DOI:10.3969/j.issn.1001-5965.2003.03.007 |



