2. 中国运载火箭技术研究院, 北京 100076
2. China Academy of Launch Vehicle Technology, Beijing 100076, China
高超声速飞行器研制过程中的气动加热问题至关重要。飞行器热防护系统、信息通讯系统、某些定位制导系统的设计研制都需要准确的气动热数据支撑,否则,设计出的飞行器就可能在飞行过程中因烧蚀过量而失去机动能力甚至损毁,也可能因未能准确预示“黑障”现象而失去信息通讯、定位制导的能力。
对于复杂外形高超声速飞行器,其表面存在激波干扰、流动分离、稀薄流效应、高温真实气体效应以及边界层转捩/湍流等复杂的流动和物理化学现象。针对此类现象,一方面,目前的模拟理论尚不完备,气动加热的预示精度还存在较大的不可信空间,对复杂外形高超声速飞行器气动热环境的准确预示仍有较大难度;另一方面,目前地面试验设备的模拟能力不足,几乎不可能复现真实飞行环境,地面试验数据无法反映真实飞行过程中的气动加热水平,这也较大程度制约了气动热环境预示技术的发展[1-2]。因此,利用热流传感器通过地面/飞行试验开展表面热流的直接测量、进而验证和完善气动热环境预示方法就显得尤为重要。美国早期开展的Reentry F研究计划[3],就是专门针对气动热环境和转捩进行测量;欧洲宇航局ESA也提出了用于高超声速飞行器气动热力学研究的EXPERT计划[4]等。
圆箔式热流传感器能够进行长时间热流测量,广泛应用于高超声速飞行试验的气动加热测量。其原理是通过测量康铜箔片中心与其周径上的温度梯度来辨识热流[5]。由于传感器与被测物体的结构和材料不同,对高超声速对流引起的气动加热的热响应存在差异,在测量过程中,传感器康铜箔片的温度会低于被测物体表面温度,形成低温区域,表面温度的差异会影响近壁面附近的边界层流动,从而影响热流测量结果,即为“冷点效应”。
国内高超声速研究刚刚起步,以飞行试验开展热流研究的工作少之又少。在采用“嵌入式”手段测量“冷壁热流”技术途径的基础上,丁小恒[6]等发展了可适应更宽工作范围的热流密度测量方法及热流辨识反问题计算方法。国外在20世纪50年代开始了相关研究工作,多个试验和分析结果[7-11]表明:在层流或湍流中,变化的表面温度分布会引起明显的热流变化。Eckert[12]和Neumann[13]注意到嵌入式传感器材料和被测表面材料不同时,测得的热流不同于材料相同时测得的热流;Diller[14]指出,传感器必然引起壁面温度分布和热流分布的变化,在对流传热中,上游热边界层的信息会随着流动对下游传热产生影响;Kandula和Reinarts[15]采用二维数值模拟手段研究了雷诺数1×106、马赫数4、壁面温度不连续条件下,以圆柱热流测量计测量热流可能产生的误差,并给出了修正方案。Mukerji[16]等研究了低速对流条件下一维温度台阶和二维温度台阶对湍流边界层内对流热流的影响,分析了传感器在该影响下产生测量误差的原因,发展了一种适用于温度台阶边界条件的新型热流评估关系式。
从以上研究可以看出,针对嵌入式传感器“冷点效应”的研究工作相对较少,且主要针对低速和超声速流动。因此,本文采用数值模拟手段分析高超声速对流环境下嵌入式传感器冷点效应的形成机理和影响因素;针对某飞行试验热流预示结果低于圆箔式热流传感器实测结果这一现象,通过流场加热和传感器热响应计算,研究分析局部冷点效应导致热流测量偏差的机制,获得试验状态下的偏差量值。
1 计算方法流场数值计算采用CFD++软件,气体模型采用完全气体假设,对流格式采用二阶精度的低耗散TVD格式。来流进口、出口分别采用超声速入口边界条件和零梯度边界条件;壁面采用无滑移边界条件。采用六面体结构化网格,为保证热流计算精度,对壁面附近网格进行加密,壁面网格雷诺数小于10。
结构温度场计算采用通用有限元ABAQUS软件,材料的物性参数通过试验获取。
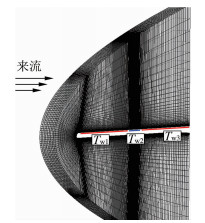
2 机理分析采用钝头-平板模型进行“冷点效应”数值模拟,计算模型和网格如图 1所示。以传感器中心为坐标原点O,-2.5mm≤x≤2.5mm为传感器表面,x<-2.5mm为传感器上游被测物体表面,x>2.5mm为传感器下游被测物体表面。
|
| 图 1 钝头-平板计算模型 Fig.1 Blunt plate calculation model |
平板壁面温度不连续,分别为Tw1、Tw2、Tw3,其中Tw2代表 5mm范围的低温区域(传感器端面直径为5mm,-2.5mm≤x≤2.5mm),用于表征真实高超声速飞行条件下高温热结构表面安装热流传感器时的壁面温度分布特点。
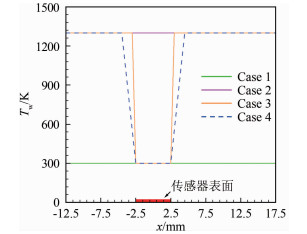
在静压p=287Pa、静温T=250K、速度v=5550m/s、迎角α=15°来流条件下,对表 1的4种壁温状态开展数值模拟(Case 4为考虑真实情况的被测物面与传感器表面之间温度渐变过渡),研究不同壁温条件下的壁面流动和加热规律。不同壁温边界条件如图 2所示。
| 状态 | Tw1/K | Tw2/K | Tw3/K | 备注 |
| Case 1 | 300 | 300 | 300 | 均匀 |
| Case 2 | 1300 | 1300 | 1300 | 均匀 |
| Case 3 | 1300 | 300 | 1300 | 间断 |
| Case 4 | 1300 | 300 | 1300 | 渐变 |
|
| 图 2 表面温度条件 Fig.2 Surface temperature conditions |
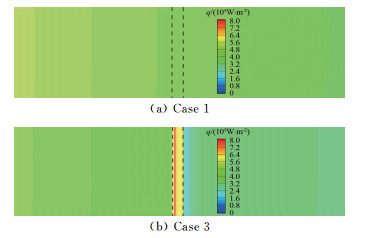
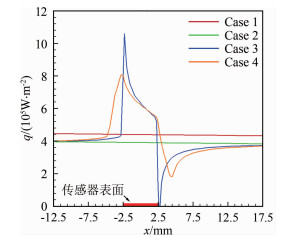
图 3给出了Case 1和3的表面热流分布,可以看出壁面温度直接影响表面热流,在局部低壁温区域,热流显著升高。传感器附近热流计算结果如图 4所示,可以看出:Case 1和2的传感器表面温度与被测物面相同,传感器表面热流也与被测物面热流相同;Case 3和4传感器表面温度低于被测物面温度,上下游被测物面的热流与相同壁温的Case 2接近,但是传感器与被测物体的间断处(上下游)热流骤变,传感器表面中心区热流也高于周围被测物面。
|
| 图 3 表面热流 Fig.3 Heat flux on the surface |
|
| 图 4 传感器及附近被测物体表面热流 Fig.4 Heat flux on the surface of sensor and in the vicinity of the measured object |
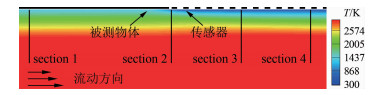
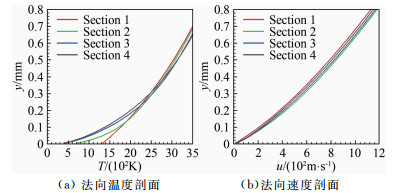
为分析“冷点效应”导致传感器表面热流增大的原因,图 5、6给出了传感器附近流场温度分布云图以及典型截面法向温度剖面和法向速度剖面(其中,Section 1位于传感器上游被测物体表面;Section 2位于被侧物体与传感器交界面;Section 3和4位于传感器表面)。可以看出:传感器局部低壁温影响了壁面的边界层流动,沿着流动方向,壁温变化对速度影响很小,但对温度影响较大。以法线方向距表面0.3mm处为界,大于该距离时,各截面法向温度梯度相近,小于该距离时,各截面法向温度梯度存在差异:Section 2的法向温度梯度最大,Section 3和4的法向温度梯度接近且小于Section 2,而Section 1的法向温度梯度最小,因此传感器表面热流高于较热的被测物面,冷热壁交界面处的传感器表面热流最高。由此可知:“冷点效应”本质是传感器上游的被测物面的高温热边界层对表面温度较低的传感器表面进行附加的加热,使得热流增大。
|
| 图 5 流场温度云图 Fig.5 Flow field temperature contour |
|
| 图 6 典型截面的法向温度和速度 Fig.6 Normal temperature profile and normal speed profile of each section |
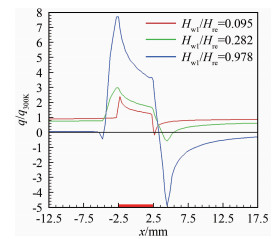
针对图 1的计算模型,研究Hw1/Hre的影响规律(Hw1、Hre分别为被测物体壁焓及其附近气流的恢复焓),Hw1/Hre分别取0.095、0.282、0.978,无量纲热流计算结果对比见图 7。可以看出:Hw1/Hre对传感器热流有较大影响,相同壁温条件下,Hw1/Hre越小(气流恢复焓越高),“冷点效应”越弱。
|
| 图 7 不同Hw1/Hre的表面无量纲热流计算结果对比 Fig.7 Comparison of non-dimensional heat flux calculation results for different values of Hw1/Hre |
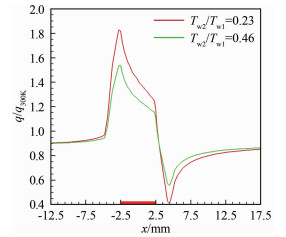
针对图 1的计算模型,研究壁温比Tw2/Tw1的影响规律。表面温度设置分别为:(1)Tw1=Tw3=1300K、Tw2=300K,Tw2/Tw1=0.23;(2)Tw1=Tw3=1300K、Tw2=600K,Tw2/Tw1=0.46。无量纲热流计算结果对比见图 8,可以看出:Tw2/Tw1比值越大,即传感器与被测物体表面温差越小,“冷点效应”越弱。
|
| 图 8 不同Tw2/Tw1的表面无量纲热流计算结果对比 Fig.8 Comparison of non-dimensional heat flux calculation results for different values of Tw2/Tw1 |
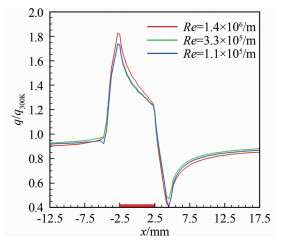
针对图 1的计算模型,研究来流雷诺数Re的影响规律。3个状态的来流单位雷诺数分别为1.4×106/m、3.3×105/m、1.1×105/m,Hw1/Hre和Tw2/Tw1相同。无量纲热流计算结果对比见图 9,可以看出:传感器表面无量纲热流变化不大,来流雷诺数对“冷点效应”的影响较小。
|
| 图 9 不同来流雷诺数下的表面无量纲热流计算结果对比 Fig.9 Comparison of non-dimensional heat flux calculation results for different Re of inflow |
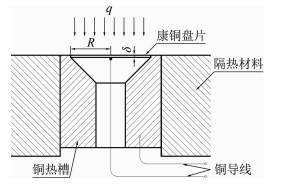
图 10为圆箔式热流传感器结构图。其原理是通过测量圆箔(康铜箔)中心的温度TO和周径上的温度Tc之间的温度差ΔT获得表面热流q[5]:
|
| 图 10 圆箔式热流传感器结构图 Fig.10 Schematic of circular foil heat flux sensor |
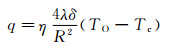 (1)
(1)
其中,圆箔厚度δ=6×10-5m,圆箔有效半径R=1×10-3m,导热系数λ=20.9×(1+0.0012ΔT)W/(m·K),η为修正系数,可通过标定获得。
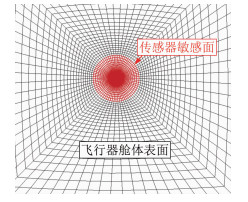
4.2 冷点效应影响研究在某高超声速飞行试验中,采用圆箔式热流传感器测量表面热流,测量过程中传感器表面温度显著低于其周围的飞行器表面温度,需要考虑“冷点效应”影响。计算模型为飞行器三维外形,传感器铜箔敏感端面直径5mm,计算模型局部表面网格如图 11所示。计算中,壁面温度采用飞行器表面和传感器敏感端面的实测温度。
|
| 图 11 计算模型局部表面网格 Fig.11 Local surface grid of model |
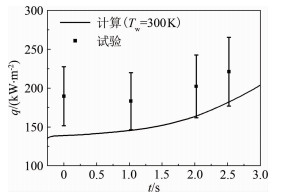
图 12给出了圆箔式热流传感器测量的热流数据与计算结果的对比(曲线为测量数据,黑点为计算结果)。传感器在工作过程中,通过自身的热沉吸热,飞行过程中传感器敏感端面的温升很小,热流测量数据为常温下的冷壁热流;气动热数值计算取等壁温300K。从图中结果对比可以看出,数值计算预示的热流比测量数据至少偏低20%。
|
| 图 12 传感器测量数据与计算结果对比 Fig.12 Comparison of sensor measurement data and calculation results |
针对来流压力p=79Pa、Ma=18的飞行状态,研究分析热流传感器测量数据与计算结果产生差异的原因。在该状态下,飞行器热结构表面温度的测量结果达到了1000K,传感器敏感端面温度约400K。
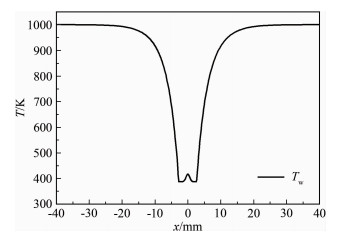
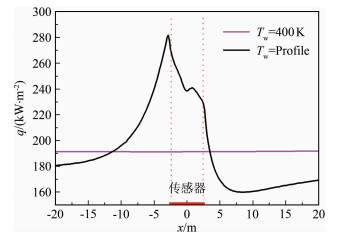
根据飞行试验来流条件,开展了400K均匀壁温以及图 13所示的变壁温分布条件(传感器局部低温)的表面热流计算。从图 14的计算结果可以看出:考虑冷点效应的传感器热流值(Tw=Profile)高于均匀壁温(Tw=400K)条件,热流比值区间为1.20~1.42。
|
| 图 13 被测物体与传感器的表面温度分布 Fig.13 Surface temperature distribution of measured object and sensor |
|
| 图 14 被测物体与传感器的表面热流分布 Fig.14 Heat flux distribution of measured object and sensor |
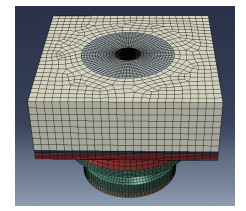
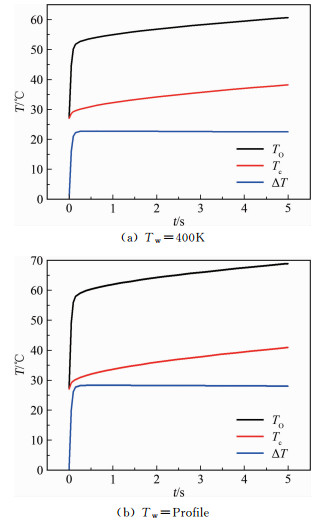
根据圆箔式热流传感器的结构和表面加热条件,建立如图 15所示的有限元分析模型开展温度场计算。分别以图 14所示的2个热流作为输入,计算传感器的温度响应,获得了传感器中心点温度TO和边缘点温度Tc的分布以及温差,结果如图 16所示。可以看出:在不考虑冷点效应和考虑冷点效应的情况下,圆箔式热流传感器的响应温差(TO-Tc)分别为22.5℃和28.0℃。
|
| 图 15 圆箔式热流传感器有限元分析模型 Fig.15 Finite element analysis model of circular foil heat flux sensor |
|
| 图 16 热流传感器响应温度和温差 Fig.16 Heat flux sensor response temperature and temperature difference |
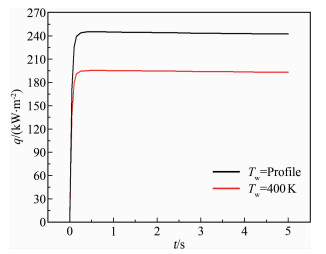
针对使用的传感器,采用500kW/m2热流对式(1)中的η进行标定,得到η=5/3。以式(1)进行热流计算,结果如图 17所示,Tw=400K表示均匀壁温、不考虑冷点效应,Tw=Profile表示考虑冷点效应,两者的热流分别为193和242kW/m2,比值约为1.25,可以看出:考虑冷点效应的影响后,理论复现了图 12中均匀壁温的热流预示结果比测量数据至少偏低20%这一现象。
|
| 图 17 热流传感器响应热流 Fig.17 Heat flux sensor response of heat flux |
(1) 在高超声速对流环境下,嵌入式热流传感器表面温度小于被测物体表面温度,会产生“冷点效应”,导致传感器上游的高温热边界层对传感器进行附加加热,使得传感器表面热流增大。
(2) 来流焓值越低、被测物体表面温度越高,“冷点效应”越明显;传感器与被测物体的表面温差越大,“冷点效应”越明显;来流雷诺数Re影响较小。
(3) 对飞行试验中圆箔式热流传感器的“冷点效应”开展了气动加热和传感器热响应计算分析,计算结果复现了均匀壁温的热流预示结果比传感器实测结果至少偏低20%的现象。
(4) 通过流场和传感器热响应仿真分析,表明“冷点效应”是导致飞行条件下圆箔式热流传感器测量结果偏高的重要原因。
| [1] |
中国科学院. 新型飞行器中的关键力学问题[M]. 北京: 科学出版社, 2008.
|
| [2] |
余平, 段毅, 尘军. 高超声速飞行的若干气动问题[J]. 航空学报, 2015, 36(1): 7-23. Yu P, Duan Y, Chen J. Some aerodynamic issues in hypersonic flight[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 7-23. |
| [3] |
James L D, Howard S C. Analysis of base pressure and base heating on a 5 degree half-angle cone in free flight near Mach 20(Reentry F)[R]. NASA-TM-X-2468, 1972.
|
| [4] |
Muylaert J, Cipollini F, Walpot L, et al. In flight research on real gas effects using the ESA EXPERT vehicles[R]. AIAA 2003-6981, 2003.
|
| [5] |
中国运载火箭技术研究院北京强度环境研究所. 结构热试验技术[M]. 北京: 宇航出版社, 2008.
|
| [6] |
丁小恒.高超声速飞行试验热流密度测量方法与装置研究[D].哈尔滨: 哈尔滨工业大学, 2017. Ding X H. Research on measuring method and device of heat flux in hypersonic flight test[D]. Harbin: Harbin Institute of Technology, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10213-1016739227.htm |
| [7] |
Rubesin M W. The effects of an arbitrary surface-temperature variation along a flat plate on the convective heat transfer in an incompressible turbulent boundary layer[R]. NACA-TN-2345, 1951.
|
| [8] |
Reynolds W C, Kays W M, Klein S J. Heat transfer in the turbulent incompressible boundary layer. Ⅱ-step wall-temperature distribution[R]. NASA Memo 12-2-58W, 1958.
|
| [9] |
Reynolds W C, Kays W M, Klein S J. A summary of experiments on turbulent heat transfer from a nonisothermal flat plate[J]. Journal of Heat Transfer, 1960, 82(4): 341-348. |
| [10] |
Conti R J. Heat-transfer measurements at Mach number of 2 in a turbulent boundary layer on a flat plate having a stepwise temperature distribution[R]. NASA-TN-D-159, 1959.
|
| [11] |
Hornbaker D R, Rall D L. Thermal perturbations caused by heat-flux transducers and their effect on the accuracy of heating-rate measurements[J]. ISA Transactions, 1964, 3(2): 123-130. |
| [12] |
Eckert E R G, Drake R M Jr. Analysis of heat and mass transfer[M]. 2nd ed. New York: McGraw-Hill, 1972.
|
| [13] |
Neumann R D. Thermal instrumentation: a state-of-the-art review[R]. WL-TR-96-2107, 1996.
|
| [14] |
Diller T E. Advances in heat flux measurements[J]. Advances in Heat Transfe, 1993, 23: 279-368. |
| [15] |
Kandula M, Reinarts T. Corrections for convective heat flux gauges subjected to a surface temperature discontinuity[R]. AIAA-2002-3087, 2002.
|
| [16] |
Mukerji D, Eaton J K, Moffat R J. Convective heat transfer near one-dimensional and two-dimensional wall temperature steps[J]. Journal of Heat Transfer, 2004, 126(2): 202-210. |



