火焰温度是燃烧过程中最重要的热力学参数之一,是对燃烧过程最直观的描述。火焰温度的精确测量对于了解火焰温度分布规律、探讨物理作用过程和化学反应机理、评估燃烧效率、了解燃烧过程有着十分重要的意义[1]。
发动机燃烧室的压强通常在0.2MPa以上,温度约为1000~3000K,且伴随有激波边界层干扰、混合边界层等现象。同时发动机燃烧试验条件极为苛刻,包括受限空间试验布局,受限空间引入的强杂散光干扰,超声速燃烧流场引起的高度湍流特性,燃烧室温度、压强分布的不均匀性等。这些因素导致发动机燃烧场的温度测量非常困难,亟需响应速度快、不干扰流场、高时空分辨率、高灵敏度和可消除杂散光干扰的燃烧场温度测量技术[2-3]。
目前,能够实现燃烧场二维温度测量的技术主要有平面激光诱导荧光技术和瑞利散射技术。平面激光诱导荧光技术通常采用双波长激发来获取燃烧场的温度信息[4-5],但在带压燃烧场环境下,分子间碰撞加剧,受碰撞淬灭的影响,荧光信号急剧下降,这给温度测量带来了极大的挑战。瑞利散射技术利用激光照射燃烧场获取瑞利散射信号来测量流场的温度,与平面激光诱导荧光技术不同,瑞利散射信号强度与气体的数密度成正比,在带压情况下,压强越高,瑞利散射信号越强,越容易实现高精度温度测量。然而,复杂的燃烧场测量环境会引入很强的杂散光(主要来自于米散射和背景散射),这会极大影响瑞利散射信号的信噪比,降低温度测量的精度[6-7]。
为消除杂散光干扰,通常采用窄带宽滤波片对信号光进行滤波处理,但由于瑞利散射光频率与杂散光频率基本相同,导致普通的窄带宽滤波片无法滤除大量的杂散光干扰。为此,20世纪90年代,Miles和Lempert[8]在传统瑞利散射技术的基础上,发展了一种用于流场诊断的滤波瑞利散射技术(FRS),通过在待测高温流场和探测器之间放置碘分子滤波池,实现了对杂散光的有效抑制,从而极大提高了瑞利散射信号的信噪比。因此,滤波瑞利散射技术一经提出,便受到国内外众多研究者的广泛关注。Forkey等[9]校正了碘分子滤波池的吸收模型;Hoffman等[10]在甲烷/空气火焰(含有轻微碳烟)中开展了二维温度测量;德国DLR研究所的Doll[11-12]和Schroll等[13]针对常压燃烧场和发动机燃烧场进行了二维温度定量测量研究;西北核技术研究所的王晟等[14]和中国空气动力研究与发展中心的郑尧邦等[15]也开展了常压燃烧场温度和密度测量的初步研究。综上所述,国内外关于FRS技术的研究主要是针对常压燃烧场温度的测量,关于带压燃烧场的温度测量工作较少。
因此,本文将滤波瑞利散射技术应用于高压火焰温度测量,针对高压平面层流火焰炉产生的带压燃烧场试验环境(1000~2000K,0.1~0.5MPa),开展了甲烷/空气预混火焰的二维温度分布测量实验研究。
1 基本原理当线宽很窄的一束激光投射到燃烧流场时,将伴随激光散射现象。通常,散射信号既包含气体分子引起的瑞利散射信号,也包含大量杂散光(来自米散射和背景散射)。如图 1所示,燃烧流场气体分子的瑞利散射,因其内部大量分子无规则的热运动,导致其谱线较入射激光有着明显的展宽。同时,对于不同的气体温度和压强,瑞利散射光谱线型也不同。但是对于杂散光,其频率和线宽均与入射激光相同,且信号较强,在燃烧场温度测量过程中属于干扰噪声。为减小杂散光的干扰,提高瑞利散射信号的信噪比,可通过在燃烧流场与探测器ICCD之间放置具有窄吸收峰的分子滤波池,并通过波长调谐技术,将窄线宽激光光源的输出波长调至滤波分子的吸收峰中心(如图 1所示),杂散光因与入射激光具有相同频率和线宽,并正好位于滤波分子的强吸收峰中心而被过滤掉;而燃烧场的瑞利散射光将部分透过吸收峰被ICCD所探测。不同的燃烧状态,所引起的瑞利散射谱线展宽不同,因此通过滤波池后,ICCD相机探测到的光强也不一样,根据滤波瑞利散射信号的强弱,可以反解出燃烧场的温度信息。

|
| 图 1 碘分子对激光散射信号吸收示意图 Fig.1 Schematic of iodine transmission profile convoluted with the molecular Rayleigh scattering spectral profile |
考虑激光能量以及实际燃烧场的其他物理量,ICCD探测到的滤波瑞利散射信号可以表示为:
 (1)
(1)
式中,C为校准常数,I0为入射激光强度,N为燃烧场的数密度,ω为激光的频率,χk和Mk为燃烧场中第k种分子的摩尔组分和质量,(∂σ/∂Ω)为瑞利散射截面,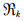
 (2)
(2)
式中, 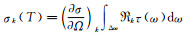
由式(2),根据燃烧条件及滤波分子透过率曲线的条件,可建立FRS相对强度与温度的对应关系S*-T曲线,将实验测得的FRS相对强度S*与理论计算的S*-T曲线比对,即可获得流场的温度信息。
2 实验装置简介 2.1 装置光路简介滤波瑞利散射温度测量装置主要由激光器、片光系统、能量波长监测系统、分子滤波池、同步时序控制器及ICCD相机组成。如图 2所示,激光器为种子注入Nd :YAG激光器,提供在532nm波长附近可调的窄线宽脉冲光源,激光器输出能量为400mJ,激光脉宽约10ns,波长选择为532.2185nm。激光器输出的激光经分束比约为24 :1的分束镜分成2束,能量低的一束进入能量波长监测系统,其中光电倍增管PMT(英国Sens-Tech公司生产,P30A-03)用于对激光输出能量监测,F-P干涉仪用于对激光波长漂移进行监测,实验时,通过对激光能量和波长的监测,可对探测到的滤波瑞利散射图像进行必要的修正;分束后,能量高的一束激光经过由柱面镜组组成的片光系统后,形成一片激光通过高压火焰炉观察窗照射高压燃烧火焰。

|
| 图 2 分子滤波瑞利散射温度测量光路示意图 Fig.2 Schematic of optical arrangement for FRS temperature measurements |
高压火焰炉如图 3(a)所示。该高压火焰炉可以实现压强0.1~1.0MPa之间连续可调,且压强控制精度为0.01MPa。同时,火焰炉为标准McKenna平面火焰炉(如图 3(b)所示),炉面尺寸为25mm,可通过调节炉内压力和CH4/空气比例,产生稳定的层流火焰。在火焰中心区域悬置热电偶用于火焰温度点测量,图 3(b)中的标记点A、B和C为实验中所用到的热电偶探测点,距离炉面的高度分别为hA=12.5mm,hB=17mm,hC=21.5mm。瑞利散射光收集成像装置如图 4所示,火焰的散射光经过一个碘分子滤波池(碘分子池的温度控制在52.3℃),实现对杂散光的过滤吸收后,被ICCD相机所探测。整个测量装置的同步时序控制由一台DG535实现。

|
| 图 3 (a) 高温高压火焰炉实物图;(b)McKenna火焰炉及其上方实验布局尺寸图 Fig.3 (a) Schematic of high temperature and pressure combustion burner; (b) The size of McKenna burner and the experiment layout |

|
| 图 4 瑞利散射光收集成像装置实物图 Fig.4 Schematic of Rayleigh scattering collecting and imaging system |
为建立FRS相对强度与温度的对应关系S*-T曲线,必须先获得不同温度和压强条件下瑞利-布里渊散射的光谱线型,进而获得不同温度和压强条件下瑞利散射信号经过滤波池后的光强透过率。
对于气体分子的瑞利-布里渊散射光谱线型,国外学者已开展了大量的深入研究,建立了许多物理模型和计算方法。其中,Tenti等[16]建立的S6模型因精度较高而被广泛使用,近年来Pan等[17]建立了S7模型,进一步提高了计算精度,其计算结果也得到了大量实验验证。本文采用S7模型,计算了不同温度、压强条件下,氮气分子的瑞利-布里渊散射光谱分布,依据式(2),建立了FRS相对强度与温度的对应关系S*-T曲线,如图 5所示。通过ICCD探测燃烧和未燃烧条件下的流场滤波瑞利散射信号,并依据S*-T曲线,即可得到燃烧火焰的二维温度分布结果。

|
| 图 5 不同压强下FRS相对强度与温度的对应关系 Fig.5 Normalized FRS signal versus flow temperature curve under different pressures |
为验证滤波瑞利散射测温装置对米散射和背景杂散光的抑制能力,按照图 2所示的光路,开展了滤波和未滤波条件下空气散射流动显示对比实验。在未添加碘分子滤波池的条件下,得到空气对入射片激光的散射图像,如图 6(a)所示。从图中可观察到很强的背景杂散光,如热电偶探针的反射光和平面火焰炉炉面的反射光,杂散光已经将瑞利散射信号全部掩盖,极大影响了探测到的瑞利散射信号的信噪比。在散射光收集光路中添加碘分子滤波池,并将入射激光波长调谐至图 1所示的吸收峰中心,获得滤波后的空气瑞利散射图像,如图 6(b)所示。可以看出,由平面火焰炉炉面和热电偶探针引起的背景杂散光几乎全部被过滤吸收掉,即系统有效实现了对杂散光的抑制,明显提高了瑞利散射信号图像的信噪比。

|
| 图 6 有/无滤波池条件的瑞利散射图像 Fig.6 Scattering images without and with the iodine filtering cell |
为进一步说明设计的滤波瑞利散射测温装置对杂散光的抑制能力,采用图 2所示光路得到了未燃条件、不同腔压下的瑞利散射信号值(图 6(b)中红色方框内的瑞利散射信号平均值),如图 7所示。由式(1)可知,瑞利散射信号强度值S与气体分子密度N成正比,而N=pV/RT,其中V为气体腔室体积,p为腔压,R为理想气体常数,T为腔内气体温度,故S∝p。由图 7中的线性拟合公式S=657704.9p+1662.9可知,由杂散光干扰引起的截距项仅为1662.9,小于总信号强度的3%,说明设计的滤波瑞利散射测温装置具有较好的背景杂散光抑制能力。其次,利用滤波瑞利散射测温装置在高压火焰炉上开展了预混燃烧火焰温度测量实验。带压燃烧实验参数如表 1所示,测量区域片激光的厚度约0.5mm,宽度约25mm,激光下边缘距炉面约8mm(如图 3(b)所示)。

|
| 图 7 ICCD相机测得的瑞利散射信号强度S(20幅累加)与腔体压强p的关系 Fig.7 The relation between the Rayleigh scattering signal S and the chamber pressure p |
| p/MPa | QCH4/SLM | QAir/SLM | φ | vpremixed/(cm·s-1) | |
| Case 1 | 0.11 | 0.6 | 4.8 | 1.19 | 16.67 |
| Case 2 | 0.30 | 0.6 | 4.8 | 1.19 | 6.11 |
| Case 3 | 0.50 | 0.6 | 4.8 | 1.19 | 3.67 |
图 8(a)显示了瞬态火焰和50幅火焰图像累加的温度场分布平均结果。可以看出,随着高压火焰炉腔内压强的增加,火焰形状变得尖锐,火焰截面变窄。这是因为当甲烷和空气的预混气体流量不变时,随着腔压的升高,单位时间内通过的预混气体体积减小(V=NRT/p),预混气体的出射速度v减小(v=V/Θ,V为单位时间内通过的气流体积,Θ为截面积),进而火焰形状变得尖锐,火焰面变窄。同时,为了对比不同压强下的滤波瑞利散射技术温度测量的相对不确定度,图 8(b)对比了火焰炉上方1.5cm且平行炉面处的瞬态瑞利散射温度分布曲线。由图可知:0.11MPa时的温度测量相对不确定度约在15%以内,0.30MPa时约在10%以内,而0.50MPa时约在7%以内。这是因为随着腔压的升高,瑞利散射信号强度增大,瑞利散射图像的信噪比增强,造成温度测量相对不确定度减小。最后,为了验证滤波瑞利散射技术的温度测量精度,分别在A、B和C点(如图 3(b)和8(a)所示)进行了热电偶温度点测量,并将热电偶测量结果与滤波瑞利散射测温装置得到的结果(50幅平均)进行对比,如图 8(c)所示。由图可知,2种测量方法均可得到:火焰距离炉面的高度越高,温度越低,这是因为火焰在向上传播时会有热损失,从而导致温度变低;压强越高,相同位置处的温度越低,这是因为当预混燃气(甲烷/空气)的总量不变时,压强越高,预混燃气向上的速度越低,从而导致层流火焰面整体向下偏移。此外,对于距离炉面较近的探测点A来说,滤波瑞利散射温度测量结果和热电偶测量结果偏差在10%以内(不同压强)。而随着探测点距离炉面高度的增加,2种测量方法之间的偏差逐渐增大,且腔压越高,偏差越大,尤其是对于腔压为0.50MPa中的探测点C来说,2种方法得到的温度值最大偏差达到18%。这是因为随着探测点距离炉面的高度的增加,燃气气流的速度减小,受热传递的影响,上方火焰出现扰动(由图 9可以看出,不同时间的火焰形状不同),进而导致2种测量方法得到的温度偏差增大。

|
| 图 8 (a) 经滤波瑞利散射技术得到的火焰温度分布图像;(b)不同腔压下,火焰炉上方1.5cm处的火焰温度分布图; (c)不同探测位置处,热电偶和FRS (50幅平均)温度测量结果 Fig.8 (a) Images of combustion temperature distribution by the FRS technique; (b) Distribution of combustion temperature at the height (1.5cm) above the burner; (c) Comparison of the temperature results between the FRS technique and the thermocouple |

|
| 图 9 腔压p=0.50MPa时,不同时间下的火焰瑞利散射信号分布图像 Fig.9 Images of combustion Rayleigh scattering signal distribution with the chamber pressure p=0.50MPa, at different times |
本文基于滤波瑞利散射原理技术,以大功率窄线宽Nd :YAG脉冲激光器为光源,以碘分子滤波池为背景光抑制器件,以ICCD相机为图像采集设备,设计了一套滤波瑞利散射温度测量装置,并利用该装置在高压火焰炉上开展了不同压强条件下甲烷/空气预混火焰温度场诊断实验。结果表明:
(1) 滤波瑞利散射测温技术能有效抑制受限空间引入的背景杂散光干扰;
(2) 滤波瑞利散射测温技术能够获得带压条件下的瞬态燃烧场温度分布结果,且温度测量的相对不确定度优于15%;
(3) 通过与热电偶温度测量实验的结果进行对比,两者的偏差约为10%,验证了滤波瑞利散射技术具备带压燃烧场温度的非接触测量能力。
本文工作对实现受限空间、带压条件下的燃烧场温度分布定量测量具有参考意义,下一步计划将FRS技术应用于内燃机燃烧场和超燃冲压燃烧场温度分布定量测量实验。
| [1] |
Liu J R, Hu Z Y, Zhang Z R. Laser spectroscopy applied to combustion diagnostics[J]. Optics and Precision Engineering, 2011, 19(2): 284-296. DOI:10.3788/OPE.20111902.0284 |
| [2] |
Fourguette D C, Zurni R M, Long M B. Two dimensional Rayleigh thermometry in a turbulent nonpremixed Methane-Hydrogen flame[J]. Combustion Science Technology, 1986, 44(30): 307-317. |
| [3] |
俞刚, 范学军. 超声速燃烧与高超声速推进[J]. 力学进展, 2013, 43(5): 449-454. Yu G, Fan X J. Supersonic combustion and hypersonic propul-sion[J]. Progress in Mechanics, 2013, 43(5): 449-454. |
| [4] |
McMillin B K, Palmer J L, Seitzman J M, et al. Two line instantaneous temperature imaging of NO in a scramjet model flow-field[R]. AIAA-93-0044, 1993.
|
| [5] |
Seitzman J M, Palmer J L, Antonio A L. Instantaneous planar thermometry of shock-heated flows using PLIF of OH[R]. AIAA-93-0802, 1993.
|
| [6] |
Elliott G S, Glumac N. Molecular filtered Rayleigh scattering applied to combustion turbulence[R]. AIAA-99-0643, 1999.
|
| [7] |
Elliott G S, Glumac N, Carter C D. Molecular filtered Rayleigh scattering applied to combustion[J]. Measurement Science and Technology, 2001, 12(4): 452-466. DOI:10.1088/0957-0233/12/4/309 |
| [8] |
Miles R B, Lempert W R. Two-dimensional measurement of density, velocity, and temperature in turbulent high-speed air flows by UV Rayleigh scattering[J]. Applied Physics B, 1990, 51(4): 1-7. |
| [9] |
Forkey J N, Lempert W R, Miles R B. Corrected and calibrated I2 absorption model at frequency-doubled Nd:YAG laser wavelengths[J]. Applied Optics, 1997, 36(27): 6729-6738. DOI:10.1364/AO.36.006729 |
| [10] |
Hoffman D, Munch K U, Leipertz A. Two-dimensional temperature determination in sooting flames by filtered Rayleigh scattering[J]. Opt Lett, 1996, 21(7): 525-527. DOI:10.1364/OL.21.000525 |
| [11] |
Doll U, Fischer M, Stockhausen G, et al. Frequency scanning filtered Rayleigh scattering in combustion experiments[C]//Proc of the 16th International Symposium on Applications of Laser Techniques to Fluid Mechanics. 2012.
|
| [12] |
Doll U, Stockhausen G, Willert C. Pressure, temperature, and three-component velocity fields by filtered Rayleigh scattering velocimetry[J]. Optical Letter, 2017, 42(19): 3773-3776. DOI:10.1364/OL.42.003773 |
| [13] |
Schroll M, Doll U, Stockhausen G, et al. Flow field characterization at the outlet of a lean burn single-sector combustor by laser-optical methods[J]. Journal of Engineering for Gas Turbines and Power, 2017, 139(6): 011503. |
| [14] |
王晟, 刘晶儒, 胡志云, 等. 用于燃烧场诊断的分子滤波瑞利散射技术[J]. 光学精密工程, 2011, 19(2): 445-461. Wang S, Liu J R, Hu Z Y, et al. Development of filtered Rayleigh scattering for combustion diagnostic application[J]. Optics and Precision Engineering, 2011, 19(2): 445-461. |
| [15] |
郑尧邦, 陈力, 苏铁, 等.滤波瑞利散射测温技术研究[C]//中国空气动力学会测控技术专委会学术交流会论文集. 2013. Zheng Y B, Chen L, Su T, et al. Study on the temperature measurement by filtered ray-leigh scattering[C]//Proc of Academic Exchange Meeting of China Aerodynamic Society Measurement and Control Technical Committee. 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=8056120 |
| [16] |
Tenti G, Boley C D, Desai R C. On the kinetic model description of Rayleigh-Brillouin scattering from molecular gases[J]. Canadian Journal of Physics, 1974, 52(2): 285-290. |
| [17] |
Pan X, Shneider M N, Miles R B. Coherent Rayleigh-Brillouin scattering in molecular gases[J]. Physical Review A, 2004, 69(3): 33814-33822. DOI:10.1103/PhysRevA.69.033814 |



