发动机小型强化技术被认为是最有前途的点燃式(Spark Ignition,SI)发动机节能减排技术措施之一[1]。然而,小型强化SI发动机热负荷的增加,导致在其燃烧过程中更容易发生爆震(Knock)[2]、超级爆震(Super-Knock)[3-4]等不正常燃烧现象,限制了小型强化SI发动机热效率进一步提升。目前爆震产生的机理尚不明确,末端气体自燃理论由于很好地解释了光学实验的结果而得到广泛的认可。Bäuerle [5]采用激光诱导荧光(Laser Induced Fluorescence,LIF)的方法检测到内燃机末端气体的热点自燃并提出热点的自燃分为诱发、起燃和传播3个阶段。Kawahara[6]在氢气燃料压缩膨胀机上通过高速摄像方法观测到爆震过程中的自燃和压力波,并提出爆震强度与末端气体数量相关。与此不同,超级爆震是由“热点”(Hot spot)先于火花点火自燃诱发的异常燃烧现象。Zahdeh[7]与Zaccardi[8]等通过内窥镜观测到了燃烧室内先于火花点火形成的“热点”,并根据形成位置及分布排除了排气门及火花塞电极等高温表面点火的可能。润滑油被认为是形成低速早燃“热点”的可能物质之一,被稀释后的润滑油通过活塞环岸积累并窜入到燃烧室内发生蒸发和氧化,最终在火花点火之前发生自燃[9],自燃后产生的火焰和压力突变在传播过程中诱导末端未燃混合气再次发生自燃,并产生具有强压力间断的爆轰波[10-11],引发燃烧峰值压力高达30MPa、压力振荡幅值超过20MPa的超级爆震[12]。综上所述,无论是常规爆震还是超级爆震,本质特征都是未燃混合气发生自燃,自燃后的湍流火焰-压力波相互作用最终导致了剧烈的压力振荡。对湍流火焰-压力波相互作用的相关研究是揭示爆震、超级爆震等非正常燃烧现象产生机理的关键。
从压力波的产生机理来看,湍流火焰在传播过程中不断加速,压缩前方未燃混合气形成压缩波,最终压缩波互相叠加形成强压力间断面。因此,研究火焰加速产生压力波的过程是火焰-压力波相互作用研究的基础性前提。近年来, 相关学者从实验、理论和数值模拟等角度出发,开展了大量有关火焰加速过程及其机理的研究,其中光滑管和阻塞管均有所涉及[13-23]。Shchelkin等[24]首次对光滑管内的火焰加速做出解释,指出已燃气体的热膨胀在未燃混合气中产生了流动并形成湍流,流动的不均匀又进一步造成火焰表面褶皱进而导致火焰加速。在此基础上,Zeldovich等[25]进一步展开对光滑管内火焰加速过程的探究,提出火焰锋面与上游不均匀的速度场相互作用导致火焰锋面延展,这是导致火焰加速的主要原因,而湍流在火焰加速过程中只起到次要作用。根据Ciccarelli和Dorofeev[13]对火焰加速过程的综述研究,层流火焰的光滑表面在发展过程中会受到水力学不稳定性(Darrieus-Landau instability)和热扩散不稳定性(Thermal-Diffusion instability)的作用而产生褶皱,进而导致胞状火焰的形成,增加火焰表面积。相比于光滑管而言,阻塞管中所设立的障碍物能在更大程度上促进湍流的形成和实现火焰加速[26-31]。Bychkov等[32]提出由于障碍物的存在,在火焰传播过程中会产生射流,射流会驱使火焰不断加速。Petchenko等[33]基于障碍物封闭管道对火焰传播过程进行了数值模拟,结果表明在强烈的Rayleigh-Taylor不稳定性作用下,声波/压力波的波动会使火焰锋面产生很大程度的褶皱。除了Kelvin-Helmholtz不稳定性对火焰-压力波相互作用有影响之外,Richtmyer-Meshkov不稳定性也会使火焰-压力波相互作用对火焰锋面产生扰动并提高能量释放率[34]。肖华华等[35-36]发现火焰在传播过程中会与侧壁面作用产生压力波,火焰与压力波或声波的相互作用会导致火焰锋面周期性振荡以及形成不同的火焰结构。
上述研究从探究火焰加速机理的角度出发,揭示了火焰加速的本质。在此基础上,相关学者对火焰加速过程的影响因素进行了探究,指出在不同发展阶段火焰加速的影响因素也有所不同。Johansen等[19]指出在阻塞管内火焰发展的初始阶段,火焰传播速度低于反应物声速时,火焰加速强度与障碍物的阻塞比表现出强烈的相关性。在这一阶段,阻塞比的增大会导致湍流更加强烈,火焰表面积增大也会使体积燃烧速率升高,从而促进火焰加速。Ciccarelli等[13]则提出随着火焰继续向前发展,火焰加速后期主要受到火焰-压力波相互作用的影响,这一相互作用过程引发了Richtmyer-Meshkov不稳定性并伴随有气流收缩,造成火焰焰舌速度的波动。Valiev等[37]在研究中指出气体压缩作用也会降低火焰加速速率以及火焰焰舌速度峰值,在燃烧的早期阶段抑制了指状火焰的加速过程。他们还指出粘度、湍流以及障碍物几何结构也是影响火焰加速的重要因素。然而, 目前火焰过障碍物加速的机理仍不完善,气流在火焰加速过程中的作用仍值得深入探讨。
本文基于自主设计的定容燃烧弹,采用高速纹影技术捕捉火焰过孔板加速的全过程,探索火焰过孔板加速的机理;通过三维数值模拟方法,研究气流在火焰加速过程中的作用。此外,通过对实验和模拟结果对比,讨论了初始压力对火焰过孔板加速的影响。
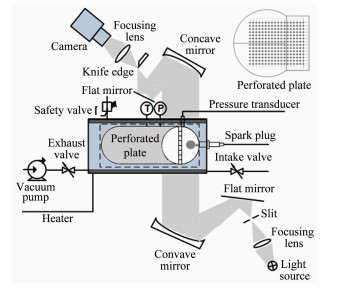
1 实验装置及仿真方法 1.1 光学定容燃烧弹实验平台整个实验系统包括定容燃烧弹本体、高速纹影摄像系统、燃烧压力采集系统、温度控制系统、进排气系统、高压点火系统和同步控制系统,如图 1所示。定容燃烧弹的燃烧室为圆柱形的腔体,长度230mm,直径100mm,容积2.32 L,弹体可承受极限压力为10MPa。在燃烧室的前后壁面分别安装直径80mm的圆形石英玻璃视窗。孔板为3mm厚的钢板,表面分布有不同孔径的圆孔。Kistler 6113B型缸压传感器安装于燃烧室上壁面,缸压采集频率为70000Hz。Z字型布置的高速纹影系统用于捕捉火焰和冲击波,高速相机的采样频率最高为210000帧/s。但是,相机的采样频率越高,采样区域越小,为捕捉火焰过孔板加速的全过程,本次研究采用的采样频率为90000帧/s。定容燃烧弹的上下壁面分别安装有1000W的加热板,使整个弹体加热到373K,防止燃烧产物中的水蒸气冷凝成液滴,影响相机拍摄。
|
| 图 1 实现火焰-冲击波相互作用的可视化定容燃烧弹 Fig.1 Schematic diagram of the experimental setup for the observation of flame acceleration |
本研究选用化学当量比的氢气-空气混合气作为测试燃料,并通过道尔顿分压定律确定氢气和空气的配比。实验开始前先将燃烧室抽真空,之后依次充入氢气和空气,待静止2min后,同步触发点火、图像和缸压采集。实验条件如表 1所示。
| 实验条件 | 数值 |
| 孔板孔径/mm | 2,5 |
| 孔板孔隙率/% | 12 |
| 初始温度/K | 362±3 |
| 初始压力/MPa | 0.1, 0.2, 0.3, 0.4, 0.5 |
| 当量比 | 1 |
使用美国Converge Science公司开发的计算流体力学软件Converge进行定容燃烧弹三维模型计算,如图 2所示。本模型使用的网格初始边长为4mm。模拟过程中,点火区域在0~1ms的过程中经过了4层16倍的固定加密;点火阶段,火焰前锋的网格边长为0.125mm。在孔板及其左右3mm, 也进行了4层16倍的固定加密。此外,在整个火焰传播过程中,根据当地温度和H2、OH浓度对当地网格进行了最大4层16倍的动态自适应加密(Adaptive Mesh Refinement,AMR)。此举可以保证火焰在层流传播、射流传播以及湍流传播3个阶段的锋前网格尺寸为0.250mm。最后的结果显示,在燃烧过程中,整个模型网格的数量在600~1000万之间, 时间步长在1×10-8~1×10-6s之间。

|
| 图 2 定容燃烧弹几何模型 Fig.2 Geometric model for simulation |
考虑到实际所用定容弹的主体结构为圆柱体,为减小模拟复杂度,使用三维建模软件Pro/E所搭建的圆柱模型近似模拟实验所用的定容弹弹体(如图 2所示),其总长230mm,直径100mm。孔板的模拟也依据实验中所用孔板完成,在图 2中用断面处的小圆柱体表示。对于不同孔径和不同位置的孔板,表现为模型中断处小圆柱体的个数及直径有所不同,到壁面的距离也有所改变。通过在UDF里添加监测点来实现对压力的监测。模拟中,监测点的位置与实验台架压力传感器的位置保持一致并紧贴壁面。模拟火焰在定容燃烧弹中加速时,为了更好地模拟壁面散热,采用了O′Rourke和Amsden模型,该模型能准确地模拟出热量经壁面传播散发的物理过程。由于燃烧进行的速度很快,壁面散热对燃烧造成的影响较小,所以壁面采用恒温模型。此外,本研究中采用大涡模拟(Large Eddy Simulation,LES)方法,即对大尺度涡团直接进行求解,对小尺度涡团则先建立亚网格模型再求解。在Converge三维数值模拟方法中,有2种亚网格模型,分别是零方程模型和一方程模型。零方程模型对于射流、混合层、边界层等的流动比较简单有效,但是其忽略了对流和扩散的影响,而一方程模型则弥补了这一缺点。本研究中选用了由Yoshizawa[38]和Menon[39]提出的一方程粘性模型。
燃烧模型方面,湍流火焰燃烧通过G方程来捕捉,其中层流火焰速度通过Gülder方程预测。本文采用将G方程和详细化学反应机理模型SAGE结合的方法来模拟火焰传播。使用G方程判定火焰面位置,并用化学平衡法计算火焰面处的反应,而在火焰内部和外部采用SAGE求解详细化学反应机理。其中,SAGE采用CVODES方法(求解常微分方程的初始值问题)求解给定的化学反应机理中每一个单元反应的反应速率,并与输运方程相耦合,可模拟宽泛的燃烧状态,包括点火、预混燃烧和非层流燃烧。需要注意的是,采用CVODES方法时,模型的求解精度与化学反应机理直接相关。在化学反应动力学机理方面,采用了包含5元素10组分21反应的详细反应机理。其中5个元素为C、H、O、N、Ar,10个组分为:H、H2、O、O2、OH、H2O、N2、HO2、H2O2、Ar。
内燃机缸内流体运动数值的模拟由质量、动量和能量守恒方程以及组分输运方程控制,控制方程如下所示:
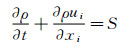 (1)
(1)
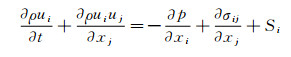 (2)
(2)
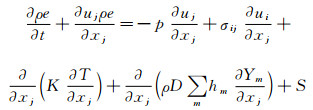 (3)
(3)
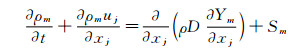 (4)
(4)
其中,u是速度,ρ是密度,S是源项,p是压力,σij为粘性应力张量,Ym是组分m的质量分数,D是质量扩散系数,e是比内能,K是导热率,hm是组分m的焓值,T是温度。
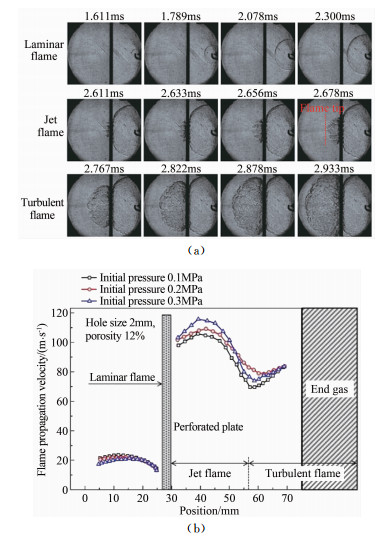
2 火焰过孔板加速 2.1 火焰过孔板加速过程图 3(a)为初始压力0.2MPa、孔板孔径2mm下火焰过孔板过程的一系列纹影图片;图 3(b)为孔板孔径2 mm、初始压力0.1、0.2和0.3MPa下火焰传播速度的变化曲线。如图 3(a)所示,本文中火焰传播速度是基于火焰前锋位移对时间的微分计算所得。
|
| 图 3 (a) 火焰过孔板加速过程;(b)火焰过孔板加速过程的速度曲线 Fig.3 (a) Chronological schlieren images of flame acceleration passing through the perforated plate; (b) Evolution of the flame tip velocity |
如图 3所示,依据火焰传播形态与速度,将封闭空间中火焰过孔板的加速过程分为3个阶段:层流火焰阶段、射流火焰阶段和湍流火焰阶段。
层流火焰阶段:在火花塞跳火之后,火焰呈球状向前传播,表面光滑。此后,由于受到水力学不稳定性和热扩散不稳定性的影响,光滑的球形层流火焰表面出现胞状结构[7]。在层流火焰阶段,火焰传播速度较低,约为20m/s左右,表现为先上升后下降的趋势。在火焰发展初期,由于出现胞状结构,导致火焰锋面面积增加,火焰传播速度略微增加。值得注意的是,本次实验采用化学当量比的氢气-空气混合气,其Effective Lewis Number约为1,因此在层流火焰发展过程中,水力学不稳定性的作用会大于热扩散不稳定性。后期火焰传播速度下降是由于燃烧膨胀流场受到孔板阻碍作用的结果。如图 3(b)所示,对比不同初始压力下的层流火焰传播速度,发现在层流燃烧阶段,火焰传播速度与初始压力呈负相关。
射流燃烧阶段:在2.611ms,层流火焰穿过孔板并被孔板分割成数股射流火焰。过孔板后,火焰传播速度迅速从16m/s上升至100m/s,增加约一个数量级。随着射流火焰的发展,火焰传播速度进一步升高,直至在距离火花塞约40mm处达到某一速度峰值,此后火焰传播速度开始急剧下降。火焰过障碍物加速一直是一个热点问题,并得到了广泛研究。根据Bychkov的理论,在火焰过孔板加速的过程中,膨胀流场过孔板产生的射流驱动了火焰的加速。在过孔板前,膨胀流场沿火焰锋面法向向四周传播,当气流穿过孔板之后,其传播方向汇聚为一(与燃烧室轴线方向平行),进而形成一股速度极高的强射流。火焰受到该强射流的驱动,传播速度急剧增加。穿过孔板后,层流火焰被孔板分割成多束细小的火焰,使得火焰表面积增加,化学反应速率加快;此外,当火焰在障碍物空间传播时,Rayleigh-Taylor不稳定性和Kelvin-Helmholtz不稳定性诱导了湍流的产生,使得火焰表面褶皱更加剧烈,表面分裂为更小的胞状结构,进一步促进燃烧速率的加快[20, 40]。
湍流火焰阶段:在2.767ms,多股射流火焰汇聚成一束湍流火焰,并在自加速机理的影响下,火焰传播速度逐渐升高。如图 3(b)所示,过孔板之后,火焰传播速度随着初始压力的增加而升高,与Chaudhuri等[41]对预混火焰爆炸的研究结果一致。
2.2 火焰过孔板加速过程中的流场分析本研究中高速纹影摄像技术只能识别并拍摄密度梯度较大的射流现象,而无法拍摄到整个燃烧室内的其他流动。因此,为了获得更多关于气流速度的信息,通过三维数值模拟对火焰过孔板过程中火焰和气流的传播展开探究。
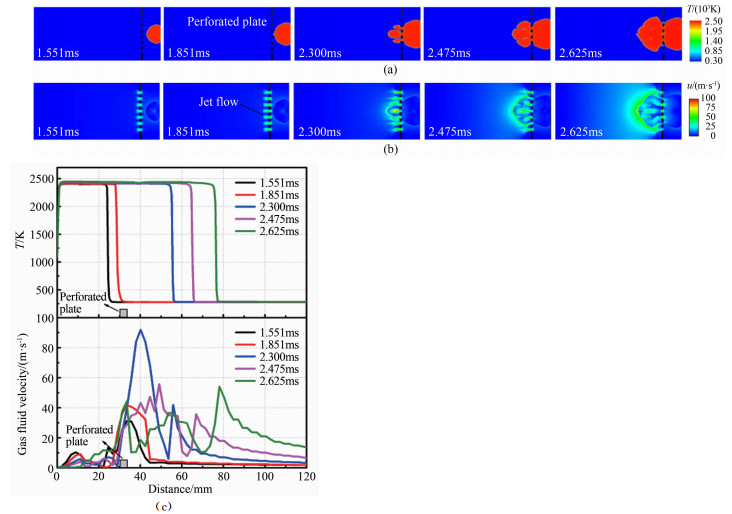
图 4(a)和(b)分别为温度和速度的分布云图;图 4(c)所示则为燃烧室中心线上温度及速度的变化曲线。以火花塞为起点延长120mm作为研究范围,依据火焰过孔板加速过程选择5个时刻展开分析,分别为1.551、1.851、2.300、2.475和2.625ms。图 4(a)中,依据温度变化可以看出红色部分即为火焰。如图 4(b)所示,由于孔板的节流作用,可以明显观察到孔板后产生了强烈的射流现象。如图 4(c)所示,在1.551和1.851ms时刻,从温度变化曲线可以看出火焰尚未穿过孔板,而在孔板附近可以观察到明显的气流速度峰值,表明此时射流已经产生,并驱使火焰过孔板加速;在2.300、2.475和2.625ms时刻,火焰穿过孔板且火焰锋面超过射流,此时可以观察到火焰锋前的气流速度随着与火焰锋面距离的增加而降低,表明该阶段下火焰不再受射流的驱动,相反,未燃区的气体流动是在火焰锋面的推动下而运动的。
|
| 图 4 初始压力0.3MPa下火焰过孔板加速过程中的(a)温度分布;(b)流场分布; (c)速度分布 Fig.4 Distribution of (a) temperature, (b) flow and (c) velocity when flame passes through the perforated plate under initial pressure of 0.3MPa |
火焰在燃烧室中的加速传播是不同因素综合影响下的结果。强烈的射流驱使火焰过孔板加速,而当射流火焰超过射流时,气体动力学对火焰传播的影响则不再占据主导地位,此时湍流燃烧理论对火焰传播起主要作用。湍流火焰传播会受到火焰-声波/压力波相互作用、Richtmyer-Meshkov不稳定性和湍流自加速的影响。根据湍流燃烧理论,当火焰与声波/压力波发生相互作用时,在Richtmyer-Meshkov不稳定性的作用下火焰表面积增加,促进了湍流火焰传播。
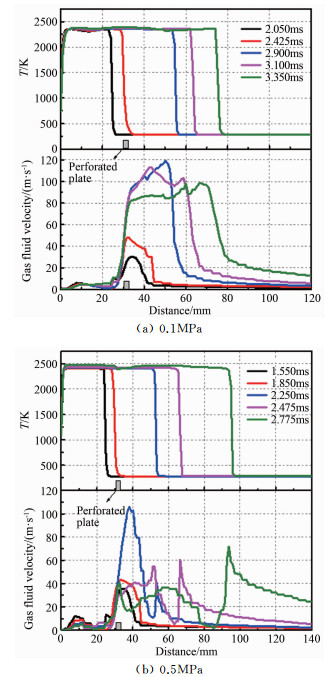
按照图 4的处理方法,绘制初始压力0.1和0.5MPa下燃烧室轴线上的温度和速度变化情况,如图 5所示。分析0.1和0.5MPa下的速度分布情况,可以得到与0.3MPa下相同的结论。在火焰未穿过孔板之前,可以观察到孔板附近有较高速度的强射流存在;当火焰接近孔板时,在该强射流的驱动下,火焰传播速度急剧增加。而当火焰穿过孔板之后,可以观察到未燃气体区域的流场是在火焰的推动下而运动的,射流对火焰发展不再起作用。纵向对比0.1、0.3和0.5MPa的情况,可以发现燃烧温度随着初始压力的升高而略有升高,同样的,过孔板之后火焰锋面的传播速度也随着初始压力的升高而增加。有意思的是,在0.1MPa下发现,当火焰过孔板之后,已燃气体区域的速度远高于火焰锋面处的速度,而在0.3和0.5MPa下,已燃区的速度在靠近锋面时已经开始衰减,火焰锋面处的速度是整个燃烧室中的最高速度。
|
| 图 5 初始压力0.1和0.5MPa下燃烧室中轴线的温度、速度变化 Fig.5 Distribution of temperature and velocity under initial pressure of 0.1 and 0.5MPa |
图 6所示为初始压力分别为0.1、0.3和0.5MPa下封闭空间中火焰加速过程的实验结果和数值模拟结果,其中彩色图片代表实验结果,黑白图片表示数值模拟结果。如图 6所示,第一排是过孔板前层流阶段的火焰传播对比图,第二排是过孔板后射流和湍流阶段的火焰传播对比图。需要指出的是,图 6中所标注的时间为分别将层流和湍流阶段的第一张图片作为起始时刻下的相对时间。将实验与数值模拟的火焰传播图片截取为相同的尺寸并保证孔板位置对齐,确保火焰锋面位置进行对比时的准确性。

|
| 图 6 初始压力0.1、0.3和0.5MPa下火焰过孔板加速的实验和数值模拟结果(彩色图片为实验结果,黑白图片为数值模拟结果) Fig.6 Comparison of combustion evolution between experiment and simulation under initial pressure of 0.1, 0.3 and 0.5MPa |
对比实验与数值模拟的结果,可以发现随着初始压力由低到高,火焰在过孔板前后的发展趋势、结构形态和传播速度上均呈现出高度的一致性。就火焰的发展趋势而言,数值模拟结果与实验结果一致,表现为层流火焰、射流火焰和湍流火焰3个发展阶段。就结构形态而言,过孔板前的层流火焰阶段,火焰表面呈现出球型结构,并在靠近孔板时受到射流的影响在火焰锋面最前方形成了一种近似毛细现象的突起。观察实验结果发现,在层流燃烧阶段火焰表面出现胞状结构,这是火焰受水力学不稳定性和热扩散不稳定性的作用而产生的[7]。而在模拟图片中则未观察到该现象,这是因为目前使用的LES方法无法对如此小尺度的结构做到精确的模拟,而继续细化网格在LES中对于模拟胞状结构而言收益较小。如果需要模拟出这种微观结构,直接数值模拟DNS是一种更好的选择。射流和湍流火焰阶段,球形层流火焰锋面最前方首先穿过孔板形成1束射流火焰,随着火焰向前发展,考虑到不同初始压力下孔板孔径均为5mm,孔板上孔数及孔的分布是固定的,因此可以看到不同初始压力下均形成3束射流火焰并最终发展合并为湍流火焰。注意到在湍流火焰阶段,数值模拟图片中可以明显观察到火焰表面出现褶皱,尽管与实验结果相比褶皱程度较低。就火焰传播速度而言,可以发现无论是层流还是湍流阶段,在经过相同或相近的时间间隔之后实验和数值模拟图片中的火焰锋面位置仍能保持接近,误差不到5%,考虑到数值模拟时许多参数设置的局限性,可认为此误差在正常范围内。这说明本次模拟的火焰传播速度与实验结果呈现出较高的一致性。
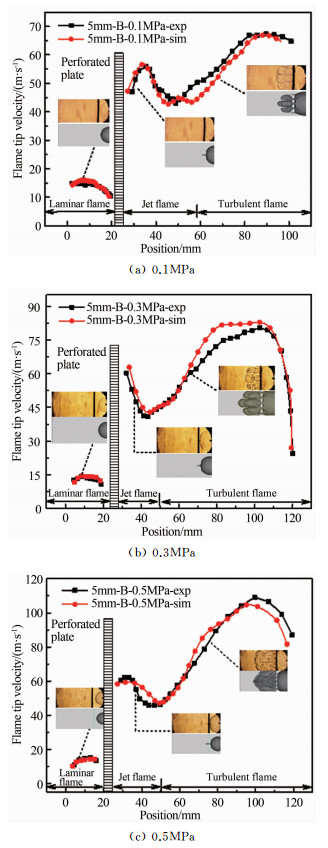
图 7所示为初始压力分别为0.1、0.3和0.5MPa下封闭空间中火焰加速过程的实验与数值模拟的速度曲线,其中黑色曲线表示实验得到的火焰传播速度,红色曲线表示数值模拟的火焰传播速度。可以看出,在不同的初始压力下,实验与数值模拟的火焰传播速度曲线在发展趋势和数值上都呈现出较高的一致性。
|
| 图 7 初始压力0.1、0.3和0.5MPa下火焰传播速度的实验和数值模拟结果 Fig.7 Comparison of flame tip velocity between experiment and simulation under initial pressure of 0.1, 0.3, 0.5MPa |
在层流火焰阶段,无论是哪一初始压力,实验和数值模拟的火焰传播速度在数值和发展趋势上都极为接近,前期均表现为上升趋势,靠近孔板时受到孔板的阻碍作用开始下降。初始压力为0.3MPa下,火焰过孔板后表现出“V”字型的变化趋势,初始压力为0.1和0.5MPa下的火焰过孔板后则表现出“S”型变化趋势。在火焰速度达到峰值之后,由于射流作用减弱,火焰传播速度下降;其后射流火焰发展为湍流火焰后由于湍流火焰的自加速作用,火焰传播速度再次表现出上升趋势。最后由于火焰和压力波/压缩波的相互作用传播速度开始下降。
对不同的初始压力横向比较可以发现,射流阶段的火焰传播速度差异较小,火焰穿过孔板后其传播速度从15m/s左右上升至60m/s左右;湍流阶段的火焰传播速度则表现出明显的差异:0.1MPa下湍流火焰传播速度峰值约为70m/s,0.3MPa下湍流火焰传播速度峰值约为90m/s,0.5MPa下湍流火焰传播速度峰值约为110m/s。
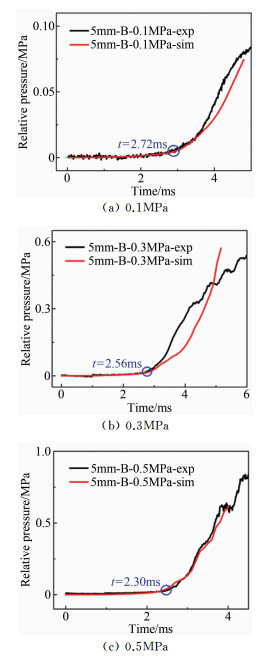
图 8所示为初始压力分别为0.1、0.3和0.5MPa下封闭空间中火焰加速过程的缸压曲线,其中黑色曲线表示实验的压力数据,红色曲线表示数值模拟的压力数据。需要指出的是,由于工作站计算能力有限,计算至压力峰值出现的时刻所需时间过长,因此本次模拟仅给出部分压力曲线。从图中可以看出,压力开始上升的时刻和压力上升的趋势在实验和数值模拟之间表现出较高的相似性。初始压力为0.1MPa下实验和数值模拟压力开始上升的时刻约为2.72ms;初始压力为0.3MPa下实验和数值模拟压力开始上升的时刻约为2.56ms;初始压力为0.5MPa下实验和数值模拟压力开始上升的时刻约为2.30ms。可以看出,随着初始压力的提高,压力上升的时刻随之提前。比较不同初始压力下的情况,初始压力为0.1和0.5MPa下实验与数值模拟的压力曲线吻合度较高,初始压力为0.3MPa下实验与数值模拟的压力曲线则表现出一定的差异,但总体趋势仍保持一致。
|
| 图 8 初始压力0.1、0.3和0.5MPa下的缸内压力实验和模拟结果对比 Fig.8 Comparison of pressure between experiment and simulation under initial pressure of 0.1, 0.3 and 0.5MPa |
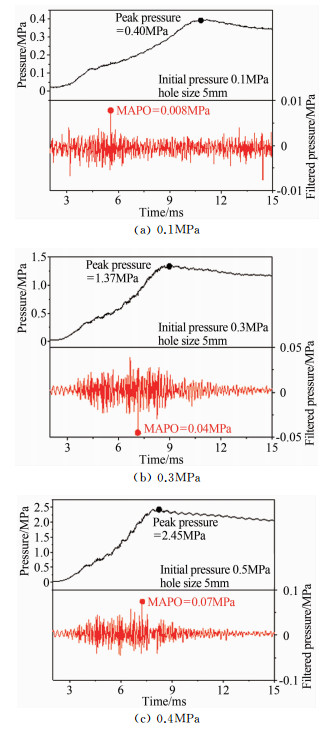
受限于工作站计算能力,模拟计算的缸压未能表现整个燃烧过程,因此对不同初始压力下的实验结果进行对比。图 9为不同初始压力下,缸内压力及其对应的高通滤波压力(带宽为4kHz)随时间的变化曲线,其中黑色曲线表示缸内压力曲线,红色曲线表示滤波压力曲线,MAPO为最大压力振荡幅值。如图所示,初始压力为0.5MPa时对应的缸内压力峰值为2.45MPa,高于初始压力为0.3MPa下的1.37MPa和初始压力为0.1MPa下的0.40MPa的压力峰值。初始压力为0.5MPa时对应的缸内最大振荡幅值为0.07 MPa,同样高于其他2个初始压力。不难发现,无论是缸内压力峰值还是缸内压力的振荡幅度,都随着初始压力的升高而升高。这是因为湍流火焰传播速度随着初始压力的升高而升高,进而对末端未燃气体产生强压缩作用,形成较强的压力波。
|
| 图 9 初始压力0.1、0.3和0.5MPa下的缸内压力和压力振荡 Fig.9 Experimental results of pressure and pressure oscillation under initial pressure of 0.1, 0.3 and 0.5MPa |
基于自主设计的定容燃烧弹和Converge三维数值模拟方法,对封闭空间中火焰过孔板加速机理及影响因素开展了研究,并讨论了不同初始压力对火焰过孔板加速过程的影响,得出以下结论:
(1) 依据火焰传播形态与速度,将封闭空间中火焰过孔板的加速过程分为3个阶段:层流火焰阶段、射流火焰阶段和湍流火焰阶段。在过孔板前的层流火焰阶段,火焰传播速度呈现先上升后下降的发展趋势:在火焰发展初期,由于受到水力学不稳定性和热扩散不稳定性的影响,火焰表面诱导出现胞状结构,导致火焰锋面面积增加,火焰传播速度略微增加。后期火焰传播速度下降是由于燃烧膨胀流场受到孔板阻碍作用的结果。此后,层流火焰穿过孔板并被孔板分割成数股射流火焰,火焰传播速度急剧增加约一个数量级。一方面,膨胀流场过孔板产生的强射流驱动了火焰的加速;另一方面,火焰在障碍物空间传播时,Rayleigh-Taylor不稳定性和Kelvin-Helmholtz不稳定性使得火焰表面褶皱更加剧烈,表面分裂为更小的胞状结构,促进燃烧速率加快。最后,多股射流火焰汇聚成一束湍流火焰,并在自加速机理的影响下火焰传播速度逐渐升高。
(2) 通过数值模拟获取了火焰过孔板过程中的流场变化情况,发现在火焰未达到孔板前,孔板附近存在速度较高的流场(强射流); 当火焰接近孔板时,在该射流的驱动下,火焰穿过孔板后速度急速上升。然而当穿过孔板之后,火焰锋面前的未燃气体区域的流场速度沿着远离火焰的方向逐渐下降,表明在该阶段射流对火焰发展不再起主导作用,相反地,火焰开始驱动前方的未燃气体运动。
(3) 对不同初始压力下的实验和数值模拟结果进行对比发现,火焰传播速度的模拟结果不论从绝对值还是发展趋势方面都能很好地吻合实验结果,验证了数值模拟结果的准确性。纵向对比不同压力下的火焰过孔板过程,发现随着初始压力的提高,孔板前的层流火焰传播速度略微降低,而孔板后的湍流火焰传播速度随着初始压力的提高而升高,进而诱导较高强度的压力波,导致较高的缸内压力和压力振荡。
| [1] |
Hancock D, Fraser N, Jeremy M, et al. A new 3 cylinder 1.2 l advanced downsizing technology demonstrator engine[R]. SAE Technical Paper, 2008-01-0611, 2008.
|
| [2] |
Heywood J B. Internal combustion engine fundamentals[M]. New York: Mcgraw-hill, 1988.
|
| [3] |
Inoue T, Inoue Y, Ishikawa M. Abnormal combustion in a highly boosted SI engine-the occurrence of super knock[R]. SAE Technical Paper, 2012-01-1141, 2012.
|
| [4] |
Attard W P, Toulson E, Watson H, et al. Abnormal combustion including mega knock in a 60% downsized highly turbocharged PFI engine[R]. SAE Technical Paper, 2010-01-1456, 2010.
|
| [5] |
Bäuerle B, Hoffmann F, Behrendt F, et al. Detection of hot spots in the end gas of an internal combustion engine using two-dimensional LIF of formaldehyde[J]. Symposium (Internatio-nal) on Combustion, 1994, 25(1): 135-141. DOI:10.1016/S0082-0784(06)80637-5 |
| [6] |
Kawahara N, Tomita E. Visualization of auto-ignition and pressure wave during knocking in a hydrogen spark-ignition engine[J]. Interna-tional Journal of Hydrogen Energy, 2009, 34(7): 3156-3163. DOI:10.1016/j.ijhydene.2009.01.091 |
| [7] |
Zahdeh A, Rothenberger P, Nguyen W, et al. Fundamental approach to investigate pre-ignition in boosted SI engines[J]. SAE International Journal of Engines, 2011, 4(1): 246-273. DOI:10.4271/2011-01-0340 |
| [8] |
Zaccardi J M, Duval L, Pagot A. Development of specific tools for analysis and quantification of pre-ignition in a boosted SI engine[J]. SAE International Journal of Engines, 2009, 2(1): 1587-1600. DOI:10.4271/2009-01-1795 |
| [9] |
Takeuchi K, Fujimoto K, Hirano S, et al. Investigation of engine oil effect on abnormal combustion in turbocharged direct injection-spark ignition engines[R]. SAE Technical Paper, 2012-01-1615, 2012.
|
| [10] |
Qi Y, Wang Z, Wang J, et al. Effects of thermodynamic conditions on the end gas combustion mode associated with engine knock[J]. Combustion and Flame, 2015, 162(11): 4119-4128. DOI:10.1016/j.combustflame.2015.08.016 |
| [11] |
Robert A, Richard S, Colin O, et al. LES study of deflagration to detonation mechanisms in a downsized spark ignition engine[J]. Combustion and Flame, 2015, 162(7): 2788-2807. DOI:10.1016/j.combustflame.2015.04.010 |
| [12] |
Luo X, Teng H, Hu T, et al. An experimental investigation on low speed pre-ignition in a highly boosted gasoline direct injection engine[J]. SAE International Journal of Engines, 2015, 8(2): 520-528. DOI:10.4271/2015-01-0758 |
| [13] |
Ciccarelli G, Dorofeev S. Flame acceleration and transition to detonation in ducts[J]. Progress in Energy and Combustion Science, 2008, 34(4): 499-550. DOI:10.1016/j.pecs.2007.11.002 |
| [14] |
Oppenheim A K, Soloukhin R I. Experiments in gasdynamics of explosions[J]. Annual Review of Fluid Mechanics, 1973, 5(1): 31-58. DOI:10.1146/annurev.fl.05.010173.000335 |
| [15] |
Lee J H S, Moen I O. The mechanism of transition from deflagration to detonation in vapor cloud explosions[J]. Progress in Energy & Combustion Science, 1980, 6(4): 359-389. |
| [16] |
Shepherd J E, Lee J H S. On the transition from deflagration to detonation[M]. New York: Springer, 1992.
|
| [17] |
Gelfand B E, Frolov S M, Nettleton M A. Gaseous detonations-A selective review[J]. Progress in Energy & Combustion Science, 1991, 17(4): 327-371. |
| [18] |
Oran E S, Gamezo V N. Origins of the deflagration-to-detonation transition in gas-phase combustion[J]. Combustion and Flame, 2007, 148(1-2): 4-47. DOI:10.1016/j.combustflame.2006.07.010 |
| [19] |
Johansen C T, Ciccarelli G. Visualization of the unburned gas flow field ahead of an accelerating flame in an obstructed square channel[J]. Combustion and Flame, 2009, 156(2): 405-416. DOI:10.1016/j.combustflame.2008.07.010 |
| [20] |
Dorofeev S B. Flame acceleration and explosion safety applica-tions[J]. Proceedings of the Combustion Institute, 2011, 33(2): 2161-2175. |
| [21] |
Zipf R K, Gamezo V N, Mohamed K M, et al. Deflagration-to-detonation transition in natural gas-air mixtures[J]. Combustion and Flame, 2014, 161(8): 2165-2176. DOI:10.1016/j.combustflame.2014.02.002 |
| [22] |
Maeda S, Minami S, Okamoto D, et al. Visualization of deflagration-to-detonation transitions in a channel with repeated obstacles using a hydrogen-oxygen mixture[J]. Shock Waves, 2016, 26(5): 573-586. DOI:10.1007/s00193-016-0660-1 |
| [23] |
Goodwin G B, Houim R W, Oran E S. Effect of decreasing blockage ratio on DDT in small channels with obstacles[J]. Combustion and Flame, 2016, 173: 16-26. DOI:10.1016/j.combustflame.2016.07.029 |
| [24] |
Shchelkin K I. Influence of tube roughness on the formation and detonation propagation in gas[J]. Zhurnal Eksperimental'noi i Teoreticheskoi Fiziki, 1940, 10(7): 823-827. |
| [25] |
Zeldovich Y B. On the theory on transition to detonation in gases[J]. Zhurnal Tekhnicheskoi Fiziki, 1947, 17(1): 3-26. |
| [26] |
Kuznetsov M, Alekseev V, Matsukov I, et al. DDT in a smooth tube filled with a hydrogen-oxygen mixture[J]. Shock Waves, 2005, 14(3): 205-215. DOI:10.1007/s00193-005-0265-6 |
| [27] |
Ciccarelli G, Fowler C J, bardon M. Effect of obstacle size and spacing on the initial stage of flame acceleration in a rough tube[J]. Shock Waves, 2005, 14(3): 161-166. DOI:10.1007/s00193-005-0259-4 |
| [28] |
Roy G D, Frolov S M, Borisov A A, et al. Pulse detonation propulsion:challenges, current status, and future perspective[J]. Progress in Energy and Combustion Science, 2004, 30(6): 545-672. DOI:10.1016/j.pecs.2004.05.001 |
| [29] |
Johansen C, Ciccarelli G. Characterization of the flow field ahead of a flame propagating in an obstructed channel[C]//Proceedings of the 21st colloquium on the dynamics of explosions and reactive systems. 2007.
|
| [30] |
Frolov S M, Semenov I V, Utkin P S, et al. Enhancement of shock-to-detonation transition in channels with regular shaped obstacles[C]//Proceedings of 21st ICDERS. 2007.
|
| [31] |
Gamezo V N, Ogawa T, Oran E S. Effect of obstacle spacing on flame acceleration and DDT in obstructed channels[C]//Proceedings of 21st ICDERS. 2007.
|
| [32] |
Bychkov V, Valiev D, Eriksson L E. Physical mechanism of ultrafast flame acceleration[J]. Physical Review Letters, 2008, 101(16): 164501. DOI:10.1103/PhysRevLett.101.164501 |
| [33] |
Petchenko A, Bychkov V, Akkerman V Y, et al. Violent folding of a flame front in a flame-acoustic resonance[J]. Physical Review Letters, 2006, 97(16): 164501. DOI:10.1103/PhysRevLett.97.164501 |
| [34] |
Brouillette M. The richtmyer-meshkov instability[J]. Fluid Mechanics, 2002, 34(34): 445-468. |
| [35] |
Xiao H H, Houim R W, Oran E S. Formation and evolution of distorted tulip flames[J]. Combustion and Flame, 2015, 162(11): 4084-4101. DOI:10.1016/j.combustflame.2015.08.020 |
| [36] |
Xiao H H, Makarov D, Sun J, et al. Experimental and numerical investigation of premixed flame propagation with distorted tulip shape in a closed duct[J]. Combustion and Flame, 2012, 159(4): 1523-1538. DOI:10.1016/j.combustflame.2011.12.003 |
| [37] |
Valiev D M, Akkerman V, Kuznetsov M, et al. Influence of gas compression on flame acceleration in the early stage of burning in tubes[J]. Combustion and Flame, 2013, 160(1): 97-111. |
| [38] |
Yoshizawa A, Horiuti K. A statistically-derived subgrid-scale kinetic energy model for the large-eddy simulation of turbulent flows[J]. Journal of the Physical Society of Japan, 1985, 54: 2834-2839. DOI:10.1143/JPSJ.54.2834 |
| [39] |
Menon S, Calhoon W H. Subgrid mixing and molecular transport modeling in a reacting shear layer[J]. Symposium (International) on Combustion, 1996, 26: 59-66. DOI:10.1016/S0082-0784(96)80200-1 |
| [40] |
Bradley D, Harper C M. The development of instabilities in laminar explosion flames[J]. Combustion and Flame, 1994, 99(3-4): 562-572. DOI:10.1016/0010-2180(94)90049-3 |
| [41] |
Chaudhuri S, Wu F J, Zhu D L, et al. Flame speed and self-similar propagation of expanding turbulent premixed flames[J]. Physical Review Letters, 2012, 108(4): 44503. DOI:10.1103/PhysRevLett.108.044503 |



