流动广泛存在于化工和能源等行业,复杂流动现象中流动参数的获取通常十分重要[1-2]。目前有很多测量颗粒速度的方法,其中非侵入式的光学测量按照原理有两大类,即基于多普勒原理的测量方法和基于TOF(Time of Flight)的测量方法[3]。前者利用激光照射颗粒产生的多普勒频移测速,后者则根据单位时间内颗粒移动的距离来计算速度[4]。
典型的基于TOF的测量方法包括PIV(Particle Image Velocimetry)和PTV(Particle Tracking Veloci-metry)。PIV是20世纪70年代末发展起来的一种非接触式流体力学测速方法,是目前应用最为广泛的全场无干扰测速手段[5]。PTV技术本质上是PIV技术的衍生,两者的不同之处在于:PIV获取的速度来自于观测区域内多个粒子位移的统计平均值,而PTV则是通过追踪单个粒子的位移来获得速度。PTV由于其追踪颗粒运动的特点,所得结果具有直观性和准确性,不过同时也具有粒子浓度不宜过高的局限性[6]。早期PTV技术由于CCD摄像系统水平的限制,其时间和空间分辨率均不高,精度也不如PIV[7]。随着计算机和CCD相机等硬件水平的不断提高,在输移现象和传送现象等尤其关注颗粒的拉格朗日运动过程的情况下,PTV的作用逐渐显现出来,因而也得到了广泛的应用[8]。
根据图像记录的方式不同,PTV可以分为3种类型:单帧单脉冲、单帧多脉冲和多帧单脉冲[9]。近年来PTV领域的研究大多集中在多帧单脉冲形式[10]。多帧单脉冲形式具有更高的精度且能很好地解决速度二义性问题,因而得到广泛应用。不过当涉及湍流这种十分复杂、瞬息万变的流动时,通常需要频率非常高的激光脉冲,才能实现对复杂流动颗粒的精确追踪,但同时也会造成成本的急剧增加。
单帧单曝光图像法,即PTV的单帧单脉冲形式,具有系统简洁、图像直观等优点。由于只有一次曝光,因此不需要功率非常大的激光器即可完成对示踪粒子的追踪。不过单帧单曝光图像法的图像处理过程相对复杂,不同于多帧单脉冲形式的PTV,单帧单曝光虽然没有粒子匹配的问题,但由于其处理对象是轨迹而非单个点,复杂度也有所提升。
近年来对PTV的研究多集中在多帧单脉冲形式,对单帧单曝光图像法的处理算法研究相对较少。其中,刘春嵘等[11]通过形心主轴的概念来计算运动轨迹的速度;陈晶丽等[12]提出针对颗粒运动轨迹采用外接矩形的方法来提取颗粒速度与粒度;Jing等[13]则提出了通过检测轨迹边缘8个特征点来计算速度与粒度的方法。上述3种方法各有优势和特点,不过三者有一个共同点,那就是针对一条轨迹处理出一个速度矢量,导致信息的利用率较低。同时,在处理弯曲轨迹时,这些方法的精度均有所下降,而复杂流场中的弯曲轨迹是无法避免的。因此,本文提出一种方法,不仅能同时提取直线段轨迹和弯曲段轨迹的速度矢量,同时也提高轨迹上运动信息的利用率。
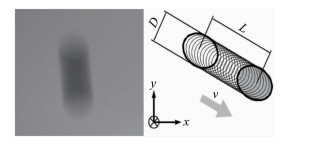
1 单帧单曝光图像法测速原理在利用单帧单曝光图像法测量示踪粒子的速度时,一般CCD相机固定不动,通过视窗记录测量区的图像,此时,离散相颗粒(如水滴、煤粉、气泡等)与CCD相机发生相对位移,其成像在曝光时间内的叠加就形成了模糊的“拖影”,如图 1所示[14]。
|
| 图 1 运动模糊图像及其成像模型 Fig.1 Motion blur image and its imaging model |
单帧单曝光运动模糊图像包含了颗粒与相机的相对位移信息。因为曝光时间已知,在物体匀速直线运动假设的前提下,可以计算出运动速度,如式(1)所示。
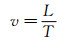 (1)
(1)
式中,T为曝光时间且已知,故速度v的计算关键就在于运动长度L的计算。现有的很多算法都将轨迹近似视为一段直线,且最终得出一个速度矢量。以外接矩形法为例,该方法求出轨迹的最小外接矩形,提取矩形的长和宽,长度减去宽度便得到了颗粒的运动距离。其他几种算法各有不同,但都具有一定的相似性。上述算法均需满足颗粒运动轨迹接近直线的前提,在颗粒轨迹为曲线的情况下会产生一定误差。所以需要提出另一种计算速度的方法,能同时适用于直线轨迹和弯曲轨迹的情况。
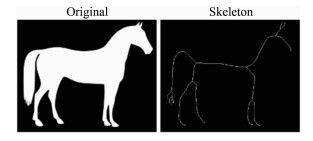
2 基于骨架提取的颗粒轨迹处理算法骨架提取,也被称为二值图像细化。这种算法能将一个连通区域细化成一个像素的宽度,同时保持图像的形态学特征,主要用于特征提取和目标拓扑表示。从图 2可以很直观地看出骨架提取的特点。
|
| 图 2 骨架提取示意图 Fig.2 Sketch of skeletonizing |
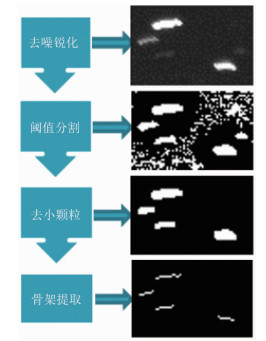
结合骨架提取的特点可以将颗粒的轨迹进行细化,得到单像素宽度的轨迹图,也就是像素精度的迹线。在此基础上进行轨迹长度计算要准确得多,且对于弯曲轨迹也更能区分各像素点处速度方向的细微区别。为得到效果更好的轨迹骨架图,需要对原图依次进行去噪、自适应阈值分割、闭运算、去除小颗粒及骨架提取等操作,主要的处理流程如图 3所示[15]。
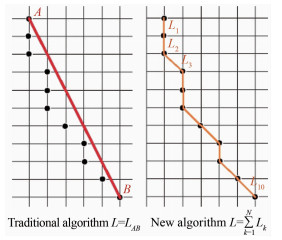
2.1 基于轨迹骨架图的速度提取在原理介绍部分已经提到,速度计算的前提是计算运动长度。在获得轨迹的单像素宽度迹线之后,通过连通区域分割函数可以识别出每条轨迹上的所有像素点,传统算法采用迹线起点与终点之间的距离作为长度,这样在处理弯曲轨迹时就会产生较大误差。本文提出类似于求线积分的求长度算法,首先将每2个像素点之间的距离求出来,然后迭加得到总的轨迹长度,2种算法的对比如图 4所示。
|
| 图 4 新旧算法求轨迹长度的对比 Fig.4 The difference on trajectory lengths between the traditional and the new algorithm |
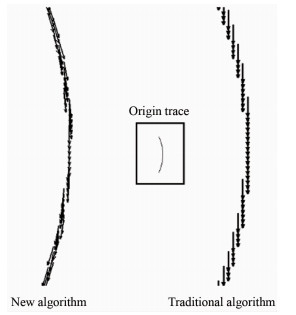
对于速度的方向,以往的计算方式是采取轨迹首尾相连的一条直线作为方向向量,如图 4中的旧算法。但这种方法在处理弯曲轨迹的时候会产生很大误差,且一条轨迹上所有的点共享一个速度矢量,十分笼统。因此,提出了求迹线切线的方法,将像素点前后若干个像素点之间的割线近似视为切线, 并作为轨迹上该点的速度方向,不仅对于弯曲轨迹能很好地提高精度,而且同一条轨迹上各个像素点的速度矢量也有区分,能很好地体现颗粒的实际运动过程。图 5显示了新旧算法求速度方向的区别,新算法(左侧)各个像素点处的速度由其切线决定,能更好地显示粒子的流动过程,旧算法(右侧)则过于笼统,所有像素点的速度矢量完全相同,不能体现实际的流动状态。此外,若将轨迹上各个点处的速度矢量逐帧播放,也能更清晰生动地显示颗粒的动态流动过程。
|
| 图 5 新旧算法求速度方向的对比 Fig.5 The difference on velocity direction between the traditional and the new algorithm |
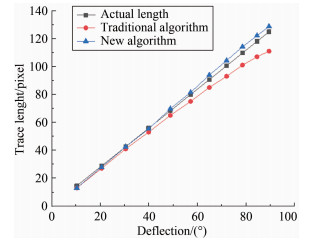
图 6为新旧算法在计算不同弯曲程度轨迹时的精度对比。从仿真圆形轨迹上截取不同弧长的轨迹,然后分别采用2种算法求长,并与弧长的理论值进行对比。图中,横坐标为轨迹的弧长,也代表了轨迹的弯曲程度,纵坐标为轨迹长度。红色圆点为旧算法计算的长度,蓝色三角点为新算法计算的长度,黑色方点为实际弧长。由图 6可见,在弧长较低,即轨迹接近直线的情况下,2种算法的结果均十分接近真值;随着弧长的增加(即轨迹弯曲程度增加),新算法则逐渐体现出了优势。
|
| 图 6 2种速度提取算法精度比较 Fig.6 Accuracy contrast between the traditional and the new algorithm |
在前文的叙述中,速度的计算忽略了一个很重要的问题,就是速度二义性的判断。对一条轨迹来说,一般有2个端点,那么轨迹是从端点A运动到B还是从B运动到A是2种完全不同的情况,所以需要对该问题进行判断。下面提供2种方法:一种是利用流体的角速度进行判断,另一种则利用多帧图像之间的运动关系进行判断。
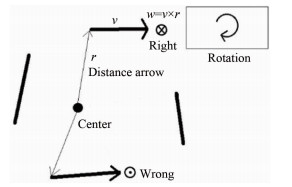
2.2.1 角速度判别法角速度判别法是一种利用右手螺旋定则来确定轨迹运动方向的方法。如图 7所示,有一组围绕同一中心点进行旋转的4条轨迹,此时执行前述的速度提取流程后,上下2条轨迹的速度方向会保持一致(水平向右)。但实际上,由于这是一组旋转轨迹,上下2条轨迹的方向应该相反。为使同一旋转中心的一组轨迹旋转方向保持一致,使用角速度判别法进行判断。图 7中,通过右手螺旋定则可以知道上方轨迹的角速度垂直纸面朝里,而下方的角速度垂直纸面向外,二者互相矛盾,通过改变其中一条轨迹的速度矢量即可解决速度二义性问题。在实际执行过程中可预先定义轨迹的旋转方向(顺时针或逆时针),从而统一各个轨迹的速度方向,消除二义性。
|
| 图 7 角速度判据 Fig.7 Angular velocity verdict |
对于直线运动状态,可以将旋转中心点选在垂直于轨迹的无穷远处。此外,对于复杂的流动,可以通过选取多个旋转中心分别进行角速度判别,由于过程比较复杂,故方法具有一定的局限性。
2.2.2 多帧连续曝光图像匹配单帧图像很难解决二义性问题,而多帧图像则可以。因此,在相机进行第一段曝光之后,立刻进行第二段曝光,这样得到2帧在时间序列上几乎衔接的图片,由于2帧图片的时间先后顺序已知,就能很方便地求出颗粒的速度方向。
在多帧图像匹配方法中,关键在于2帧图片中同一条轨迹的匹配识别[16]。由于2次曝光之间的时间间隔非常短暂,所以2段轨迹理论上是能首尾相连的。实际处理中,对于第一帧图片里的所有轨迹,于2个端点附近搜索其在第二帧图片中是否有轨迹,搜索半径由2段曝光之间的间距时间以及流场的速度决定。为了保证在搜索半径中只有该轨迹的下一帧轨迹出现,因此颗粒密度不宜太大。此外,考虑到边缘部分的轨迹可能由于进出视场而导致无法匹配,故应提前将边缘部分的轨迹剔除。图 8展示了2帧连续曝光图片(曝光时间为7ms,间隔时间为0.077ms)匹配并叠加的过程,其轨迹匹配率为84.5%。

|
| 图 8 2帧图片的匹配与叠加过程 Fig.8 Match and compound processing of two frame images |
在完成2帧图片之间的轨迹匹配之后,速度二义性就解决了。举例来说:假设AB是第一帧图片的某条轨迹,端点分别是A和B,而CD是该轨迹在第二帧图片上的位置,端点分别是C和D;若B和C是2条轨迹的连接点,则轨迹的方向就依次是A—B—C—D。
多帧图像匹配之后,不仅解决了速度二义性问题,同时,由于得到了不同时间序列上的速度值,也能因此获得加速度。
2.3 二值化与骨架提取的误差分析基于骨架提取的轨迹处理算法可以分成2部分:图像处理部分和速度计算部分。速度计算部分的误差已经在2.1节进行了描述,此处对二值化和骨架提取的误差进行分析。
2.3.1 二值化过程误差分析单阈值分割通常采用Ostu (最大类间方差)阈值,其通过图像灰度将图像分为背景和目标,通过最大化背景和目标之间的类间方差来找寻最优阈值。考虑到单阈值分割在灰度分布不均的情况下并不适用,故使用了自适应阈值分割。这是一种多阈值分割方法,通过分析像素周围局部范围的灰度特性来决定该像素点的阈值,能够使阈值分割后的图片保留更多信息。
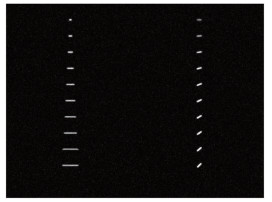
二值化过程的误差分析实验采用了仿真的运动模糊图片,如图 9所示。根据实际射流实验图片,将仿真颗粒图像的背景灰度设为40,目标灰度设为200,粒径为5pixel,将颗粒图像进行卷积并添加方差为0.008的高斯加性噪声即得到仿真运动模糊图像,卷积核则由运动长度决定。
|
| 图 9 多种运动的仿真运动模糊图片 Fig.9 Simulation image contains different motion blur |
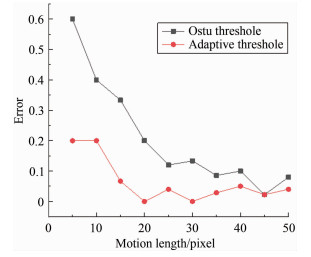
仿真实验的结果如图 10所示,可见随着运动长度的增加,2种阈值分割的误差均显著下降,且自适应阈值分割的误差要明显低于Ostu阈值分割。
|
| 图 10 不同二值化过程的误差 Fig.10 Error by different binary options |
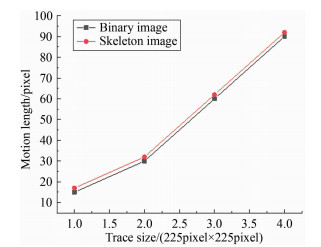
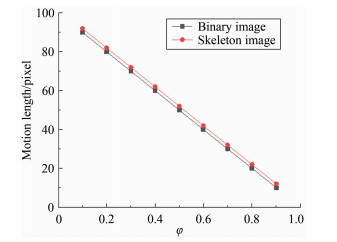
骨架提取过程将二值图转变成骨架图,故误差分析过程采用仿真的轨迹二值图(由一系列圆形叠加形成的类似于椭圆的图形)进行一系列仿真实验。初步认为骨架提取的结果受轨迹大小、轨迹长短轴比、轨迹方向(位置)三方面的影响。实验过程中分别计算二值图与骨架图中轨迹对应的运动长度。在二值图中,运动长度为轨迹的长度减去宽度;在骨架图中,轨迹长度即为像素距离迭代求和的长度。仿真实验结果如图 11~13所示。

|
| 图 11 骨架提取结果与轨迹方向的关系 Fig.11 Relation between skeletonizing and trajectory direction |
|
| 图 12 不同轨迹尺寸下二值图与骨架图的运动长度 Fig.12 Motion length of binary and skeleton image on different trajectory sizes |
|
| 图 13 不同长宽比(φ)下二值图与骨架图的运动长度 Fig.13 Motion length of binary and skeleton image with different width/length rate (φ) |
从图 11可以看出骨架提取结果与轨迹的方向无关;从图 12和13看出,骨架提取操作对运动长度的影响很小。进一步考察原始数据发现,在所有情况下,骨架图中的运动长度都比二值图的运动长度大一个固定值1,这是由于长度计量的起点不同所导致的。举例来说,假设有一个仅包含一个像素点的轨迹,其长度应该为1,但长度减去宽度却等于0,从而导致了二者相差1的现象,这种情况在实际应用过程中统一即可。
3 流场重构算法在执行了上述轨迹处理算法之后,可以得到每条轨迹的速度信息。然而多数情况下实际需要的是整个流场的速度信息,因此需要进行流场重构工作。
3.1 RBF插值法重构流体速度场从随机的数据拟合出整个平面场的信息属于数学上插值的范畴。选用径向基函数(Radial Basis Function, RBF)插值的方法得出流场的速度场。该插值方法的基本假设是插值点的函数值受插值源函数值影响,且影响程度与插值点和插值源之间的距离有关,其数学表达式如下:
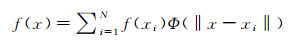 (2)
(2)
根据不同应用实例,可以选取不同的距离系数函数Φ以达到最佳的插值效果。比较多种函数的插值效果,从中选取名为“multiquadric”的距离系数,其距离系数函数如下:
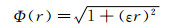 (3)
(3)
考虑到流体速度场的特点,任意一点的速度受来流方向速度值的影响大于下游方向速度值的影响。需要在RBF插值的基础上进行类似于“迎风插值”的优化。优化的基本思想是在插值点的上游增加对插值点的影响;在插值点的下游减弱对插值点的影响。因此,可以构建迎风修正系数函数ψ,ψ的值由插值点与已知点之间速度向量的夹角决定,当夹角为锐角时,ψ大于0,对结果进行增强;当夹角为钝角时,ψ小于0,对结果削弱。其表达式如下:
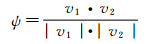 (4)
(4)
修正后的插值表达式如下:
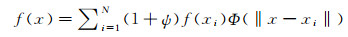 (5)
(5)
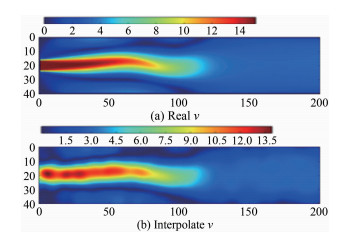
对插值的误差进行分析,采用仿真输出的流场结果,随机选取一定的数据点之后进行插值,分析插值结果与原流场的差别即可。原流场与插值流场的速度云图如图 14所示。
|
| 图 14 仿真流场(a)与插值流场(b)对比 Fig.14 Contrast between simulation flow field (a) and interpolation flow field (b) |
为了量化2幅图之间的相似度,以便更直观地获知不同插值方法的优劣,定义2幅图像之间的平均距离δ,如式(6)所示。δ越大,表示两者之间的差别越大,δ越小,表示两者越为接近。
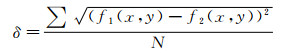 (6)
(6)
表 1显示了选用不同插值函数并采用“迎风插值”优化之后的插值结果的平均距离。从中可以看出基于“multiquadric”并采用“迎风插值”优化之后得到插值效果是最好的,与肉眼直观相符。
| Interpolation function | δ |
| multiquadric | 1.057 |
| gaussian | 5.645 |
| linear | 1.444 |
| log | 1.647 |
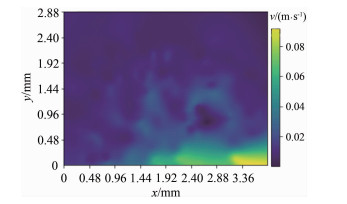
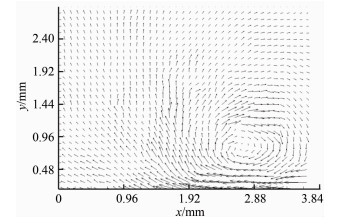
为验证本文算法在实际情况下的适用性,采用射流实验中拍摄的图片作为处理对象,如图 15所示。实验中射流出口流速为0.15m/s,拍摄部位为射流口上部的卷吸区域。射流口位于图片右下方,视场大小为2.88mm×3.86mm。图 16展示了轨迹骨架图,图 17和18分别是最终速度场的云图和矢量图。

|
| 图 15 原始图像 Fig.15 Original image |

|
| 图 16 轨迹骨架图 Fig.16 Skeleton image of trajectory |
|
| 图 17 速度云图 Fig.17 Contour of the velocity field |
|
| 图 18 速度矢量图 Fig.18 Velocity field vector diagram |
在速度云图中,每个像素点处的颜色代表了该处的速度大小,因而能直观地看出速度场在空间上的能量分布;在速度矢量图中,箭头方向为速度方向,箭头长度表征了速度大小,从而可以看出流场整体运动趋势。
为验证实验结果的可信度,利用插值后的速度场来计算速度的散度场。考虑到此处速度场并非连续,因此采用变分方式来计算散度,同时假定流场为二维流动,散度计算公式如下:
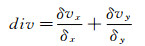 (7)
(7)
采用云图方式展示计算的散度场,如图 19所示,由于常温常压下水流可视为不可压流动,速度的散度应处处为零,图 19中大多数散度值接近为零,少数几处出现稍大的散度值(正值或负值),不过总体上结果符合事实。

|
| 图 19 速度的散度云图 Fig.19 Contour of the divergence of velocity |
为获取颗粒的速度分布,针对单帧单曝光图像的处理提出一种颗粒轨迹处理算法。通过骨架提取获得轨迹的迹线,然后对迹线的像素坐标进行迭代求和来计算轨迹长度,同时通过求迹线的切线来计算速度方向。相比传统算法,该算法在速度大小和方向上均有更高精度,且不同于传统算法一条轨迹一个速度矢量的模式,该算法的一条轨迹可以获得轨迹上任意点处的速度矢量,大大提高了信息利用率。
在得到原始的离散速度场之后,利用迎风优化后的RBF插值算法,可以重构一个相对连续且平滑的全分布流场,可在此基础上计算加速度、散度等参数,方便后续研究;也可以很方便地与CFD等仿真模拟结果进行比较。
本算法处理结果的精度上限取决于阈值分割过程,因而需要在拍摄过程中调整曝光时间、光源、颗粒浓度等因素,尽可能提高所拍摄图像中轨迹的清晰度,以期达到好的阈值分割效果,减少图片中的干扰轨迹,从而获得更高精度的结果。
| [1] |
Koeninger B, Henslers T, Schug S, et al. Horizontal secondary gas injection in fluidized beds:solid concentration and velocity in multiphase jets[J]. Powder Technology, 2017, 316: 49-58. DOI:10.1016/j.powtec.2017.01.057 |
| [2] |
Yang Y, Kang B S. Development and validation of digital holographic particle velocity measurement system for rotational flows[J]. Optik-International Journal for Light and Electron Optics, 2015, 126(19): 2223-2227. DOI:10.1016/j.ijleo.2015.05.103 |
| [3] |
Andreas F. Model-based review of Doppler global velocimetry techniques with laser frequency modulation[J]. Optics and Lasers in Engineering, 2017, 93: 19-35. DOI:10.1016/j.optlaseng.2017.01.004 |
| [4] |
Komine H. System for measuring velocity field of fluid flow utilizing a laser-Doppler spectral image converter: US4919536[P]. 1990-04-24.
|
| [5] |
金光, 焦晶晶, 吴晅. 典型流场测速技术应用研究进展[J]. 矿山机械, 2015, 43(12): 10-15. Jin G, Jiao J J, Wu X. Research progress on application of typical flow field velocimetry technology[J]. Mining & Processing Equipment, 2015, 43(12): 10-15. |
| [6] |
胡涛. PTV匹配算法的对比分析[D].北京: 清华大学, 2010. Hu Tao. Comparison of particle matching algorithms for PTV[D].Beijing: Tsinghua University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10003-1011280837.htm |
| [7] |
申功炘. 全场观测技术概念、进程与展望[J]. 北京航空航天大学学报, 1997, 23(3): 332-340. Shen G X. Concept trace trend on fullfield observation and measurement techniques[J]. Journal of Beijing University of Aeronautics and Astronautics, 1997, 23(3): 332-340. |
| [8] |
周云龙, 宋连状, 周红娟. 稀相颗粒二维速度场测量PTV法的研究进展[J]. 化工进展, 2010, 29(z2): 17-21. Zhou Y L, Song L Z, Zhou H J. Research progress of PTV method in two-dimensional dilute phase particle velocity measurement[J]. Chemical Industry and Engineering Progress, 2010, 29(z2): 17-21. |
| [9] |
禹明忠. PTV技术和颗粒三维运动规律的研究[D].北京: 清华大学, 2002. Yu M Z. Study on the PTV technique and 3D movement of particles[D]. Beijing: Tsinghua University, 2002. http://cdmd.cnki.com.cn/Article/CDMD-10003-2004032001.htm |
| [10] |
杨福胜, 张早校, 王斯民, 等. 粒子追踪测速(PTV)技术及其在多相流测试中的应用[J]. 流体机械, 2014, 42(2): 37-42. Yang F S, Zhang Z X, Wang S M, et al. Particle tracking velocimetry and its application to the measurement of multiphase flow[J]. Fluid Machinery, 2014, 42(2): 37-42. DOI:10.3969/j.issn.1005-0329.2014.02.009 |
| [11] |
刘春嵘, 刘波. 基于形心主轴的二维DPTV算法[J]. 实验流体力学, 2007, 21(3): 66-69. Liu C R, Liu B. Two-dimensional DPTV algorithm based on central principal axis[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(3): 66-69. DOI:10.3969/j.issn.1672-9897.2007.03.014 |
| [12] |
陈晶丽, 李琛, 蔡小舒, 等. 流动多参数场的单帧图像法测量方法研究[J]. 实验流体力学, 2015, 29(6): 67-73. Cheng J L, Li C, Cai X S, et al. Research on single frame imaging method for measuring multi-parameter fields in flow field[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(6): 67-73. |
| [13] |
Jing J Q, Xiao F, Yang L, et al. Measurements of velocity field and diameter distribution of particles in multiphase flow based on trajectory imaging[J]. Flow Measurement and Instrumenta-tion, 2018, 59: 103-113. DOI:10.1016/j.flowmeasinst.2017.12.005 |
| [14] |
张晶晶.基于单帧单曝光图像法的多相流速度场和粒度分布测量研究[D].上海: 上海理工大学, 2011. Zhang J J. Study on measurement for velocity vector field and granularity distribution of multi-phase flow based on single-frame and single-exposure imaging[D]. Shanghai: University of Shanghai for Science and Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10252-1013010566.htm |
| [15] |
Maas H G, Gruen A, Papantoniou D. Particle tracking velocimetry in three-dimensional flows:part 1-photogram-metric determination of particle coordinates[J]. Experiments in Fluids, 1993, 15(2): 133-146. DOI:10.1007/BF00190953 |
| [16] |
Malik N A, Dracos T, Papantoniou D A. Particle tracking velocimetry in three-dimensional flows:part 2-particle tracking[J]. Experiments in Fluids, 1993, 15(4-5): 279-294. |