水能作为一种清洁、储量大的可再生能源,一直是全球范围内关注的能源类型之一。水力转轮是转化水动能的关键装置。Savonius转轮是典型的垂直轴阻力型转轮,结构简单、静态力矩大、启动性能良好[1],最早被应用于风力发电。将多个转轮组合为转轮组,理论上可以更好地利用流体动能,但实际上转轮之间的相互影响有时会降低部分转轮的能量利用系数。目前相关研究尚不充分,尤其是对上游叶轮尾流与下游叶轮之间相互作用的研究,鲜见报道。
已有的单个转轮流场研究,主要集中于不同相位角下的瞬态流场与转轮结构对流场的影响2个方面。Kacprzak等采用计算流体动力学(Computational fluid dynamics,CFD)方法研究了转轮叶片形状对尾流流场的影响,发现叶片间的重叠削弱了叶片凹面产生的旋涡,从而使尾流宽度减小[2]。Jaohindy等在对Savonius风力机周围流场的数值模拟中,指出转轮内部及周围流场中的部分旋涡区在一定程度上来源于旋转过程中剪切应力造成的低压区[3]。Nasef等在对Savonius风力机的性能评估中,指出在0°~90°范围内尾流宽度随转轮安放角增大而增大[4]。Zhang等提出一种新型Savonius转轮的设计方法,并通过数值模拟与粒子群算法对转轮流场进行了研究[5]。Kang等利用数值模拟对螺旋形Savonius转轮的湍流特性及动力学性能进行了研究,发现尾流区的大尺度旋涡多出现在凸面迎流的叶片后方[6]。Kumar等分析并对比了不同相位角下扭曲叶片Savonius水力转轮的流场[7]。Fujisawa与Gotoh采用颜料可视化方法研究了不同相位角下Savonius转轮的瞬态流场,描述了转轮周围的流动结构[8]。Torresi等在风洞中对Savonius风力机的性能及流场进行了测试,获得的结果接近工程数据[9]。Sarma等的评估结果表明,Savonius水力转轮的性能优于风力转轮,证实了其在水动能利用中的巨大潜力[10]。
在转轮组合的研究中,以优化转轮布置方案及探讨转轮之间的流动特征为主。Gao等[11]与Park等[12]的研究表明,在风电场中增加风力机数量可以提高经济效益。Zhang等研究了Savonius风力机尾流利用的新型布置方案,结果表明下游风力机的最佳位置处于上游风力机尾流的周期性高速区域内[13]。Zuo等利用数值模拟方法研究了间距对串列H形垂直轴风力机性能的影响,发现随着间距的增大,上游风力机的尾流效应减弱[14]。Lam与Peng通过二维与三维数值模拟研究了垂直轴风力机的尾流特性,分析了风力机尾流中各断面的速度及涡量分布[15]。Shaheen等采用数值模拟分析Savonius风力机群时,发现60°为风力机的最佳错列角度,可以避开上游风力机尾流的影响[16]。Shigetomi等在研究错列布置的Savonius风力机相干流场时,发现与单个风力机相比,两风力机之间的流线较弯曲且速度较慢[17]。孙科等利用OpenFOAM软件分析了水轮机间距对下游水轮机水动力学性能的影响,结果表明两水轮机的间距大于40倍转轮直径时,上游水轮机尾流场对下游水轮机性能的影响可以忽略[18]。Ahmadi-Baloutaki等在利用风洞对阵列垂直轴风力机相互影响的研究中,发现2个并列风力机旋向相反时性能会有所提升[19]。杨瑞等在串列风力机三维尾流场的实验研究中发现,风力机串列布置时,上游风力机尾流对下游风力机的功率输出影响较大[20]。
尽管目前在转轮尾流场及转轮布置方案的研究中已经获得了一些结论,但多数研究建立于数值模拟基础之上,其与实际工程应用仍存在较大差距。在串列水力转轮组的流场研究中,虽然下游转轮对上游转轮的效率几乎没有影响[21],但是上游转轮尾流场速度与涡量分布会对下游转轮产生影响,并呈现出受到复杂壁面干扰的尾流特征。在实际工程应用中,转轮尺寸相对较大、应用环境复杂,开展流动可视化实验研究成本较高、难度较大。在已有文献中,关于下游转轮的安放角对上游转轮尾流场的影响鲜见报道。
为描述受到转轮干扰的尾流特征,采用基于时间解析的PIV(Time-resolved particle image velocimetry,TR-PIV)系统对2个水力转轮间的流动进行测量,重点考虑下游转轮安放角与来流速度对转轮之间流场的影响。在各实验工况下,获得流场中的速度分布、涡量分布和流动结构,并进行系统的对比分析,进而使用本征正交分解(Proper orthogonal decomposition,POD)算法分析周期性流动中占主导地位的流动模态,以解释Bach转轮的尾流受到另一转轮干扰时呈现出的特征,并为水力转轮布置方案优化提供参考。
1 实验装置及方法 1.1 实验装置及模型实验在江苏大学能源与动力工程学院的低速循环水洞实验台上进行。实验段尺寸为500mm×315mm×50mm(长×宽×高),壁面以厚35mm的有机玻璃制成。通过变频器(0~50Hz范围内可连续调节)调节循环泵转速,从而控制转轮来流速度。实验中采用2个Bach水力转轮模型(直径D=60mm、高H=48mm)组成串列转轮组。如图 1所示。

|
| 图 1 Bach转轮模型实物图 Fig.1 Bach rotor |
相比于传统的Savonius转轮,Bach转轮的水动能利用系数更高。实验采用的转轮模型采用铜合金加工,以防止在水流冲击或部分转轮安放角下可能出现的振动及变形问题;同时,为防止模型表面反光影响PIV拍摄,使用黑色亚光漆将其表面涂黑;另外,转轮基座通过销钉固定于实验段侧壁面上,转动基座可以分别调节下游转轮安放角θ1与上游转轮安放角θ2。
1.2 TR-PIV系统低频PIV系统在高雷诺数工况下难以捕捉旋涡的高频脱落。TR-PIV不但能实现瞬时、全场测量,还能达到较高的时间和空间分辨率[22]。实验采用LaVision公司的TR-PIV系统,主要组件为DM30高频激光发生器(最高频率10kHz,最大能量70mJ,双脉冲工作方式)、Highspeed Star UX100相机(分辨率1280pixel×1024pixel,最大满帧4000帧/s,配备Nikon 50mm f/1.4D相机镜头)、脉冲激光同步器等。以直径为20μm的空心玻璃微珠作为示踪粒子。采用Davis与Tecplot软件进行数据处理,其中Davis软件主要完成图像采集和初步处理。实验中每个工况拍摄500张图片,基于该样本获得平均流场参数。
1.3 实验方案参考Torresi[9]与Zhou等[23]的转轮实验及模拟结果,将上游转轮固定(θ2=36°),下游转轮选取0°、36°、72°、108°、128°和144°等6个具有代表性的安放角。转轮间距为3倍转轮直径(3D)。实验装置如图 2所示。

|
| 图 2 实验装置 Fig.2 Experimental rig |
激光片光由实验段底部中间截面垂直于转轮轴线射入流场;高速相机垂直于片光进行拍摄。为确保拍摄到上游转轮尾流受到下游转轮影响后产生的形态变化,拍摄区域(长220mm×高176mm)的中心选取在2个转轮之间偏下游转轮的位置。拍摄区域及Tecplot图像软件默认的坐标系如图 3所示,上下游转轮中心分别位于x=65和100mm处。
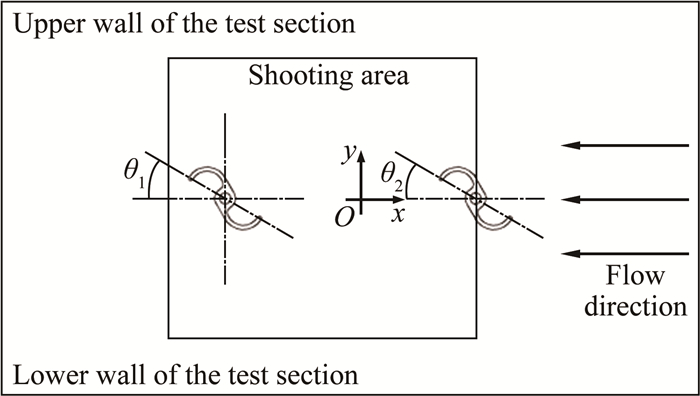
|
| 图 3 拍摄区域示意图 Fig.3 Schematic diagram of the monitored area |
实验中,设置来流速度v的范围为1.3~4.0m/s,对应的雷诺数(Re=ρvD/μ,D为转轮直径,μ为水的动力粘度)范围是0.8×105~2.4×105;同时设置PIV采样频率为1kHz、标定因子为6.1pixel/mm、相邻计算区域的重叠率为75%及32pixel×32pixel的PIV互相关算法窗口。在此拍摄条件下,空间分辨率为0.98mm×0.98mm。
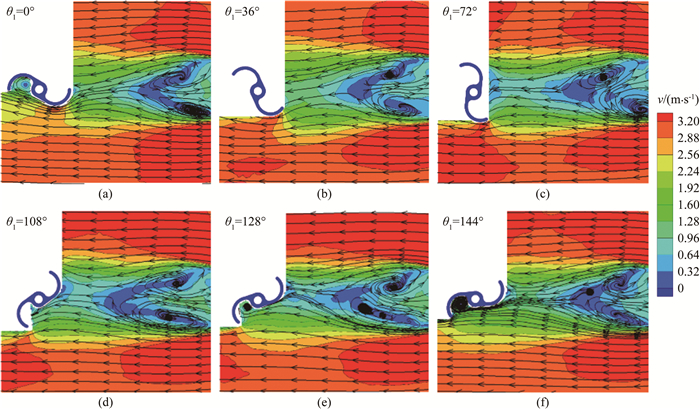
2 结果与分析 2.1 下游转轮安放角对尾流的影响图 4为不同下游转轮安放角时的上游转轮尾流形态及速度分布平均结果。为使上游转轮的尾流更加直观明显,仅截取显示了两转轮之间的流场信息。图中空白区域是金属转轮遮挡激光所致(图中给出了下游转轮安放角的示意)。
|
| 图 4 不同下游转轮安放角时的上游转轮尾流形态及速度分布 Fig.4 Wake patterns and velocity distributions at different setting angles of the downstream rotor |
从图 4(a)~(f)可以看出:上游转轮的尾流在流经下游转轮时,扩散的尾流区域被破坏,且在下游转轮的上下叶片边缘区域出现流动加速,与Torresi等[9]与Hassanzadeh等[24]在研究中发现的现象类似。这是由于下游转轮的存在对尾流产生了阻挡,使尾流区域的流体被迫挤向转轮两侧从而造成加速。
受下游转轮安放角的影响,图 4中尾流流线的走向分别呈现向下偏转、水平和向上偏转等3种状态。其中,在θ1=0°和36°时,流线向下偏转,如图 4(a)和(b)所示。θ1=0°时,下游转轮接近水平状态,其迎流叶片凹面形成的附着涡一般不会超出凹面,因此对流线走向的影响较小,且尾流中上侧旋涡尺寸较下侧旋涡大,对流体的影响不均衡,因此流线向下偏转。θ1=36°时,下游转轮迎流叶片凹面附着涡对尾流的聚集效应以及叶片凸面附近低压区对尾流的诱导作用使局部流线向下偏转,此现象与Jaohindy等[3]对Savonius风力机进行数值模拟获得的结果相似。因此,θ1=36°时,下游迎流叶片凹面能较好地接受尾流能量,有利于能量转化。
当θ1=72°时,转轮接近竖直状态;当θ1=144°时,转轮接近水平状态。在2种角度下,转轮对尾流的整体阻碍作用都较为均匀,流线走向基本水平,如图 4(c)和(f)所示。θ1=72°时,尾流流线在接近下游转轮时急转向下,流体冲击迎流叶片凹面;而θ1=144°时,由于受到转轮直线段的影响,大部分流体流向迎流叶片凹面。72°、144°这2个安放角都有利于转轮的顺时针旋转。
当θ1=108°和128°时,靠近上游转轮下侧的旋涡沿流向被拉伸,尾流形态受此旋涡影响较大,流线呈现整体向上偏转的状态,导致上侧返回叶片的顺时针旋转受阻,转轮的负力矩增大。如图 4(d)和(e)所示。
尾流区域中的旋涡明显受到了下游转轮的影响。整体来看,当θ1从0°变化到72°时,上侧旋涡涡心位置逐渐向下游移动,但旋涡大小变化不明显,而下侧旋涡逐渐变大。这是由于下游转轮的迎流叶片逐渐远离上侧旋涡、同时其凹面对尾流的诱导作用造成的。与之相比,当θ1从108°变化到144°时,上侧旋涡涡心位置向上游偏移,下侧旋涡沿流向被明显拉伸,形状更加细长、扁平,特别是在θ1=128°时,旋涡被拉伸后分解为多个小尺寸旋涡,对流场的扰动加剧。在θ1变化过程中,下游转轮的上侧叶片逐渐靠近上游转轮,使上侧旋涡沿流线的发展被限制;同时,下侧叶片对尾流的诱导聚集作用主要体现在下侧旋涡附近,因此下侧旋涡被拉伸。由于下游转轮对上游转轮尾流发展的阻碍,上游转轮尾流中的旋涡难以脱落,并且在部分安放角下,旋涡向上游转轮靠近,阻碍上游转轮的旋转,因此有可能导致上游转轮性能下降。
为了进一步分析下游转轮安放角对上游转轮尾流的影响,在两转轮的中间位置提取了竖直方向上的尾流速度分布,如图 5所示。从整体来看,6种安放角条件下的尾流速度分布相似,呈中心低、两侧高的V形分布,最小速度的位置保持在两转轮中心的连线附近。在0°~108°范围内,随着安放角增大,尾流的最小速度逐渐减小,中心线两侧速度梯度随着安放角增大而升高,预示着尾流区的扰动增强,能量耗散加剧;与之相反,在108°~144°范围内,随着安放角增大,最小速度逐渐增大,速度下降梯度逐渐降低,说明受转轮影响的低速区域范围变小,这与图 4(d)~(f)中显示的低速区域逐渐向上游移动相对应。

|
| 图 5 两转轮中间位置的竖直方向速度分布 Fig.5 Velocity distributions in vertical direction at the middle cross section between the two rotors |
图 6为不同下游转轮安放角时两转轮中心连线上的速度分布。可以看出,6条曲线都呈现双峰模式。以每条曲线峰谷处的速度最小值为参考,左侧为2个旋涡之间的回流区域,右侧为速度恢复区域。结合图 4的速度云图可以判断,峰谷处速度转折点的位置大致在2个旋涡所形成的三角区域的“角尖”处。在2个旋涡的相互作用下,峰谷左侧回流区域的流体速度上升,其后受到上游转轮阻挡,速度下降,形成左侧曲线峰值;峰谷右侧的尾流流体逐渐远离旋涡区域,在主流区的作用下速度逐渐上升,其后受到下游转轮阻挡,速度下降,形成右侧曲线峰值。由于2个旋涡的存在,回流区域内的流体能量被耗散,且速度恢复区域沿流向长度相对较大,速度恢复时间充足,从而左侧峰值小于右侧峰值;但在108°与128°时,其速度曲线峰谷位置靠近下游转轮,速度恢复区域长度相对较短,因而其左侧峰值大于右侧峰值。此外,在速度恢复区域中,0°与36°、72°与128°的速度曲线斜率近似相等,速度则是以108°为界先减小后恢复;而在回流区域内,速度变化并无明显规律。

|
| 图 6 两转轮中心连线上的速度分布 Fig.6 Velocity distributions along the center line between the two rotors |
图 7为上、下游转轮安放角固定不变时,不同来流速度条件下的流动形态及速度分布。从整体来看,不同来流速度对应的尾流区流动形态相似。随着来流速度增大,集中在2个旋涡附近的低速区域逐渐被压缩;但由于2个旋涡的相互作用,在上游转轮与2个旋涡之间的回流区内出现的高速区域面积逐渐增大。同时,尾流区的流线分布也受到了速度变化的影响。对比不同来流速度下的流线分布可以看出,Re=0.8×105和1.6×105时,尾流区的流线受下游转轮影响更加严重,偏转趋势更加明显;而Re=2.4×105时,2个转轮之间的流线更加平直。

|
| 图 7 上游转轮尾流的形态及速度分布随来流速度的变化 Fig.7 Variations of wake pattern and velocity distributions with the upstream velocity for the upstream rotor |
此外,随着来流速度增大,上游转轮下游的2个旋涡在流向与竖直方向上的发展都受到了限制,旋涡整体向上游转轮移动,涡心位置更加对称,但其占据的面积逐渐减小,特别是在Re=2.4×105时,2个旋涡被限制在上游转轮下游的三角形区域内。当来流速度增大(即水流的动能增大)时,尾流区内的低速流体与主流区的高速流体之间的动量交换增强,旋涡引起的能量耗散被抑制,从而其影响范围减小,两转轮之间水平流线长度增加。因此,高雷诺数时尾流分布更加均匀,接近无下游转轮的情况;来流携带的动能较高时,有利于下游转轮对水能的转化。
图 8为不同来流速度条件下两转轮中间位置竖直方向上的速度分布。从整体来看,各组速度分布相似。由曲线转折点的位置可以推断,随着来流速度增大,尾流在竖直方向上的宽度有逐渐减小的趋势;但在图 8(a)中的Re=0.8×105时,两转折点之间的宽度却明显小于高速时(Re=1.6×105和2.4×105)的宽度,这是来流速度与转轮安放角对流场的共同影响造成的。同时,随着来流速度增大,V形曲线凹陷部分的底部由平坦变得尖耸(即靠近中心区域的曲线斜率随来流速度增大而增大),这说明尾流区中心部分的能量耗散随速度增大而增强,同时尾流中心与主流区的速度相差较大,速度恢复所需时间延长。
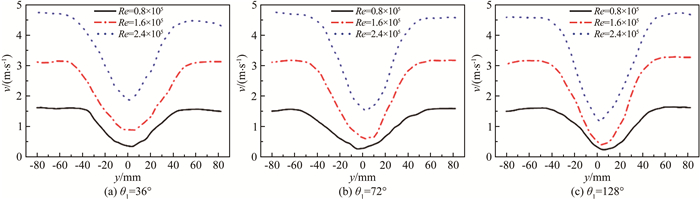
|
| 图 8 不同来流速度时两转轮中间位置竖直方向上的速度分布 Fig.8 Velocity distributions in vertical direction at the middle cross section between the two rotors at different upstream flow velocities |
图 9为不同来流速度条件下两转轮中心连线上的速度分布。从图中可以看出,3组曲线整体都呈现双峰模式,而曲线上升或下降的趋势都与转轮安放角和旋涡有关,原因与图 6相同。但是,在-100mm<x<-80mm区域内,图 9(c)中的3条曲线都呈现出与图 9(a)、(b)不同的上升趋势。分析图 7的速度云图可知,由于下游转轮安放角的影响,速度分布相对于两转轮的中心连线并不对称,而是出现低速区向上或向下偏移的形态,从而在靠近下游转轮时,速度上升。同时,雷诺数的改变对尾流沿流向的速度分布有较明显影响。随着雷诺数增大,峰谷处的转折点逐渐向上游移动,这与图 7中旋涡区随来流速度增大而逐渐向上游转轮偏移相呼应。
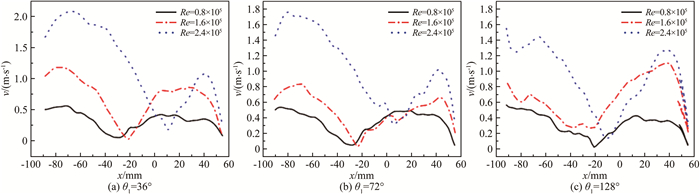
|
| 图 9 不同来流速度时两转轮中心连线上的速度分布 Fig.9 Velocity distributions along the center line of the two rotors at different upstream flow velocities |
涡量分布反映了旋涡在向尾流发展过程中的变化。图 10为在相同来流速度、不同下游转轮安放角情况下尾流中z方向的涡量分布平均结果。其中,正涡量对应的旋转方向为逆时针方向,负涡量对应的旋转方向为顺时针方向。从图中可以看出,由于水力转轮相对于两转轮中心连线并不对称,上下涡量区呈现不对称分布。涡量向下游和主流区的扩散能力与下游转轮在不同安放角下的迎流面积密切相关。对比6幅图可以发现,θ1=0°和144°时,上游尾流高能涡量区的面积较小;而在θ1=72°、108°与128°的尾流场中,涡量区向下游和主流区扩散明显,高能涡量区已经发展到下游转轮位置,几乎与下游转轮的高能涡量区相连通。θ1=0°和144°时,由于转轮迎流面积较小,主流区动能较高的流体与尾流中的流体之间的能量交换作用增强,自上游转轮脱落的涡崩塌,因此高能涡量区沿流向发展的长度有限;而在其他安放角下,下游转轮能接触到绝大部分脱落旋涡并使其破碎,流场中的小尺度涡数量增加。
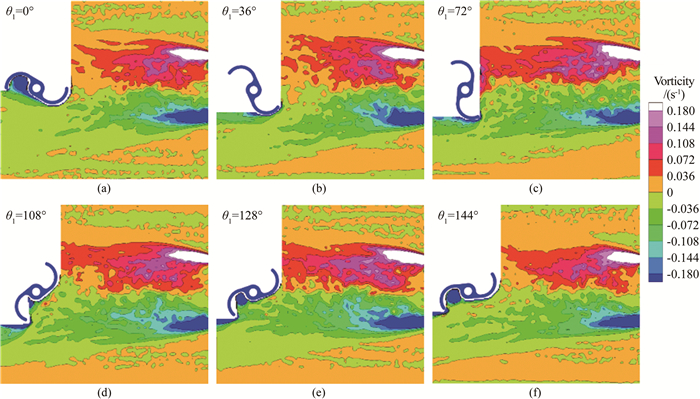
|
| 图 10 不同下游转轮安放角对应的涡量分布(Re=1.6×105) Fig.10 Variations of the vorticity distribution with the different setting angles of the downstream rotor (Re=1.6×105) |
图 11为不同来流速度时尾流中z方向的涡量分布平均结果。从图中可以看出,随着来流速度增大,图 11(a)和(b)中的涡量带逐渐向中心收拢,尾流宽度与转轮直径接近,向主流区的扩散减弱。来流速度较小时,高能涡量区集中于上游转轮的上下叶尖位置;随着来流速度增大,上游转轮上下两侧的涡量增大,并且不断向尾流中心和下游发展,导致尾流中的离散小尺度涡增多,逐渐占据整个尾流区,并与下游转轮附近的涡量区相连接,加剧了上游转轮尾流中的能量耗散,但在较高的来流速度条件下,转轮能够吸收的流体动能显著增加。

|
| 图 11 涡量分布随来流速度的变化 Fig.11 Variations of the vorticity distribution with the upstream flow velocity |
本征正交分解可以将流场信息分解为与时间和空间相关的本征模态的线性组合,旨在获取多维度系统的低维度近似描述,可以反映占主导地位的流动结构,从而对复杂流动进行降阶处理与分析[25]。
图 12、13分别为Re=0.8×105与1.6×105时前3阶的POD模态结构及能量分布。从2组图中可以看出,在低来流速度条件下,第1~3阶模态中的涡量分布区域沿流向的宽度基本不变,而在高来流速度条件下,涡量区沿流向呈明显的扩散状,这与图 11前2列(Re=0.8×105与1.6×105时)的涡量分布相一致。图 12(d)和图 13(d)分别为2种来流速度条件下的各阶模态的能量分布。Re=0.8×105时,涡量场的第1阶模态占据了55%的能量份额,在涡量场中处于支配地位;第2阶模态的能量份额也达到了30%,该模态对应的流动结构对决定尾流场特征也具有重要贡献。随着阶数增加,能量占比曲线急剧下降并趋于平缓,第3阶模态的能量占比约为3%,更高阶模态的能量占比更低,可以认为前3阶模态包含了大部分流动结构的信息,而较高阶模态以小尺度的流动结构为主,粘性耗散和湍流耗散是引起能量损失的主要因素。

|
| 图 12 POD模态结构及能量分布(Re=0.8×105) Fig.12 Flow structures and energy distribution at different POD modes (Re=0.8×105) |

|
| 图 13 POD模态结构及能量分布(Re=1.6×105) Fig.13 Flow structures and energy distribution at different POD modes (Re=1.6×105) |
第1~3阶模态中的涡量分布相似,以正涡量和负涡量混合、错列排列为主要特征。同时,随着模态阶数的增加,尾流中小尺度涡元增加,大尺寸涡元减少,这意味着随着阶数增加,能量逐渐由大尺度涡向小尺度涡传递。在较高来流速度条件下,涡量区在垂直于主流方向显著拓展,涡量整体增大,流场中的湍动加剧,如图 13所示。
3 结论(1) 上游转轮尾流在向下游发展的过程中形成速度恢复区域和回流区域。来流速度增大时,速度恢复区域向上游转轮延伸,回流区域被压缩。在速度恢复区域,0°与36°、72°与128°的速度曲线斜率近似相等;速度则是以安放角108°为界先减小后恢复;而回流区域内,速度的变化不存在明显规律。
(2) 尾流中旋涡的发展受到下游转轮安放角的影响,旋涡涡心位置随安放角变化而上下偏移,在部分角度下,旋涡被拉伸变得扁平,流线也因此呈现出与无下游转轮时不同的偏转状态。来流速度增大使尾流区的宽度减小,尾流中的旋涡区域在流动方向与竖直方向上受到压缩,逐渐向上游转轮靠拢,同时涡心的位置更加对称。
(3) 在一定的下游转轮安放角条件下,随着来流速度增大,流场中高能涡量区向尾流中心和下游发展,脱落涡的破碎加剧,尾流中的高能涡量区逐渐与下游转轮的涡量区相连通,小尺度涡数量不断增加。尾流中的大尺度涡结构和大部分能量包含于前3阶POD模态中,而高阶POD模态主要表征小尺度的流动结构。
| [1] |
王蔚峰, 康灿, 杨敏官. 新型垂直轴螺旋型风力叶轮的研究[J]. 太阳能学报, 2013, 34(8): 1421-1426. Wang W F, Kang C, Yang M G. Research of a novel spiral vertical-axis wind turbine rotor[J]. Acta Energiae Solaris Sinica, 2013, 34(8): 1421-1426. DOI:10.3969/j.issn.0254-0096.2013.08.020 |
| [2] |
Kacprzak K, Liskiewicz G, Sobczak K. Numerical investigation of conventional and modified Savonius wind turbines[J]. Renewable Energy, 2013, 60(4): 578-585. |
| [3] |
Jaohindy P, Ennamiri H, Garde F. Numerical investigation of airflow through a Savonius rotor[J]. Wind Energy, 2014, 17(6): 853-868. DOI:10.1002/we.v17.6 |
| [4] |
Nasef M H, El-Askary W A, AbdEl-Hamid A A, et al. Evaluation of savonius rotor performance:static and dynamic studies[J]. Journal of Wind Engineering and Industrial Aerody-namics, 2013, 123(Part A): 1-11. |
| [5] |
Zhang B S, Song B W, Mao Z Y, et al. A novel parametric modeling method and optimal design for Savonius wind turbines[J]. Energies, 2017, 10(3): 1-20. |
| [6] |
Kang C, Yang X, Wang Y L. Turbulent flow characteristics and dynamics response of a vertical-axis spiral rotor[J]. Energies, 2013, 6(6): 2741-2758. DOI:10.3390/en6062741 |
| [7] |
Kumar A, Saini R P. Performance analysis of a single stage modified Savonius hydrokinetic turbine having twisted blades[J]. Renewable Energy, 2017, 113: 461-478. DOI:10.1016/j.renene.2017.06.020 |
| [8] |
Fujisawa N, Gotoh F. Visualization study of the flow in and around aSavonius rotor[J]. Experiments in Fluids, 1992, 12(6): 407-412. DOI:10.1007/BF00193888 |
| [9] |
Torresi M, de Benedittis F A, Fortunato B, et al. Performance and flow field evaluation of a Savonius rotor tested in a wind tunnel[J]. Energy Procedia, 2014, 45: 207-216. DOI:10.1016/j.egypro.2014.01.023 |
| [10] |
Sarma N K, Biswas A, Misra R D. Experimental and computational evaluation of Savonius hydrokinetic turbine for low velocity condition with comparison to Savonius wind turbine at the same input power[J]. Energy Conversion and Manage-ment, 2014, 83: 88-98. DOI:10.1016/j.enconman.2014.03.070 |
| [11] |
Gao X X, Yang H X, Lu L. Optimization of wind turbine layout position in a wind farm using a newly-developed two-dimensional wake model[J]. Applied Energy, 2016, 174: 192-200. DOI:10.1016/j.apenergy.2016.04.098 |
| [12] |
Park J, Law K H. Layout optimization for maximizing wind farm power production using sequential convex programming[J]. Applied Energy, 2015, 151: 320-334. DOI:10.1016/j.apenergy.2015.03.139 |
| [13] |
Zhang B S, Song B W, Mao Z Y, et al. A novel wake energy reuse method to optimize the layout for Savonius-type vertical axis wind turbines[J]. Energy, 2017, 121: 341-335. DOI:10.1016/j.energy.2017.01.004 |
| [14] |
Zuo W, Wang X D, Kang S. Numerical simulations on the wake effect of H-type vertical axis wind turbines[J]. Energy, 2016, 106: 691-700. DOI:10.1016/j.energy.2016.02.127 |
| [15] |
Lam H F, Peng H Y. Study of wake characteristics of a vertical axis wind turbine by two- and three-dimensional computational fluid dynamics simulations[J]. Renewable Energy, 2016, 90: 386-398. DOI:10.1016/j.renene.2016.01.011 |
| [16] |
Shaheen M, El-Sayed M, Abdallah S. Numerical study of two-bucket Savonius wind turbine cluster[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 137: 78-89. DOI:10.1016/j.jweia.2014.12.002 |
| [17] |
Shigetomi A, Murai Y, Tasaka Y, et al. Interactive flow field around two Savonius turbines[J]. Renewable Energy, 2011, 36(2): 536-545. DOI:10.1016/j.renene.2010.06.036 |
| [18] |
孙科, 李岩, 王凯, 等. 串列竖轴水轮机尾流场影响CFD模拟分析[J]. 哈尔滨工业大学学报, 2018, 50(5): 185-191. Sun K, Li Y, Wang K, et al. CFD simulation analysis on the wake effect of tandem vertical axis tidal turbines[J]. Journal of Harbin Institute of Technology, 2018, 50(5): 185-191. |
| [19] |
Ahmadi-Baloutaki M, Carriveau R, Ting D S-K, et al. A wind tunnel study on the aerodynamic interaction of vertical axis wind turbines in array configurations[J]. Renewable Energy, 2016, 96(Part A): 904-913. |
| [20] |
杨瑞, 张志勇, 王强, 等. 串列风力机三维尾流场的实验研究[J]. 兰州理工大学学报, 2017, 43(5): 60-64. Yang R, Zhang Z Y, Wang Q, et al. Experimental study of three-dimensional wake of tandem windturbines[J]. Journal of Lanzhou University of Technology, 2017, 43(5): 60-64. DOI:10.3969/j.issn.1673-5196.2017.05.011 |
| [21] |
郭峰山, 贾明, 林伟豪, 等. 竖轴潮流能水轮机群数值模拟研究[J]. 太阳能学报, 2014, 35(9): 1810-1815. Guo F S, Jia M, Lin W H, et al. Numerical investigation of vertical tidal turbine arrays[J]. Acta Energiae Solaris Sinica, 2014, 35(9): 1810-1815. DOI:10.3969/j.issn.0254-0096.2014.09.039 |
| [22] |
王勇, 郝南松, 耿子海, 等. 基于时间解析PIV的圆柱绕流尾迹特性研究[J]. 实验流体力学, 2018, 32(1): 64-70. Wang Y, Hao N S, Geng Z H, et al. Measurements of circular cylinder's wake using time-resolved PIV[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(1): 64-70. |
| [23] |
Zhou T, Rempfer D. Numerical study of detailed flow field and performance of Savonius wind turbines[J]. Renewable Energy, 2013, 51(2): 373-381. |
| [24] |
Hassanzadeh A R, Yaakob O B, Ahmed Y M, et al. Numerical simulation for unsteady flow over marine current turbine rotors[J]. Wind and Structures, 2016, 23(4): 301-311. DOI:10.12989/was.2016.23.4.301 |
| [25] |
谢龙, 靳思宇, 王玉璋, 等. 阀体后90°圆形弯管内部流场PIV测量及POD分析[J]. 实验流体力学, 2012, 26(3): 21-25, 31. Xie L, Jin S Y, Wang Y Z, et al. PIV measurement and POD analysis of inner flow flied in 90° bending duct of circular-section with fore-end valve[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(3): 21-25, 31. DOI:10.3969/j.issn.1672-9897.2012.03.004 |



