2. 北卡罗来纳州立大学 机械与航空航天系, 美国 罗利 27607
2. Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh 27607, USA
针对液滴以一定速度撞击固体表面的瞬态动力学行为的研究,在喷墨打印[1]、发动机燃烧[2]、工业喷涂[3]、飞行器飞行安全[4]、液冷散热系统[5]、农作物种植[6]、自然界物质输运[7]、新能源开发[8]等领域都有着重要的意义。
长期以来,相关研究局限于液滴撞击刚性固体表面。近年来,柔性材料因其柔韧、延展性高、可自由弯曲等显著区别于刚性材料的独特性能而逐渐获得研究人员的关注。在种类繁多的柔性材料基底中,聚二甲基硅氧烷(PDMS)以其化学性质稳定、透光度高、热稳定性好等优势成为研究者的首选。Beemer等基于粘附力学,利用PDMS设计出一种与冰具有极低粘结强度的柔性防冰涂层,能够防止冰层粘附于固体表面[9]。Wang等基于高分子材料之间的表面接触起电效应,利用PDMS薄层与聚酯纤维薄片的摩擦,在两层聚合物薄膜间形成电势差,开发出摩擦纳米发电机,将微小的机械能转化为电能[10]。Sun等开发出混合材料太阳能电池板,通过在太阳能电池板表面覆盖PDMS和PEDOT:PSS薄膜,可以将雨滴撞击电池板的机械能转化为电能,该装置的能量转化效率很大程度上取决于水滴撞击PDMS表面后的铺展面积[8]。
液滴撞击固体表面的铺展面积主要由液滴在铺展阶段的移动接触线直径所确定。在铺展阶段,液滴在惯性力的作用下从撞击点向外边缘铺展,动能减小,表面能增大。当移动接触线的速度降为0时,液滴达到最大铺展直径。对于液滴撞击刚性固体表面,决定最大铺展直径的主导因素是液体的粘性能量耗散和表面张力(分别由雷诺数Re和韦伯数We表征)[11]。Hung等研究了固体表面的润湿性对液滴铺展速度的影响[12]。毕菲菲等通过研究液滴撞击金属材料表面的铺展过程,认为液体的粘度对铺展过程起主导作用,而表面张力对液滴的回缩起主导作用[13]。Scheller[14]、Mao[15]和Roisman[16]等分别给出了预测最大铺展直径的经验公式、半经验公式和纯理论模型。Lee[17]和Huang[18]等针对液滴以较低韦伯数撞击固体表面的最大铺展直径预测值与实验结果误差较大的问题,采用不同的方法修正了最大铺展直径的预测公式,与实验结果得以更好的吻合。
与刚性材料不同,液滴撞击柔性材料时,由于柔性材料的可变形特征以及伴随而来的能量吸收和损耗,必然会在一定程度上改变液滴撞击后的铺展行为[19-22]。Carre等指出,当固体足够“软”时,液滴的铺展速度和界面的形成由软固体物质的力学特性决定[23]。Alizadeh等对比了液滴在多种柔性和刚性材料表面铺展和收缩过程的特性,发现液滴的收缩随着材料弹性的降低而减弱,认为与软物质的粘弹性能量耗散相比,液体的粘性能量耗散可以忽略不计[24]。Chen等研究了液滴在不同剪切模量的柔性材料表面的铺展过程,发现铺展过程的持续时间由固体材料的柔性决定,并认为柔性材料的强度不影响液滴撞击后的铺展过程,但会影响其后的收缩过程及振荡过程[25-26];Chen等还指出液滴在撞击柔性材料表面时,由于软材料的变形将会在液体与固体之间产生空气薄层,该空气薄层会在一定程度上改变系统的表面能并影响液滴在软材料表面的铺展行为[27]。Howland通过实验研究了乙醇液滴撞击不同强度硅凝胶表面的飞溅过程,指出液滴撞击软基底时,需要比硬基底多70%的动能才能出现飞溅现象[22]。
对于液滴撞击刚性材料表面的铺展过程,国内外学者已有较为系统的研究,但对于液滴撞击柔性固体表面后的铺展过程,尚未开展系统和细致的分析,铺展直径随柔性材料力学性能参数的变化规律也没有统一的结论。为进一步研究液滴撞击柔性材料表面的铺展行为,本文从铺展阶段的能量守恒角度出发,综合考虑柔性材料受压导致的粘性变形耗能、移动接触线处润湿脊[19, 23]导致的柔性材料粘弹性能量耗散和液体铺展导致的液体内部粘性能量耗散,对液滴最大铺展系数随柔性材料的强度和厚度的变化规律进行实验研究,进一步揭示液滴在柔性材料表面铺展过程的内在机理。
1 实验装置 1.1 PDMS样品制备柔性材料样品由美国道康宁公司生产的PDMS预聚物和固化剂制成(Dowcorning 184),预聚物和固化剂使用了2种质量配比(10:1和40:1)。将充分混合的PDMS混合液敷设于直径100mm的Prime级硅片表面,放入真空环境静置20min,待PDMS混合液中的气泡完全释放后,保持120℃恒温加热15min,获得厚度在0.3mm以上的PDMS样品。使用Laurell甩胶机,通过调整转速和时间,在直径100mm的Prime级硅片上旋涂得到厚度为0.03和0.09mm的PDMS样品。每种配比制作了5个不同厚度的样品。各样品的预聚物和固化剂质量配比Ratio、厚度b、剪切弹性模量G[26]如表 1所示。
| No. | Ratio | b/mm | G/kPa |
| 1 | 10:1 | 0.03 | 710 |
| 2 | 10:1 | 0.09 | 710 |
| 3 | 10:1 | 0.30 | 710 |
| 4 | 10:1 | 1.00 | 710 |
| 5 | 10:1 | 3.60 | 710 |
| 6 | 40:1 | 0.03 | 36 |
| 7 | 40:1 | 0.09 | 36 |
| 8 | 40:1 | 0.30 | 36 |
| 9 | 40:1 | 1.00 | 36 |
| 10 | 40:1 | 3.60 | 36 |
实验装置如图 1所示。实验液体为美国Millipore制水仪制成的去离子水。微量进液器在针头前端稳定地生成液滴(实验中产生的液滴直径约2.36mm),在重力作用下自由下落,以一定初速度垂直撞击下方水平放置的PDMS样品表面,通过调节针头前端与PDMS样品上表面的距离获得不同的撞击速度。实验中使用Phantom V4.3高速摄影机(水平放置),Nikon AF Micro 60mm f/2.8D微距镜头。以LED灯作为照明光源,使用凸透镜获得均匀的平行光场。采用背光法拍摄,拍摄速率设定为4400帧/s。所有实验过程均在20℃的恒温下完成。
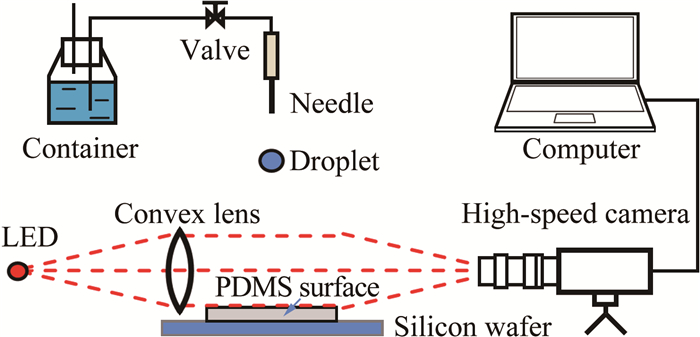
|
| 图 1 实验装置示意图 Fig.1 Sketch of the experimental setup |
在3种不同材料表面(配比分别为10:1和40:1的PDMS样品表面、高纯硅表面),利用微量进液器测量了实验液体的平衡接触角θe、前进接触角θa和收缩接触角θr,结果如表 2所示。
| Surfaces | θe | θa | θr |
| PDMS 10:1 | 120°±2° | 116°±2° | 88°±2° |
| PDMS 40:1 | 125°±3° | 123°±2° | 24°±2° |
| Silicon | 80°±2° | 92°±2° | 74°±2° |
由于液滴从针头脱落瞬间的表面张力扰动影响以及空气阻力的作用,液滴在下落过程中的形状会有轻微振荡,且逐渐趋于稳定,近似为椭球。采用名义直径D0定义液滴的平均直径:
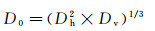 (1)
(1)
式中,Dh、Dv分别为液滴的最大水平直径和最大竖向直径。
实验共设置9个不同的液滴自由下落高度H。每个实验工况均重复3次,获得的液滴撞击参数如表 3所示。经过对实验结果的初步分析,本实验具有很高的可重复性。
| D0/mm | H/mm | v0/(m·s-1) | Re | We |
| 2.36±0.07 | 6 | 0.216±0.006 | 481±18.0 | 1.52±0.09 |
| 12 | 0.409±0.002 | 899±14.5 | 5.39±0.10 | |
| 25 | 0.623±0.007 | 1429±26.3 | 13.05±0.36 | |
| 50 | 0.881±0.007 | 1954±29.2 | 25.23±0.52 | |
| 100 | 1.311±0.018 | 2882±56.4 | 55.38±1.63 | |
| 200 | 1.864±0.009 | 4099±43.1 | 111.96±1.52 | |
| 400 | 2.602±0.017 | 6017±90.4 | 229.44±3.99 | |
| 800 | 3.544±0.057 | 7995±210.0 | 415.18±20.90 | |
| 1600 | 4.743±0.142 | 10 520±301.0 | 731.12±48.70 |
表 3中,H为液滴的下落高度,v0为液滴与PDMS样品表面撞击瞬间的液滴质心速度,该速度通过液滴与固体表面接触瞬间之前的连续10帧高速摄影图像序列中液滴质心的位移计算获得。Re和We分别为撞击瞬间液滴的雷诺数和韦伯数:
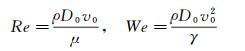 (2)
(2)
式中,ρ、μ和γ分别为实验液体的密度、粘性系数和表面张力系数。
2 实验结果分析 2.1 液滴撞击柔性材料表面的铺展过程分析图 2为典型的液滴撞击PDMS样品表面的高速摄影照片,可见液滴撞击样品表面的过程大致分为3个阶段:初始接触阶段(图 2(b))、铺展阶段(图 2(c))和收缩阶段(图 2(d)和(e))。液滴撞击样品表面前的形状并非理想圆球,由于其自身的振荡及空气阻力的作用,其外形近似为椭球(图 2(a))。撞击后液滴形状发生急剧变化,前端与固体表面接触部分的竖向速度迅速降低为0,而液滴的上部仍然在惯性作用下继续下落,此时液滴的形状类似于草帽形。在撞击速度较低的情况下,可以清晰地看到由于表面张力波的传递,在液滴表面出现的阶梯状特征,如图 2(b)所示。

|
| 图 2 高速摄影照片(Ratio=10:1, v0=0.623m/s) Fig.2 Photos of impact procedure (Ratio=10:1, v0=0.623m/s) |
初始接触阶段之后,液滴随即进入铺展阶段,以轴对称的形式沿径向向外铺展。该过程中,液滴的表面积逐渐增大,动能转换为表面能,并有部分能量通过液滴内部粘性能量耗散的方式消耗。铺展的液滴薄片的前缘速度逐渐降低,并在薄片边缘逐渐汇聚,形成一个环状凸起(图 2(c))。此后,由于表面张力的作用,液滴开始回缩,进入后期的收缩阶段。液滴与固体表面的接触面直径逐渐减小,在撞击点位置产生回弹。在不同实验条件下,液滴可能会出现部分回弹甚至是全回弹。
液滴在柔性材料表面的铺展过程中,其表面张力的垂直分量将导致柔性表面在移动接触线附近发生微小变形,该变形称为“润湿脊”[19, 23]。润湿脊的高度取决于柔性材料的弹性模量,与γ/G(液体表面张力系数/固体剪切弹性模量)成正比。随着移动接触线的运动,润湿脊也随之沿径向移动。柔性材料在润湿脊处变形的产生及消失过程会导致系统能量的粘弹性能量耗散。
当液滴在铺展阶段末期达到最大铺展直径Dmax时,液滴薄层前缘的速度降为0。忽略此时的液滴动能,则系统满足能量守恒方程:
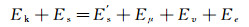 (3)
(3)
等式左侧为液滴撞击柔性材料表面之前的系统初始总能量,Ek、Es分别为撞击初始时刻液滴的动能和表面能。等式右侧为液滴达到最大铺展直径时的系统总能量,其中E's为达到最大铺展直径时液滴的表面能[28]、Eμ为液滴内部的粘性能量耗散[18]、Ev为润湿脊随接触线移动导致的柔性材料粘弹性能量耗散[24]、Ee为液滴撞击过程中柔性材料沿厚度方向发生受压变形所吸收的应变能:
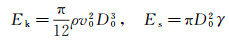 (4)
(4)
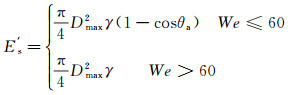 (5)
(5)
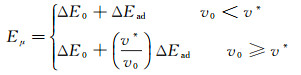 (6)
(6)
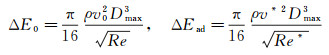 (7)
(7)
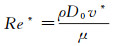 (8)
(8)
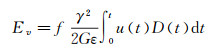 (9)
(9)
其中,ΔE0为经典理论计算的液体粘性能量耗散,ΔEad为低韦伯数条件下的附加粘性能量耗散,v*、Re*分别为附加粘性能量耗散对应的临界速度和临界雷诺数,f为粘弹性材料耗能模量与复模量的比值,ε为移动接触线附近的特征截断距离,u为移动接触线的运动速度。
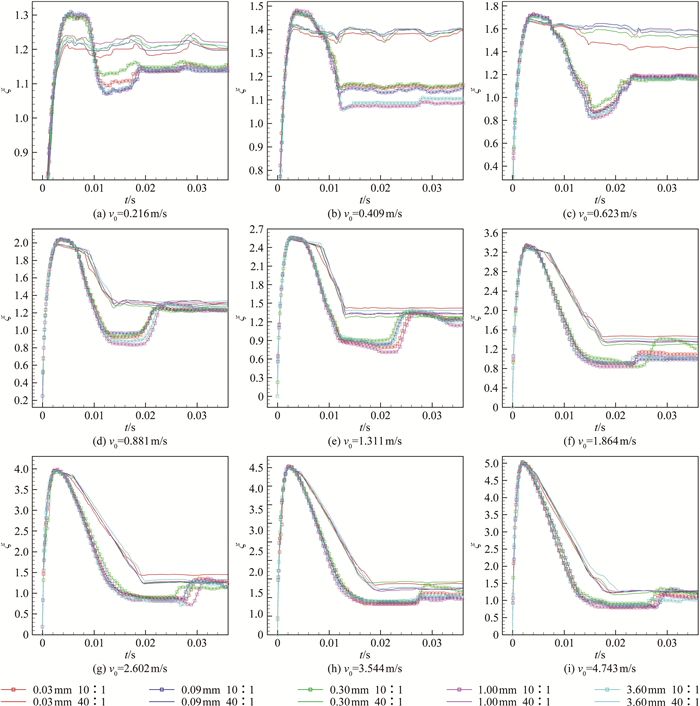
2.2 柔性材料厚度对最大铺展系数的影响通过自行编制的Matlab程序,可以对高速摄影图像序列进行判读,获取液滴与固体表面的接触面直径。不同实验条件下的液滴铺展系数ξ(ξ=D(t)/D0,D(t)为移动接触线直径)随时间t的变化如图 3所示。
|
| 图 3 不同实验条件下的液滴铺展系数 Fig.3 Spread factor of liquid droplet |
由图 3可以看出,在实验的测量精度范围内,相同直径的液滴以相同的速度撞击配比相同、厚度不同的PDMS样品表面,移动接触线在前期的铺展过程中基本一致,且液滴的最大铺展系数也基本相同。
实验所使用的基底材料为硅片,其弹性模量的数量级约为1011Pa,比实验所使用的柔性材料高出6个数量级以上,可作为刚体处理。当液滴以一定速度撞击PDMS样品时,PDMS样品在碰撞方向上会形成相应的受压变形。按照经典粘弹性理论,此类粘弹性材料除了发生弹性变形之外,还将产生能量的粘性耗散,而该部分能量耗散是不可恢复的,将会在一定程度上降低系统的总能量,减小液滴的最大铺展系数。当PDMS样品的厚度仅为0.03mm时,样品能够产生的粘性能量耗散非常小,可近似认为等于0。随着厚度的增加,PDMS样品能够吸收的粘性能量耗散随之增加。但由图 3的实验结果可以看出,在保持其他参数不变的情况下,随着厚度逐渐增加到3.60mm,最大铺展系数并没有发生明显改变。说明在本实验参数范围内,液滴撞击PDMS样品使其受压所导致的柔性材料粘性能量耗散与系统的总能量相比很小,不会对液滴的铺展过程产生明显影响。
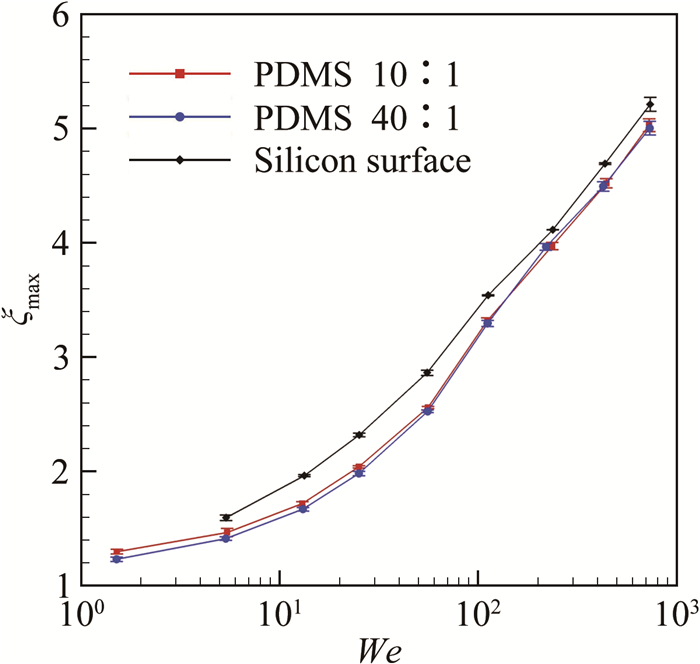
2.3 PDMS弹性模量对最大铺展系数的影响图 4为液滴撞击3种不同表面(2种不同弹性模量的PDMS样品表面、没有覆盖PDMS的高纯硅表面)的最大铺展系数ξmax(ξmax=Dmax/D0)随韦伯数We的变化曲线。可以看出,随着韦伯数的增大,3种表面上的最大铺展系数均随之增大。在本实验的韦伯数范围内,液滴撞击硅片表面后的最大铺展系数明显高于柔性材料表面。在相对较低的韦伯数下(We<20),韦伯数基本相同的液滴撞击不同弹性模量的PDMS样品表面所获得的最大铺展系数存在一定差别,在弹性模量较低的样品表面上将获得较小的最大铺展系数。随着韦伯数的增大,这种差异逐渐消失。该现象可尝试通过液滴铺展过程中的能量转换进行解释。
|
| 图 4 液滴撞击不同材料表面的最大铺展系数 Fig.4 Spread factor of liquid droplet |
液滴撞击柔性材料表面并达到最大铺展直径时,系统初始总能量中的一部分转换为铺展液体的表面能E's,另一部分通过润湿脊的粘弹性能量耗散Ev和液体内部的粘性能量耗散Eμ而损失(根据上节的分析,忽略柔性材料受压变形所导致的能量耗散)。当液滴撞击刚性的硅片表面时,硅片表面不会形成润湿脊,不存在由润湿脊所导致的粘弹性能量耗散。
从式(9)可以看出,在其他参数基本保持不变的条件下,润湿脊导致的粘弹性能量耗散与柔性材料的剪切弹性模量G成反比关系,即柔性材料越“软”,导致的粘弹性能量耗散越多。与质量配比为10:1的样品相比,40:1的样品的剪切弹性模量G要低1个数量级以上,由此导致的粘弹性能量耗散高出1个数量级。
定义系统初始总能量Etotal为液滴初始动能Ek与初始表面能Es之和:
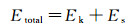 (10)
(10)
式中各项可由式(4)计算得出。定义Ψ为润湿脊导致的粘弹性能量耗散与系统初始总能量之比:
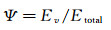 (11)
(11)
表 4列出了液滴撞击2种不同配比的PDMS样品表面的液滴初始总能量Etotal、粘弹性能量耗散Ev以及Ψ的数值。可见,随着韦伯数的增大,粘弹性能量耗散Ev占总能量的比例降低,柔性材料的弹性模量对液滴在其表面铺展行为的影响逐渐降低。
| We | PDMS 10:1 | PDMS 40:1 | |||||
| Etotal | Ev | Ψ | Etotal | Ev | Ψ | ||
| 1.5 | 1.43×10-6 | 3.78×10-8 | 2.64% | 1.43×10-6 | 4.94×10-7 | 34.5% | |
| 5.4 | 1.86×10-6 | 4.74×10-8 | 2.55% | 1.85×10-6 | 6.16×10-7 | 33.3% | |
| 13.1 | 2.61×10-6 | 7.16×10-8 | 2.74% | 2.61×10-6 | 9.31×10-7 | 35.7% | |
| 25.2 | 3.93×10-6 | 9.19×10-8 | 2.34% | 3.94×10-6 | 1.19×10-6 | 30.3% | |
| 55.4 | 7.18×10-6 | 1.45×10-7 | 2.02% | 7.20×10-6 | 1.89×10-6 | 26.2% | |
| 112.0 | 1.31×10-5 | 2.46×10-7 | 1.87% | 1.32×10-5 | 3.20×10-6 | 24.2% | |
| 229.0 | 2.55×10-5 | 3.82×10-7 | 1.50% | 2.51×10-5 | 4.97×10-6 | 19.8% | |
| 415.0 | 4.69×10-5 | 4.81×10-7 | 1.03% | 4.72×10-5 | 6.26×10-6 | 13.3% | |
| 731.0 | 7.34×10-5 | 5.61×10-7 | 0.76% | 7.48×10-5 | 7.29×10-6 | 9.74% | |
定义最大铺展总能量E'total为液滴达到最大铺展直径时的表面能、液滴铺展过程中的润湿脊粘弹性能量耗散以及液滴的粘性能量耗散之和:
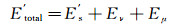 (12)
(12)
式中各项可由式(4)~(9)计算得出。
图 5为系统初始总能量Etotal以及液滴在不同柔性表面的最大铺展总能量E'total随韦伯数的变化曲线。利用理论公式获得的E'total与通过实验数据直接计算得到的Etotal基本吻合,最大相对误差为16.9%,表明本文所建立的能量模型能够比较准确地反映液滴撞击柔性材料铺展过程的能量转化及耗散规律。
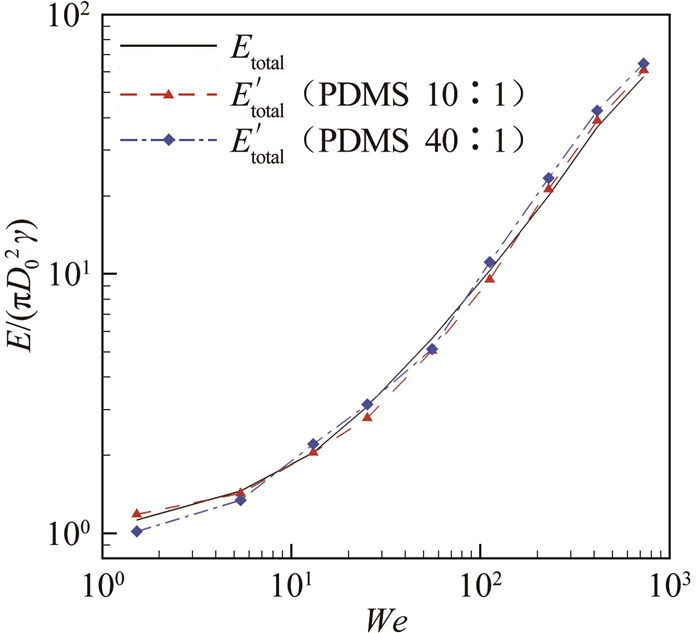
|
| 图 5 初始总能量与最大铺展总能量的比较 Fig.5 Comparison of Etotal and E'total |
进一步分析表明,当液滴以中等速度(We≈50)撞击柔性材料表面时,最大铺展总能量E'total与系统初始总能量Etotal的吻合程度较好。在更高或更低的韦伯数条件下,偏差增大。分析认为,该现象主要由以下3个原因导致:(1)低韦伯数时,液滴的力学行为主要由液体表面张力控制。由于此时液滴铺展的直径较小,达到最大铺展直径时所形成的液体薄层的厚度较大,形状较为不规则,因此利用式(5)计算得到的液滴达到最大铺展直径时的表面能与真实情况差别较大,误差主要由表面能的计算所引起。(2)高韦伯数时,液滴的力学行为主要由液体的粘性力控制。液滴在铺展过程中的粘性能量耗散逐渐占据系统能量耗散的主导地位,润湿脊导致的粘弹性能量耗散影响逐渐减小,误差主要由液体内部粘性能量耗散的计算所引起。(3)根据式(9),润湿脊导致的柔性材料粘弹性能量耗散的计算准确度在很大程度上依赖于柔性材料的动态力学性能参数的测量。因此,柔性材料力学性能参数的选择对分析结果也有较大的影响。
3 结论建立了用于观测液滴撞击柔性材料的实验平台,用高速摄影机获取了液滴撞击不同厚度、不同弹性模量的柔性PDMS样品表面的全过程, 得到以下结论:
(1) 在液滴撞击柔性材料过程中,柔性材料受压变形所导致的粘性能量耗散与系统的总能量相比很小,不会对液滴的铺展过程产生明显影响。
(2) 分析了柔性材料弹性模量对最大铺展系数的影响,讨论了液滴铺展过程中的能量转换过程,在系统能量守恒方程中引入了润湿脊导致的柔性材料粘弹性能量耗散。分析表明,该能量方程模型能较好地反映液滴撞击柔性材料铺展过程的能量转化及耗散规律。
| [1] |
van Dam D B, Le Clerc C. Experimental study of the impact of an ink-jet printed droplet on a solid substrate[J]. Physics of Fluids, 2004, 16(9): 3403-3414. DOI:10.1063/1.1773551 |
| [2] |
Gavaises M, Theodorakakos A, Bergeles G. Modeling wall impaction of diesel sprays[J]. International Journal of Heat and Fluid Flow, 1996, 17(2): 130-138. DOI:10.1016/0142-727X(95)00097-A |
| [3] |
Sampath S, Jiang X. Splat formation and microstructure development during plasma spraying:deposition temperature effects[J]. Materials Science and Engineering:A, 2001, 304-306: 144-150. DOI:10.1016/S0921-5093(00)01464-7 |
| [4] |
张洪, 张文倩, 郑英. 过冷大水滴结冰探测技术研究进展[J]. 实验流体力学, 2016, 30(3): 33-39. Zhang H, Zhang W Q, Zheng Y. Research progress on supercooled large droplet icing detection technology[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(3): 33-39. |
| [5] |
叶学民, 李永康, 李春曦. 受热基底上的液滴铺展及换热特性[J]. 物理学报, 2016, 65(23): 234701. Ye X M, Li Y K, Li C X. Spreading and heat transfer characteristics of droplet on a heated substrate[J]. Acta Physica Sinica, 2016, 65(23): 234701. DOI:10.7498/aps.65.234701 |
| [6] |
贾卫东, 朱和平, 董祥, 等. 喷雾液滴撞击大豆叶片表面研究[J]. 农业机械学报, 2013, 44(12): 87-94, 113. Jia W D, Zhu H P, Dong X, et al. Impact of spray droplet on soybean leaf surface[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(12): 87-94, 113. DOI:10.6041/j.issn.1000-1298.2013.12.015 |
| [7] |
Joung Y S, Buie C R. Aerosol generation by raindrop impact on soil[J]. Nature Communications, 2015, 6: 6083. DOI:10.1038/ncomms7083 |
| [8] |
Liu Y Q, Sun N, Liu J W, et al. Integrating a silicon solar cell with a triboelectric nanogenerator via a mutual electrode for harvesting energy from sunlight and raindrops[J]. ACS Nano, 2018, 12(3): 2893-2899. DOI:10.1021/acsnano.8b00416 |
| [9] |
Beemer D L, Wang W, Kota A K. Durable gels with ultra-low adhesion to ice[J]. Journal of Materials Chemistry A, 2016, 4(47): 18253-18258. DOI:10.1039/C6TA07262C |
| [10] |
Cao X, Yang J, Wang N, et al. Triboelectric nanogenerators driven self-powered electrochemical processes for energy and environmental science[J]. Advanced Energy Materials, 2016, 6(23): 1600665. DOI:10.1002/aenm.201600665 |
| [11] |
Bennett T, Poulikakos D. Splat-quench solidification:estimating the maximum spreading of a droplet impacting a solid surface[J]. Journal of Materials Science, 1993, 28(4): 963-970. DOI:10.1007/BF00400880 |
| [12] |
Hung Y L, Wang M J, Liao Y C, et al. Initial wetting velocity of droplet impact and spreading:Water on glass and parafilm[J]. Colloids and Surfaces A:Physicochemical and Engineering Aspects, 2011, 384(1-3): 172-179. |
| [13] |
毕菲菲, 郭亚丽, 沈胜强, 等. 液滴撞击固体表面铺展特性的实验研究性[J]. 物理学报, 2012, 61(18): 184702. Bi F F, Guo Y L, Shen S Q, et al. Experimental study of spread characteristics of droplet impacting solid surface[J]. Acta Physica Sinica, 2012, 61(18): 295-300. |
| [14] |
Scheller B L, Bousfield D W. Newtonian drop impact with a solid surface[J]. AIChE Journal, 1995, 41(6): 1357-1367. DOI:10.1002/(ISSN)1547-5905 |
| [15] |
Mao T, Kuhn D C S, Tran H. Spread and rebound of liquid droplets upon impact on flat surfaces[J]. AIChE Journal, 1997, 43(9): 2169-2179. DOI:10.1002/(ISSN)1547-5905 |
| [16] |
Roisman I V, Rioboo R, Tropea C. Normal impact of a liquid drop on a dry surface:model for spreading and receding[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2002, 458(2022): 1411-1430. DOI:10.1098/rspa.2001.0923 |
| [17] |
Lee J B, Laan N, de Bruin K G, et al. Universal rescaling of drop impact on smooth and rough surfaces[J]. Journal of Fluid Mechanics, 2016, 786(4): R4. |
| [18] |
Huang H M, Chen X P. Energetic analysis of drop's maximum spreading on solid surface with low impact speed[J]. Physics of Fluids, 2018, 30(2): 022106. |
| [19] |
Shanahan M E R, Carre A. Viscoelastic dissipation in wetting and adhesion phenomena[J]. Langmuir, 1995, 11(4): 1396-1402. DOI:10.1021/la00004a055 |
| [20] |
Pepper R E, Courbin L, Stone H A. Splashing on elastic membranes:The importance of early-time dynamics[J]. Physics of Fluids, 2008, 20(8): 082103. DOI:10.1063/1.2969755 |
| [21] |
Rioboo R, Voué M, Adão H, et al. Drop impact on soft surfaces:beyond the static contact angles[J]. Langmuir, 2010, 26(7): 4873-4879. DOI:10.1021/la9036953 |
| [22] |
Howland C J, Antkowiak A, Castrejon-Pita J R, et al. It's harder to splash on soft solids[J]. Physical Review Letters, 2016, 117(18): 184502. DOI:10.1103/PhysRevLett.117.184502 |
| [23] |
Carre M, Shanahan M E R. Direct evidence for viscosity-independent spreading on a soft solid[J]. Langmuir, 1995, 11(3): 24-26. |
| [24] |
Alizadeh A, Bahadur V, Shang W, et al. Influence of substrate elasticity on droplet impact dynamics[J]. Langmuir, 2013, 29(14): 4520-4524. DOI:10.1021/la304767t |
| [25] |
Chen L Q, Auernhammer G K, Bonaccurso E. Short time wetting dynamics on soft surfaces[J]. Soft Matter, 2011, 7(19): 9084-9089. DOI:10.1039/c1sm05967j |
| [26] |
Chen L Q, Bonaccurso E, Deng P G, et al. Droplet impact on soft viscoelastic surfaces[J]. Physical Review E, 2016, 94(6): 063117. DOI:10.1103/PhysRevE.94.063117 |
| [27] |
Chen L Q, Li Z G. Bouncing droplets on nonsuperhydrophobic surfaces[J]. Physical Review E, 2010, 82(1): 016308. DOI:10.1103/PhysRevE.82.016308 |
| [28] |
Pasandideh-Fard M, Qiao Y M, Chandra S, et al. Capillary effects during droplet impact on a solid surface[J]. Physics of Fluids, 1996, 8(3): 650-659. DOI:10.1063/1.868850 |



