2. 中国科学院大学 工程科学学院, 北京 100049;
3. 北京机电工程总体设计部, 北京 100854
2. School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China;
3. Beijing System Design Institute of Mechanical-electrical Engineering, Beijing 100854, China
高超声速进气道(以下简称高超进气道)作为超燃冲压发动机的重要气动部件,其工作状态将直接影响发动机整体效能的发挥[1]。不起动作为进气道的一种非正常工作状态,其带来的流场脉动将严重影响发动机的推力性能,甚至对结构造成破坏[2]。由于在实际飞行中导致进气道不起动的诱因繁多,因此,一旦进气道进入到不起动状态,在不起动诱因消失后进气道还能否恢复起动状态下的自起动能力也是衡量进气道性能的重要指标。
针对自起动问题,Kantrowitz[3-4]最早通过假设自起动时进气道内收缩段入口处存在正激波,自起动过程中喉道处为声速,并基于一维流动分析提出了仅与来流马赫数相关的Kantrowitz极限作为进气道的自起动设计准则。然而在高超进气道实际自起动过程中,内收缩段波系结构复杂且存在着大分离,明显有别于Kantrowitz理论假设。进而在高超进气道试验中发现[5-9],即使在内收缩比大于Kantrowitz极限的条件下,进气道依然具有自起动能力。可见,要解决高超进气道自起动内收缩比极限预测问题,有必要先对进口段内的激波边界层干扰问题进行研究和分析,这其中的影响因素远不止来流马赫数一项。
在考虑粘性后,Goldberg和Hefner[10-11]在马赫数6.0条件下,结合简化的二元进气道对唇口角度、唇口高度以及边界层相对厚度等参数进行了多方面研究。研究发现,进气道的总压恢复能力决定了进气道是否可以实现自起动,并且边界层厚度对进气道自起动性能影响较大。Van Wie[12]通过来流马赫数3.0风洞试验对小尺度、有粘、矩形的简化进气道起动-不起动转换过程进行了观察,将进气道的不起动/自起动过程分为“硬”和“软”2种。通过分析不同唇口长度和高度条件下的试验结果,以唇口高度和长度粗略地划分了“软”/“硬”不起动/自起动分界线。Yue[13]深入开展了进口薄边界层下唇罩压缩角度对简化进气道自起动性能影响的试验研究,获得了其影响规律,并指出可通过分级压缩提升进气道的自起动能力。Flock和Gülhan[14]通过来流马赫数6.0~7.0之间的风洞试验对三维进气道自起动过程流场进行观测,发现与平唇口相比,V型唇口由于增加了溢流量而对进气道自起动性能有提升作用。
尽管之前已有大量关于进气道自起动的研究,但是研究对象大多为简化的进气道构型,并未考虑实际进气道的肩部膨胀扇结构以及不同的压缩方式。因此有必要结合现有的结果与上述影响因素下的结果进行对比,获得其在进气道自起动过程中的影响规律,为提升进气道自起动能力设计提供参考和依据。
1 研究对象和试验方法 1.1 研究对象为研究膨胀波及压缩方式对自起动性能的影响,尽量减小单一影响因素变化时其他因素的干扰,采用文献[13]中的简化模型作为基准,如图 1(a)所示。简化进气道模型中的激波发生器为唇罩,对侧为底板。其中唇罩压缩角度α,唇口上游底板长度L,唇口高度H以及进气道喉道高度Ht等值均可通过替换部件实现对唇罩激波强度、边界层相对厚度以及内收缩比的单独调节。与此同时,保证进气道进口流场的均匀性不受喷管外流动的干扰,对唇口上游底板长度L大于300mm的模型底板边缘增加侧翼结构,如图 1(b)所示。进气道内压缩段宽度为80mm,唇口前底板为矩形,宽度为180mm。进气道唇口高度H与喉道高度Ht的比值为进气道的内收缩比(Internal Contraction Ratio, ICR)。对于唇罩压缩角度(α=7°、11°和15°)、唇口上游底板长度L、唇口高度H相同的,试验设计加工了一系列斜劈厚度的唇罩,通过选配不同厚度的唇罩部件改变Ht来获得不同的进气道内收缩比ICR,其调节精度可达到0.05。本文用能保证进气道实现自起动的最大内收缩比Maximum ICR来表征进气道的自起动性能。

|
| 图 1 简化进气道模型示意图与实物图 Fig.1 Schematic (a) and photograph (b) of the test inlet model |
作为研究肩点膨胀波对进气道自起动性能影响的对比模型,设计了仅带1道外压缩激波的二元进气道模型(如图 2所示),其外压缩角度α分别为7°、11°和15°,内压缩段宽度为80mm,侧板上游底板宽度为200mm,长度为300mm,压缩面两侧加装侧翼结构。由于唇口激波强度对自起动能力的极大影响,本试验设计保证唇口激波气流转角与简化模型相同。试验进气道喉道高度Ht=24mm,通过调节水平唇罩前后位置,改变进气道唇口的进口面积,以调节进气道内收缩比ICR。

|
| 图 2 二元进气道模型示意图与实物图 Fig.2 Schematic (a) and photograph (b) of the test two-dimensional inlet model |
为对比研究压缩方式对进气道自起动性能的影响,设计加工了如图 3所示的侧压进气道模型。侧压进气道唇罩与来流方向持平,对气流无压缩, 前端与侧压板齐平,侧板为零后掠角设计。气流仅由进气道侧板诱导的侧压激波进行压缩,试验中侧板角度α分别为7°、11°和15°,通过改变侧板的厚度实现对进气道内收缩比的控制。唇口高度H为20和40mm。模型采用5种底板,长度L分别为200、300、400、500和600mm。为避免底板边缘的侧向流动干扰,对唇口上游底板长度L>300mm的模型底板边缘增加侧翼结构。侧挡板在侧壁压缩外侧,与侧压板之间存在边界层排移通道,如图 3所示。侧挡板的边界层会随溢流排出,不进入内通道。进气道的侧压式进气道内压缩段进口宽度为80mm,唇口前底板宽度为180mm。试验中进气道内收缩比ICR的调节精度可达到0.05。

|
| 图 3 侧压进气道模型图 Fig.3 Photographs of the side-compression inlet model |
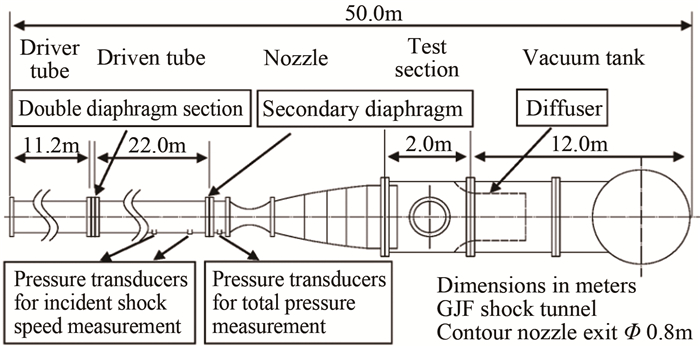
试验在中国科学院力学研究所高温气体动力学国家重点实验室的GJF激波风洞中展开。激波风洞主要由驱动段、双膜段(中压段)、被驱动段、型面喷管、实验舱和真空罐组成。风洞的结构布局及尺寸说明见图 4, 其中,激波风洞的驱动段长度为11.2m,被驱动段长度为22.0m,驱动段与被驱动段内径均为405mm,拉瓦尔喷管出口直径为800mm。
|
| 图 4 GJF激波风洞布局及尺寸示意图 Fig.4 Sketch of the GJF shock tunnel |
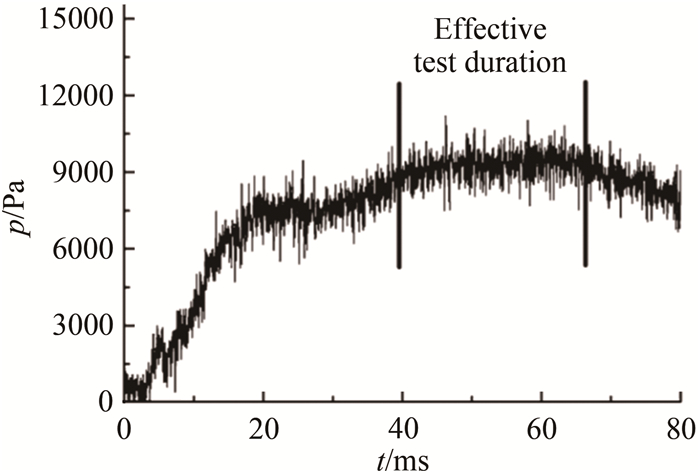
驱动段和被驱动段中的气体都为室温下的压缩空气,通过激波压缩气体焓值被提高,经过拉瓦尔喷管加速到试验所需要的马赫数,喷管可模拟的马赫数分别为3.5、4.0、5.0、6.0和7.0,试验均在马赫数4.0喷管下开展。对应的试验段气流参数如表 1所示,激波风洞的气流总压随时间的变化曲线如图 5所示,可以看到静压曲线在40~65ms间相对稳定。
| Ma | 总压p0/MPa | 总温T0/K | 静压p/Pa | 单位雷诺数Re/m-1 |
| 4.0 | 1.4 | 430.0 | 9220.51 | 3.58××107 |
|
| 图 5 GJF激波风洞的静压变化曲线(Ma=4.0) Fig.5 Variation of static pressure with time in GJF shock tunnel (Ma=4.0) |
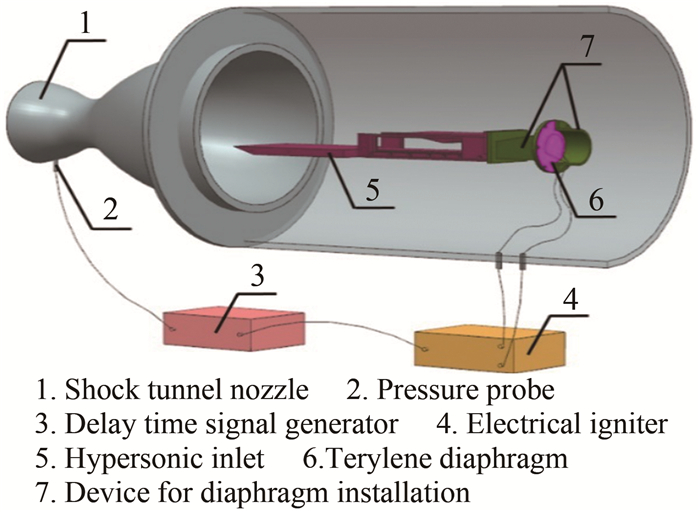
为了在风洞毫秒量级的运行时间内实现进气道不起动及自起动过程,采用了基于激波风洞的电弧破膜进气道起动试验技术。图 6为进气道破膜装置示意图。进气道出口处连接转接法兰,法兰盘之间安装涤纶膜片,在试验初始阶段可以实现进气道出口面积全堵塞。膜片上贴有电阻丝,并与点火器连接,试验前将点火器提前充入1800V的高电压,试验过程中由延时脉冲信号发生器控制点火器放电破膜。延时信号发生器的触发信号为风洞总压传感器的放大电压信号,在设定的延时后,信号发生器输出脉冲电压信号触发点火器电阻丝放电。
|
| 图 6 进气道自起动破膜装置示意图 Fig.6 Schematic of experimental devices for inlet restarting in shock tunnel |
激波风洞流场建立后,由于进气道出口处于壅塞状态,进气道处于不起动喘振流态,到达设定时间后,延时信号发生器发出脉冲电压信号给点火器,触发电阻丝在短时间内烧毁膜片,进气道出口处的膜片在5~10ms时由于内外流场压差的作用而完全打开,进气道下游堵塞消失以考察进气道的自起动能力。整个过程能在激波风洞的稳定运行时间段内完成,可以准确地判断进气道在高反压扰动消失后是否能够自起动。通过该试验方法对轴对称进气道在激波风洞中的试验结果与常规风洞的试验结果对比,发现进气道自起动能力基本一致[15],证明该方法能较好地研究进气道自起动特性。
1.2.3 试验观测手段借助于双镜平行光纹影系统对进气道自起动流场进行显示和记录,辅助判断其是否正常起动。该纹影系统光源为氙灯,对于纹影流场的记录采用FASTCAM SA4的高速摄影系统完成,拍摄镜头光圈为f/2.8,焦距为200mm,高速相机设置的拍摄帧率为5000帧/s,曝光时间为6.2μs,图片分辨率为896pixel×896pixel。纹影拍摄系统由风洞总压信号来触发拍摄记录图片,每次试验记录风洞起动后200ms内的气流流动特性,可涵盖风洞运行的整个过程。
2 膨胀波对进气道自起动性能的影响基准构型进气道(图 1)的试验结果已在文献[13]中总结,下面给出图 2中二元进气道模型试验结果。受进气道出口处涤纶膜片的阻挡,风洞起动后进气道内首先形成不起动大喘振流场。在t=30.0ms时,延时脉冲信号发生器控制点火器放电使出口处膜片烧毁,进气道出口附近压强降低,破膜产生的膨胀波前传,导致大喘振分离激波向唇口方向回退。图 7为喘振激波向下游移动过程中进气道流场的纹影图。在t=38.8ms时,进气道唇口内出现一道激波,且不断向下游运动。这是来流在下游高压下滞止出的激波,且随着下游膜片的破坏,通道背压下降,该激波将被吞入到通道内。通过激波不同时刻的相对位置关系可以估算出激波运动速度,约为283.5m/s。

|
| 图 7 二元进气道破膜后流场纹影示意图(α=7°,ICR=1.89) Fig.7 Schlieren images of two-dimensional inlet model after the diaphragm ruptures (α=7°, ICR=1.89) |
试验发现,自起动过程中唇口外向下游移动的分离激波角度几乎不变,迎风角大约为27°,如图 8所示。根据Chapman[16]提出的自由相互作用理论与Zhukoski对湍流边界层诱导分离进行综合分析,当雷诺数满足3.0×104 < Reδ < 1.2×106时,分离激波前后压比满足p2/p1=1+0.5Ma1。根据Rankine-Hugoniot公式,在主流马赫数Ma=4.0、外压缩角度为7°时,分离激波波前马赫数为Ma1=3.5,斜激波前后压比p2/p1约为2.75,在该压比下对应的激波角为26.9°。可见试验观察得到的激波角与理论值符合良好。在t=42.4ms时,大尺度分离区进入进气道内压缩段,分离区诱导的斜激波打在进气道唇口处。分离区进入内压缩段后至t=51.8ms时,分离激波角度几乎不变,但其向下游移动的速度明显减慢。随后,分离激波的激波角减小,在t=56.6ms时激波角减小至23.5°。分离区迎风面角度减小,分离区形态逐渐偏平,最终全部消失,在t=61.4ms时进气道起动流场建立,进气道肩点处存在明显的膨胀波结构。

|
| 图 8 二元进气道自起动过程纹影示意图(α=7°, ICR=1.89) Fig.8 Schlieren images of two-dimensional inlet restart process (α=7°, ICR=1.89) |
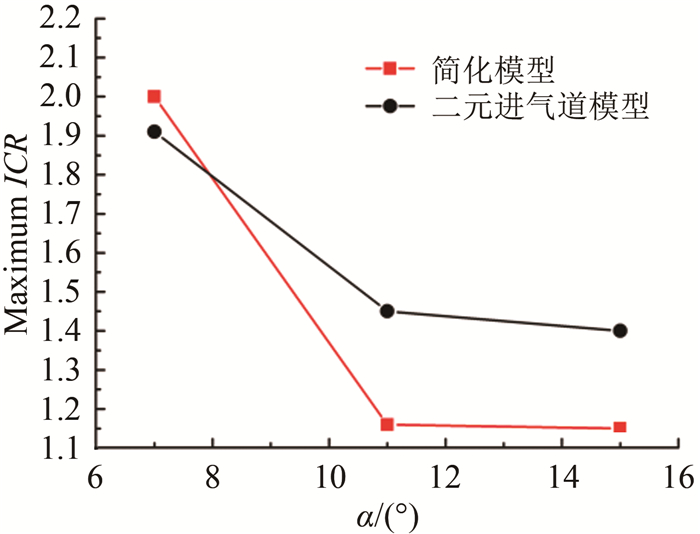
二元进气道与简化进气道在不同压缩角度下的自起动性能如图 9所示。与简化模型相同,随着气流偏转角度的增加,唇罩激波强度增大,由唇罩激波带来的总压损失增大,唇罩激波诱导的激波-边界层相互作用更加剧烈,进气道自起动极限收缩比随气流偏转角度α的增加而减小。由于外压缩激波的存在,7°、11°和15°偏转角度下进气道唇口处的主流马赫数分别为3.5、3.2和2.9,小于简化进气道模型的唇口马赫数4.0。唇口马赫数减小,其对应的Kantrowitz极限与等熵压缩极限值降低,进气道需要更大的喉道面积使捕获流量全部通过,自起动极限收缩比减小。因此, 气流偏转角度为7°的二元进气道自起动极限收缩比为1.90,小于对应简化模型的自起动极限收缩比2.00。然而,对于气流偏转角度较大(11°和15°)的模型,二元进气道的自起动性能优于简化进气道。对于大角度模型,进气道是否能够实现自起动取决于分离区是否形成气动喉道限制进气道流量的捕获。与分离区同侧的肩点膨胀波对局部流场进行加速减压,增强了其抗反压能力,并促进了分离区向下游移动。因此,对于受分离区影响的大角度进气道,同侧膨胀波能有效提高其自起动能力。
|
| 图 9 二元进气道自起动性能随气流偏转角变化曲线 Fig.9 Variation of the maximum ICR with deflection angle |
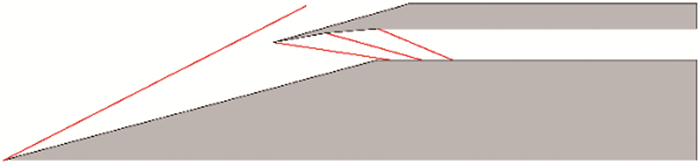
对于二元进气道模型,气流经过外压激波后偏转,到达唇口处反向偏转, 流向恢复为水平状态。当压缩角度较大,进气道自起动性能较差。参考文献[13]对唇罩激波进行分级压缩优化,对进气道(见图 2)自起动能力对压缩角度变化曲线进行研究,将压缩角度为15°的进气道模型唇罩进行分级,分散为5°+5°+5°(如图 10所示),3道激波分散不相交。
|
| 图 10 二元进气道唇罩分级压缩示意图 Fig.10 Multiple-shockes design of two-dimensional inlet model |
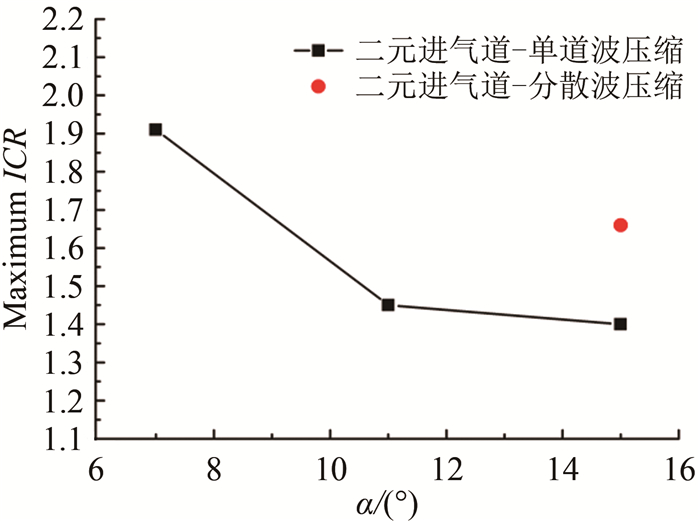
唇罩分级压缩模型的自起动性能如图 11所示,其自起动极限收缩比为1.66,较单波压缩模型提高了18.6%。对于压缩角度为15°的二元进气道模型,其唇罩截面主流马赫数为2.9。若将唇罩进行单级压缩,气流经过外压激波与唇罩激波后, 马赫数为2.2,无粘总压恢复系数为72.4%。而对于唇罩5°+5°+5°的分级压缩模型,气流经过4道压缩激波并恢复水平方向时, 马赫数为2.26,无粘总压恢复系数为79.4%。分级压缩不仅减小了由压缩激波带来的总压损失,而且激波强度的减小也降低了激波-边界层相互作用的剧烈程度,减小了分离区尺度。可见这种将强激波压缩分级为若干弱激波的方式对简化进气道模型与二元进气道模型均适用。
|
| 图 11 唇罩分级压缩对二元进气道自起动性能影响 Fig.11 Influence of multiple-shocks design on inlet restart capability |
Trexler[17-18]在20世纪70年代首次提出了利用侧板对气流进行压缩的侧压式进气道,其最大的优点是结构简单,起动马赫数低,可以在很厚的前体边界层来流条件下工作。仅利用侧板对气流进行压缩的进气道[19-21]现已很少在实际应用中被采用,一般是作为三维压缩的部分出现,但对纯侧压式进气道的自起动性能规律的研究,可以有助于对三维进气道起动特性的深化理解。
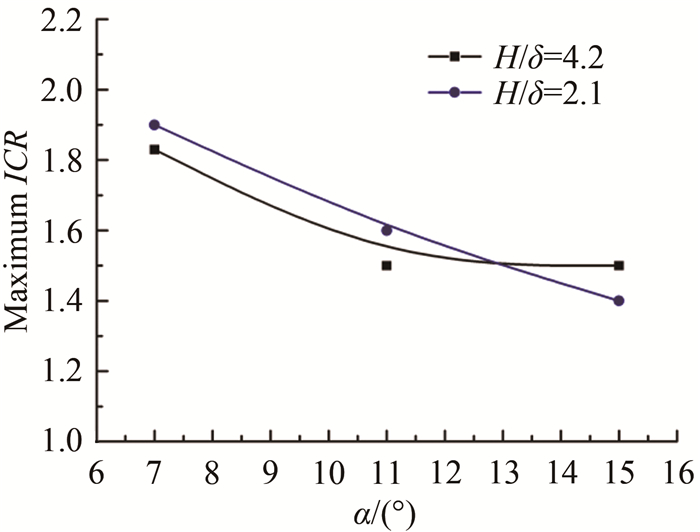
3.1 压缩激波强度和边界层厚度对侧压式进气道自起动性能影响图 12给出了唇罩截面薄边界层(L=600mm,H=40mm,H/δ=4.2)与截面厚边界层(L=600mm,H=20mm,H/δ=2.1)条件下侧压式进气道的自起动性能随压缩角度α的变化,其中边界层厚度均借助皮托管测得。在来流马赫数Ma=4.0条件下,压缩角度α直接决定了压缩激波的强度。对于唇罩截面存在薄边界层的进气道,当侧压角度由7°增加至11°,进气道自起动极限收缩比下降18.0%,由1.83减小至1.50;当侧压角度由11°增加至15°,进气道自起动收缩比变化很小。对于唇罩截面厚边界层的进气道,当侧压角度由7°增加至11°,进气道自起动极限收缩比下降15.7%,由1.90减小至1.60;当侧压角度由11°增加至15°,进气道自起动极限收缩比下降12.5%,由1.60减小至1.40。可以看到,压缩角由7°增加至11°时,进气道自起动性能明显下降,而由11°增加至15°时,唇口截面薄边界层的进气道性能变化较为平缓,唇口截面厚边界层的进气道性能仍明显下降。唇罩角度的增加使压缩激波强度增加,激波总压损失增大,进气道自起动性能呈现下降趋势。
|
| 图 12 侧压式进气道自起动性能随压缩角度α的变化 Fig.12 Variation of the maximum ICR with the cowl angle of side-compression inlet model |
由于侧板诱导的平面扫掠激波与壁板边界层发生相互干扰,扫掠激波前后的压力梯度会在边界层内引发二次流,有可能引发主分离、主再附、二次分离、二次再附等流动结构。流场模式与压缩角度α及扫掠激波的强度相关。但是侧压试验缺乏直观观测试验手段,进气道内部的流场结构无法直接获得。为进一步研究流动机理,参考了试验环境与GJF激波风洞相近的T-333风洞[22]中扫掠激波边界层干扰的试验数据对现有试验结果进行辅助分析。T-333风洞的来流马赫数为Ma=3.92,总压p0=1.48MPa,单位雷诺数Re=8.9×105/m,压缩前缘处底板边界层厚度为δ=3.5mm,侧板高度为100mm,其进气道唇口截面边界层厚度相对较薄。T-333试验发现,在对称轴附近,一些流线直接向下游流动,汇聚成一个特征喉道(Characteristic Throat)。当侧压压缩角为7°,气流经过特征喉道时没有出现分离现象。对于唇口截面薄边界层的进气道模型,当压缩角由7°增加至11°时,对称轴特征喉道下游开始出现大尺度分离,进而导致所观测到的进气道自起动性能出现明显下降现象;压缩角度由11°增加至15°时,对称轴分离区一直存在,尺度随压缩角增长而扩大,进气道自起动性能降低但变化较为平缓。对于唇口截面厚边界层的进气道模型,边界层相对厚度带来的影响趋势较为复杂。
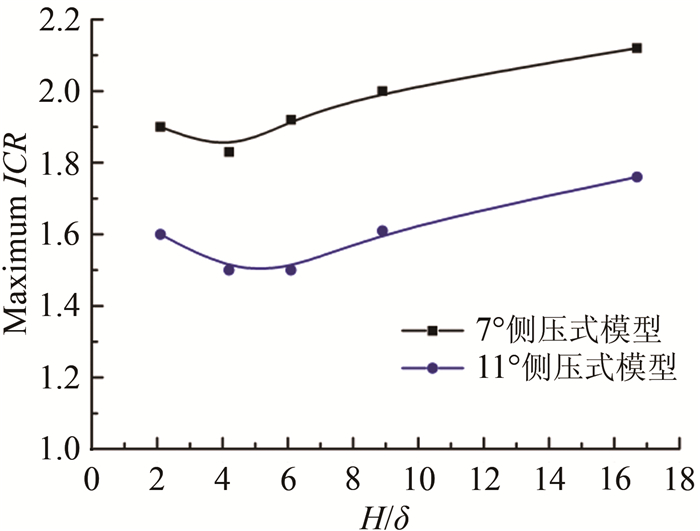
图 13给出了α=7°、11°时侧压式进气道的自起动极限收缩比随唇口截面边界层相对厚度H/δ的变化曲线。当模型唇罩截面边界层相对较薄(4.2 < H/δ < 16.7)时,随着边界层相对厚度增加,7°进气道模型的自起动极限收缩比由2.12下降至1.83,下降了13.7%;而11°进气道模型的自起动极限收缩比由1.76下降至1.50,下降了14.8%。该结果与顶压式进气道在薄边界层条件下自起动性能几乎不受唇罩截面边界层相对厚度影响的规律不同。对于顶压模型自起动过程中的激波-边界层干扰,Prandtl[23]发展的理论适用,但对于扫掠激波-边界层干扰,其存在明显的三维结构,二维分析手段不再适用。此外,当唇罩截面边界层的相对厚度增加至H/δ < 4.2时,侧压进气道的自起动性能存在小幅提升。但由于三维激波-边界层作用十分复杂,随着边界层相对厚度增加,maximum ICR反而增大的现象还需要进一步研究分析。
|
| 图 13 侧压式进气道自起动性能随唇罩截面边界层相对厚度H/δ的变化 Fig.13 Variation of the maximum ICR with H/δ of side-compression inlet model |
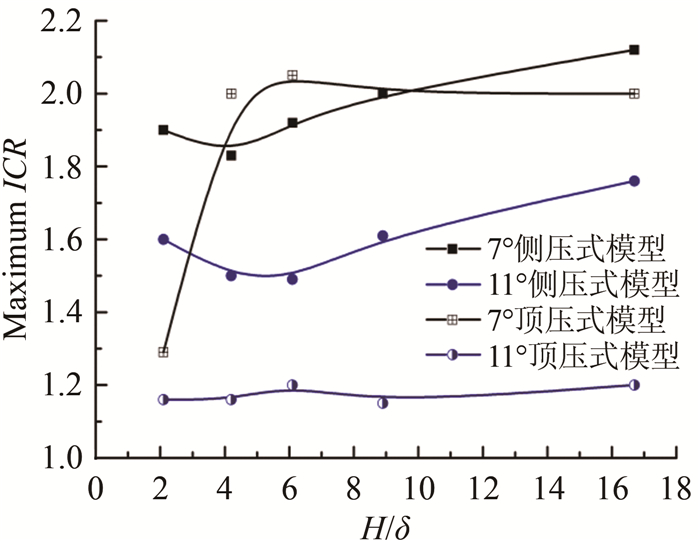
侧压式进气道侧板扫掠激波与边界层干扰,三维效应带来的影响使其自起动特性与顶压式进气道存在显著差别。图 14所示为α=7°、11°时,侧压式进气道与顶压式进气道的自起动极限收缩比随唇口截面边界层相对厚度H/δ的变化曲线。对于压缩角度α=11°的进气道,唇罩压缩顶压模型的自起动能力始终很差,自起动极限收缩比在1.20左右,而侧压模型的maximum ICR始终大于1.50。侧板压缩使进气道的自起动性能提升25.0%以上,在H/δ=16.7时,侧压带来的性能优化达到最大,与顶压相比,自起动极限收缩比提升46.7%。11°顶压模型的自起动性能受内收缩段大尺度分离区形成的气动喉道限制,在内收缩比很小时才能实现自起动。但11°侧压模型的扫掠激波与底板边界层的干扰强度受三维效应影响,其引发的分离尺度小于二维激波-边界层引发的分离区尺度。因此,压缩角度较大的侧压式进气道自起动性能明显优于顶压式进气道模型。
|
| 图 14 侧压进气道与顶压进气道自起动性能随唇罩截面边界层相对厚度H/δ的变化 Fig.14 Variation of the maximum ICR with H/δ of side-compression and cowl-compression inlet models |
对于压缩角度α=7°的进气道,在唇罩截面边界层较薄(4.2 <H/δ < 16.7)时,侧压式进气道与顶压式进气道的自起动极限收缩比在2.00附近浮动。参考文献[13]提到:7°进气道模型能否自起动取决于几何喉道能通过的最大流量,受激波-边界层干扰引发的分离区影响较小,此时2种进气道模型自起动性能相近。但是,当唇罩截面为厚边界层(H/δ < 4.2)时,7°顶压式进气道模型的自起动性能发生突降,降低至maximum ICR=1.29,唇口处厚边界层使进气道能通过的最大流量从由几何喉道约束转变为气动喉道的控制。此时,侧压式进气道的自起动性能稳定保持在maximum ICR=1.90,侧板压缩使进气道的自起动性能提升了47.3%。而由于压缩激波-边界层干扰诱导分离区形成的气动喉道将决定进气道能否自起动,侧压式进气道的自起动性能要优于顶压式进气道。
4 结论为了探究实际进气道肩部膨胀扇以及压缩方式对进气道自起动性能的影响,结合多套具体的进气道构型,针对不同的压缩角、边界层厚度开展了激波风洞试验,在Ma4.0进气道进口马赫数条件下,获得了其极限内收缩比变化规律,研究结果表明:
(1) 通过二元进气道与简化进气道的风洞试验对比,发现与分离区同侧的膨胀扇会对当地气流加速,降低局部压强,进而对压缩激波较强的进气道自起动过程有明显的改善作用。唇罩分级压缩对于二元进气道的自起动能力也具有提高效果。
(2) 由于侧压扫掠激波与底板边界层干扰中三维效应的影响,边界层厚度对侧压式进气道自起动性能的影响趋势与顶压式进气道存在明显的差异。当边界层较薄时,进气道自起动极限随边界层喉道增加略有下降,而当边界层喉道增加时,进气道自起动性能将小幅提升。
(3) 通过对比侧压模型与顶压模型的试验结果发现,自起动受限于几何喉道的进气道构型,压缩方式对进气道自起动性能的影响不明显。对于由压缩激波-边界层干扰诱导分离区形成的气动喉道决定能否起动的进气道,侧压方式有利于提高进气道的自起动性能。
| [1] |
Bowcutt K G. Multidisciplinary optimization of airbreathing hypersonic vehicles[J]. Journal of Propulsion and Power, 2001, 17(6): 1184-1190. DOI:10.2514/2.5893 |
| [2] |
McClinton C R, Hunt J L, Ricketts R H. Airbreathing hypersonic technology vision vehicles and development dreams[R]. AIAA-99-4987, 1999.
|
| [3] |
Kantrowitz A, Donaldson C D. Preliminary investigation of supersonic diffusers[R]. NACA-ACR-L5D20, 1945.
|
| [4] |
Kantrowitz A. The formation and stability of normal shock waves in channel flows[R]. NACA-TN-1225, 1947.
|
| [5] |
Li Z F, Huang B, Yang J M. A novel test of starting characteristics of hypersonic inlets in shock tunnel[R]. AIAA-2011-2308, 2011.
|
| [6] |
李祝飞, 黄舶, 贾立超, 等.激波风洞中高超声速进气道起动问题实验研究[C]//十四届全国激波与激波管学术会议论文集. 2010. Li Z F, Huang B, Jia L C, et al. Starting characteristics of hypersonic inlets in shock tunnel[C]//Proc of the 14th Chinese National Symposium on Shock Waves. 2010. |
| [7] |
王成鹏, 程克明. 高超进气道临界起动特征[J]. 航空动力学报, 2008, 23(6): 997-1002. Wang C P, Cheng K M. Critical starting characteristics of hypersonic inlets[J]. Journal of Aerospace Power, 2008, 23(6): 997-1002. |
| [8] |
Sun B, Zhang K Y. Empirical equation for self-starting limit of supersonic inlets[J]. Journal of Propulsion and Power, 2010, 26(4): 874-875. DOI:10.2514/1.46798 |
| [9] |
Hohn O M, Gülhan A. Experimental investigation on the influence of sidewall compression on the flowfield of a scramjet inlet at Mach 7[R]. AIAA-2011-2350, 2011.
|
| [10] |
Goldberg T J, Hefner J N. Starting criterion for hypersonic inlets[J]. Journal of Aircraft, 1970, 7(3): 275-277. DOI:10.2514/3.44160 |
| [11] |
Goldberg T J, Hefner J N. Starting phenomena for hypersonic inlet with thick turbulent boundary layers at Mach 6[R]. NASA TN D-6280, 1971.
|
| [12] |
Van Wie D M, Kwok F T, Walsh R F. Starting characteristics of supersonic inlets[C]. The 32nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Lake Buena Vista, USA, 1996.
|
| [13] |
Yue L J, Jia Y N, Xu X, et al. Effect of cowl shock on restart characteristics of simple ramp type hypersonic inlets with thin boundary layers[J]. Aerospace Science and Technology, 2018, 74: 72-80. DOI:10.1016/j.ast.2017.12.018 |
| [14] |
Flock A K, Gülhan A. Experimental investigation of the starting behavior of a three-dimensional scramjet intake[J]. AIAA Journal, 2015, 53(9): 2686-2693. DOI:10.2514/1.J053786 |
| [15] |
岳连捷, 刘红, 徐骁, 等.激波风洞进气道自起动实验方法[C]//第九届全国实验流体力学论文集. 2013. Yue L J, Liu H, Xu X, et al. Experimental method for hypersonic inlet self-starting in shock tunnel[C]//Proc of the 9th national conference on experimental fluid mechanics. 2013. |
| [16] |
Chapman D R, Kuehn D M, Larson H K. Investigation of separated flows in supersonic and subsonic streams with emphasis on the effect of transition[R]. NACA-TN-3869, 2011.
|
| [17] |
Trexler C A. Performance of an inlet for an integrated scramjet concept[J]. Journal of Aircraft, 2015, 11(9): 589-591. |
| [18] |
Trexler C A. Inlet performance of the integrated langley scramjet module[C]. The 11th Propulsion Conference. Anaheim, USA, 1975.
|
| [19] |
袁化成, 梁德旺. 高超声速侧压式模型进气道不起动特性分析[J]. 南京航空航天大学学报, 2004, 36(6): 683-687. Yuan H C, Liang D W. Characteristic analysis of unstart performance for hypersonic side-wall inlet model[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2004, 36(6): 683-687. DOI:10.3969/j.issn.1005-2615.2004.06.003 |
| [20] |
向安宇, 岳连捷, 肖雅彬, 等. 侧压式超燃进气道流场特性研究[J]. 力学与实践, 2007, 29(3): 7-10. Xiang A Y, Yue L J, Xiao Y B, et al. Investigation on sidewall compression scramjet inlet[J]. Mechanics in Engineering, 2007, 29(3): 7-10. DOI:10.3969/j.issn.1000-0879.2007.03.002 |
| [21] |
龚鹏, 岳连捷, 肖雅斌, 等. 带中心支板侧压进气道流场特性研究[J]. 实验流体力学, 2008, 22(1): 31-35. Gong P, Yue L J, Xiao Y B, et al. Investigation on flow pattern of sidewall compression scramjet inlet with single central strut[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(1): 31-35. DOI:10.3969/j.issn.1672-9897.2008.01.007 |
| [22] |
Zheltovodov A A, Maksimov A I, Shevchenko A M. Topology of three-dimensional separation under the conditions of symmetric interaction of crossing[J]. Thermophysics and Aeromechanics, 1998, 5(3): 293-312. |
| [23] |
Prandtl L. Über Flüßigkeitsbewegung bei sehr kleiner Reibung[C]. The Verhandlungen des dritten internationalen Mathematiker-Kongresses. Heidelberg, Germany, 1904.
|



