2. 中国空气动力研究与发展中心 超高速空气动力研究所, 四川 绵阳 621000;
3. 中国空间技术研究院 载人航天总体部, 北京 100010
2. Hypervelocity Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China;
3. Institute of manned space system engineering, China academy of space technology, Beijing 100010, China
几十年来,考虑复杂结构和各种防热材料的流-热-固耦合一体化计算方法逐步应用于航天工程[1]。数值计算基本采用高精度CFD技术求解N-S方程与固体求解器相耦合的方式开展流-热-结构耦合研究[2-3],对高超声速飞行器进行建模与分析仿真工作,并与对应的高超声速风洞试验的气动力、气动热和热响应测试数据进行对比与验证。但耦合计算中固体热传导和结构变形的求解大多是采用有限元[4-6]和有限差分技术[7],而非效率更高的边界元求解。当前对高超声速流动与固体之间的耦合换热问题已进行了大量研究,提出了多种耦合方法和策略[8-10]。
随着各国在临近空间和火星探测的太空竞赛,新一代高马赫数、长航时、高机动飞行器和火星再入探测器壁面将面临严重的催化效应[11-15]。研究表明飞行器关键部位防热材料表面的催化效应最高可带来近50%以上的气动热载荷[16],使其成为非平衡气动热研究领域的热点。针对此问题,诸多学者[17-20]在高温气体非平衡效应和气动热环境的数值模拟与理论分析方面做了大量研究工作,通过设定材料为非催化、完全催化和有限催化特性,基于CFD方法分析类返回舱[21]和有翼飞行器[22]等材料表面催化对热防护系统和气动热的影响,特别是对催化特性发生变化时的热流载荷预测进行了解析与修正[23]。催化效应会对飞行器翼身结合处的激波与湍流边界层相互作用产生影响[24],数值分析与试验结果的对比分析表明[25],壁面催化特性、表面温度和马赫数等参数都对激波/边界层相互作用和气动热载荷有重要影响。其中,催化热的出现很大程度增大了激波/边界层相互作用分离区的下游气动热[26]。对于壁面催化不连续和壁面滑移条件下的气动加热问题也进行了研究,在壁面催化不连续的条件下,会导致壁面温度产生“跳跃”现象[27],而壁面滑移对壁面温度的“跳跃”几乎没有任何影响[28],数值计算结果表明温度“跳跃”现象会导致航天飞机表面产生大约150K的温度跳跃,与测量结果相比该计算结果偏低[29]。遗憾的是,对于考虑表面催化效应的流动/传热多场耦合分析,研究甚少,董维中等[30]针对C/C材料,考虑由氧化反应和催化反应引起的热化学烧蚀和热效应,建立了表面温度分布与气动热的耦合计算方法,实现了流场非平衡、表面的热辐射以及热防护层内部的热传导效应的部分耦合。但是,该研究尚未考虑具体的催化反应过程,缺少针对飞行器表面的物理化学计算模型和内部热响应计算模型,进而建立完善的非平衡流场/表面催化/热传导多场耦合模型与求解策略,分析材料表面催化效应对耦合传热过程的影响。
基于此,本文在高超声速非平衡流动求解器与结构热力多场耦合计算框架之上,建立超高速流动/催化反应/传热多场耦合分析模型,基于高频等离子风洞开展ZrB2-SiC超高温陶瓷防热材料表面催化特性的测试,对比简化原子复合催化模型和有限速率催化反应模型对气动热的影响,揭示非烧蚀防热材料表面催化效应对耦合传热的根本原因,进而大幅度提升多场耦合计算对热载荷预测的可靠性,有效避免非耦合计算给防热设计带来的过高估计。
1 考虑表面催化反应的耦合计算策略在非平衡条件下,材料表面会发生氧分子和氮原子的催化复合反应(如表 1所示),定义防热材料表面催化复合反应程度的参数为催化复合系数(简称催化系数)γ,大多数情况下γ被拟合为温度的函数,在CFD模拟中作为催化边界条件使用。本文主要针对简化催化原子复合模型和有限速率表面反应模型表征表面催化效应对耦合传热过程的影响,并对2种模型的计算结果进行对比分析。其中相对于反应3和4,形成异相的NO的反应5通常在气动热模拟中不予考虑,因此在简化催化原子复合模型忽略异相的NO生成。然而,研究发现等离子体风洞中的试样附近有NO生成[31],并且在与OREX再入飞行数据的匹配过程中也证明了NO生成的重要性[32],因此在有限速率表面反应模型中考虑扩散至邻近表面原子与气相中原子复合反应(E-R机制)以及与另一吸附原子复合反应(L-H反应),其中S0为吸附系数,γer为反应效率,E为反应放热量。在之前建立的超高速流动-传热耦合模型[33]的基础之上,将表面相互作用模型嵌入CFD中实现其表面反应建模能力,并与FEM程序相耦合,具体计算流程如图 1所示。这里仅研究催化效应对耦合传热过程的影响。
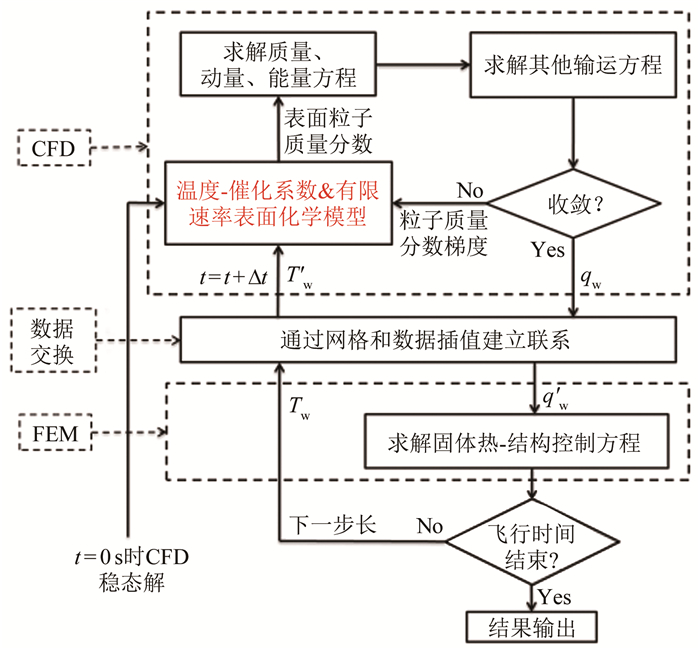
|
| 图 1 考虑表面反应后的耦合策略 Fig.1 Coupling approach with surface reaction considered |
| Reaction | Type | S0 / γer | E/(J·mol-1) | |
| 1 | O+(s)→O(s) | ads | 0.050 | 0 |
| 2 | N+(s)→N(s) | ads | 0.050 | 0 |
| 3 | O+O(s)→O2+(s) | ER | 0.001 | 9000 |
| 4 | N+N(s)→N2+(s) | ER | 0.001 | 9000 |
| 5 | O(s)+ N(s)→NO+2(s) | LH | 0.200 | 300000 |
为了获得材料表面催化系数与温度的函数关系,为耦合计算提供边界条件,采用中国空气动力研究与发展中心的高频等离子风洞,对ZrB2-SiC典型非烧蚀类超高温陶瓷材料的表面催化性能进行测试。分别选用驻点压力ps为3.32和5.81kPa、焓值为19.27~35.86MJ/kg的测试环境。表 2给出了各状态下氧、氮原子浓度(CO、CN)以及驻点压力ps、焓值ht等试验状态参数。试样模型为Φ20mm×3mm圆片,测试方法与SiO2[34]、C/SiC[35]表面催化系数测试方法相同。测试试样表面必须达到热平衡,以实现准确的测量热流。在每种测试环境下的测试时间均不少于100s,以确保试样表面温度趋于稳定,保证试样处于热平衡状态,不同状态下热流密度和材料表面温度如图 2所示。
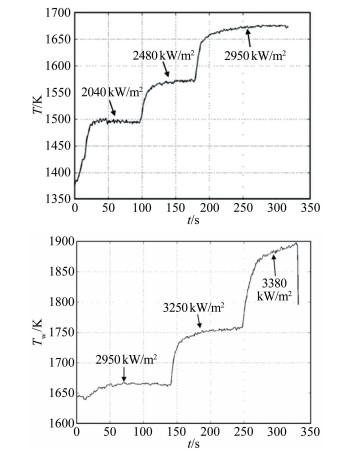
|
| 图 2 不同试验状态下试样表面热流密度和温度历程 Fig.2 Change curve of surface heat flux and temperature with increasing time under different states |
| State | ps/kPa | ht/(kJ·kg-1) | CO | CN | ps/kPa | |
| A | A01 | 3.10 | 19271 | 0.233 | 0.209 | 3.32 |
| A02 | 3.17 | 24087 | 0.233 | 0.316 | ||
| A03 | 3.21 | 27067 | 0.234 | 0.382 | ||
| A04 | 3.25 | 29824 | 0.234 | 0.445 | ||
| A05 | 3.48 | 32840 | 0.234 | 0.518 | ||
| A06 | 3.46 | 43343 | 0.234 | 0.691 | ||
| B | B01 | 5.57 | 20250 | 0.233 | 0.187 | 5.81 |
| B02 | 5.76 | 23977 | 0.233 | 0.268 | ||
| B03 | 5.80 | 28154 | 0.233 | 0.351 | ||
| B04 | 5.86 | 30509 | 0.233 | 0.407 | ||
| B05 | 6.07 | 35859 | 0.233 | 0.511 | ||
得到ZrB2-SiC材料表面催化系数随温度的变化如图 3所示,可拟合为与材料表面温度相关的函数:
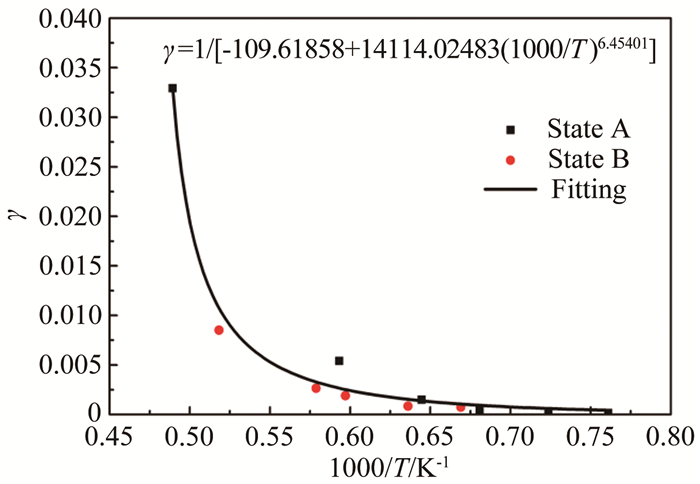
|
| 图 3 不同状态下试样表面催化系数 Fig.3 The catalytic coefficient with different states |
γ=1/[-109.61858+14114.02483(1000/T)6.45401]
从试验结果可以看出,ZrB2-SiC材料表现出较低的催化系数且随着材料表面温度升高而逐渐增大,当表面温度低于1600K时,γ小于0.001且变化不大;而在更高的温度下,γ仍小于0.035。
3 考虑催化反应的多场耦合计算分析 3.1 耦合传热模型对热载荷的影响针对ZrB2-SiC低催化非烧蚀防热材料,开展考虑表面催化效应的多场耦合计算,计算对象为轴对称头锥,几何尺寸如图 4所示,自由来流马赫数、压力和温度分别为15、1090.2Pa和223.1K,飞行高度30.48km。不考虑气体辐射的影响,此时壁面处于气动加热、辐射散热、催化加热(完全催化)以及固体传热的热平衡机制,计算中假设氮原子和氧原子具有相同的壁面复合系数。首先对比催化和非催化壁面条件下非耦合的壁面辐射平衡和耦合传热对表面温度和热流分布的影响,如图 5和6所示。

|
| 图 4 几何模型 Fig.4 Geometry model |

|
| 图 5 有无固体热传导时的表面温度分布 Fig.5 Comparison of surface temperature distributions with and without heat conduction |

|
| 图 6 有无固体热传导时的表面热流分布 Fig.6 Comparison of surface heat flux distributions with and without heat conduction |
从图 5中可以看出,非耦合的辐射平衡假设结果高估了驻点温度并低估了锥面温度。这是由于超高温陶瓷材料具有较高的热导率,鼻锥处的一部分热载荷向内部快速进行热传导,而此热传导的存在降低了驻点温度并使后面锥面的温度升高。对于具有更高热导率的材料,这种效应会更明显。在非催化壁面条件下,考虑固体热传导时的驻点温度比辐射平衡假设结果低了780K,而在完全催化条件下则低了960K。
假定定常有限催化系数0.100~0.001,得到耦合传热下驻点压力、热流和温度如表 3所示。结果表明壁面催化特性对壁面热流和温度有很大影响,而对压力没有影响。最低的非催化壁面热流与最高的完全催化热流相差了4.78MW/m2。
| Test Case | γw | p/kPa | qs/(MW·m-2) | T/K |
| Fully catalytic | 1.000 | 336.5 | 30.53 | 4046.90 |
| Partially catalytic | 0.100 | 336.5 | 27.20 | 3722.82 |
| Partially catalytic | 0.010 | 336.5 | 26.02 | 3601.71 |
| Partially catalytic | 0.001 | 336.5 | 25.88 | 3570.50 |
| Non catalytic | 0 | 336.5 | 25.75 | 3550.44 |
材料表面催化系数是壁面温度的函数,由于壁面附近原子发生复合,改变了壁面附近组分质量分数,因此气体混合物的热导率也发生了改变。类似的, 可知模型表面不同时间、不同位置因温度不同其催化特性也有所不同。根据半经验Wilke公式[36]计算的热导率以及催化系数变化, 得到材料表面催化系数(反应速率)与热导率、时间和表面位置的关系,如图 7所示。图 7(a)结果表明,随着壁面催化系数增大,混合气体的热导率略有增加。而催化反应速率随表面温度升高而逐渐增大。此外,由于催化系数是温度的函数,直接导致锥体表面不同部位的催化性能有所差异,用定常催化系数不能准确地对其进行表征,在后续的气动热环境计算中,上述物理量均非定值。

|
| 图 7 材料表面催化特性随热导率、时间和位置的变化 Fig.7 The change of material surface catalytic property with thermal conductivity, time and surface location |
针对自由来流马赫数、压力和温度分别为9、574.6Pa和236.5K,飞行高度35km的飞行工况,分别采用简化原子复合催化模型和有限速率催化反应模型计算驻点热流随时间的变化,结果如图 9所示。考虑固体结构内的瞬态传导过程,给出了2种化学反应模型计算的t=500s时刻的表面温度对比,如图 10所示。由图可知,2种模型计算的结果基本一致,其中有限速率表面反应模型在驻点处温度稍低于简化反应模型,而在锥体后部温度则略高,二者的细微差别是由表面组分分布的不同所致。简化催化模型在对不同材料表面催化效应的初步研究中可以作为基准模型,更精细的研究则需要采用有限速率催化反应模型。

|
| 图 8 几何模型和计算网格 Fig.8 Geometry and computational grid |

|
| 图 9 驻点热流随时间变化 Fig.9 Time evolution of the stagnation point heat flux |

|
| 图 10 t=500s时表面温度分布 Fig.10 Surface temperature distributions at t=500s |
在上述耦合计算的基础之上,开展耦合传热过程中催化效应和壁面温度对换热系数影响规律的研究。耦合模型计算的有限催化和非催化壁面条件下的驻点处换热系数随时间变化的对比如图 11所示。这里的换热系数定义为CH= q/(Tfilm, w-Tref),表示物体表面与附近空气温差1K,单位时间单位面积上通过对流与附近空气交换的热量,单位为W/(m2·K)。Tfilm, w为流体边界层平均温度,Tref=226.91K。可以看出在整个耦合换热过程中,驻点处的换热系数整体上随时间变化呈上升趋势,尤其是在初始的短时间内变化较剧烈,而后逐渐趋缓,但是整体绝对值变化不大。另外由于催化效应的影响,有限催化壁面的换热系数整体上略高于非催化壁面的换热系数,表明催化效应的存在增强了周围气体的换热能力。

|
| 图 11 驻点处换热系数随时间变化 Fig.11 The heat transfer coefficient of stagnation point varying with time |
将有限催化和非催化壁面条件下的驻点处换热系数随壁面温度的变化进行了对比,如图 12所示。2种情况下的驻点换热系数均随壁面温度的升高呈现出近似线性增大的规律,且有限催化壁面的换热系数整体上略高于非催化壁面的换热系数。

|
| 图 12 驻点处换热系数随温度变化曲线 Fig.12 The heat transfer coefficient of stagnation point varying with temperature |
(1) 建立了超高速流动/催化反应/传热多场耦合分析模型与计算策略,并通过高频等离子风洞获得了ZrB2-SiC超高温陶瓷材料催化系数与温度的函数关系。壁面的总热流取决于流动非平衡状态和材料表面催化特性,对于具有较高热导率材料的热响应,耦合传热分析能够有效避免非耦合计算带来的过度高估的结果。
(2) 材料表面气体热导率随着壁面催化系数的增大略有增加,从而使得飞行器表面的传热能力有所增加。简化催化模型在不同材料表面催化效应的初步研究中可以作为基准模型,更精细的研究则需要采用有限速率催化反应模型。
(3) 催化效应的存在增强了周围气体的换热能力,有限催化壁面周围气体的换热系数整体上略高于非催化壁面的换热系数,因此在传热分析中需要考虑表面催化效应以精确获得结构热响应。
| [1] |
Chen Y K, Henline W D, Tauber M E. Mars pathfinder trajectory based heating and ablation calculations[J]. Journal of Spacecraft and Rockets, 1995, 32(2): 225-230. DOI:10.2514/3.26600 |
| [2] |
Adam J C. Coupled fluid-thermal-structural modeling and analysis of hypersonic flight vehicle structures[D]. Columbus: Ohio State University, 2010.
|
| [3] |
Olynick D R, Henline W D. Navier-Stokes heating calculations for benchmark thermal protection system sizing[J]. Journal of Spacecraft and Rockets, 1996, 33(6): 807-814. DOI:10.2514/3.26842 |
| [4] |
Calvo J, Mack A, Bozic O. Study of the heating of a hypersonic projectile through a multidisciplinary simulation[C]//Proc of European Conference on Computational Fluid Dynamics. 2006.
|
| [5] |
Molvik G A, Milos F S, Chen Y K, et al. Computation of high speed flow fields with multidimensional heat conduction[R]. AIAA-1995-2116, 1995.
|
| [6] |
Yamamoto Y, Yoshioka M. CFD and FEM coupling analysis of OREX aerothermodynamic flight data[R]. AIAA-1995-2087, 1995.
|
| [7] |
Thornton E A, Dechaumphai P. Coupled flow, thermal, and structural analysis of aerodynamically heated panels[J]. Journal of Aircraft, 1988, 25(11): 1052-1059. DOI:10.2514/3.45702 |
| [8] |
桂业伟, 袁湘江. 类前缘防热层流场与热响应耦合计算研究[J]. 工程热物理学报, 2002, 23(6): 733-735. Gui Y W, Yuan X J. Numerical simulation on the coupling phenomena of aerodynamic heating with thermal response in the region of the leading edge[J]. Journal of Engineering Thermophysics, 2002, 23(6): 733-735. DOI:10.3321/j.issn:0253-231X.2002.06.022 |
| [9] |
张兵, 韩景龙. 多场耦合计算平台与高超声速热防护结构传热问题研究[J]. 航空学报, 2011, 32(3): 400-409. Zhang B, Han J L. Multi-field coupled computing platform and thermal transfer of hypersonic thermal protectionstrucutres[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(3): 400-409. |
| [10] |
Zhang S T, Chen F, Liu H. Interated of fluid-thermal-structural analysis for predicting aerothermal environment of hypersonic vehicles[R]. AIAA-2014-1394, 2014.
|
| [11] |
孟松鹤, 金华, 王国林, 等. 热防护材料表面催化特性研究进展[J]. 航空学报, 2014, 35(2): 287-302. Meng S H, Jin H, Wang G L, et al. Research advances on surface catalytic properties of thermal protection materials[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 287-302. |
| [12] |
Paterna D, Monti R, Savino R, et al. Experimental and numerical investigation of martian atmosphere entry[J]. Journal of Thermophysics and Heat Transfer, 2002, 39(2): 227-236. |
| [13] |
Wright M, Loomis M, Papadopoulos P. Aerothermal analysis of the project fire Ⅱ afterbody flow[J]. AIAA-2001-3065, 2001.
|
| [14] |
杨肖峰, 唐伟, 桂业伟. MSL火星探测器高超声速流场预测及气动性分析[J]. 宇航学报, 2015, 36(4): 383-389. Yang X F, Tang W, Gui Y W. Hypersonic flow field prediction and aerodynamics analysis for MSL entry capsule[J]. Journal of Astronautics, 2015, 36(4): 383-389. DOI:10.3873/j.issn.1000-1328.2015.04.003 |
| [15] |
刘宗庆, 董维中, 丁明松, 等. 火星探测器气动热环境和其动力特性的数值模拟研究[J]. 空气动力学学报, 2018, 36(4): 642-650. Liu Q Z, Dong W Z, Ding M S, et al. Numerical simulation of aerothermal environments and aerodynamic characteristics of Mars entry capsules[J]. Acta Aerodynamics Sinica, 2018, 36(4): 642-650. DOI:10.7638/kqdlxxb-2016.0053 |
| [16] |
Voinov L, Zalogin G N, Lunev V V, et al. Comparative analysis of laboratory and full-scale data on the catalycity of the heat shield for the Bor and Buran orbital vehicles[J]. Cosmonautics and Rocket Production, 1994, 2: 51-57. |
| [17] |
董维中, 乐嘉陵, 刘伟雄. 驻点壁面催化速率常数确定的研究[J]. 流体力学实验与测量, 2000, 14(3): 1-6. Dong W Z, Le J L, Liu W X. The determination of catalyticreate constant of surface materials of testing model in the shock tube[J]. Experiments and Measurements in Fluid Mechanics, 2000, 14(3): 1-6. DOI:10.3969/j.issn.1672-9897.2000.03.001 |
| [18] |
苗文博, 程晓丽, 艾邦成. 壁面催化条件对热环境预测的影响[J]. 航天器环境工程, 2009, 26(增刊): 45-49. Miao W B, Cheng X L, Ai B C. The influence of catalyze condition on the thermal environment predicting[J]. Spacecraft Environment Engineering, 2009, 26(S): 45-49. |
| [19] |
苗文博, 程晓丽, 艾邦成, 等. 高超声速流动壁面催化复合气动加热特性[J]. 宇航学报, 2013, 34(3): 442-446. Miao W B, Cheng X L, Ai B C, et al. Surface catalysis recombination aero heating characteristics of hypersonic flow[J]. Journal of Astronautics, 2013, 34(3): 442-446. DOI:10.3873/j.issn.1000-1328.2013.03.021 |
| [20] |
李海燕, 石安华, 马平, 等.高超声速非平衡流研究进展[C]//中国力学大会论文集. 2017. Li H Y, Shi A H, Ma P, et al, Recent advances in hypersonic non-equilibrium flows[C]//Proc of the Chinese Congress of Theoretical and Applied Mechanics. 2017. |
| [21] |
Inger G R, Gnoffo P A. Hypersonic entry heating with discontinuous surfacecatalycity-A combined analytic/CFD approach[R]. AIAA-1996-2150, 1996.
|
| [22] |
Prabhu D K, Venkatapathy E, Kontinos D A, et al. X-33 catalytic heating[R]. AIAA-1998-2844, 1998.
|
| [23] |
Scott C D, Derry S M. Catalytic recombination and space shuttle heating[R]. AIAA-1982-0841, 1982.
|
| [24] |
Ranuzzi G, Grass F, Bisceglia S. Effects of the surface catalysis on high-enthalpy shock- wave/turbulent boundary-layer interactions[R]. AIAA-2005-3219, 2005.
|
| [25] |
Viviani A, Pezzella G. Influence of surface catalyticity on reentry aerothermodynamics and heat shield[R]. AIAA-2007-4047, 2007.
|
| [26] |
Grumet A A, Anderson J D. The effects of surface catalysis on the hypersonic shock wave/boundary layer interaction[R]. AIAA-1994-2073, 1994.
|
| [27] |
Mizoguchi M, Iwata N, Hayashi K, et al. Reduction of aerodynamic heating with wall catalysis by film cooling[R]. AIAA-2006-8068, 2006.
|
| [28] |
Shirouzu M, Inouye Y, Watanabe S, et al. Overview of aero and aerothermodynamic researches on HOPE-X and related activities in Japan[R]. AIAA-2004-2426, 2004.
|
| [29] |
Peigin S, Kazak V. 3D Thermochemical nonequilibrium viscous gas flow over blunt bodies with catalytic surface at attack and slip angles[R]. AIAA-99-3628, 1999.
|
| [30] |
董维中, 高铁锁, 丁明松, 等. 高超声速飞行器表面温度分布与气动热耦合数值研究[J]. 航空学报, 2016, 36(25): 311-324. Dong W Z, Gao T S, Ding M S, et al. Numerical study of coupled surface temperature distribution and aerodynamic heat for hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2016, 36(25): 311-324. |
| [31] |
Laux T, Feigl M, Stöckle T, et al. Estimation of the surface catalyticity of PVD coatings by simultaneous heat flux and LIF measurements in high enthalpy air flows[R]. AIAA-2000-2364, 2000.
|
| [32] |
Kurotaki T. Catalytic Model on SiO2-based surface and application to real trajectory[J]. Journal of Spacecraft and Rockets, 2001, 38(5): 798-800. DOI:10.2514/2.3749 |
| [33] |
周印佳, 孟松鹤, 解维华, 等. 高超声速飞行器热环境与结构传热的多场耦合数值研究[J]. 航空学报, 2016, 37(9): 2739-2748. Zhou Y J, Meng S H, Xie W H, et al. Multi-field coupling numerical analysis of aerothermal environment and structureal heat transfer of hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(9): 2739-2748. |
| [34] |
刘丽萍, 王国林, 王一光, 等. 高焓化学非平衡流条件下防热材料表面催化特性的试验方法[J]. 航空学报, 2017, 38(10): 121317-1. Liu L P, Wang G L, Wang Y G, et al. Test methods for determining surface catalytic properties of thermal protection materials in high enthalpy chemical non-equilibrium flows[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(10): 121317-1. |
| [35] |
刘丽萍, 王国林, 王一光, 等. 高焓化学非平衡流条件下C/SiC复合材料的催化性能[J]. 航空学报, 2018, 39(5): 621696-1. Liu L P, Wang G L, Wang Y G, et al. Catalytic performance of C/SiC composites in high enthalpy chemical non-equilibrium flow[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(5): 621696-1. |
| [36] |
Anderson J D. Hypersonic and high temperature gas dynamics[M]. New York: McGraw-Hill, 2006.
|



