高超声速飞行器在大气层中飞行时,具有极高的飞行速度,会面临非常严酷的高焓非平衡气动热环境[1-3],而结构设计的精细化要求对气动热预测精准度提出了很高的要求。电弧风洞作为高焓风洞中的一种,是目前唯一能模拟高超声速飞行器长时间所经历的高焓非平衡气动热环境的地面设备[4],主要用于热防护结构考核试验。
风洞试验的最终目的是给出飞行器实际飞行条件下各种气动特性的准确测量结果;或者通过对风洞试验数据的研究,给出飞行器实际飞行条件下气动特性的准确预测结果。但在风洞试验实现过程中,很难达到实际飞行条件的完全模拟。由于各种限制(场地、能量等),试验段的来流条件与实际飞行条件常常存在很大差别。因此,在试验测量数据使用时,必须采用一定方法,将风洞试验数据外推,获得真实飞行条件下的气动特性数据。
在高焓风洞的驻室中,试验气体处于高温高压状态,并可以近似认为处于热化学平衡状态;随后试验气体历经喷管膨胀加速,到达试验段时往往会出现振动能量和化学组分的冻结现象,这就使得试验段来流与真实飞行条件有很大差别[5]。在这种情况下,来流的非平衡特性会对试验模型的气动热环境产生重要影响,使得试验数据的外推较常规风洞更加复杂。
风洞试验数据外推到真实飞行状态,一般需要采用相似参数的方法。国内外对高温气体非平衡流动模拟的相似参数已进行了很多研究,提出了一些模拟准则。例如,张涵信[6]在分析流体力学和化学动力学方程的基础上指出,在三体反应可以忽略的情况下,高温非平衡流动的模拟参数为双尺度参数ρ∞L(ρ∞为自由来流密度、L为特征长度);董维中[7-8]在对高焓脉冲风洞F4试验数据外推飞行条件的研究中指出,在保持总焓和双尺度参数ρ∞L一致的情况下,头部区域的热流可以外推到飞行条件,但在身部区域误差较大;曾明[9]通过数值模拟研究指出,在流场中三体碰撞反应趋于平衡或者冻结的情况下,双尺度模拟参数ρ∞L可以对全流场适用,但是这种适用存在一个有效范围,要求ρ∞L值不能太大。Gokcen[10]、袁军娅[11]等在研究电弧风洞试验模型非平衡气动热环境时指出,应用部分相似模拟(Partial Simulation)理论,即保持总焓和驻点压力一致,可以模拟飞行条件下的气动热环境,但要求模型边界层外缘达到热力学平衡状态。可以看出,对于不同高焓风洞及其运行状态,应用何种相似参数将试验数据外推到飞行条件存在很大差别,不同相似准则的适用范围和准确性还需进一步研究。
此外,高焓风洞流动的数值研究中,大多采用分步计算喷管和试验模型流场的方法,即先通过数值计算获取喷管出口参数,然后将其作为试验模型流场的均匀来流开展研究[12-15]。这种分步处理方法,计算效率很高,应用十分广泛。但实际上,喷管出口和试验段参数分布存在一定非均匀性[16],试验段存在沿流向的膨胀效应及非平衡效应[17-18],置入模型会对试验段气流造成影响[19],分步计算方法与实际风洞试验流场的边界条件也存在差别,这些问题都是分步处理方法所忽略的。因此为了真实地反应电弧风洞的试验过程,有必要采用喷管/试验段/试验模型流场的一体化数值模拟方法。
在笔者所在团队研制的高超声速飞行器气动物理流场计算软件(AEROPH_Flow)基础上,以中国空气动力研究与发展中心的FD-15电弧风洞为研究对象,基于一体化数值模拟思路,开展了风洞典型运行状态下喷管/试验段/试验模型流场的一体化数值模拟研究,在此基础上研究了如何将试验数据外推到飞行条件的问题,分析了改变驻室总压对于试验数据外推的影响。
1 计算方法及物理化学模型 1.1 控制方程及求解方法控制方程是三维两温度热化学非平衡Navier-Stokes方程,其无量纲化形式如下[8, 20]:
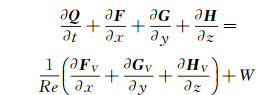 (1)
(1)
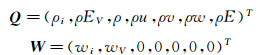
式中Q是守恒变量,ρ是混合气体总密度,ρi是组分i的密度,u、v、w为直角坐标下3个方向的速度,E为总能,EV为分子组分总振动能,Re是雷诺数,F, G, H和FV, GV, HV分别对应3个方向的对流项和粘性项,W为热化学非平衡源项,其中wi是组分i的化学非平衡源项,wV是振动非平衡源项。采用结构网格的有限差分方法离散控制方程(1),对流项采用AUSMPW+(Advection Upstream Splitting Method by Pressure-based Weight functions)格式离散,粘性项采用中心差分格式离散,时间离散采用LU-SGS(Lower-Upper Symmetric Gauss Seidel)隐式方法。为了克服方程刚性,非平衡源项、对流项和粘性项均采用全隐式处理,具体处理方法详见文献[8]和[20]。
1.2 热化学反应模型常见的空气化学反应模型有Park模型[21]、Gupta模型[22]和Dunn-Kang[23]模型,本文计算选用5组分(O2、N2、NO、O、N)的Dunn-Kang空气化学反应模型。化学反应生成源项计算具体详见文献[21]。
热力学模型采用两温度振动非平衡模型,能量关系式、振动非平衡源项计算和输运系数等计算详见文献[8]、[21和[24]。
1.3 表面催化模型表面催化特性采用了完全催化条件(Full Catalytic Wall, FCW)和非催化条件(Non-Catalytic Wall, NCW)。对于非催化条件,壁面组分满足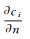
为了与主流场的化学反应计算保持一致,本文在文献[8]的基础上改进了驻室气体组分计算方法,具有较高的计算精度和稳定性。对于5组分的高温空气化学反应模型,独立的平衡化学反应有如下3个:
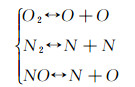 (2)
(2)
假定组分O2,N2,NO,O,N对应的分压为p1,p2,…,p5,则有如下3个化学平衡方程、2个原子数守恒方程:
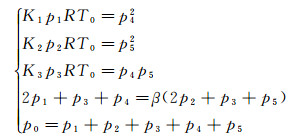 (3)
(3)
其中β=0.265808,Ki=kfi/kbi为第i个平衡化学反应的平衡常数,可由流场数值计算中的高温空气化学反应模型的相应化学反应常数求得,R为气体普适常数,p0为驻室总压,T0为驻室总温。
令p4=x,p5=y,则求解方程组(3)变为求解方程:
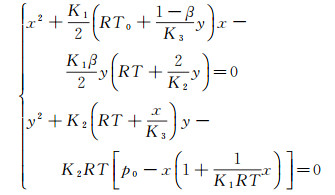 (4)
(4)
通过2个方程相互迭代求出x,y,即p4、p5,再由(3)求出其他组分分压。通过分压就可求出驻室高温空气组分的质量分数ci。
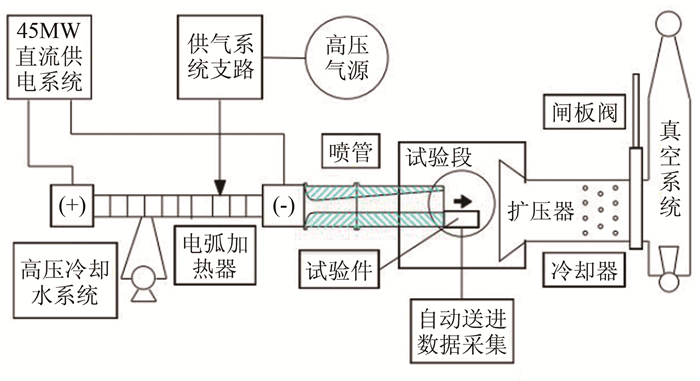
1.5 FD-15电弧风洞FD-15电弧风洞是中国空气动力研究与发展中心的主要试验设备之一,主要用于高超声速飞行器防热材料筛选和防热结构性能评估试验,其结构示意图如图 1所示。该电弧风洞可以根据实际试验需要配置片式或管式加热器,结合各种锥形、半椭圆或矩形喷管,具有灵活、宽广的试验能力,既可以开展平板试验,也可以利用驻点、钝楔试验技术开展自由射流试验。在本文涉及的计算中,喷管为锥形喷管,喉道直径为30mm,出口直径500mm,喉道前收缩角15°,喉道后扩张角8°,试验段为圆筒型,直径2m,长度3m。
|
| 图 1 FD-15电弧风洞结构示意图 Fig.1 Sketch of FD-15 arc-jet tunnel |
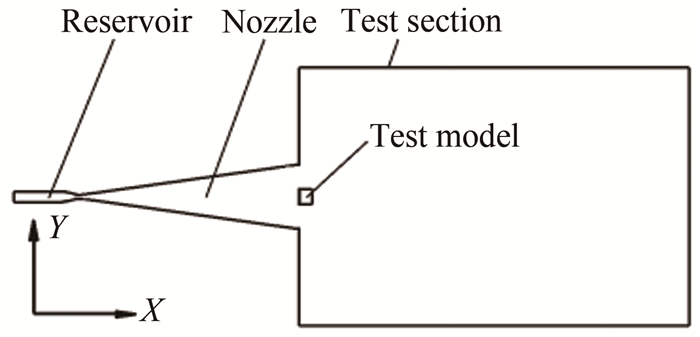
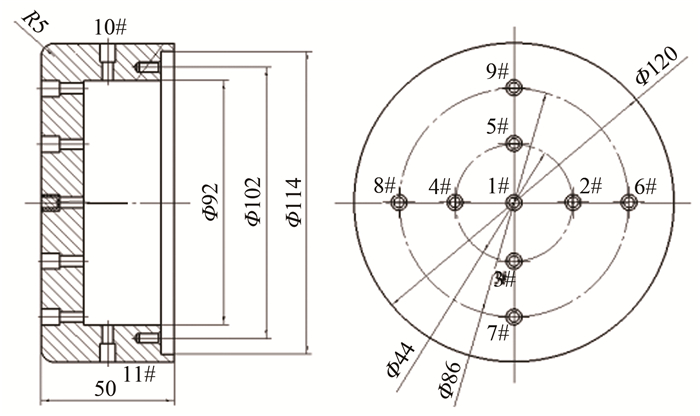
在以往研究中,作者所在团队对本文采用的计算模型、方法等进行了较为充分的验证和研究[1-3]。这里针对FD-15电弧风洞的平头热流校核试验,开展了喷管/试验段/试验模型一体化流场的数值模拟,并与试验结果进行对比,验证计算方法的合理性。计算外形如图 2所示。图 3为平头模型的结构示意图,平头直径120mm,倒角半径5mm,长50mm,头部共有9个热流测量点。共进行了2组试验,表 1给出了2组试验的风洞运行状态参数,H0为驻室气体总焓,T0为驻室温度,p0为驻室总压,G为气体流量,其中总温T0通过总焓和总压使用前述的驻室高温气体组分计算方法迭代计算得出。试验气体为空气。壁面条件采用等温壁Tw=500K、零压力梯度、无滑移、完全催化(FCW)和非催化(NCW)条件,入口条件由驻室参数获得。
|
| 图 2 一体化计算域示意图 Fig.2 Sketch of integrated computational domain |
|
| 图 3 平头模型示意图 Fig.3 Sketch of cylinder test model |
| Condition | H0/(MJ·kg-1) | T0/K | p0/MPa | G/(g·s-1) |
| 1 | 9.8 | 5070 | 0.27 | 95 |
| 2 | 17.5 | 6783 | 0.39 | 108 |
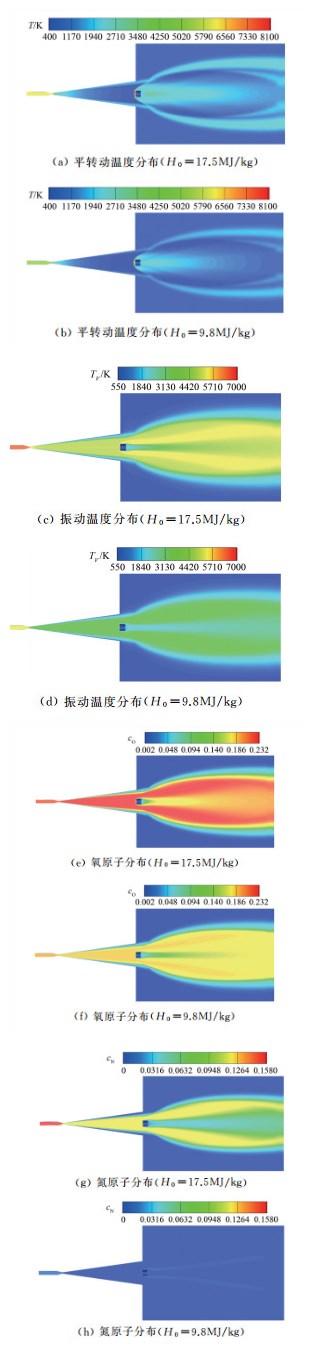
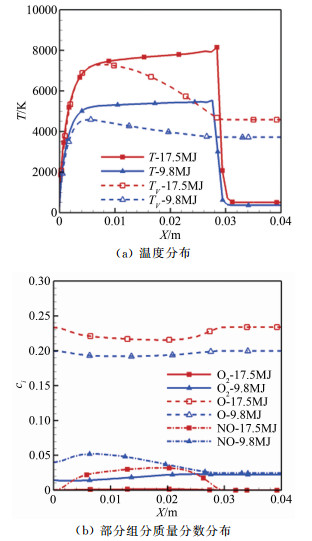
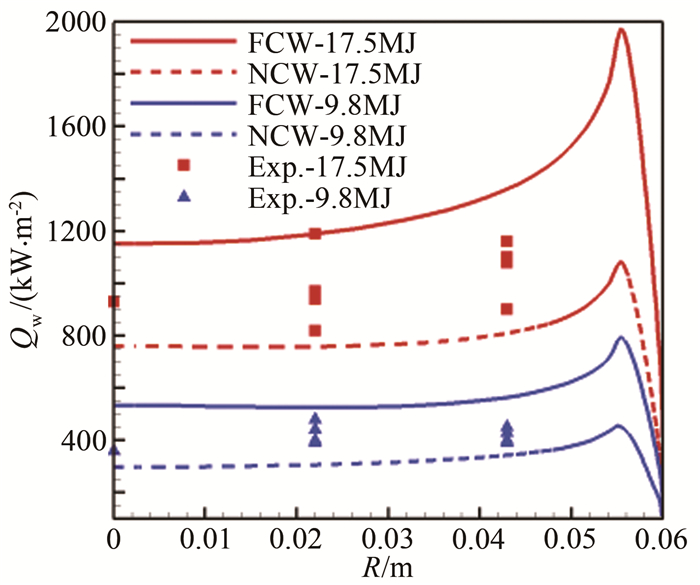
图 4给出了流场参数分布云图。从图中可以看出,试验模型头部产生的弓形激波与试验段超声速气流外边界存在强烈的相互干扰,流动结构十分复杂,试验段来流存在振动温度和组分的冻结现象,高总焓(17.5MJ/kg)试验条件下来流的振动温度冻结在更高温度,同时含有更多的氮、氧原子组分。图 5给出了NCW条件下模型驻点线上温度、压力和组分质分数分布,从图中可以看出,高总焓(17.5MJ/kg)试验条件下的波后振动温度和平转动温度更高,氧分子几乎完全离解,组分反应更加剧烈。图 6给出了计算结果与试验数据的对比,可以看出,试验得到的热流数据值几乎处于完全催化(FCW)热流和非催化(NCW)热流之间,说明数值计算方法和程序适用于电弧风洞的高温气体非平衡流场气动热环境的计算。
|
| 图 4 流场参数分布云图 Fig.4 Parameter distribution contour of flow field |
|
| 图 5 沿模型对称轴线上的参数分布(NCW条件) Fig.5 Parameter distribution along the axis of test model (NCW) |
|
| 图 6 表面热流分布对比 Fig.6 Comparison of surface heat flux |
为了研究FD-15电弧风洞的试验数据外推问题,这里选取了特征尺寸明显的球头模型作为试验模型。球头模型外形如图 7所示,其头部半径为60mm,长度为120mm。

|
| 图 7 球头模型示意图 Fig.7 Sketch of sphere test model |
计算状态为:驻室总焓17.5MJ/kg,总压0.39MPa。计算采用两温度热力学模型,化学反应模型采用5组分Dunn-Kang模型,壁面采用无滑移、零压力梯度和等温壁Tw=500K条件,表面催化条件为完全催化(FCW)、非催化(NCW)条件。
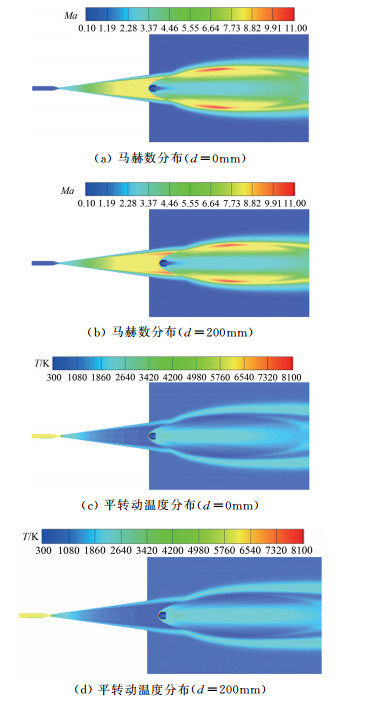
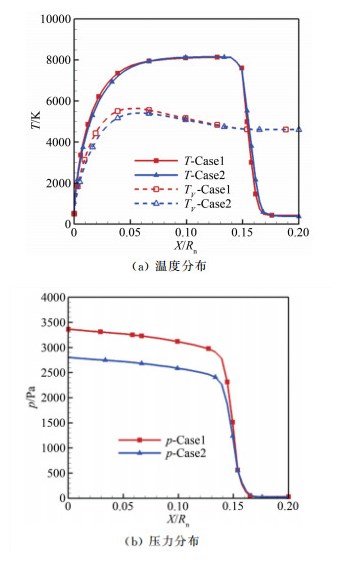
3.1 模型位置对试验模型气动特性的影响选取的计算状态为:模型迎角为0°,模型距喷管出口距离d分别为0和200mm。图 8给出了2种情况下的流场马赫数、温度分布云图。从图中可以看出,试验模型头部激波与试验段气流外边界存在相互干扰,模型位置的变化引起了试验段尾流的一定变化;试验模型距喷管出口越远,其实际来流马赫数会更高。图 9给出了NCW条件下模型驻点线上温度和压力分布对比,图中Case1表示d=0mm的计算结果,Case2表示d=200mm的计算结果。从图中可以看出:二者的平转动温度分布基本重合,Case2的波后振动温度略低于Case1;由于试验段气流沿流向的膨胀作用,Case2波前来流的压力略低,导致波后压力明显偏低。图 10给出了模型表面热流分布对比,从图中可以看出,随着模型距喷管出口距离增加,模型表面热流有一定下降,FCW条件下驻点处热流下降了9.3%,NCW条件下下降了9.7%。由此可以看出,模型位置对于试验模型表面压力、热流分布影响较大,这在试验和计算中应引起重视。
|
| 图 8 流场马赫数、温度分布云图对比 Fig.8 Comparison of Mach number and temperature contour |
|
| 图 9 模型驻点线上的参数分布(NCW条件) Fig.9 Parameter distribution along stagnation line of test model (NCW) |

|
| 图 10 模型表面热流分布对比 Fig.10 Comparison of heat flux on model surface |
对于高焓风洞试验数据外推的方法,主要有2种准则:一是非平衡流动的双尺度模拟准则,二是部分相似模拟准则。文献[6]~[9]指出,在主要发生离解反应的流动中,保持总焓和双尺度参数ρ∞L一致,可以将试验热流外推到飞行条件。目前电弧风洞中开展热防护试验时,由于很多情况下试验条件难以满足双尺度模拟准则,故提出了部分相似模拟准则,文献[25]~[26]指出,通过模拟总焓和驻点压力可以模拟飞行条件下的气动热环境。因此,这里在球头模型试验一体化数值模拟的基础上,研究了以上2种方法外推热流到飞行条件的可行性。
3.2.1 部分模拟准则表 2给出了采用部分模拟准则时风洞和飞行条件下的来流参数,对应飞行条件的确定原则是总焓和驻点压力基本一致,风洞试验的来流参数取自一体化流场数值模拟结果,表中ps是驻点压力,Rn是头部半径,V、p、T、TV为来流速度、压力、平转动温度和振动温度。从表中可以看出,飞行条件下的状态参数大致相当于65km高度下的大气条件,风洞试验来流条件则存在明显的振动温度和化学组分冻结,氧分子几乎完全离解,除了占较高质量分数的氮分子和氧原子外,来流中还存在着一定数量的氮原子。
| Parameter | Tunnel | Flight |
| H0/(MJ·kg-1) | 17.5 | 17.5 |
| ps/Pa | 5067 | 5102 |
| Rn/m | 0.06 | 0.06 |
| V/(m·s-1) | 4335 | 5900 |
| p/Pa | 56.8 | 10.3 |
| T/K | 509 | 232 |
| TV/K | 4584 | 232 |
| cN2 | 0.6572 | 0.7670 |
| cO2 | 7.3900×10-5 | 0.2330 |
| cNO | 5.5600×10-6 | 0 |
| cN | 0.1090 | 0 |
| cO | 0.2340 | 0 |
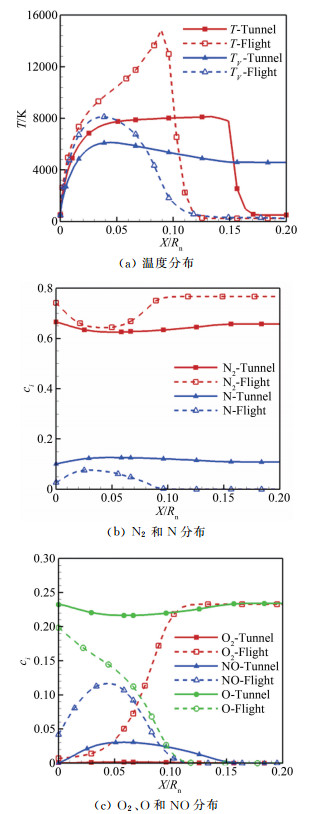
图 11给出了NCW条件下模型头部驻点线上的流场参数分布,可以看出:(1)风洞条件下试验模型激波脱体距离明显大于飞行条件;(2)风洞条件下的来流含有大量原子组分,同样地,其波后流场中原子组分质量分数也明显高于飞行条件,而分子组分则明显低于飞行条件,风洞条件下流场中的氧分子几乎完全离解;(3)在壁面附近边界层内,风洞条件下的原子组分明显高于飞行条件,尤其是氮原子,风洞试验未能模拟飞行条件边界层外缘气体的离解程度。
|
| 图 11 模型驻点线上流场参数分布(NCW条件) Fig.11 Parameters distribution along stagnation line of test model (NCW) |
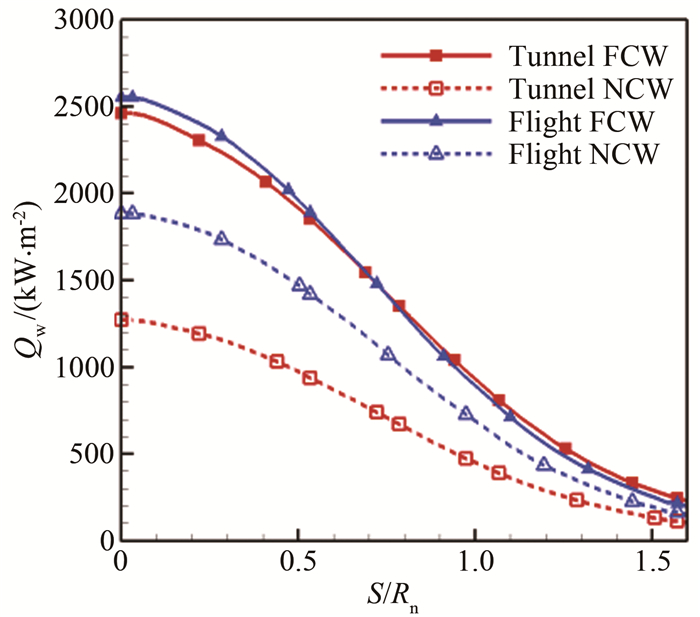
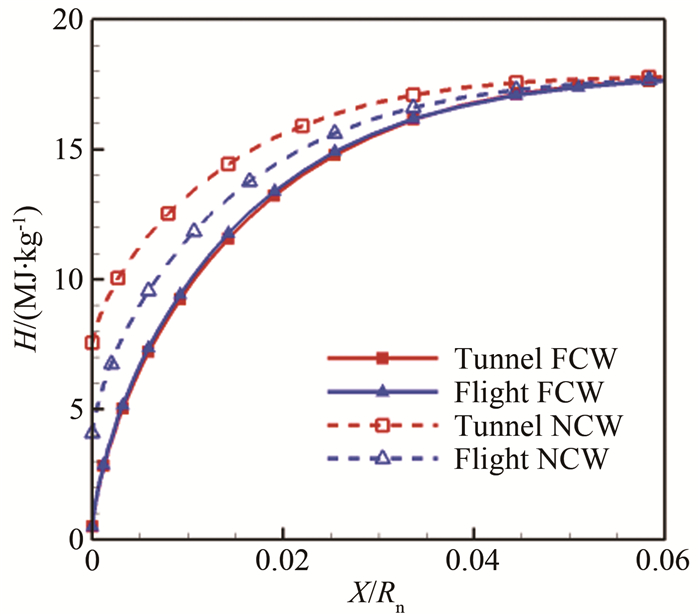
图 12给出了风洞和飞行条件下模型表面热流分布对比,从图中可以看出,在FCW条件下,二者热流接近,飞行条件驻点热流比风洞条件高5%左右;在NCW条件下,飞行条件驻点热流比风洞条件高48%,此时风洞试验的气动热环境模拟明显偏低,将风洞热流试验数据外推飞行条件存在较大误差。为了研究NCW条件下热流差异的原因,图 13进一步给出了风洞和飞行条件下模型驻点壁面附近的气体总焓分布对比,可以看出,FCW条件下,边界层内二者的气体总焓分布基本重合,而NCW条件下,风洞条件的气体总焓明显高于飞行条件,这是由于风洞条件下壁面附近原子组分更高、存在更多化学焓导致,而这些化学焓在NCW条件下难以转化为壁面热流,因此导致总热流偏低。
|
| 图 12 模型表面热流分布对比 Fig.12 Comparison of heat flux on model surface |
|
| 图 13 模型驻点边界层内的总焓分布 Fig.13 Total enthalpy distribution in the boundary layer of stagnation point |
总的来说,在此试验状态下,采用部分模拟准则外推热流出现较大误差,尤其是非催化条件下。
3.2.2 双尺度模拟准则表 3给出了采用双尺度模拟准则时风洞和飞行条件下的来流参数,对应飞行条件的确定原则是总焓和双尺度参数ρ∞L基本一致,表中ρ∞为来流密度。从表中可以看出,飞行条件下模型尺寸放大了3倍,相应的密度减小3倍,其状态参数大致相当于69km高度下的大气条件,处于热化学平衡状态。
| Parameter | Tunnel | Flight |
| H0/(MJ·kg-1) | 17.5 | 17.5 |
| ρ∞L | 3.48×10-5 | 3.48×10-5 |
| ρ∞/(kg·m-3) | 5.80×10-4 | 1.93×10-4 |
| Rn/m | 0.06 | 0.18 |
| V/(m·s-1) | 4335 | 5900 |
| p/Pa | 56.800 | 6.175 |
| T/K | 509 | 223 |
| TV/K | 4584 | 223 |
| cN2 | 0.6572 | 0.7670 |
| cO2 | 7.3900×10-5 | 0.2330 |
| cNO | 5.5600×10-6 | 0 |
| cN | 0.1090 | 0 |
| cO | 0.2340 | 0 |
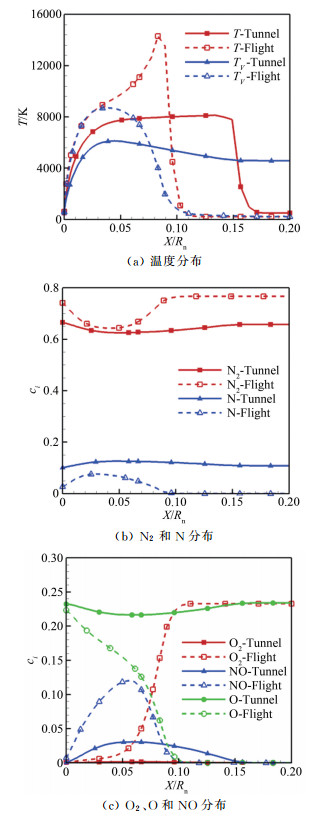
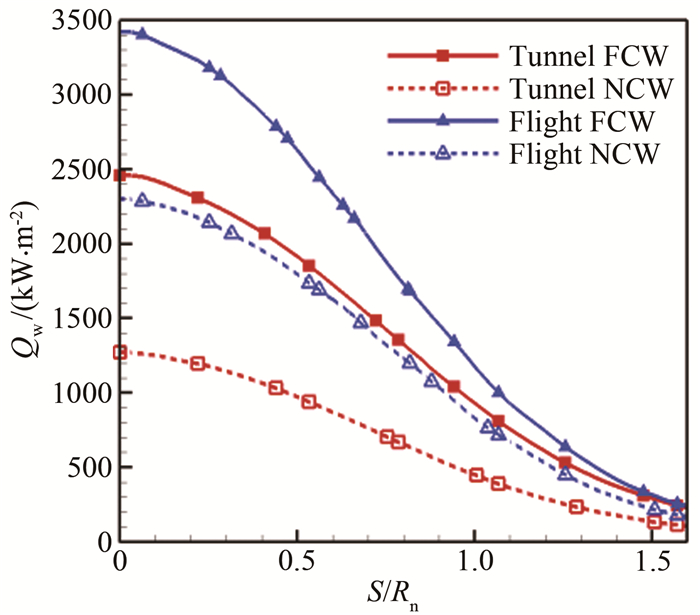
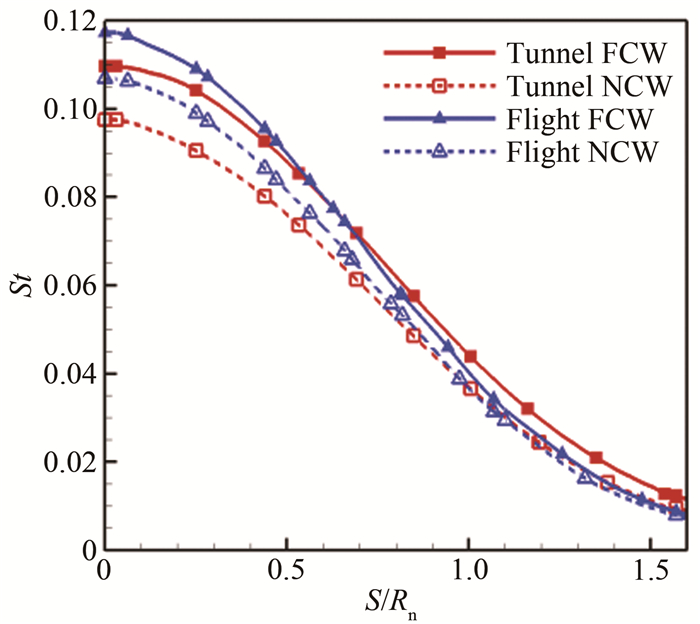
图 14给出了NCW条件下试验模型头部驻点线上的流场参数分布。与图 11类似,风洞条件下模型的激波脱体距离明显大于飞行条件,波后化学反应剧烈,壁面附近边界层内,组分质量分数变化剧烈,风洞条件下的原子组分明显高于飞行条件。图 15给出了以缩比尺度外推热流的对比,本文与文献[7]、[8]和[27]采用了相同方法,风洞和飞行条件的密度相差3倍因子,因此将飞行热流乘以缩比尺度3后与风洞热流对比。可以看出,FCW热流值比风洞试验热流高39%,NCW热流值更是高80%,因此,使用缩比尺度外推热流是失效的。图 16给出了2种条件下的表面Stanton数(St)对比,在FCW条件下,驻点处Stanton数相差7.0%,沿驻点向后发展误差逐渐加大。这种差别可能是由于沿驻点向后复合反应逐渐占优导致双尺度准则失效造成的,在NCW条件下,驻点处Stanton数相差9.5%。
|
| 图 14 模型驻点线上流场参数分布(NCW条件) Fig.14 Parameters distribution along stagnation line of test model (NCW) |
|
| 图 15 模型表面热流分布(尺度为3) Fig.15 Heat flux distribution on model surface (by scale 3) |
|
| 图 16 模型表面Stanton数分布 Fig.16 Stanton number distribution on model surface |
从上面的分析可以看出,在本文的计算状态下,风洞试验采用双尺度准则模拟时,使用缩比尺度外推热流是失效的,使用Stanton数外推热流时,结果有一定误差,因此,认为本文的电弧风洞运行状态下难以通过双尺度模拟准则模拟实际飞行状态。
3.3 提高驻室压力对数据外推的影响从上节的结果可以看出,由于电弧风洞的来流存在更多的原子组分,热化学非平衡效应严重,导致一些条件下外推热流出现失效的问题。本节将研究通过提高驻室压力来改善电弧风洞数据外推的可行性。
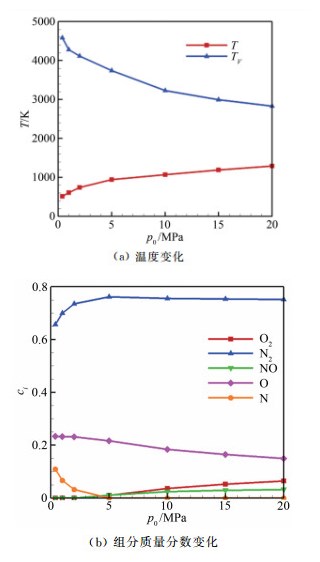
图 17给出了喷管出口参数随驻室压力变化的情况。从图中可以看出,随着驻室压力增加,喷管出口平转动温度更加接近于振动温度,同时原子组分质量分数不断下降,氧分子、一氧化氮分子质量分数有一定上升,这是由于驻室压力升高导致密度增加,使得振动松弛和化学反应特征时间变短,振动松弛和化学反应更容易达到平衡状态,因此提高驻室压力可以抑制试验段来流的非平衡特性。
|
| 图 17 喷管出口参数随驻室压力变化关系 Fig.17 Relationship between reservoir pressure and parameters at nozzle exit |
在保持总焓不变的情况下,取驻室总压为5MPa,对FD-15电弧风洞中的球头试验进行一体化数值模拟。作为对比,同时计算了2组飞行条件:采用部分模拟准则和双尺度模拟准则时对应的飞行来流条件。
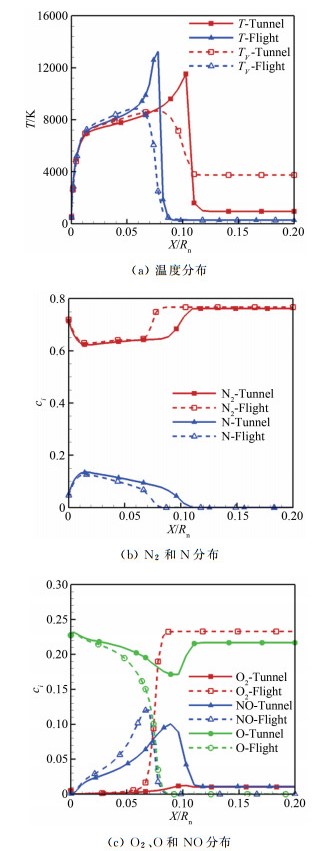
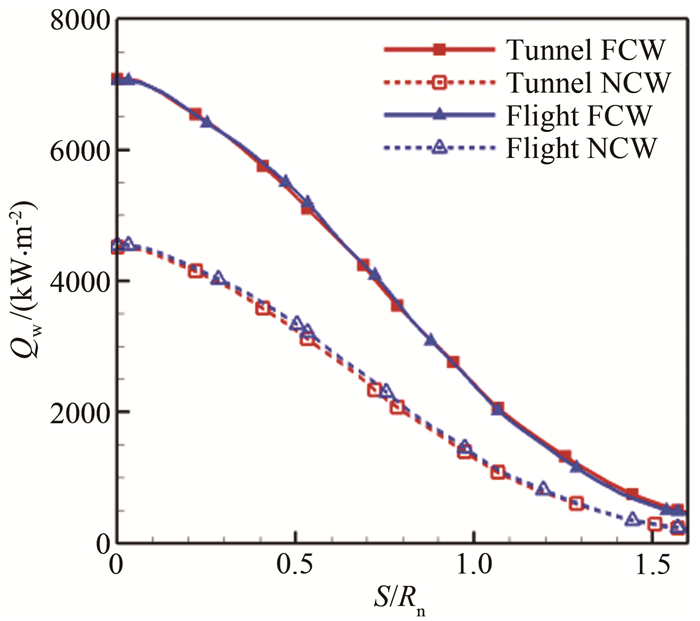
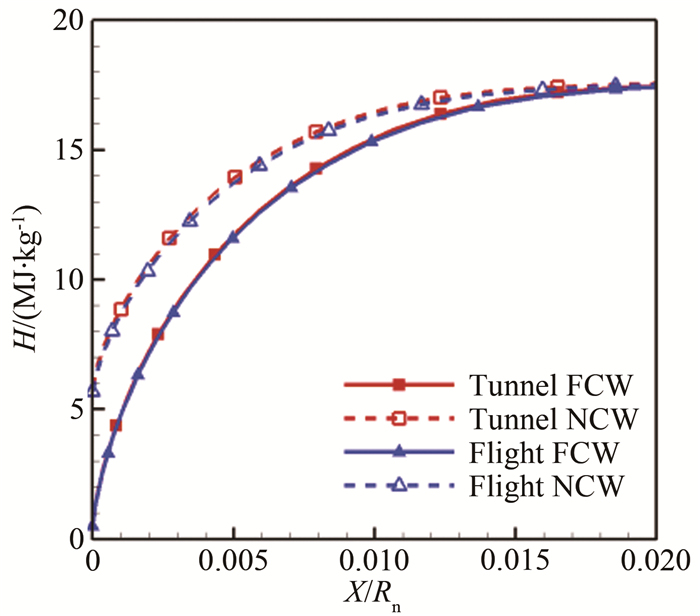
3.3.1 部分模拟准则表 4给出了采用部分模拟准则时风洞和飞行条件下的来流条件。图 18给出了驻室总压为5MPa时,NCW条件下模型头部驻点线上的流场参数分布。相较于图 11(驻室总压0.39MPa),可以看出:(1)随着驻室压力升高,风洞和飞行条件下激波脱体距离均有所减小,并且二者差距也有所缩小,波后平转动温度和振动温度更加接近,表明提高驻室压力使波后更接近热力学平衡状态;(2)随着驻室压力的升高,壁面边界层内风洞与飞行条件的组分分布差异减小,在高驻室压力情况下风洞试验很好地模拟了飞行条件边界层外缘的气体离解程度;(3)随着驻室压力升高,风洞和飞行条件下边界层内的复合反应均有所增强。图 19给出了驻室压力为5MPa时模型表面热流对比。可以看出,相较于图 12(驻室总压0.39MPa),模型表面的热流升高,风洞和飞行条件的热流差别减小,二者的热流分布最大相差不超过5%。由此可知,提高驻室压力可以很好地改善使用部分模拟准则外推热流的误差情况。图 20给出了驻室压力为5MPa时驻点边界层内的总焓对比。可以看出,相较于图 13(驻室总压0.39MPa),风洞和飞行条件的边界内总焓分布基本重合,这正是由于其化学组分分布逐渐吻合所致,表明风洞和飞行条件的气动热环境十分接近。
| Parameter | Tunnel | Flight |
| H0/(MJ·kg-1) | 17.5 | 17.5 |
| ps/Pa | 40739 | 41008 |
| Rn/m | 0.06 | 0.06 |
| V/(m·s-1) | 5052 | 5900 |
| p/Pa | 542.00 | 96.13 |
| T/K | 939 | 271 |
| TV/K | 3740 | 271 |
| cN2 | 0.7620 | 0.7670 |
| cO2 | 0.0100 | 0.2330 |
| cNO | 0.1091 | 0 |
| cN | 1.2100×10-6 | 0 |
| cO | 0.2171 | 0 |
|
| 图 18 模型驻点线上流场参数分布(p0=5MPa,NCW条件) Fig.18 Parameters distribution along stagnation line of test model (p0=5MPa, NCW) |
|
| 图 19 模型表面热流分布对比(p0=5MPa) Fig.19 Comparison of heat flux on model surface (p0=5MPa) |
|
| 图 20 模型驻点边界层内的总焓分布(p0=5MPa) Fig.20 Total enthalpy distribution in the boundary layer of stagnation point (p0=5MPa) |
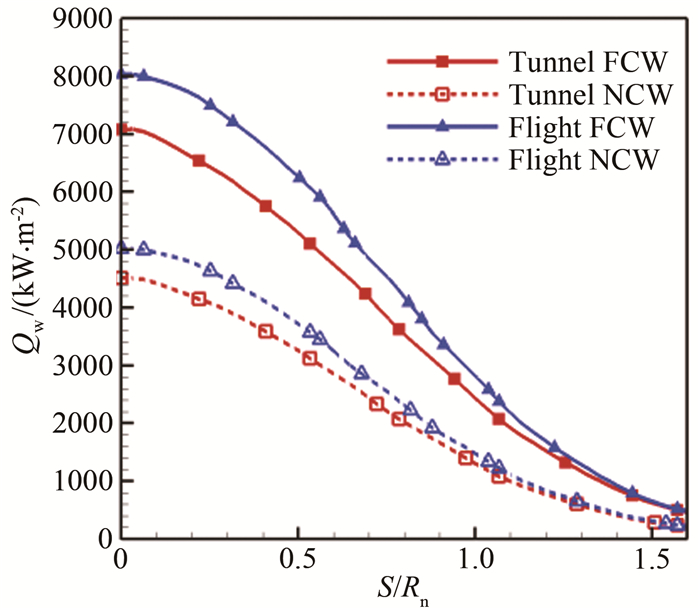
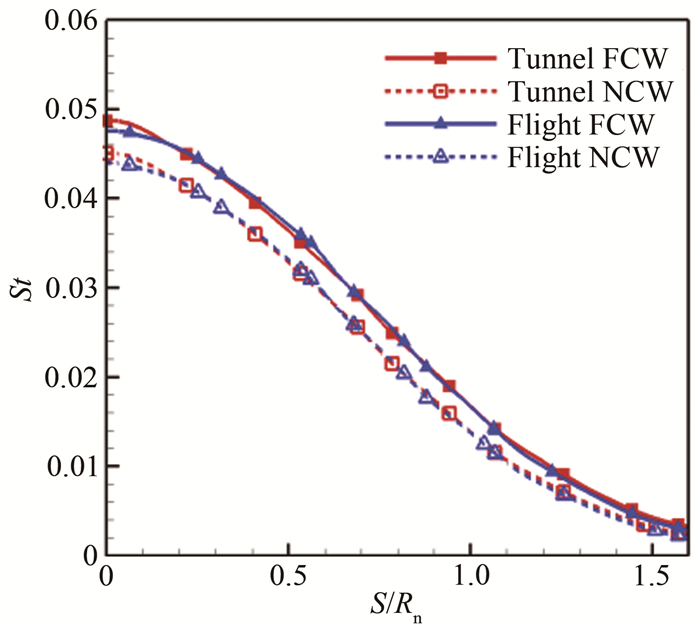
表 5给出了采用双尺度参数模拟准则时风洞和飞行条件下的来流条件。图 21给出了以缩比尺度外推热流的对比,其中飞行条件下的模型尺寸放大3倍,因此将飞行热流乘以缩比尺度3后与风洞热流对比。可以看出,提高驻室压力使外推误差减小,驻室压力提高到5MPa,FCW条件下相差13.5%,而NCW条件下为11.3%。图 22给出了表面Stanton数对比。可以看出,提高驻室压力使风洞和飞行条件的Stanton数误差减小,驻室压力提高到5MPa时,2种表面催化条件下的最大误差下降到2.3%。
|
| 图 21 模型表面热流分布(尺度为3,p0=5MPa) Fig.21 Heat flux distribution on model surface (by scale 3, p0=5MPa) |
|
| 图 22 模型表面Stanton数分布(p0=5MPa) Fig.22 Stanton number distribution on model surface (p0=5MPa) |
| Parameter | Tunnel | Flight |
| H0/(MJ·kg-1) | 17.5 | 17.5 |
| ρ∞L | 1.005×10-4 | 1.005×10-4 |
| ρ∞/(kg·m-3) | 5.80×10-4 | 1.93×10-4 |
| Rn/m | 0.06 | 0.18 |
| V/(m·s-1) | 5052 | 5900 |
| p/Pa | 542.0 | 41.7 |
| T/K | 939 | 260 |
| TV/K | 3740 | 260 |
| cN2 | 0.7620 | 0.7670 |
| cO2 | 0.0100 | 0.2330 |
| cNO | 0.1091 | 0 |
| cN | 1.2100×10-6 | 0 |
| cO | 0.2171 | 0 |
研究结果表明:提高驻室总压可以抑制试验段来流的非平衡特性,同时增强试验模型波后的化学反应,使风洞试验与飞行条件下模型波后的流场参数分布更加接近,从而明显减小使用部分模拟准则和双尺度模拟准则外推热流的误差。
4 结论通过本文的研究,可以得到以下结论:
(1) 验证了高焓风洞三维热化学非平衡流场一体化数值模拟的计算方法和计算程序,热流校核试验测量数据位于一体化数值模拟的完全催化热流和非催化热流之间,分布合理,计算方法和程序正确。
(2) 由于试验段流场沿流向的非均匀性,随着模型距喷管出口距离d增大,模型表面的压力和热流值有一定降低,这在试验和计算中应引起重视。
(3) 在驻室总压较低的试验条件下(0.39MPa),数值模拟表明,风洞试验与飞行条件下的模型边界层外缘气体离解程度差别很大, 采用不同模拟准则将风洞热流试验数据外推飞行条件存在差别。采用部分模拟准则时,风洞试验的完全催化热流与飞行条件接近,但非催化热流明显偏低;在完全催化和非催化条件下,风洞试验均难以通过双尺度模拟准则模拟实际飞行状态。
(4) 提高驻室总压可以抑制试验段来流的非平衡特性,同时增强试验模型波后的热化学效应,使风洞试验与飞行条件下模型波后的流场参数分布更加接近,从而明显减小使用部分模拟准则和双尺度模拟准则外推热流的误差。
基于本文的高焓风洞一体化数值模拟思想,可以更加真实地反映高焓风洞试验过程,改善风洞试验数值模拟精度,还可以应用于其他高焓风洞设备、复杂试验模型以及试验数据外推飞行条件等方面的研究,为高焓风洞试验方案设计以及测量数据对比分析奠定坚实基础。为了完善高焓风洞一体化数值模拟方法,还需要开展以下几个方面的研究:重叠网格技术的计算研究;试验模型表面催化特性计算模型的研究;湍流效应对高焓风洞试验流场的影响研究;考虑多个振动温度的高焓风洞热化学非平衡流动研究。
致谢: 本文的研究得到了中国空气动力研究与发展中心唐志共研究员负责的某项基础理论研究课题的支持,中国空气动力研究与发展中心超高速空气动力研究所提供了FD-15电弧风洞的参数以及试验数据,在此特别感谢!| [1] |
董维中, 高铁锁, 丁明松, 等. 高超声速飞行器表面温度分布与气动热耦合数值研究[J]. 航空学报, 2015, 36(1): 311-324. Dong W Z, Gao T S, Ding M S, et al. Numerical study of coupled temperature distribution and aerodynamic heat for hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 311-324. |
| [2] |
丁明松, 董维中, 高铁锁, 等. 局部催化特性差异对气动热环境影响的计算分析[J]. 航空学报, 2018, 39(3): 121588. Ding M S, Dong W Z, Gao T S, et al. Computational analysis of influence of differences in local catalytic properties on aero-thermal environment[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(3): 121588. |
| [3] |
丁明松, 董维中, 高铁锁, 等. 传感器催化特性差异对气动热影响的计算分析[J]. 宇航学报, 2017, 38(12): 1361-1371. Ding M S, Dong W Z, Gao T S, et al. Computational analysis of influence on aero-thermal environments caused by catalytic property distinction of heat flux sensor[J]. Journal of Astronautics, 2017, 38(12): 1361-1371. |
| [4] |
Lu F K, Marren D E. Advanced hypersonic test facilities[M]. Virginia: American Institute of Astronautics and Aeronautics, 2002.
|
| [5] |
汪球, 赵伟, 滕宏辉, 等. 高焓激波风洞喷管流场非平衡特性研究[J]. 空气动力学学报, 2015, 33(1): 66-71. Wang Q, Zhao W, Teng H H, et al. Numerical simulation of none-equilibrium characteristics of high enthalpy shock tunnel:nozzle flow[J]. Acta Aerodynamica Sinica, 2015, 33(1): 245-254. |
| [6] |
张涵信. 真实气体流动的相似规律[J]. 空气动力学学报, 1990, 8(1): 1-8. Zhang H X. The similarity law for real gas flow[J]. Acta Aerodynamica Sinica, 1990, 8(1): 1-8. |
| [7] |
董维中, 乐嘉陵, 高铁锁. 钝体标模高焓风洞试验和飞行试验相关性的数值分析[J]. 流体力学实验与测量, 2002, 16(2): 1-8. Dong W Z, Le J L, Gao T S. Numerical analysis for correlation of standard model testing in high enthalpy facility and flight test[J]. Experimental Measurements in Fluid Mechanics, 2002, 16(2): 1-8. DOI:10.3969/j.issn.1672-9897.2002.02.001 |
| [8] |
董维中.热化学非平衡效应对高超声速流动影响的数值计算与分析[D].北京: 北京航空航天大学, 1996. Dong W Z. Numerical simulation and analysis of thermal-chemical non-equilibrium effects at hypersonic flows[D]. Beijing: Beijing University of Aeronautics and Astronautics, 1996. |
| [9] |
曾明, 林贞彬, 柳军, 等. 非平衡模拟参数ρ∞L有效性的数值分析[J]. 力学学报, 2009, 41(2): 177-184. Zeng M, Lin Z B, Liu J, et al. Numerical analysis of the validity of binary scaling parameter ρ∞Lin nonequilibrium flow[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(2): 177-184. DOI:10.3321/j.issn:0459-1879.2009.02.005 |
| [10] |
Gokcen T. Effects of flow field nonequilibrium on convective heat transfer to a blunt body[R]. AIAA-96-0352, 1996.
|
| [11] |
袁军娅, 蔡国飙, 杨红亮, 等. 高焓非平衡气动热环境的试验模拟及影响[J]. 实验流体力学, 2012, 26(6): 35-39. Yuan J Y, Cai G B, Yang H L, et al. Test simulation of heat environment in high enthalpy nonequilibrium flow and effects[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(6): 35-39. DOI:10.3969/j.issn.1672-9897.2012.06.008 |
| [12] |
Ishihara T, Ogino Y, Ohnishi N, et al. Numerical study on anomalous heating over blunt-body in free-piston shock tunnel HIEST[R]. AIAA-2013-0909, 2013.
|
| [13] |
Ishihara T, Aizawa R, Ogino Y, et al. Numerical analysis on aerothermodynamic characteristics of blunt-nosed cone in free-piston shock tunnel HIEST[R]. AIAA-2014-1390, 2014.
|
| [14] |
Holden M S, Wadhams T P, MacLean M, et al. Experiment research analysis in supersonic and hypervelocity flows in the LENS shock tunnels and expansion tunnel[R]. AIAA-2015-3660, 2015.
|
| [15] |
Vasilevskii E B, Zhestkov B E, Sakharov V I. Numerical simulation and experiment in the induction plasmatron of the VAT-104 wind tunnel[J]. TsAGI Science Journal, 2016, 47(5): 457-474. DOI:10.1615/TsAGISciJ.v47.i5 |
| [16] |
Clemente M D, Trifoni E, Marini M. Numerical and experimental analyses on re-entry vehicle control surface[R]. AIAA-2013-5331, 2013.
|
| [17] |
曾明.高焓风洞流场测量的数值重建和非平衡效应的数值分析[D].北京: 中国科学院力学研究所, 2006. Zeng M. Numerical rebuilding of free-stream measurement and analysis of none-equilibrium effects in high enthalpy tunnel[D]. Beijing: Institute of Mechanics, Chinese Academy of Science, 2007. |
| [18] |
曾明, 林贞彬, 郭大华, 等. 高焓激波风洞自由流参数的数值重建[J]. 空气动力学学报, 2009, 27(3): 358-362. Zeng M, Lin Z B, Guo D H, et al. Numerical rebuilding of free stream measurement in the high enthalpy shock tunnel[J]. Acta Aerodynamica Sinica, 2009, 27(3): 358-362. DOI:10.3969/j.issn.0258-1825.2009.03.017 |
| [19] |
Numerical and experimental study of high enthalpy flows in a hypersonic plasma wind tunnel: L3K[R]. AIAA-2011-3777, 2011.
|
| [20] |
董维中. 气体模型对高超声速再入钝体气动参数计算影响的研究[J]. 空气动力学学报, 2001, 19(2): 197-202. Dong W Z. Thermal and chemical model effect on the calculation of aerodynamic parameter for hypersonic reentry blunt body[J]. Acta Aerodynamica Sinica, 2001, 19(2): 197-202. DOI:10.3969/j.issn.0258-1825.2001.02.010 |
| [21] |
Park C. Non-equilibrium hypersonic aerothermodynamics[M]. New York: John Wiley &Sons, 1990.
|
| [22] |
Gupta R N, Yos J M, Thompson R A. A review of reaction rates and thermodynamic and transport properties for 11-species air model for chemical and thermal non-equilibrium calculation to 30000K[R]. NASA-TM-101528, 1989.
|
| [23] |
Dunn M G, Kang S W. Theoretical and experimental studies of reentry plasmas[R]. NASA-CR-2232, 1973.
|
| [24] |
Anderson J D. Hypersonic and high temperature gas dynamics[M]. New York: McGraw-Hill Book Company, 1989.
|
| [25] |
Fay J A, Riddle, F R. Theory of stagnation point heat transfer in dissociatedair[J]. Journal of the Aeronautical Science, 1958, 25(2): 73-85. |
| [26] |
Goulard R. On catalytic recombination rates in hypersonic stagnation heat transfer[J]. Jet Propulsion, 1958, 25(2): 733-745. |
| [27] |
Muylaert J, Walpot L, Hauser J, et al. Standard model testing in the European high enthalpy facility F4 and extrapolation to flight[R]. AIAA-92-3905, 1992.
|



