二维粒子图像速度测量技术(Two-dimensional Particle Image Velocimetry,2D-PIV)是20世纪70年代末发展起来的一种激光流体测速方法,与激光多普勒测速、热线风速仪等单点测速手段相比,其具有瞬态、多点、无接触式的优点, 因此经过几十年的不断完善与发展,该技术在实验流体力学、空气动力学、燃烧学和叶轮机械等诸多领域都有着广泛的应用[1-3]。然而, 由于基础科学研究和实际工程应用中的诸多流动现象都具有复杂的三维特征,二维流场的速度信息不足以反映流动现象的数学物理本质,因此,如何精确测量三速度分量的三维(3D-3C)速度场成为了近几十年来PIV领域的一个研究热点。
利用双目视觉仿生学的原理,先后有学者提出了使用2台相机并采用不同布局方式的Stereo PIV技术,该技术首先获得激光片光源所在平面中的示踪粒子在2个相机图片中各自的二维位移速度场,然后联立求解该平面中的三维速度场,从而来获得一个平面内的三速度分量(2D-3C)[4]。与此同时也有学者提出了Scanning PIV技术,该技术利用可以旋转的反射镜装置,使激光片光源旋转扫描整个待测流场,用单目或者双目高速相机测量多个切面的速度矢量场,但受限于激光扫描和相机存储的速度,该技术的最大可测量速度一般小于1m/s[5]。数字离焦PIV(Defocusing PIV,DPIV)则采用了带有光阑的镜头拍摄示踪粒子图像,光阑具有一定的图案,如带有3个圆孔的掩模,示踪粒子离相机聚焦平面距离不同时,由于光阑的作用,粒子离焦图像的模糊程度不同并且会发生上下翻转,因此可以计算出粒子的三维空间位置,带有光阑的单相机即可完成三维流场测速,但DPIV技术的示踪粒子浓度一般较低[6]。全息PIV(Holographic, HPIV)则利用全息照相技术将示踪粒子的三维图像记录在银盐感光胶片或者数码相机中,进而通过三维互相关获得粒子的速度场。利用感光胶片成像时,HPIV具有目前PIV技术中最高的空间分辨率,然而由于该技术中粒子全息相片处理过程的时间和资金成本都较高,而且全息技术本身的光路布置比较复杂,目前这一技术并没有得到广泛应用[7-9]。层析PIV(Tomographic PIV,Tomo-PIV)则是一种近十多年逐步发展起来的三维流动测试技术,该技术一般采用4~8台数字相机在不同角度拍摄同一流体区域,进而利用得到的粒子图像通过MART重构算法和三维互相关算法计算出速度矢量[10-11],其测量结果精准,测量区域较大,粒子浓度高并且空间分辨率较高,因此已经被广泛应用于多个领域的流动测试,但该技术也存在着校准过程复杂、需要的光学窗口较多等不足,因此并不适合光学窗口数目受限情形的三维流场测量。鉴于Tomo-PIV操作的复杂性,有国内学者提出利用一块三视野的分光镜来实现单相机的3D-3C测量[12],由于被拍摄区域与相机之间有一块特殊的三视野分光棱镜,相机CCD芯片被划分成了3个不同的成像区域,每个区域对应示踪粒子的一个观察视角,该技术的图像数据处理过程类似于Tomo-PIV,但实验装置及操作过程的复杂性得到了极大的降低,不过由于3个视角对应的观察角总体比较小,因而在沿光轴方向上的空间分辨率不及垂直于光轴方向的空间分辨率。合成孔径PIV(Synthetic Aperture PIV,SAPIV)是另外一种利用多相机来测量流体速度矢量场的三维测试技术,通常该技术采用了包含至少5台以上的相机阵列来获取粒子图像,并进一步用合成孔径重聚焦算法获取多个重聚焦平面的粒子强度[13],从而获得三维粒子光照强度场和速度矢量场。与Tomo-PIV相比,SAPIV能够消除粒子之间的相互遮挡作用,因此可以测量粒子浓度更高的流场,而且其在景深方向的测量范围能够达到与垂直光轴方向测量范围同等大小的水平,这一技术的最大缺陷在于其结构复杂且成本高昂的相机阵列。
不同于上述的三维PIV测试技术,光场PIV(Light-field PIV, LF-PIV)是一种近些年来发展起来的能够仅利用单台相机即可比较精准测量三维速度场的PIV技术[14-15],其既不需要复杂的光路系统,又不需要多台相机,因此极大地简化了试验操作难度并降低了硬件成本,特别适合光学窗口较少情形下的流体三维速度场测量。LF-PIV的硬件是基于斯坦福大学Ng于2005年利用现有高分辨率相机开发出来的紧凑型光场相机,其科研成果转化产品为Lytro品牌的光场相机[16],但由于这种面向普通消费者的相机不具备PIV所需的双曝光功能,因此无法实际应用到PIV技术中。市场上另外一种比较流行的光场相机是德国Raytrix公司旗下推出的面向工业界的产品[17],但由于Raytrix光场相机的相关硬件结构、微透镜参数和重构算法均对用户封闭,因此使用者很难利用该相机针对不同条件下的流场测试问题进行自主开发粒子重构算法[18]。
基于上述情况,本文作者所在的课题组和美国学者Brian领导的团队分别展开了对光场相机的硬件开发和粒子三维重构算法的研究。LF-PIV利用带有微透镜阵列(Microlens Array, MLA)和高分率CCD的光场相机记录下示踪粒子的4D光场图像,进一步通过光场重聚焦算法或者光线跟踪算法重构粒子强度场[19-20]。尽管LF-PIV能够仅凭借单台光场相机即可实现3D-3C测量,但由于光场相机整体的视角较小,因此重构出的粒子强度在沿光轴方向上会被拉长,从而影响了粒子重构沿光轴方向的空间分辨率,这一现象在Tomo-PIV中也比较常见,被称为拉长效应(Elongation Effect)[10]。针对这一问题,已有学者在HPIV中提出利用2台相机呈光轴相互垂直布置来达到最佳的空间分辨率[21]。参照该想法,本文作者提出了双光场相机PIV技术,通过利用2个光场相机增大视角来消除或抑制这一效应,由此提高景深空间分辨率以及沿光轴方向的测量精度。
本文阐述了双光场相机系统,包括双光场相机PIV系统概述、光场相机成像原理、基于光线跟踪的数字合成图像以及基于光场相机校准的双光场相机MART三维粒子重构算法。利用DNS射流数据生成了数字合成图像,通过水射流涡环验证实验得到实验图像,并根据这两者的结果对双光场相机和单光场相机进行详细对比分析。
1 双光场相机PIV技术 1.1 双光场相机PIV系统为了增大相机系统对示踪粒子的观察视角以消除或抑制单光场相机粒子重构中的拉长效应,本文采用2个光场相机的光轴相互垂直呈90°的布置方式,以达到最大的相机观察视角。
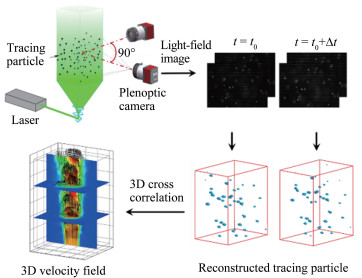
双光场相机PIV的工作流程为(如图 1所示):将示踪粒子注入待测试流体,这些粒子在Nd:YAG激光照射下因反射作用变得高亮可见,随后用2台光轴互相垂直的光场相机同时拍摄同一流场区域并采用双曝光模式记录下示踪粒子的光场图像。对获得的原始图像减去由于环境反射光造成的背景噪声后,利用基于光场相机校准的MART算法重构三维粒子强度场,最后由基于FFT算法的多重网格互相关计算出3D-3C速度场。
|
| 图 1 双光场相机PIV系统工作流程示意图 Fig.1 Working principle of dual light-field cameras PIV |
与传统相机相比,光场相机的不同之处在于其不仅能够记录进入相机的每一根光线的空间坐标,也能记录下其相应的传播方向,即能够记录下进入相机的“光场”(Light Field)。“光场”这一概念由Arun Gershun于1936年首次提出,他将其定义为在空间中各点处向各个方向传播的辐射光线的集合[22]。而当光线在自由空间中传播且能量不发生损失时,每根光线可以表示为4D函数的形式[23]:
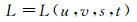 (1)
(1)
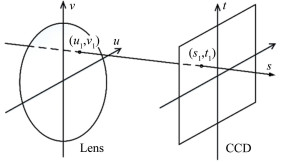
式中, (u, v)和(s, t)分别代表某根光线沿传播方向与2个平行平面的交点坐标(如图 2所示)。这2组坐标不仅包含了某根光线的空间坐标信息,也包含了其传播方向信息。
|
| 图 2 光场4D函数 Fig.2 4D parameterization of light field |
光场相机与常规相机不同,其在主透镜和CCD感光器件之间存在一个微透镜阵列,CCD平面处于微透镜阵列的焦平面上,因此一个点光源的入射光线经过主透镜后,会透过若干个微透镜投影到它们每个微透镜后的一个或者若干个像素上[24]。由相机针孔模型可以看出,同一个微透镜下的不同像素代表着不同的主透镜位置,即角度信息,而入射光线到达的不同微透镜则代表着入射点光源的不同空间位置,即空间信息。
基于上述光场相机成像原理,作者所在的课题组自主开发了适用于PIV测量的高分辨率光场相机[22],相机实物和得到的原始图片如图 3所示。

|
| 图 3 光场相机实物和原始图片 Fig.3 Light field camera and its raw image |
由于微透镜的形状、尺寸等参数会对光场相机成像产生很大影响,在进行了前期研究之后,该光场相机采用了六边形的微透镜填充铺满整个CCD芯片,以提高CCD利用率并平衡光场相机的角度和空间分辨率[25]。
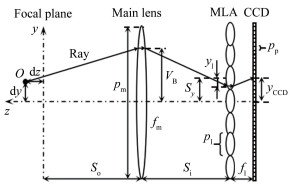
1.3 基于光线跟踪的光场相机数字合成图像对光场相机,从点光源发出的光线的传播过程如图 4所示[24]。图中dy, dz表示点光源O的相机坐标系坐标,其参考坐标系原点为光场相机聚焦平面与光轴的交点,pm为主透镜的直径,fm为主透镜的焦距,So和Si分别为物距和像距,pl和fl是微透镜的圆形通光部分的直径和焦距,pp是正方形像素的边长,VB, yl和yCCD分别表示该光线在主透镜、微透镜阵列和CCD芯片上的坐标,Sy表示其击中的微透镜的光心坐标。
由光场理论可知,进入光场相机的每根入射光线都可以用一个四维向量表示,而且根据矩阵光学,光线传播过程中的透镜器件、一定厚度的均匀介质对光线的作用都可以用一个矩阵表达[26],因此从一个点光源发出的入射光线,经过主透镜、微透镜后最终到达CCD平面的传播过程可以视为对一个四维向量进行的连续线性变换,最终所有连续变换的结果可以用式(2)表示:
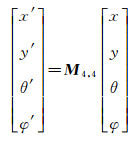 (2)
(2)
式中,x, y是光线的空间坐标,θ, φ是光线的传播方向,而x′, y′, θ′, φ′为最终传播到CCD平面的光线相应的4D参数,矩阵M是一个4行4列的光线传播矩阵,物理意义是光路中所有的传播介质和光学器件对4D向量的线性变换。光场相机数字合成图像的具体过程见文献[25]。
由上述方法追踪单个点光源发出的每一根光线,可将有一定空间体积大小的示踪粒子离散成发光强度在空间中遵循高斯分布的若干个点光源,由此获得示踪粒子的光场相机数字合成图像[25]。假如同一时刻的单个粒子处于离相机聚焦平面不同距离时,或者同一时刻多个粒子处于不同空间位置时,由光线跟踪得到的数字合成图像如图 5所示。

|
| 图 5 数字合成粒子光场图像 Fig.5 Synthetic light field images of the particle |
在Tomo-PIV中,常用的粒子图像重构算法被称为MART,其数学原理如式(3)所示[10]。
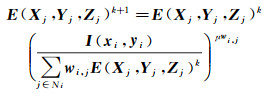 (3)
(3)
式中, E(Xj, Yj, Zj)代表第j个体素的强度值,其初始值设为1;I(xi, yi)是第i个像素;wi, j是权重系数,代表从第j个体素发出的光线中,有多大比例的能量传递给了第i个像素;式中的分母代表所有可以影响第i个像素的体素映射到第i个像素位置上的加权值之和,μ是迭代时的松弛系数,一般大于等于1。
由式(3)可以看出,实现MART算法的关键在于:(1)精准计算单个体素影响到的像素位置;(2)精准计算每个体素对受其影响的像素的权重系数。对Tomo-PIV, 校准方法采用的是计算机视觉中常用的相机针孔模型矩阵映射函数[27],而其相应的权重系数计算比较简单,通过圆柱体-立方体假设模型实现[10-11],由于光场相机的单个像素可以受到不同空间位置的多个体素影响,因此这一假设模型并不适用。作者所在的课题组曾利用矩阵光学提出了密集光线跟踪及其相应的权重系数计算方法[18],这一方法能够被应用的前提条件是光路中的光线传播矩阵参数可知,同时由光学元器件本身或者其安装误差导致的相机成像畸变较小。然而实际成像过程中由于畸变、光学元器件的加工和安装误差对光线传播矩阵的影响不可忽略,而且考虑到对多相机系统,存在未知的多个相机坐标系之间的相互转换关系,作者所在的课题组提出了一种针对光场相机的弥散圆模型校准算法[28],利用校准步骤得到的结果可以精准定位单个或多个相机中受到拍摄区域中某个点光源影响的像素位置。
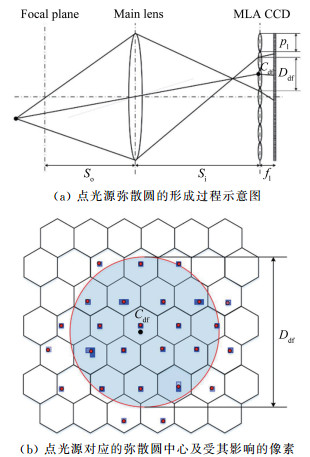
校准算法原理如图 6所示,当一个在世界坐标系中定义为(X,Y,Z)的点光源位于离聚焦平面一定距离时,从点光源向各个方向发出的光线进入主透镜后会投射到微透镜阵列上,形成一个圆斑并且覆盖多个微透镜,该圆斑被称为弥散圆,其中心被称为弥散圆中心[28]。
|
| 图 6 点光源的弥散圆及其影响的像素位置示意图 Fig.6 Diffusion circle and the affected pixels of a point source |
由于六边形微透镜的通光部分也是圆形的,因此进入某个微透镜的光线投射到CCD后点亮的区域也会形成一个比弥散圆更小的圆斑,微透镜下面会有一个或者若干个像素被点亮,其数量取决于该圆斑的尺寸和位置;弥散圆中心与主透镜光心、点光源三点共线。
前期研究发现,点光源的弥散圆中心、受影响像素对应的微透镜下的圆斑中心、点光源的弥散圆直径存在着如式(4)所示的关系式[28]:
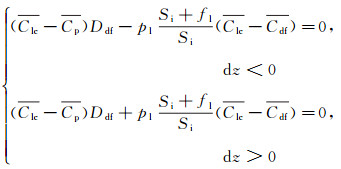 (4)
(4)
式中,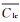
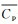
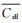
根据上述光场相机成像模型,根据作者所在课题组提出的光场相机校准算法,能精准计算某一个点光源对应的弥散圆中心、弥散圆直径以及微透镜中心像素坐标,从而精确计算出该点光源影响到的所有像素位置,其具体校准过程见文献[28]。
计算出受影响像素的坐标以后,进一步对每个受影响像素的权重系数计算,原理如图 7所示。对一个特定像素,其权重系数由两部分相乘得到:点光源发出的所有光束中击中某个微透镜的光束面积与总的光束面积之比为权重系数w1;被击中的微透镜下一个CCD像素上的光束面积与进入这个微透镜的光束面积之比为w2。

|
| 图 7 权重系数计算原理示意图 Fig.7 Schematic diagram of calculating principle of weight coefficient |
w1, w2都可以采用亚网格计数的方法计算得到,即对一个像素进一步细分为多个亚网格,计算某个像素内有多少个亚网格落入微透镜下的圆斑之中以及该微透镜下落入圆斑的亚网格的总数,前者除以后者即是该像素的w2,同样的方法可以计算出w1。
基于上述的校准、权重系数计算和MART粒子重构原理,最终双相机系统的整个校准及粒子重构算法过程如图 8所示,该算法亦可拓展应用到多台光场相机的粒子三维光照强度场重构算法之中。

|
| 图 8 体校准及重构算法流程图 Fig.8 Flowchat of the volumetric calibration and reconstruction algorithm |
为了验证双光场相机能够消除或抑制单光场相机PIV中的拉长效应,作者首先利用直接数值模拟(Direct Numerical Simulation, DNS)得到的射流数据生成光场相机数字合成图像,然后分别利用单光场相机和双光场相机测量速度场,对比两者的速度测量精度,尤其是对比两者沿景深方向的速度测量误差。
DNS数据模拟了一个圆形喷管的流动,喷管直径D=20mm, 雷诺数Re=2500,测试数据抽取自该喷管出口大约1D处的速度场,大小为0.66D×0.66D×0.66D[29]。粒子浓度取1.0ppm(Particle per Microlens), 即在该区域随机生成一些粒子的空间位置并由光线跟踪生成第一帧图像,这些粒子的浓度符合上述浓度值,然后根据DNS数据得到这些粒子所在位置点的速度矢量,给定时间间隔(2ms), 由这些速度矢量计算出下一帧的粒子空间位置并生成合成图像。单相机的体素数目为800×800×267voxels, 体素像素比为3:3:10,因此体素的空间分辨率为0.0165mm×0.0165mm×0.055mm,双相机体素数目为800×800×800voxels, 像素体素比为3:3:3,相应的空间分辨率为0.0165mm×0.0165mm×0.0165mm。为节约时间成本,所有图像均采用NVIDIA GTX 1080Ti显卡CUDA C并行计算处理,得到粒子强度场后同样利用并行程序进行基于FFT的两重网格互相关算法计算出速度矢量,最终对计算得到的速度矢量场进行中值滤波和线性插值等后处理。
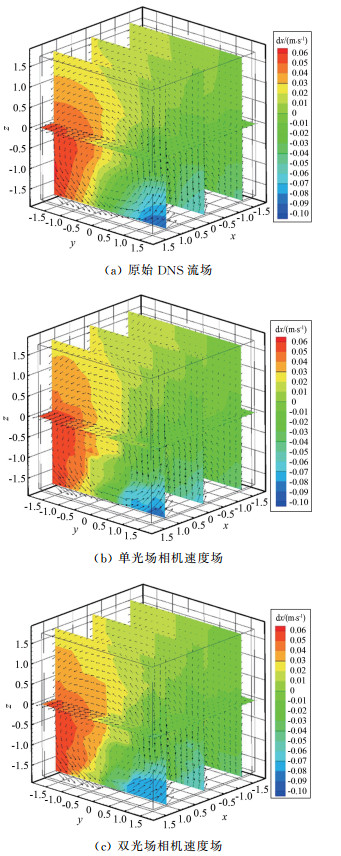
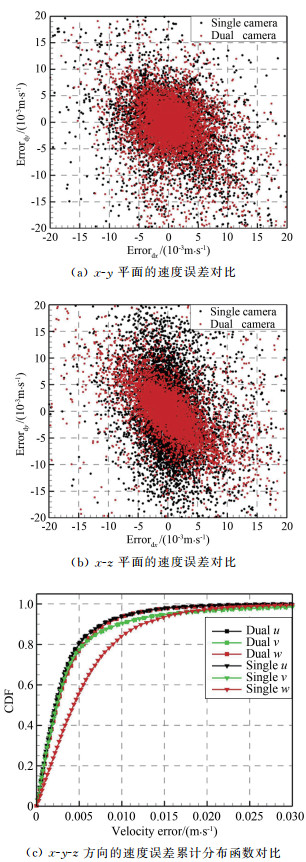
DNS原始速度场、单光场相机速度场及双光场相机速度场如图 9所示。计算结果表明,无论是单光场相机还是双光场相机,其计算结果和原始数据场都比较吻合,均能捕捉到流场中的涡系结构。为定量对比分析两者的速度测量误差,图 10分别展示了两者在x-y和x-z平面的速度测量绝对误差分布散点图以及两者在x-y-z 3个方向上的累计误差分布函数(Cumulative Distribution Function, CDF)的对比(其中坐标系的定义为:x-y平面为垂直于某一个相机光轴的平面,z方向为光轴方向)。由结果可以清楚地看出,单相机和双相机在x-y平面上的测量精度相近,但在单个相机坐标系的z方向上(即其光轴方向上),双相机的测量精度明显高于单相机,并且达到了与x-y平面精度大小相近的水平。由累计误差分布函数可以看出,双相机沿光轴方向的测量误差与单个相机相比明显减小。
|
| 图 9 DNS射流合成图像计算结果对比 Fig.9 Comparison of calculation results of synthetic images of DNS jet |
|
| 图 10 测量误差结果对比(z方向为光轴方向) Fig.10 Comparison of measurement errors between single and dual cameras |
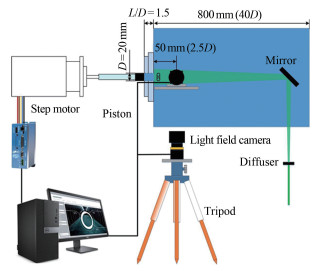
由于数字合成图像没有考虑到实验条件下的如背景噪声、光照不均匀等诸多限制因素,为进一步验证双光场相机技术的可行性,开展了水射流涡环PIV测量验证实验。验证实验的装置系统如图 11所示。2台光场相机布置时保持光轴互相垂直。为产生实验所需的涡环,采用一台步进电机来驱动一个可以作直线冲击运动的活塞,活塞运动时挤压圆柱形流道中的流体,从而向静止的水缸中注入一股圆柱形的射流,由于活塞所在流道的壁面无滑移速度边界条件,壁面有着很大的速度梯度,因此在流道的出口处形成了一个涡环[30]。
|
| 图 11 涡环实验装置示意图 Fig.11 Schematic of vortex-ring experimental apparatuses |
活塞的行程与直径之比L/D为1.5,直径D=20mm,对应的层流状态下雷诺数Re=2000。2台相机相互垂直90°放置,光圈数为2.8,放大系数为1,由此可以得到测量体积大约为36mm×24mm×36mm。测量区域在喷嘴出口前方2.5D处,示踪粒子型号为Dantec PSP-50,其平均粒子直径为50μm。
重构的体素像素比在x, y, z 3个方向上分别为3:3:3,速度采用两重网格互相关,第一重网格的窗口大小为200×200×200voxels, 第二重网格的窗口大小为100×100×100voxels,互相关窗口重叠率为0.75,由此得到的速度矢量空间分辨率为1.65mm×1.65mm×1.65mm, 速度场的矢量总数为73×53×73。
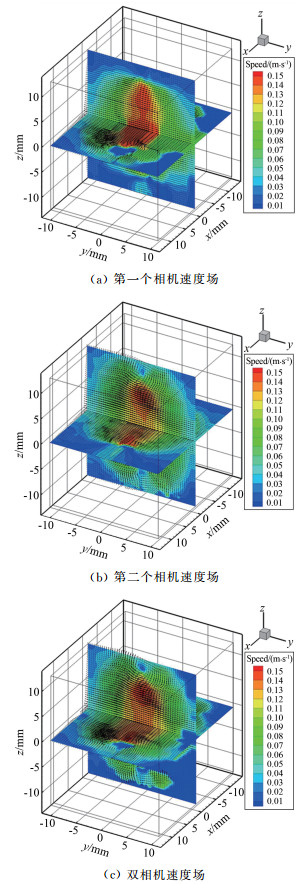
由测量实验得到的速度场可以看出(见图 12),2个光场相机各自对涡环进行测量时, 在上述互相关参数下,在各自的光轴方向(由于2个相机光轴相互垂直,所以对第一个相机而言,其光轴方向为图中坐标系的z轴方向,对第二个相机而言则为x轴方向)的测量精度有限,无法准确捕捉到该方向的涡环速度矢量,而双相机系统则可以比较精准地测出涡环在3个方向的速度场。
|
| 图 12 涡环实验速度场对比(z方向为光轴方向) Fig.12 Velocity fields of the vortex-ring experiment |
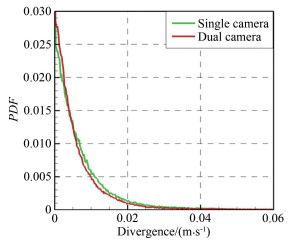
测量速度的散度对比分析如图 13所示。由于水射流的速度场是不可压流体的速度场,因此由不可压流体的连续性方程可知速度的梯度应满足:
|
| 图 13 单光场相机和双光场相机的速度散度概率密度函数对比 Fig.13 Comparison of the probability density function on the divergence error of the single- and dual-camera configurations |
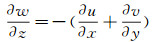 (5)
(5)
式中,u, v, w分布表示沿x,y,z方向的速度。
为定量分析测量速度的梯度对式(5)的偏离程度,测量误差由式(6)所示的散度绝对值来定义:
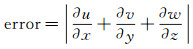 (6)
(6)
从图 13中的速度散度的概率密度分布函数(Probability Density Function,PDF)可以看出,双相机的测量结果更加符合不可压流体的连续性方程。
4 结论本文阐述了基于双光场相机的高分辨率光场三维PIV技术,基于针对光场相机的校准算法和MART权重系数算法,发展了适用于双光场相机乃至多台光场相机的三维粒子强度场重构技术,通过数字合成图像仿真分析和涡环测量实验对比分析发现,双光场相机与单相机相比,在光轴方向上有更高的空间分辨率,而且精度达到了和垂直光轴方向的分辨率同等大小的水平;双相机对水射流的测量结果更加符合不可压流体的连续性方程,从而表明双光场相机可以更加精准地测量景深方向的速度矢量,提高了测量的准确性。
| [1] |
Adrian R J, Westerweel J. Particle image velocimetry[M]. Cambridge: Cambridge University Press, 2011.
|
| [2] |
Schroeder A, Willert C E. Particle image velocimetry:new developments and recent applications[M]. New York: Springer, 2008: 1-33.
|
| [3] |
Raffel M, Willert C E, Wereley S, et al. Particle image velocimetry a practical guide[M]. 2nd ed. New York: Springer, 2007.
|
| [4] |
Prasad A K, Adrian R J. Stereoscopic particle image velocimetry applied to liquid flows[J]. Experiments in Fluids, 1993, 15(1): 49-60. DOI:10.1007/BF00195595 |
| [5] |
Brücker C. 3-D scanning particle image velocimetry:technique and application to a spherical cap wake flow[J]. Applied Scientific Research, 1996, 56(2-3): 157-179. DOI:10.1007/BF02249379 |
| [6] |
Hori T, Sakakibara J. High-speed scanning stereoscopic PIV for 3D vorticity measurement in liquids[J]. Measurement Science and Technology, 2004, 15(6): 1067-1078. DOI:10.1088/0957-0233/15/6/005 |
| [7] |
Hinsch K D. Holographic particle image velocimetry[J]. Measurement Science and Technology, 2002, 13(7): R61-R72. DOI:10.1088/0957-0233/13/7/201 |
| [8] |
Arroyo M, HinschK. Recent developments of PIV towards 3D measurements[M]. New York: Springer, 2008.
|
| [9] |
Katz J, Sheng J. Applications of holography in fluid mechanics and particle dynamics[J]. Annual Review of Fluid Mechanics, 2010, 42(1): 531-555. |
| [10] |
Scarano F. Tomographic PIV:principles and practice[J]. Mea-surement Science and Technology, 2013, 24(1): 1-28. |
| [11] |
Elsinga G E, Scarano F, Wieneke B, et al. Tomographic particle image velocimetry[J]. Experiments in Fluids, 2006, 41(6): 933-947. DOI:10.1007/s00348-006-0212-z |
| [12] |
Gao Q, Wang H P, Wang J J. A single camera volumetric particle image velocimetry and its application[J]. Science China Technological Sciences, 2012, 55(9): 2501-2510. DOI:10.1007/s11431-012-4921-7 |
| [13] |
Belden J, Truscott T T, Axiak M C, et al. Three-dimensional synthetic aperture particle image velocimetry[J]. Measurement Science and Technology, 2010, 21(12): 1-21. |
| [14] |
Ng R, Levoy M, Bredif M, et al. Light field photography with a hand-held plenoptic camera[R]. Tech report CTSR 2005-02, California: Stanford University, 2005.
|
| [15] |
Ng R. Digital light field photography[D]. California: Stanford University, 2006.
|
| [16] |
Lytro Inc. Lytroillum[EB/OL].[2016-09-10]. https: //www.lytro.com.
|
| [17] |
Raytrix GmbH Inc. 3D light field camera solutions.. https: //www.raytrix.de/produkte.
|
| [18] |
Chen H, Sick V. Plenoptic particle tracking velocimetry for internal combustion engine measurements[C]. The 11th International Symposium on Particle Image Velocimetry-PIV15, Santa Barbara, California, 2015.
|
| [19] |
Ding J F, Wang J H, Liu Y Z, et al. Dense ray tracing based reconstruction algorithm for light field volumetric particle imagevelocimetry[C]. The 7th Australian Conference on Laser Diagnostics in Fluid Mechanics and Combustion. Melbourne, Australia, 2015.
|
| [20] |
Fahringer T W, Lynch K P, Thurow B S. Volumetric particle image velocimetry with a single plenoptic camera[J]. Measurement Science and Technology, 2015, 26(11): 115201. DOI:10.1088/0957-0233/26/11/115201 |
| [21] |
Soria J, Atkinson C. Towards 3C-3D digital holographic fluid velocity vector field measurement tomographic digital holographic PIV (Tomo-HPIV)[J]. Measurement Science and Technology, 19(7): 074002. DOI:10.1088/0957-0233/19/7/074002 |
| [22] |
Levoy M. Light fields and computational imaging[J]. Computer, 2006, 39(8): 46-55. DOI:10.1109/MC.2006.270 |
| [23] |
Levoy M, Hanrahan P. Light field rendering[J]. ACM Trans Graph, 1996, 31-42. |
| [24] |
Shi S X, Wang J H, Ding J F, et al. Parametric study on light field volumetric particle image velocimetry[J]. Flow Measurement and Instrumentation, 2016, 49: 70-88. DOI:10.1016/j.flowmeasinst.2016.05.006 |
| [25] |
丁俊飞, 许晟明, 施圣贤. 光场单相机三维流场测试技术[J]. 实验流体力学, 2016, 30(6): 51-58. Ding J F, Xu S M, Shi S X. Light field volumetric particle image velocimetry[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(6): 51-58. |
| [26] |
Georgiev T, Zheng K, Curless B, et al. Spatio-angular resolution tradeoff in integral photography[C]. The 17th Eurographics Symposium on Rendering. Cyprus, 2006.
|
| [27] |
马颂德, 张正友. 计算机视觉[M]. 北京: 科学出版社, 1998.
|
| [28] |
Shi S X, Ding J F, New T H, et al. Volumetric calibration for single-camera light field PIV[J]. Experiments in Fluids, 2019, 60: 21. DOI:10.1007/s00348-018-2670-5 |
| [29] |
Shi S X, Ding J F, Atkinson C, et al. A detailed comparison of single-camera light-field PIV and tomographic PIV[J]. Experiments in Fluids, 2018, 59(3): 46. DOI:10.1007/s00348-018-2500-9 |
| [30] |
Couch L D, Krueger P S. Experimental investigation of vortex rings impinging on inclined surfaces[J]. Experiments in Fluids, 2011, 51(4): 1123-1138. DOI:10.1007/s00348-011-1135-x |