2. 空气动力学国家重点实验室, 四川 绵阳 621000
2. State Key Laboratory of Aerodynamics, Mianyang Sichuan 621000, China
碳基材料(包括普通人工石墨、热解石墨、碳/碳复合材料等),是当前高超声速飞行器非常重要的一类高温烧蚀型防热材料[2-14],被广泛应用于战略导弹端头区、战术导弹空气舵前缘、固体火箭发动机尾喷管喉道等重点防热部位。
当飞行器在大气层中高速飞行时,用于防热的碳基材料可能会发生表面烧蚀。随着表面温度升高,碳与空气之间一般会依次出现碳的氧化、碳氮反应和碳的升华等反应过程。在较低温度下,碳首先氧化,生成二氧化碳(CO2)和一氧化碳(CO)气体。此时,氧化过程由反应速率控制,烧蚀率由表面化学反应动力学条件决定,与氧气向表面的扩散过程无关,属于氧化速率控制区。随着温度升高,碳的氧化反应速率加快,氧气供应逐渐不足,边界层内输送氧气的快慢程度对烧蚀率起着控制作用,这时达到氧化扩散控制区。介于氧化速率控制区和氧化扩散控制区之间的区域,称为过渡区。在过渡区中,氧化率由表面化学反应动力学条件和边界层内对流-扩散因素共同决定。在更高温度下,碳氮反应和碳的升华逐渐显著,升华过程也是由速率控制(动力学升华)过渡到扩散控制(平衡升华)的。
对碳和氧气反应的研究,迄今已有150余年历史,但仍有许多问题没有完全搞清楚。对于近现代的石墨类和碳/碳复合材料,由于原始材料和加工工艺不同,其碳化程度、晶格方位、密度、孔度、结构强度、杂质含量、热力学和化学动力学特性等都有所不同,即使在其他实验条件完全相同的情况下,也可能获得不同的氧化速率数据[15]。
20世纪60年代初,Scala[2]针对石墨烧蚀进行了深入研究,发现存在两种极限动力学数据,并由此提出了著名的“快反应”和“慢反应”模型,前者的反应速率系数比后者大4个数量级。根据“快反应”模型计算的烧蚀速率与普通商业用石墨烧蚀实验测量结果吻合较好,而“慢反应”模型与人工热解石墨烧蚀实验结果一致。Scala认为两个模型之间没有内在联系,其差别是由于材料微观结构不同引起的。快/慢反应模型被研究者普遍接受并沿用至今[3-11]。对于飞行器碳基防热材料(包括碳/碳编织体材料和以热解碳为主形成碳化层的热解材料)烧蚀而言,基本都属于人工石墨类材料,采用“快反应”模型预测的烧蚀量都比实验结果大很多,而“慢反应”模型预测结果与实验较为接近。因此,近半个世纪以来,研究者在工程计算中普遍采用“慢反应”模型[5, 9, 16],而“快反应”模型实际上几乎被弃置了。
前段时间,本文作者曾就反应模型问题进行了研究,建立了碳基材料氧化烧蚀的双平台理论[1],解决了一些学术上的争议问题,如:
(1) 烧蚀计算到底应该使用“快反应”模型还是“慢反应”模型?它们之间有没有联系?
(2) 无量纲烧蚀速率存在“一个平台”还是“两个平台”?
(3) CO2到底能不能忽略?
通过研究发现:原本认为毫无关系的“快反应”和“慢反应”之间是有内在联系的,过去常被忽略的CO2恰恰是实现由“快反应”曲线向“慢反应”曲线转化的桥梁和纽带,并得到了实验证实。本文就此问题进行更为深入的分析,发现沿用了50余年的“慢反应”模型根本不存在,没有实质物理意义,而被弃置的“快反应”模型却具有重要的应用价值。
为全面阐述问题,本文部分内容与之前发表的内容[1]有所重复,特此说明。
1 Scala快/慢反应动力学模型20世纪60年代以来,针对高超声速飞行器所达到的表面温度和压力范围,人们对碳基材料的烧蚀机理开展了大量研究,建立了众多计算模型[3],其中最著名的当属Scala[2]提出的“碳氧反应控制理论”和“快反应”、“慢反应”模型。
Scala认为,碳氧反应过程受控于边界层的氧向表面的输运速率和表面碳与氧的反应速率,氧化过程的真正表面质量流率应由这两个因素共同决定,即:
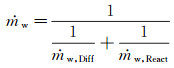 (1)
(1)
其中,ṁw, Diff为扩散质量流率,ṁw, React为反应质量流率,ṁw为总的质量流率。低壁温时反应项起主导作用,高壁温时扩散项起主导作用,在过渡区由两者共同控制。
上式中的扩散项可由边界层扩散方程求得;而化学反应项的问题则十分复杂。虽然对碳氧反应的研究为时已久,但迄今对其反应步骤和反应级数仍未完全搞清楚。实际上,气-固反应包含一系列连续独立的、相互竞争的动力学步骤(如反应物被表面吸附、反应物在表面移动到活性位置、在活性位置上与碳原子结合、反应产物从表面解附等),随着表面温度和压力的变化,每个步骤的重要性或增强或减弱;除此之外,如果反应物发生离解(如O2↔2O),或者产生更多生成物(如同时生成CO2和CO),或者起稀释作用的其他组元(如N2)占据活性位置,或者不止有一种类型的活性位置等,都可能会出现更为复杂的反应步骤。研究表明,这些动力学步骤是与温度和压力相关的。为了定量描述碳和氧的气-固反应过程,通常采用Arrhenius表达式来关联异相反应动力学数据。Scala总结了前人给出的动力学数据,提出了著名的“快反应”和“慢反应”模型。
快反应:
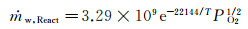 (2)
(2)
慢反应:
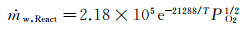 (3)
(3)
其中,ṁw, React的单位为kg/(m2·s),温度T的单位为绝对温度K,氧气分压PO2的单位为标准大气压atm。可以看出,快反应和慢反应的速率系数相差4个数量级。
我们注意到,Scala的模型并没有明确反应产物中CO/CO2的比值。后继很多研究者[5-8]认为:一般情况下,当温度大于1000K时,CO2的浓度很小,碳的氧化生成物几乎全为CO气体。因此,在一般烧蚀计算中,通常忽略CO2,仅考虑CO。研究者普遍认为,绝大部分碳氧反应动力学数据都可归类到所谓“快反应”和“慢反应”两种情形。前者通常用于商业用天然石墨,后者用于人工热解石墨。这里不免让人产生一些疑问:虽然材料的热力学和传热学特性可能与微观结构有关,但化学反应通常只与温度和压力相关,既然它们都是石墨类材料,为什么反应动力学数据差异如此之大?“快反应”和“慢反应”之间到底有无内在联系?难道碳的氧化反应有其特殊性?在发表论文[1]之前,这些问题一直没有解决。
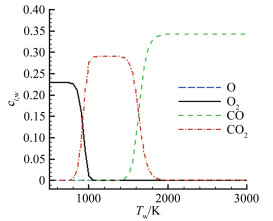
2 CO2在烧蚀计算中的重要作用及快/慢反应的关系在飞行器烧蚀量计算中,一般认为,当温度大于1000K时,与CO相比,CO2的浓度已很小,可以忽略。但也有文献表明[1, 11-12],壁温800~1700K范围内,CO2都是存在的,不应忽略。本文针对典型实验条件下碳氧反应组元进行了筛选计算,结果如图 1所示。可以看到,在1500K以下,生成物主要是CO2,在1700K以上,生成物才以CO为主。
|
| 图 1 实验条件烧蚀组元浓度计算结果 Fig.1 Dependence of concentration on surface temperature |
一般认为,CO2是不稳定的,极易分解成CO和O2,可采用如下平衡反应来考虑它们的相对含量:
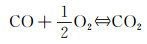 (4)
(4)
其中,平衡常数定义为:
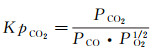 (5)
(5)
我们发现一个有趣的现象:如果对固态碳的氧化反应(见式(6))采用“快反应”动力学数据进行计算,同时考虑式(4)的平衡反应,那么在扩散控制平台ṁC/ṁd=1出现之前,会出现一个ṁC/ṁd=0.5的新平台(见图 2),两个平台的数值刚好相差一倍。这里,碳的氧化烧蚀质量流率ṁC由后文式(15)计算获得,氧的扩散质量流率ṁd=ρeueCH(MC/MO)cO2, e,其中ρe和ue为边界层外缘气流密度和速度,CH为传热系数,MC和MO分别为碳原子C、氧原子O的分子量,cO2为氧气质量浓度,下标e表示边界层外缘值。
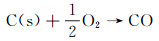 (6)
(6)
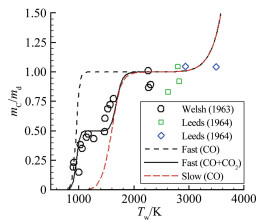
进一步研究发现:当Tw<1100K时,考虑了CO2影响的新模型计算结果与忽略CO2时的“快反应”结果一致;当Tw>1500K时,新模型与忽略CO2时的“慢反应”结果基本一致;而在1100K<Tw<1500K时,则自动从所谓的“快反应”区过渡到“慢反应”区。那么,这是否意味着:此前人为区分的“快反应”和“慢反应”,只是抓住了上下边界两种极端情况,并没有注意到它们之间的内在联系,而本文的新模型则将它们统一起来了。图 2给出的新模型计算结果与实验结果[12]的一致性,应该能够证明这一观点,并且说明化学动力学数据实际上只有一套,即ṁC=3.29×109e-22144/TP1/2O2,并不存在所谓的“快反应”和“慢反应”。因为从物理直观层面讲,无论是商业用石墨还是人工热解石墨,其元素都是碳,而化学反应一般只与温度和压力相关,两者的反应动力学数据不会有非常大的差别。关于碳的氧化从速率控制区到扩散控制区为何出现两个平台以及如何划分氧化控制区的问题,可以通过以下理论分析来阐明。
|
| 图 2 ATJ石墨烧蚀计算与实验结果比较 Fig.2 Comparison of the ATJ graphite oxidation rate between calculated results and experimental data |
众所周知,碳的表面氧化由两个基本过程组成:一是固体表面上的化学动力学过程,二是反应物向表面输送的过程。在这两个基本过程中,速率较小的过程起主导作用。当其中一个过程的速率远远小于另一过程,该过程就控制着整个烧蚀过程,其速率实际上就等于此时烧蚀过程的真正速率。如果表面化学反应速率比对流扩散速率小得多,则称之为速率控制;与此相反的极限情况,称为扩散控制;介于两者之间的区域称为过渡区。
不失一般性,可以采用如下化学计量方程表示碳和氧的反应:
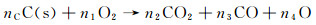 (7)
(7)
可以看出,式(7)实际上包含了固体碳的异相非平衡氧化反应式(6)、两种烧蚀产物之间的平衡反应式(4)以及氧气的离解平衡反应。令反应生成物CO与CO2的分压比为δ,O与CO2的分压比为γ,则式(7)可表示为:
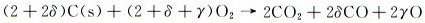 (8)
(8)
在氧化区,设碳氧异相反应级数为n,由表面氧化动力学决定的质量流率可由下式确定:
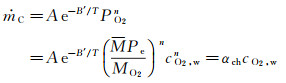 (9)
(9)
式中,A为反应速度的频率因子,B′为活化性温度,MO2为氧气分子量,M为混合物平均分子量,Pe为表面压力(等于边界层外缘压力),下标e、w分别表示边界层外缘值、壁面值。αch为氧化速率系数,表征表面在一定氧气浓度下进行氧化反应的快慢程度:
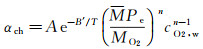 (10)
(10)
由边界层内对流-扩散因素决定的氧气质量流率ṁO2为:
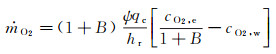 (11)
(11)
其中,B为无因次烧蚀质量流率,定义为:
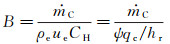 (12)
(12)
其中,ψ为质量引射系数,qc为冷壁热流,hr为恢复焓。
由边界层扩散到达壁面的氧气,一部分用于离解-复合反应,另一部分用于碳的氧化反应。由边界层内对流-扩散因素决定的碳消耗的潜在质量流率为:
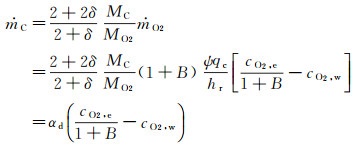 (13)
(13)
其中,αd为当量扩散系数,表征氧气向表面输送的快慢程度,是与边界层有关的复杂函数:
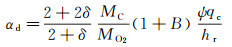 (14)
(14)
氧化过程的真正表面质量流率,应由表面碳与氧的反应速率和边界层的氧向表面的输运速率这两个因素共同决定,则由式(9)和(13)得到:
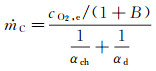 (15)
(15)
讨论:
(1) 当表面温度较低时,有αch≪αd,则式(15)可近似为:
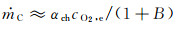 (16)
(16)
根据式(9),则:
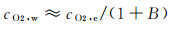 (17)
(17)
引入元素质量浓度概念,低温时可不考虑氧原子、碳氮反应和碳的升华,则不难得到:
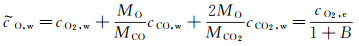 (18)
(18)
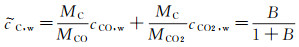 (19)
(19)
由此可得:
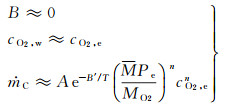 (20)
(20)
这就是氧化速率控制区的烧蚀关系式,它相当于表面有过剩氧气存在(氧气在表面的浓度等于边界层外缘值)的极限情形,这个烧蚀量与边界层对流-扩散因素无关,仅取决于表面动力学数据。
(2) 当表面温度较高时,有αch≫αd,则由式(15)可近似得到:
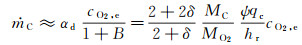 (21)
(21)
由式(21)、(12)和(13)得:
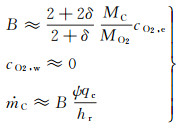 (22)
(22)
这就是氧化扩散控制区方程,它相当于氧气在表面完全燃尽的极限情形,这时氧化率与表面动力学因素无关。
由式(22)可知,这时的B值与反应生成物CO、CO2的分压比δ有关。在温度较低的情况下(1200K附近),生成物主要是CO2,CO浓度较小;高温情况下(1700K以上),生成物主要是CO,CO2浓度很小。因此,不妨考虑两种极限情形,一种是假设生成物主要是CO2,忽略CO,即δ=0,则:
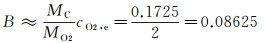 (23)
(23)
另一种是假设生成物只有CO,忽略CO2,即δ=∞,则:
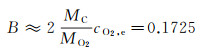 (24)
(24)
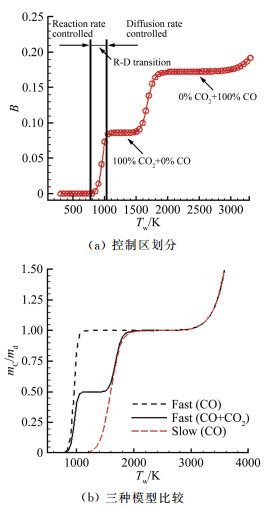
由此可见,在扩散控制区,由于反应产物的成分不同,会出现两个不同的平台(见图 2和图 3)。第一个平台出现在温度较低的情况下,反应产物主要是CO2;第二个平台出现在温度较高的情况下,反应产物主要是CO。
|
| 图 3 无量纲烧蚀质量流率随温度变化 Fig.3 Dependence of un-dimensional ablation rate on surface temperature |
(3) 在氧化速率控制区与扩散控制区之间的区域,αch和αd具有数值相当的量级,这时氧化率与表面动力学因素和边界层因素都有关。如果定义φch=αd/αch为氧气的表面输送速度与表面氧化动力学速度之比,则式(15)可改写为:
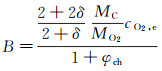 (25)
(25)
显然,φch→∞时,式(25)变为速率控制的极限情况(式(20));φch→0时,则变为扩散控制的极限情况(式(22))。事实上,在某个有限φch值处,氧化已很接近速率控制区或扩散控制区的数值,可据此来确定过渡区的范围。若取φch=100和φch=0.01分别作为速率控制区的上限值和扩散控制区的下限值,则由式(25)就能确定出对应的B值,将B值代入式(15),就能确定对应的温度上限值和下限值(见表 1[9])。
结合图 2和图 3(b),可以看出,在飞行器表面温度1000~1700K这个重要的区间内,“快反应”模型(忽略CO2)的计算结果比“慢反应”模型高出很多,“慢反应”结果与实验结果更为接近,特别是对于温度较高、烧蚀较快的情况。因此,此前国内外的碳基材料烧蚀计算大都采用“慢反应”数据,而“快反应”模型基本上被抛弃了。然而真实情况并非如此。
图 3(a)给出了烧蚀过程控制区的划分情况。参考图 2的实验结果可以看出,“快反应”在反应速率控制区是真实存在的;而所谓的“慢反应”,实际上处于扩散速率控制区,如图 3(b)所示,第一平台与第二平台之间的连接过渡线(即与所谓“慢反应”曲线重合的部分),完全是由反应生成物CO与CO2的分压比δ从0到∞变化引起的,与反应动力学无关。因此,“慢反应”实际上并不存在,只是因为烧蚀在Tw>1700K时变得显著、恰好模型的这段曲线能够与实验结果吻合而造成的假象。“慢反应”是为了拟合扩散控制区部分实验结果而被臆造出来,并被广泛使用了50余年;而“快反应”模型由于使用不当(忽略了CO2,致使其预测结果大大高于实验结果),则被长期束之高阁。
基于以上分析,可以认为:对碳基材料的烧蚀计算,采用“快反应”动力学数据才是真实可靠的;但需要注意的是,必须同时考虑CO和CO2两个烧蚀产物,否则无法得到准确的烧蚀量计算结果,因为以往常常被忽略的CO2恰恰扮演了重要角色,由它产生的第一平台,起到了由“快反应”曲线向“慢反应”曲线转化过渡的桥梁作用。由此推论,对任何表面烧蚀的化学反应,在反应速率控制区拟合化学动力学数据是有实质物理意义的;而在过渡区和扩散控制区,不能不考虑反应产物种类和边界层中氧化剂扩散而单纯拟合反应动力学数据。
上述研究的碳氧反应,仅适用于壁温小于2000K的情况;当温度更高时,需进一步考虑碳氮反应和碳的升华。沿典型弹道对碳端头表面烧蚀组分所做的筛选计算[6]表明,在全温区范围内,生成CO、CO2、C1、C2、C3、C2N和CN的反应对碳的烧蚀是不可忽略的主要因素,为此我们建立了全温区计算模型,限于篇幅,此处从略。
4 结论本文研究了碳基材料氧化动力学模型,得出如下结论:
(1) CO2在烧蚀计算中不能忽略。由于CO2的作用,在扩散控制区,无因次质量烧蚀速率随温度变化的曲线存在两个平台,而不是此前普遍认为的只有一个平台。在温度稍低情况下出现的第一平台对应的主要烧蚀产物是CO2,在温度稍高情况下出现的第二平台对应的主要烧蚀产物是CO,而且第一平台数值恰好是第二平台数值的1/2。第一平台与第二平台之间的连接过渡线,完全是由反应生成物CO与CO2的分压比δ从0到∞变化引起的,与反应动力学无关。
(2) 所谓“慢反应”模型,尽管它与实验数据吻合较好,但并无实质物理意义,且在800~1500K壁温范围内会低估烧蚀量。此前50余年,国内外的碳基材料烧蚀计算大都采用“慢反应”数据是有问题的。
(3) 碳基材料烧蚀计算应采用“快反应”动力学数据,且必须同时考虑CO和CO2两个烧蚀产物,否则无法得到准确的烧蚀量计算结果。对任何表面烧蚀的化学反应,在反应速率控制区拟合化学动力学数据有实质物理意义,而在过渡区和扩散控制区,不能抛开反应产物种类和边界层中氧化剂扩散而单纯拟合反应动力学数据。
| [1] |
国义军, 代光月, 桂业伟, 等. 碳基材料氧化烧蚀的双平台理论和反应控制机理[J]. 空气动力学学报, 2014, 32(6): 755-760. Guo Y J, Dai G Y, Gui Y W, et al. A dual platform theory for carbon based material oxidation with reaction diffusion rate controlled kinetics[J]. Acta Aerodynamica Sinica, 2014, 32(6): 755-760. DOI:10.7638/kqdlxxb-2014.0047 |
| [2] |
Scala S M. The ablation of graphite in dissociated air, Part Ⅰ: Theory[R]. AD289298, 1962.
|
| [3] |
Diaconis N S, Gorsuch P D, Sheridan R A. The ablation of graphite in dissociated air, Part Ⅱ: Experimental investigation[R]. AD290051, 1962.
|
| [4] |
Maahs H G. Oxidation of carbon at high temperatures: reaction-rate control or transport control[R]. NASA TN D-6310, 1971.
|
| [5] |
Swann R T, Pittman C M, Smith J C. One-dimensional numerical analysis of the transient response of thermal protection systems[R]. NASA TN D-2976, 1965.
|
| [6] |
黄振中. 烧蚀端头的瞬变外形及内部温度分布[J]. 空气动力学学报, 1981(1): 53-65. |
| [7] |
卞荫贵, 钟家康. 高温边界层传热[M]. 北京: 科学出版社, 1986.
|
| [8] |
国义军. 炭化材料烧蚀防热的理论分析与工程应用[J]. 空气动力学学报, 1994, 12(1): 94-99. Guo Y J. An analysis of a charring ablative thermal protection system with its engineering application[J]. Acta Aerodynamica Sinica, 1994, 12(1): 94-99. |
| [9] |
Milos F S, Chen Y K. Comprehensive model for multicomponent ablation thermochemistry[R]. AIAA-97-0141, 1997.
|
| [10] |
黄海明, 杜善义, 吴林志, 等. C/C复合材料烧蚀性能分析[J]. 复合材料学报, 2001, 18(3): 76-80. Huang H M, Du S Y, Wu L Z, et al. Analysis of the ablation of C/C composites[J]. Acta Materiae Compositae Sinica, 2001, 18(3): 76-80. DOI:10.3321/j.issn:1000-3851.2001.03.018 |
| [11] |
张志成, 潘梅林, 刘初平. 高超声速气动热和热防护[M]. 北京: 国防工业出版社, 2003.
|
| [12] |
Welsh W E, Chung P M. A modified theory for the effect of surface temperature on the combustion rate of carbon surface in air[C]//Proc of Heat Transfer and Fluid Mechanics Institute.: Stanford University Press, 1963: 146-159.
|
| [13] |
Baron J R, Bernstein H. Heterogeneous rate coupling for graphite oxidation[J]. AIAA Journal, 1971, 9(8): 1588-1595. DOI:10.2514/3.49961 |
| [14] |
Milos F S. Comparison of ablation predictions for carbonaceous materials using CEA and JANAF-based species thermodynamics[C]. Proc of the 35th Annual Conference on Composites, Materials, and Structures. 2011.
|
| [15] |
益小苏, 杜善义, 张立同. 复合材料手册[M]. 北京: 化学工业出版社, 2009.
|
| [16] |
Clark R K. An analysis of a charring ablator with thermal nonequilibrium, chemical kinetics, and mass transfer[R]. NASA TN D-7180, 1973.
|



