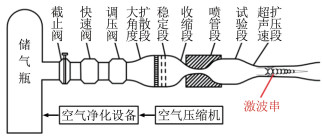
超声速喷管是高速风洞和高速流动基础研究的基本气动部件,其功能是产生超声速气流。超声速喷管广泛存在于风洞、高速飞行器等设备或部件中,具有广泛的航空、航天和军事应用背景。喷管及其下游扩压段的流动特性关系着超声速气流的稳定运行[1]。在超声速喷管起动过程中形成的含激波超声速流动结构具有速度快、梯度大、间断强、力热耦合复杂、扰动区域传播有限等特点,含有类似流动结构的气动部件(如超声速扩压器、超燃冲压发动机隔离段等)的设计技术和流场特性十分复杂,其中包含的定常或非定常激波附面层干扰[2]主导的复杂流场,也是高速空气动力学领域的基础流场。
拉瓦尔喷管为典型的超声速喷管,通过管道横截面的变化来实现气流流速的控制。气流在亚声速流动时,管道收缩,在超声速时,管道扩张,从而使气流速度不断增大。目前,拉瓦尔喷管的理论研究已经较为深入,在经典教科书中,对不同压比下拉瓦尔喷管出口截面处的超声速气流工作状态均有详细分析[3-4]。拉瓦尔喷管不同工况下的工程应用非常广泛,但针对工程实际中超声速喷管起动过程所形成的复杂激波附面层干扰结构,相关认识还远远没有达到透彻的地步,学术界和工程应用界还在持续不断地开展研究。
在拉瓦尔喷管上游调压阀逐步开启、来流总压逐步增大的喷管起动过程中,喷管及下游扩压器内形成的含激波流动结构通常是一种具有一定长度的、在核心流中耦合复杂多重激波结构以及在靠近壁面附面层形成分离流的“激波串”结构[5]。这种“激波串”结构常见的工程应用背景是超/高超声速风洞扩压器[6](图 1)、超燃冲压发动机隔离段[7]、超声速流动引射装置和火箭发动机尾喷管等。其特点是:在激波与附面层的相干结构中,气流经历了较为平缓的减速增压过程,即上游来流不是经过一道正激波使得气流参数发生剧烈间断,而是逐渐经过一段激波与附面层相互干扰的区域,在这一区域,壁面附面层通常会发生分离和再附。在实际流动中,这种激波串结构在受到上、下游流场参数变化等各种扰动时,会呈现出一定程度的非定常特性,这些非定常特性和前文提及的风洞扩压器等部件的气动设计和性能密切相关(比如风洞的稳定运行时间等)。
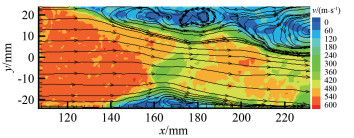
|
| 图 1 南京航空航天大学NH-1风洞扩压器的激波串 Fig.1 Shock train in NH-1 wind tunnel diffuser |
通常,承载这种激波串结构的工程部件是等截面或近似等截面直管道。一方面,超声速气流在其中减速增压;另一方面,又要求激波串结构具备一定的抗反压能力,即该等直管道能够隔离下游反压扰动对上游的影响。这种部件应用于超/高超声速风洞,称为“扩压器”;应用于吸气式超声速燃烧冲压发动机,则称为“隔离段”;另外,在气体激光器、超声压气机叶栅中均有功能类似的部件。而起“扩压”和“隔离”作用的,便是前文提到的激波串结构。“扩压”是超声速气流在摩擦和下游反压影响下形成激波串过程的自然属性;而激波串“隔离”下游压力扰动,有时则成为隔离段功能的核心。比如,在风洞试验段保证流场稳定、保证高超声速进气道流动不受下游燃烧形成的高压前传的影响等[8]。
基于上述应用背景开展超声速喷管流动研究,在“拉瓦尔喷管+等直管道”试验模型内,在喷管上游调压阀逐步开启、来流总压逐步增大的喷管起动过程中,观察到喷管及下游扩压器内所形成的含激波流动结构[9-14]以及上、下游气流参数变化导致的非定常激波串结构包含了很多上述工程应用所关心的流动细节。
采用风洞试验的方式,在一种“拉瓦尔喷管+等直管道”试验模型内,研究和分析马赫数2.7的二维对称拉瓦尔喷管起动过程中的流场激波结构变化情况,从试验角度给出常见的拉瓦尔喷管流动理论示意图的流动图谱。
1 理论分析假设喷管内为一维定常等熵流动,在不同大小的外界反压pb的影响下,拉瓦尔喷管内的气流可能出现7种流动形态。图 2直接给出相应的分析结果(p、p0分别为静压、总压,p*为速度等于当地声速的截面的临界压力)。
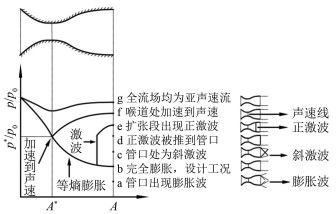
|
| 图 2 拉瓦尔喷管中气体流动状态理论示意图 Fig.2 Schematic illustration of flow state in Laval nozzle |
第一种工况(Ⅰ)pb≤pe(pe为喷管处于设计工况时的出口压力):当pb<pe时,喷管处于膨胀不足状态(图 2的工况a),出口处产生膨胀波;当pb=pe时,喷管处于设计工况状态(工况b)。
第二种工况(Ⅱ):当pb>pe时,超声速气流在喷管出口截面外受压缩产生激波,气流通过激波后,压力迅速上升(工况c)。激波强度随着pb的增大而不断增大,并由斜激波逐渐变为正激波,在出口截面形成封口正激波,压力变化如工况d所示。
第三种工况(Ⅲ):反压pb继续增大,激波向喷管内移动,此时,激波波前马赫数减小。当激波移动到扩张段某个截面时,压力分布如工况e所示。此时,喷管内气流状态由亚声速(收缩段)、声速(喉部)、超声速(激波前)、亚声速(激波后)组成。当pb继续升高至某值时,喷管内正激波正好移动到喉部位置;此时,喷管内气流状态由亚声速(收缩段)、声速(喉部)、亚声速(扩张段)组成,如工况f所示。
第四种工况(Ⅳ):当反压pb继续升高,整个喷管内全为亚声速流,喉部达不到声速;此时反压变化引起的扰动将传入喷管,影响喷管内的流动状态。管内压力分布如工况g所示。
2 试验模型在南京航空航天大学高超声速风洞实验室的Ф50mm高速风洞中进行试验。试验来流马赫数2.7,上游总压最高可达800kPa,下游连通于大气环境,总温290K。当来流总压达到350kPa时,风洞喷管即可完全起动,流场建立,整个试验气流稳定时间约60s。
为简化研究对象,设计了马赫数2.7的二维对称拉瓦尔喷管加等直段模型。喷管段长146.7mm,喉道高度14.2mm,进、出口高度均为45.1mm;等直段长400.0mm,垂直于流向的等直段截面水平宽度为40.0mm,下壁面设计为0.5°外扩张角以进行附面层干扰修正。在喷管出口和等直段处的侧面布置360mm×70mm的光学玻璃观察窗,上壁面布置120mm×20mm的PIV拍摄的激光入射窗口(图 3)。模型下壁面沿流向中心线共布置38个压力测点,其中前5个测点布置在喷管扩张段上,后33个测点布置在等直段上,相邻测点间距为10.0mm,在图 3中示意标注了测点位置。该模型能很好地模拟超声速喷管起动激波演化及斜激波串在管道内的发生、发展和移动情况。
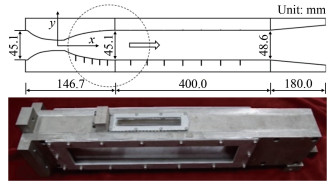
|
| 图 3 试验模型示意图 Fig.3 Schematic illustration of test model |
试验中,在风洞稳压段处以Kulite动态压力传感器监测来流总压,以量程为15PSI的DTC Initium电子压力扫描阀测量壁面沿程压力分布,采集频率333Hz,测试精度0.5%。纹影系统口径Ф200mm,采用Hotshot系列高速相机进行拍摄,采集频率5000Hz,图片像素640dpi×448dpi。
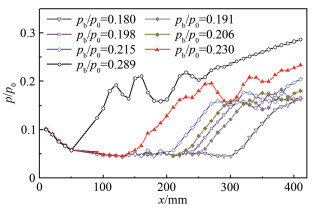
3 试验结果分析 3.1 沿程压力分布图 4为试验中管道下壁面沿程静压随总压变化的分布情况。横坐标为沿来流方向的坐标值,以喷管喉道处为坐标原点;纵坐标为沿程壁面静压p与来流总压p0的无因次比值。由图 4可知,当来流总压大于350kPa时(如pb/p0=0.230的情况),起动激波串首道激波被推出喷管出口(喷管出口处位置为x=93.7mm),马赫数2.7的超声速流场建立。壁面静压在波后并不是呈现陡增,而是缓步上升,产生的激波串首道激波为斜激波,纹影结果(图 5(b))也说明了这一点。另外,图 5也表明首道斜激波后出现了大分离区,反射激波与分离区附面层相互作用,在波后的一段区域内,压力出现较大幅度的振荡变化(如pb/p0=0.289的情况)。随着来流总压逐渐增大,激波串逐渐向管道下游移动。
|
| 图 4 下壁面沿程压力分布曲线 Fig.4 Pressure distribution along the bottom wall |

|
| 图 5 规则反射和马赫反射纹影结果 Fig.5 Schlieren images of Mach reflection and regular reflection |
当来流总压逐渐增大,喷管起动,超声速流场建立,超声速流场对应的低压与下游风洞出口大气压联合作用,在等直段部分形成包含激波和附面层分离结构的激波串结构。在上壁面附近,激波串出现大范围分离区(见图 5),上壁面附面层在视窗内没有再附;下壁面反射激波与附面层干扰所产生的小范围附面层分离则可以清楚地观察到。由于上、下壁面激波与附面层干扰后分离区的差异性,激波串呈现非对称性,偏向下壁面。激波串呈现非对称性的具体原因还有待进一步研究。
图 5为从纹影观察窗观测到的两种典型状态的纹影图像。图 5(a)中激波串首道激波反射为马赫反射,形成λ型激波,图 5(b)中激波串首道激波反射为规则反射[14-15],形成X型激波,波系简化结构如图 6所示。图 5(b)对应的PIV速度场如图 7所示,该激波波系大致可分为4个区域:1区为自由来流区,流场未受下游压力扰动;2区为首道斜激波后流场,经过斜激波压缩后,该区域流场压力逐渐上升;3区为斜激波串首道斜激波与附面层相互干扰的分离区;4区为反射激波后的混合流场区域。首道激波后气流转角与附面层分离区分离角相关。

|
| 图 6 马赫反射和规则反射示意图 Fig.6 Mach reflection and regular reflection |
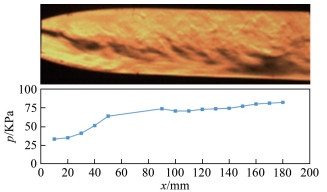
对应图 2中的理论工况g到工况a,在试验中通过逐步增加来流总压来实现。通观图 8~11的纹影结构,可见在总压逐渐增大的初期,喉道下游形成的起动气流剪切层在纵向上就呈现出上下不对称的结构,整体偏向下壁面(图 8);一直到激波串形成、往下游移动,整个起动激波串结构始终偏向下壁面(图 9~11)。
|
| 图 8 pb/p0=0.633喷管内纹影图和下壁面压力分布 Fig.8 Schlieren image and pressure distribution on the bottom wall under the condition of pb/p0=0.633 |

|
| 图 9 喷管内纹影图和下壁面压力分布 Fig.9 Schlieren image and pressure distribution on the bottom wall under the conditions of pb/p0=0.509 and pb/p0=0.436 |
|
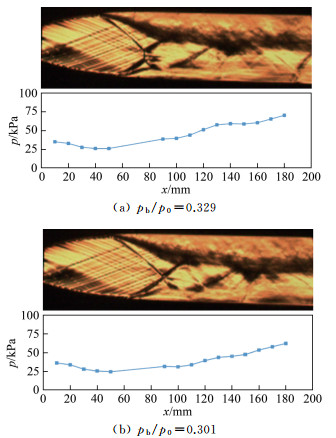
| 图 10 喷管内纹影图和下壁面压力分布 Fig.10 Schlieren image and pressure distribution on the bottom wall under the conditions of pb/p0=0.329 and pb/p0=0.301 |
|
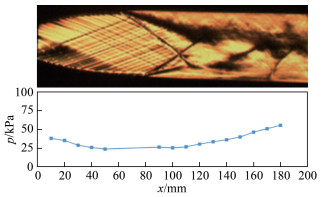
| 图 11 pb/p0=0.240喷管内纹影图和下壁面压力分布 Fig.11 Schlieren image and pressure distribution on the bottom wall under the condition of pb/p0=0.240 |
随着来流总压的不断增大,喷管和扩压器内包含激波串的流动结构的产生与发展分别经历了全亚声速流、喉道正激波、扩张段内正激波、等直管内马赫反射、等直管内规则反射等过程,分别对应理论分析图 2中的各个工作状态。
对应前述第四种工况:由于来流总压较低,喷管内流速较低。如图 8中的纹影所示,喷管和扩压器中未观测到激波结构,有条带状剪切层结构存在。
对应前述第三种工况:随着来流总压增大,喷管扩张段内形成首道激波为λ型的正激波串,如图 9(a)所示;来流总压继续增大,扩张段内正激波串强度逐渐增强,正激波串首道激波前缘逐渐到达喷管出口位置,如图 9(b)所示。此时,喷管内气流状态由亚声速(收缩段)、声速(喉部)、超声速(首道激波前)、亚声速(激波串后)以及上、下壁面分离区亚声速流动组成。
对应前述第二种工况:喷管喉部声速,扩张段超声速。随着来流总压增大,激波串逐渐向下游移动,扩张段内首道激波逐渐由马赫反射结构转变为规则反射结构(即λ型转变为X型),从而由正激波串逐渐演变为斜激波串,如图 10(a)和(b)所示。
对应前述第一种工况:喷管喉部声速,扩张段及喷管出口均为超声速流动,气流在喷管出口下游扩压段内形成X型激波,即激波结构为规则反射结构,构成斜激波串的首对交叉激波,达到设计工况,如图 11所示。此时,超声速气流不能逆向影响喷管内部的流动状态。
3.4 起动激波结构的初步三维特征探索以上试验结果,基本上是从二维角度或沿流向对称面角度获得。对于上述拉瓦尔喷管下游的矩形截面扩压器(高45.1mm×宽40.0mm)内的起动激波串结构,三维特征也是学术界和工程界广泛关注的问题。针对这一问题开展了初步研究,采用玻璃组成扩压器段四壁,通过旋转超声速喷管和扩压器模型90°的办法,获得了斜激波串首道激波垂直截面和水平截面的纹影图像,以帮助刻画起动激波串的初步三维结构。图 12给出了垂直和水平截面上纹影的对应流态结果。从图中可见,虽然斜激波串结构在垂直截面上呈现上下不对称结构,但首道激波在水平截面上呈现对称结构。

|
| 图 12 起动斜激波串位于扩压段时首道斜激波三维特征 Fig.12 3D characteristics of the leading oblique shocks when the starting shock train locates in the diffuser |
需要说明的是,图 12的垂直截面和水平截面的纹影是在两个测试下采用高速摄像机(5000帧/s)获得,在所关心的区域细致调整首道激波位置,综合压力分布、液晶涂层摩擦力显示结果,获得图 12(a)和(b)。纹影试验完成后,将扩压段底板换为发黑金属板,通过喷涂剪切敏感液晶涂层获得底板上的激波附面层干扰流场分布。图 12(c)为壁面摩擦力分布云图,红色对应摩擦力小尺度区域,黄色和绿色对应摩擦力大尺度区域。由图中可见,在下壁面首道分离激波后的分离区内,摩擦应力大大降低,对应的流场结构同水平截面上的纹影结果一致,斜激波串基本呈现为对称形状;下壁面的分离激波起始位置沿展向几乎为一条直线,在两侧壁面处弯曲,而分离激波再附位置沿展向呈现出“M”型锯齿形状。剪切敏感液晶技术的细节详见文献[16]。
4 结论(1) 通过试验手段获得了马赫数2.7的二维对称拉瓦尔喷管起动时的流态变化情况,从试验角度给出了对应拉瓦尔喷管流动理论示意图的流动图谱。
(2) 试验中的超声速流场建立和理论中的流场建立同样经历了喷管起动激波从喉道发展到喷管出口、而后过渡到设计工况的历程;不同的是,由于壁面附面层干扰,试验流态更加复杂,比如激波串的不对称结构、首道激波从λ型激波向Х型激波的转变等。
(3) 综合运用不同光路布置的纹影和剪切敏感液晶摩阻测量技术,初步获得了起动激波串首道激波的三维特征。
| [1] |
王铁城. 空气动力学实验技术[M]. 北京: 航空工业出版社, 1985: 36-48. Wang T C. Experimental technique for aerodynamics[M]. Beijing: Aviation Industry Press, 1985: 36-48. |
| [2] |
Babinsky H, Harvey J K. Shock wave-boundary-layer interactions[M]. Cambridge: Cambridge University Press, 2011: 48-51.
|
| [3] |
童秉纲, 孔祥言, 邓国华. 气体动力学[M]. 北京: 高等教育出版社, 1990: 82-90. Tong B G, Kong X Y, Deng G H. Gasdynamics[M]. Beijing: Higher Education Press, 1990: 82-90. |
| [4] |
陆志良. 空气动力学[M]. 北京: 北京航空航天大学出版社, 2009: 109-113. Lu Z L. Aerodynamics[M]. Beijing: Beihang Press, 2009: 109-113. |
| [5] |
Matsuo K, Miyazato Y, Kim H D. Shock train and pseudo-shock phenomena in internal gas flows[J]. Progress in Aerospace Sciences, 1999, 35(1): 33-100. DOI:10.1016/S0376-0421(98)00011-6 |
| [6] |
李桦, 范晓樯, 丁猛. 超声速扩压器中激波串结构的数值模拟[J]. 国防科技大学学报, 2002, 24(1): 18-21. Li H, Fan X Q, Ding M. Numerical simulation of the shock train structure in the supersonic diffuser[J]. Journal of National University of Defense Technology, 2002, 24(1): 18-21. DOI:10.3969/j.issn.1001-2486.2002.01.005 |
| [7] |
Gnani F, Zare-Behtash H, Kontis K. Pseudo-shock waves and their interactions in high-speedintakes[J]. Progress in Aerospace Sciences, 2016, 82: 36-56. DOI:10.1016/j.paerosci.2016.02.001 |
| [8] |
Chang J T, Li N, Xu K J, et al. Recent research progress on unstart mechanism, detection and control of hypersonic inlet[J]. Progress in Aerospace Sciences, 2017, 89: 1-22. DOI:10.1016/j.paerosci.2016.12.001 |
| [9] |
Hornung H G, Taylor J R. Transition from regular to Mach reflection of shock waves Part 1. The effect of viscosity in the pseudosteady case[J]. Journal of Fluid Mechanics, 1982, 123: 143-153. DOI:10.1017/S0022112082002997 |
| [10] |
Hornung H G, Robinson M L. Transition from regular to Mach reflection of shock waves Part 2. The steady-flow criterion[J]. Journal of Fluid Mechanics, 1982, 123: 155-164. DOI:10.1017/S0022112082003000 |
| [11] |
Gao B, Wu Z N. A study of the flow structure for Mach reflection in steady supersonic flow[J]. Journal Fluid Mechanics, 2010, 656: 29-50. DOI:10.1017/S0022112010001011 |
| [12] |
Xiang G X, Wang C, Teng H H, et al. Study on Mach stems induced by interaction of planar shock waves on two intersecting wedges[J]. Acta Mechanica Sinica, 2016, 32(3): 362-368. DOI:10.1007/s10409-015-0498-2 |
| [13] |
Hu Z M, Myong R S, Kim M S, et al. Downstream flow condition effects on the RR→MR transition of asymmetric shock waves in steady flows[J]. Journal Fluid Mechanics, 2009, 620: 43-62. DOI:10.1017/S0022112008004837 |
| [14] |
Ben-Dor G. Shock wave reflection phenomena[M]. Berlin: Springer Press, 2007: 3-6.
|
| [15] |
Wang D, Yu Y. Shock wave configurations and reflection hysteresis outside a planar Laval nozzle[J]. Chinese Journal of Aeronautics, 2015, 28(5): 1362-1371. DOI:10.1016/j.cja.2015.07.010 |
| [16] |
焦运.带入射激波高速流动的全局表面摩擦力场测量方法研究[D].南京: 南京航空航天大学, 2017: 14-19. Jiao Y. Global surface shear stress measurement in high-speed flow including incident shock waves[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2017: 14-19. |