2. 中国科学院力学研究所, 北京 100190;
3. 中国科学院大学 工程科学学院, 北京 100049
2. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China;
3. School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
具有自相似性的图形称为分形, 分形几何用于定量描述分形的不规则程度[1-2].近年来, 分形几何方法应用于科学问题分析取得了很多进展. Sreenivasan等[3]最早把分形理论引入流体力学实验测量中, 并系统分析了剪切层、射流和边界层等典型流场的分形维数.赵玉新等[4]应用分形几何方法, 测量了超声速混合层转捩区和完全发展湍流区湍流界面的分形维数, 发现湍流界面分形维数随着湍流脉动的增强而增大。杨洪旻等[5]应用分形几何方法, 提出了一种基于分形理论的湍流预混火焰传播速度模型, 该模型将小尺度涡团对湍流火焰的强化扩散效应归结为旋涡对锋面结构的改变。蒋德明等[6]使用分形几何方法分析了内燃机预混湍流火焰图像, 结果表明预混湍流火焰结构具有分形特征, 可以用分形维数来定量描述火焰褶皱、扭曲及其与湍流强度的关系。Hiraoka等[7]通过直接数值模拟来分析湍流预混射流火焰的分形特征, 结果表明火焰锋面的分形维数随着下游距离的增加而增大。
超声速燃烧的火焰分布与火焰形态是决定燃烧效率和燃烧室性能的关键因素。超声速燃烧是涉及燃料喷注、混合、化学反应、激波以及湍流的多物理复杂过程, 其火焰形态及其传播特性受到燃料种类、来流条件以及喷注参数的影响, 并且火焰形态具有很强的非定常脉动特性。因此, 如何定量研究超声速湍流火焰及其传播速度一直是研究的难点。以往研究工作多将分形几何用于低速燃烧的火焰形态分析, 用于分析超声速燃烧火焰的研究并不多见。为此, 本文将分形几何用于超声速燃烧的火焰形态分析中, 特别是采用分形几何方法系统分析不同燃料、不同当量比的超声速火焰分形特征变化, 并考察分形特征与超声速燃烧湍流火焰传播速度的关系。类似的超声速火焰研究尚未见公开报道。
本文基于高速摄影获得的火焰CH*自发光图像, 应用分形几何方法, 采用分形维数表征火焰锋面的褶皱、扭曲程度, 验证超声速燃烧火焰形态的自相似性, 建立湍流火焰传播速度与火焰边界分形维数的关系。基于分形几何表征方法, 研究马赫数2.5的超声速来流下, 乙烯及氢/乙烯混合燃料的火焰分形维数变化规律, 探讨燃料当量比、燃料组分对湍流火焰传播速度的影响。
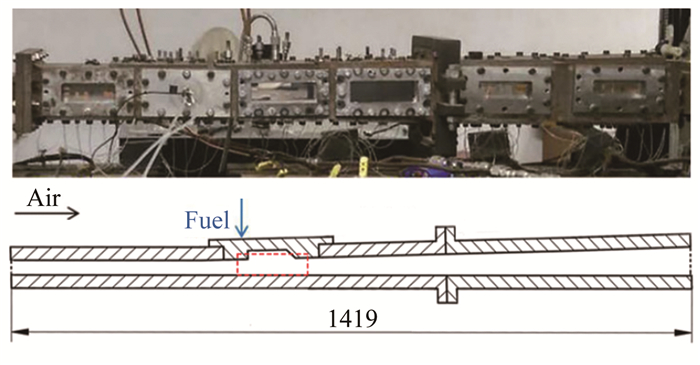
1 实验设计与分析方法 1.1 实验设计图 1为实验使用的超声速燃烧室结构示意图[8-9]。图中红框为主燃区, 在该区域通过石英窗口对CH*自由基发光进行拍摄。由于CH*自由基发光的波长在430nm左右, 因此实验通过高速相机配备中心波长为430nm的带通滤光片进行拍摄, 拍摄频率为10 000帧/s, 曝光时间为1/16 000s, 分辨率为1280pixel×240pixel。在燃烧室壁面布置了一系列静压测点, 能够得到实验条件下燃烧室壁面的沿程静压分布。
|
| 图 1 超声速燃烧实验台及其结构示意图(单位:mm) Fig.1 Supersonic combustion test facility and its structure diagram (unit: mm) |
实验的来流条件均为马赫数2.5, 总温1850K, 总压1.23MPa, 质量流量1.35kg/s。来流总温、马赫数分别通过烧氢补氧加热器与拉瓦尔喷管获得。燃料均为气态, 成分如表 1所示。燃料通过位于上壁面凹腔上游10mm处的壁面小孔垂直喷入燃烧室。燃烧当量比在0.1~0.3之间。燃料点火后稳定燃烧时间为实验的有效时间, 共2s。拍摄CH*发光的高速相机在燃烧前0.5s开始工作, 拍摄时间共持续3.7s。
| 编号 | H2 | C2H4 |
| A | 100 | |
| B | 20 | 80 |
| C | 50 | 50 |
根据Helmhotz定理, 流体中的涡管在运动中将不断地拉伸和折叠, 从而使湍流结构呈现出分形特征[10]。湍流流场中存在很多尺度不同且连续变化的涡团, 这些涡团的几何特征和运动规律具有一定的统计意义上的自相似性。不同尺度的涡团在同一时间和空间内互相重叠, 呈现出混沌和无序的现象。这种现象背后隐含着一定的有序性与相干结构。因此, 分形几何可以用来很好地描述湍流这种拟序特征。沈学会等[11]将分形理论用于湍流研究中, 研究结果表明分形理论有助于理解湍流的内在规律和机理。
湍流火焰与层流火焰的不同主要在于:湍流火焰锋面在湍流涡团的强扰动下无法保持为规则而光滑的薄层。湍流火焰锋面在受到剧烈扭曲和拉伸后发生褶皱和破碎, 其表面积迅速增加, 导致燃烧从局限在一个薄层发展到整个空间, 从而使火焰传播速度显著增大。湍流火焰锋面这种褶皱不规则表面, 正是分形几何可以研究的对象。前人的研究表明, 低速条件下湍流火焰锋面具有统计意义上的自相似性[12], 但其满足分形特征的尺度是有边界的, 两端的边界分别称为内外截止点。
Kolmogorov认为, 湍流具有不同尺度的旋涡结构。流体的动能通过不同尺度结构之间的传递过程, 由积分尺度结构把能量逐渐传递给最小尺度旋涡, 即Kolmogorov尺度η。Kolmogorov尺度是湍流的最小尺度, 此时动能仅能够以热能的形式耗散掉。因此, 湍流火焰锋面的内截止点, 即最小尺度为Kolmogorov尺度η。外截止点, 即最大尺度为湍流积分尺度l[13-14]。Gouldin等[15]最早将分形理论应用于湍流火焰的分析中, 其提出的湍流火焰传播速度模型建立在3个假设的基础上:(1)湍流燃烧速率并不是由卷吸作用所控制, 而主要是由火焰面上的褶皱变形率控制, 其表面的褶皱变形程度可以用分形理论来计算; (2)湍流与层流的火焰传播速度之比等于其火焰锋面的面积之比[16], 这与火焰锋面的分形维数相关; (3)层流火焰与湍流火焰的特征尺度分别为内外截止点尺度。因此, 有:
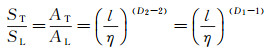 (1)
(1)
其中, ST和SL分别为湍流和层流火焰传播速度, AT和AL分别为湍流和层流的火焰锋面面积, D2和D1分别为火焰锋面和火焰锋面边界曲线的分形维数, 曲面与曲线分形维数之差为1。如果火焰锋面边界为具有分形特征的曲线, 其分形维数将大于1。由式(1)可知, 火焰边界的分形维数越大, 湍流火焰传播速度越大。
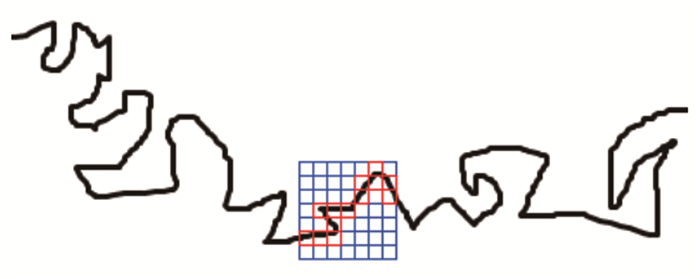
1.3 分形维数计算方法记盒数法是计算分形维数的一种常用方法。以图 2中曲线分形维数的计算为例, 来说明该方法的应用。用边长为S的正方形盒子来互不交叉地覆盖曲线, 完全覆盖曲线所需的最小盒子数为N(图中红色盒子数)。
|
| 图 2 计盒数法示意图 Fig.2 Schematic diagram of box counting |
显然, 盒子边长S越小, 所需的盒子数N越大。该曲线的分形维数即为盒子数N与盒子边长S自然对数之比的相反数, 如下式所示:
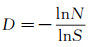 (2)
(2)
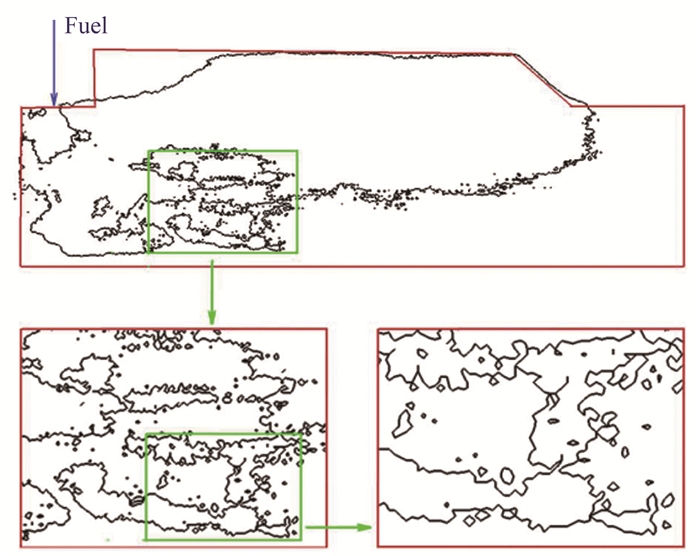
如果曲线的分形维数大于1, 则说明该曲线具有自相似性。选取燃料乙烯、当量比0.30的工况, 通过CH*自发光图像分析, 来考察其火焰边界的自相似性。图 3为该工况在稳定燃烧时间内某一瞬时的火焰边界。如图所示, 上图为火焰的整体边界, 红色框为观察窗的视野, 绿色框内为待考察的局部边界。将绿色框的局部边界放大到原来的两倍, 得到左下图所示的图像。重复该放大过程, 得到右下图所示的图像。如果我们以不同的尺度来测量火焰边界的长度, 显然在右下图所在的尺度下, 测量值更大。
|
| 图 3 稳定燃烧时乙烯瞬态火焰边界 Fig.3 Transient flame boundary of ethylene during steady combustion |
采用计盒数法计算火焰边界的分形维数。该灰度图像由一系列正方形像素排列而成, 每个像素具有单一的灰度值。因此选取盒子边长时以像素的宽度p为单位。选取不同的盒子边长, 覆盖图 3火焰边界所需的盒子数在表 2中给出。
| 盒子边长S(p) | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
| 盒子数N | 4640 | 2562 | 978 | 366 | 129 | 46 | 18 | 8 | 2 |
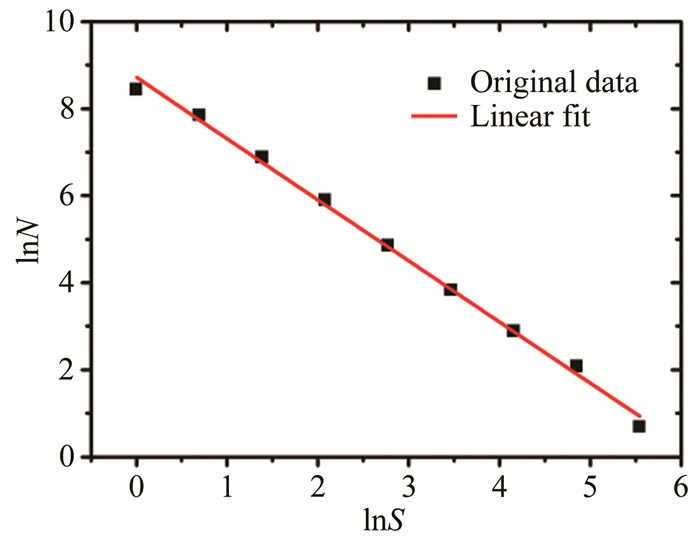
将盒子数和盒子边长的自然对数lnN和lnS进行线性拟合, 结果如图 4所示。图中的拟合优度达0.996, 线性度较好。根据式(2)得到火焰边界的分形维数为1.404, 说明该火焰边界具有典型的自相似性。
|
| 图 4 乙烯火焰边界分形维数计算结果与拟合曲线 Fig.4 Calculation results and fitting curves of fractal dimension of ethylene flame boundary |
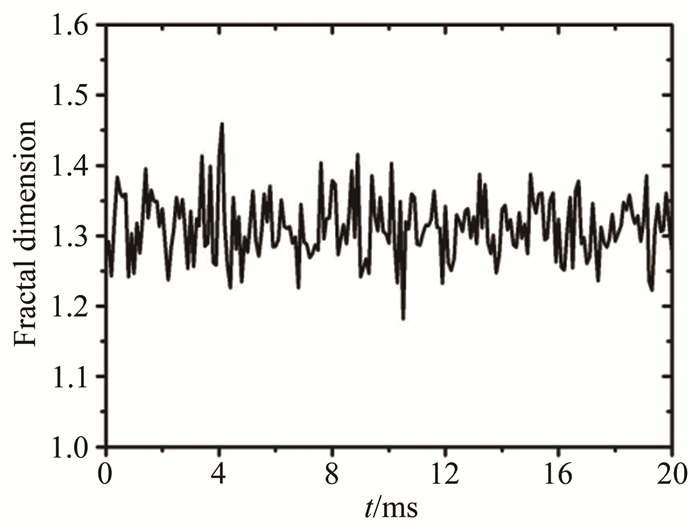
由于湍流具有强非定常性, 湍流火焰边界在不断变化, 其边界的卷曲、褶皱程度也在不断变化, 因此有必要考察火焰边界分形维数随时间的变化规律。仍以图 3火焰为例, 在稳定燃烧的0.02s时间段内, 选取200个时刻, 计算每个瞬态时刻火焰边界的分形维数, 结果如图 5所示。图中分形维数随时间上下波动, 但其时均值基本不变, 因此采用其时均值1.312来表征准稳态燃烧下该火焰边界的分形维数。
|
| 图 5 分形维数随时间的变化 Fig.5 The change of fractal dimension with time |
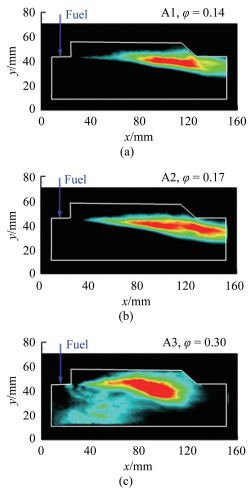
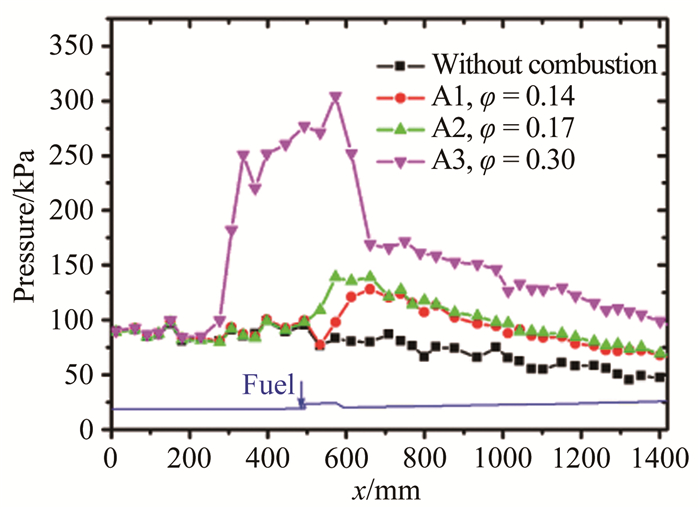
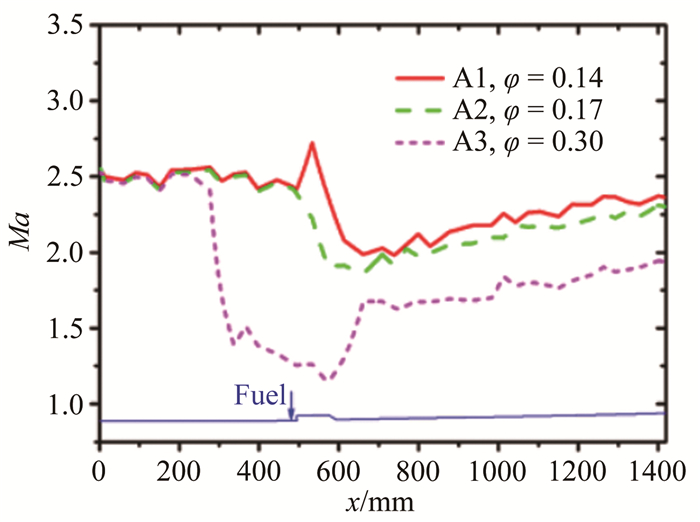
图 6给出了乙烯在不同当量比下的典型瞬态火焰图像, 图中将原始的灰度图像进行了伪彩处理。图 7为不同当量比下燃烧室壁面压力测量数据沿程分布。图 8为根据压力测量数据以及燃烧室一维流动分析方法得到的平均马赫数沿程分布[15]。如图 6所示, 超声速火焰形态随当量比φ的增大逐渐由凹腔稳焰模式过渡到射流稳焰模式, 火焰分布区域向上游移动, 同时火焰区域扩大, 并且火焰边界变得更加不规则。随着释热开始位置的前移, 相应的燃烧室压力抬升位置和马赫数开始迅速下降的位置也从凹腔区域前移到燃料喷注点上游, 如图 7和8所示。
|
| 图 6 不同当量比条件下乙烯瞬态火焰分布 Fig.6 Transient flame distribution of ethylene at different equivalent ratios |
|
| 图 7 不同当量比下燃烧室压力分布 Fig.7 Pressure distribution of combustor at different equivalent ratios |
|
| 图 8 不同当量比下燃烧室平均马赫数分布 Fig.8 Average Mach number distribution of combustor at different equivalent ratios |
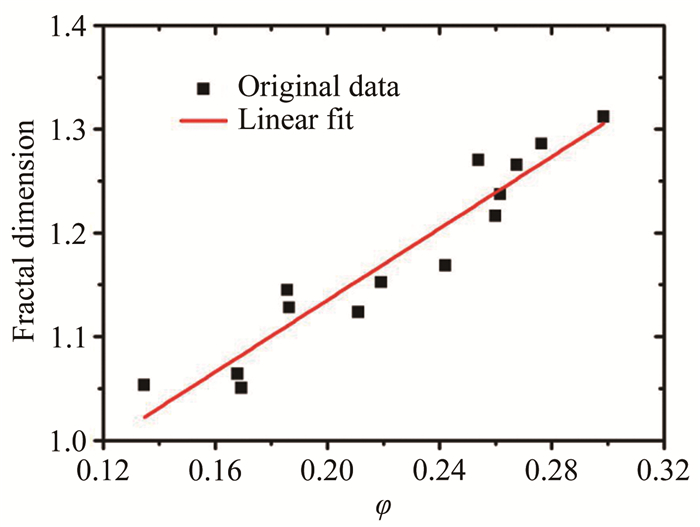
图 9给出了不同当量比条件下乙烯火焰边界的分形维数, 分形维数在1.05~1.32之间。如图所示, 随着当量比的提高, 火焰边界的分形维数逐渐增大。
|
| 图 9 乙烯火焰边界分形维数随当量比的变化 Fig.9 Variation of fractal dimension of ethylene flame boundary with equivalent ratio |
对图中的数据点进行线性拟合, 其拟合优度为0.902, 这说明火焰边界的分形维数随当量比近似线性增加, 线性关系如下式所示:
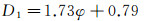 (3)
(3)
呈现这种变化, 是因为低当量比时, 火焰主要稳定在凹腔后缘位置, 火焰受到超声速气流的冲刷, 相对稳定; 随着当量比增大, 火焰区逐渐前移至喷注点附近, 这时燃料射流穿透增强, 喷注点前形成弓形激波, 并导致边界层分离, 压力抬升位置前移, 火焰边界变形与破碎程度加剧, 从而使得火焰边界的分形维数增大。分形维数的增大意味着火焰面积在不断增大, 湍流火焰传播速度也逐渐增大。
根据湍流尺度理论[17], Kolmogorov尺度η与湍流积分尺度l有以下关系:
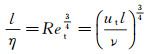 (4)
(4)
其中, ut为湍流脉动特征速度, ν为运动粘性系数, Ret为以ut为特征速度的雷诺数。结合式(1)、(3)和(4), 可得湍流、层流火焰传播速度之比与当量比的关系:
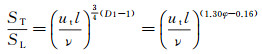 (5)
(5)
如式(5)所示, 如果已知湍流脉动特征速度ut、湍流积分尺度l和运动粘性系数ν, 就可以获得该工况下不同当量比湍流和层流火焰传播速度之比。
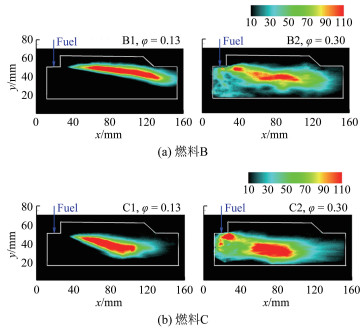
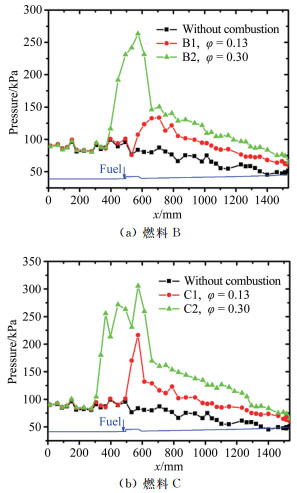
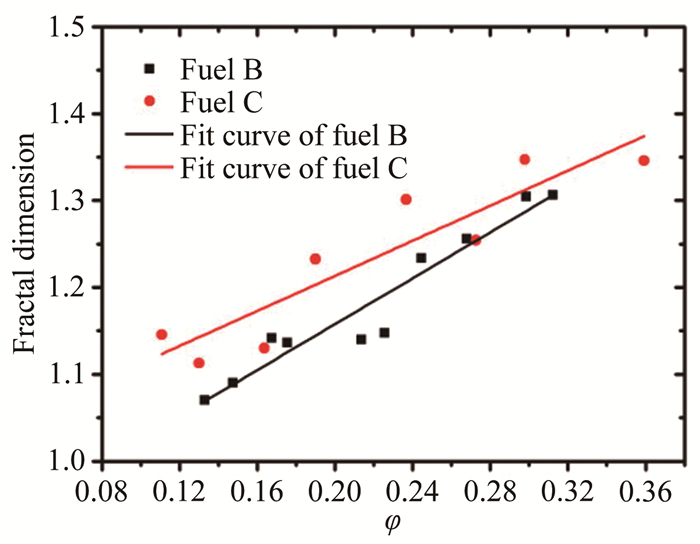
2.3 分形维数随燃料成分的变化图 10为燃料B(20%H2+80%C2H4)和C(50%H2+50%C2H4)在不同当量比条件下的瞬时火焰形态。图 11为不同当量比下燃烧室的压力分布。如图所示, 随着当量比增大, 燃烧区域前移, 压力抬升位置前移到喷注点上游。相同当量比下, 氢含量更高的燃料C燃烧明显更强, 压力峰值更大。图 12为燃料B和C火焰边界分形维数随当量比的变化, 分形维数在1.05~1.36之间。对图 12中的数据点进行线性拟合, 两条曲线的拟合优度分别为0.919和0.815, 说明燃料B、C火焰边界分形维数随当量比近似线性增大。在当量比增大过程中, 火焰边界分形维数的增大反映了湍流火焰传播速度的增大, 其机理与乙烯燃烧类似。对比燃料B和C的数据可见, 随着氢含量的增加, 相同当量比下, 火焰边界分形维数有所增大, 湍流火焰传播速度增大, 和图 10中的火焰形态结果一致。
|
| 图 10 不同当量比燃料B和C火焰瞬时形态 Fig.10 Instantaneous form of fuel B and C at different equivalent ratios |
|
| 图 11 不同当量比下燃烧室的压力分布 Fig.11 Pressure distribution of combustor at different equivalent ratios |
|
| 图 12 不同当量比燃料B和C火焰边界分形维数及其拟合曲线 Fig.12 Fractal dimension of flame boundary of fuel B and C at different equivalent ratios and their fitting curves |
本文将分形几何用于超声速燃烧火焰形态的定量分析, 采用计盒数法确定了火焰边界的分形维数, 建立了湍流火焰传播速度与火焰边界分形维数的关系, 验证了超声速燃烧火焰形态的自相似性, 获得了火焰边界分形维数随当量比和燃料组分的变化结果。主要结论有:
(1) 超声速燃烧火焰边界具有自相似性, 分形维数在1.05~1.36之间变化。在燃烧稳定的时间段内, 火焰边界的瞬态分形维数随时间上下波动, 但时均值基本不变。
(2) 在本文研究的当量比范围内, 超声速火焰边界的分形维数随当量比近似线性增加, 说明火焰边界的卷曲、褶皱程度增加, 湍流火焰传播速度增大。
(3) 火焰边界的分形维数随氢含量的增加而增大, 这说明氢的加入导致燃烧增强, 火焰边界的卷曲、褶皱程度增加, 湍流火焰传播速度增大。
本文尝试采用分形几何方法对超声速燃烧的火焰形态进行定量分析, 初步获得了可以定量表征火焰特性的数据与变化规律。研究的最大当量比为0.3, 对于单路喷油来说, 已不算小。如果继续增大当量比, 受燃烧室小扩张角的影响, 该构型燃烧室容易出现热壅塞, 从而影响入口条件。在今后工作中, 针对大扩张角燃烧室, 将研究高当量比条件下是否依然遵循该规律。随着光学测试手段的不断提高, 如平面激光诱导荧光等技术的应用, 可以获得更为清晰的火焰锋面图像, 从而采用分形几何方法可以获得更准确的火焰表征结果。
| [1] |
Yoshikawa I, Shim Y S, Nada Y, et al. A dynamic SGS combustion model based on fractal characteristics of turbulent premixed flames[J]. Proceedings of the Combustion Institute, 2013, 34(1): 1373-1381. |
| [2] |
Mandelbrot B B. The fractal geometry of nature[M]. New York: Times Books, 1982.
|
| [3] |
Sreenivasan K R, Meneveau C. The fractal facets of turbulence[J]. Journal of Fluid Mechanics, 1986, 173: 357-386. DOI:10.1017/S0022112086001209 |
| [4] |
赵玉新, 易仕和, 田立丰, 等. 超声速湍流混合层实验图像的分形度量[J]. 中国科学(G辑:物理学力学天文学), 2008, 38(5): 562-571. Zhao Y X, Yi S H, Tian L F, et al. Fractal measurement of experimental images of supersonic turbulent mixing layer[J]. Science in China (Series G:Physics, Mechanics & Astronomy), 2008, 38(5): 562-571. |
| [5] |
杨宏旻, 顾璠, 刘勇, 等. 湍流预混火焰传播速度的分形模型研究[J]. 工程热物理学报, 2001, 22(4): 507-510. Yang H M, Gu P, Liu Y, et al. The investigation on fractal model of the propagating speed of turbulent premixed flame[J]. Journal of Engineering Thermophysics, 2001, 22(4): 507-510. DOI:10.3321/j.issn:0253-231X.2001.04.032 |
| [6] |
蒋德明, 马凡华, 杨迪. 预混湍流火焰结构的分形特征[J]. 西安交通大学学报, 1999, 33(2): 22-24. Jiang D M, Ma F H, Yang D. The fractal nature of turbulent premixed flame structure[J]. Journal of Xi'an Jiaotong University, 1999, 33(2): 22-24. DOI:10.3321/j.issn:0253-987X.1999.02.006 |
| [7] |
Hiraoka K, Minamoto Y, Shimura M, et al. A fractal dynamic SGS combustion model for large eddy simulation of turbulent premixed flames[J]. Combustion Sciences & Technology, 2016, 188(9): 1472-1495. |
| [8] |
Cheng L W, Zhong F Q, Wang Z P, et al. Experimental study of ignition and flame characteristics of surrogate of cracked hydrocarbon fuels in supersonic crossflow[R]. AIAA-2017-2295, 2017.
|
| [9] |
程柳维, 仲峰泉, 王知溥, 等.超声速燃烧室乙烯/氢混合燃料点火及火焰形态的实验研究[C].第九届全国高超声速科技学术会议, 西安, 2016. Cheng L W, Zhong F Q, Wang Z P, et al. Experimental study of ignition and flame shape of blended fuel of ethylene/hydrogen in a supersonic combustor[C]//Proc of the 9th National Conference on Hypersonic Science and Technology. 2016. |
| [10] |
王玲玲, 金忠青. 分形理论及其在紊流研究中的应用[J]. 河海大学学报, 1997, 25(1): 1-5. Wang L L, Jin Z Q. Fractal theory and its application to turbulence study[J]. Journal of Hohai University, 1997, 25(1): 1-5. DOI:10.3321/j.issn:1000-1980.1997.01.001 |
| [11] |
沈学会, 陈举华. 分形与混沌理论在湍流研究之中的应用[J]. 河南科技大学学报:自然科学版, 2005, 26(1): 27-30. Shen X H, Chen J H. Application of fractal and chaos theory in turbulence study[J]. Journal of Henan University of Science and Technology:Natural Science, 2005, 26(1): 27-30. |
| [12] |
孟艳玲.汽油机燃烧火焰的分形特征研究[D].天津: 天津大学, 2007. Meng Y L. Study on fractal characteristics of combustion flame in gasoline engine[D]. Tianjin: Tianjin University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10056-2008184277.htm |
| [13] |
Fureby C. A fractal flame-wrinkling large eddy simulation mo-del for premixed turbulent combustion[J]. Proceedings of the Combustion Institute, 2005, 30(1): 593-601. |
| [14] |
Cintosun E, Smallwood G L, Gülder Ömer L. Flame surface fratcal characteristics in premixed turbulent combustionat high turbulence intensities[J]. AIAA Journal, 2007, 45(11): 2785-2789. DOI:10.2514/1.29533 |
| [15] |
Gouldin F C. An application of fractals to modeling premixed turbulent flames[J]. Combustion and Flame, 1987, 68(3): 249-266. DOI:10.1016/0010-2180(87)90003-4 |
| [16] |
Peters N. The turbulent burning velocity for large-scale and small-scale turbulence[J]. Journal of Fluid Mechanics, 1999, 384: 107-132. DOI:10.1017/S0022112098004212 |
| [17] |
Cant R S, Mastorakos E. An introduction to turbulent reacting flows[M]. UK: Imperical College Press, 2007.
|



