2. 北京理工大学 宇航学院, 北京 100081
2. School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China
燃烧是燃料化学能转化为热能的主要形式, 可分为缓燃燃烧和爆震燃烧两种模式.与基于缓燃燃烧的传统发动机相比, 基于爆震燃烧的发动机具有自增压、熵增低和热循环效率高的优点[1].旋转爆震发动机是一种以爆震波在燃烧室内沿圆周方向传播为典型特点的新型动力装置, 具有一次点火起爆即可稳定工作、结构紧凑、对来流适应能力强等诸多优点, 近年来逐渐成为航空航天推进技术领域的研究热点[2].
典型的旋转爆震燃烧流场中包含运动激波、化学反应和亚-跨-超声速强耦合的复杂流动过程.近半个世纪以来, 国内外学者对这种燃烧流动过程进行了大量研究。20世纪60年代, Dabora等[3]在一侧为惰性气体自由边界、另一侧为壁面的二元流道内, 实验研究了爆震波传播流场, 观测到了爆震波诱导的斜激波和滑移线。Sommers和Morrison[4]建立了斜激波和滑移线的理论分析模型, 而后Sichel和Foster[5]结合特征线理论对爆震波后参数分布进行了初步计算。这些早期的研究成果为其后旋转爆震燃烧及发动机建模奠定了理论基础。
随着计算机硬件及CFD技术的不断发展, 国内外学者针对旋转爆震流场开展了大量数值模拟工作, 对旋转爆震燃烧的触发与发展过程[6-7]、流场内部精细结构[8-10]以及非稳态的复杂流动过程[11-12]等进行研究。Schwer和Kailasanath[8]采用诱导参数化学反应模型, 通过二维数值模拟对比了氢气与小分子碳氢燃料对应的旋转爆震流场精细结构和发动机燃烧室主要性能参数。Tsuboi等[9]采用基元反应模型进行数值模拟, 对比了二维和三维氢气/氧气预混气旋转爆震发动机燃烧室流场结构和性能参数, 结果表明:在同样的入口条件下, 二维和三维流场宏观参数较为接近, 爆震波平均传播速度均大约为C-J理论速度的96%。Hishida等[11]采用两步化学反应模型, 数值模拟得到了旋转爆震流场中爆震波面上的胞格结构, 分析了未燃混气与燃烧产物接触面上的Kelvin-Helmholtz不稳定性。上述对旋转爆震流场的数值研究, 通过在实验室坐标系下求解非稳态带化学反应的流动控制方程, 可以获得丰富的瞬态流场信息。然而, 对于旋转爆震发动机的参数化设计, 重点关注的是设计参数对流场宏观波系结构和发动机性能的影响, 并且希望快速获得给定设计参数条件下流场主要宏观流动和状态参数分布, 进而完成对设计参数的修正反馈及优化改进。采用数值模拟方法研究旋转爆震流场往往需要消耗大量的计算资源和时间, 因此不适合开展大规模的参数化研究。为此, 文献[13-15]根据旋转爆震流场特点建立了低阶理论分析模型, 对旋转爆震发动机开展参数化研究, 分析了喷注参数和燃烧室尺寸等对发动机性能的影响。这些低阶模型虽然具有很高的计算效率, 但在模型简化中引入了与实际情况存在较大差别的假设, 如忽略旋转爆震流场中斜激波与滑移线角度的变化等。Fievisohn和Yu[16]采用迭代方式处理斜激波和滑移线的弯曲, 将特征线法推广应用于旋转爆震发动机流场的稳态分析, 计算了氢气/空气预混气旋转爆震发动机性能参数。与数值模拟相比, 采用特征线法求解旋转爆震流场具有很高的计算效率, 通常仅需要几次迭代计算即可得到收敛流场; 且与针对旋转爆震流场的一维流动分析方法不同, 采用特征线法可计算得到入口和出口参数沿流场圆周方向的变化、斜激波和滑移线的弯曲等旋转爆震流场二维参数分布特征[16]。目前国内学者尚未开展相关研究工作。
本文对旋转爆震流场进行简化处理, 采用特征线理论并结合流场计算基本单元过程, 建立基于特征线理论的旋转爆震流场计算方法, 计算氢气/空气、甲烷/空气和辛烷/空气3种均匀预混气对应的旋转爆震稳态流场, 并分析混气当量比、喷注总温和喷注总压对爆震波高度、倾斜角度以及爆震波后宏观流场结构的影响, 为后续利用本文计算方法和结果开展发动机整机性能评估提供支撑。
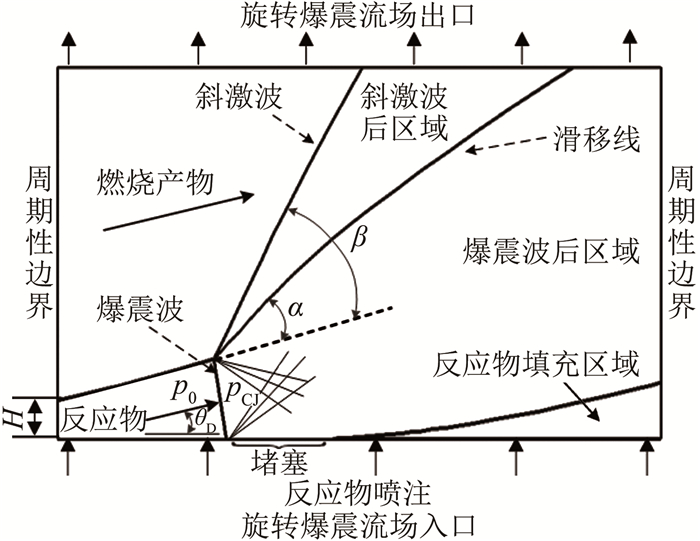
1 模型与方法 1.1 流动模型将坐标系固定在爆震波上的二维旋转爆震流场结构如图 1所示。整个流场可分为爆震波后区域、斜激波后区域和反应物填充区域。根据C-J理论, 爆震波后气流为声速流动, 向下游膨胀加速, 变为超声速流动。因此, 若忽略粘性和导热, 并且不考虑爆震波前来流参数不均匀所导致的爆震波弯曲, 此时的流动控制方程为具有明确特征走向的双曲型方程。根据特征线理论, 从初值线开始, 沿着流场特征线求解控制方程, 即可快速计算得到整个旋转爆震流场。
|
| 图 1 旋转爆震流场示意图 Fig.1 Schematic diagram of a rotating detonation flow field |
采用特征线法对旋转爆震流场的求解, 需要给出紧邻爆震波后区域的初值, 然后沿特征线推进计算整个流场, 如图 1所示。假设爆震波前来流参数(压力p0和温度T0等)已知, 根据C-J理论计算爆震波后参数(压力pCJ、温度TCJ以及爆震波速度等), 同时根据Prandtl-Meyer流动方程计算滑移线与爆震波前来流方向夹角α。另外, 滑移线角α、斜激波角β(斜激波与爆震波前来流方向夹角)以及斜激波前来流马赫数Mas0需要满足斜激波关系式。最后, 结合斜激波前后关系式、等熵膨胀关系式以及滑移线两侧的压力匹配关系, 计算得到爆震波后紧邻爆震波区域流场计算的初值参数。旋转爆震流场周期性边界条件导致斜激波前来流参数不均匀, 使得斜激波和滑移线发生弯曲。因此, 在紧邻爆震波后区域求解上述爆震波-斜激波关系, 仅用于提供流场推进计算的初值, 后续计算需根据来流条件迭代确定流场下游斜激波和滑移线的角度等参数。
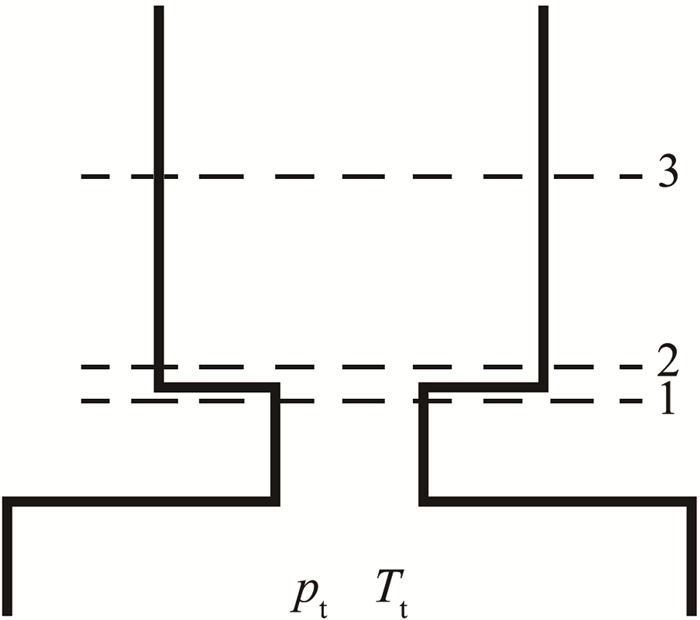
1.1.2 反应物喷注模型对于旋转爆震流场入口条件, 借鉴文献[16]中提出的适用于特征线法的反应物喷注模型给出。高压集气腔中反应物通过带有几何喉部的突扩通道进入燃烧室, 如图 2所示。截面1为喷孔喉部, 截面2紧邻喷孔喉部后端, 截面3为喷孔出口流动已经稳定的位置。假设整个过程绝热, 由于气流在突扩段存在流动损失, 因此流动是非等熵的。计算时, 反应物喷注过程要与爆震波后高压产物膨胀过程同时迭代求解。随着爆震波后高压产物逐渐膨胀, 喷孔出口(截面3)压力会随之变化, 喷孔喉部(截面1)会出现堵塞(Ma1=0)、壅塞(Ma1=1)和未壅塞(Ma1 < 1)3种状态。
|
| 图 2 反应物喷注模型 Fig.2 Reactant injection model |
气流在截面2和截面3之间满足拟一维无粘流动的质量、动量和能量守恒方程[16]。给定高压集气腔内总温Tt、总压pt, 以及截面1和截面3的面积A1和A3, 喷孔出口截面3处压力p3, 即可通过迭代求解得到喷孔三个截面处的流动参数。需要说明的是:给定截面3压力p3, 通过上述拟一维流动方程组计算得到的截面3气流的速度v3是在实验室固定坐标系下反应物的轴向速度。在爆震波坐标系下, 截面3气流的速度需要叠加爆震波在实验室坐标系下的传播速度ulab, 即在爆震波坐标系下, 截面3的合速度为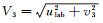
直角坐标系下二维稳态等熵流动控制方程为欧拉方程, 由有旋流动的特征线理论可知, 若流场内为超声速流动, 沿流场特征线可将原始偏微分方程转化为常微分方程。对于二维问题, 可以将原始欧拉方程组转化为沿着特征线的4个相容方程。采用文献[18]预估-矫正法, 即可沿流场特征线求解相容方程。特征线法的详细理论和计算单元过程见文献[18-19]。
1.2.1 旋转爆震流场计算主要单元过程由于沿入口边界反应物非等熵喷注以及旋转爆震流场内弯曲的斜激波, 使得流场内部存在较大的熵梯度, 此时按照传统内点单元过程计算流场中内点会出现较大的计算误差[20], 因此采用流函数-熵方法对内点单元过程进行修正来提高计算精度[16]。其基本思想是:对于等熵流动, 沿着流线, 熵不发生变化, 即同一条流线上总参数处处相等, 可以通过计算待求内点的流函数来确定该点的总参数, 再结合沿特征线的相容方程, 计算得到待求点的所有参数。
反应物喷注单元过程的计算方法与基于特征线理论的斜激波单元过程计算方法[18]类似。斜激波单元过程根据斜激波关系式和沿特征线相容方程, 迭代计算斜激波参数。反应物喷注单元过程则利用上述拟一维流动方程组和沿特征线的相容方程, 迭代确定喷孔出口处流动参数。
旋转爆震流场内, 反应物填充区域未燃混气与爆震燃烧产物之间, 以及爆震燃烧产物与经过斜激波压缩后的上一轮爆震燃烧产物之间都会形成滑移线, 因此需要采用滑移线单元过程计算滑移线两侧参数。滑移线单元过程[18]的计算, 主要通过在滑移线两侧分别采用逆置壁面点单元过程和自由压力点单元过程, 并根据滑移线两侧流动需要满足的压力和流动角度匹配条件进行迭代计算。
1.2.2 流场插值对于全流场的首次计算, 可以先假定爆震波高度H、倾斜角度θD以及爆震波前气流的压力p0和温度T0。斜激波前气流初始参数, 可取为爆震燃烧后气流等熵膨胀至爆震波前来流压力时对应的状态参数。后续迭代计算中, 根据燃烧室周向长度和周期性边界条件, 将爆震波与反应物填充区域滑移线相交点对应的轴向位置作为新的爆震波高度。同时, 在反应物填充区域插值计算新爆震波位置处的流动参数, 并对得到的流动参数进行质量加权平均, 作为新一轮迭代爆震波倾斜角度以及波前来流参数。斜激波前来流参数同样需要在上一轮计算得到的流场中插值确定, 以满足二维旋转爆震流场的周期性边界条件[15]。
1.2.3 化学反应参数计算计算中假定反应物和燃烧产物均为理想气体, 并利用Cantera[21]中爆震工具箱, 调用基元反应模型计算爆震波后C-J状态参数。利用Cantera计算不同燃料在不同当量比条件下, C-J爆震波波前和波后比热比和气体常数。全流场计算时, 反应物的计算采用波前比热比和气体常数, 燃烧产物的计算则采用波后比热比和气体常数。采用gri30_highT反应机理[21]分别计算氢气/空气和甲烷/空气的化学反应参数, 采用文献[22]中针对大分子碳氢燃料提出的化学反应机理计算辛烷/空气的化学反应参数。
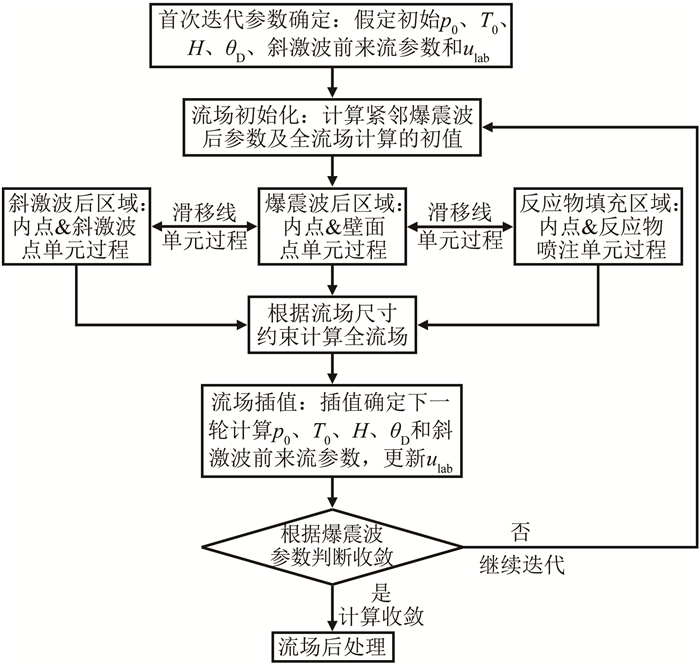
综上所述, 采用特征线理论对旋转爆震流场迭代计算的流程如图 3所示。
|
| 图 3 旋转爆震全流场迭代流程图 Fig.3 Flow chart of the rotating detonation flow field iteration |
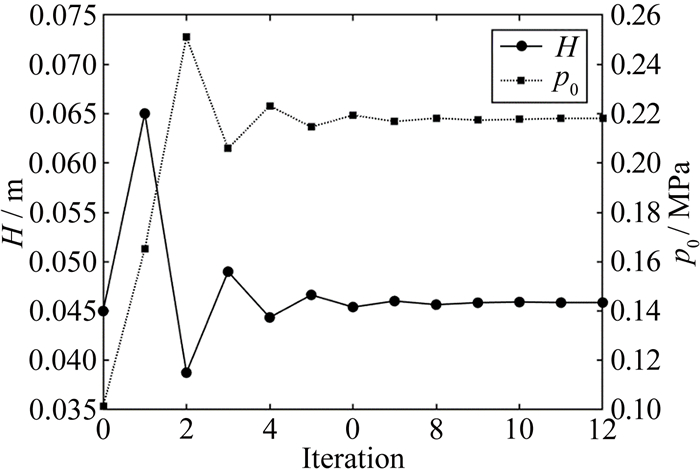
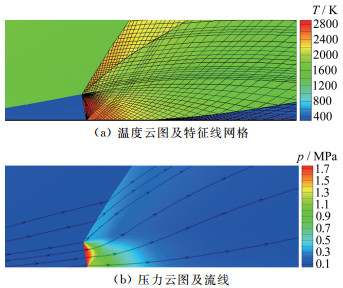
为验证本文计算方法和计算程序, 选取文献[16]中针对化学恰当比的氢气/空气预混气旋转爆震流场计算工况进行对比。图 4为本文迭代计算过程中, 爆震波轴向高度H和爆震波前来流压力p0收敛过程。可以看出:采用特征线法计算旋转爆震流场, 仅需要几次迭代即可得到收敛流场, 具有很高的计算效率。图 5为本文计算得到的旋转爆震流场温度云图、压力云图及流线图。从图中可以看到, 流场中爆震波后区域、斜激波后区域以及反应物喷注区域中的特征线网格, 与文献[16]中给出的计算结果基本一致。
|
| 图 4 流场迭代收敛过程 Fig.4 Convergence history of the flow field iteration |
|
| 图 5 旋转爆震流场计算结果 Fig.5 Calculation results of the rotating detonation flow field |
值得注意的是, 采用特征线方法无法计算未燃混气与爆震波后燃烧产物之间的接触燃烧, 以及斜激波后沿滑移线的Kelvin-Helmholtz不稳定性。其原因在于:特征线方法需要假设旋转爆震流场的反应物全部通过爆震燃烧转化为燃烧产物, 而忽略了反应物与爆震燃烧后高温产物之间的接触燃烧; 斜激波后滑移线的计算所采用的滑移线单元过程也是一种简化处理, 仅考虑了滑移线两侧气流流动需满足的压力及速度方向的匹配条件, 而忽略了斜激波后气流与爆震波后气流在滑移线界面存在的不稳定性现象。
另外, 计算了不同喷孔面积比A1/A3时, 化学恰当比的氢气/空气预混气旋转爆震流场。其中计算得到的不同A1/A3时燃料质量流量, 与采用数值模拟的文献[23]和采用特征线方法的文献[16]的计算结果对比如图 6所示。可以看出, 本文定量计算结果与文献结果基本一致。以上验证说明了本文所采用的计算方法和计算程序的有效性和正确性。

|
| 图 6 本文计算结果与文献结果对比 Fig.6 Comparison of fuel mass rates among this paper and references |
利用上述流动模型和计算方法, 分别选用氢气(H2)/空气、甲烷(CH4)/空气和辛烷(C8H18)/空气3种预混气, 计算不同当量比φ、不同喷注总温Tt和不同喷注总压pt条件下的爆震波轴向高度H、倾斜角度θD及波后流场。计算采用旋转爆震流场周向长度l=43.98cm, 喷孔面积比A1/A3=0.3。采用控制变量的方式, 保持喷注总压pt=0.1MPa、喷注总温Tt=300K不变, 研究当量比φ的影响; 保持当量比φ=1.0、喷注总压pt=0.1MPa不变, 研究喷注总温Tt的影响; 保持当量比φ=1.0、喷注总温Tt=300K不变, 研究喷注总压pt的影响。
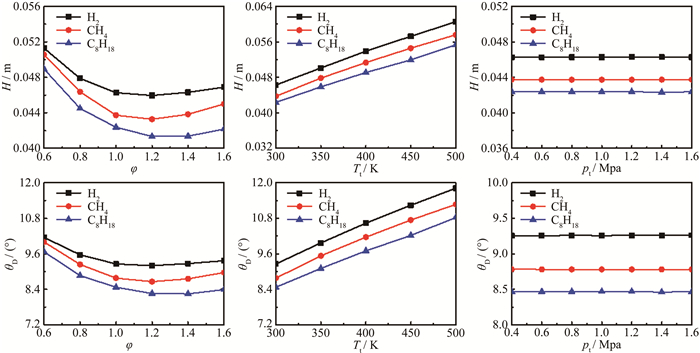
2.1 爆震波高度、倾斜角度的变化规律混气当量比φ、喷注总温Tt和喷注总压pt对3种混气的爆震波高度H和倾斜角度θD的影响如图 7所示。从图中可以看出:
|
| 图 7 当量比、喷注总温和喷注总压对爆震波高度和倾斜角度的影响 Fig.7 Effect of equivalence ratio, the plenum stagnation temperature and plenum stagnation pressure on detonation wave height and inclination angle |
(1) 相同当量比条件下, 以氢气为燃料时混气的爆震波高度最高, 以辛烷为燃料时最低; 当量比较低(贫油)时爆震波高度大, 倾斜角度也大, 随着当量比逐渐接近化学恰当比, 爆震波高度下降, 倾斜角度也变小。在当量比1.2附近, 两个参数达到最小值, 再进一步增加当量比, 二者变化较小。
(2) 对于3种混气, 随着喷注总温从300K增大到500K, 爆震波高度和倾斜角度也都随之增大。
(3) 对于3种混气, 喷注总压从0.4MPa变化到1.6MPa, 爆震波高度和倾斜角度变化不明显。
一般来说, 爆震波高度H主要取决于反应物喷注速度v和爆震波传播周期T。若给定燃烧室周向长度l, 则传播周期T由爆震波周向传播速度ulab决定, 则爆震波高度可近似由式(1)表示, 其中n为爆震波头数目。因此, 当爆震波头数目相同时, 喷注速度增大以及爆震波传播速度降低都有利于爆震波前反应物的积累, 进而使得爆震波高度增大。而爆震波的倾斜角度θD主要取决于反应物的喷注速度v和爆震波的周向传播速度ulab, 可近似由式(2)表示。喷注速度越大、爆震波传播速度越小, 会使得爆震波倾斜角度越大。燃料的当量比主要影响反应放热量, 进而影响爆震波传播速度。需要说明的是, 爆震波后喷注壁面压力分布, 以及反应物的性质都会对反应物的喷注速度产生影响。喷注壁面的压力分布受爆震波后高压燃烧产物膨胀的影响, 燃烧产物越快膨胀至喷注总压以下, 反应物能越早进入燃烧室内。
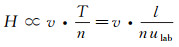 (1)
(1)
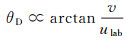 (2)
(2)
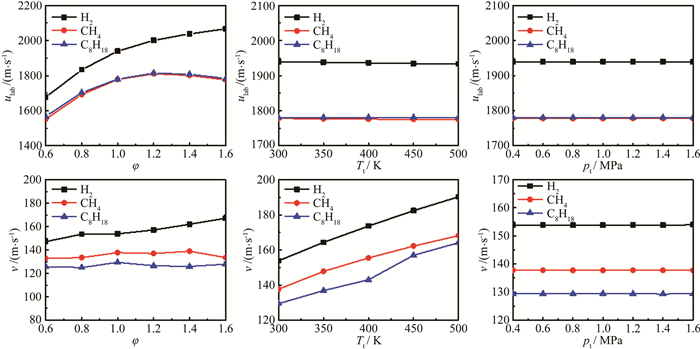
为此, 统计了3种混气在不同当量比、喷注总温和喷注总压条件下, 爆震波在实验室坐标系下的周向传播速度ulab以及反应物沿轴向喷注速度v, 如图 8所示。其中, 喷注速度取为沿喷注壁面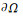
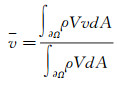 (3)
(3)
|
| 图 8 当量比、喷注总温和喷注总压对爆震波周向传播速度与反应物喷注速度的影响 Fig.8 Effect of equivalence ratio, the plenum stagnation temperature and plenum stagnation pressure on the circumferential velocity of detonation wave and the velocity of reactant injection |
(1) 混气当量比φ的影响
从图 8可以看出, 相同当量比时, 以氢气为燃料的爆震波周向传播速度最大, 其对应的反应物喷注速度也最大。氢气爆震波的周向传播速度大约为甲烷爆震波的1.11倍, 而氢气/空气反应物的喷注速度大约为甲烷/空气反应物的1.15倍。与甲烷/空气反应物相比, 氢气/空气反应物虽然积累时间比较短, 但却具有更大的喷注速度, 因此氢气/空气爆震波高度比甲烷/空气的大。而对于甲烷和辛烷对应的混气, 相同当量比时, 两者爆震波周向传播速度比较接近, 而甲烷/空气反应物喷注速度比辛烷/空气反应物大。因此, 在相同当量比条件下, 甲烷/空气反应物的爆震波高度要比辛烷/空气反应物的大。
随着当量比增大, 氢气/空气反应物爆震波周向传播速度逐渐增大, 因此爆震波传播周期逐渐减小, 对应的反应物积累时间也会缩短, 使得爆震波高度减小。而随着当量比增大, 反应物中氢气含量增加, 喷孔出口平均速度也逐渐增大, 这又有利于爆震波前反应物的积累, 使得爆震波高度逐渐增大。在这两种因素的共同作用下, 使得以氢气为燃料的爆震波高度随着当量比增大先降低而后升高。而对于甲烷、辛烷分别与空气组成的混合物, 随着当量比的增大, 爆震波周向传播速度先增大而后略有减小, 而反应物的喷注速度则变化不大。因此, 爆震波高度主要取决于爆震波的周向速度, 并且与爆震波周向传播速度变化呈现相反的趋势。对于3种燃料, 同样的原因使得爆震波倾斜角度随着当量比的增大也先减小而后略有增大。
(2) 喷注总温Tt的影响
从图 8可以看出, 对于相同混气, 爆震波周向传播速度随着喷注总温的增大略有减小。这是因为喷注总温增大会增大爆震波前来流的温度, 导致爆震波传播速度略有降低[24]。同时, 反应物的喷注速度随着喷注总温的增大而明显增大。对于本文所采用的喷注模型, 当喷注总压、喷孔喉道与出口面积比以及喷孔出口压力保持不变时, 喷注总温越高, 喷孔出口喷注速度越大, 如氢气/空气反应物在喷注总温为300K时, 喷注速度约为154m/s, 而喷注总温为500K时, 其对应喷注速度约为190m/s, 大约增大了23%。周向传播速度降低和喷注速度增大, 都会使得爆震波高度和倾斜角度增大。因此随着喷注总温增大, 3种混合物的爆震波高度和倾斜角度都逐渐增大。
(3) 喷注总压pt的影响
对于本文的喷注构型, 当给定喷孔喉道与出口面积比A1/A3以及喷注总温时, 若喷孔喉道处于壅塞状态, 则喷孔出口速度与喷注总压无关。此时增大喷注总压只会增大喷孔出口压力, 而压力对爆震波传播速度影响很小。因此, 随着喷注总压增大, 爆震波周向传播速度变化不大, 爆震波高度和倾斜角度受喷注总压影响较小。
2.2 旋转爆震波后流场的宏观变化规律爆震波诱导的斜激波和滑移线构成了爆震波后流场宏观结构。图 9给出了3种混气在当量比、喷注总温和喷注总压变化时, 爆震波下游流场宏观波系结构的变化情况。从图中可以看出:(1) 3种混气经爆震燃烧后, 流场的宏观结构(包括斜激波和滑移线的变化趋势)类似。(2)混气当量比由0.6增加到1.0, 斜激波角度逐渐减小, 滑移线角度也相应减小; 当量比进一步增加, 爆震燃烧进入富油状态, 斜激波与滑移线几乎不变。(3)反应物喷注总温变化对爆震波后宏观流场结构的影响比较明显; 当喷注总温由300K增加到500K时, 斜激波和滑移线角度均有所增大, 且前者增大更明显。(4)反应物喷注总压由0.4MPa增加到1.6MPa时, 流场宏观结构未发生明显变化。

|
| 图 9 当量比、喷注总温和喷注总压对爆震波后宏观流场的影响 Fig.9 Effect of equivalence ratio, the plenum stagnation temperature and plenum stagnation pressure on the macroscopic flow field behind the detonation wave |
如图 1所示, 爆震波、斜激波及滑移线构成了旋转爆震流场的典型结构特征。新一轮爆震燃烧高压产物向下游的侧向膨胀形成了对上一轮燃烧产物作用的斜激波。斜激波后气体与当前燃烧产物在一定位置保持压力相等, 速度方向相同, 从而形成了新旧燃烧产物之间的接触间断, 即滑移线。斜激波和滑移线的变化趋势与爆震波的速度、压比等强度参数和上一轮爆震燃烧产物的膨胀程度紧密相关。一般而言, 爆震波强度越大, 对应斜激波前气流马赫数越大(在爆震波坐标系下), 斜激波角度越小。因此, 斜激波角度直观反映了爆震波的强度, 而滑移线则作为分界线将爆震波后新一轮燃烧产物与上一轮燃烧产物区分开。
对于给定几何尺寸的燃烧室, 旋转爆震流场宏观结构主要取决于爆震波的强度, 而爆震波的强度主要受波前来流参数影响。随着来流混气当量比增大, 反应放热量相应增大。越接近化学恰当比, 爆震波的速度和爆震波前后压比越高, 则斜激波前来流马赫数越大, 从而使得斜激波角度越小。而随着当量比的进一步增大, 爆震燃烧处于富油状态, 反应放热量变化较小, 爆震波强度也变化不大, 导致此时流场宏观波系结构变化较小。同样道理, 随着反应物喷注总温增大, 爆震波前来流温度增加, 则爆震波强度(爆震波速度和爆震波前后压比)略有变弱, 导致斜激波和滑移线角度随着喷注总温增大而增大。同时, 喷注总温增大使得混气的填充速度增加, 导致爆震波的高度明显增加, 从而使斜激波和滑移线起始位置向下游移动。而在本文所研究的范围内, 喷注总压变化对爆震波参数影响较小, 爆震波后流场宏观结构随喷注总压变化不明显。
3 结论通过将坐标系建立在爆震波上, 应用特征线理论建立了旋转爆震稳态流场参数分布的计算模型, 计算了氢气/空气、甲烷/空气及辛烷/空气3种不同预混气对应的旋转爆震流场, 研究了爆震波高度、倾斜角度以及爆震波后宏观流场结构随混气当量比、喷注总温和喷注总压的变化规律, 得到了以下结论:
(1) 混气由低当量比(贫油)变化为高当量比(富油)时, 爆震波高度和倾斜角度均先减小后增大; 爆震波高度和倾斜角度随着喷注总温增大而增大, 而在所研究范围内受喷注总压影响较小。
(2) 燃料由小分子氢燃料变为大分子碳氢燃料时, 随着分子量的增加, 爆震波高度和倾斜角度逐渐减小。
(3) 混气当量比和喷注总温主要通过影响爆震波传播速度、高度和倾斜角度而影响爆震波后宏观流场特征趋势。
| [1] |
Wolański P. Detonative propulsion[J]. Proceedings of the Combustion Institute, 2013, 34(1): 125-158. |
| [2] |
Lu F K, Braun E M. Rotating detonation wave propulsion:experimental challenges, modeling, and engine concepts[J]. Journal of Propulsion and Power, 2014, 30(5): 1125-1142. DOI:10.2514/1.B34802 |
| [3] |
Dabora E K, Nicholls J A, Morrison R B. The influence of a compressible boundary on the propagation of gaseous detonations[J]. Symposium (International) on Combustion, 1965, 10(1): 817-830. DOI:10.1016/S0082-0784(65)80225-9 |
| [4] |
Sommers W P, Morrison R B. Simulation of condensed-explosive detonation phenomena with gases[J]. Physics of Fluids, 1962, 5: 241-248. DOI:10.1063/1.1706602 |
| [5] |
Sichel M, Foster J C. The ground impulse generated by a plane fuel-air explosion with side relief[J]. Acta Astronautica, 1979, 6(3-4): 243-256. DOI:10.1016/0094-5765(79)90096-1 |
| [6] |
林伟, 周进, 林志勇, 等. 热射流起爆过程的数值模拟[J]. 国防科技大学学报, 2015, 37(1): 70-77, 89. Lin W, Zhou J, Lin Z Y, et al. Numerical simulation of detonation onset by hot jets[J]. Journal of National University of Defense Technology, 2015, 37(1): 70-77, 89. |
| [7] |
姜孝海, 范宝春, 董刚, 等. 旋转爆轰流场的数值模拟[J]. 推进技术, 2007, 28(4): 403-407. Jiang X H, Fan B C, Dong G, et al. Numerical investigation on the flow field of rotating detonation wave[J]. Journal of Propulsion Technology, 2007, 28(4): 403-407. DOI:10.3321/j.issn:1001-4055.2007.04.014 |
| [8] |
Schwer D, Kailasanath K. Fluid dynamics of rotating detonation engines with hydrogen and hydrocarbon fuels[J]. Proceedings of the Combustion Institute, 2013, 34(2): 1991-1998. |
| [9] |
Tsuboi N, Eto S, Hayashi A K, et al. Front cellular structure and thrust performance on hydrogen-oxygen rotating detonation engine[J]. Journal of Propulsion and Power, 2016, 33(1): 100-111. |
| [10] |
Tsuboi N, Watanabe Y, Kojima T, et al. Numerical estimation of the thrust performance on a rotating detonation engine for a hydrogen-oxygen mixture[J]. Proceedings of the Combustion Institute, 2015, 35(2): 2005-2013. DOI:10.1016/j.proci.2014.09.010 |
| [11] |
Hishida M, Fujiwara T, Wolanski P. Fundamentals of rotating detonations[J]. Shock Waves, 2009, 19(1): 1-10. DOI:10.1007/s00193-008-0178-2 |
| [12] |
Zhou R, Wang J P. Numerical investigation of flow particle paths and thermodynamic performance of continuously rotating detonation engines[J]. Combustion and Flame, 2012, 159(12): 3632-3645. DOI:10.1016/j.combustflame.2012.07.007 |
| [13] |
Mizener A R, Lu F K. Low-order parametric analysis of a rotating detonation engine in rocket mode[J]. Journal of Propulsion and Power, 2017, 33(6): 1543-1554. DOI:10.2514/1.B36432 |
| [14] |
Kaemming T, Fotia M L, Hoke J, et al. Thermodynamic mo-deling of a rotating detonation engine through a reduced-order approach[J]. Journal of Propulsion and Power, 2017, 33(5): 1170-1178. DOI:10.2514/1.B36237 |
| [15] |
Sousa J, Braun J, Paniagua G. Development of a fast evaluation tool for rotating detonation combustors[J]. Applied Mathematical Modelling, 2017(52): 42-52. |
| [16] |
Fievisohn R T, Yu K H. Steady-state analysis of rotating detonation engine flowfields with the method of characteristics[J]. Journal of Propulsion and Power, 2017, 33(1): 89-99. DOI:10.2514/1.B36103 |
| [17] |
Fievisohn R, Yu K. Method of characteristic analysis of gaseous detonations bounded by an inert gas[C]//Proc of the 25th International Colloquium on the Dynamics of Explosions and Reactive Systems, Leeds, 2015.
|
| [18] |
Zucrow M J, Hoffman J D. Gas dynamics. Volume 2-multidimensional flow[M]. New York: John Wiley and Sons, Inc., 1977: 185-266.
|
| [19] |
Thompson P A. Compressible-fluid dynamic[M]. New York: McGraw-Hill, 1971: 454-455.
|
| [20] |
Oneill J B, Powers S A. Determination of hypersonic flow fields by the method of characteristics[J]. AIAA Journal, 1963, 1(7): 1693-1694. DOI:10.2514/3.1897 |
| [21] |
Goodwin D G, Moffat H K, Speth R L. Cantera: an object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes. Version 2.3.0[CP/OL].[2018-03-01] http://www.cantera.org.
|
| [22] |
Westbrook C K, Pitz W J, Herbinet O, et al. A comprehensive detailed chemical kinetic reaction mechanism for combustion of n-alkane hydrocarbons from n-octane to n-hexadecane[J]. Combustion and flame, 2009, 156(1): 181-199. DOI:10.1016/j.combustflame.2008.07.014 |
| [23] |
Schwer D, Kailasanath K. Numerical study of the effects of engine size on rotating detonation engines[R]. AIAA-2011-581, 2011.
|
| [24] |
严传俊, 范玮. 脉冲爆震发动机原理及关键技术[M]. 西安: 西北工业大学出版社, 2005: 37-38. Yan C J, Fan W. Principles and crucial techniques of pulse detonation engine[M]. Xi'an: Northwestern Polytechnical University Press, 2005: 37-38. |



