2. 陕西省航空动力系统热科学重点实验室, 西安 710129
2. Shaanxi Key Laboratory of Thermal Sciences in Aero-engine System, Xi'an 710129, China
脉冲爆震发动机(PDE, Pulse Detonation Engine)是一种利用间歇式爆震燃烧产生的高温高压燃气来获得周期性推力的动力装置.按照是否自带氧化剂, PDE可分为火箭式、吸气式两种类型.其中, 吸气式脉冲爆震发动机(APDE, Air-Breathing Pulse Detonation Engine)比冲更大, 在工程上更具吸引力。然而, 当APDE的进气道与爆震燃烧室连通后, 由于爆震燃烧的自增压作用, 工作时的燃气压力将远高于来流, 高压燃气会向位于上游的进气道反传。反传的高压和燃气将改变上游流场结构, 不仅影响进气道正常工作, 而且会造成较大的推力损失。
为解决该问题, 国内外学者主要对机械阀、气动阀(无阀)以及流体阀展开研究。机械阀采用机械作动方式周期性地开闭阀门。阀门开启时, 空气流入爆震室进行填充; 阀门关闭后, 爆震室与进气道阻断, 爆震燃烧后的高温高压燃气只能向后排出产生推力。机械阀能较好地控制燃气反传, 但存在阀门瞬时开合引起的进气道流场突变[1-3]、在大流量下难以高频作动且容易损毁(采用单管电磁阀方案时)[4-5]以及额外驱动机构[6-8]导致的系统复杂性增加等问题。相比于机械阀, 气动阀(无阀)与流体阀因无作动机构而更易在工程中实现。其中, 流体阀采用特殊设计的流道, 使流体正向流动顺畅、逆向流动困难, 以达到单向阀的效果, 从而抑制燃气以及压力的反传。何小民[9]、李建中[10]以及郑殿峰[11]在加装了旋流器、钝体等形式的APDE原理样机上进行了大量的实验, 但一直未能达到较高的工作频率。
王可[12]、鲁唯[13]等曾在火箭式PDE上采取无阀工作方式实现了140Hz的稳定工作。但火箭式PDE的工作方式与吸气式截然不同。美国海军研究生院[14]所进行的无阀APDE研究中, 多次提到需要设计合理的隔离段以隔离爆震室工作时产生的反压。邱华[15]、彭畅新[5]、卢杰[16]等曾对不同形式的隔离段及其组合结构进行研究, 结果表明, 与来流方向呈锐角布置的刺型结构在削减反压时有突出效果。Sha等[17]针对激波衰减开展的研究表明, 迎风面(相对于激波运动方向)为钝角的三角形削减激波的能力最佳。然而, 在相同防反压结构下, 以上研究未对不同长度爆震室的反压特性进行探讨。另外, 为减小压力反传, 王治武[18]等在进气道与燃烧室之间使用了一种极小间距的环缝泄去反压。这种泄压缝的方式与上述刺型结构, 在削减反压上究竟孰优孰劣, 亦缺乏相关研究。
为研究APDE反压的传播规律, 进一步比较上述反压抑制结构的优劣, 研究设计了一种带特殊构型的隔离段, 与长径比为20的爆震室构成的发动机流道为基准模型, 同时设置4组对照模型。以化学恰当比的H2/Air为燃料和氧化剂, 研究单次爆震时的反压传播规律, 分析所设计隔离段的防反传机制以及爆震室长径比对反传的影响。
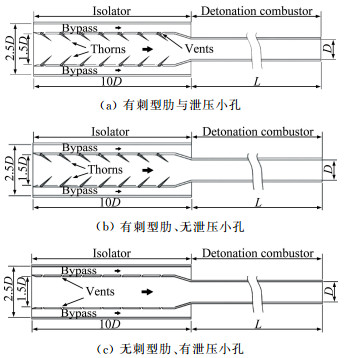
1 物理模型采用的物理模型如图 1所示。按进气方向, 气流先经过隔离段, 再流入爆震室。以图 1(a)为基准模型, 隔离段与长为L、直径为D爆震室相连(长径比L/D=20)。隔离段总长为10D, 由内径为1.5D的内涵道与内径为2.5D的外涵道组成。刺型肋(Thorns)位于内涵道中, 共设7级。泄压小孔(Vents)位于刺型肋尾部, 使得内外涵道连通。基于图 1(a), 分别设置L/D=10和40的爆震室作为基准模型的对照。另外, 针对有/无刺型肋、有/无泄压小孔, 分别考虑图 1(b)和(c)两种构型, 其爆震室的长径比均为20。为便于表述, 表 1列出了不同模型的设置及编号(ID), 表中第三列为爆震室(DC, Detonation Combustor)的长径比(L/D)。
|
| 图 1 物理模型示意图 Fig.1 Schematic of physical models |
| Case ID | Isolator config. | L/D of DC | Notes |
| A-10 | Thorns + Vents | 10 | |
| A-20 | Thorns + Vents | 20 | Base model |
| A-40 | Thorns + Vents | 40 | |
| B-20 | Thorns | 20 | |
| C-20 | Vents | 20 |
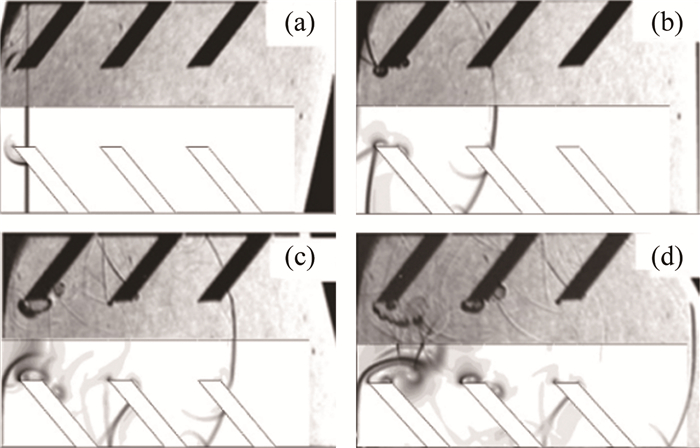
参考文献[1, 19-23]的数值方法, 采用有限体积法求解包含realizable k-ε湍流模型与组分输运的可压缩雷诺平均Navier-Stokes方程组(RANS)。因不关注爆震波的结构, 在此仅考虑单步H2/Air化学反应机理, 用基于Arrhenius的有限速率模型求解能量方程中的源项与质量分数, 并用真实气体状态方程[24]求解密度。对于网格的尺度, 实验测得的H2/Air混合物的胞格尺寸[25]在化学恰当比下约为8~15mm, 若欲捕捉爆震波的细微结构, 需保证反应区长度内至少有一个网格。但文献[26]指出, 网格尺寸为0.5mm时, 获得的爆震波宏观参数(包括爆震波速、von Neumann压力、von Neumann温度以及C-J温度), 除von Neumann温度外, 与0.1mm网格的计算值最大相差不超过5%。在此, 分别考虑0.5、0.4、0.25mm三种尺度的网格, 计算获得的爆震波C-J压力与CEA软件所计算出的C-J压力的相对误差分别为11.85%、5.69%以及4.43%。由于在隔离段中反传的燃气已完全燃烧, 本质上是求解带组分输运的流动问题, 而非求解爆震波传播的细微结构, 因此, 综合考虑采用的最大网格尺寸为0.4mm。采用上述数值方法, 对文献[27]中激波Ma=1.2的工况进行模拟, 所得的数值纹影与该文献实验拍摄的纹影序列对比如图 2所示, 可知所采用的数值方法在刺型肋结构附近可很好地捕捉入射波与反射波的传播规律。文献[27]与本文工作采用了类似结构, 且所讨论的问题同为激波在气流通道中的衰减规律, 故本数值方法满足要求, 可用于计算爆震燃烧形成的反压在气流通道内的衰减过程。
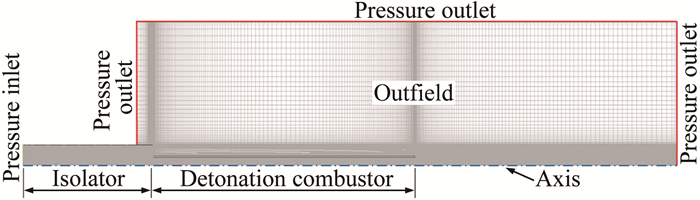
计算域如图 3所示, 包括隔离段、爆震室以及外场。需要指出, 由于不关注外流场, 其网格尺寸按等比数列从0.4mm逐渐过渡到2mm。图 3中也标出了计算域中所采用的边界条件。其中, 压力进口边界条件的总压和总温分别为202.13kPa和363K;压力出口边界的压力和温度分别为101.33kPa和288.15K;壁面绝热、无滑移。计算时, 先用给定的边界条件计算出稳态流场, 待计算收敛后, 填充化学恰当比的H2/Air混合物至爆震室, 并在爆震室头部配置厚度为10mm的高温高压区(2000K, 1.5MPa)以直接起爆。为保证收敛性, 时间步长为50ns, 单个时间步长内迭代次数为100。
|
| 图 3 计算域、网格及边界条件 Fig.3 Computational domain, grids and boundary conditions |
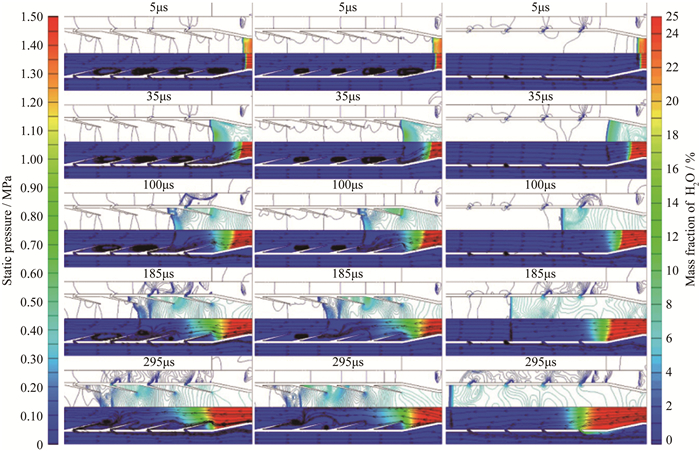
图 4给出了5~295μs时间段内, A-20、B-20和C-20在隔离段中的压力等值线图(上)、H2O的质量分数云图与流线图(下)。从图中可以看到, 反压的形成直接导致流动反向。在扩张段中, C-20靠近壁面处的反流因扩压而减速, 与A-20、B-20相比, 由于C-20的流通面积更宽, 来流中靠近轴线的流动速度较慢, 因此C-20中的反压面向左凸, 如图 4中35μs时刻所示。与此同时, A-20部分反流从泄压小孔中流出。在100μs时刻, A-20与C-20部分高压通过泄压小孔溢向外涵道, 从对应的流线图可知, 溢向外涵道的高压并未对流动造成较大影响。可以看到, A-20与B-20反压的传播速度得到了有效降低, 反压强度有效削减。此外, B-20具有最佳抑制燃烧产物前传的能力, 如图 4中295μs时刻所示。A-10、A-40反压的传播规律与A-20类似, 不再给出。为更好地比较反压在各构型中传播规律的差异, 后文将对具体数值进行分析与说明。
|
| 图 4 压力等值线图(上)、H2O的质量百分数云图及流线图(下) Fig.4 Pressure isolines(upper), mass fraction contours of H2O and streamline diagram(lower) |
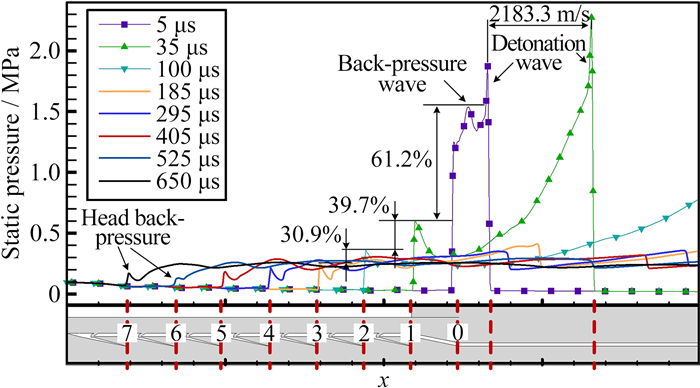
图 5给出了基准模型A-20中轴线上各时刻的静压分布, 下方的序号0~7标记了刺型肋不同级数对应的轴向位置。在5μs时刻, 因直接起爆, 爆震室头部的高压分两部分传播:一部分为向下游传播的爆震波, 一部分为向上游传播的反压。由5μs和35μs时刻的波形, 可粗略估算出爆震波波速约为2183.3m/s, 与CEA软件计算出的C-J爆震波波速1965.6m/s的相对误差为11.1%。分析认为, 过驱爆震是起爆初期爆震室头部波速较高的可能原因。由于隔离段中无可燃混气维持反压的强度, 当反压抵达第1级刺型肋时, 其静压峰值降低了61.2%;当反压抵达第2、3级刺型肋时, 其静压峰值分别降低了39.7%和30.9%。随后, 反压在持续传播过程中, 强度并未发生显著变化, 如图 5中295~650μs时刻所示。
|
| 图 5 基准模型(A-20)各时刻中轴线上的静压分布 Fig.5 Static pressure history along the central axis of the base model (A-20) |
按照图 5的方式, 可得到各模型反压传播至各级刺型肋时(即图 5中红色虚线1~7位置; C-20无刺型肋, 取与其他模型相同的几何位置)所对应的静压在中轴线上的分布。各模型反压抵达各级刺型肋的时刻如表 2所示。从表 2最右列可以看出:(1) C-20的反压抵达第7级刺型肋所需时间最短, 反传速度最快; A-10的反压抵达第7级刺型肋所需时间最长, 反传速度最慢。(2) A-40的反压传播速度稍快于A-20, A-20与B-20的反压传播速度比较接近, 这说明刺型肋能较为有效地控制反压的传播速度。(3)在有刺型肋时, 爆震室长径比越大, 所含的燃料与氧化剂越多, 反压的传播速度越快。(4)有刺型肋、且爆震室长径比相同时, 无泄压孔的反压传播速度更快。
| Case ID | Stage of thorns | |||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| A-10 | 5 | 45 | 135 | 255 | 400 | 550 | 705 | 920 |
| A-20 | 5 | 35 | 100 | 185 | 295 | 405 | 525 | 650 |
| A-40 | 5 | 35 | 90 | 165 | 260 | 355 | 465 | 580 |
| B-20 | 5 | 35 | 95 | 175 | 285 | 390 | 505 | 615 |
| C-20 | 5 | 35 | 95 | 150 | 215 | 285 | 360 | 440 |
为进一步比较不同模型的优劣, 在反压传播至各级刺型肋的标记位置(即图 6中红色虚线1~7位置), 分别对各模型中轴线上的静压曲线提取特征参数——"反压波头峰值"和"隔离段压力峰值"进行分析。反压波头峰值指的是隔离段反压波头的压力最大值(图 6左箭头所指处)。反压波头总存在这样的峰值, 相对于来流静压明显增加、随后又有一定幅度的降低, 同时该峰值随压力波的反传逐渐降低, 因此将其作为特征参数之一。隔离段压力峰值指的是各时刻下整个隔离段中轴线压力曲线的最大值(图 6右箭头所指处)。隔离段压力峰值和反压波头峰值的数值可能相同, 也可能不同, 区别在于, 反压波头峰值所对应的压力波传播方向相对于来流反向, 而隔离段压力峰值所对应的压力波传播方向并不确定, 需要结合流场进行具体分析。

|
| 图 6 反压波头峰值与隔离段压力峰值示意图 Fig.6 Schematic diagram of the head back-pressure and the isolator pressure peak |
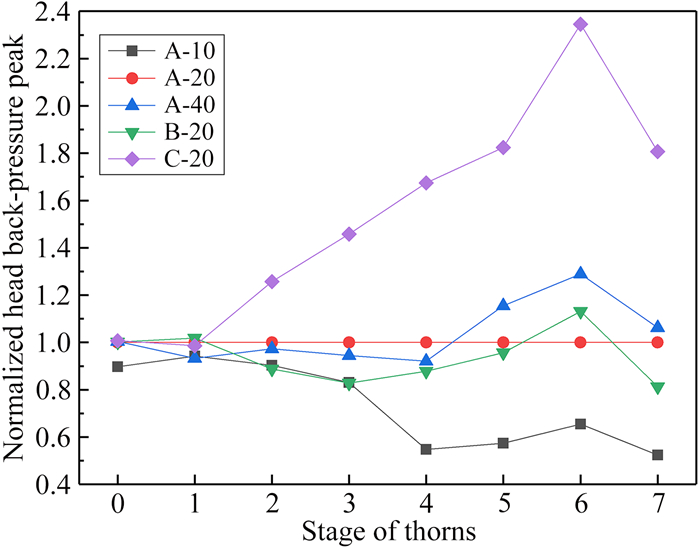
将各模型的反压波头峰值和隔离段压力峰值按照基准模型A-20归一化处理后, 可较为清晰地比较出反压传播至各级刺型肋时所对应的反压波头峰值与隔离段压力峰值变化的相对差异, 如图 7、8所示。
|
| 图 7 按A-20归一化的反压波头峰值 Fig.7 Head back-pressure peaks normalized by A-20 |

|
| 图 8 按A-20归一化的隔离段压力峰值 Fig.8 Isolator pressure peaks normalized by A-20 |
由图 7可知, 对于A-10、A-20和A-40, 反压波头峰值在经过前3级刺型肋结构时无显著差异, 到达第4级刺型肋结构后, A-10的反压波头峰值约减少为A-20的一半。而A-40的反压波头峰值在到达第5级刺型肋后, 约增加为A-20的1.2倍。在图 8中, 当反压传播至第3级刺型肋时, A-10、A-20和A-40的隔离段压力峰值就产生了差异。其中, A-10的隔离段压力峰值开始相对于A-20减小, 当反压传播至第7级刺型肋时, 约减小为A-20的40%;而A-40的隔离段压力峰值则增加到A-20的1.2倍。以上结果表明, 当隔离段结构相同时, 爆震室长径比越大, 反压强度越大。原因是:一方面, 爆震室长径比越大, 所含的可燃混气越多, 燃烧释放的能量更大; 另一方面, 爆震室长径比越大, 其流动阻力越大, 排气过程更加缓慢, 抑制反压愈加困难。
从图 7可知, 对于B-20, 反压沿各级刺型肋传播过程中, B-20的反压波头峰值总体上略低于A-20。而在图 8中, B-20的隔离段压力峰值却在反压经过第3级刺型肋后, 增加为A-20的1.3倍, 说明泄压小孔可有效降低隔离段压力峰值。而对于C-20, 当反压传播到第2级刺型肋时, 其反压波头峰值便已大于A-20;当反压传播到第6级刺型肋时, C-20的反压波头峰值约为A-20的2.3倍。由图 8可知, 当反压传播到第2级刺型肋时, C-20的隔离段压力峰值较A-20增加了20%左右; 当反压继续前传, 其隔离段压力峰值相对于B-20有所降低, 亦可说明泄压小孔在降低隔离段压力峰值上有一定优势。以上对比说明, 刺型肋结构在控制反压波头峰值上有较为突出的效果, 在仅有刺型肋、无泄压小孔时(B-20), 其抑制反压波头峰值的能力最为突出。然而, 同样由于无泄压小孔, 导致隔离段中的压力一直维持在较高水平。
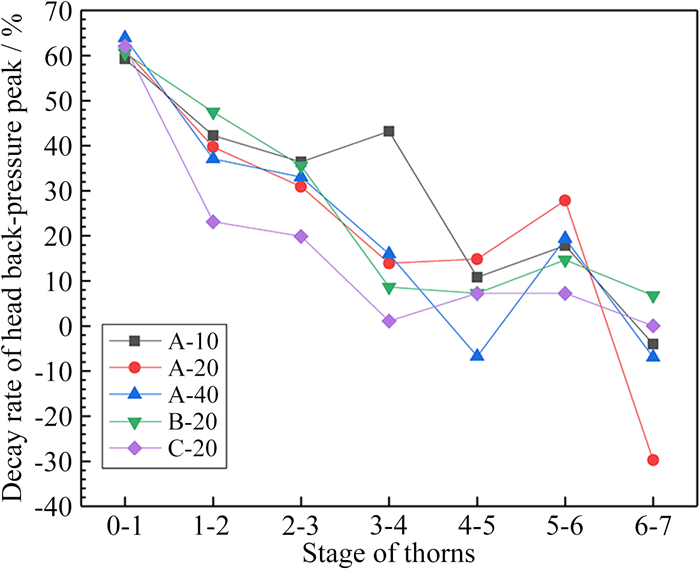
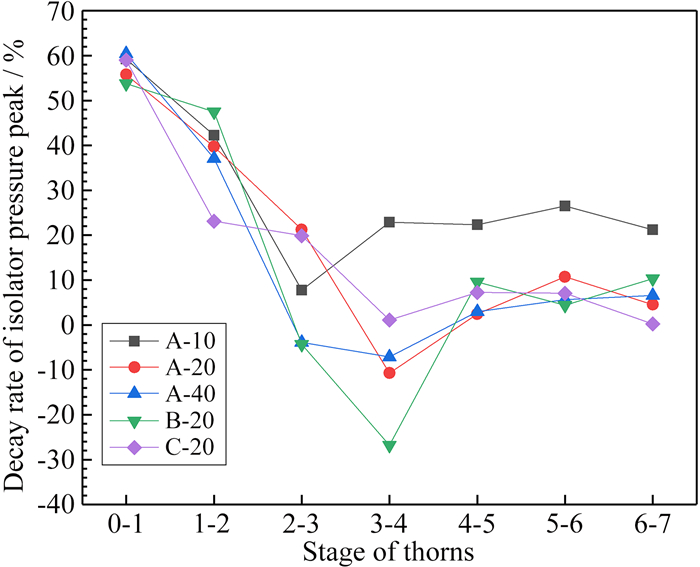
图 9、10分别为反压沿隔离段各级刺型肋传播时, 反压波头峰值和隔离段压力峰值相对于反压传播至前一级刺型肋时的衰减率。从图中可见, 在本研究的所有模型中, 反压在经过0~1级位置时, 反压波头峰值和隔离段压力峰值相对于起爆压力均衰减了约60%。其原因:一是通道扩张使反压膨胀降压; 二是与爆震相比, 缺乏化学反应释放的能量来维持反压的强度。当反压于0~3级刺型肋之间传播时, A-10、A-20与A-40的反压波头峰值衰减率几乎相同, 其反压波头峰值在反压于3~4级刺型肋之间传播时才开始产生差异, 如图 9所示。当反压于3~4级刺型肋之间传播时, A-10的反压波头峰值仍维持着近40%的衰减率, 而当反压在4~5级刺型肋之间传播时, A-40的反压波头峰值的衰减率为负。当反压在6~7级刺型肋之间传播时, A-10、A-20以及A-40也出现了不同程度的负衰减率。对于隔离段压力峰值, A-10一直维持着约20%的衰减率, 而A-20、A-40则维持着5%~10%的衰减率, 如图 10所示。当反压于2~4级刺型肋之间传播时, 隔离段压力峰值亦出现了负衰减率。对于压力峰值出现负衰减率的原因, 将在下文讨论。
|
| 图 9 反压波头峰值沿各级刺型肋的衰减率 Fig.9 Decay rate of head back-pressure peaks along various stages of thorns |
|
| 图 10 隔离段压力峰值沿各级刺型肋的衰减率 Fig.10 Decay rate of isolator pressure peaks along various stages of thorns |
从图 9可以看到, 对于不同隔离段结构(A-20、B-20与C-20), 当反压在1~3级刺型肋之间传播时, B-20的反压波头峰值衰减率略高于A-20;当反压经过第4级刺型肋后, A-20的反压波头峰值衰减得更快。对于C-20, 其反压波头峰值的衰减率普遍比A-20低10%左右, 再次说明刺型肋结构可更为有效地降低反压波头峰值。从图 10可以看到, 当反压在2~4级刺型肋之间传播时, B-20的隔离段压力峰值出现了负衰减率。其余时刻, 其隔离段压力峰值衰减率与A-20几乎相同。对于C-20, 当反压在1~2级刺型肋之间传播时, 其隔离段压力峰值衰减率约为A-20的一半; 当反压在4~7级刺型肋之间传播时, 其衰减率与A-20几乎一致。说明对于整个隔离段而言, 当爆震室长度一定时, 在反压传播的初期, 压力峰值的衰减率主要受隔离段结构的影响, 随后, 衰减率主要取决于反传距离。
另外, 推测出现负衰减率的原因是由于刺型肋的存在:当其受到反压冲击, 将在隔离段中形成压力振荡[28], 该过程本质上是加速隔离段与爆震室的压力平衡。选取的特征参数——"反压波头峰值"和"隔离段压力峰值"仅是给定时刻下的瞬态参数, 并非平衡后的稳定值, 因此在计算衰减率时出现了负数。在图 9、10中, 无刺型肋的C-20未出现负衰减率, 可以很好地证明这一点。
爆震起始后, 形成的高压同时向两个方向传播, 一部分为沿下游方向传播的爆震波, 一部分为沿上游反传的压力波。当爆震波在爆震室中传播时(尚未传出爆震室), 隔离段与爆震室的压力分布如图 11所示。此时, 爆震波的压力最高, 约在1.5MPa及以上量级; 爆震波后的已燃气体压力较低, 约在300~400kPa量级; 来流以及未燃气体的压力最低, 约在100~200kPa量级。因此, 在爆震波尚未传出爆震室时, 高压只能反传, 以平衡前后不同的压力。
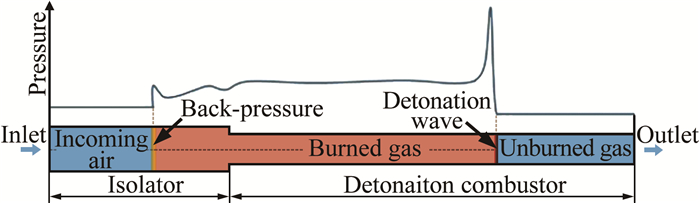
|
| 图 11 隔离段与爆震室中的典型压力分布 Fig.11 Typical pressure distribution in an isolator and a detonation combustor |
在反传过程中, 反压可通过与来流的动量交换而衰减, 也可通过在隔离段中设置合适的结构提升其衰减率; 然而在爆震波传出爆震室前, 波后高压的已燃气体便成为了维持反压强度的来源。因此, 在采用大长径比的爆震室时, 填充的可燃混气更多, 爆震波在爆震室中的传播时间亦更长, 故抑制反压的难度越大。需要指出, 爆震波相对于未燃气体以Ma=5~8的速度向下游传播的同时, 反压的起始强度较大, 传播速度大于当地声速, 在随后的传播过程中强度有所衰减, 直到衰减为以当地声速进行传播的弱波, 而未燃气体的声速与来流的当地声速基本相同。换言之, 反压的传播速度并未远小于爆震波的传播速度, 因此即使爆震波在爆震室中传播的时间极短, 反压亦将在隔离段中传播相当长的距离, 进而改变了反压波后的流场, 这无疑对防反压提出了非常严峻的要求。本研究采用特殊设计的结构, 虽在一定程度上抑制了反压前传速度、削减了反压波头峰值和隔离段压力峰值, 但当隔离段的压力降低后, 隔离段与爆震室形成了新的压力梯度, 反压会源源不断地从爆震室中产生, 直到爆震波从爆震室传出、膨胀波进入爆震室后, 才可得到缓解。也就是说, 当来流压力一定时, 爆震产生的反传高压, 仍需依赖于排气过程, 而长径比越小的爆震室, 其排气过程越迅速, 反压降低得越快, 对比图 7~10中A-10、A-20和A-40的压力峰值曲线和衰减率, 都能很好地证明这一点:A-10率先进入排气过程, 其隔离段压力峰值也最早开始下降, 且一直维持着较高的衰减率; 而A-40较迟进入排气过程, 其隔离段维持较高压力峰值的时间也最长。
在设计隔离段结构时, 为减小流动损失, 考虑使内涵道中心流通面积与爆震室通径相同。图 12给出了在海平面大气条件下, 采用稳态计算方法, 以A-20隔离段的内涵道进出口为检测截面, 采用质量加权平均与面积加权平均两种方式提取的总压恢复系数σ随来流马赫数变化的数值计算结果。由图 12可知, 总压恢复系数符合随来流流速的提高而降低的基本规律。当来流马赫数为0.15时, 质量加权平均的总压恢复系数约为99.51%, 面积加权平均的总压恢复系数约为99.37%;当来流马赫数为0.80时, 质量加权平均的总压恢复系数约为90.34%, 面积加权平均的总压恢复系数约为84.96%。以上结果表明, 所设计的隔离段满足设计初衷, 未造成大的流动损失。
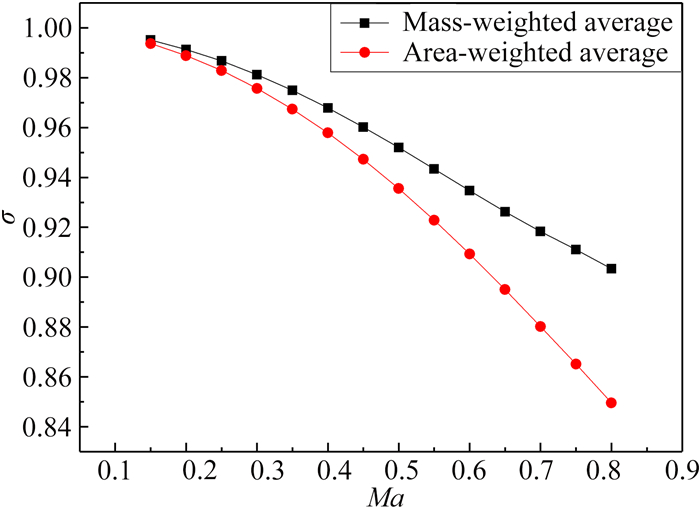
|
| 图 12 海平面大气条件下隔离段总压恢复系数随来流马赫数的变化 Fig.12 Total pressure recovery coefficient of the isolator versus Mach number of incoming flow under sea level conditions |
本文设计了一种带特殊构型的隔离段, 与长径比为20的爆震室构成的发动机流道为基准模型, 同时设置4组对照模型。以化学恰当比的H2/Air为燃料和氧化剂, 研究单次爆震时的反压传播规律, 并计算了基准模型的总压恢复系数, 得出以下结论:
(1) 刺型肋能有效地降低反压的传播速度, 在削减反压波头峰值方面有较为突出的效果, 泄压小孔可有效降低隔离段压力峰值。
(2) 采用相同隔离段结构时, 爆震室的长径比越大, 反压的传播速度越快, 排气过程开始得越晚, 反压越难以抑制。
(3) 反压相对于起爆压力衰减60%的原因, 一是通道扩张使其膨胀降压, 二是与爆震相比, 缺乏化学反应释放能量来维持其强度。在反压传播的初期, 压力峰值的衰减率主要受隔离段结构的影响, 随后, 其衰减率主要取决于反传距离。
(4) 当来流压力一定时, 爆震产生的反传高压, 需依赖于排气过程才能有效降低, 而长径比越小的爆震室, 排气过程越迅速。
(5) 在海平面大气条件下, 来流马赫数在0.15~0.80范围内, 所设计的隔离段未造成大的流动损失。
本文仅关注了所设计隔离段抑制反压的效果以及反压传播规律, 分析了隔离段内涵道的总压损失, 未细致考虑流阻损失、流量脉动、缓燃向爆震转变等因素, 在后续研究中将进一步完善并综合考虑。
| [1] |
Zangiev A E, Ivanov V S, Frolov S M. Thrust characteristics of an airbreathing pulse detonation engine in flight at Mach numbers of 0.4 to 5.0[J]. Russian Journal of Physical Chemistry B, 2016, 10(2): 272-283. DOI:10.1134/S1990793116020135 |
| [2] |
Xiong C, Yan C J, Qiu H. Analysis of an air-breathing pulsed detonation engine with bypass and ejector[J]. International Journal of Turbo and Jet Engines, 2008, 25(2): 129-136. |
| [3] |
European commission. Aeronautics and air transport research-7th framework programme 2007-2013. Project synopses-volume 1-calls 2007& 2008[R]. doi: 10.2777/83373.
|
| [4] |
Wang K, Fan W, Zhu X D, et al. Experimental studies on rotary valves for single-tube pulse detonation rocket engines[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2013, 228(2): 262-270. |
| [5] |
彭畅新.脉冲爆震外涵加力燃烧室关键技术研究[D].西安: 西北工业大学, 2013. Peng C X. Investigation on key technologies of pulse detonation combustor as bypass burner[D]. Xi'an: Northwestern Polytechnical University, 2013. |
| [6] |
范玮, 陈文娟, 严传俊.一种吸气式脉冲爆震发动机防反流机构: 中国, CN201020109153.7[P]. 2010-10-27. Fan W, Cheng W J, Yan C J. Device for back-flow prevention of air-breathing pulse detonation engine: China, CN201020109153.7[P]. 2010-10-27. |
| [7] |
Matsuoka K, Morozumi T, Takagi S, et al. Flight validation of a rotary-valved four-cylinder pulse detonation rocket[J]. Journal of Propulsion and Power, 2015, 1-9. |
| [8] |
温玉芬.吸气式脉冲爆震发动机进气道的流动特性研究[D].南京: 南京航空航天大学, 2012. Wen Y F. Research on the flow characteristics of the inlet for air-breathing pulse detonation engine[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10287-1012041309.htm |
| [9] |
何小民, 王家骅. 气动阀式两相脉冲爆震发动机研究[J]. 航空学报, 2004, 25(6): 529-533. He X M, Wang J H. Investigation on the aerovalve two phase pulse detonation engine[J]. Acta Aeronautica et Astronautica Sinica, 2004, 25(6): 529-533. DOI:10.3321/j.issn:1000-6893.2004.06.001 |
| [10] |
李建中, 王家骅, 范育新, 等. 煤油气动阀式脉冲爆震发动机爆震波压力特性试验[J]. 推进技术, 2005, 26(5): 443-447. Li J Z, Wang J H, Fan Y X, et al. Detonation pressure properties of kerosene aero-valve pulse detonation engine[J]. Journal of Propulsion Technology, 2005, 26(5): 443-447. DOI:10.3321/j.issn:1001-4055.2005.05.015 |
| [11] |
郑殿峰, 杨义勇, 王家骅. 吸气式脉冲爆震发动机钝体气动阀的设计与实验研究[J]. 北京大学学报:自然科学版, 2012, 48(3): 347-353. Zheng D F, Yang Y Y, Wang J H. Design and experimental investigation of blunt aero-valve for air-breathing pulse detonation engine[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2012, 48(3): 347-353. |
| [12] |
Wang K, Fan W, Lu W, et al. Study on a liquid-fueled and valveless pulse detonation rocket engine without the purge process[J]. Energy, 2014, 71: 605-614. DOI:10.1016/j.energy.2014.05.002 |
| [13] |
Lu W, Fan W, Wang K, et al. Operation of a liquid-fueled and valveless pulse detonation rocket engine at high frequency[J]. Proceedings of the Combustion Institute, 2016, 36(2): 2657-2664. |
| [14] |
Brophy C M, Sinibaldi J O, Ma L, et al. Effects of non-uniform mixture distributions on pulse detonation engine performance[R]. AIAA-2005-1304, 2005.
|
| [15] |
Qiu H, Xiong C, Yan C J, et al. Effect of aerodynamic valve on backflow in pulsed detonation tube[J]. Aerospace Science and Technology, 2013, 25(1): 1-15. DOI:10.1016/j.ast.2011.12.003 |
| [16] |
卢杰.脉冲爆震涡轮发动机关键技术研究[D].西安: 西北工业大学, 2016. Lu J. Investigation on key technologies of pulse detonation turbine engine[D]. Xi'an: Northwestern Polytechnical University, 2016. |
| [17] |
Sha S, Chen Z, Jiang X. Influences of obstacle geometries on shock wave attenuation[J]. Shock Waves, 2014, 24(6): 573-582. DOI:10.1007/s00193-014-0520-9 |
| [18] |
Wang Z W, Wang Y Q, Peng C X, et al. Experimental study of pressure back-propagation in a valveless air-breathing pulse detonation engine[J]. Applied Thermal Engineering, 2017, 110: 62-69. DOI:10.1016/j.applthermaleng.2016.08.144 |
| [19] |
Lu F K, Umapathy N K, Thirumangalath S C. Multi-port filling of pulsed detonation engines[R]. AIAA-2017-2119, 2017.
|
| [20] |
李舒欣, 范玮, 王永佳, 等. 流体障碍物对爆震管中初始火焰加速作用的数值研究[J]. 推进技术, 2017, 38(8): 1893-1899. Li S X, Fan W, Wang Y J, et al. Numerical simulation of effects of fluidic obstacles on initial flame speed acceleration in a detonation tube[J]. Journal of Propulsion Technology, 2017, 38(8): 1893-1899. |
| [21] |
Wang Y J, Fan W, Li H B, et al. Numerical simulations of flame propagation and DDT in obstructed detonation tubes filled with fluidic obstacles[R]. AIAA-2017-2382, 2017.
|
| [22] |
Zhang Q B, Fan W, Wang K, et al. Numerical investigation on the performance of the pulse detonation engine with injected flows[R]. AIAA-2017-2242, 2017.
|
| [23] |
Peace J T, Lu Frank K. Numerical study of pulse detonation engine nozzle and exhaust flow phenomena[R]. AIAA-2015-4189, 2015.
|
| [24] |
Aungier R H. A fast, accurate real gas equation of state for fluid dynamic analysis applications[J]. Journal of Fluids Engineering, 1995, 117(2): 277-281. DOI:10.1115/1.2817141 |
| [25] |
Kaneshige M, Shepherd J E. Detonation database[R]. Explosion Dynamics Laboratory Report FM97-8, 1997.
|
| [26] |
王丁喜.脉冲爆震发动机进气道内流场和爆震燃烧的数值研究[D].西安: 西北工业大学, 2005. Wang D X. Numerical investigation on internal flow of inlet and detonation of pulse detonation engine[D]. Xi'an: Northwestern Polytechnical University, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10699-2005064149.htm |
| [27] |
Berger S, Sadot O, Ben-Dor G. Experimental investigation on the shock-wave load attenuation by geometrical means[J]. Shock Waves, 2010, 20(1): 29-40. DOI:10.1007/s00193-009-0237-3 |
| [28] |
Gamezo V N, Oran E S. Unidirectional propagation of gas detonations in channels with sawtooth walls[R]. NRL/MR/6404-10-9255, 2010.
|