2. 浙江大学 结构工程研究所, 杭州 310000;
3. 浙江华云电力工程设计咨询有限公司, 杭州 310000
2. Institute of Structural Engineering, Zhejiang University, Hangzhou 310000, China;
3. Zhejiang Huayun Electric Power Engineering Design & Consulting Co., Ltd., Hangzhou 310000, China
圆柱绕流是流体动力学的经典问题之一。不同于其他带锐边的钝体,圆柱绕流分离点的位置并不固定,其受到来流雷诺数、湍流度、圆柱表面粗糙度等因素的共同影响。Schewe[1]在亚临界至超高临界雷诺数范围内进行了圆柱绕流试验,研究了阻力系数随雷诺数的变化规律;Zhou[2]研究了圆柱表面粗糙度对阻力系数及圆柱表面风压分布的影响;Younis[3]研究了湍流度和湍流积分尺度对圆柱阻力系数的影响。
与二维圆柱相比,有限长悬臂圆柱的气动力特性存在较大的差异。Sumner[4]对悬臂圆柱绕流研究成果进行了文献综述,认为长径比和雷诺数对悬臂圆柱气动力特性的影响并未得到系统研究。王汉封等[5]对层流中长径比为5的悬臂圆柱进行研究,认为在亚临界区间悬臂圆柱阻力系数小于二维圆柱。Wang等[6]研究了亚临界区间不同长径比的悬臂圆柱阻力系数的变化规律。Sumner等[7]认为二维圆柱和悬臂圆柱绕流特性的差异主要是由于流经悬臂圆柱自由端后的气流出现下沉现象,对圆柱尾流的涡脱落产生干扰,从而减小圆柱背压绝对值,导致阻力系数的减小。Park等[8]认为随着悬臂圆柱长径比的减小,亚临界雷诺数下悬臂圆柱绕流的涡脱落频率也会降低。Rostamy等[9]对不同长径比的悬臂圆柱尾流流场特性进行了研究。Sumner等[10]采用粒子图像测速(PIV)技术对悬臂圆柱绕流特性进行研究。
从目前国内外对悬臂圆柱绕流特性的研究成果来看,大部分的研究仅讨论了层流来流下的绕流特性,对脉动风压特性的讨论较少,高湍流度下超临界雷诺数来流条件下悬臂圆柱气动力特性的研究尚不多见,而大风对实际圆柱形结构的作用大多属于高湍流度下超临界雷诺数悬臂圆柱绕流问题。
本文以风洞试验为手段,对亚临界至超临界雷诺数、高湍流度下的悬臂圆柱绕流的气动力特性,包括阻力系数、平均风压分布、脉动风压分布等进行研究,并与层流下的试验结果进行对比。本文研究工作补充了圆柱绕流已有的研究成果,丰富了悬臂圆柱气动力系数取值,为圆截面结构物抗风设计气动力参数取值提供了试验依据。
1 风洞试验 1.1 试验设备和模型圆柱绕流风洞试验在浙江大学实验室ZD-1边界层风洞内进行。该风洞是一座闭口回流式矩形截面单试验段风洞,试验段尺寸为4m(宽)×3m(高)×18m(长)。试验段风速范围为3~55m/s,控制精度达到1.0%以上。均匀湍流场通过竖向格栅进行模拟,实测风洞试验段0.5m高度处的湍流度为9.5%,湍流积分尺度约为0.55m。
圆柱模型采用亚克力材料加工制成,外直径D=0.5m,展长L=1.0m, 风洞阻塞率为4.2%,当风洞试验中的阻塞率≤5%时,则不考虑风洞阻塞率的修正。对圆柱外表面进行喷涂处理,经哈量2205型表面粗糙度仪测量(如图 1所示),测得模型外表面平均粗糙高度Rz=6.155μm,低于《输变电钢管结构制造技术条件》(DL/T 646-2006)规定的钢管构件表面热喷涂防腐处理时要求的粗糙度,与热浸镀锌处理的表面粗糙度较为接近,对比结果如表 1所示。

|
| 图 1 外表面粗糙度测量 Fig.1 Measurement of surface roughness |
圆柱展向中心(0.5m高度处)的周向上每隔5°布置一个测压孔,共72个,其中0°测压孔正对来流方向。风洞试验采用美国Scanivalve扫描阀公司的电子扫描阀、A/D数据采集板、PC机以及自编的信号采集及数据处理软件组成风压测量、记录及数据处理系统,扫描阀量程为±10inch水柱,测量精度为±0.15%FS。采样频率设定为300Hz,每个试验工况下同步采集圆柱模型共10 000个时程数据。
试验测压管长度为0.8m,采用数学方法对测压管路引起的脉动风压畸变[16]进行修正。圆柱模型竖直固定于风洞底面,试验模型布置如图 2所示。圆柱轴线位置处风洞边界层厚度约为150mm,即本文试验悬臂圆柱体绝大部分处在均匀流中,忽略其影响。来流风速为5~20m/s,对应雷诺数范围为Re=1.73×105~6.90×105。在层流和湍流来流下(Iu=9.5%)分别开展长径比L/D=2.0悬臂圆柱绕流试验,研究不同雷诺数下悬臂圆柱绕流特性,来流均为均匀流。

|
| 图 2 风洞模型试验 Fig.2 Wind tunnel test |
圆柱周向θ处测压孔测得的风压系数时程为Cp(θ, t)定义为:
 (1)
(1)
式中,p(θ, t)为θ处测点t时刻的表面风压,Pa; p∞为参考静压,Pa; ρ为试验环境下的空气密度,kg/m3; U∞为来流风速, m/s。
平均风压系数定义为:
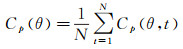 (2)
(2)
脉动风压系数定义为:
 (3)
(3)
基于同步测压技术,可通过圆柱周向压力积分,得到阻力系数时程CD(t)和升力系数时程CL(t),分别定义为:
 (4)
(4)
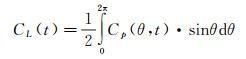 (5)
(5)
阻力系数(CD)随雷诺数的变化是圆柱绕流研究中的重点关注内容。三维圆柱绕流的气动特性在高度方向是不均匀的,与二维圆柱具有明显的差异。但王汉封等[5]对悬臂圆柱在不同高度进行测压试验,获得的总体阻力系数和1/2高度阻力系数误差不超过10%。因此本文认为可以将悬臂圆柱1/2高度处的阻力系数作为名义阻力系数来代替总体阻力系数进行研究。
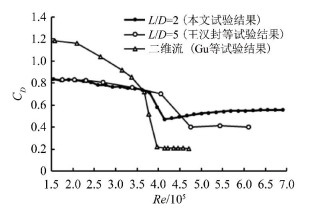
图 3将Gu等[11],王汉封等[5]在层流来流下圆柱阻力系数的实测结果与本文进行对比。对比结果表明阻力系数随雷诺数的变化存在相同的规律和趋势,即阻力系数在亚临界区间波动较为平缓,在临界区急剧下降,进入超临界区间后缓慢上升。对阻力系数进行定量分析后发现,二维圆柱和不同长径比悬臂圆柱的阻力系数存在较为明显的差异。从图 3可看出:
|
| 图 3 阻力系数 Fig.3 Drag coefficient |
(1) 亚临界雷诺数区间,悬臂圆柱的阻力系数明显小于二维圆柱,本文实测L/D=2悬臂圆柱的阻力系数约为0.83,略小于王汉封等[5]L/D=5的悬臂圆柱实测结果。
(2) 临界雷诺数下,本文L/D=2悬臂圆柱实测临界雷诺数下阻力系数为0.47,相较于亚临界区间阻力系数下降了43%;王汉封等[5]L/D=5悬臂圆柱在临界雷诺数下的阻力系数为0.40,相较于亚临界区间阻力系数减小了53%;Gu等二维圆柱阻力系数在临界雷诺数下则下降到了0.21,下降幅度约为82%,由此说明长径比越大,临界雷诺数区间阻力系数下降幅度越大,即长径比越大,阻力系数在临界区间对雷诺数越敏感,各区间参数如表 2所示。
(3) 超临界雷诺数区间,本文实测阻力系数从最低点0.47开始缓慢增长,逐渐趋近于0.56;王汉封等[5]实测阻力系数结果稳定于0.40;Gu等的二维圆柱实测阻力系数则稳定于0.21。由此可见,超临界雷诺数区间阻力系数与长径比存在较为明显的关系,长径比越小,阻力系数越大。
2.2 表面平均风压分布对圆柱表面平均风压分布进行进一步分析以确定圆柱绕流形态以及造成上述阻力系数差异的原因。由图 4可知:

|
| 图 4 圆柱表面平均风压分布 Fig.4 Mean pressure distribution on the circular cylinder |
(1) 亚临界雷诺数下,本文试验结果与王汉封等[5],Achenbach[12]的试验结果进行了对比,如图 4(a)所示。本文L/D=2悬臂圆柱背部平均风压稳定于-0.60附近,略大于王汉封等[5]L/D=5悬臂圆柱的相应值。上述两类悬臂圆柱与二维圆柱表面平均风压分布存在较为明显的差异,具体表现为:(1)本文平均风压最小值出现在θmin=65°,绕流分离发生于θs=70°附近,而二维圆柱的平均风压最小值和绕流分离点均略向圆柱背部移动;(2)悬臂圆柱绕流分离点后侧平均风压分布较二维圆柱整体偏高,主要是由于圆柱尾流区域处于负压状态,导致气流流经悬臂圆柱自由端后出现下沉,这部分气流的补充使悬臂圆柱尾流区域负压的绝对值降低,从而导致悬臂圆柱背部风压的增加。
(2) 超临界雷诺数下,本文试验结果与王汉封等[5]、顾志福等[13]试验结果进行了对比,如图 4(b)所示。对比圆柱表面平均风压分布曲线可知,超临界下不同长径比的悬臂圆柱和二维圆柱的Cp在距驻点0°~45°和135°~180°范围内基本吻合,尾流区压力系数Cpb均收敛至-0.5左右,说明超临界下悬臂圆柱自由端后的下沉气流对圆柱背部压力的影响明显减小;45°~135°之间Cp分布则存在较大的差异。总体而言,二维圆柱的最小风压系数Cpmin小于悬臂圆柱。
2.3 表面脉动风压分布图 5给出了层流来流下不同雷诺数条件下L/D=2悬臂圆柱表面脉动风压C′p分布情况。由图可知,亚临界雷诺数区间和超临界雷诺数区间悬臂圆柱表面脉动风压分布存在较为明显的差异,主要表现为脉动风压峰值C′pmax大小和出现位置的不同以及背部脉动风压C′pb大小的不同:

|
| 图 5 L/D=2悬臂圆柱表面脉动风压分布 Fig.5 Fluctuating pressure distribution on the cantilevered circular cylinder with L/D=2 |
(1) 亚临界雷诺数区间,L/D=2悬臂圆柱脉动风压峰值均出现在距驻点约70°位置,脉动风压峰值在0.10~0.15区间内波动;背部脉动风压C′pb稳定在0.09附近。
(2) 超临界雷诺数区间,悬臂圆柱脉动风压峰值出现于距驻点110°~115°附近,最大值达到0.39,与亚临界雷诺数下的试验结果存在明显差异。此外随着雷诺数的增加,脉动风压峰值位置略向背部偏移,峰值大小也明显下降,如表 3所示;背部脉动风压C′pb在临界雷诺数下达到最小值0.06,此后随着雷诺数的增加而逐渐增大,最后趋近于0.14。
| Re | C′pmax | C′pmax出现位置 | C′pb | |
| 亚临界 | 2.8×105 | 0.13 | 70° | 0.10 |
| 3.5×105 | 0.12 | 70° | 0.08 | |
| 超临界 | 4.1×105 | 0.39 | 110° | 0.06 |
| 5.2×105 | 0.24 | 115° | 0.13 | |
| 6.0×105 | 0.17 | 115° | 0.14 |
由于实际工程结构位于大气边界层之中,所处的来流条件均带有一定的湍流度,尤其是在接近地面时,湍流度甚至可达到40%左右。因此有必要研究湍流条件下圆柱绕流特性。
为研究湍流度对圆柱绕流特性的影响,本文通过在风洞入口安装竖向格栅的方法获得均匀湍流场,实测湍流强度Iu=9.5%。从图 6中可以看出,湍流来流下的CD-Re曲线并未出现陡降现象,本文实测阻力系数随雷诺数的增加而缓慢减小,最后逐渐趋近于0.55。由此说明在本文实测雷诺数范围内,高湍流度下L/D=2悬臂圆柱阻力系数对雷诺数不敏感。

|
| 图 6 阻力系数 Fig.6 Drag coefficient |
Cheung等[14]二维圆柱在来流相近湍流度(Iu=9.1%, L=90mm)下的CD-Re曲线同样表明高湍流度下阻力系数在本文实测雷诺数范围内对雷诺数不敏感,阻力系数比本文试验结果略高。然而,顾志福等[15]在近似湍流度下进行的二维圆柱绕流试验测得的阻力系数在Re=6.5×105下仅为0.47,根据Younis[3]对圆柱绕流阻力系数和湍流度及湍流积分尺度关系的研究成果,推测来流湍流积分尺度可能是导致上述阻力系数差异的原因之一。
3.2 表面平均风压分布从图 7中可以看出,高湍流度下本文L/D=2悬臂圆柱表面风压分布在Re=1.7×105时已接近超临界下的风压分布,说明来流湍流度的增加会使圆柱绕流提前进入类似超临界状态。高湍流度下,悬臂圆柱表面平均风压分布在本文实测雷诺数范围内几乎不随雷诺数的改变而改变,即对雷诺数不敏感。随着雷诺数的进一步增加,圆柱背部压力系数Cpb逐渐减小,最后趋近于-0.60。

|
| 图 7 圆柱表面平均风压分布 Fig.7 Mean pressure distribution on the circular cylinder |
与顾志福等[19]在近似雷诺数(Re=6.5×105)和湍流度(Iu=10%)的二维圆柱绕流试验结果相比,本文L/D=2悬臂圆柱最小风压系数Cpmin为-0.22,与上述二维圆柱实测结果基本一致;背侧风压分布亦与上述结果相吻合,稳定于-0.58附近,说明高湍流度下悬臂圆柱自由端后的下沉气流对圆柱背部压力的影响相较层流流场明显减小,上述现象与本文超临界层流来流下的结果一致。
3.3 表面脉动风压分布图 8给出了湍流来流下不同雷诺数下悬臂圆柱表面脉动风压C′p分布情况。由图可知,高湍流度下悬臂圆柱表面脉动风压分布受雷诺数影响较小。从亚临界雷诺数到超临界雷诺数范围内,脉动风压峰值C′pmax在0.24~0.28区间波动,且均在距驻点110°~115°附近出现,与层流来流下超临界雷诺数下的结果一致;背部脉动风压C′pb均收敛到0.09。

|
| 图 8 L/D=2悬臂圆柱表面脉动风压分布 Fig.8 Fluctuating pressure distribution on the cantilevered circular cylinder with L/D=2 |
本文以L/D=2的悬臂圆柱为研究对象,在亚临界雷诺数至超临界雷诺数范围内(1.73×105~6.90×105)对悬臂圆柱在层流来流和湍流来流下(Iu=9.5%)进行风洞试验,实测得到上述两类来流下悬臂圆柱绕流特性,结论如下:
(1) 由于气流流经悬臂圆柱自由端后存在下沉现象,导致悬臂圆柱背部风压分布与二维圆柱存在较为明显的差异,超临界雷诺数或带有较大湍流度的来流条件下,上述影响明显减小。
(2) 层流来流下,悬臂圆柱在亚临界区间阻力系数明显小于二维圆柱;临界区间,悬臂圆柱长径比越大,阻力系数降幅越大,即对雷诺数越敏感;超临界区间,悬臂圆柱长径比越小,阻力系数越大。
(3) 层流来流下,亚临界区间L/D=2悬臂圆柱脉动风压峰值均在距驻点70°位置出现;超临界区间,脉动风压峰值位于110°~115°,较亚临界区间峰值位置大幅度后移,脉动风压分布出现明显尖峰,峰值最大值达到0.39,随雷诺数的增加而逐步减小。
(4) 湍流来流下,本文L/D=2悬臂圆柱阻力系数在实测雷诺数范围内对雷诺数不敏感,实测阻力系数随雷诺数的增加从0.61缓慢减小到0.55;脉动风压峰值随雷诺数的变化较为平缓,且均出现于距驻点110°~115°位置,峰值出现位置与层流来流超临界雷诺数下的结果一致,但脉动风压分布并未出现明显尖峰。
| [1] |
Schewe G. On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers[J]. Journal of Fluid Mechanics, 1983, 133: 265-285. DOI:10.1017/S0022112083001913 |
| [2] |
Zhou B, Wang X K, Gho W M, et al. Force and flow characteristics of a circular cylinder with uniform surface roughness at subcritical Reynolds numbers[J]. Applied Ocean Research, 2015, 49: 20-26. DOI:10.1016/j.apor.2014.06.002 |
| [3] |
Younis N, Ting D S K. The subtle effect of integral scale on the drag of a circular cylinder in turbulent cross flow[J]. Wind and Structures, 2012, 15(6): 463-480. DOI:10.12989/was.2012.15.6.463 |
| [4] |
Sumner D. Flow above the free end of a surface-mounted finite-height circular cylinder:a review[J]. Journal of Fluids and Structures, 2013, 43: 41-63. DOI:10.1016/j.jfluidstructs.2013.08.007 |
| [5] |
王汉封, 邹超, 王启文, 等. 均匀流中悬臂圆柱体气动力雷诺数效应[J]. 湖南大学学报:自然科学版, 2015, 42(5): 65-71. Wang H F, Zou C, Wang Q W, et al. Reynolds number effects on the aerodynamic forces of a cantilevered circular cylinder in uniform flow[J]. Journal of Hunan University:Natural Sciences, 2015, 42(5): 65-71. |
| [6] |
Wang H F, Zhou Y, Mi J. Effects of aspect ratio on the drag of a wall-mounted finite-length cylinder in subcritical and critical regimes[J]. Experiments in Fluids, 2012, 53(2): 423-436. DOI:10.1007/s00348-012-1299-z |
| [7] |
Sumner D, Heseltine J L, Dansereau O J P. Wake structure of a finite circular cylinder of small aspect ratio[J]. Experiments in Fluids, 2004, 37(5): 720-730. DOI:10.1007/s00348-004-0862-7 |
| [8] |
Park C W, Lee S J. Free end effects on the near wake flow structure behind a finite circular cylinder[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2000, 88(2-3): 231-246. |
| [9] |
Rostamy N, Sumner D, Bergstrom D J, et al. Local flow field of a surface-mounted finite circular cylinder[J]. Journal of Fluids and Structures, 2012, 34: 105-122. DOI:10.1016/j.jfluidstructs.2012.04.014 |
| [10] |
Sumner D, Rostamy N, Bergstrom D J, et al. Influence of aspect ratio on the flow above the free end of a surface-mounted finite cylinder[J]. International Journal of Heat and Fluid Flow, 2015, 56: 290-304. DOI:10.1016/j.ijheatfluidflow.2015.08.005 |
| [11] |
Gu Z F, Sun T F. On interference between two circular cylinders in staggered arrangement at high subcritical Reynolds numbers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 80(3): 287-309. DOI:10.1016/S0167-6105(98)00205-0 |
| [12] |
Achenbach E. Distribution of local pressure and skin friction around a circular cylinder in cross-flow up to Re=5×106[J]. Journal of Fluid Mechanics, 1968, 34(4): 625-639. |
| [13] |
顾志福, 孙天风, 贺德馨, 等. 高雷诺数时串列双圆柱脉动压力的实验研究[J]. 空气动力学学报, 1992, 10(2): 176-189. Gu Z F, Sun T F, He D X, et al. Pressure fluctuations on the surface of two circular cylinders in tandem arrangements at high Reynolds numbers[J]. Acta Aerodynamica Sinica, 1992, 10(2): 176-189. |
| [14] |
Cheung J C K, Melbourne W H. Turbulence effects on some aerodynamic parameters of a circular cylinder at supercritical numbers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1983, 14(1-3): 399-410. DOI:10.1016/0167-6105(83)90041-7 |
| [15] |
顾志福, 孙天风, 贺德馨, 等. 大湍流度高雷诺数时并列双圆柱的平均和脉动压力分布[J]. 力学学报, 1992, 24(5): 522-528. Gu Z F, Sun T F, He D X, et al. Pressure distributions on two circular cylinders of side-by-side arrangements in high-turbulence flow at high Reynolds number[J]. Chinese Journal of Theoretical and Applied Mechanics, 1992, 24(5): 522-528. |
| [16] |
马文勇, 刘庆宽, 刘小兵, 等. 风洞试验中测压管路信号畸变及修正研究[J]. 实验流体力学, 2013, 27(04): 71-77. Ma W Y, Liu Q K, Liu X B, et al. Study on correction and distortion effects caused by tubing systems of pressure measurements in wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(04): 71-77. DOI:10.3969/j.issn.1672-9897.2013.04.013 |



