以电弧风洞为代表的地面模拟试验设备能够较好地模拟飞行器进入大气层的加热过程[1-2],用于其热防护结构[3-4]性能的考察,同时也能进一步验证防护材料热载荷设计与计算的合理性并加以改进[5-7]。在地面模拟试验的众多参数中,热流无疑是最为关键的参数之一,其测量精准度直接关系到流场模拟的准确性[8]。
塞块式量热计[9]因其结构简单、测试方便,经常用于电弧加热设备等超高声速风洞试验的热流测量。塞块式量热计基于能量平衡原理,假定除了气动加热面以外,其他面为绝热壁面,但在实际应用中很难保证其他面没有任何热传递,因此,如何最大程度地减少其他面的热损失[10]成为了塞块式量热计研制的关键问题之一。
常见的用以减少热损失的隔热方式有两种:一种是用隔热材料制作隔热套;另一种是在量热基体和安装结构之间设计空气隙。美国Ames Research Center的Nawaz等[11]比较研究了空气隙、气凝胶以及铜镍合金等隔热套(环)对塞块式量热计的影响,证明了空气隙隔热性能较好;但同时也指出空气隙结构在平板、端头和球头试验中差异比较明显[12],因为在空气隙中会形成不同情形的绕流,从而不同程度地影响测试结果;另外,空气隙尺寸控制对工艺要求较高,与隔热套结构相比制作成本较高,使用也较为不便。中国空气动力研究与发展中心的杨庆涛等[13]将传统隔热套结构塞块式量热计的隔热套前段改进设计为尖楔状,以减小高温气流对隔热套的烧损和侧向传热,但所测热流偏低9%~20%,因此在其文中基于该结构设计了修正方法。中国航天空气动力技术研究院的许考等[14]也对此类隔热套结构塞块式量热计进行了改进,使量热基体与待测模型安装孔之间的前段存在一部分线接触,但对后段未作改变,仍有较大部分隔热材料与量热基体直接接触,所以测量结果比其文中给出的参考值偏低约10%~15%。上述两种改进方式都仅减少了前段少部分侧向传热,而后段大部分的量热基体会从侧面和底部向温度相对较低的隔热材料传热,产生较多热损失,测试结果都不同程度偏低。因此,本文对此类隔热套结构塞块式量热计的隔热结构进行改进,以减小这种热损失,从而达到提高塞块式量热计测量精准度的目的。
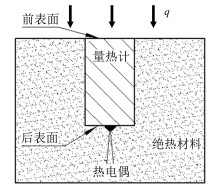
1 塞块式量热计隔热结构的改进 1.1 隔热套结构的改进图 1为塞块式量热计测热原理图。中间圆柱体为塞块式量热计的量热基体(材料一般为无氧铜),其前表面置于热流为q的高温气流中,后表面连着热电偶,用于测量量热计的温升率,其整体安装在理想的绝热材料中。
|
| 图 1 塞块式量热计测热原理 Fig.1 Principle of heat flux measurement for slug calorimeter |
基于能量平衡原理,可得到前表面热流q的计算公式[5]:
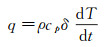 (1)
(1)
其中,dT/dt为后表面的温升率,ρ、cp和δ为量热计基体材料的密度、比热和长度。
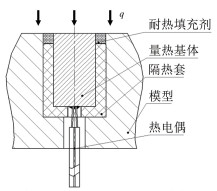
图 2为传统隔热材料塞块式量热计的隔热结构和使用方式。将焊接有热电偶的量热基体塞入隔热套,然后将其整体放入测试模型的预先开孔中,再用可直接暴露于高温气流中的耐热填充剂密封前端。如果耐热填充剂和整个隔热套都是绝热的,就可直接根据式(1)得出表面热流。但在实际测试中,量热基体与隔热套之间总会产生不可忽略的传热,传热量的大小与二者温差、接触面积以及接触面的光滑度和紧密度有关。
|
| 图 2 传统塞块式量热计结构及其使用方式 Fig.2 Traditional structure and usage method of slug calorimeter |
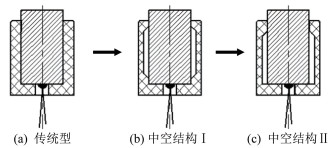
在图 2所示的结构中,量热基体与隔热套接触面积较大,会导致较大的热损失。针对这一缺陷,在不破坏隔热套外部结构的前提下,将其内部设计为中空结构,如图 3(b)、(c)所示。中空结构的轴向尺寸占比越大,量热基体与隔热套的接触面积越小,侧向传热就越少。与图 3(a)的传统结构相比,中空结构有两个优点:一是大幅度减小量热基体与隔热套的接触面积;二是减小量热基体与隔热套的接触紧密度。这两点都有利于减少侧向传热。一般风洞试验使用图 3(c)结构的隔热套即可满足要求,加工制作相对也更方便;对于某些压力过高的流场,可以使用图 3(b)结构,这种结构可以使隔热套对量热基体的紧固作用更强。
|
| 图 3 3种隔热套结构 Fig.3 Three kinds of structures of insulating sleeve |
将隔热套设计为中空结构后,侧向传热会减少很多,但并未完全消除:一是侧面仍有少部分隔热材料、耐热填充剂与量热基体发生传热;二是量热基体后表面也会和隔热材料发生传热。以式(1)计算热流,仍然会存在一定误差。因此,在采用塞块式量热计测试热流前,需要对其标定以获取修正系数,用修正系数对所测热流进行修正。
为使通过标定获取的修正系数能够合理应用于热流测量,需使隔热结构在标定、测试过程中尽量保持一致;而图 2所示的安装方式并不能保证这一点。因为图 2的安装方式一般是先将塞块式量热计安装在标定设备中进行标定,然后再将其拆装到测试模型中,而此时隔热结构已经发生改变:一是与隔热套外表面直接接触的材料和受热情况发生了改变;二是受加工工艺限制,测试模型安装孔尺寸与标定设备安装孔尺寸并不一致,从而导致接触面的紧密度、光滑度等并不一致;三是耐热填充剂需要重新制作、填充,并不是此前经过标定的填充剂。
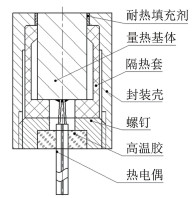
因此,为将标定时的隔热结构及其传热特性保留至测试环境中,在前述改进隔热套结构的基础上,设计增加了封装壳,对塞块式量热计进行封装处理,如图 4所示。封装壳前段设计为台阶孔,小孔直径略大于量热基体直径,两者之间的环缝灌封耐热填充剂;大孔用于隔热套的轴向、径向限位,使量热基体前表面与封装壳端面平齐以及小孔与量热基体之间的环缝均匀。封装壳材料与量热基体一致,这样可使二者轴向上的传热特性相近,有利于减少侧向传热。封装壳后段的内螺纹与螺钉配合,紧固整个结构。
|
| 图 4 改进的塞块式量热计隔热结构 Fig.4 Improved insulating structure of slug calorimeter |
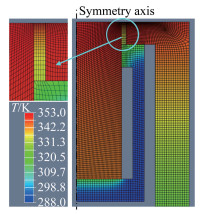
针对图 4的几何结构(量热基体直径为4mm, 长为7mm),对改进后的隔热结构进行了数值计算分析和优化。基于傅里叶定律,以有限元分析软件建立了如图 5所示的轴对称一维传热计算模型。其中,各元件无相互接触的表面部分视为绝热面,热载荷为辐射加热,无对流换热。由于温度不高,忽略各元件自身的辐射热损失。起始温度300K,加热时间均为1.5s。
|
| 图 5 塞块式量热计的数值计算模型 Fig.5 Numerical calculation model of slug calorimeter |
量热基体(铜)、封装壳(铜)前端间隙之间的耐热填充剂的主要成分为氧化铝,则间隙宽度即为氧化铝的径向宽度dAl2O3。量热基体的侧面和后表面以玻璃钢套与封装壳隔开。定义铜与氧化铝、铜与玻璃钢(FRP)、氧化铝与玻璃钢之间的接触热阻分别为RCu-Al2O3,RCu-FRP,RAl2O3-FRP。接触热阻与材料表面粗糙度和压力大小有密切关系,且不易测量。根据文献[15],预估3个接触热阻为10-3m2·K/W量级。为充分考察其影响程度,数值计算时可放大或缩小一个数量级。本文选择1×10-2、2×10-2、1×10-3、2×10-3和1×10-4m2·K/W等5个接触热阻值进行仿真对比。
第一步,考察耐热填充剂对热流测试的影响。填充剂深度(轴向)越小,则侧向传热面积越小,但综合考虑机械强度、热防护等因素,深度不宜过小,结合工程经验将其取值为1mm。在此基础上,重点考察填充剂氧化铝的径向宽度以及氧化铝与铜基体的接触热阻。
填充剂宽度不宜过小,否则易受加工精度和同轴度偏差影响,导致铜基体和封装壳直接接触;但也不宜过大,否则易被高速气流吹出间隙,影响模型表面气流加热效果。本文重点考察0.15、0.20和0.25mm等3个宽度。
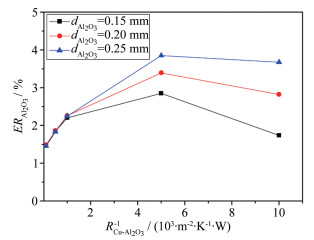
将氧化铝与玻璃钢、铜与玻璃钢之间的接触近似为绝热接触,即将其接触热阻设为较大值,令RAl2O3-FRP=RCu-FRP=1×10-2m2·K/W。当输入热流为1MW/m2时,数值计算结果如图 6所示。图中,横轴为铜与氧化铝的接触热阻倒数,值越大,则接触热阻越小;纵轴为计算热流偏差ERAl2O3,表示后表面计算得到的热流值与前表面输入热流值的偏差百分比。
|
| 图 6 RCu-Al2O3对热流输出的影响 Fig.6 Effects of RCu-Al2O3on heat flux |
从图 6可知:在同一接触热阻条件下,随着氧化铝填充剂变宽,计算热流偏差略微变大;在填充剂为同一宽度时,计算热流偏差随接触热阻变化而出现一定波动,但波动较小。总的来看,当接触热阻在1×10-3m2·K/W附近波动时,填充剂宽度和接触热阻对测量结果影响较小。基于以上结果,本文将氧化铝宽度设为0.20mm。
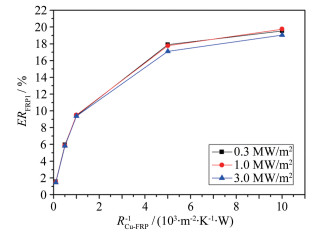
第二步,在确定了耐热填充剂宽度后,对两种隔热套结构对热流输出的影响进行对比研究。图 7是采用传统隔热套结构(图 3(a))的计算结果(模型仍为轴对称计算模型),图 8是改进隔热套(图 3(c))的计算结果。图 7、8的横轴均为铜与玻璃钢的接触热阻的倒数,纵轴均为后表面计算热流值与前表面输入热流值的偏差百分比。根据模型结构和图 6可知,氧化铝与玻璃钢、铜与氧化铝之间的接触热阻影响较小,均设为中间值1×10-3m2·K/W。
|
| 图 7 传统隔热结构RCu-FRP对热流输出的影响 Fig.7 Effects of RCu-FRP on heat flux in the traditional insulating structure |
|
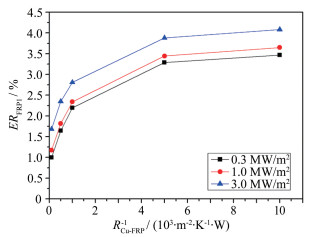
| 图 8 改进隔热结构RCu-FRP对热流输出的影响 Fig.8 Effects of RCu-FRP on heat flux in the improved insulating structure |
从图 7可知:在同一接触热阻条件下,不同输入热流值所引起的偏差百分比相差不大(图 8也是如此);同一输入热流条件下,计算热流偏差会随着热阻减小而呈明显增大趋势(从2%增大到20%)。在RCu-FRP=1×10-3m2·K/W时,偏差百分比约9%。由此可见,在传统隔热结构中,RCu-FRP的变化对计算热流偏差有较大影响,原因就是铜基体和隔热套接触面积较大,装配时不同的光滑度和紧密度能带来较大的侧向传热变化。而在图 8中,同一输入热流条件下,随着接触热阻减小,计算热流偏差变化较小,在RCu-FRP=1×10-3m2·K/W时,偏差百分比仅有约2.5%。由此可见,改进隔热结构能够大幅度减小热损失,有利于避免因装配等因素造成的热损失波动,减小不同塞块式量热计测试性能的个体差异。
(1) 数值计算结果表明,隔热套前端内侧与铜基体直接接触面积越小(轴向长度越短),计算热流偏差百分比就越小。但隔热套前端还有夹持固定铜基体、保持同轴度的作用,太短则夹持力度减小,综合权衡取较优长度1mm。
(2) 图 5是图 4的简化模型,并未体现一些较小的影响因素:一是未体现隔热套底面中心的一个穿线孔(在实际应用时,该孔会用少许高温胶进行填充,以加固热电偶焊点)。在图 5中,以隔热套的玻璃钢代替了高温胶(两者热导率都较低)。二是未考虑螺钉与隔热套、螺钉与封装壳、热电偶和铜基体之间的相互换热以及辐射换热,因为同铜基体与隔热套之间的换热相比,这些换热均是小量。
3 基于热流标定的性能评估 3.1 建立评价准则基于热流标定原理[16],给出塞块式量热计测试性能的评价指标,即单个塞块式量热计的准度和多个塞块式量热计的精度。中国空气动力研究与发展中心超高速空气动力研究所的弧光灯热流标定系统[17]由氙灯、椭球镜和积分器等部件构成,能够为热流标定提供稳定、均匀、可控的辐射光源[18]。标定时与经过溯源校准的商用戈登计比对,以获取被标传感器的修正系数。
修正系数获取方式如下:在一定热流范围内,选取不少于5个不同的热流状态,在每个热流状态下分别得到标准戈登计的测量热流(纵轴)和塞块式量热计的测量热流(横轴),然后对其进行线性拟合(线性拟合后的残差平方和不小于0.999),其斜率即为修正系数η。由于总有侧向传热存在,修正系数η的值总是大于1。修正系数越接近1,塞块式量热计测量偏差越小,其准度越高。在实际应用时,较为真实的输入热流qin应等于计算热流qc乘以修正系数η, 即:
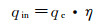 (2)
(2)
在考察整个模型表面热流分布的工程实际应用中,很多大模型需要上百个塞块式量热计。若塞块式量热计个体差异较大(表现为η差别大),则每个塞块式量热计都需要标定,工作量很大;而且使用时需“对号入座”,测试安装和后期数据处理较为不便。因此,有必要减小这种个体差异,提高多个塞块式量热计的测量精度,以达到可以不加区分地使用同一个修正系数的目的,从而极大地方便标定试验和热流测量,提高效率,节省成本。
假设对某批次n个塞块式量热计进行抽样标定,可定义该批次塞块式量热计修正系数η为:
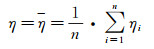 (3)
(3)
其中,ηi为第i个(i=1, 2,…, n)塞块式量热计的修正系数。基于极差概念,定义该批次塞块式量热计的测量精度ξ(≥0)为:
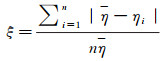 (4)
(4)
ξ越接近0,表明该批次塞块式量热计精度越高。
3.2 标定试验与结果讨论加工制作了传统隔热结构和改进结构的塞块式量热计各10支,量热基体直径为4mm, 长为7mm,如图 9所示。图 9(a)为传统隔热结构,内部配备的是传统隔热套;图 9(b)是改进隔热结构,配备的是改进后的中空结构隔热套和新设计的封装壳。

|
| 图 9 两种塞块式量热计实物 Fig.9 Two kinds of slug calorimeters |
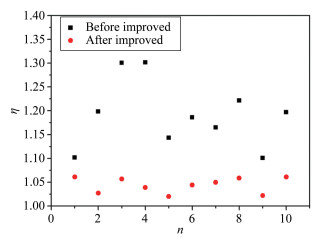
每个塞块式量热计均标定了5个热流点,由标准戈登计测得的参考热流值分别为0.35、0.65、1.00、1.50和2.00MW/m2。20个塞块式量热计的修正系数η的分布如图 10所示,横轴为传感器编号,纵轴为修正系数η。由图 10可知,传统塞块式量热计的修正系数(黑色方块)普遍较大(η=1.170),测量值比参考热流值平均偏低约14.5%,准度较低,且分布较散(ξ=6.3%),表现为个体差异大。其主要原因是:(1)量热基体与隔热套接触面积较大,量热基体向隔热套传递了较多热量,因此测量结果偏低,修正系数较大;(2)量热基体与隔热套之间属于紧密过盈配合,加工精度很难控制,接触面越光滑、装配越紧密,传热量及其波动就越大,导致多个量热计个体差异大,测量精度较低。反观改进后的量热计,无论是单个量热计的测量准度(η=1.044),还是多个量热计的测量精度(ξ=1.3%)都优于前者,其原因正是减小了量热基体与隔热套的接触面积,使装配紧密度和接触面光滑度的影响变小,侧向传热减小。
|
| 图 10 塞块式量热计修正系数分布 Fig.10 Distribution of corrected coefficient of slug calorimeters |
为进一步考察改进塞块式量热计的实用性,在某电弧风洞中开展了考核试验。试验使用了两个半径为35mm的平头模型,如图 11所示。两个平头模型外形尺寸完全一致,边缘圆角半径为5mm。图 11(a)平头模型为不锈钢材料,安装塞块式量热计;图 11(b)为无氧铜材料,内部设计为水冷结构,安装水冷戈登计。图中的1、2、3号为塞块式量热计,量热基体直径为4mm,长为7mm,经标定获得其共同修正系数为1.036;4号为水冷戈登计[19],热流感应面直径为2mm,标定后的灵敏度系数为1.1955MW·m-2/mV。

|
| 图 11 两个试验模型 Fig.11 Two kinds of test models |
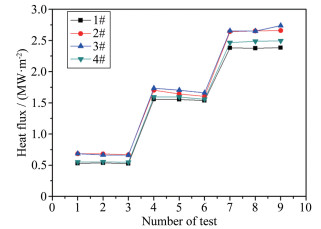
共考核3个试验状态,每个试验状态重复3次,共计9次试验,试验结果如图 12所示,横轴为试验次数,纵轴为4支热流传感器测得的热流值。从3个角度分析塞块式量热计在风洞试验中的测试性能:
|
| 图 12 风洞试验考核结果 Fig.12 Results of wind tunnel assessment |
(1) 在每个试验状态下,3个塞块式量热计的3次重复测量值都比较接近,其重复性精度值依次为0.51%、1.62%和2.42%,说明单个塞块式量热计重复性精度较高。另外,在同一状态下,2、3号测量值明显高于1号,其趋势较好地反应了平头模型热流分布规律[20](从圆心往圆周方向,半径越大热流越高)。
(2) 2、3号可视为热流对称位置测点(与圆心距离均为12mm,流场绝对均匀的理想状况下两者的热流测量值应该相同),在3个不同状态下的测量偏差分别为0.34%、2.43%和1.52%,说明不同塞块式量热计在风洞试验中个体差异较小、性能稳定。
(3) 1号塞块式量热计和4号戈登计所测热流均为平头模型中心点热流。塞块式量热计感应面直径为4mm,戈登计为2mm。仅从感应面尺寸和平头模型热流分布规律看,塞块式量热计测量值应略高于戈登计;但在3个状态下,塞块式量热计比戈登计测试结果分别偏低3.6%、2.8%和3.7%,导致这一结果的原因尚不明确,可能与两种传感器的测热原理以及传感器表面催化氧化程度有一定关系;但两者偏差的绝对量并不大(小于4.0%),能够较好地说明塞块式量热计在风洞热流测量中的准确性和可信性。
5 结论综合以上传热分析、数值计算、热流标定以及风洞考核试验结果,得到以下结论:
(1) 相比传统隔热套,改进后的中空结构隔热套能够较大程度降低侧向传热及其不稳定性。
(2) 新设计的封装壳结构能够将热流标定时的塞块式量热计内部隔热结构完整保留到测试环境中,且方便尺寸控制和加工制作。
(3) 改进后的塞块式量热计重复性精度高、个体差异小、测试性能稳定、热流测量数据可靠。
| [1] |
张松贺, 杨远剑, 王茂刚, 等. 电弧风洞热/透波联合试验技术研究及应用[J]. 空气动力学学报, 2017, 35(1): 141-145. Zhang S H, Yang Y J, Wang M G, et al. Studies and applications of thermal/wave-transmission test technique in arc-heated wind tunnel[J]. Acta Aerodynamics Sinica, 2017, 35(1): 141-145. DOI:10.7638/kqdlxxb-2015.0146 |
| [2] |
侯玉柱, 郑京良, 董威. 高超声速飞行器瞬态热试验[J]. 航空动力学报, 2010, 25(2): 343-347. Hou Y Z, Zheng J L, Dong W. Transient test of aerodynamic heating for hypersonic vehicle[J]. Journal of Aerospace Power, 2010, 25(2): 343-347. |
| [3] |
韩海涛, 陈智, 胡龙飞, 等. 基于高温热管的超燃燃烧室热防护结构[J]. 航空动力学报, 2017, 32(5): 1043-1049. Han H T, Chen Z, Hu L F, et al. High temperature heat pipe enhanced thermal protection structure for scramjet combustion chamber[J]. Journal of Aerospace Power, 2017, 32(5): 1043-1049. |
| [4] |
刘强, 崔赢午, 陈志会, 等. 高气动加热环境下运载器局部防热设计与试验研究[J]. 强度与环境, 2016, 43(1): 54-59. Liu Q, Cui Y W, Chen Z H, et al. The study on topical TPS design for hypersonic aerocraft[J]. Structure & Environment Engineering, 2016, 43(1): 54-59. DOI:10.3969/j.issn.1006-3919.2016.01.010 |
| [5] |
吴大方, 周岸峰, 郑力铭, 等. 瞬态热冲击环境下金属蜂窝板结构的热防护特性[J]. 航空动力学报, 2014, 29(6): 1261-1271. Wu D F, Zhou A F, Zheng L M, et al. Thermal protection performances of metallic honeycomb panel structure at transient at transient thermal shock environment[J]. Journal of Aerospace Power, 2014, 29(6): 1261-1271. |
| [6] |
张志豪, 孙得川. 飞行器气动加热烧蚀工程计算[J]. 兵工学报, 2015, 36(10): 1949-1954. Zhang Z H, Sun D C. Calculation of aerodynamic heating and ablation of multi-layer thermal protection material[J]. Acta Armamentarii, 2015, 36(10): 1949-1954. DOI:10.3969/j.issn.1000-1093.2015.10.017 |
| [7] |
蒋友娣, 董葳, 陈勇. 高超声速钝头体变熵流表面热流计算[J]. 航空动力学报, 2008, 23(9): 1591-1594. Jiang Y D, Dong W, Chen Y. Surface heat flux calculation of variable entropy flow for hypersonic blunt bodies[J]. Journal of Aerospace Power, 2008, 23(9): 1591-1594. |
| [8] |
杨庆涛, 王辉, 朱新新, 等. 无水冷条件下温度与热流复合传感器设计与试验[J]. 兵工学报, 2016, 37(2): 193-202. Yang Q T, Wang H, Zhu X X, et al. Design and test of a hybrid sensor for temperature and heat flux measurement without water-cooling[J]. Acta Armamentarii, 2016, 37(2): 193-202. DOI:10.3969/j.issn.1000-1093.2016.02.001 |
| [9] |
刘初平. 气动热与热防护试验热流测量[M]. 北京: 国防工业出版社, 2010. Liu C P. Heat flux measurement in aerothermodynamics and thermal protection test[M]. Beijing: National Defense Industry Press, 2010. |
| [10] |
Hightower T M, Olivares R A, Philippidis D. Thermal capa-citance (slug) calorimeter theory including heat losses and other decaying processes[R]. NASA/TM-2008-215364.
|
| [11] |
Nawaz A, Santos J A. Assessing calorimeter evaluation methods in convective and radiative heat flux environment[R]. AIAA-2010-4905, 2010.
|
| [12] |
Nawaz A, Gorbunov S, Terrazas-Salinas I, et al. Investigation of slug calorimeter gap influence for plasma stream characterization[R]. AIAA-2012-3186, 2012.
|
| [13] |
杨庆涛, 白菡尘, 张涛, 等. 隔热结构对塞块式量热计热流测量的影响[J]. 实验流体力学, 2014, 28(5): 92-98. Yang Q T, Bai H C, Zhang T, et al. Effects of adiabatic structure on heat flux measurement using a slug calorimeter[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(5): 92-98. |
| [14] |
许考, 陈连忠. 导管内塞式量热计热流测量试验及数值模拟研究[J]. 实验流体力学, 2015, 29(2): 84-89. Xu K, Chen L Z. Experimental and numerical simulation studies on heat flux measurement for slug calorimeters in the conduit[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(2): 84-89. |
| [15] |
吴登倍.接触热阻试验与数值模拟[D].北京: 北京交通大学, 2011. Wu D B. Experiment and numerical simulation of thermal contact resistance[D]. Beijing: Beijing Jiaotong University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10004-1011051030.htm |
| [16] |
Murthy A V, Tsai B K, Saunders R D. Radiative calibration of heat-flux sensors at NIST:facilities and techniques[J]. Journal of Research of the National Institute of Standards and Technology, 2000, 105(2): 293-305. DOI:10.6028/jres |
| [17] |
朱新新, 王辉, 杨庆涛, 等. 弧光灯热流标定系统的光学设计[J]. 光学学报, 2016, 36(11): 234-240. Zhu X X, Wang H, Yang Q T, et al. Optical design of arc lamp heat flux calibration system[J]. Acta Optical Sinica, 2016, 36(11): 234-240. |
| [18] |
朱新新, 王辉, 刘洪波, 等. 弧光灯热流标定系统光源的仿真设计[J]. 光学学报, 2016, 36(4): 246-252. Zhu X X, Wang H, Liu H B, et al. Simulation design of the arc lamp system for heat flux sensor calibration[J]. Acta Optical Sinica, 2016, 36(4): 246-252. |
| [19] |
罗跃, 杨凯, 黄伟, 等. 用于高温高压剪切流场的Gardon计研制[J]. 科学技术与工程, 2017, 17(29): 139-143. Luo Y, Yang K, Huang W, et al. Design and fabrication of Gardon gage used in shear flow field of high temperature/pressure[J]. Science Technology and Engineering, 2017, 17(29): 139-143. DOI:10.3969/j.issn.1671-1815.2017.29.020 |
| [20] |
张志成, 潘梅林, 刘初平, 等. 高超声速气动热与热防护[M]. 北京: 国防工业出版社, 2003. Zhang Z C, Pan M L, Liu C P, et al. Hypersonic aerothermodynamics and thermal protection[M]. Beijing: National Defense Industry Press, 2003. |



