对于吸气式空空导弹动力系统固冲压发动机的设计, 动压、马赫数、迎角和侧滑角是4个非常关键的飞行来流设计参数, 它们决定了吸气式空空导弹进气道乃至整个气动布局的设计。精确实时的飞行来流参数测量能够确保固冲压发动机的最佳飞行性能。由于惯性导航系统的安装及其性能的影响, 不能反映大气的变化及风速等外界条件的干扰, 因此无法准确获得飞行来流参数。嵌入式大气数据传感(Flush Air Data Sensing, FADS)系统依靠压力传感器阵列测量飞行器表面的压力分布, 通过特定算法间接获得动压、总压、迎角、侧滑角等大气数据, 具有精度高、成本低和维护简单等特点, 因此, 采用FADS系统测量吸气式空空导弹的飞行来流参数作为控制系统输入, 对提高吸气式空空导弹的总体性能、降低研制成本具有重要意义。
相比其他飞行器, 由于受到作战环境、弹体空间、列装成本和过载要求等诸多方面的约束, 吸气式空空导弹FADS系统技术更加复杂。在国外, FADS技术已经成功运用于X-15、F/A-18、X-31、X-33、X-34、X-38、X-43A、航天飞机和"好奇号"火星探测器等多种飞行器[1-4]。国内对FADS技术也开展了大量探索性研究。南京航空航天大学陆宇平教授课题组针对算法、校准、系统误差、标定、FADS与INS组合、故障检测等方面开展了FADS理论的系列研究[5-8]。中国空气动力研究与发展中心李其畅分析了嵌入式大气数据三点解算方法的可行性[9]。西北工业大学李清东探讨了FADS快速智能故障检测和诊断技术[10]。中国航天空气动力技术研究院在FADS理论、风洞试验和飞行试验测试等方面开展了工程应用初步研究[11-17]。但是, 针对吸气式空空导弹FADS系统风洞试验标定等相关研究比较少。
FADS系统风洞试验标定研究的主要目的是测试系统的集成兼容性、实时数据采集和解算能力, 初步验证系统的设计测量精度、故障诊断与容错性能, 是FADS系统研究过程的一项重要关键技术。本文针对自主研发的吸气式空空导弹FADS系统先后开展了两次标定风洞试验。首次风洞试验验证了系统实时解算性能和部分马赫数的设计测量精度, 分析了首次标定试验存在的各种影响因素, 提出新的标定方案并完成了第二次风洞试验标定。
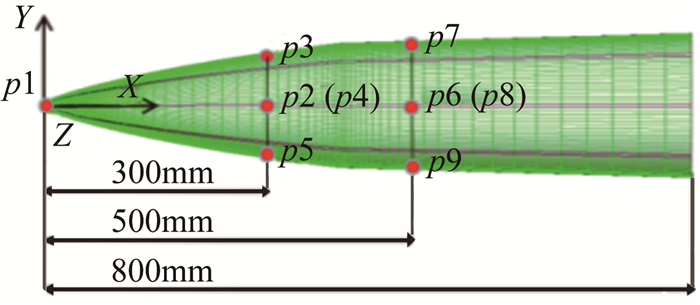
1 FADS系统介绍及标定分析针对典型的吸气式空空导弹外形(见图 1), 开发了吸气式空空导弹嵌入式大气数据传感系统CA-FADS原理样机(见图 2)。系统采用9个测压点的"十字"阵列布局(如图 3所示), 集成了压力测量模块、解算机模块和算法模型。系统测量范围:马赫数1.5~4.0, 海拔高度0~25km, 迎角和侧滑角-10°~10°。FADS系统的设计测量精度目标为:自由来流静压测量绝对误差≤500Pa(3%); 飞行马赫数测量绝对误差≤0.1;飞行迎角和侧滑角测量绝对误差≤0.5°。

|
| 图 1 欧洲"流星"远程吸气式空空导弹 Fig.1 European "Meteor" long range air-to-air missile |

|
| 图 2 FADS系统原理样机 Fig.2 Prototype of FADS system |
|
| 图 3 测压点布局 Fig.3 Layout of pressure measurement points |
压力测压模块采用高精度硅压阻式测压传感器单元, 解算机利用FPGA+DSP(Field-Programmable Gate Array:现场可编程门阵列; Digital Signal Processor:数字信号处理器)构架设计, 由FPGA采集压力数据, 送入DSP进行FADS算法实时解算获得来流参数, 再将解算结果发送回FPGA, 最后通过FPGA与飞行控制系统通信传输FADS解算结果并接收飞行控制系统的指令。算法设计采用CFD+BP神经网络技术, CFD方法可生成高精度的样本数据库, 特别是在大迎角、大分离状态下, 流场压力计算CFD方法具有非常明显的优势, 通过神经网络建立测压点压力值与来流参数的非线性映射关系而获得FADS算法模型。算法采用主动容错设计, 测压点故障诊断点数3个, 可容错的点数2个, 即在测压点出现2个故障点的情况下, FADS系统仍可以正常工作。
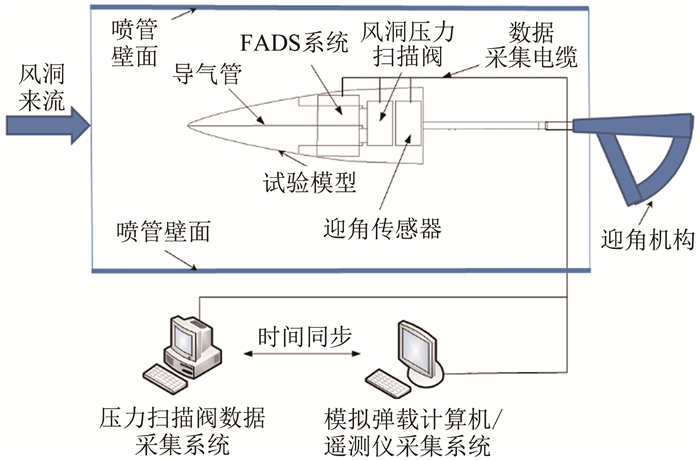
系统标定试验包括风洞试验和飞行试验。由于吸气式空空导弹飞行试验总体技术非常复杂、研制经费昂贵、靶场协调困难和试验准备周期长等原因, 开展飞行试验标定难度非常大。因此, 地面风洞试验成为FADS系统标定的主要技术手段, 标定示意图如图 4所示。
|
| 图 4 风洞标定示意图 Fig.4 Sketch of wind tunnel calibration |
FADS系统风洞试验标定是一项极其精细的特种试验, 受到流场品质、模型设计加工和安装等多方面因素的影响。其工作原理是依靠压力传感器阵列测量飞行器表面的压力分布, 通过特定算法间接获得飞行器来流大气数据。因此, 系统标定的第一项关键技术难点是获得稳定、均匀的高品质风洞流场, 保证模型上测点的压力值不受外界其他因素影响, 才能准确标定FADS系统的测量精度。如果未能排除外界其他因素干扰, 即无法准确标定FADS系统测量精度, 将导致FADS系统研制失败。
国内现有的生产型风洞的流场品质设计通常是按照国军标技术标准设计的, 主要满足飞行器测力和测压等常规试验任务要求, 风洞试验段内部分位置流场品质无法满足FADS系统标定等特种试验的要求。因此, 要完成风洞试验标定必须对风洞流场结构进行深入分析研究, 避开各种干扰, 以寻找适合FADS系统标定的流场区域。风洞试验中影响流场品质的因素主要有台阶波和洞壁干扰两个方面。台阶波由风洞喷管与试验段对接的缝隙产生的膨胀波系组成, 其影响无法消除, 只能避开; 而洞壁干扰是由试验模型头部脱体激波"打"到洞壁反射造成, 只能通过设计模型堵塞比和控制试验最大迎角来降低其影响。以上两种因素均会影响FADS系统测压点阵列布局上的压力值, 造成算法解算结果出现偏差, 严重影响FADS系统标定测量精度。系统标定的第二项关键技术难点是模型设计和加工, 此过程必须保证测压点的位置误差, 测压孔与壁面垂直度, 确保模型对接处的安装结构强度, 防止试验过程中超声速高频抖振导致模型松动造成测量误差。第三项关键技术难点是试验模型的安装精度控制。对于吸气式导弹的轴对称模型, 模型安装最容易出现周向偏差, 将对迎角和侧滑角测量误差产生明显影响。因此, 在安装模型后必须按照一定标准进行相应的检测和微调。
2 标定方案设计吸气式空空导弹FADS系统建成后, 先后进行了两次风洞试验标定。两次试验均在中国航天空气动力技术研究院FD-12风洞内进行。该风洞是一座暂冲式三声速风洞, 马赫数范围是0.30~1.20、1.50、1.75、2.00、2.25、2.50、3.00、3.50和4.00。试验段截面尺寸为1.2m×1.2m。亚跨声速试验时, 利用声速喷管改变前室总压的方法来获得不同的马赫数; 超声速试验时, 通过更换不同的喷管箱来改变马赫数。首次试验标定只有部分马赫数状态的测量精度达到设计指标, 通过分析首次标定试验中存在的各种问题, 提出新的标定方案, 此次标定试验中, 全部马赫数状态的系统测量精度均达到设计指标要求。
2.1 首次标定设计与结果系统首次试验标定是按照普通测压试验设计的, 完成了马赫数2.0、2.5、3.0、3.5和4.0的吹风试验。迎角范围-2°~ 12°, 迎角12°的试验数据仅作研究参考, 用以检验求解算法模型的外插预测能力, 不参加考核。试验详细参数见表 1。风洞试验模型安装如图 5所示。本次试验按照常规测压试验设计, 未考虑流场品质、模型设计加工和安装精度等因素的影响。风洞系统只测量总压、马赫数和迎角, 马赫数是风洞系统测量给出的平均值, 总压和迎角均与FADS同步进行实时测量, FADS系统的采样频率为100Hz, 按照采样频率, 每个迎角状态采样6000~8000个点(每个点时间间隔为0.01s)。侧滑角由已标定的支杆机构直接给出, 试验中不作测量。风洞静压是根据风洞系统测量总压和马赫数, 按照等熵流动换算获得, 见式(1)。式中, pt为总压, p∞为静压, γ=1.4为空气比热比。
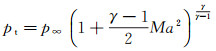 (1)
(1)

|
| 图 5 风洞试验模型 Fig.5 Wind tunnel test model |
| 序号 | 来流参数 | 参数范围 |
| 1 | Ma | 2.0, 2.5, 3.0, 3.5, 4.0 |
| 2 | 迎角α/(°) | -2, 0, 2, 4, 6, 10, 12 |
| 3 | 侧滑角β/(°) | 0, -3, -5 |
| 4 | 静压p∞/kPa | 参考风洞实际静压 |
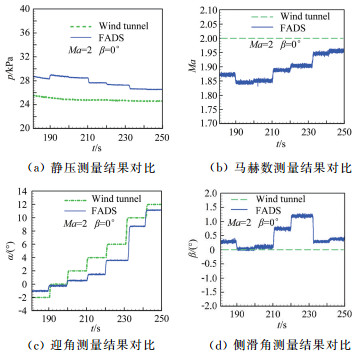
从图 6中可以看出, Ma=2.0状态的标定结果误差很大, 静压最大误差达到3000Pa, 马赫数最大误差0.15, 迎角最大误差2.5°, 侧滑角最大误差1.2°。从测量结果来看, 该状态的标定是失败的。
|
| 图 6 Ma=2, β=0°测量结果对比 Fig.6 Comparison of measurement results of β=0°, Ma=2 case |
表 2为风洞试验马赫数2.0~4.0共5个马赫数试验结果误差的统计表。Ma=2.5时, 各参数测量正常, 但静压最大误差还是达到了970Pa。随着马赫数增加, 静压的绝对误差减小, 相对误差先减小后增大, 这是由静压绝对值减小造成的。在迎角为-2°~10°, Ma=2.5~4.0时, 马赫数误差均小于0.1, 已经达到设计指标; 而迎角和侧滑角的误差均小于1°, 但是大于0.5°, 未达到设计指标。Ma=4.0, 迎角12°时马赫数误差达到最大, 为0.12。试验结果表明, 求解算法模型还具有一定的外插预测能力。从表 2可以得出, Ma=2.0、2.5时, 标定的试验结果误差很大, 未能达到设计要求, 并且Ma=2.0状态下的测量结果出现畸变。Ma=3.0、3.5和4.0时, 标定静压和马赫数误差精度基本上达到设计指标要求。由于首次风洞试验标定是按照普通测压试验的标准设计的, 未考虑风洞试验流场对FADS系统的影响, 造成标定结果误差较大甚至出现畸变。
| 实验状态 | 静压误差 /Pa |
静压相对误差 | 马赫数误差 | 迎角误差 /(°) |
侧滑角误差/(°) |
| Ma=2.0 | ≤3000 | ≤11.5% | < 0.15 | ≤2.5 | ≤1.2 |
| Ma=2.5 | ≤970 | ≤6.0% | < 0.10 | < 1.0 | < 1.0 |
| Ma=3.0 | < 400 | ≤4.4% | < 0.10 | < 1.0 | < 1.0 |
| Ma=3.5 | < 300 | ≤3.3% | < 0.10 | < 1.0 | < 1.0 |
| Ma=4.0 | < 300 | ≤6.9% | < 0.10 | < 1.0 | < 1.0 |
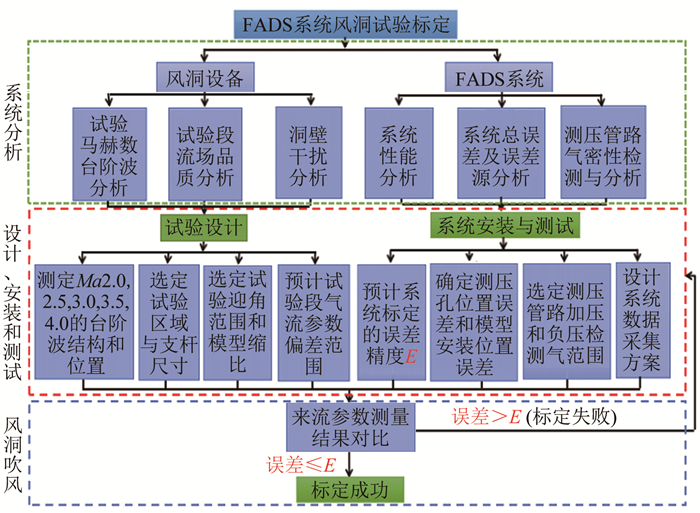
总结第一次标定试验出现的各种问题, 提出了新的标定方案。风洞试验标定设计流程如图 7所示, 包括系统分析, 设计、安装和测试以及风洞吹风三大部分。系统分析主要是对风洞设备的流场和FADS系统的性能、误差和管路气密性等进行分析, 通过分析确定试验设计、FADS系统安装与测试的相关参数, 制定试验方案。最后, 对安装FADS系统的试验模型进行吹风, 将风洞系统和FADS系统测量的来流数据进行对比, 误差小于或等于FADS系统的设计测量误差精度E, 则试验标定成功, 否则试验标定失败, 需要重新调整试验方案再进行吹风, 直到标定成功。
|
| 图 7 FADS系统风洞试验标定设计流程 Fig.7 Flowchart of design in calibration of FADS system |
利用台阶波位置、试验段喷管几何尺寸、模型尺寸、实验迎角范围和支杆位置等参数, 可以计算出标定试验的最佳流场区域; 通过确定支杆长度, 可以确保模型安装在最佳流场区域。
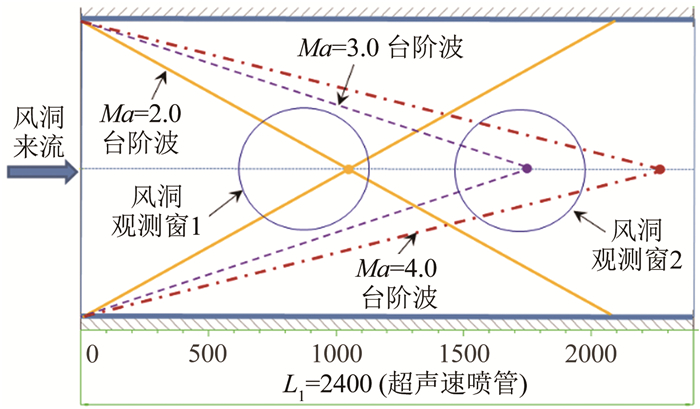
首先, 利用纹影技术测量超声速风洞台阶波结构和交点位置, 通过观察窗纹影绘制台阶波几何尺寸。图 8所示为喷管截面台阶波结构示意图, 从图中可以看出, 台阶波由喷管左侧接缝台阶产生, 在中线上形成交点, 随着马赫数增大, 交点位置由左侧向右侧移动。Ma=2.0时, 台阶波在中线相交后再回到喷管壁面上, 随着马赫数的增大, 如Ma=3.0、4.0时, 台阶波不再回到喷管壁面上。
|
| 图 8 Ma=2.0, 3.0, 4.0的台阶波结构 Fig.8 Step shock wave structure of Ma=2.0, 3.0, 4.0 cases |
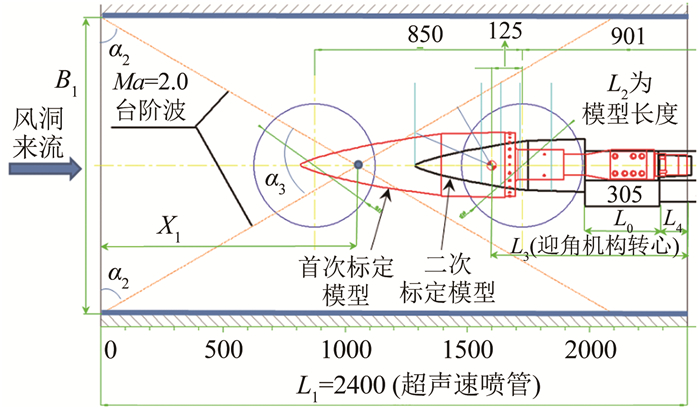
其次, 选定试验区域、支杆尺寸、模型缩比、迎角范围及测定气流偏角等。在风洞试验标定过程中, 为了确保模型能避开台阶波, 利用台阶波交点位置计算获得模型缩比值和支杆长度。在超声速风洞中进行FADS系统试验标定, 喷管长度为L1, 截面尺寸为B1×B1, 在喷管中进行嵌入式大气数据传感系统标定试验, 试验马赫数为2.0~4.0, 模型长度为L2, 等效直径为D。迎角机构转动中心距离喷管出口为L3, 迎角机构接头距离喷管出口L4。试验预估的迎角范围为AOA1~AOA2, 支杆长度为L0。各参数定义如图 9所示。
|
| 图 9 风洞标定模型位置和各参数定义 Fig.9 Position of the wind tunnel calibration model and the definition of each parameter |
利用纹影技术测量超声速喷管中马赫数2.0~4.0时的台阶波结构和上下波交点的位置, 测量交点位置尺寸X1, 以此确定台阶波的影响范围。根据X1选定超声速风洞喷管中前段(0~X1)或者后段((L1-X1)~L1)三角区域作为嵌入式大气数据传感系统标定的风洞流场区域, 以X1为高计算三角域的底角α2和顶角α3。根据试验预估迎角范围AOA1~AOA2、迎角机构转心L3、台阶波交点X1、台阶波三角区域底角α2和顶角α3, 先取模型缩比的比例值Sc=1和安装支杆的长度L0, 支杆长度为迎角机构接头与模型底部的距离尺寸(其中Ma=2.0~4.0)。确保在试验过程中, 迎角状态下所有模型均可以避开台阶波, 并且保证模型表面上的点距离台阶波最近位置不小于100mm。为了保证模型的安装位置, 将支杆长度限制在0.1L1≤L0≤0.6L1范围内。按照以上计算参数, 推导得到可以满足特定迎角和马赫数条件的支杆长度计算公式, 即可获取最佳流场区域。
当台阶波交点X1≥1200mm, 选定前段试验区域, 即利用长支杆将模型向前安装以避开台阶波, 支杆长度计算公式为(长度单位:mm, 角度单位:(°)):
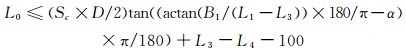 (2)
(2)
当台阶波交点X1 < 1200mm, 选定后段试验区域, 即选定短支杆将模型向后安装以避开台阶波, 支杆长度计算公式为(长度单位:mm, 角度单位:(°)):
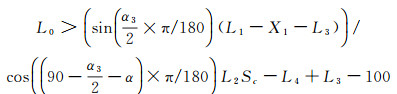 (3)
(3)
式(2)和(3)均为参照迎角机构转动中心与模型头部位置, 为确保模型头部在迎角变化的过程中避开台阶波而推导的求解支杆长度的几何关系式。如果无法获得符合条件的支杆长度L0, 则需调整迎角范围或缩比模型参数, 直到获得满足要求的支杆长度L0。
根据式(2)和(3)计算得出:Ma=2时, 单独使用一个有效长度为300mm的短支杆, Ma=2.5、3.0和3.5时, 使用同一个1300mm的长支杆, 模型缩比值Sc=0.8, 迎角范围取-12°~12°, 如图 10和11所示。由于Ma=3.5与4.0状态的流场特性接近, 为降低试验成本, 二次标定取消了Ma=4.0状态的试验吹风。

|
| 图 10 Ma=2模型位置 Fig.10 Model location of Ma=2 case |

|
| 图 11 Ma=2.5~3.5模型位置 Fig.11 Model location of Ma=2.5~3.5 case |
此外, 可以根据风洞系统流场测定获得气流偏角, 修正风洞吹风标称来流参数。
2.2.2 系统安装与测试首先是加工试验模型, 即FADS系统安装载体。模型的加工精度对试验影响非常明显, 系统设计时已作相关分析[15], 不再赘述。模型加工表面各尺寸精度通常在±0.02mm以内, 一般的数控机床加工均能满足要求。模型上测压孔位置要求:顶点的位置偏差相对于安装面可以取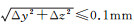
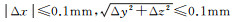
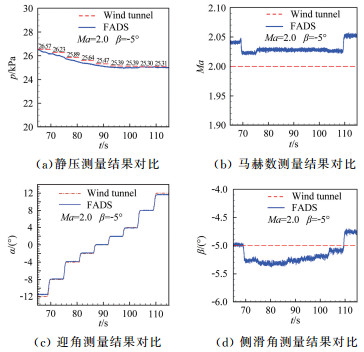
Ma=2、β=-5°状态下, FADS系统测量结果与风洞试验测量结果的对比如图 12所示。从图中可以得出静压的测量误差≤400Pa, 马赫数误差≤0.05, 迎角和侧滑角误差均≤0.5°, 与首次标定试验相比测量误差明显改善。
|
| 图 12 Ma=2, β=-5°测量结果对比(短支杆) Fig.12 Comparison of measurement results of Ma=2, β=-5°(short pole) |
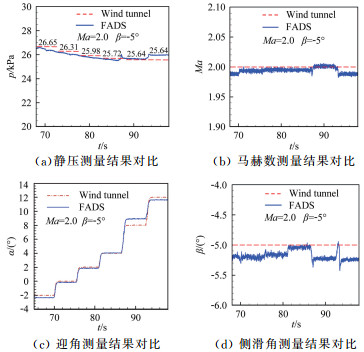
从图 13可以看出, 长短支杆对静压、马赫数和侧滑角的测量误差影响较小。对于迎角测量误差, 在α=8°状态时, 测量误差达到1°, 出现明显偏差, 此时台阶波已经"打"到模型壁面测压孔上, 造成解算出现较大偏差。
|
| 图 13 Ma=2, β=-5°测量结果对比(长支杆) Fig.13 Comparison of measurement results of Ma=2, β=-5°(long pole) |
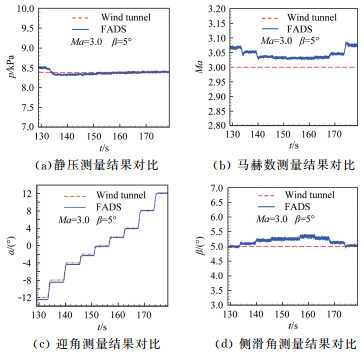
图 14所示为Ma=3、β=5°状态FADS系统测量结果与风洞试验测量结果的对比, 从图中可以得出静压的测量误差≤200Pa, 马赫数误差≤0.05(不考核迎角±12°状态), 迎角和侧滑角均≤0.5°。
|
| 图 14 Ma=3, β=5°测量结果对比 Fig.14 Comparison of measurement results of Ma=3, β=5° |
两次标定的测量误差结果对比见表 3。从表中可以看出, 第二次标定FADS系统的测量误差明显降低。静压误差≤490Pa, 马赫数误差≤0.1, 迎角和侧滑角误差≤0.5°。两次试验结果对比表明, 台阶波对标定产生严重干扰, 试验过程中必须避开台阶波影响。
| 试验马赫数 | 模型 | 静压误差 /Pa |
静压相对误差 | 马赫数误差 | 迎角误差 /(°) |
侧滑角误差/(°) |
| 2.0 | 首次 | ≤3000 | ≤11.5% | ≤0.15 | ≤2.5 | ≤1.2 |
| 二次 | ≤490 | ≤1.9% | ≤0.05 | ≤0.5 | ≤0.5 | |
| 2.5 | 首次 | ≤970 | ≤6.0% | ≤0.10 | ≤1.0 | ≤1.0 |
| 二次 | ≤400 | ≤2.4% | ≤0.05 | ≤0.5 | ≤0.5 | |
| 3.0 | 首次 | ≤400 | ≤4.4% | ≤0.10 | ≤1.0 | < 1.0 |
| 二次 | ≤200 | ≤2.4% | ≤0.05 | ≤0.5 | ≤0.5 | |
| 3.5 | 首次 | ≤300 | ≤3.3% | ≤0.10 | ≤1.0 | ≤1.0 |
| 二次 | ≤200 | ≤3.0% | ≤0.10 | ≤0.5 | ≤0.5 | |
| 4.0 | 首次 | ≤300 | ≤6.9% | ≤0.10 | ≤1.0 | ≤1.0 |
(1) 基于FD-12风洞试验平台, 提出了一种FADS系统风洞试验标定方法, 并完成了吸气式空空导弹FADS系统的标定研究。风洞标定测量误差与FADS系统设计测量误差基本吻合, 验证了系统的算法、硬件和集成等设计方法。
(2) 首次标定结果中, Ma=2.0、2.5标定的试验结果测量误差很大, 未能达到设计要求, Ma=2.0状态下模型所在流场位置受到台阶波严重干扰, 造成测量结果出现畸变。
(3) 改进试验方案后, 本次标定试验结果表明, 在Ma=2.0~3.5范围内, FADS系统测量误差为:静压最大误差约490Pa(Ma=2.0), 马赫数误差≤0.1, 迎角和侧滑角误差≤0.5°。FADS系统测量误差基本达到预期目标, 验证了FADS算法设计;
(4) 通过调整模型位置可以有效避开台阶波, 在Ma=2、α=8°迎角长支杆时, 台阶波"打"到模型上, 迎角误差约为0.9°~1°; 短支杆时, 台阶波未"打"到模型上, 迎角误差 < 0.5°。在本次标定的长支杆位置, 台阶波对其他参数测量影响较小;
(5) 本方法可以为其他风洞试验平台的FADS系统标定研究提供技术参考。
下一步, 还需要开展飞行试验搭载和测试验证研究, 相关研究正在筹备中。
| [1] |
Karlgaard C, Kutty P, Schoenenberger M, et al. Mars entry atmospheric data system trajectory reconstruction algorithms and flight results[R]. AIAA-2013-28, 2013.
|
| [2] |
Baumann E, Pahle J W, Davis M C, et al. X-43A flush airdata sensing system flight-test results[R]. AIAA-2008-657, 2008.
|
| [3] |
Ellsworth J C, Whitmore S A. Simulation of a flush air-data system for transatmospheric vehicles[J]. Journal of spacecraft and rocket, 2008, 45(4): 716-73. DOI:10.2514/1.33541 |
| [4] |
柏楠, 时兆峰, 苑景春, 等. 嵌入式大气数据传感技术研究[J]. 飞航导弹, 2010, 8: 79-85. |
| [5] |
方习高, 陆宇平. 嵌入式大气数据传感系统的求解算法研究[J]. 计算机测量与控制, 2008, 16(3): 398-400. Fang X G, Lu Y P. Research on algorithms of flush airdata sensing system[J]. Computer Measurement & Control, 2008, 16(3): 398-400. |
| [6] |
杨雨, 陆宇平, 吴在桂. 嵌入式大气数据传感系统中的组合滤波技术[J]. 传感器与微系统, 2009, 28(5): 117-120. Yang Y, Lu Y P, Wu Z G. Combination filter technology in flush air data sensing system[J]. Transducer and Microsystem Technologies, 2009, 28(5): 117-120. DOI:10.3969/j.issn.1000-9787.2009.05.038 |
| [7] |
沈国清, 陆宇平, 徐志晖. 嵌入式大气数据传感系统误差分析[J]. 传感器与微系统, 2012, 31(6): 62-65. Shen G Q, Lu Y P, Xu Z H. Error analysis of flush air data sensing system[J]. Transducer and Microsystem Technologies, 2012, 31(6): 62-65. DOI:10.3969/j.issn.1000-9787.2012.06.019 |
| [8] |
赵磊, 陆宇平. 基于RBF神经网络的FADS系统及其算法研究[J]. 飞机设计, 2012(1): 43-47. Zhao L, Lu Y P. Research of algorithms of flush airdate sensing system based on RBF neural network[J]. Aircraft Design, 2012(1): 43-47. |
| [9] |
李其畅, 刘劲帆, 刘昕, 等. 嵌入式大气数据三点解算方法初步研究[J]. 空气动力学学报, 2014, 32(3): 360-363. Li Q C, Liu J F, Liu X, et al. The primary study of 3-point calculation method for the flush air data system[J]. Acta Aero-dynamica Sinica, 2014, 32(3): 360-363. |
| [10] |
李清东, 陈璐璐, 张孝功, 等. FADS快速智能故障检测和诊断技术[J]. 系统工程与电子技术, 2009, 31(10): 2544-2546. Li Q D, Chen L L, Zhang X G, et al. Flush airdata sensing system fast intelligent fault detection and diagnosis technology[J]. Systems Engineering and Electronics, 2009, 31(10): 2544-2546. DOI:10.3321/j.issn:1001-506X.2009.10.058 |
| [11] |
王鹏, 金鑫, 张卫民. FADS系统在各型号飞行器中的应用[J]. 飞航导弹, 2013, 2: 75-79. |
| [12] |
王鹏, 李秋红, 胡远思, 等. 尖楔前体飞行器FADS-α的求解精度研究[J]. 中国科学:物理学力学天文学, 2015, 45(12): 124709. Wang P, Li Q H, Hu Y S, et al. Research on solving accuracy for FADS-α applied to the vehicle with sharp wedged fore-bodies[J]. Sci Sin:Phys Mech Astron, 2015, 45(12): 124709. |
| [13] |
王鹏, 金鑫, 张卫民. FADS系统在尖楔前体高超声速飞行器中的应用[J]. 中国科学:物理学力学天文学, 2013, 43(9): 1105-1110. Wang P, Jin X, Zhang W M. Application of FADS system in hypersonic flight vehicles with sharp wedged fore-bodies[J]. Sci Sin:Phys Mech Astron, 2013, 43(9): 1105-1110. |
| [14] |
秦永明, 张春, 董金刚. 嵌入式大气数据传感系统风洞标定试验研究[J]. 空气动力学学报, 2015, 33(4): 488-492. Qin Y M, Zhang C, Dong J G. Experimental Study on flush air data sensing system calibration in wind tunnel[J]. Acta Aerodynamica Sinica, 2015, 33(4): 488-492. |
| [15] |
陈广强, 刘吴月, 豆修鑫, 等. 吸气式空空导弹FADS系统设计[J]. 中国科学:技术科学, 2016, 46(11): 1193-1206. Chen G Q, Liu W Y, Dou X X, et al. Flush air data sensing system design for air breathing air-to-air missile[J]. Sci Sin Tech, 2016, 46(11): 1193-1206. |
| [16] |
陈广强, 王贵东, 陈冰雁, 等. 低成本飞行试验平台FADS技术研究[J]. 宇航学报, 2015, 36(10): 1195-1202. Chen G Q, Wang G D, Chen B Y, et al. Study of flush air data system technology for low cost flight test platform[J]. Journal of Astronautics, 2015, 36(10): 1195-1202. DOI:10.3873/j.issn.1000-1328.2015.10.014 |
| [17] |
陈广强, 王贵东, 陈冰雁, 等. 高超声速飞行器FADS算法研究[J]. 飞机设计, 2015, 35(6): 1-7. Chen G Q, Wang G D, Chen B Y, et al. Study of flush air data system algorithms for hypersonic vehicle[J]. Aircraft Design, 2015, 35(6): 1-7. |



