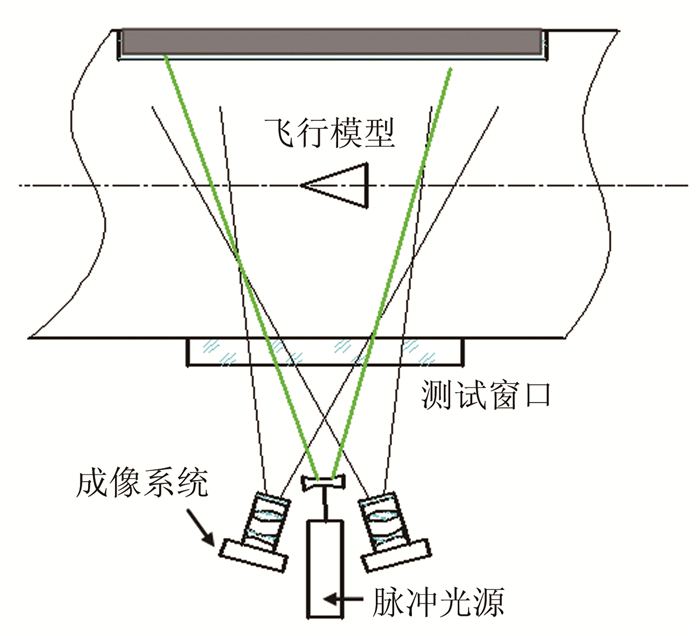
弹道靶具有试验模型自由飞行、流场无支架干扰、靶室环境真实可控等优点, 是获得模型超高声速飞行时的气动力参数尤其是动态稳定性参数的理想设备之一。2013年之前, 中国空气动力研究与发展中心(简称气动中心)的200m自由飞弹道靶上配置有口径300~500mm正交阴影仪, 其具有技术成熟、可显著消除测试区域的强烈自发光、定位精度高等优点, 是获得模型位姿变化参数的唯一设备。开展弹道靶试验时, 缩比模型在靶室内自由飞行, 沿靶室分布的正交阴影测量系统获得模型的飞行姿态图像及成像时序, 利用图像处理等方法获得模型的飞行位姿参数, 最终通过辨识获得模型气动力参数。NASA阿姆斯研究中心的弹道靶至今仍采用阴影成像系统获得飞行模型的位姿[1]。近年来, 国内重点针对阴影成像系统的数据处理方法[2]和成像接收端优化[3]、测试精度提高[4]等方向开展了相关的研究工作。
2013年, 气动中心的200m自由飞弹道靶上新建了120和203mm口径二级轻气炮[5], 模型位姿测量系统的视场达到Φ1m以上。如果仍采用正交阴影测量系统, 其光学元件的尺寸将达到Φ1m以上。由于国内Φ1m量级光学元件加工能力不足, 研制Φ1m正交阴影测量系统风险巨大, 且成本极高。
随着计算机视觉及图像处理技术的发展, 双目视觉定位技术得到极大发展, 在粒子测速[6]、物体轮廓测量[7]、机场飞机和车辆位置实时测量[8]、低速风洞自由飞模型单站位姿测量[9]等领域得到广泛应用。通过开展改进标定算法[10]、复杂外形的三维测量[11]、模型姿态的轮廓测量方法研究[12]等工作, 使得双目视觉定位技术的测试视场更大、测试精度更高、技术更成熟[13]。
前光成像技术是在模型飞行过程中通过外界光源进行瞬间照明, 实现模型姿态的瞬间"冻结", 图像的有效曝光时间为外界光源照射的时间。
本文将技术成熟的双目视觉定位技术和前光照相技术结合, 在200m自由飞弹道靶上建立超高声速飞行模型视觉位姿测量系统。该系统采用多个测量站沿飞行方向依次对模型进行成像, 实现200m长度内、视场Φ1m的飞行模型位姿测量。由于模型飞行速度高、测试区域自发光强、测试范围大, 如何实现模型清晰成像以及测量站全局关联等是视觉位姿测量系统获取有效测量数据的关键, 而模型表面标记点的制作、建模是获取高精度测量数据的保证。
本文介绍了200m自由飞弹道靶模型视觉位姿测量系统的组成及测量原理、关键技术的解决以及获得的锥模型弹道靶自由飞试验的气动力参数测试结果。
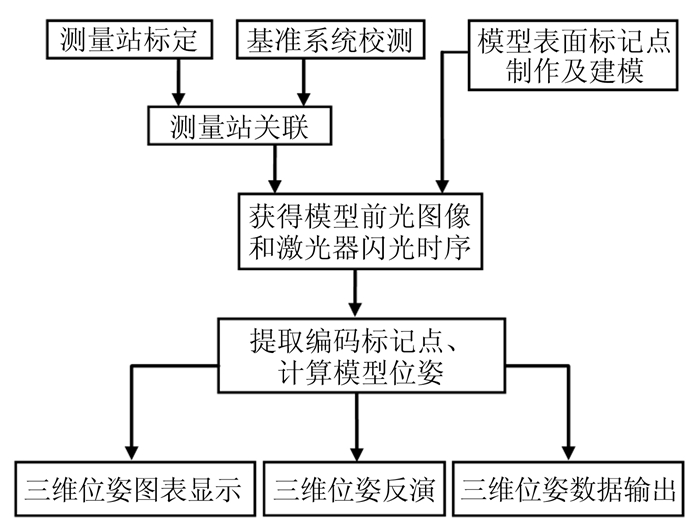
1 200m自由飞弹道靶视觉姿态测量系统组成及测量原理 1.1 系统组成及工作流程200m自由飞弹道靶视觉位姿测量系统主要由以下系统组成:双目前光照相定位系统[14]、基准及关联系统、模型表面标记点制作及建模系统、时间关联系统以及数据处理系统等。系统的工作流程如图 1所示。
|
| 图 1 视觉姿态测量系统工作流程图 Fig.1 The workflow of the vision measurement system |
(a) 双目前光照相定位测量站标定。单站双目前光照相定位测量站(简称双目测量站)的现场布置如图 2所示, 主要由1台200mJ脉冲绿激光器及扩束系统、2台4872pixel×3248pixel相机及镜头组成。通过标定获得2个相机的空间位置以及镜头焦距。
(b) 基准系统校测及双目测量站全局关联。校测靶室内由多个基准点组成基准坐标系, 将每个双目测量站的坐标系关联到基准坐标系。
(c) 模型表面标记点制作与建模。在模型表面制作圆形的标记点, 并对其进行编码; 采用质心测量系统获得其质心位置, 并利用三维扫描系统[15]获得模型表面标记点之间的空间位置关系, 通过数据处理将标记点转换到模型质心坐标系下。
(d) 获得模型超高声速自由飞行前光图像和测量站激光器出光时序。模型在弹道靶靶室内自由飞行, 各双目测量站获得模型的双目前光图像, 同时采集测量各测量站激光器的出光时序。
(e) 图像处理、模型位姿解算。根据各双目测量站获得的双目前光图像, 通过图像处理, 提取双目前光图像中模型表面可同时识别的至少3个编码标记点, 再根据标记点的坐标、双目测量站标定结果和全局关联数据解算出模型的位姿参数。
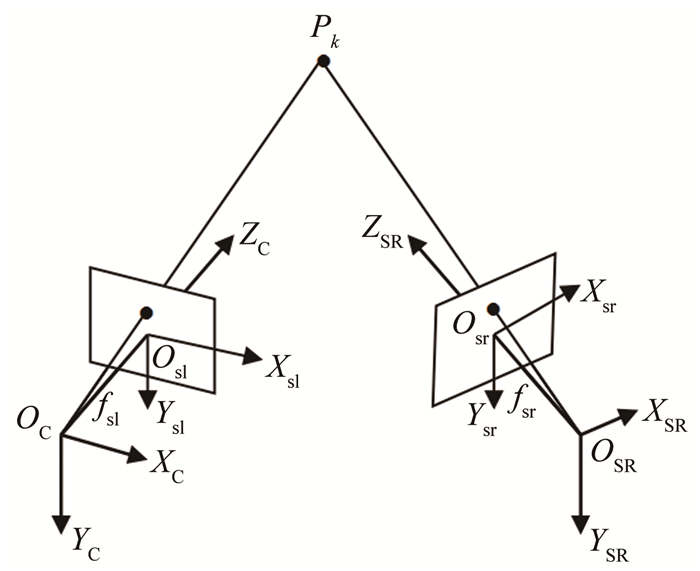
1.2 双目视觉测量系统测量原理双目视觉测量技术[13]基于编码标记点实现坐标关联和飞行位姿解算, 从二维图像获取物体表面的三维信息。双目视觉测量原理如图 3所示。将双目测量系统的世界坐标系OC-XCYCZC建立在左相机上, 图像坐标系为Osl-XslYsl, 有效焦距为fsl; 右相机坐标系为OSR-XSRYSRZSR, 图像坐标系为Osr-XsrYsr, 有效焦距为fsr。根据相机透视投影变换模型, 可得Pk点(k=1, 2, …, n为空间点编号)在双目左相机坐标系的坐标, 如式(1)所示, 其中OC-XCYCZC坐标系与OSR-XSRYSRZSR坐标系之间的旋转矩阵R和平移矢量T如式(2)所示, 最后再进行重投影误差最小优化, 获得更高精度的位置坐标。
 (1)
(1)
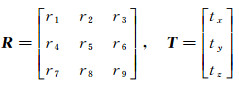 (2)
(2)
|
| 图 3 双目立体视觉中空间点的三维重建 Fig.3 3-D rebuild of space point in binocular stereovision |
双目视觉测量系统的相机距离影响测量精度[15]。弹道靶双目测量站2个相机的距离为1.2m, 采用传统基于平面标定板的标定方法[13]进行标定, 同时, 将双目窗口玻璃作为成像光路的一部分进行标定。图 4所示为所使用的600mm×800mm平面标定板。

|
| 图 4 双目测量站标定板 Fig.4 Calibration plate of binocular measurement station |
双目测量站视场水平及垂直方向的测量精度可达0.1mm, 沿景深方向的测量精度约0.4mm, 标定完成后采用距离精度优于0.01mm的标杆检测测量站精度, 特征点距离的测量精度优于0.5mm[14]。此外, 发展了同时对多块标定板成像的标定方法, 大大缩短了单站标定的时间。
利用模型在每个测量站位置获得的2张前光图像中的至少3个公共标记点, 解算出模型在每个测量站的位姿。再根据每个测量站的坐标系和全局基准坐标系的关系, 获得模型在基准坐标系下的位姿参数。
2 200m自由飞弹道靶视觉位姿测量系统关键技术弹道靶试验时, 模型发射过程中过载大且气流温度高, 模型上的标记点易变形或变色, 同时模型飞行速度快, 测试区域自发光强。200m自由飞弹道视觉位姿测量系统涉及的关键技术有:清晰成像、测量站关联、模型表面标记点制作与建模、数据处理等。
2.1 双目测量站清晰成像 2.1.1 弹道靶靶室杂光及模型自发光滤除200m自由飞弹道靶通过二级轻气炮将模型加速到超高声速, 二级轻气炮压缩管内的高压氢气进入靶室可能产生氢爆, 弹托和模型撞击拦截装置会产生强烈的火光, 都会造成双目相机获得的前光图像过曝(见图 5), 使图像中模型表面标记点不清晰, 甚至无法分辨。

|
| 图 5 过曝前光图像 Fig.5 The overexposure front light image |
为有效降低靶室内氢爆或超高声速撞击发光造成前光图像过曝, 采用了双目测量站相机序列开启、微秒级曝光等控制模式。根据测控系统获得的模型到达双目测量站测试视场中心的时刻, 序列控制双目测量站相机曝光和光源(脉冲激光器)出光, 每个双目测量站脉冲激光器出光的时刻在相机曝光时间内。目前双目测量站使用的相机最短曝光时间为233μs, 相机短时间曝光能有效降低相机所得图像中的噪点。前光成像的光源为532nm脉冲激光, 在相机镜头前安装532nm窄带滤光片(带宽10nm、透过率大于90%), 能够有效滤除大部分模型自发光。未安装滤光片时模型自发光的前光图像见图 6。

|
| 图 6 模型自发光前光图像 Fig.6 Front light image with model spontaneous light |
缩短相机的曝光时间是降低靶室杂光以及模型自发光对前光图像影响的最有效方法之一。随着工业相机技术的快速发展, 在保证分辨率的情况下, 采用最短曝光时间达到1μs的相机, 可进一步提高前光图像的质量。
2.1.2 前光脉冲光束匀化为实现前光照相过程中对模型飞行姿态的冻结、减小图像模糊量, 采用了技术成熟、脉宽小于10ns的多模脉冲激光器。但这种多模脉冲激光器的脉冲光束对双目相机成像有较明显的噪声干扰, 使得相机获得的图像质量较差, 影响标记点的识别和模型位姿测量精度。通过在脉冲激光器出口增加相位器实现光束匀化、提高光斑品质、减小激光光束噪声干扰等, 使前光图像清晰, 利于标记点的识别。激光器光斑品质改进前后获得的前光图像如图 7所示。图 7(a)中激光器出口未安装相位器, 前光图像较图 7(b)亮, 但图像中噪点较多; 激光器出口安装相位器, 激光脉冲光束扩束后在靶室轴线形成的光斑尺寸增加, 造成图 7(b)中图像的亮度降低, 但噪点明显减少、标记点清晰。

|
| 图 7 激光光斑品质改进前后获得的图像比较 Fig.7 Comparison of front light images |
目前, 采用的激光光束匀化方法还存在能量利用率较低等问题, 下一步将改进脉冲光束匀化方法, 提高脉冲激光光束能量的利用率, 以提高前光成像的信噪比。
2.2 双目测量站全局关联30站双目测量站分布在靶室150m范围, 相邻2个测量站的最小距离为3.8m。为避免全局关联过程中各双目测量站的误差累加, 采用TM30全站仪分别将30站双目测量站坐标系关联到靶室的基准坐标系下, 全站仪的标称精度为0.6mm+10-6mm/m×S(S为全站仪到测量站的距离, 单位:m); 同时, 设计了如图 8所示的测量站立体关联装置, 主要由4个棱镜与平面标定板固连组成。

|
| 图 8 双目测量站立体关联装置 Fig.8 Tridimensional correlation device of binocular measurement station |
双目测量站关联方法如下:
(a) 在靶室内沿轴线选择18个位置作为临时基准点, 每个基准点上安装棱镜, 用全站仪标定18个位置的坐标以建立基准坐标系。
(b) 选择某一个内外参数已标定的双目测量站, 将立体关联装置放置于测量站视场内至少10个不同位置, 通过双目测量站拍摄图像获得标定板的移动刚体变换, 同时利用全站仪获得4个棱镜的移动刚体变换, 结合手眼标定方法[16]即可标定出标定板上至少3个点((xF1, yF1, zF1), (xF2, yF2, zF2), (xF3, yF3, zF3))所建坐标系与至少3个棱镜((xP1, yP1, zP1), (xP2, yP2, zP2), (xP3, yP3, zP3))所建坐标系的旋转矩阵RFP和平移矢量TFP。
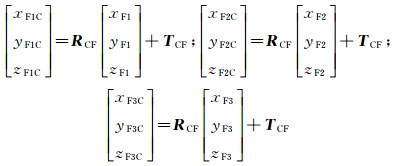
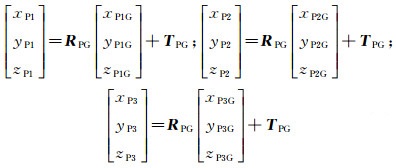
(c) 依次将该立体关联装置放置于各双目测量站视场内, 通过双目图像获得标定板上至少3个点在测量站下的坐标(xF1C, yF1C, zF1C), (xF2C, yF2C, zF2C)以及(xF3C, yF3C, zF3C), 同时通过全站仪测量侧面至少3个棱镜在基准坐标系下的坐标(xP1G, yP1G, zP1G), (xP2G, yP2G, zP2G)以及(xP3G, yP3G, zP3G), 根据式(3)和(4)解算出双目测量站坐标系到标定板坐标系的旋转矩阵RCF和平移矢量TCF、棱镜坐标系到基准坐标系的旋转矩阵RPG和平移矢量TPG。
(d) 结合(b)、(c)两步结果, 完成双目测量站坐标系在基准坐标系的关联。为了提高测量站关联的精度, 将立体关联装置放置在同一双目测量站视场内的至少4个不同位置, 双目测量站坐标系与基准坐标系的平移向量TCG和旋转矩阵RCG由式(5)解算。
基准点建立在靶室内, 各测量站的关联精度达到2mm。靶室变形会降低基准点的精度, 因此根据试验需要适时对基准系统重新校测。后续将采用精度更高的关联设备(如激光跟踪仪)以提高测量站之间的关联精度。
 (3)
(3)
 (4)
(4)
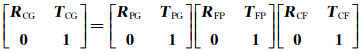 (5)
(5)
自由飞弹道靶模型主要由金属加工而成, 当光束照射模型前光成像时会产生明显的眩光, 造成图像中模型表面的部分标记点不清晰。图 9给出了Φ70mm铝球表面处理成不同颜色时获得的静态前光图像。可以看出, 模型表面处理成黑色可有效降低眩光影响, 提高标记点的清晰度。为了不影响模型的外形, 且在前光图像中得到清晰的模型表面标记点, 采用表面阳极化发黑处理技术, 在模型表面形成很薄的黑色膜层。模型表面通过激光烧蚀形成与背景对比明显的编码标记点, 标记点的深度控制在0.05mm以内。采用三维扫描系统[17]扫描模型表面标记点并建立其空间位置关系, 结合扫描数据和质心位置数据获得标记点在模型质心坐标系下的坐标。

|
| 图 9 模型表面处理成不同的颜色获得的前光图像对比 Fig.9 Comparison of front light images for the different surface colors of model |
该模型表面标记点制作方法主要适用于以铝合金为代表的金属模型, 非金属模型表面标记点的制作需探索新方法。
模型表面标记点的建模精度越高, 数据处理获得的模型位姿精度越高。目前, 使用的模型表面标记点建模设备的算法还不够优化, 经过多次拼接后标记点在模型质心坐标系的位置精度约0.2mm。采用摄影测量系统对模型表面的标记点进行建模, 可将精度提高到0.1mm。
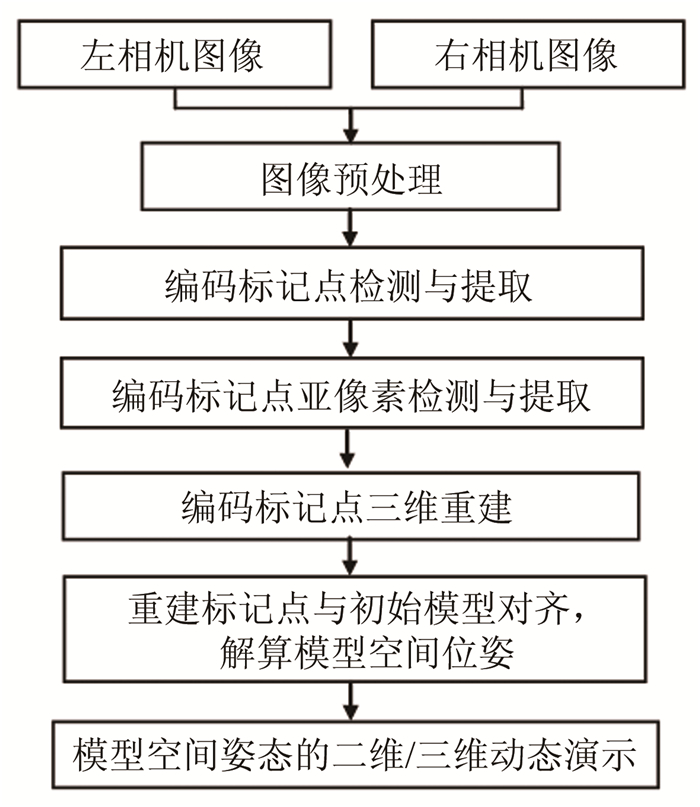
2.4 图像处理及位姿解算根据各双目测量站获得的前光图像, 通过图 10所示的流程进行图像处理、标记点识别与提取, 解算模型的飞行位姿。靶室基准坐标系OG-XGYGZG下编码标记点三维坐标为(xjG, yjG, zjG), j=1, 2..., n为标记点编号; 设模型质心坐标系OM-XMYMZM到OG-XGYGZG的转换关系为RMG、TMG, 则有式(6):
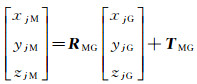 (6)
(6)
|
| 图 10 前光图像处理及模型位姿解算流程 Fig.10 The work flow of pre-process on the images and calculation on the model poses |
通过分解旋转矩阵线性解法, 可以计算出2个坐标系之间的旋转矩阵RMG和平移向量TMG, 其中-RMGTTMG为模型质心在全局下的坐标。根据模型俯仰角θ、偏航角γ和滚转角φ的定义, 模型姿态由式(7)表示。
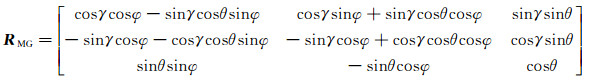 (7)
(7)
提取的双目前光图像中公共标记点越多、标记点分布的范围越大, 模型位姿解算的精度越高。为了提高自动识别、提取标记点的精度, 发展了灰度梯度方向的二次曲线拟合以实现标记点中心的亚像素提取。
考虑到试验环境的复杂性及自动提取标记点中心的稳定性, 图像处理中保留了手动方式提取标记点中心。标记点中心的匹配阈值为1pixel, 匹配误差大于阈值的标记点不参与姿态解算。
弹道靶模型发射过程中高温气流和自由飞行过程中靶室杂光的影响, 造成前光图像中模型表面的部分标记点不清晰, 很难自动识别和提取。因而, 在图像处理时有部分标记点需要手动提取, 影响了数据处理的精度和速度。下一步将改进数据处理软件的适应性, 提高数据处理的精度和速度。
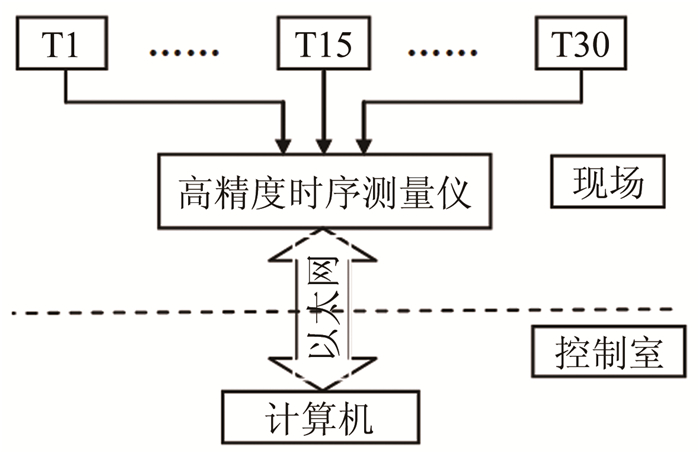
2.5 双目测量站出光时间关联视觉位姿测量系统通过测量双目测量站激光器出光时序获得模型的成像时序。双目测量站激光器的出光时序集中采集, 考虑不同位置信号传输延时, 实现激光器出光时序测量精度优于50ns。测量布局如图 11所示。双目测量站激光器出光时间数据可与弹道靶试验中其他测试数据进行关联, 建立统一时间基准, 便于数据分析。
|
| 图 11 激光器出光时间关联系统布局图 Fig.11 The sketch of collecting the sequence time of lasers flashing |
目前, 在200m自由飞弹道靶上已经开展了锥及复杂外形等模型的超高声速自由飞试验的位姿测量。文献[18]开展了20°锥模型的超高声速自由飞行位姿测量和气动力参数辨识。为了和文献的结果对比, 下面介绍开展的锥模型超高声速自由飞试验和气动力参数辨识。
3.1 锥模型超高声速自由飞试验位姿测量采用长度165mm的20°锥模型在200m自由飞弹道靶上开展了试验。锥模型表面进行了阳极化发黑处理, 再通过激光烧蚀形成Φ3mm的标记点。模型飞行速度约2.7km/s, 自由飞行试验段压力15kPa。利用双目测量站获得了模型飞行过程中27站前光图像, 单站前光图像如图 12所示。试验中, 由于靶室内部截弹、防护等原因, 造成部分双目测量站测试窗口被遮挡, 无法获得模型飞行时的双目前光图像。

|
| 图 12 单站双目前光图像 Fig.12 The binocular front light images of one station in the test |
由图 12可见, 该双目测量站左相机获得的图像受到眩光影响, 而右相机获得图像未受眩光影响。锥模型表面光洁度高, 该双目测量站的脉冲激光器扩束光斑照射到模型表面时, 反射光大部分进入左相机, 造成左相机获得的图像有一定的眩光, 但通过前光图像可清晰地识别多个标记点, 不影响模型位姿的解算。
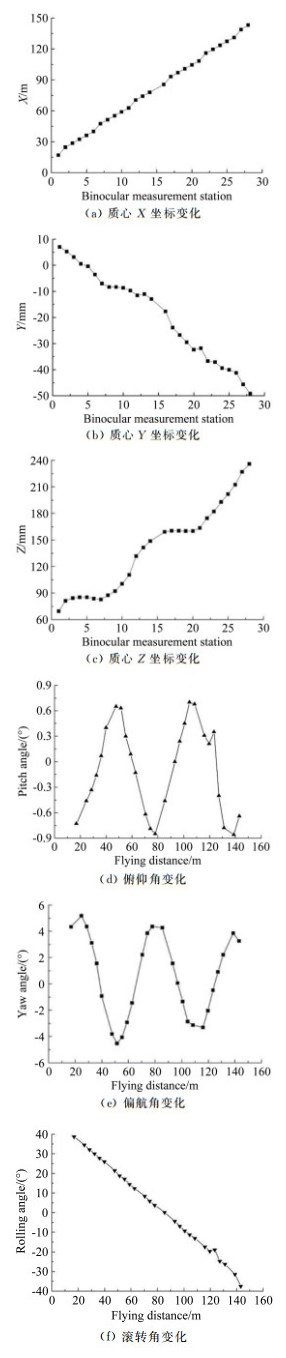
试验后, 利用数据处理软件对获得的双目前光图像进行处理, 1h内可获得模型飞行过程中的位姿参数(如图 13所示)。全局坐标系定义为:X轴正向为模型发射方向, Y轴正向为垂直X轴向上, Z轴由右手准则确定。
|
| 图 13 锥模型飞行位姿变化 Fig.13 The poses changes of the cone model |
从图 13可以看出, 在近130m的飞行范围内, 模型的质心下降了56mm, 向右偏离了166mm。模型俯仰角和偏航角变化趋势与文献[18]基本一致。
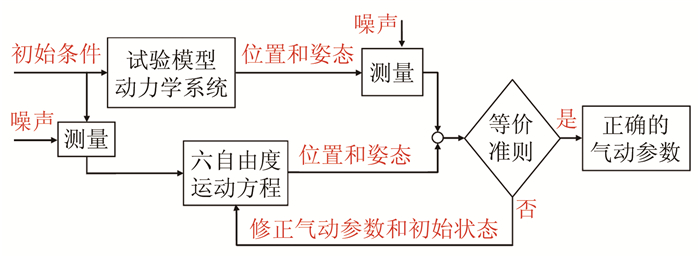
3.2 锥模型气动力参数辨识弹道靶自由飞试验气动力参数采用最大似然法辨识, 原理如图 14所示。以六自由度运动方程作为试验模型动力学系统的数学模型, 给定气动力参数的一组估计值, 计算六自由度运动方程在该条件下的响应与实际测量值的偏差, 判断是否满足一定的等价准则, 如不满足, 则修正气动力参数, 通过迭代直至得到正确的气动力参数。
|
| 图 14 气动力参数辨识原理 Fig.14 The principle of identifying aerodynamic parameters |
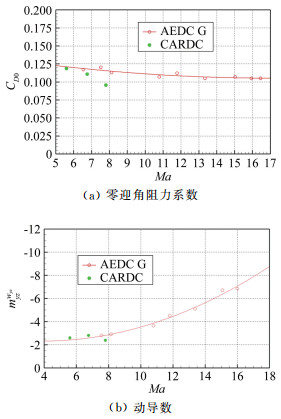
结合视觉位姿测量系统各测量站获得的位姿参数及激光器出光时序, 通过开发的软件辨识气动力参数。图 15对比了Ma=5.6、6.8和7.9这3个试验状态的锥模型零迎角阻力系数和动导数与AEDC G靶的结果[18], 可以看出二者趋势基本一致。本文采用的试验模型尺寸较文献[18]的大, 可能是造成辨识出的气动力参数有差异的原因之一。
|
| 图 15 气动力参数辨识结果与AEDC G靶的对比 Fig.15 Comparison of the identified results with those of AEDC G Range |
在解决测试区域强自发光和靶室其他杂光滤除、前光光源出口光斑匀化、双目测量站全局关联、模型表面处理及标记点制作等问题的基础上, 在200m自由飞弹道靶上建立了测试视场Φ1m的模型高精度视觉位姿测量系统, 实现了模型清晰成像, 获得了高精度测量数据, 视觉位姿测量系统全局定位精度达到2mm。双目前光图像还可直接观测模型超高声速飞行过程中的结构完整性、表面损伤等情况, 为弹道靶试验开展与能力拓展提供了技术支撑。利用试验获得的超高声速飞行模型双目前光图像解算出模型飞行位姿变化后, 通过辨识可获得模型阻力系数和动导数等气动力参数。
在200m自由飞弹道靶上开展了长165mm的20°锥模型飞行试验, 试验环境压力15kPa、飞行速度约2.7km/s, 利用发展的视觉位姿测量系统得到了锥模型的位姿参数, 通过辨识得到的气动力参数结果与AEDC G靶上的结果趋势基本一致。
致谢: 在测量技术的调试及试验过程中, 罗锦阳、简和祥、陈鲲、罗庆、龙耀、姜林、周毅、覃金贵等同志提出了宝贵建议并给予了很多帮助, 全体试验人员付出了辛勤劳动, 在此表示衷心感谢。| [1] |
Wilder M C, Bogdanoff D W, Cornelison C J. Hypersonic testing capabilities at the NASA Ames ballistic ranges[R]. AIAA 2015-1339, 2015.
|
| [2] |
刘世平, 易文俊, 顾金良, 等. 弹道靶数据判读与处理方法研究[J]. 兵工学报, 2000, 21(3): 201-204. Liu S P, Yi W J, Gu J L, et al. A new method for image analysis and data extraction of projectiles in flight[J]. Acta Armamentarii, 2000, 21(3): 201-204. DOI:10.3321/j.issn:1000-1093.2000.03.003 |
| [3] |
顾金良, 陈平, 夏言, 等. 数字式靶道阴影照相系统[J]. 弹道学报, 2009, 21(4): 38-41. Gu J L, Chen P, Xia Y, et al. Digital ballistic range shadowgraph system[J]. Journal of Ballistics, 2009, 21(4): 38-41. |
| [4] |
王唯, 唐志华, 罗红娥, 等. 照相站空间基准标定方法及测量误差分析[J]. 兵工学报, 2014, 35(9): 1414-1418. Wang W, Tang Z H, Luo H E, et al. Calibration of shadow-graphy system and analysis of measuring error[J]. Acta Armamentarii, 2014, 35(9): 1414-1418. DOI:10.3969/j.issn.1000-1093.2014.09.013 |
| [5] |
焦德志, 黄洁, 平新红, 等. 200m自由飞弹道靶升级改造[J]. 实验流体力学, 2014, 28(2): 95-98. Jiao D Z, Huang J, Ping X H, et al. Upgrading of 200 meter free-flight ballistic range at CARDC[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(2): 95-98. |
| [6] |
Du H, Li M G. The study for particle image velocimetry system based on binocular vision[J]. Measurement, 2009, 42(4): 619-627. DOI:10.1016/j.measurement.2008.10.011 |
| [7] |
Zhou W J, Yu L, Qiu W W, et al. Utilizing binocular vision to facilitate completely blind 3D image quality measurement[J]. Signal processing, 2016, 129: 130-136. DOI:10.1016/j.sigpro.2016.06.005 |
| [8] |
Wang J, Wang X J, Liu F, et al. Modeling of binocular stereo vision for remote coordinate measurement and fast calibration[J]. Optics and Lasers Engineering, 2014, 54(1): 269-274. |
| [9] |
宋晋, 马军, 蒋敏, 等. 双目视觉系统在风洞伞摆角测量中的应用与研究[J]. 计算机测量与控制, 2012, 20(8): 2042-2044. Song J, Ma J, Jiang M, et al. Research and application of parachute swing angle in wind tunnel test based on stereo vision measurement system[J]. Computer Measurement & Control, 2012, 20(8): 2042-2044. |
| [10] |
钟凯, 李中伟, 史玉升, 等. 组合式大尺寸三维测量系统中的结构参数标定算法[J]. 天津大学学报, 2011, 44(5): 425-429. Zhong K, Li Z W, Shi Y S, et al. Calibration algorithm of structure parameters in combined large-scale 3D metrology system[J]. Journal of Tianjin University, 2011, 44(5): 425-429. |
| [11] |
Liu X J, Zhao H S, Zhan G M, et al. Rapid and automatic 3D body measurement system based on a GPU-Steger line detector[J]. Applied Optics, 2016, 55(21): 5539-5547. DOI:10.1364/AO.55.005539 |
| [12] |
Zhao P, Ni G Q. Simultaneous perimeter measurement for 3D object with a binocular stereo vision measurement system[J]. Optics and Lasers Engineering, 2010, 48(4): 505-511. DOI:10.1016/j.optlaseng.2009.08.007 |
| [13] |
马颂德, 张正友. 计算机视觉[M]. 北京: 科学出版社, 2003. Ma S D, Zhang Z Y. Computer vision[M]. Beijing: Science Press, 2003. |
| [14] |
Ke F W, Huang J, Xie A M, et al. Photo and location techno-logy of binocular front light used to obtain the attitude of flying model with hypervelocity in the free flight ballistic range[C]//Proc of the 13th Asian Symposium on Visualization. 2015.
|
| [15] |
Xu G, Li X T, Su J, et al. Comprehensive evaluation for mea-surement errors of a binocular vision system with long virtual baseline generated from double reflection mirrors[J]. Optik, 2015, 126(23): 4621-4624. DOI:10.1016/j.ijleo.2015.08.063 |
| [16] |
Daniilidis K. Hand-eye calibration using dual quaternions[J]. The International Journal of Robotics Research, 1999, 18(3): 286-298. DOI:10.1177/02783649922066213 |
| [17] |
文雪忠, 郑蕾, 李毅, 等.三维光学扫描技术在超高声速碰撞毁伤测量中的初步应用[C]//第七届全国空间碎片学术交流会论文集. 2013. Wen X Z, Zheng L, Li Y, et al. The preliminary application of 3D optical scanning technique in hypervelocity impact damage measurement[C]//Proc of the 7th National Conference on Space Debris. 2013. |
| [18] |
Welse C J, Winchenbach G L, Madagan A N. Free-flight investigation of the aerodynamic characteristics of a cone at high Mach number[J]. AIAA Journal, 1970, 8(2): 294-300. DOI:10.2514/3.5659 |