石蜡类相变材料具有较高的热量贮存能力和较好的恒温特性, 其潜热吸收过程可用于延缓或控制表面产生的高热流现象, 因而在航天器热控制领域得到了广泛应用[1-4]。然而, 石蜡类相变材料热导率通常较低, 较大程度限制了相变蓄热系统的热量存储和释放速率, 进而影响系统的热控制性能。近年来, 国内外在如何有效提高该类材料热导率及储、放热速率方面开展了大量研究工作, 尤其是使用高导热泡沫材料(如C和SiC泡沫)进行复合, 可以极大改善该类材料的储热性能[5]。
C和SiC泡沫不仅具有较高的比热导率(热导率与密度的比值), 而且具有较好的机械性能和较强的耐化学腐蚀性。这些优良的物理和化学性质, 使C和SiC泡沫与石蜡类相变材料复合而成的材料体系(即本文所指复合相变材料, PCM)在能量储存及新一代飞行器热控制/热管理研究领域得到了越来越广泛的关注[6-7]。
由于微观结构及传热机理的复杂性, 目前, 复合相变材料传热过程的准确预测还存在较大难度, 而相应传热特性预测模型及计算方法的研究也不尽完善。目前主要采用体积分数法或质量分数法获得该类材料的等效热物性参数, 因而在材料传热特性的精细化预测方面还存在较大程度的局限性和不确定性[8-11]。针对上述问题, 本文采用扫描电子显微镜测试了材料微观结构, 并基于微结构特征建立了复合相变材料单胞体计算模型。采用双温度法和显热热容法建立了相变过程的细观和宏观尺度数值预测模型, 利用有限容积法对热扩散控制方程进行离散, 发展了复合相变材料的传热特性计算方法。为验证数值方法的有效性, 通过自主搭建的复合相变材料实验测试系统, 开展了复合相变材料传热特性的实验研究。
1 数值仿真 1.1 数值方法以SiC泡沫/正二十二烷复合相变材料为研究对象, 通过电子显微镜扫描, 获得其微观结构如图 1所示。从复合相变材料的微结构特征可以看出, 对于材料单胞体, 一方面由于微细尺度导致比表面积增大, 传热的边缘和端部效应增强, 因而三维效应不能忽略; 另一方面由于胞体特征尺寸远大于载体粒子的平均自由程, 连续介质的假定依然成立, 傅立叶导热定律仍可适用。针对复合相变材料既具有复杂性、随机性, 又具有周期性及自相似性的特点, 在典型微结构形式及尺度特征分析的基础上, 建立了单胞体内相变材料的传热分析模型。

|
| 图 1 电镜扫描下的复合相变材料微结构 Fig.1 Micrograph of composite PCM by SEM test |
为简化分析求解, 计算模型中可引入以下假设:(1)SiC泡沫及相变材料均为各向同性; (2)单相区内材料的热物性为常数; (3)导热为材料内部的主要传热机制; (4)忽略相变材料热膨胀对其传热特性的影响。在上述假设基础上, 基于双温度法[12]复合相变材料传热过程的能量控制方程可表示为:
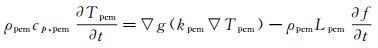 (1)
(1)
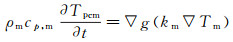 (2)
(2)
相变材料与泡沫骨架材料的耦合传热边界可表示为:
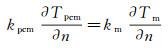 (3)
(3)
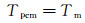 (4)
(4)
式(1)~(4)中, 下标pcm和m分别对应于相变材料和泡沫骨架材料, 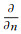
根据傅立叶定律, 复合相变材料单胞结构的等效热导率可以描述为:
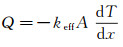 (5)
(5)
其中, Q为热流量, A为导热面积, keff为等效导热系数。
实际的复合相变材料是无数单胞体材料的集合。在整体传热性能预测中, 为了有效表征复合相变材料微结构的复杂细观传热特性, 同时降低材料整体宏观传热特性计算带来的计算代价, 采用等效比热容方法对整体材料传热特性进行了研究。对于复合相变材料, 假定熔化潜热为线性逐步释放, 则液相率可表达为:
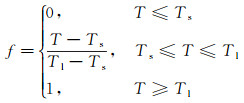 (6)
(6)
其中, Ts和Tl分别为相变材料的熔化和凝固温度。
伴随有相变过程的三维非稳态导热微分方程可表示为:
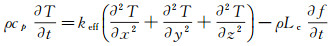 (7)
(7)
其中, Lc为胞体等效相变潜热, 等效导热系数keff可以通过式(5)获得, 而其他热物性参数可分别表示为:
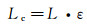 (8)
(8)
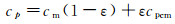 (9)
(9)
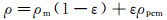 (10)
(10)
其中, ε为复合相变材料泡沫骨架的孔隙率。
引入附加比热:
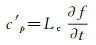 (11)
(11)
包含相变材料与骨架材料整个区域上的比热可表示为:
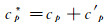 (12)
(12)
根据cp'的定义, 其包含了固液相界面上的所有信息。因此, 控制方程可简化为:
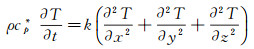 (13)
(13)
根据上述方法, 复合相变材料的复杂传热过程可视为具有相变性质的特殊材料的纯导热过程。采用基于非结构网格的三维有限体积方法进行空间离散[13], 同时使用二阶显式Runge-Kutta方法进行时间推进[14], 实现对该方程的数值求解。
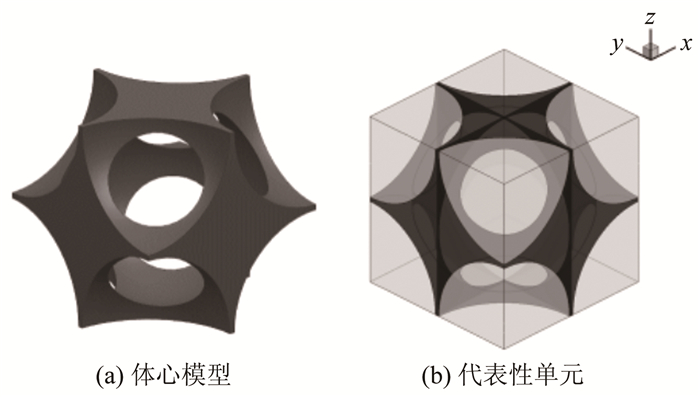
1.2 计算分析在建立上述数值计算方法的基础上, 根据图 1所示的材料微结构建立了对应的单胞体模型, 如图 2所示。其中, 基于单胞体的代表性单元(Representative Volume Element, RVE)边长为0.2mm, 孔隙率为0.9, 材料热物性参数见表 1。为保证计算精度, RVE内网格单元数约为105, 相变模糊区的温度范围设为1K, 能量方程的收敛残差取为10-8。计算时, RVE上/下表面分别取318K恒温加热边界和绝热边界, 四周则取对称周期边界, 初始温度为313K。
|
| 图 2 复合相变材料单胞体模型 Fig.2 Unit-cell model of composite PCM |
| 物性 | 密度 /(kg·m-3) |
比热 /kJ·(kg·K)-1 |
热导率 /W·(m·K)-1 |
相变温度 /K |
潜热 /(kJ·kg-1) |
| SiC | 3200 | 0.75 | 200 | —— | —— |
| PCM | 790 | 0.65 | 0.3 | 316 | 252 |
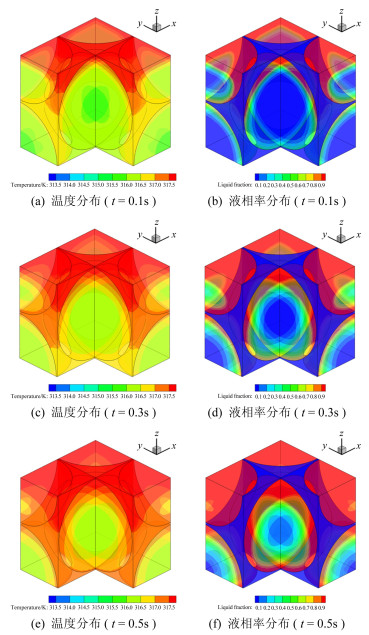
图 3给出了不同时刻复合相变材料RVE内温度分布及液相率分布特性。可以看出, 由于SiC的热导率明显高于纯相变材料, 在加热过程中, 从RVE上表面进入的大部分热量将首先沿SiC骨架快速扩散, 然后才逐步向相变材料内部释放。因此, 复合相变材料RVE的熔化过程呈现由SiC骨架周围往相变材料中心逐渐发展的趋势, 且SiC骨架的温度明显高于其周围相变材料的温度。
|
| 图 3 复合相变材料RVE热响应特性 Fig.3 Thermal response of RVE of composite PCM |
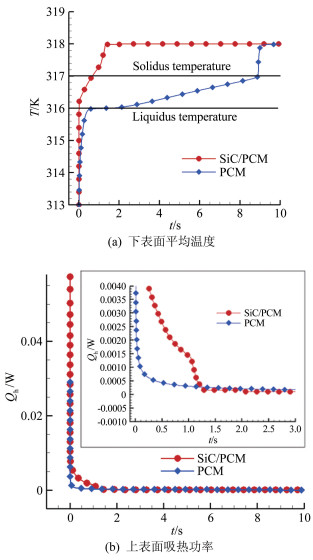
图 4分别比较了上表面加热条件下, 复合相变材料RVE与纯相变材料RVE的下表面温度响应特性和上表面吸热特性。可以看出, 由于SiC泡沫的导热增强作用, 在加热初期, 复合相变材料上表面的吸热速率明显高于纯相变材料, 其下表面的温升速率也明显更快。然而, 对于相同尺寸的RVE, 纯相变材料由于具有更多的相变潜热, 其熔化过程将平缓地持续较长时间, 此时复合相变材料内的正二十二烷已经完全熔化。因此, 在加热后期, 纯相变材料的吸热功率将高于复合相变材料, 其总吸热量也会更高。
|
| 图 4 RVE传热特性比较 Fig.4 Thermal characteristic comparisons of RVE |
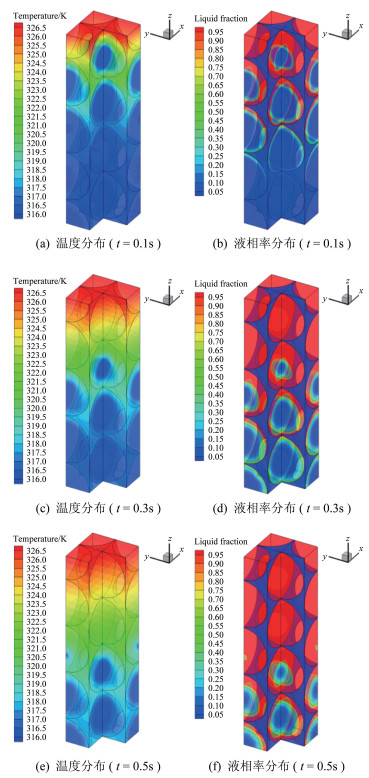
在单胞体传热特性研究的基础上, 图 5显示了多胞体复合相变材料温度与液相率分布随时间的变化特性。可以看出, 随着加热的进行, 高温区由加热面向底部冷端逐步推进, 材料内部的温度梯度也呈逐渐降低趋势。
|
| 图 5 复合相变材料多胞结构的热响应特性 Fig.5 Thermal response of multi-cells of composite PCM |
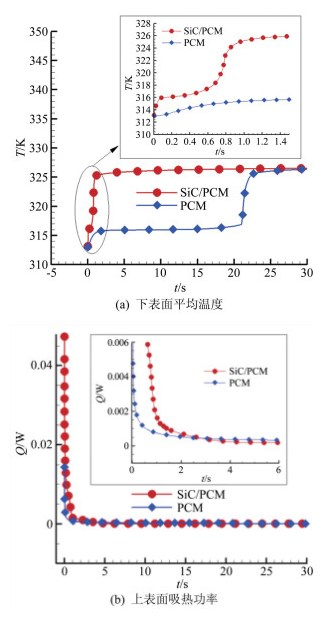
图 6显示了复合相变材料多胞结构顶部加热过程中底部平均温度及顶部吸热功率变化特性。可以看出, 与单胞体传热特性类似, 相对于纯相变材料, 在上表面加热条件下, 由于高热导率SiC骨架的导热增强作用, 复合相变材料底部温升速率更快; 在吸热过程中, 复合相变材料与纯相变材料上表面吸热功率均呈逐步降低趋势, 但由于复合相变材料热导率相对较高, 其上表面吸热功率的降低速率要快于纯相变材料。
|
| 图 6 复合相变材料与纯相变材料多胞结构热特性的比较 Fig.6 Thermal characteristic comparisons of multi-cell of composite PCM and pure PCM |
通过材料细观传热特性的计算分析, 可获得不同几何结构及孔隙率条件下复合相变材料的等效导热系数, 从而为实现复合相变材料整体热响应特性的精细化预测提供重要依据。
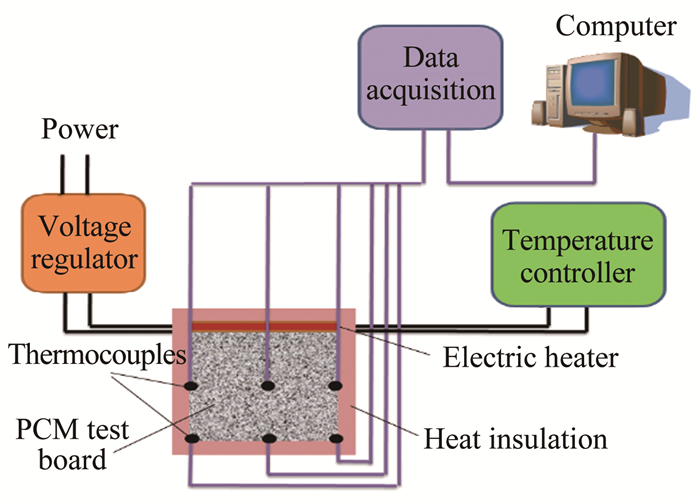
2 实验验证为验证数值计算方法的有效性, 开展了复合相变材料传热特性实验研究。如图 7所示, 实验系统主要由电加热模块、温度控制模块(ANV TF100 PID, 温度控制误差为±0.1℃)、测量与数据采集模块以及红外热成像模块(FLIR E60)等组成。复合相变材料尺寸为100mm×100mm×30mm, 其孔隙率为0.95, 相变材料填充量为225g, 其中内埋热电偶以获得复合相变材料典型位置的温度变化曲线。实验开始时, 先打开温度控制器, 将加热温度设为65℃, 然后启动电加热模块, 待温度稳定后再与复合相变材料进行接触, 同时打开红外热成像仪与数据采集器。实验结束后, 依次关闭电加热模块、温度控制器、红外热成像仪与数据采集器。
|
| 图 7 复合相变材料传热特性研究实验装置示意图 Fig.7 Experimental setup for heat transfer test of composite PCM |
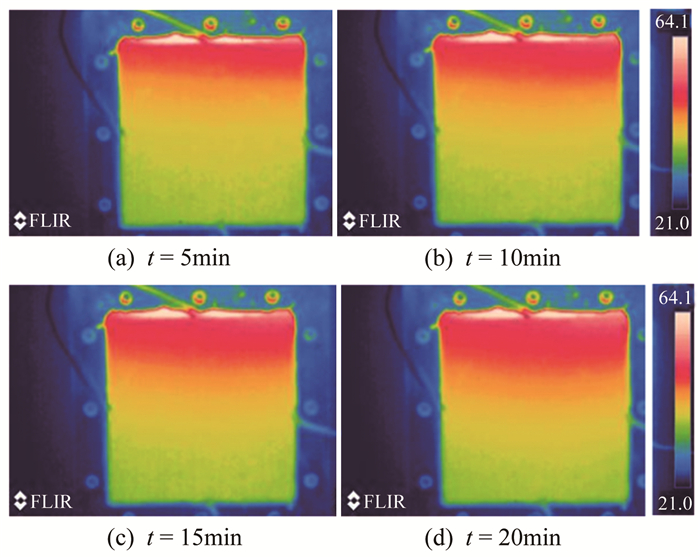
图 8和9分别给出了红外热成像仪监控下复合相变材料的表面温度变化及固/液界面推进的过程。可以看出, 复合相变材料在熔化过程中固/液界面较为清晰, 由于大部分加热热量将汇集于该界面, 因此相应区域的温度梯度也相对较大。
|
| 图 8 复合相变材料熔化过程的红外热成像图(单位:℃) Fig.8 Experimental temperature contours at various time by thermal imager (unit: ℃) |

|
| 图 9 复合相变材料固/液界面随时间变化情况 Fig.9 The liquid/solid fraction of composite PCM |
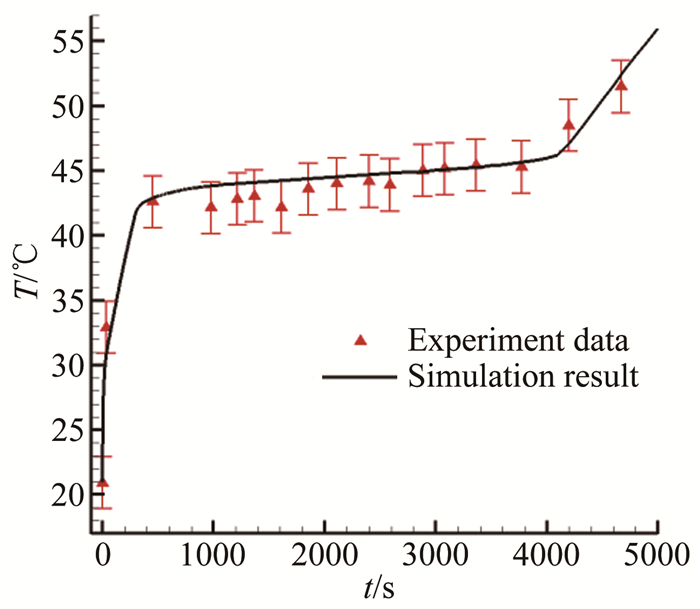
图 10对比了复合相变材料监控位置(距顶端加热面30mm处)温度响应的数值计算结果和实验测量数据。可以看出, 在加热初期, 由于复合相变材料的高导热性, 对应点温度快速上升直至熔点, 在熔化过程中温度变化趋于平缓, 而当所在区域相变材料完全熔化时, 其温度将再次迅速上升。结果表明, 数值计算结果与实验测量数据吻合较好(其绝对误差在±2℃之内), 因此采用本文建立的计算方法对复合相变材料传热特性进行性能预测是可行的。
|
| 图 10 数值计算与实验结果比较 Fig.10 The comparison of the experimental and simulated results |
针对复合相变材料的复杂微结构特点及复杂传热过程, 以SiC泡沫填充石蜡类相变材料为研究对象, 采用有限容积法与等效热容法相结合的方法, 建立了考虑材料细观与宏观传热特性的复合相变材料传热特性数值预测方法, 搭建了实验平台并开展了材料传热特性实验研究。研究表明, 所建数值方法可有效预测复合相变材料的传热特性。相对于传统体积分数法和质量分数法, 本文所建方法既可有效表征复合相变材料微结构内部的复杂细观传热特性, 又可降低工程应用中材料宏观传热特性计算带来的计算效率问题。相关方法可为开展材料孔隙率、微结构等特征对复合相变材料传热特性的影响规律研究以及材料蓄热性能的优化提供参考。
| [1] |
Yendler B, Poffenbarger N. A new approach for thermal protection system of a probe during entry[C]//Proc of the 2nd International Planetary Probe Conference. 2004.
|
| [2] |
Fukai J, Hamada Y, Morozumi Y, et al. Effect of carbon fiber brushes on conductive heat transfer in phase change materials[J]. International Journal of Heat and Mass Transfer, 2002, 45(24): 4781-4792. DOI:10.1016/S0017-9310(02)00179-5 |
| [3] |
Elgafy A, Lafdi K, Mesalhy O. Carbon nanofibers in passive cooling[C]//Proc of the International conference of carbon. 2004.
|
| [4] |
Wirtz R, Shuo P, Fuchs A. A polymer-based thermal energy storage composite for temperature control of sensors and electronics[C]//Proc of the 6th ASME-JSME thermal engineering joint conference. 2003.
|
| [5] |
Osama M, Khalid L, Ahmed E. Carbon foam matrices satura-ted with PCM for thermal protection purposes[J]. Carbon, 2006, 44(10): 2080-2088. DOI:10.1016/j.carbon.2005.12.019 |
| [6] |
Patricio A, Espinoza V, Chris D. Carbon foam filled with phase change materials for passive temperature management[C]. Proc of the COMSOL Multiphysics User's Conference. 2005.
|
| [7] |
Jankovsky R S, Smith T D. High-area-ratio rocket nozzle at high combustion chamber pressure-experimental and analytical validation[R]. NASA TP-1999-208522, 1999.
|
| [8] |
Alawadhi E M, Amon C H. PCM thermal control unit for por-table electronic devices:experimental and numerical studies[J]. IEEE Transactions on Components and Packaging Technologies, 2003, 26(1): 116-125. DOI:10.1109/TCAPT.2003.811480 |
| [9] |
Yoo D, Joshi Y K. Energy efficient thermal management of electronic components using solid-liquid phase change materials[J]. IEEE Transactions on Device and Materials Reliability, 2005, 4(4): 641-649. |
| [10] |
Lafdi K, Mesalhy O, Elyafy A. Graphite foams infiltrated with phase change materials as alternative materials for space and terrestrial thermal energy storage applications[J]. Carbon, 2008, 46(1): 159-168. DOI:10.1016/j.carbon.2007.11.003 |
| [11] |
Zhao C Y, Lu W, Tian Y. Heat transfer enhancement for thermal energy storage using metal foams embedded within phase change materials(PCMs)[J]. Solar Energy, 2010, 84(8): 1402-1412. DOI:10.1016/j.solener.2010.04.022 |
| [12] |
Hu X, Patnaik S S. Numerical simulations of cyclic melting and freezing of phase change material in micro-foam[C]//Proc of the 43rd AIAA Thermophysics Conference. 2012.
|
| [13] |
Versteeg H K, Malalasekera W. An introduction to computational fluid dynamics:the finite volume method[M]. 北京: 世界图书出版社公司, 1995.
|
| [14] |
Teschl G. Ordinary differential equations and dynamical systems[M]. Providence: American Mathematical Society, 2012.
|



