对于Ma6一级的大气层内飞行的高超声速飞行器, TBCC发动机无疑是最为理想的动力装置。TBCC动力通常采用涡轮发动机与双模态超燃冲压发动机组合, 但最为突出的问题是如何实现两种发动机的"推力衔接"。现役涡轮发动机的最大工作马赫数为2.0到2.3, 而双模态冲压发动机起动马赫数一般在4.0左右。如何提高涡轮发动机的马赫数上限、降低冲压发动机的马赫数下限并实现两种发动机的"推力衔接", 是Ma6一级的TBCC的主要技术问题之一。目前, 国内外TBCC组合动力存在多种技术方案, 包括采用"超级燃烧室"的串联TBCC技术方案[1-2]、预冷却(射流预冷[3-4]和换热预冷[5-9])涡轮发动机技术方案以及采用额外的引射火箭的三组合T/RBCC技术方案[10-11]等。针对上述组合动力方案的对比分析研究相对较少, 究竟何种组合动力方案更加适合高超声速巡航飞行器, 需要开展相关研究。本文遵循"一种平台, 多种动力"的研究思路, 基于相同的高超声速飞行器飞行任务和气动特性, 对比分析涡轮/亚燃冲压/双模态超燃冲压组合动力方案、涡轮/引射冲压/双模超燃冲压组合(Trijet)动力方案、射流预冷涡轮/双模态超燃冲压组合动力方案和空气涡轮火箭(ATR)/双模态超燃冲压组合动力方案, 比较不同动力方案下的飞行器航程、巡航距离和爬升加速时间等飞行性能参数。
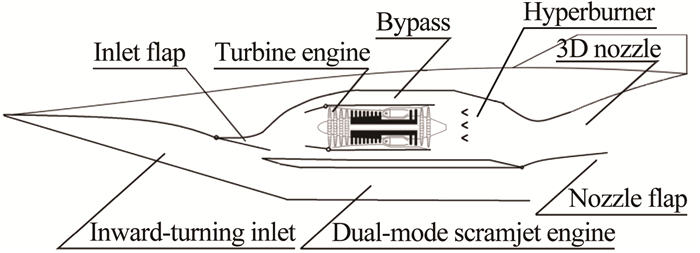
1 多种组合动力方案 1.1 涡轮/亚燃冲压/双模态超燃冲压组合发动机(方案1)在涡轮/亚燃冲压/双模态超燃冲压组合发动机方案中, 将涡轮发动机与亚燃冲压发动机串联作为低速通道, 再与作为高速通道的双模态超燃冲压发动机并联, 如图 1所示。该方案中, 涡轮发动机工作马赫数0~2.3, 亚燃冲压发动机工作马赫数2.0~4.0, 双模态超燃冲压发动机的工作马赫数4.0~6.5。涡轮发动机采用小涵道比涡扇发动机, 其与亚燃冲压发动机在马赫数2.0~2.3时进行模态转换。
|
| 图 1 涡轮/亚燃冲压/双模态超燃冲压组合发动机 Fig.1 Turbine/Ramjet/Dual-mode Scramjet |
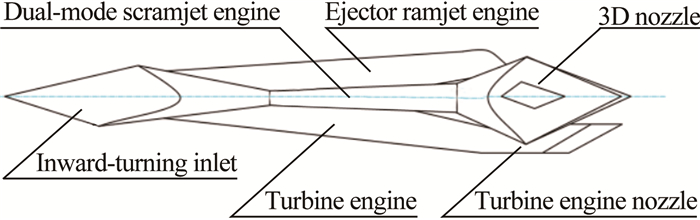
在涡轮/引射冲压/双模态超燃冲压组合发动机方案中, 采用涡轮发动机、引射冲压发动机与双模态超燃冲压发动机三者并联的形式, 如图 2所示。该方案中, 涡轮发动机工作马赫数0~2.3;引射冲压发动机工作马赫数0.8~4.0。其中, 马赫数0.8~2.0时, 引射冲压发动机工作在引射模态, 而在马赫数2.0~4.0时, 引射冲压发动机工作在冲压模态; 双模态超燃冲压发动机工作马赫数4.0~6.5。
|
| 图 2 涡轮/引射冲压/双模态超燃冲压组合发动机 Fig.2 Turbine/Ejector Ramjet/ Dual-mode Scramjet |
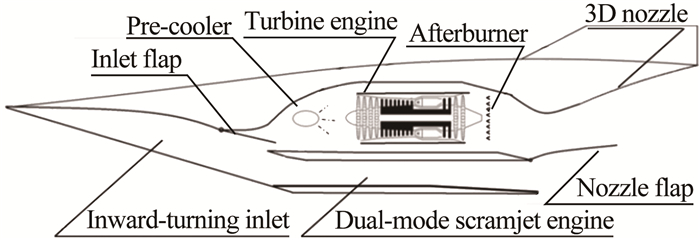
在射流预冷涡轮/双模态超燃冲压组合发动机方案中, 采用射流预冷涡轮发动机与双模态超燃冲压发动机并联的形式, 如图 3所示。射流预冷涡轮发动机工作马赫数0~3.5, 射流预冷的工质为水; 双模态超燃冲压发动机的工作马赫数3.5~6.5。
|
| 图 3 射流预冷涡轮/双模态超燃冲压组合发动机 Fig.3 Pre-cooled Turbine /Dual-mode Scramjet |
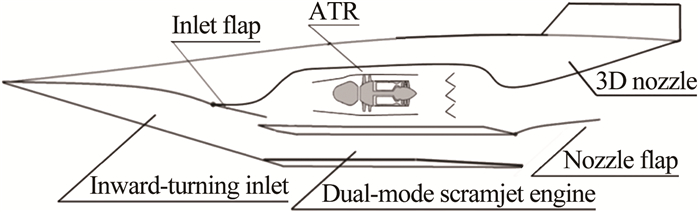
在空气涡轮火箭/双模态超燃冲压组合发动机方案中, 采用空气涡轮火箭发动机(ATR)与双模态超燃冲压发动机并联的形式, 如图 4所示。空气涡轮火箭发动机工作马赫数0~3.5, 双模态超燃冲压发动机工作马赫数3.5~6.5。
|
| 图 4 空气涡轮火箭/双模态超燃冲压组合发动机 Fig.4 Air-turbo-rocket/ Dual-mode Scramjet |
表 1给出了上述4种组合发动机方案在不同马赫数范围工作的发动机状态。方案1和方案2中的涡轮发动机均基于现阶段涡轮发动机水平, 其工作马赫数范围0~2.3;方案3通过射流预冷手段将涡轮发动机的工作马赫数上限提高到3.5;方案4的空气涡轮火箭发动机的工作马赫数上限为3.5。
| No. | Scheme of combined engine | Mode of engine | Mach number |
| 1 | TE/RJ/DMSJ | Turbine | 0~2.3 |
| Ramjet | 2.0~4.0 | ||
| Dual-mode Scramjet | 4.0~6.5 | ||
| 2 | TE/ERJ/DMSJ | Turbine | 0~2.3 |
| Ejector-mode of Ejector Ramjet | 0.8~2.0 | ||
| Ramjet-mode of Ejector Ramjet | 2.0~4.0 | ||
| Dual-mode Scramjet | 4.0~6.5 | ||
| 3 | PCTE/DMSJ | Pre-cooled Turbine | 0~3.5 |
| Dual-mode Scramjet | 3.5~6.5 | ||
| 4 | ATR/DMSJ | Air-turbine-rocket | 0~3.5 |
| Dual-mode Scramjet | 3.5~6.5 |
针对组合动力方案的评估, 首先需要开展的是组合动力的性能计算, 获得其高度、速度特性。参考文献[12-14], 本文采用基于部件法的性能计算模型和计算方法进行涡轮发动机和冲压发动机的高度、速度计算。
2.2 射流预冷涡轮发动机性能计算方法随着飞行马赫数增加, 自由流的总温增加, 导致传统涡轮发动机的换算转速下降, 压气机压比和效率会有所下降, 使得涡轮发动机性能下降; 在涡轮前温度和加力燃烧室出口温度受限的情况下, 燃烧室加热量也会随自由流总温的增加而减小, 这些因素都导致单位推力Fs随着飞行马赫数的增加而下降。射流预冷涡轮发动机与传统发动机的不同在于:在压气机前利用液体冷却剂喷射装置, 蒸发冷却进入压气机的高温气流, 使压气机前空气总温降低或维持在某一温度, 增大流量, 从而扩大发动机的飞行包线。
在射流预冷发动机性能计算过程中, 除涡轮发动机计算模型外, 还需要考虑热交换系统计算模型。射流预冷的热交换系统主要由热交换器、射流冷却器组成。不饱和态的水在热交换器中通过热交换转化为过热蒸汽, 在射流冷却器中通过对流掺混来冷却来流总温。射流预冷的热交换系统相当复杂, 在对其特性的计算中, 本文采用简化数学模型[15]。
2.3 空气涡轮火箭发动机性能计算方法空气涡轮火箭发动机性能计算方法, 是在航空发动机性能计算方法的基础上建立的。在设计点计算时, 依次计算进气道、压气机、涡轮、内外涵混流器、燃烧室、尾喷管出口参数, 由推力公式计算ATR的推力[16-18]。ATR的非设计点数学模型可由非线性方程组来描述[18]。方程组的自变量包括物理转速、压气机压比、涡轮前温度和涡轮进口燃气流量。ATR必须满足3个共同工作的条件:压气机与涡轮功率平衡、混流器进口内外涵气流静压相等、燃烧室出口与尾喷管的流量平衡。在给定发动机调节规律下(如涡轮前温度), 通过求解这3个共同工作方程, 即可确定ATR的共同工作点, 再根据设计点的计算方法得到ATR的推力。
2.4 引射冲压发动机性能计算方法引射冲压发动机的基本工作机理是:高温高压的一次流的高速流动通过引射作用吸入环境的二次流, 两股气流之间的动量和能量进行组合分配形成一股气流, 再经过燃烧释热并通过尾喷管将高温燃气排出, 从而产生推力。引射冲压发动机主要包括进气道、燃气发生器、引射器、燃烧室和尾喷管。燃气发生器主气流为超声速, 进气道二次流为亚声速, 引射器部分具有恒定的面积和几何形状, 其出口平面气流处于堵塞或临界状态。理想的引射冲压发动机如图 5所示。

|
| 图 5 引射冲压发动机模型示意图 Fig.5 Ejector Ramjet model |
引射冲压发动机的性能计算采用准一维计算方法。火箭喷管出口的高温燃气一次流与从进气道进入的空气二次流在引射器内充分混合, 并假设在引射器出口(e截面)达到热壅塞状态(Ma=1), 充分混合的气流在冲压燃烧室内组织燃烧, 最后经喷管排入大气中。在引射器进出口截面, 一次流与二次流满足流量守恒、动量守恒和能量守恒, 并且在i截面处一次流与二次流需要满足静压相等, 以此可以根据引射器进口气流参数确定其出口气流参数。详细计算过程见文献[19]。
2.5 双模态超燃冲压发动机性能计算方法双模态超燃冲压发动机性能计算采用一维计算方法。针对超声速燃烧室求解流量平衡、动量平衡和能量平衡的方程组获得沿燃烧室轴向变化的气流参数[26]。
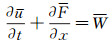 (1)
(1)
其中,
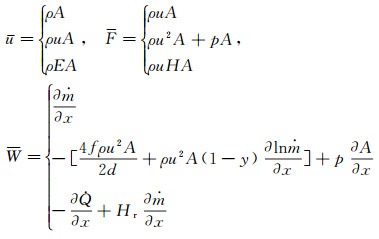
式中:ρ为气流密度; u为气流速度; A为燃烧室横截面积; Q为放热量; m为质量流量; d为水力直径; y为喷氢后的气流动量增量, y=sinγ, 其中γ为喷射角, 垂直喷射时γ=90°, 平行喷射时γ=0°; H为气流总焓; Hr为燃烧总焓; p为气流静压, 假设其仍满足热状态方程; E为总内能。
采用MacCormack有限差分格式对式(1)进行求解[26]。
2.6 同参数对比方法发动机热力循环参数、部件参数和空气流量等参数不同, 则计算得到的发动机性能也会不同。因此, 针对上述多种组合动力方案, 尽可能在相同的热力循环参数下进行性能对比。射流预冷发动机与传统涡轮发动机在设计点具有相同的热力循环参数和空气流量; ATR发动机依靠燃气发生器出口较小的燃气流量驱动涡轮, 带动压气机来压缩较大流量的来流空气, 根据涡轮和压气机的功率平衡, 该发动机压气机的压比一般比较低, 而涡轮落压比相对较大, 因此, ATR发动机无法具有与传统涡轮发动机完全相同的热力循环参数, 本文在计算中仅保持ATR与涡轮发动机涡轮前温度和部件效率相同。此外, 多种组合动力方案之间的对比还基于以下同参数条件:
(1) 飞行马赫数0~6.5;
(2) 飞行高度0~30km;
(3) 模态转换前后两种发动机推力相等;
(4) 所有组合动力方案的推力特性都进行无量纲化处理, 即T=T/TSL, 其中T为相对推力, T为实际飞行条件下的推力, TSL为海平面标准状态下加力状态的推力。
各种组合动力方案均采用相同的燃料。
表 2给出了部分发动机设计点的热力循环参数。
| Thermodynamic cycle parameter of engine | value |
| Total temperature of Turbine inlet/K | 1650 |
| Total temperature of afterburner outlet/K | 2050 |
| Pre-cooled temperature of PCTE/K | 420 |
| Temperature of ATR gas generator outlet/K | 1650 |
| Equivalence ratio of RJ | 0.95 |
| Equivalence ratio of DMSJ | 0.90 |
| Ratio of total temperature of ERJ primary flow to static temperature of free flow | 10 |
| Ratio of total pressure of ERJ primary flow to static pressure of free flow | 20 |
此外, 针对上述不同发动机类型, 分别采用如下进气道总压恢复系数模型进行计算。低速流道发动机采用式(2)和(3)的进气道模型, 而高速流道发动机则采用式(4)的进气道模型。
 (2)
(2)
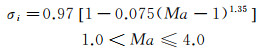 (3)
(3)
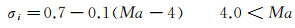 (4)
(4)
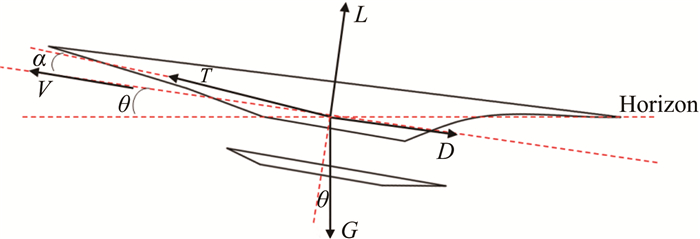
高超声速飞行器的飞行性能与传统飞行器一样, 是由作用其上的外力来决定的, 这些力包括:发动机推力(安装推力)、空气动力(升力和阻力)和飞行器的重力。此外, 当飞行高度小于40km时, 地球曲率和自转对飞行性能的影响可以不加考虑。因此, 针对本文研究对象, 即大气层内的高超声速巡航飞行器, 可以采用传统飞行器的平面平行地球引力场假设进行性能计算。飞行器在铅垂平面(飞行平面)内的"质点"受力分析如图 6所示, 其中L为升力, D为阻力, T为发动机推力, G为飞行器本身重力, θ为航迹倾角, α为迎角, V为飞行速度。
|
| 图 6 飞行器受力分析图 Fig.6 Force analysis on aircraft |
根据受力分析, 可以得到飞行器运动控制方程为:
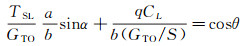 (5)
(5)
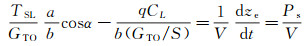 (6)
(6)
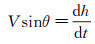 (7)
(7)
式中, 发动机在高度h、飞行速度V下的推力T与海平面起飞推力TSL的比值记为a; 飞行器在高度h、飞行速度V下的重力G与海平面的起飞最大重力GTO的比值记为b; h为飞行高度, 且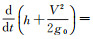
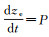
一般地, 升力系数CL和阻力系数CD可以表示为飞行马赫数Ma和迎角α的函数关系:
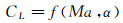 (8)
(8)
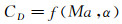 (9)
(9)
因此, 在给定的飞行器推力和升阻特性下, 可以根据式(5)~(9)计算出飞行器在该飞行状态下的剩余功率Ps, 则某一航段(从V1到V2, 从h1到h2)的飞行时间为:
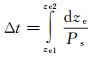 (10)
(10)
在计算过程中, 每一任务航段飞行区间较小时, 可用平均剩余功率Ps, avg进行简化计算:
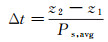 (11)
(11)
在飞行过程中, 由于燃油的消耗, 飞行器自身重力不断变化。重力变化的计算, 将根据航段中剩余功率Ps的不同分为两种形式[20]:
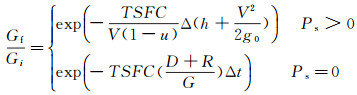 (12)
(12)
式中, Gi为航段开始时的重力; Gf为航段结束时的重力; TSFC为安装推力下的耗油率; 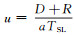
因此, 在给定飞行器的起飞重力、燃油重力、发动机推力和升阻特性以及飞行剖面后, 沿任务剖面依次计算每一航段的飞行时间和飞行器重力变化, 并将每一航段结束时的重力作为下一航段开始时的重力。最终根据剩余燃油重力计算其能够维持的巡航时间(巡航阶段Ps=0), 总的航程即为燃油完全消耗时所有任务航段的飞行距离之和:
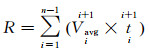 (13)
(13)
图 7和8给出了涡轮/亚燃冲压/双模态超燃冲压组合发动机的高度、速度特性。图 7为组合发动机的推力特性(不同高度和不同速度下的推力, 通过除以海平面推力进行了无量纲化处理)。图中左侧红色曲线、浅蓝色曲线分别表示涡轮发动机的最大状态(开加力状态)和中间状态(不开加力状态)。从图中可以看到:(1)在最大状态下, 涡轮发动机推力随着飞行马赫数的增大而增大; 当马赫数接近2.0时, 推力变化趋于平缓; Ma=2.2时, 推力达到最大; Ma=2.3时, 推力略微下降。(2)在中间状态下, 涡轮发动机推力在Ma=1.5时达到最大; 随着马赫数继续增大, 推力开始下降。(3) Ma=2.3~4.0时, 亚燃冲压发动机的推力随着飞行马赫数的增大而增大。(4)双模态超燃冲压发动机的推力随着飞行马赫数的增大而增大。在相同马赫数下, 发动机推力随着飞行高度增大而下降, 主要是由于飞行高度增大、空气密度减小而使得发动机空气流量减小。

|
| 图 7 涡轮/亚燃冲压/双模态超燃冲压组合发动机推力特性 Fig.7 Thrust performances of Turbine/Ramjet/Dual-mode Scramjet |
|
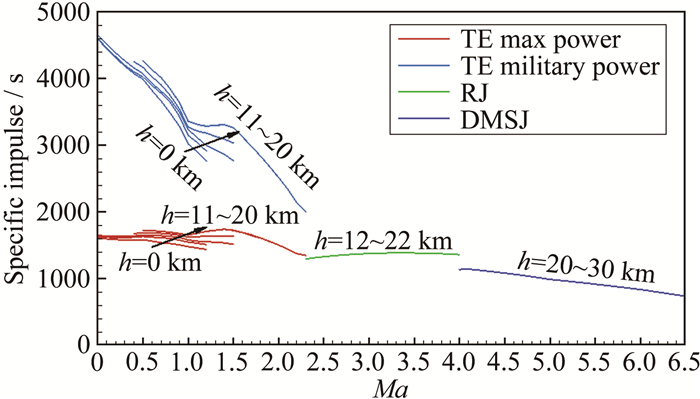
| 图 8 涡轮/亚燃冲压/双模态超燃冲压组合发动机比冲特性 Fig.8 Specific impulse performances of Turbine/Ramjet/Dual-mode Scramjet |
图 8为组合发动机的比冲特性。在中间状态下, 涡轮发动机的比冲范围在2000~4000s左右, 在最大状态下, 比冲范围在1400~1800s左右; 冲压发动机的比冲范围在1200~1400s左右; 双模态超燃冲压发动机的比冲范围在800~1000s左右。计算得到的发动机比冲在其马赫数范围内与典型的发动机比冲范围[21]一致。
4.2 涡轮/引射冲压/双模态超燃冲压组合发动机性能分析图 9和10给出了涡轮/引射冲压/双模态超燃冲压组合发动机的高度、速度特性。图 9中的绿色曲线表示引射冲压发动机的推力变化。Ma=0.8~2.3时, 引射冲压发动机工作在引射模态下(即火箭开启状态下), 其推力如图中绿色虚线表示, 推力随着马赫数增大而增大; Ma=2.3~4时, 引射冲压发动机的火箭关闭, 此时引射冲压发动机工作在冲压模态下。Ma= 4~6.5时, 双模态超燃冲压发动机的推力依然随马赫数增大而增大。

|
| 图 9 涡轮/引射冲压/双模态超燃冲压组合发动机推力特性 Fig.9 Thrust performances of Turbine/Ejector Ramjet/Dual-mode Scramjet |
|
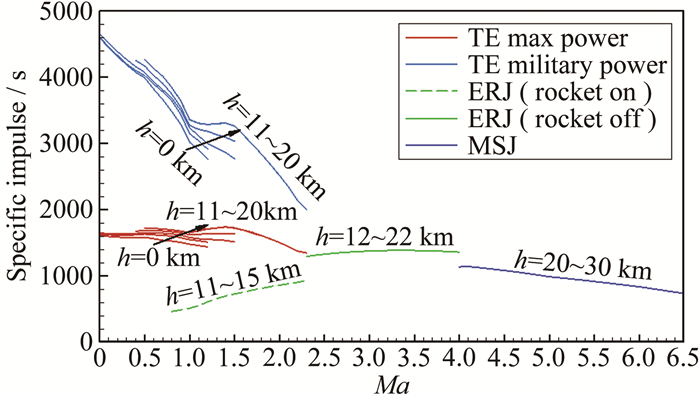
| 图 10 涡轮/引射冲压/双模态超燃冲压组合发动机比冲特性 Fig.10 Specific impulse performances of Turbine/Ejector Ramjet/Dual-mode Scramjet |
图 10为组合发动机的比冲特性。Ma=0.8~2.3时, 引射冲压发动机的比冲随着马赫数的增大而增大, 火箭发动机的比冲明显低于冲压发动机的比冲; 而随着马赫数的增大, 引射冲压发动机的冲压能力增强, 发动机工作状态中冲压所占的比例也随之提高, 因此其比冲也随之提高。当火箭关闭时, 引射冲压发动机在冲压模态下的比冲明显提高。
4.3 射流预冷涡轮/双模态超燃冲压组合发动机性能分析图 11和12给出了射流预冷涡轮/双模态超燃冲压组合发动机的高度、速度特性。图 11为组合发动机的推力特性。Ma=0~2.2时, 射流预冷涡轮发动机冷却装置不工作, 此时作为传统涡轮发动机工作。Ma>2.2时, 发动机的冷却装置开始工作, 在进气道中喷入冷却水, 使得压气机入口总温保持在420K, 直到Ma=3.5。从其推力曲线的变化可以看到, 在Ma=2.2~3.5时, 射流预冷发动机的推力随着马赫数增大而大幅度增加。其原因是:保持压气机入口总温不变, 则发动机的共同工作点基本不变, 此时发动机能保持在一个固定的换算转速和换算流量下工作, 因此, 发动机的空气流量随着来流马赫数的增大而显著增大; 虽然发动机单位推力随着马赫数的增大而下降, 但其下降程度小于空气流量的增加程度, 最终使得发动机推力随着马赫数的增大而继续增加。

|
| 图 11 射流预冷涡轮/双模态超燃冲压组合发动机推力特性 Fig.11 Thrust performances of Pre-cooled Turbine /Dual-mode Scramjet |
|
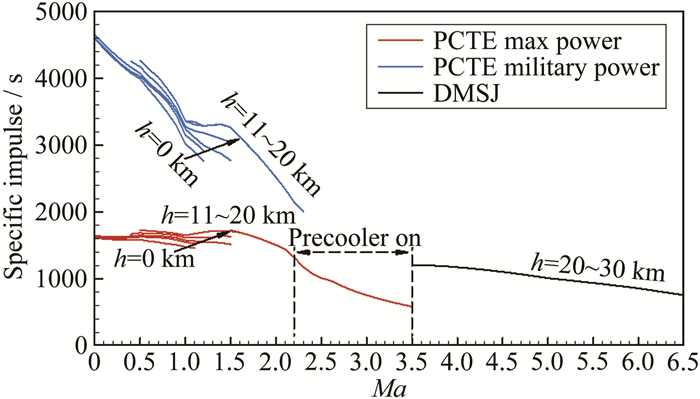
| 图 12 射流预冷涡轮/双模态超燃冲压组合发动机比冲特性 Fig.12 Specific impulse performances of Pre-cooled Turbine /Dual-mode Scramjet |
图 12为组合发动机的比冲特性。Ma=0~2.2时, 射流预冷发动机的比冲特性与传统涡轮发动机相同; Ma=2.2~3.5时, 射流预冷发动机的比冲明显下降, 这是因为冷却水作为飞行器所携带的消耗工质, 需与发动机燃料一同包含在比冲计算中; 随着飞行马赫数增大, 自由流总温增加, 单位空气流量冷却至420K时的冷却水流量也随之增加, 因而其比冲随马赫数的增大而大幅度下降。Ma=3.5时, 射流预冷发动机的比冲已低于600s。
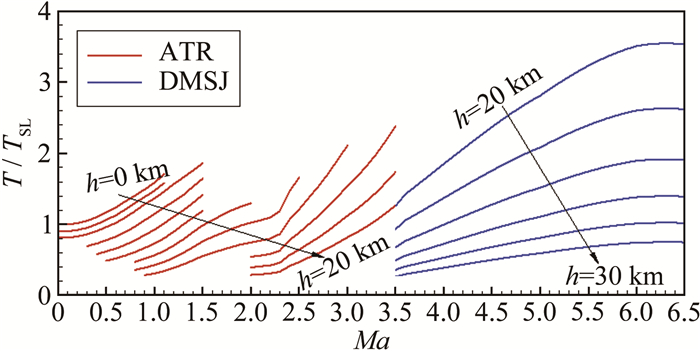
4.4 空气涡轮火箭/双模态超燃冲压组合发动机性能分析空气涡轮火箭/双模态超燃冲压组合发动机的高度、速度特性如图 13和14所示。图 13为组合发动机的推力特性。可以看到, 空气涡轮火箭发动机的推力随着飞行马赫数的增大而增大, 与引射冲压发动机相类似, 随着马赫数的增大, 其冲压能力有所提高, 同时涡轮机械的换算转速下降, 其风扇压比接近于1, 此时空气涡轮火箭发动机的工作模态类似于冲压发动机, 因此其推力随着马赫数的增大而增大。
|
| 图 13 空气涡轮火箭/双模态超燃冲压组合发动机推力特性 Fig.13 Thrust performances of Air-turbo-rocket/ Dual-mode Scramjet |

|
| 图 14 空气涡轮火箭/双模态超燃冲压组合发动机比冲特性 Fig.14 Specific impulse performances of Air-turbo-rocket/Dual-mode Scramjet |
图 14为组合发动机的比冲特性。与引射冲压发动机相类似, Ma=0~3.5时, 空气涡轮火箭发动机的比冲随着飞行马赫数的增大而增大, 但Ma=2.6~3.0时, 其比冲略微下降; 与引射冲压发动机在引射冲压模态时的比冲相比, 空气涡轮火箭的比冲较高。与之类似的是文献[19]在相同热力参数下对比了空气涡轮火箭发动机和引射冲压发动机的性能, 空气涡轮火箭发动机的比冲要高于引射冲压发动机的比冲, 这也说明了旋转机械的能量传递机理比粘性能量的传递机理更加有效[19]。尽管空气涡轮火箭发动机的比冲要高于引射火箭发动机, 但在低飞行马赫数范围内, 其比冲相比于传统涡轮发动机要低得多。
4.5 多种组合动力方案性能对比分析为进一步分析多种组合动力方案性能的差异, 在高度、速度特性图上选取若干点进行对比, 选取的飞行马赫数和飞行高度如表 3所示。
| Parameter | Value | ||||||||
| Ma | 0 | 0.5 | 1.0 | 2.0 | 3.0 | 3.5 | 4.0 | 5.0 | 6.0 |
| h/km | 0 | 3 | 11 | 13 | 18 | 20 | 22 | 24 | 28 |
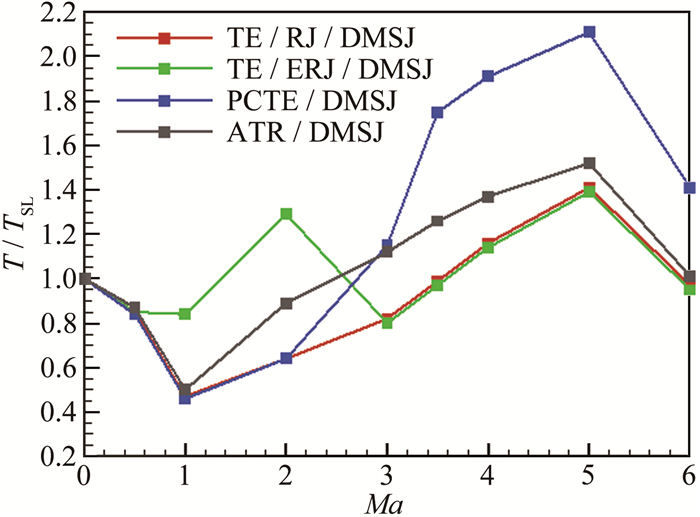
不同飞行马赫数和高度下的多种组合动力方案的推力和比冲分别如图 15和16所示。其中, 推力均作了归一化处理, 即多种组合动力均具有相同的起飞推力。从推力对比图可以看到:Ma=1.0~2.0时, 涡轮/引射冲压/双模态超燃冲压组合动力方案下的引射冲压发动机与涡轮发动机共同工作, 其推力明显提高; Ma>3.0时, 射流预冷涡轮/双模态超燃冲压组合动力具有明显的推力优势。从比冲对比图可以看到:Ma=0~6.0时, 涡轮/亚燃冲压/双模态超燃冲压组合动力具有较高的比冲; 涡轮/引射冲压/双模态超燃冲压组合动力在引射火箭工作时, 其比冲大幅度下降; Ma>3.0时, 射流预冷涡轮/双模态超燃冲压组合动力比冲较低。空气涡轮火箭/双模态超燃冲压组合动力的推力和比冲在4种组合动力方案中处于中间水平。因此, 多种组合动力方案的推力和比冲无法在单独的飞行状态点上进行一一比较, 并进而用来说明其性能优劣。"产品"性能的优劣, 还需要从"用户"体验角度进一步评判。组合动力的"用户"是高超声速飞行器, 因此, 需要开展基于多种组合动力的高超声速飞行器飞行性能对比研究。
|
| 图 15 4种组合动力方案推力对比 Fig.15 Thrust comparison of four different combined schemes |

|
| 图 16 4种组合动力方案比冲对比 Fig.16 Specific impulse comparison of four different combined schemes |
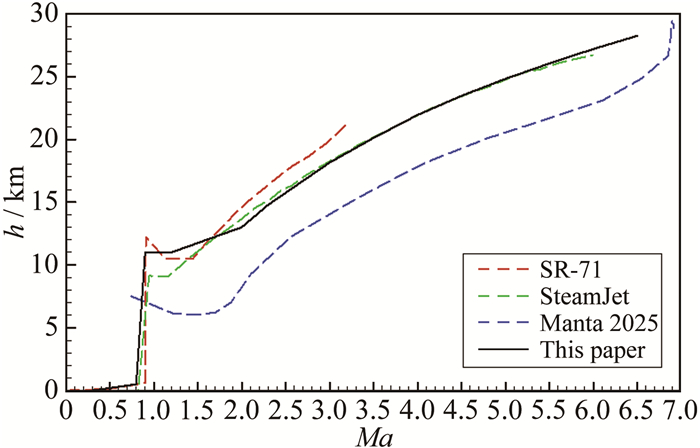
进行高超声速飞行器飞行性能计算, 首先需要确定高超声速飞行器的飞行轨迹。图 17中的红色、绿色和蓝色曲线分别给出了SR-71[22]、SteamJet[4]和Manta 2025[23]的飞行轨迹。虽然每个飞行器的飞行轨迹不尽相同, 但一般包括:(1)从海面起飞, 水平加速至Ma=0.8~0.9;(2)等马赫数爬升至h=8~11km; (3)水平加速或俯冲加速至Ma=1.2~1.5的跨声速航段; (4)爬升加速至等动压段的起始马赫数和高度, 等动压段范围依据机体结构、热防护、燃烧室燃烧稳定性等诸多因素, 一般在24~96kPa之间选取[19], SR-71、SteamJet和Manta 2025飞行器的等动压段范围为34~96kPa; (5)等动压爬升至巡航马赫数和高度; (6)等马赫数和等高度巡航。
基于上述飞行轨迹, 本文所确定的飞行轨迹如图 17中的黑色曲线所示。该飞行轨迹的关键航段包括:海平面起飞, 爬升加速至Ma=0.8、h=0.5km; 等速爬升至h=11km; 水平加速至Ma=1.2;爬升加速至Ma=2.0、h=13km, 此时动压为46.3kPa; 等动压爬升至Ma=6.5、h=28km; 此后飞行器开始进行等马赫数、等高度巡航。为了简化计算, 飞行轨迹中忽略了下滑和着陆航段, 这是因为在下滑和着陆航段中不需要发动机做功, 飞行器依靠自身阻力或减速伞减速下降, 发动机仅工作在慢车状态, 其对整个飞行任务的燃油消耗影响较小。详细的飞行马赫数和飞行高度沿飞行轨迹的变化如表 4所示。
| Phase | Initial Mach number | Final Mach number | Initial attitude/km | Final attitude/km |
| 1-2 | 0.00 | 0.29 | 0.0 | 0.0 |
| 2-3 | 0.29 | 0.80 | 0.0 | 0.5 |
| 3-4 | 0.80 | 0.90 | 0.5 | 11.0 |
| 4-5 | 0.90 | 1.20 | 11.0 | 11.0 |
| 5-6 | 1.20 | 2.00 | 11.0 | 13.0 |
| 6-7 | 2.00 | 2.30 | 13.0 | 14.8 |
| 7-8 | 2.30 | 2.50 | 14.8 | 15.7 |
| 8-9 | 2.50 | 3.00 | 15.7 | 18.1 |
| 9-10 | 3.00 | 3.50 | 18.1 | 20.1 |
| 10-11 | 3.50 | 4.00 | 20.1 | 21.9 |
| 11-12 | 4.00 | 4.50 | 21.9 | 23.5 |
| 12-13 | 4.50 | 5.00 | 23.5 | 24.8 |
| 13-14 | 5.00 | 5.50 | 24.8 | 26.0 |
| 14-15 | 5.50 | 6.00 | 26.0 | 27.2 |
| 15-16 | 6.00 | 6.50 | 27.2 | 28.2 |
| 16-17 | 6.50 | 6.50 | 28.2 | 28.2 |
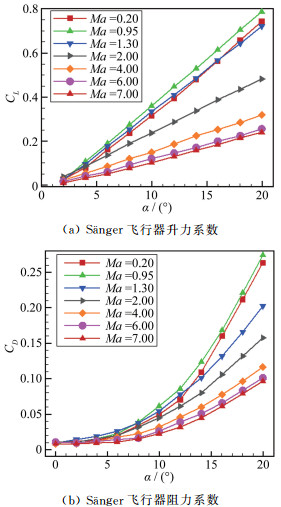
在给定飞行轨迹后, 还需要高超声速飞行器的升阻特性作为飞行性能计算的输入条件。高超声速飞行器具有宽广的飞行马赫数范围, 必须采用具有高升阻比的气动外形设计。目前, 高超声速飞行器常采用升力体、乘波体和高的长细比气动外形。不同气动外形的高超声速飞行器所针对的飞行任务有所不同。对于高超声速巡航飞行器, 其气动外形应综合考虑不同马赫数下的气动性能, 在上述3种气动外形中进行折中[24]。本文采用典型的高超声速飞行器——Sänger飞行器的升阻特性[25], 如图 18所示。可以看到, 该飞行器的阻力系数和升力系数在跨声速附近(Ma=0.95)达到最大。
|
| 图 18 Sänger飞行器升力系数和阻力系数 Fig.18 Lift coefficient and drag coefficient of Sänger |
在上述给定的飞行任务、飞行器升阻特性以及相同的起飞重力和推进剂重力下(推进剂包含燃料、氧化剂和冷却水等, 共占飞行器起飞总重的45%), 分别计算了不同起飞推重比下的各组合动力方案的飞行性能。
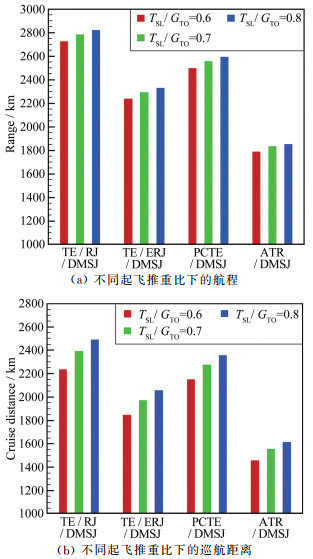
翼载为4000Pa时, 起飞推重比分别为0.6、0.7和0.8下的不同组合动力方案的航程和巡航距离如图 19所示。从图中可以看到:飞行器的航程和巡航距离随着起飞推重比的增大而增加; 涡轮/亚燃冲压/双模态超燃冲压组合发动机的航程和巡航距离最大, 而射流预冷涡轮/双模态超燃冲压组合发动机和涡轮/引射冲压/双模态超燃冲压组合发动机次之, 空气涡轮火箭/双模态超燃冲压发动机的航程和巡航距离最小。
|
| 图 19 不同起飞推重比下的多种组合动力方案航程和巡航距离 Fig.19 The range and the cruise distance of different takeoff thrust-loading |
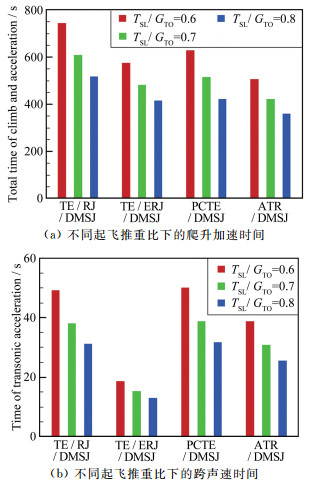
图 20给出了不同起飞推重比下的多种组合动力方案的总爬升加速时间和跨声速时间。从图中可以看到, 随着起飞推重比的增大, 飞行器的加速时间明显减少。空气涡轮火箭/双模态超燃冲压组合发动机的总爬升加速时间最短; 而在跨声速段, 涡轮/引射冲压/双模态超燃冲压组合发动机的飞行时间最短。
|
| 图 20 不同起飞推重比下的多种组合动力方案爬升加速时间和跨声速时间 Fig.20 The climb and acceleration time and the transonic time of different takeoff thrust-loading |
由上述结果可以看到, 飞行器的飞行性能随着起飞推重比的增大而提高, 其原因为:在飞行器升阻特性和发动机高度、速度特性不变的情况下, 在飞行过程中, 随着起飞推重比的增大, 加速性能提高, 飞行器可以更快地爬升加速至巡航点, 因而有更多燃料可以用于巡航, 巡航距离也因此增大。
从4种组合动力方案的飞行性能比较可以看到:在相同的翼载和起飞推重比下, 涡轮/亚燃冲压/双模态超燃组合冲压发动机具有最大的航程和巡航距离, 但其爬升加速时间也最长; 而空气涡轮火箭/双模态超燃冲压组合发动机的航程和巡航距离最短, 但其加速性能较高, 爬升加速的时间最短。
6 结论针对涡轮/亚燃冲压/双模态超燃冲压组合发动机、涡轮/引射冲压/双模态超燃冲压组合发动机、射流预冷涡轮/双模态超燃冲压组合发动机和空气涡轮火箭/双模态超燃冲压组合发动机等4种组合动力方案进行了性能计算与对比分析, 基于相同的高超声速飞行器飞行任务和气动特性, 比较了不同动力组合方案下的飞行器航程、巡航距离和加速时间等性能参数。主要结论如下:
(1) 在4种方案中, 涡轮/亚燃冲压/双模态超燃冲压组合发动机方案具有较高的比冲。
(2) Ma=1.0~2.0时, 涡轮/引射冲压/双模态超燃冲压组合发动机方案下的引射冲压发动机与涡轮发动机共同工作, 推力明显提高; Ma>3.0时, 射流预冷涡轮/双模态超燃冲压组合发动机方案具有明显的推力优势; 在引射火箭工作时, 涡轮/引射冲压/双模态超燃冲压组合发动机方案的比冲大幅度下降; Ma>3.0时, 射流预冷涡轮/双模态超燃冲压组合发动机方案的比冲较低; 在4种方案中, 空气涡轮火箭/双模态超燃冲压组合发动机方案的推力和比冲处于中间水平。
(3) 在4种方案中, 飞行器航程、巡航距离均随着起飞推重比的增大而增大, 而爬升加速时间随着起飞推重比的增大而明显缩短。
(4) 在相同的翼载和起飞推重比下, 涡轮/亚燃冲压/双模态超燃冲压组合发动机方案具有最大的航程和巡航距离, 但其爬升加速时间也最长; 而空气涡轮火箭/双模态超燃冲压组合发动机方案的航程和巡航距离最短, 但其加速性能较高, 爬升加速的时间最短。
| [1] |
Bartolotta P A, McNelis N B, Shafer D G. High speed turbines: development of a turbine accelerator (RTA) for space access[R]. AIAA-2003-6943, 2003.
|
| [2] |
Hagseth P E, Benner K W, Gillen S, et al. Technology deve-lopment for high speed/hypersonic applications[R]. AIAA-2005-3212, 2005.
|
| [3] |
Carter P, Balepin V V. Mass injection and precompressor cooling engines analyses[R]. AIAA-2002-4127, 2002.
|
| [4] |
Balepin V. Liston G W. The SteamJetTM: Mach 6+ turbine engine with inlet air conditioning[R]. AIAA-2001-3238, 2001.
|
| [5] |
Sato T, Tanatsugu N, Hatta H, et al. Development study of the ATREX engine for TSTO spaceplane[R]. AIAA-2001-1839, 2001.
|
| [6] |
Isomura K, Omi J, Murooka T, et al. A feasibility study of an ATREX engine at approved technology levels[R]. AIAA-2001-1836, 2001.
|
| [7] |
Sawai S, Sato T, Kobayashi H, et al. Flight test plan for ATREX engine development[R]. AIAA-2003-7027, 2003.
|
| [8] |
Harada K, Tanatsugu N, Sato T. Development study on precooler for ATREX engine[R]. AIAA-1999-4897, 1999.
|
| [9] |
Kojima T, Tanatsugu N, Sato T, et al. Development study on axisymmetric air inlet for ATREX engine[R]. AIAA-2001-1895, 2001.
|
| [10] |
Bulman M J, Siebenhaar A. Combined cycle propulsion: aerojet innovations for practical hypersonic vehicles[R]. AIAA-2011-2397, 2011.
|
| [11] |
Siebenhaar A, Bogar T J. Integration and vehicle performance assessment of the aerojet "Trijet" combined-cycle engine[R]. AIAA-2009-7420, 2009.
|
| [12] |
廉筱纯, 吴虎. 航空发动机原理[M]. 西安: 西北工业大学出版社, 2005.
|
| [13] |
Sellers J F, Daniele C J. DYNGEN: a program for calculating steady-state and transient performance of turbojet and turbofan engines[R]. NASA-TN-D-7901, 1975.
|
| [14] |
骆广琦, 桑增产, 王如根, 等. 航空燃气涡轮发动机数值仿真[M]. 北京: 国防工业出版社, 2007.
|
| [15] |
商旭升, 蔡元虎, 陈玉春, 等. 高速飞行器用射流预冷却涡轮基发动机性能模拟[J]. 中国空间科学技术, 2005, 25(4): 54-58. Shang X S, Cai Y H, Chen Y C, et al. Performance simulation of the mass injection pre-cooled TBCC engine for hypersonic vehicles[J]. Chinese Space Science and Technology, 2005, 25(4): 54-58. DOI:10.3321/j.issn:1000-758X.2005.04.009 |
| [16] |
陈湘, 陈玉春, 屠秋野, 等. 空气涡轮火箭发动机的性能研究[J]. 弹箭与制导学报, 2009, 29(2): 162-165. Chen X, Chen Y C, Tu Q Y, et al. Research on performance of air-turbo-rocket[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(2): 162-165. DOI:10.3969/j.issn.1673-9728.2009.02.046 |
| [17] |
李文龙, 郭海波, 南向谊. 空气涡轮火箭发动机热力循环特性分析[J]. 火箭推进, 2015, 41(4): 48-54. Li W L, Guo H B, Nan X Y. Analysis on thermodynamic cycle characteristics of air-turbo-rocket engine[J]. Journal of Rocket Propulsion, 2015, 41(4): 48-54. DOI:10.3969/j.issn.1672-9374.2015.04.008 |
| [18] |
潘宏亮, 林彬彬, 刘洋. 加力式空气涡轮火箭发动机特性研究[J]. 固体火箭发动机技术, 2010, 33(6): 650-665. Pan H L, Lin B B, Liu Y. Performance study on air turbo rocket in augmented mode[J]. Journal of Solid Rocket Technology, 2010, 33(6): 650-665. |
| [19] |
Heiser W H, Pratt D T, Daley D H, et al. Hypersonic airbreathing propulsion[M]. Reston, VA: AIAA Education, 1994.
|
| [20] |
Mattingly J D, Heiser W H, Pratt D T. Aircraft engine design[M]. 2nd ed. Reston, VA: AIAA Education, 2002.
|
| [21] |
Walker S, Tang M, Mamplata C. TBCC propulsion for a Mach 6 hypersonic airplane[R]. AIAA-2009-7238, 2009.
|
| [22] |
Kloesel K J, Ratnayake N A, Clark C M. A technology pathway for airbreathing, combined-cycle, horizontal space launch through SR-71 based trajectory modeling[R]. AIAA-2011-2229, 2011.
|
| [23] |
Tzong G, Jacobs R, Liguore S. Predictive capability for hypersonic structural response and life prediction: Phase 1-identification of knowledge gaps[R]. Air Force Research Laboratory-RB-WP-TR-2010-3068, 2010.
|
| [24] |
Tang M, Mamplata C. Two steps instead of a giant leap-an approach for air breathing hypersonic flight[R]. AIAA-2011-2237, 2011.
|
| [25] |
Hirschel E H, Weiland C. Selected aerothermodynamic design problems of hypersonic flight vehicles[M]. Berlin: Springer Science and Business Media, 2009.
|
| [26] |
Anderson D, Tannehill J C, Pletcher R H. Computational fluid mechanics and heat transfer[M]. 3rd ed. Boca Raton: CRC Press, 2012.
|