麦克风相位阵列测量技术的应用[1-5],使得声学风洞试验能够对试验模型的主要噪声源进行定位,获取声源强度、频率等丰富的声学特性信息,成为当前飞行器声学试验研究中不可或缺的测量手段。
麦克风相位阵列测量性能主要通过阵列分辨率(Resolution)和最大旁瓣水平(Maximum Sidelobe Level, MSL)进行衡量。阵列分辨率和最大旁瓣水平会随着目标声源频率的改变而发生明显变化。同一期声学风洞试验中模型构型、来流风速等试验状态的不同,可能导致主要声源位置、尺寸和噪声频率的显著改变,对麦克风阵列分辨率和最大旁瓣水平的需求也随之变化,从而超出了原有阵列的最佳适用范围,导致某些状态下测量结果的精准度受到影响。为了实现最佳测量效果,麦克风相位阵列也应针对声源特性的变化而实时改进,但是,这一改进过程必须满足风洞试验对现场操作的高效率要求。目前声学试验中普遍采用格栅式快速插拔阵列支架,能够支持麦克风阵列的快速拆装,因此,需要解决的问题是:根据试验状态对阵列分辨率和最大旁瓣水平的需求,如何在较短的时间内完成麦克风相位阵列的优化设计。
在麦克风相位阵列设计方面,国内外研究人员研究了阵列尺寸和麦克风布置方式等因素对阵列分辨率和最大旁瓣水平的影响,并且将粒子群算法、模拟退火法等优化设计方法引入了麦克风阵列设计中[4, 6-13]。但是以上研究方法并未考虑阵列设计的耗时问题。尽管阵列设计中通常采用计算量较小的点扩散函数进行阵列性能分析,但是当声源定位面内扫描点数较多,优化搜索空间较大时,计算量将会显著增加,完成整个阵列优化工作可能需要耗时数小时至数十个小时不等。这种计算耗时无法满足风洞试验过程中及时改进麦克风阵列的应用需求,必须研究更加高效的麦克风相位阵列设计方法。
基于Kriging模型的优化方法很好地解决了计算量与计算精度的问题,显著提升了优化效率,已经在飞行器气动设计领域得到了大量的应用[14-21]。文献[14]开展了旋翼桨尖气动与噪声综合优化设计研究,其中旋翼的气动性能和噪声特性需要应用非定常流场求解方法进行计算,单点计算耗时较高。如优化过程中全部采用非定常方法进行目标函数计算,则其计算量将急剧增加,无法满足工程应用需求。文章采用Kriging模型代替复杂费时的非定常计算,采用遗传算法进行优化,有效解决了计算耗时问题,建立了一种工程实用的旋翼桨尖优化设计方法。此外,为了解决计算量过大的问题,文献[15]应用Kriging模型进行了机翼气动/结构刚度耦合优化设计,文献[16]将Kriging模型应用于高升力翼型的优化设计研究。可见,Kriging模型的应用是提升优化效率的有效方法。
为了最大限度提升麦克风相位阵列设计效率,本文借鉴飞行器气动优化设计领域的研究方法,创新性地将Kriging代理模型方法引入阵列优化设计研究中。采用点扩散函数进行样本点性能分析,建立Kriging模型,应用遗传算法进行优化,形成了一种效率极高的麦克风阵列设计方法。该方法可有效改善阵列对目标声源的测量性能,满足声学风洞试验中针对特定声源及时改进麦克风相位阵列的需求,有助于改善试验测量精准度,提升试验效率。
1 基于代理模型的阵列优化设计方法 1.1 阵列性能分析方法阵列性能分析是通过给定模拟点声源,计算阵列对该声源激励的波束形成响应来评估阵列性能的一种技术手段。阵列设计过程中,进行阵列性能量化分析时,波束形成响应通常表示为点扩散函数(Point Spread Function, PSF)[22]。采用基于点扩散函数的计算方法分析阵列对模拟声源的定位效果,是阵列设计过程中较为常用且可靠的性能分析方法,可以定量地评价麦克风阵列定位性能。计算方法如下:
阵列测量位于yj处的单位声源,获得互谱矩阵(Cross Spectrum Matrix, CSM):
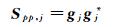 (1)
(1)
其中,gj*为gjT的共轭矩阵,gjT=[G (x1, yj), G (x2, yj), …, G (xm, yj)],G (x, y)为如下非奇次Helmholtz方程的解:
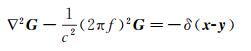 (2)
(2)
则位于yj的单位声源在扫描点k处的波束形成输出可表示为:
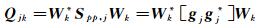 (3)
(3)
上式为PSF的定义式,Wk为对应麦克风的权向量,是关于引导向量g的函数,取决于麦克风阵列与扫描平面的位置、测量环境与声源频率。
采用点扩散函数完成全部扫描点上的波束形成输出计算后,阵列性能分析结果通常以声压级云图的形式给出,从中可以获取阵列分辨率和最大旁瓣水平两个主要性能参数。其中,阵列分辨率描述了阵列定位声源和分辨临近声源的能力;阵列的最大旁瓣水平表明阵列放大目标声源、抑制背景噪声的能力。
1.2 设计变量与约束条件与其他阵列形式相比,多臂螺旋阵列能够在较宽的频率范围内保持良好的旁瓣抑制性能,因此在声学试验中得到了广泛应用,本文主要针对这种阵列进行优化设计举例。已有的多臂螺旋阵列设计方法中,螺旋线上麦克风的位置主要采用等弧长分布,或者等环形区域面积分布的方式确定[22],无需进行优化计算,但是设计空间较为单一。本文将多臂螺旋阵列的螺旋线轨迹、麦克风分布位置、旋臂数等信息进行参数化,拓展了阵列设计空间,通过对设计参数的优化,搜索得到性能优良的阵列方案。多臂螺旋阵列设计参数包括:悬臂数目n,螺旋线系数a和k,麦克风沿螺旋线分布参数q。
对数螺旋线可用极坐标表示如下:
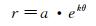 (4)
(4)
其中,r为极径,θ为极角,a、k为常系数。
当系数a、k确定之后,螺旋线的轨迹即为确定值。麦克风在螺旋线上的分布通过参数q进行确定,具体方法如下:
相邻两麦克风间螺旋线弧长成等比增长,比值为q。对于最大极径为R的对数螺旋线,当q=1时,螺旋线上麦克风为均匀分布;q≠1时,第m个麦克风的极坐标为:
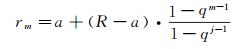 (5)
(5)
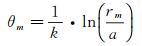 (6)
(6)
其中,j为单条悬臂上麦克风数量,由整个阵列可用的麦克风总数和悬臂条数决定。
对于有n条旋臂的螺旋阵列,将阵列面板按2π/n弧度等分为n份,并通过麦克风坐标点的旋转复制得到整个阵列坐标。
试验环境、设备以及试验对象等因素决定了麦克风阵列设计需要考虑的约束条件。试验场地的空间限制和声源定位范围约束了阵列最大直径;试验中可供使用的麦克风总数量决定了阵列单元数;麦克风尺寸和安装方式决定了两麦克风最小间距。因此,优化过程中的约束条件包括:阵列直径、麦克风数量、麦克风最小间距。
1.3 基于Kriging模型的遗传算法遗传算法不仅具有全局性优化的特点,而且具有良好的鲁棒性、可靠性和移植性,在工程优化设计领域应用较为广泛。但是遗传算法通常需要的种群规模庞大,容易导致计算量过大。本文采用基于Kriging模型的遗传算法开展阵列优化设计。Kriging模型在保证阵列性能预测精度的同时,极大地提升了优化效率,同时使遗传算法的种群规模不再受到计算量的限制,有效拓展了优化搜索空间。
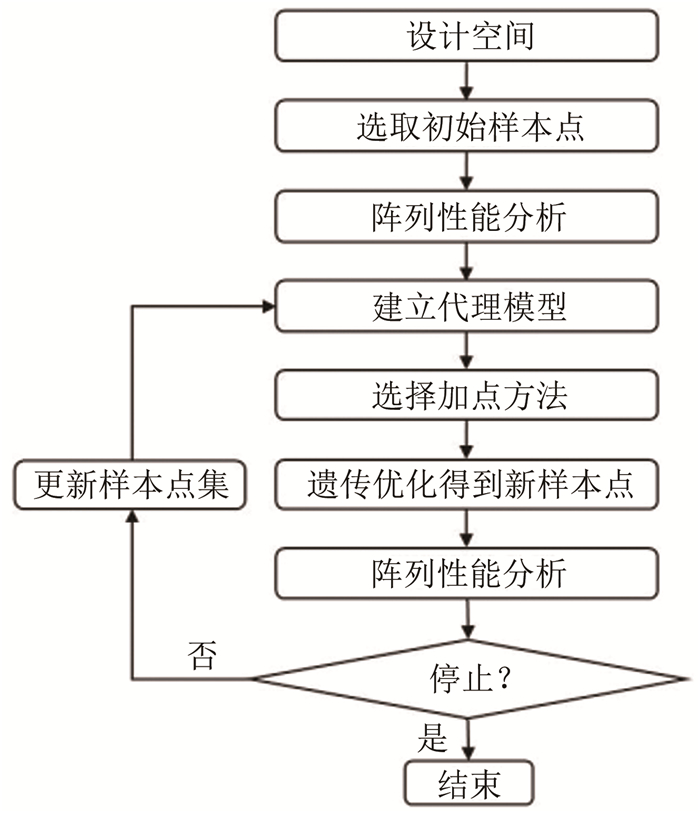
Kriging代理模型是一种插值模型,由一个参数模型和一个非参数随机过程构成,通过选择适当的优化算法计算得到模型参数最优值,进而建立Kriging模型[18-19]。图 1给出了基于代理模型的阵列优化方法流程图。其基本思想为:
|
| 图 1 优化设计方法流程图 Fig.1 Flowchart of the optimization design method |
(1) 采用试验设计方法生成设计空间内的样本点;
(2) 通过阵列性能分析程序计算样本点的响应值;
(3) 由样本信息及其响应值构建代理模型;
(4) 采用遗传算法进行优化,种群适应度计算由代理模型完成;
(5) 按照选定的加点方法,搜索性能更优的样本点;
(6) 采用阵列性能分析程序对最优样本点进行分析;
(7) 判断是否达到设计目标,若是,则输出结果,停止优化;若否,则对原样本集进行更新,以建立更加精确的代理模型,返回步骤(3),重复优化过程直至满足停止条件。
2 麦克风阵列优化设计算例针对分辨率和最大旁瓣水平两个指标分别进行阵列优化,以验证该优化设计方法的实用性。当分辨率为目标函数时,设置满足试验测量要求的最大旁瓣水平下限指标作为约束条件;以最大旁瓣水平为目标函数时,则给定分辨率指标作为约束。
2.1 多臂螺旋阵列分辨率优化针对1m直径量级63通道多臂螺旋阵列进行优化设计,优化问题总结如下:
设计状态:2kHz单极子模拟声源,定位区域1m×1m;
目标函数:分辨率最小,最大旁瓣水平≤-14dB;
设计变量:悬臂数目n,螺旋线系数a,k,分布参数q;
设计约束:阵列直径D=1m,麦克风最小间距dmin≥0.02m,麦克风总数Nm=63。
共调用60次阵列性能分析程序进行样本点计算,建立了代理模型。表 1给出了Kriging代理模型的预测结果与数值模拟分析结果对比,代理模型预测误差小于1%,预测精度完全满足优化设计需求。遗传算法优化过程中,以代理模型进行种群适应度计算,种群规模为200,交叉概率0.8,变异概率0.05,共进行了100代遗传优化。优化程序采用单核运行,整个优化过程耗时约10min,获得了性能较优异的阵列方案。可见,Kriging代理模型的应用显著减少了计算时间,极大地拓展了优化搜索的范围。
| 最大旁瓣水平/dB | 分辨率/m | |
| 阵列性能分析结果 | -14.696 | 0.1467 |
| 代理模型预测结果 | -14.680 | 0.1460 |
| 相对误差 | 0.07% | 0.45% |
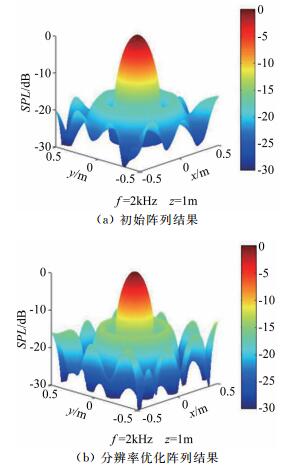
取每个设计变量上、下限的平均值为初始阵列,作为设计参考,优化前后设计变量取值如表 2所示。优化前后阵列单元分布情况如图 2所示,可见优化后阵列从中心向边缘方向,单条螺旋线上麦克风间距逐渐减小,阵列单元的分布有向阵列边缘移动的趋势。图 3给出了2kHz模拟声源下阵列响应云图,可见优化阵列的分辨率有明显改善。
| 设计变量 | n | k | a | q |
| 变量范围 | 8~10 | 0.60~1.40 | 0.050~0.200 | 0.600~1.400 |
| 初始阵列变量值 | 9 | 1.00 | 0.150 | 1.000 |
| 优化阵列变量值 | 9 | 0.89 | 0.147 | 0.716 |
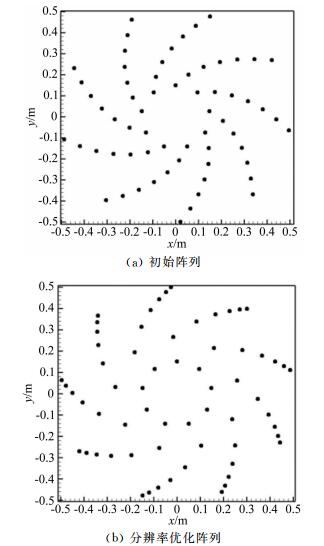
|
| 图 2 初始阵列与分辨率优化多臂螺旋阵列示意图 Fig.2 Schematic of initial array and resolution optimized multi-arm spiral microphone array |
|
| 图 3 初始阵列与分辨率优化阵列响应图 Fig.3 Responses of initial array and resolution optimized microphone array |
与全尺寸飞机相比,航空声学风洞试验中的试验模型通常是经过大幅缩比的,主要噪声的频率被相应放大。因此,本文主要进行1~6kHz频率范围内麦克风阵列测量性能分析,能够满足航空声学风洞试验的大部分测量需求。表 3给出了优化后阵列与初始阵列性能对比数据,在1~6kHz频率范围内,优化阵列的分辨率均优于初始阵列,以设计点2kHz频率性能为例,优化阵列分辨率从0.187m改善为0.164m,旁瓣声压级(SPL)略有升高,但最大旁瓣水平(MSL)满足-14dB的约束要求。
| 初始阵列 | 优化阵列 | |||
| 频率/ kHz |
最大旁瓣水平/dB | 分辨率 /m |
最大旁瓣水平/dB | 分辨率 /m |
| 1 | -17.412 | 0.388 | -14.237 | 0.341 |
| 2 | -16.882 | 0.187 | -14.330 | 0.164 |
| 3 | -15.535 | 0.123 | -11.868 | 0.108 |
| 4 | -15.252 | 0.089 | -11.934 | 0.080 |
| 5 | -14.771 | 0.070 | -11.992 | 0.061 |
| 6 | -14.188 | 0.057 | -10.235 | 0.048 |
麦克风阵列最大旁瓣水平优化算例的设计状态、设计变量、设计约束等均保持不变,目标函数变化为:最大旁瓣水平降低、分辨率≤0.2m。
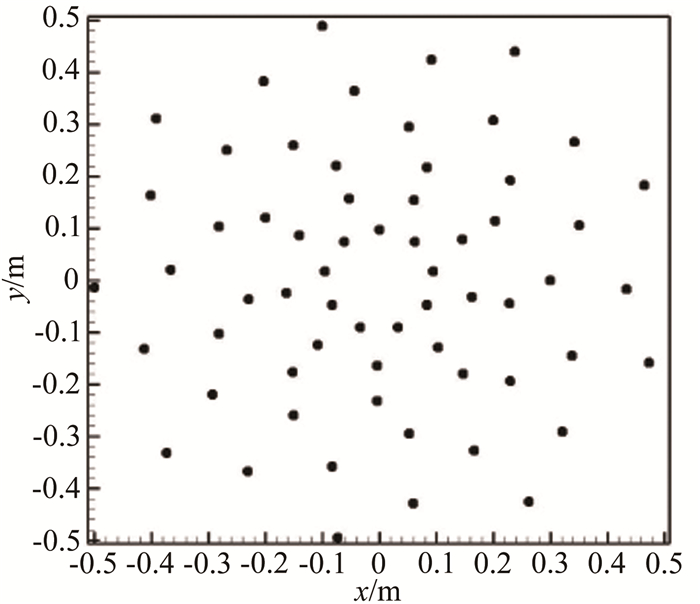
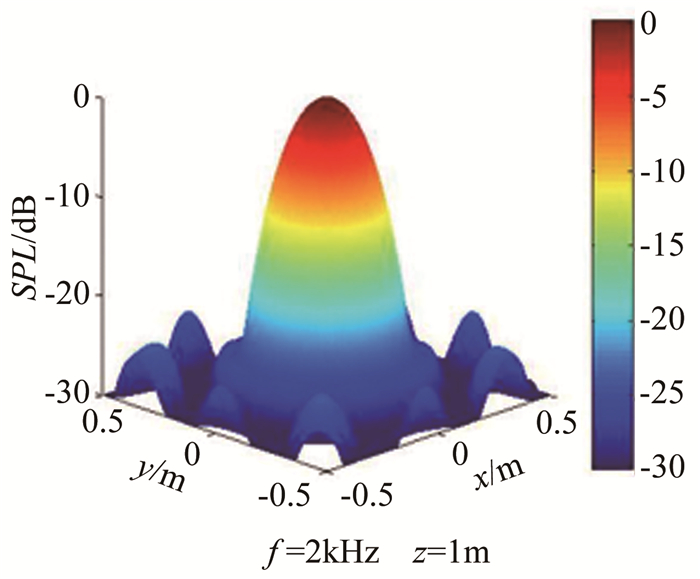
优化后阵列单元分布如图 4所示,可见优化后阵列单元向中心区域集中。图 5给出了2kHz模拟声源下的阵列响应云图,可见优化阵列的最大旁瓣水平有明显改善。表 4给出了优化后阵列与初始阵列性能对比数据,可以看出在1~6kHz频率范围内,优化阵列的最大旁瓣水平明显优于初始阵列,以设计点2kHz频率下性能为例,优化阵列最大旁瓣水平有5dB的改善,分辨率满足0.2m的优化约束条件。
|
| 图 4 最大旁瓣水平优化阵列示意图 Fig.4 Schematic of MSL optimized microphone array |
|
| 图 5 最大旁瓣水平优化阵列响应图 Fig.5 Responses of MSL optimized microphone array |
| 初始阵列 | 优化阵列 | |||
| 频率 /kHz |
最大旁瓣水平/dB | 分辨率 /m |
最大旁瓣水平/dB | 分辨率 /m |
| 1 | -17.412 | 0.388 | -20.537 | 0.412 |
| 2 | -16.882 | 0.187 | -21.922 | 0.198 |
| 3 | -15.535 | 0.123 | -19.346 | 0.129 |
| 4 | -15.252 | 0.089 | -16.105 | 0.094 |
| 5 | -14.771 | 0.070 | -15.698 | 0.074 |
| 6 | -14.188 | 0.057 | -14.009 | 0.061 |
以上阵列优化算例表明:本文发展的麦克风相位阵列设计方法能够根据试验具体需求,优化设计出性能优良的阵列方案,且优化效率极高,满足声学试验过程中随时改进麦克风阵列的特殊需求。对最大旁瓣水平进行优化时,阵列单元沿螺旋线分布有向阵列中心聚集的趋势,同时分辨率会略变差。相反,对阵列分辨率进行优化时,阵列单元沿螺旋线分布有向阵列边缘移动的趋势,最大旁瓣水平则会略变差。可见,最大旁瓣水平和分辨率这两个性能指标在一定条件下是此消彼长的关系,无法同时优化到最优值。阵列设计工作需要考虑声学试验的声源强度、特征尺寸等具体因素,在一个指标满足基本约束的情况下,尽量提升最重要的核心指标。作为约束的指标可能会有所下降,但仍满足基本需求,而核心指标的大幅提升则能够明显改善试验测量结果的精准度。
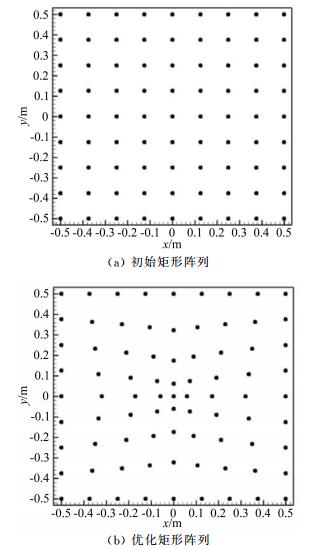
2.3 矩形阵列设计该阵列优化设计方法具有较强的可拓展性,只需针对参数化部分进行修改,即可应用于其他形式的阵列设计。针对81通道的1m边长矩形阵列,将阵列单元的横、纵坐标作为设计参数。以阵列单元在平面内的均匀分布作为初始方案,通过对阵元分布趋势的优化,提升阵列最大旁瓣水平。图 6给出了优化前后矩形阵列单元分布示意图。
|
| 图 6 初始阵列与最大旁瓣水平优化矩形麦克风阵列对比 Fig.6 Comparison of initial array and MSL optimized rectangular microphone array |
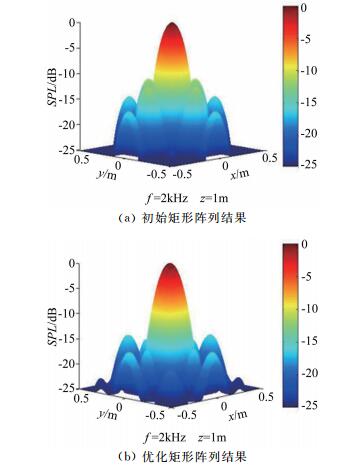
图 7给出了2kHz模拟声源下阵列响应云图,可见旁瓣水平有明显改善。表 5给出了1~6kHz频率下阵列性能对比数据,优化阵列的最大旁瓣水平改善显著,分辨率略变差。其中,声源频率为2kHz时,优化后矩形阵列最大旁瓣水平改善了4.2dB,提升约35.85%;分辨率下降约5.62%。整体而言,阵列性能有明显提升。
|
| 图 7 初始阵列与最大旁瓣水平优化矩形麦克风阵列响应图 Fig.7 Responses of initial array and MSL optimized rectangular microphone array responses |
| 初始阵列 | 优化阵列 | |||
| 频率 /kHz |
最大旁瓣水平/dB | 分辨率 /m |
最大旁瓣水平/dB | 分辨率 /m |
| 1 | -12.545 | 0.302 | -16.101 | 0.320 |
| 2 | -11.786 | 0.146 | -16.012 | 0.155 |
| 3 | -11.798 | 0.094 | -15.450 | 0.101 |
| 4 | -11.800 | 0.068 | -15.252 | 0.073 |
| 5 | -11.806 | 0.053 | -15.147 | 0.056 |
| 6 | -6.523 | 0.042 | -11.271 | 0.046 |
将基于Kriging代理模型的遗传算法引入麦克风相位阵列设计研究中,形成了高效率麦克风相位阵列设计方法,得到研究结论如下:
(1) 阵列优化结果表明:该优化设计方法可以根据试验研究的具体需求进行麦克风相位阵列设计,有效提升麦克风相位阵列的分辨率或最大旁瓣水平性能,是一种可靠实用的麦克风相位阵列设计方法。
(2) Kriging代理模型的引入使得阵列优化设计过程耗时极短,可以满足声学风洞试验中随时针对声源特点而改进麦克风相位阵列的特殊应用需求,有利于改善声学风洞试验测量数据的精准度,显著提升试验效率。
(3) 麦克风相位阵列的两个主要性能参数(分辨率和最大旁瓣水平)通常无法同时达到极值,阵列设计时需要根据试验测量的实际需求,搜寻阵列性能的最佳平衡点。
(4) 该阵列优化设计方法具有较强的可拓展性,针对参数化部分进行修改后,即可应用于其他类型阵列的设计工作。
| [1] |
Brooks T F, Marcolini M A, Pope D S. A directional array approach for the measurement of rotor noise source distributions with controlled spatial resolution[J]. Journal of Sound and Vibration, 1987, 112(1): 192-197. DOI:10.1016/S0022-460X(87)80105-0 |
| [2] |
Ahmad D V, Radhakrishnan S. Review of acoustic measurement techniques in wind tunnels[R]. AIAA-2000-2204, 2000.
|
| [3] |
Wei Q K. Compressive sensing based beamforming and its application in aeroacoustic experiment[R]. AIAA-2014-2918, 2014.
|
| [4] |
周家检, 郝璇, 张卫民, 等. 相阵列技术在民机机体气动噪声研究中的应用[J]. 空气动力学学报, 2016, 34(1): 91-97. Zhou J J, Hao X, Zhang W M, et al. Application of phased array technique in the research of civil airplane airframe noise[J]. Acta Aerodynamic Sinica, 2016, 34(1): 91-97. |
| [5] |
陈正武, 王勋年, 李征初, 等. 基于声学风洞的麦克风阵列测试技术应用研究[J]. 实验流体力学, 2012, 26(3): 84-90. Chen Z W, Wang X N, Li Z C, et al. Application investigation of microphone array measuring and testing technique in anechoic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(3): 84-90. DOI:10.3969/j.issn.1672-9897.2012.03.016 |
| [6] |
Gade S, Hald J. Array designs optimized for both low-frequency NAH and high-frequency Beamforming[R]. SAE Technical Paper 2005-01-4014, 2015.
|
| [7] |
Underbrink J R. Practical considerations in focused array design for passive broadband source mapping applications[D]. Pennsylvania: Pennsylvania State University, 1995.
|
| [8] |
黄奔.气动噪声源的麦克风阵列识别定位技术研究[D].绵阳: 中国空气动力研究与发展中心, 2014. Huang B. Investigation of aerodynamic noise sources identification technique based on microphone arrays[D]. Mianyang: China Aerodynamics Research and Development Center, 2014. |
| [9] |
William M, Humphreys J R. Design and use of microphone direction arrays for aeroacoustic measurement[R]. AIAA-98-0471, 1998.
|
| [10] |
Thomas F B, William M, Humphreys J R. Effect of directional array size on the measurement of airframe noise components[R]. AIAA-99-1958, 1999.
|
| [11] |
Takeshi Ito. Aeroacoustic noise measurements in aerodynamic low-speed wind tunnels[C]//Proc of the 26th International Congress of the Aeronautical Sciences. 2008.
|
| [12] |
Sijtsma P. Phased array beamforming in wind tunnels[R]. NLR-TP-2006-732, 2006.
|
| [13] |
陈宝, 李周复, 谭啸, 等. 声衬试验段环境下航空声学定位试验技术研究[J]. 实验流体力学, 2015, 29(5): 78-83. Chen B, Li Z F, Tan X, et al. Investigation of aeroacoustic localization technique in lining test section[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(5): 78-83. |
| [14] |
郭旺柳, 宋文萍, 许建华, 等. 旋翼桨尖气动/降噪综合优化设计研究[J]. 西北工业大学报, 2012, 30(1): 73-79. Guo W L, Song W P, Xu J H, et al. An effective aerodynamics/acoustic optimization of blade tip planform for helicopter rotors[J]. Journal of Northwestern Polytechnical University, 2012, 30(1): 73-79. |
| [15] |
聂雪媛, 刘中玉, 杨国伟. 基于Kriging代理模型的飞行器结构刚度气动优化设计[J]. 气体物理, 2017, 2(2): 8-16. Nie X Y, Liu Z Y, Yang G W. Aircraft structure stiffness and aerodynamics optimization design based on Kriging surrogate model[J]. Physics of Gases, 2017, 2(2): 8-16. |
| [16] |
Kanazaki M, Tanaka K, Jeong S, et al. Multi-objective aerodynamic optimization of elements' setting for high-lift airfoil using Kriging model[R]. AIAA-2006-1471, 2006.
|
| [17] |
Han Z H. Improving adjoint-based aerodynamic optimization via gradient-enhanced Kriging[R]. AIAA-2012-0670, 2012.
|
| [18] |
刘俊.基于代理模型的高效气动优化设计方法及应用[D].西安: 西北工业大学, 2015. Liu J. Efficient surrogate-based optimization method and its application in aerodynamic design[D]. Xi'an: Northwestern Polytechnical University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10699-1016909342.htm |
| [19] |
韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. Han Z H. Kriging surrogate model and its application to design optimization:a review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225. |
| [20] |
夏露, 王丹. 基于Kriging自适应代理模型的气动优化方法[J]. 航空计算技术, 2013, 43(1): 13-17. Xia L, Wang D. Aerodynamic optimization method based on Kriging adaptive surrogate model[J]. Aeronautical Computing Technique, 2013, 43(1): 13-17. DOI:10.3969/j.issn.1671-654X.2013.01.004 |
| [21] |
Zhang Y, Han Z H, Shi L X, et al. Multi-round surrogate-based optimization for benchmark aerodynamic design problems[R]. AIAA-2016-1545, 2016.
|
| [22] |
Thomas J M. Aeroacoustic measurements[M]. Berlin: Springer, 2002.
|



