自喷气式发动机出现以来,进气道与发动机一体化就成为飞机研制的一个重要问题,其中最关键的是评估进气道流场畸变对发动机稳定性的影响[1-3]。对这一问题,国际上相关学者对总压畸变图谱的测量进行了大量研究[4-12],一是以美国为主的总压畸变图谱评估方法,即测量分析出口截面的动态总压图谱并进行模拟[13];二是以俄罗斯为主的总压畸变强度评估方法[14-15]。无论哪种方法,都以准确测量进气道出口总压为基础;两者区别在于,后者不模拟畸变图谱,只模拟畸变强度。目前,中国主要采用俄罗斯的方法体系。
对于传统S弯进气道,其长度较长,曲率不大,出口流场畸变不大,紊流度也较小,因此采用总压耙测量方法就可以获得可信赖的结果。例如,郁新华等人[16]在低亚声速来流情况下使用总压耙对出口流场进行测量。对于大S弯进气道,因其具有更大的流道曲率,截面变化也十分复杂,出口流场不均匀度和紊流度大增,从而使得总压耙测量方法难以准确测量总压并评估畸变强度[17-18]。国内外鲜有将五孔探针作为进气道出口总压测量的工具,而主要用于压气机叶片排进出口流场测量。例如,德国慕尼黑燃气轮机研究院(MTU)与法国国家航天研究院(ONERA)力能部[19]将五孔探针被用于压气机性能测量;Gilarranz等[20]设计的“L”型五孔探针被用于多级离心压气机级间测量。在国内,姜健[21]曾使用五孔探针测量进气道入口旋流,但探针数量较多,对流场干扰较大且未达到高密度的测量。江勇等人[22]以总压耙为主、局部使用三孔探针对出口截面进行测量。
针对传统测量方法的不足,本文提出基于五孔探针的总压测量方法,这在国内外尚无相关报道。采用多种方法处理数据,对比数值计算(Computational fluid dynamics, CFD)、测量耙两种方法,然后选取最合理、准确、连续的总压测量结果,再采用美国ASME协会的进气道畸变评估标准[23]对本文大S弯进气道模型进行评估。
1 五孔探针总压测量段 1.1 大S弯进气道总压测量面临的问题国内传统进气道试验使用固定的总压测量耙测量其出口截面的总压分布。测量耙上一般安装了5根直径1mm左右的总压管,测量耙的间隔在30°~60°之间(分别对应12耙和6耙),风洞小缩比模型通常采用60°间隔测量耙。当进气道出口气流角度较大时,总压管的测值会产生误差,测量管也可能发生抖动,使得总压恢复系数、畸变强度和流量等出现较大的评估误差。同时,由于进气道出口流场沿周向变化剧烈,当测量耙间隔过大时,有可能不能分辨出真实的畸变图谱,进而影响总压畸变的评估结果。因此,需要发展一种对流向角敏感度不高、能够加密测量点的测量手段。本文采用可径向移动和周向转动的五孔探针进行测量。
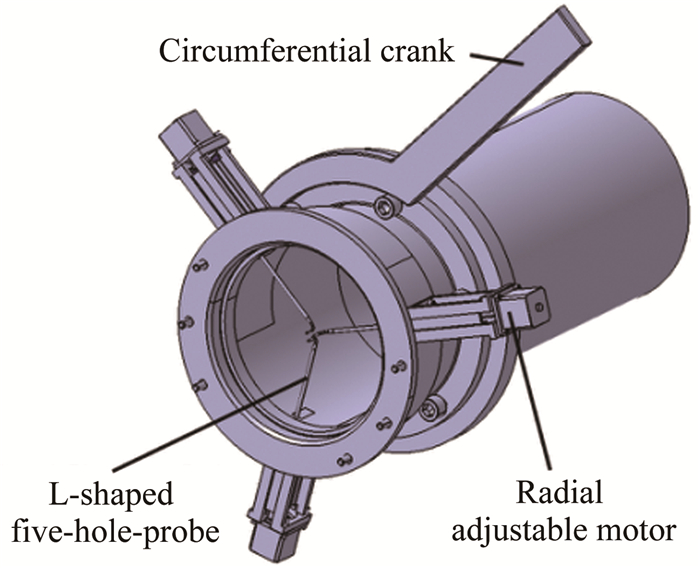
1.2 五孔探针测量段结构设计五孔探针测量段如图 1所示。探针由测量段的外壁面嵌入进气道出口流场中,受探针制造、校准等诸多因素的影响,在周向仅安装了3个L型五孔探针,探针间隔120°,呈人字形。探针尾部与轴向步进电机连接,由电机自动控制其径向移动。在轴向电机上集成了相对编码器,配合专用的电机驱动器,使步长达到了0.0079mm。电机驱动器与大S弯进气道试验台的控制系统相连,接收控制系统的控制信号,并将位置信息反馈给控制系统。测量段的周向转动采用的是手动方式,探针会随着测量段一起转动,从而实现任意周向站位的测量。
|
| 图 1 五孔探针测量段示意图 Fig.1 Five-hole-probe measurement |
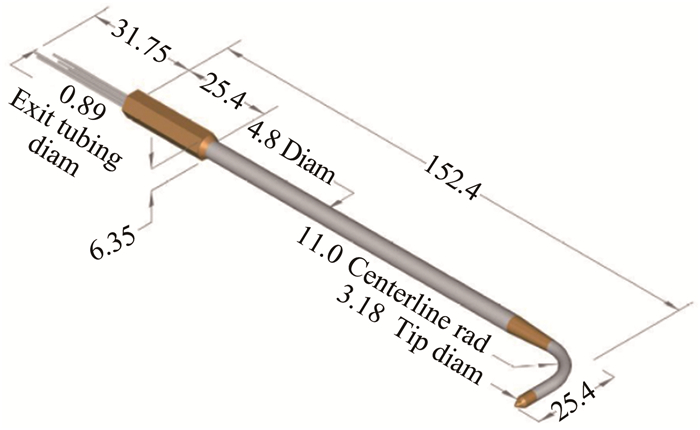
本文使用Aeroprobe公司的3个L型五孔探针,如图 2所示。探针头部为圆锥型,探针轴的长度为152.4mm、直径为4.8mm,头部长25.4mm、直径3.18mm,尾部的5根测压管连接到压力扫描阀的测压端口。校准马赫数0.1~1.5,流向角精度为0.4°,速度精度为0.8%,气流测量角为±60°[24]。
Aeroprobe推荐的五孔探针测量数据处理方法为局部最小二乘拟合方法[25](Local-Least Squares,LLS),其搜寻算法使用了专门的多区域搜寻程序和角度范围验证程序。另外还有一种分区拟合方法[26](Sector-Fitting,SF), 使用探针压力测值最大的几个点确定一个分区,读取对应分区的拟合系数,再进行快速拟合。分区拟合方法的精度不如前者,但是运算效率更高、速度更快,适用于实时数据处理。
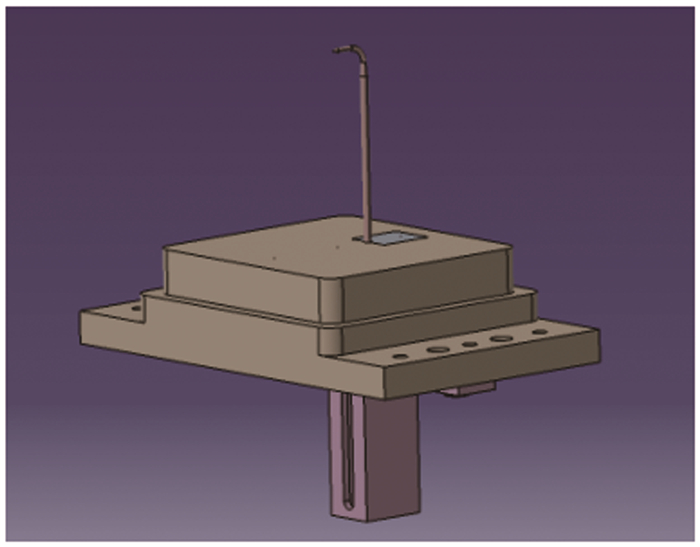
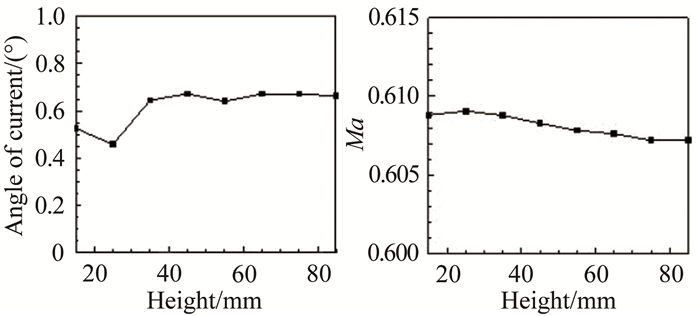
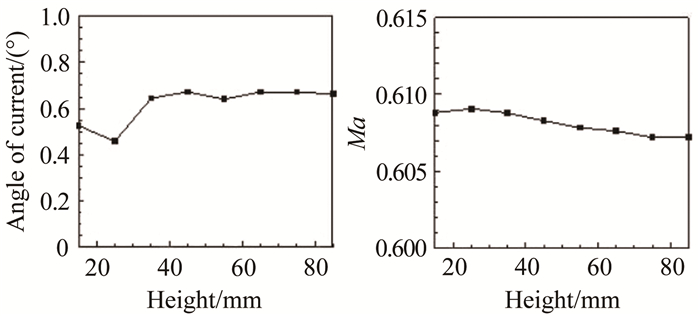
1.4 五孔探针的校准在开展试验以前,应对五孔探针进行校准。使用L型五孔探针测量了纵向速度场分布,入口马赫数在0.2~0.6之间。探针安装在等直段的下表面,其头部与中间截面标齐,等直段直径为3.2mm、长度为21mm,纵向直管段直径4.75mm,如图 3所示。试验数据表明,这种安装对下表面静压的测量值影响较大,由五孔探针反算的静压比壁面实测静压低了约1kPa,而反算的总压要高于稳定段总压约200~300Pa,因此造成马赫数计算误差,但对均匀性影响不大。如图 4、5所示,在马赫数为0.5和0.6时,实测值达到了0.515和0.608。该截面具有约0.5°的流向角,但马赫数的均方根仅为0.0009和0.0007。0.5°流向角远高于风洞流向角要求,但考虑到探针的安装误差和测量误差,认为该数据是可以接受的。
|
| 图 3 探针校准装置 Fig.3 L-shaped five-hole-probe calibration |
|
| 图 4 等直段中截面流场校核结果(马赫数0.5) Fig.4 Results of calibration(Ma=0.5) |
|
| 图 5 等直段中截面流场校核结果(马赫数0.6) Fig.5 Results of calibration(Ma=0.6) |
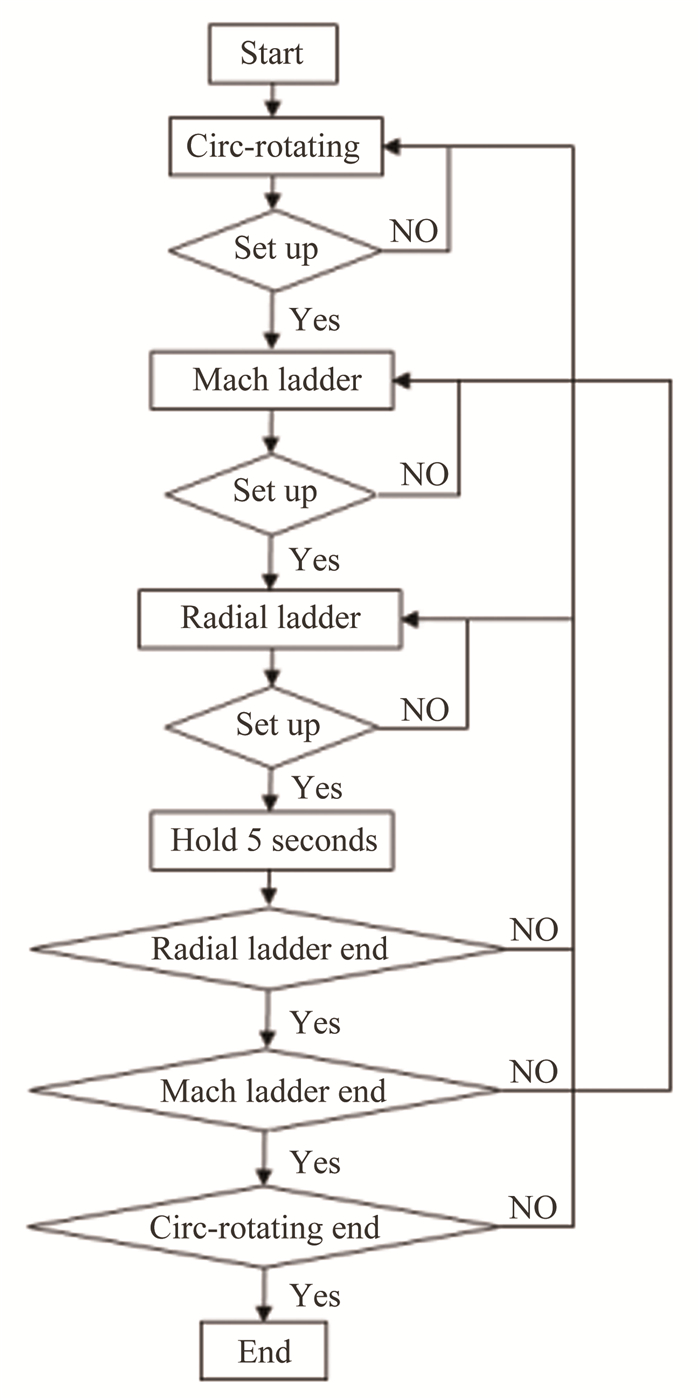
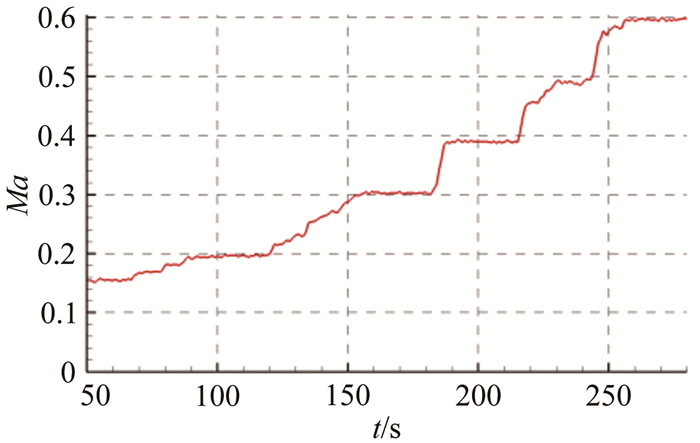
试验过程中需要调整的参数包括探针的周向位置、进气道入口马赫数和探针径向位置。试验过程中,先通过Circ-rotating改变周向角,再利用Mach ladder改变马赫数,最后使用Radial ladder改变径向位置,流程如图 6所示。将改变周向角的过程置于流程的最外环,可以减小周向转动次数,也可以在每个周向位置独立开车试验,以减少单次车吹风时间。在每个测量点,探针测量时间为5s,大约能获取50个测量数据。图 7给出了单次试验的马赫数控制曲线,马赫数阶梯从0.15到0.60。得益于气源容量优势和试验台小流量特性,虽然进气道试验台采用了开环控制方式,但在单次试验过程中马赫数能稳定在目标范围,且精度达到了2‰。
|
| 图 6 五孔探针测量试验流程 Fig.6 Flow chart of the measurement by five-hole-probe |
|
| 图 7 马赫数试验阶梯 Fig.7 Ladder of changing Mach number |
借助CFD计算结果对管内流动进行分析。虽然CFD在模拟大S弯进气道强分离流方面还存在一些不足,但可为认清基本流动状态提供依据,也可以为试验提供参考。
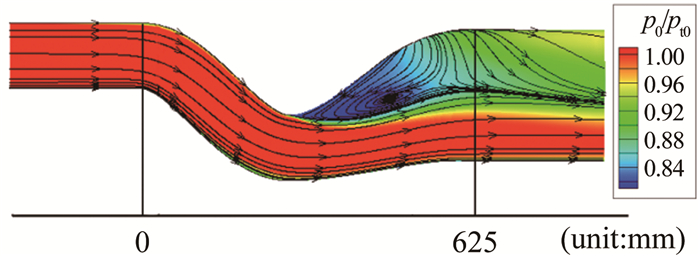
计算域包含入口等直段、进气道和出口等直段,计算网格约780万,选用Spalart-Allmaras模型,入口给定总温、总压边界条件,出口给定流量边界条件,雷诺数取实验值。图 8给出了计算得到的Ma0.5时的大S弯进气道轴向剖面的总压恢复系数云图和流线图,其中pt0为入口总压,p0为当地总压,x=625mm截面为进气道出口截面,x=0mm截面为进气道入口截面。其他马赫数下的畸变图谱和流线分布与图 8十分类似,本文不再给出。从图 8可以看出,尽管在第二弯道处存在较大分离区,但出口截面并不存在回流现象。
|
| 图 8 进气道流线图(Ma=0.5) Fig.8 Streamline graph of inlet (Ma=0.5) |
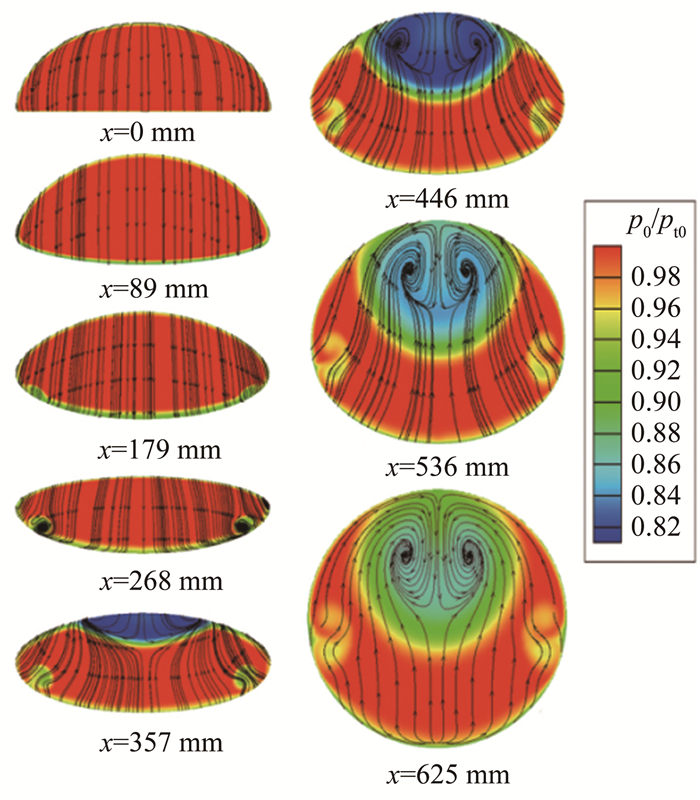
图 9展示了大S弯进气道的8个剖面,每个截面包含总压恢复系数云图和流线分布,x表示距离进气道入口截面的轴向距离。可以看出,从入口至出口,管道剖面形状从半椭圆形演变为直径250mm的圆形。x= 0mm,89mm时,截面位于进气道第一弯区域,气流随着弯道均匀地向下流动,总压几乎不存在损失。当x= 179mm时,截面下方两侧出现较小的圆形低压区,存在较弱的总压损失,但当x= 268mm时,截面位于大S弯进气道最大偏移截面,同时也是第一个弯道的末端、第二个弯道的始端,截面左/右下角出现漩涡,总压损失区域逐渐扩大。当气流进入第二个弯道时,上部流动分离区增大,总压恢复系数下降到0.82,为全流道最低数值。在进气道后半段,上部较大低压区与下部两侧较小低压区的作用范围不断扩大,但总压恢复系数在提高。总体来看,CFD结果和理论推导[27]表现出的规律是相符的。
|
| 图 9 内部截面旋流图(Ma=0.5) Fig.9 Swirl contours of internal sections (Ma=0.5) |
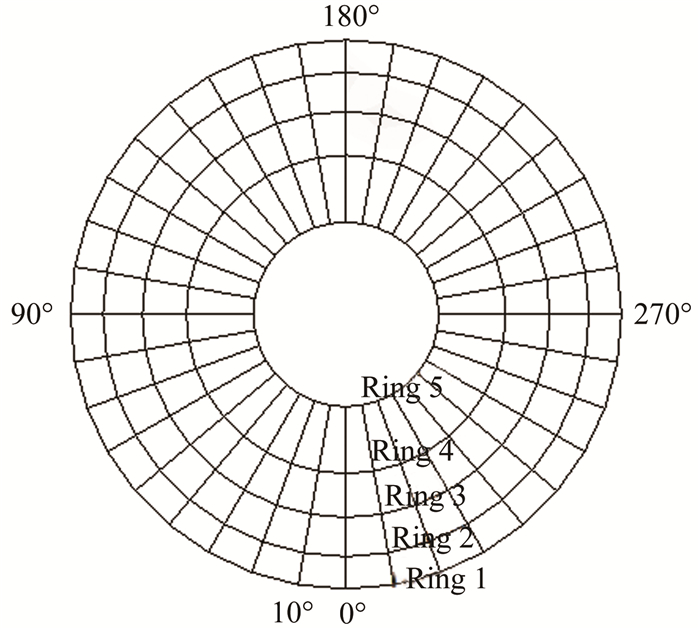
根据美国SAE的总压测量规范,在进气道出口截面(即图 8中x=625mm处)径向等面积中心布置5个测量点,周向测量角度间隔10°,总测点数为180个,如图 10所示。由于探针为120°等间隔分布,进气道流场左右对称,因此实际上只需要7个周向测量角度,共计105个测量点,从外向内依次标识为1~5环,底部位置的周向角标识为0°,并沿顺时针方向递增。
|
| 图 10 测量点位置 Fig.10 Positions of measurement |
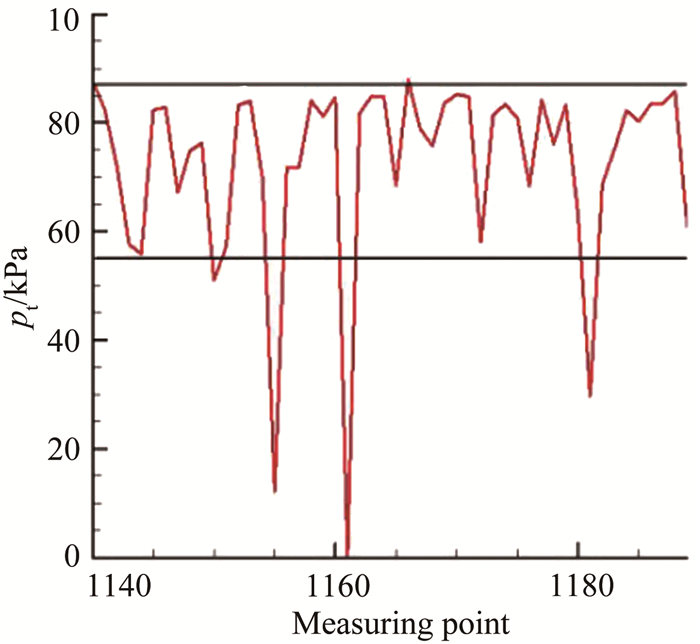
使用LLS方法直接处理每个状态所有的测压数据,得到各测点的流场结果,然后取这些结果的平均值。图 11是Ma0.6时第4环170°角位置5s内的处理结果,横坐标是测量点,纵坐标pt是总压。可以看出,LLS方法具有很好的鲁棒性,几乎所有测量点都能处理出结果。但是,某些状态的处理效果很差。除1161测量点外,其余点都有结果输出,但总压在55~ 87kPa之间剧烈波动,而某些奇异点测得的压力数据远远超过平均值,如图 11中超出水平黑线区域的几个测量数据。数据组表现出的较强的不连续性导致其没有统计上的意义,应根据特定且合适的数据处理法则予以剔除,可见,这种方法得到的单个测量点数据存在较大波动,如果不寻找一套适合的数据处理方法,可能不能有效地控制误差。
|
| 图 11 第4环170°角位置结果(LLS) Fig.11 LLS results at 170° in 4th ring |
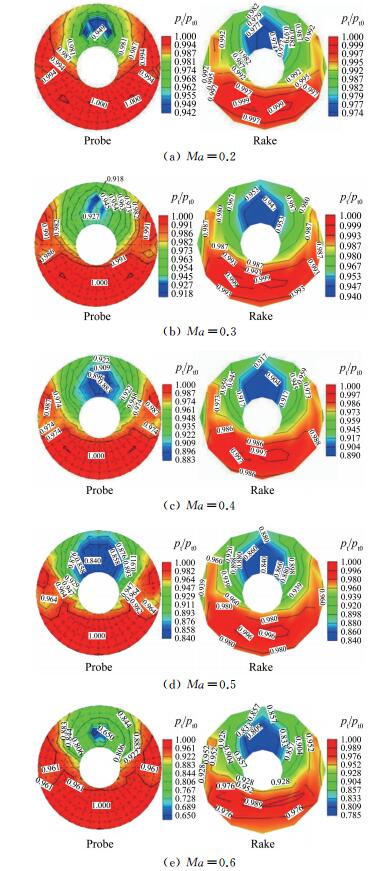
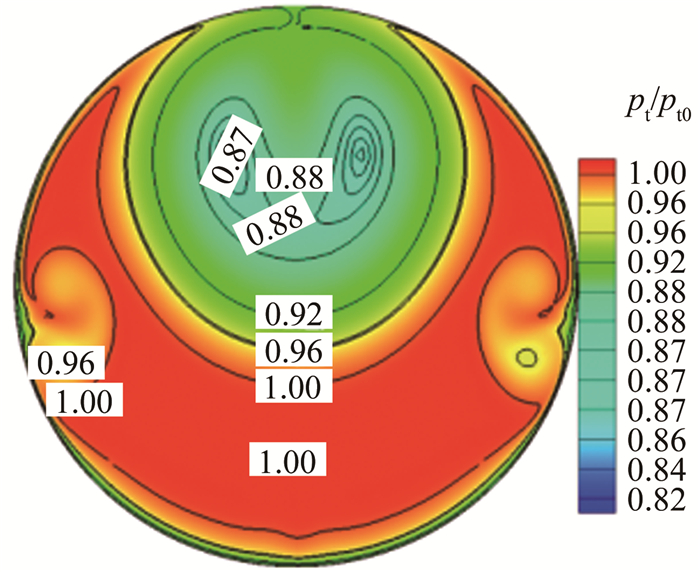
如图 12所示,左侧云图为五孔探针测得总压恢复系数(采用LLS方法得到数据),右侧云图为总压耙测得的总压恢复系数,Ma为入口马赫数,pt为当地总压,pt0为入口总压。对于Ma0.2~0.6,五孔探针和总压耙的相同点表现为:上半部分因流动分离造成的低压区及左右两侧范围较小的低压区,双方均能捕捉到;不同点表现为:五孔探针测得的上部低压区总压畸变强度明显弱于总压耙测得的结果,且五孔探针测得的左右两侧小低压区更靠近中心。可以看出,对于进气道出口总压分布规律,两者的测量结果大体一致。例如,Ma0.5时,左右两侧小低压区的压力测值(图 12(d))与计算值(图 13)云图分布一致,三者在数值上误差也很小。不难发现,尽管LLS方法能够在高压区得到稳定连续的数据,但其在低压区多个测量点数据表现出来的连续性却不尽人意:在大的低压区内出现一些异常点,使得低压区不连续;Ma0.3时第3环180°角位置、Ma0.6时第4环170°/190°角位置处总压值突然下降,这与CFD计算结果、总压耙测压结果均不相符。
|
| 图 12 测量总压对比图谱 Fig.12 Contour of total pressure by measurement |
|
| 图 13 数值计算总压图谱(Ma=0.5) Fig.13 Contour of total pressure by numerical calculation(Ma=0.5) |
表 1给出了入口Ma0.5时,180°角位置各环的俯仰角、偏航角、流向角、滚转角、总压、静压、马赫数数据处理结果。除第4环以外,其余4点处理结果的总压均在80kPa以上,马赫数也在0.2左右,唯有第4环的数据出现了异常,其俯仰角高达3377.4°,马赫数高达0.5以上,而总压则降低近20kPa。在确保试验流场稳定的情况下,这些数据的出现显然是奇异的。可以得出,LLS方法得到的大部分数据是合理的,但是个别点的数据误差很大,使得总压图谱不连续、不可靠。
| ring | 1 | 2 | 3 | 4 | 5 |
| Pitch/(°) | -33.408 | -28.496 | -17.936 | -3377.420 | 7.654 |
| Yaw/(°) | -4.949 | -23.493 | -49.459 | 115.071 | -42.099 |
| Cone/(°) | 33.730 | 36.293 | 51.800 | 71.820 | 42.661 |
| Roll/(°) | -98.938 | -132.335 | -165.244 | 17.564 | 171.615 |
| pt/Pa | 88312.7 | 86932.7 | 85204.2 | 65674.4 | 83000.8 |
| ps/Pa | 85256.7 | 84466.9 | 83228.9 | 54878.2 | 82311.1 |
| Ma | 0.225 | 0.203 | 0.183 | 0.513 | 0.109 |
在以上两种LLS方法处理结果均存在异常的情况下,考虑两种改进措施:一种以LLS方法为基础,剔除奇异值后取平均;另一种则是SF方法。前者数据处理的难点是如何给出奇异值评判标准。本项目尝试了3σ原则(即三倍均方根原则,数据与平均值的偏差大于3σ时视为异常值,予以剔除),但并不能剔除异常值;如果采用1σ原则,虽然能够剔除奇异值,但需要多轮处理才能够得到较好的结果,剩余的数据量很少,连续性并不好,故寻找一种合适的数据处理方法也是非常不易且耗时的。
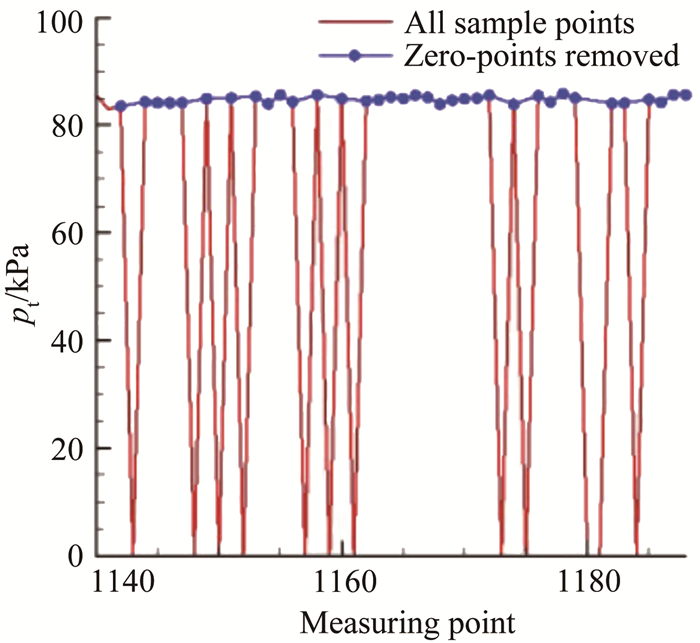
应用中发现,相比LLS,SF方法具有更好的处理结果及更高的处理效率。对于测量结果不理想的点,SF方法不能获得结果,此时所有量返回值为0,这样就可以方便地将这些异常值剔除。如图 14所示,SF方法产生的异常值有13个,而正常值则有35个。这些正常值的波动量要显著优于LLS方法:总压波动量均方根为495Pa,统计样本数达到了35个,因此具有统计意义。
|
| 图 14 第4环170°角位置处理结果(SF) Fig.14 SF results at 170° in 4th ring |
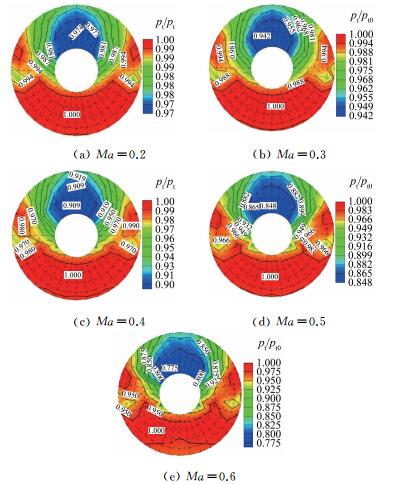
图 15是使用SF方法得到的总压图谱。可以看出,SF方法与LLS方法(图 12左侧)、总压耙(图 12右侧)、CFD(图 13)相比,四者都表现出前文所述的S弯进气道特有的总压畸变规律。首先,SF与LLS不同的是,前者得到的上部大低压区数据更加连续、对于左右两侧小低压区的细节捕捉更加精准、出口截面总压恢复系数也更高。其次,SF法五孔探针图谱与总压耙图谱在左右两侧小低压区位置的捕捉存在差异。旋流的产生会使得总压恢复系数降低而出现低压区,而大S弯进气道出口截面两侧存在的小低压区是由于第一个S弯道的流动分离所导致的,故低压区与旋流区总存在一个对应的关系,通过测量大S弯进气道的旋流分布[28]可以得到。第一个S弯道所产生的旋流应存在于两侧的第2环位置处(即低压区存在位置),由于传统总压耙布置的测量点密度不及旋转测量段基础上的五孔探针测量点精密,其测得数据难免会存在较大测量误差,所呈现出的两侧壁面低压区并不符合真实流场。最后,SF虽然在上部大低压区数值上略低于CFD结果,同时在两侧小低压区数值略高于CFD结果,但两者图谱表现出的高度一致性是其他方法所不及的。
|
| 图 15 SF总压畸变图谱 Fig.15 Contour of total pressure distortion by SF method |
由于本文的大S弯进气道是基于S弯进气道改进设计而来,国内外鲜有试验参考数据,综合传统S弯进气道测量数据、大S弯进气道的理论分析以及本文测得的大量试验数据,经过前文对两种LLS法五孔探针测量、SF法五孔探针测量、传统总压耙测量以及CFD数值计算结果的综合对比分析,我们可以判断SF法五孔探针测量是讨论范围内最适用于本文大S弯进气道模型的测量方法。
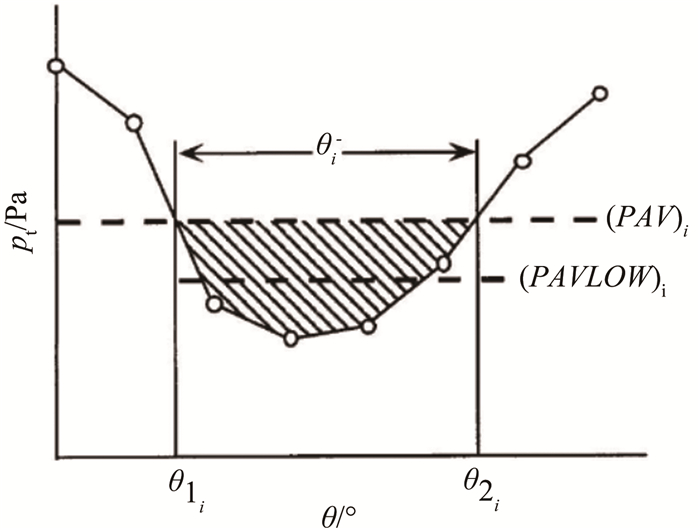
3.3 总压畸变评估采用美国ASME协会的进气道畸变评估标准计算进气道的周向、径向畸变指数和总压恢复系数[23]。根据标准,本文所研究大S弯进气道属于单畸变模式,其周向畸变指数(DPCP)所包含的各项参数如图 16所示。
|
| 图 16 周向总压畸变参数示意图 Fig.16 Parameters of total pressure circumferential distortion |
图中,i表示环数;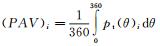
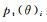
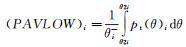
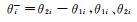
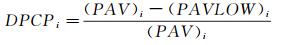 (1)
(1)
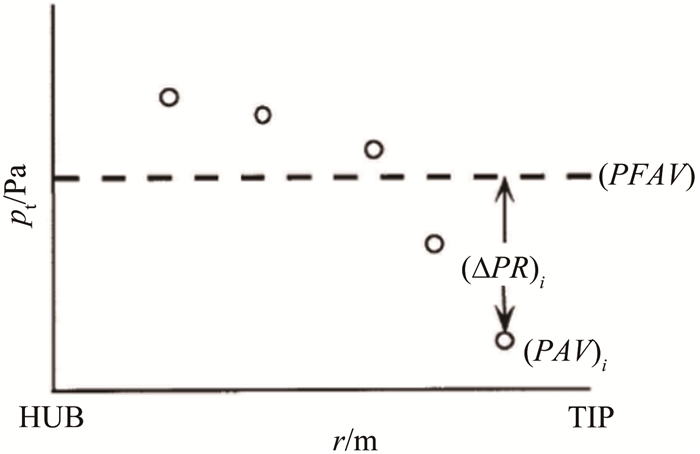
径向总压畸变指数(DPRP)采用面积平均总压计算,如图 17所示。图中,HUB表示轮毂,TIP代表叶尖。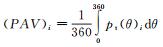
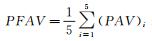
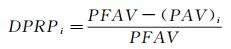 (2)
(2)
|
| 图 17 径向总压畸变参数示意图 Fig.17 Parameters of total pressure radial distortion |
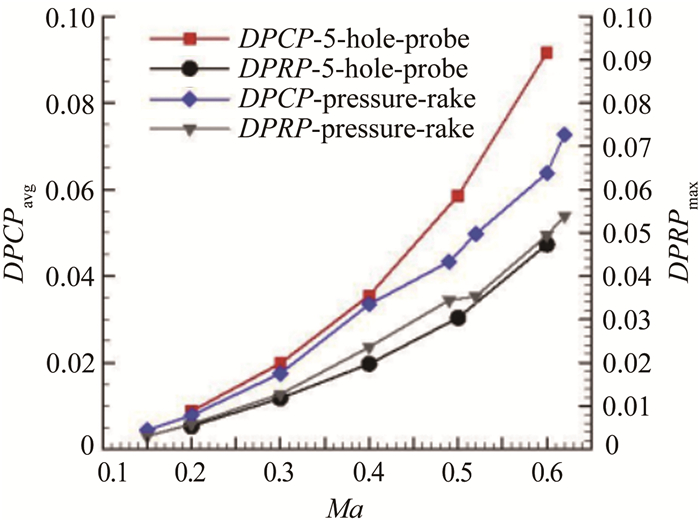
图 18给出了总压畸变指数的对比结果。横坐标是入口马赫数,左纵坐标是平均周向总压畸变指数,右纵坐标是最大径向总压畸变指数。大体来说,随着马赫数的增加,畸变指数也同时上升,畸变程度加剧。可以看出,低马赫数时,周向畸变程度与径向畸变相近;高马赫数时,周向畸变占主导。与总压耙相比,五孔探针测得的两种畸变数据更加光滑连续,其中,基于五孔探针的径向畸变指数较小,而周向畸变指数较大。特别的是,Ma0.4以下时,两者差距较小且趋势相同,但在Ma0.4以上时,五孔探针测得周向畸变指数显著大于总压耙。由此推断, 在高马赫数时,总压耙更加容易受流场干扰,测量不稳定;相比之下,五孔探针的测量数据尽管与真实流场存在一定误差,但在流场变化时,其测量数据连续性很好,误差并未发散,表现出较高的稳定性。
|
| 图 18 总压畸变指数对比 Fig.18 Coefficient of DPCPavg and DPRPmax |
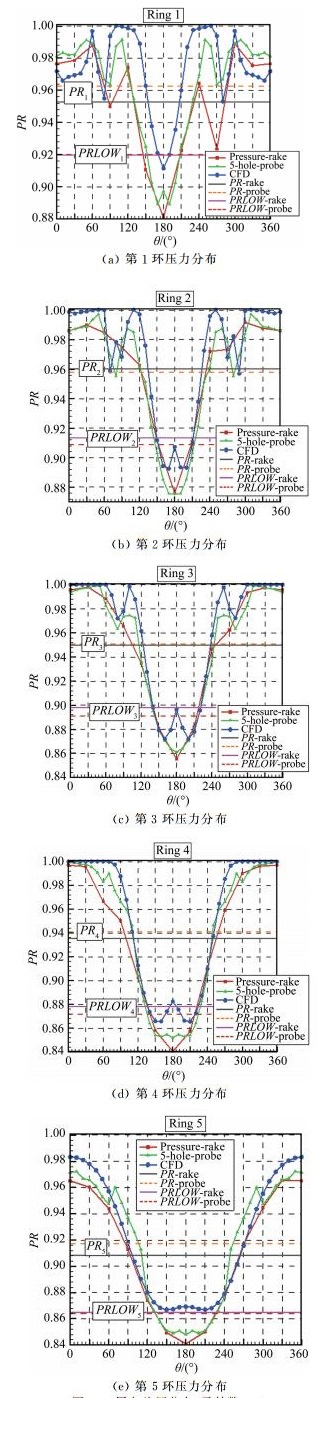
总压恢复系数为出口总压与入口总压的比值,图 19给出了Ma0.5时各环总压恢复系数变化曲线。可以看出,周向0°~360°,各环总压恢复系数大致呈现一个先降低后升高的趋势。出口180°附近大低压区总压恢复系数是最低的,此处应是第二个弯道引起的高强度对旋涡,造成总压急剧降低。第2环至第4环周向180°处CFD结果存在总压恢复系数激增,因为理论判定两侧对旋涡涡核处总压更低,非涡核处总压会升高,但试验测量并未捕捉到此特征。另外,从第2、3环的周向压力分布看,五孔探针捕捉到了左右两侧的低压区,但其压力值小于CFD结果;在无流动损失区(即总压恢复系数PR=1),CFD预测结果也高于五孔探针测量值,如第4环中0°~30°的周向位置。推测这一问题的根本原因在于CFD并未考虑真实流场脉动和流场损失,所以结果数值往往也偏高一些,这也是在第3、4环中,CFD计算的总压恢复系数结果为1这种理想情况的原因。总压耙测量结果是最低的,同时在细节捕捉上并没有五孔探针好。由于大S弯进气道属于对称进气道,其流场也应显示较高对称性,但总压耙测得的对称性并不及五孔探针,尤其是第1环,大于180°一侧的畸变强度显著强于另一侧。
|
| 图 19 周向总压分布(马赫数0.5) Fig.19 Curves of circumferential total pressure(Ma=0.5) |
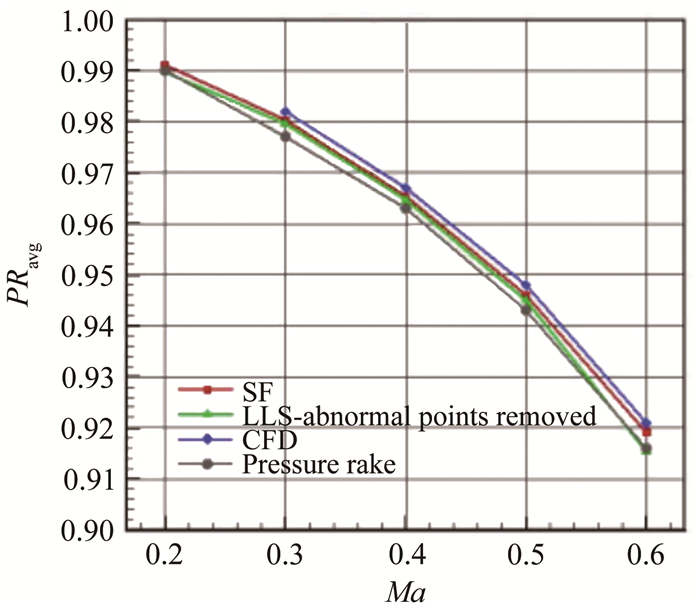
图 20给出了总压恢复系数的处理结果,横坐标是入口马赫数,纵坐标是平均总压恢复系数。大体上,随着入口马赫数的提高,总压恢复系数是降低的。显然, CFD计算结果未考虑真实流场的损失效应,其总压恢复系数是最高的,其次是SF方法,然后是LLS方法,最后是总压耙。在剔除奇异值后,采用1σ原则的LLS结果与SF结果比较接近,但在Ma0.6时偏差增大。与CFD结果相比,SF结果在各个马赫数的值都有约为0.002的下降,而总压耙则达到了0.005。需要说明的是,CFD计算的总压恢复系数是整个出口面的总压平均值,而试验测量的总压恢复系数是所有测量点的总压平均值。如果取CFD结果在测量点的总压平均值,那么总压恢复系数将比面平均值更大。
|
| 图 20 总压恢复系数 Fig.20 Coefficient of PR |
综上所述,随着马赫数的增大,大S弯进气道出口总压畸变程度更加剧烈。出口截面上部大低压区畸变程度尤为严重,总压恢复系数最低不及0.85,造成进气道/发动机一体化设计困难,而如何高效地去除高总压畸变影响有待进一步研究。
4 结论通过本文分析,明确了基于五孔探针的可旋转测量段测量进气道出口总压的可行性;对比总压参数,分析SF方法与LLS方法两者优劣点;综合畸变指数,分析五孔探针相比总压耙的优越性,并对畸变结果进行评估。研究结果主要有以下两方面:
(1) 在测量方面,本文采用三探针式旋转测量段,通过加密测量点,在对流场干扰很小的情况下,实现了可控的任意周向位置和局部径向位置的测量;同时,使用五孔探针测量流场、SF法处理数据,解决了传统总压测量图谱不连续、不对称的问题,结果更加合理。
(2) 在评估方面,分析测量结果发现,随着入口马赫数的增加,大S弯进气道出口截面总压畸变增强,周向总压畸变逐渐占据主导。出口总压畸变主要分布于第二弯道引发的大低压区,其总压恢复系数最低不及0.85,而第一弯道引发的小低压区位于两侧,强度较小。
| [1] |
Yang H, Li F, Song Y Y, et al. Numerical investigation of Electrohydrodynamic(EHD) flow control in an S-shaped duct[J]. Plasma Science and Technology, 2012, 14(10): 897-904. DOI:10.1088/1009-0630/14/10/08 |
| [2] |
Da X Y, Fan Z L, Fan J C, et al. Microjet flow control in an ultra-compact serpentine inlet[J]. Chinese Journal of Aeronautics, 2015, 28(5): 1381-1390. DOI:10.1016/j.cja.2015.07.008 |
| [3] |
屠宝锋, 胡骏, 张凯. 对涡旋流影响压气机转子性能和稳定性的研究[J]. 推进技术, 2016, 37(4): 640-645. Tu B F, Hu J, Zhang K. Effects of twin swirl on performance and stability of compressor rotor[J]. Journal of Propulsion Technology, 2016, 37(4): 640-645. |
| [4] |
Beale D K, Zelenak M. Development and validation of a free jet technique for inlet-engine compatibility testing[R]. AIAA-1992-3921, 1992.
|
| [5] |
Kimzey W F. An investigation and calibration of a device for the generation of turbulent flow at the inlet of a turbojet engine[R]. AEDC-TR-65-195, 1965.
|
| [6] |
Oates G C, Sherman D A, Motycka D L. Experimental study of inlet-generated pressure fluctuations[R]. AFAPL-TR-70-103, 1970.
|
| [7] |
Plourde G A, Brimelow B. Pressure fluctuations cause compressor instability[R]. AFAPL-TR-70-103, 1970.
|
| [8] |
Younghans J L, Moore M T, Collins T P, et al. Inlet flow field simulation techniques for engine/compressor testing[R]. AIAA-970-591, 1970.
|
| [9] |
Anderson R E. Aircraft engine inlet pressure distortion testing in a ground test facility[R]. AIAA-1983-1233, 1983.
|
| [10] |
Kutschenreuter P H, Collins T P, Vier I W. P 3G-a new dynamic distortion generator[R]. AIAA-73-1317, 1973.
|
| [11] |
Overall B W, Harper R E. The airjet distortiongenerator system-a new tool for aircraft turbine engine testing[R]. AIAA-1977-993, 1977.
|
| [12] |
Beale D, Cramer K, King P. Development of improved methods for simulating aircraft inlet distortion in turbine engine ground test[R]. AIAA-2002-3045, 2002.
|
| [13] |
Yuhas A J, Ray R J, Burley R R, et al. Design and development of an F/A-18 inlet distortion rake: a cost and time saving solution[R]. NASA-TM-4722, 1995.
|
| [14] |
姜健, 于芳芳, 赵海刚, 等. 进气道/发动机相容性评价体系的完善与发展[J]. 科学技术与工程, 2009, 9(9): 6474-6483. Jiang J, Yu F F, Zhao H G, et al. Perfection and development of engine/intake compatibility evaluate criterion[J]. Science Technology and Engineering, 2009, 9(21): 6474-6483. DOI:10.3969/j.issn.1671-1815.2009.21.041 |
| [15] |
刘大响, 叶培梁. 俄罗斯的发动机进口流场畸变评定指南[J]. 燃气涡轮试验与研究, 1994, 4(3): 436-441. |
| [16] |
郁新华, 刘斌, 陶于金, 等. 背负式进气道设计及其气动性能研究[J]. 西北工业大学学报, 2007, 25(2): 270-273. Yu X H, Liu B, Tao Y J, et al. Top-mounted inlet design and its aerodynamic performance[J]. Journal of Northwestern Polytechnical University, 2007, 25(2): 270-273. DOI:10.3969/j.issn.1000-2758.2007.02.024 |
| [17] |
Stoll F, Tremback J W, Arnaiz H H. Effect of number of probes and their orientation on the calculation of several compressor face distortion descriptors[R]. NASA-TM-72859, 1979.
|
| [18] |
Lawley T, Price D. A miniature three-dimensional pressure probe[J]. Review of Scientific Instruments, 1971, 42(1): 158-160. DOI:10.1063/1.1684855 |
| [19] |
吴岳庚. 当代压气机试验与测试技术[J]. 科技与实践, 1998, 2: 30-39. |
| [20] |
Gilarranz J L, Ranz A J, Kopko J A, et al. On the use of five-hole probes in the testing of industrial centrifugal compressors[J]. ASME Journal of Turbomachinery, 2004, 127(1): 91-106. |
| [21] |
姜健, 屈霁云, 赵海刚, 等. 进气道旋流模拟及测量地面试车台试验研究[J]. 燃气涡轮试验与研究, 2012, 25(3): 36-39. Jiang J, Qu J Y, Zhao H G, et al. Simulation and measurement of inlet swirl in ground test bed[J]. Gas Turbine Experiment and Research, 2012, 25(3): 36-39. |
| [22] |
江勇, 陶增元, 张发启, 等. 某型飞机进气道与发动机地面匹配实验研究[J]. 航空动力学报, 2003, 18(4): 554-557. Jiang Y, Tao Z Y, Zhang F Q, et al. Matching test of an aircraft inlet and engine on the ground[J]. Journal of Aerospace Power, 2003, 18(4): 554-557. DOI:10.3969/j.issn.1000-8055.2003.04.021 |
| [23] |
Society of automotive engineers. Gasturbine engine inlet flow distortion guidelines[R]. ARP-2002-1420, 2002.
|
| [24] |
AllianTech S. A. S. Multi-hole velocity probes[S]. Gennevilliers: Aeroprobe Corporation, 2010.
|
| [25] |
Johansen E S, Rediniotis O K, Jones G. The compressible calibration of miniature multi-hole probes[J]. ASME Journal of Fluids Engineering, 2001(123): 128-138. |
| [26] |
Ramakrishnan V, Rediniotis O K. Calibration and data reduction algorithms for non-conventional multi-hole pressure probes[J]. International Journal of English Studies, 2004, 12(5): 133-150. |
| [27] |
Society of automotive engineers. A methodology for assessing inlet swirl distortion[R]. ARP-2010-5686, 2010.
|
| [28] |
徐诸霖, 达兴亚, 范召林, 等. 基于五孔探针的大S弯进气道旋流畸变评估[J]. 航空学报, 2017, 38(12): 48-57. Xu Z L, Da X Y, Fan Z L. Assessment of swirl distortion of serpentine inlet based on five-hole-probe[J]. Acta Aeronautica ET Astronautica Sinica, 2017, 38(12): 48-57. |