2. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621000
2. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China
航空声学风洞为飞机气动噪声研究提供了一种有效的试验平台。为准确评估大型客机机体噪声指标和指导飞机的降噪研究,需要针对声学风洞的特点发展一种有效的噪声测试技术来精确测量机体噪声源的分布[1-2]。声学试验过程中,通常将试验模型放置在气流内部,传声器阵列放置在气流外部。这样可以避免气流与传声器相互作用产生的流致噪声,但是声波在到达传声器之前需要穿过射流剪切层。射流剪切层是一种非均匀介质,声波在传播过程中将受到反射、折射和散射等效应的影响,声场特性会因此发生改变。因此,需要开展剪切层修正方法研究,对测量数据进行修正,才能获得真实的声源信息。
20世纪中后期,Miles[3]和Ribner[4]分别对声波穿过具有相对运动速度的气流的传播效应进行了分析研究。Schlinker[5]和Amiet[6-7]等人基于无限薄剪切层的假设,针对声波穿过开口风洞剪切层产生的折射、散射等效应进行了理论分析和系统试验研究,其剪切层修正方法被广泛用于声学风洞数据修正。Amiet推导的修正公式主要针对声源位于射流中心线上、且与传声器在同一平面内的情况;而在测量过程中,并非所有传声器阵列的阵元都与目标声源同平面。Candel[8]、Ahuja[9]等人也针对开口风洞剪切层对声波的折射和散射效应进行了相关的理论和试验研究工作。近年来,王毅刚[10]等人根据数值模拟和试验测量结果,提出了一种基于有限厚度剪切层假设的声漂移量修正模型。
本文主要研究剪切层折射效应引起的声波相位失配修正,没有考虑剪切层内湍流散射效应的影响。首先,通过湍流边界层流场的Gortler理论解[11]给出风洞剪切层速度剖面,分析剪切层速度场的变化规律;其次,针对传声器阵列声源定位的特点研究了4种剪切层修正方法,从计算精度方面对不同修正方法进行对比;最后,通过风洞实验验证理论方法的有效性。
1 波束形成算法风洞噪声源定位一般采用波束形成算法。传声器阵列数据处理时,首先根据各通道采集的时域声压数据生成互谱矩阵:先将每个通道的信号数据分块平均(以减小背景噪声的影响),然后采用快速傅里叶变换将时域数据转换为频域数据。传声器阵列的互谱矩阵可以表示为:
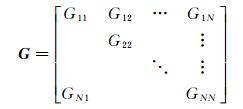 (1)
(1)
其中,N为阵列传声器的数量,互谱矩阵G为Hermite型矩阵,Gmm′可表示为:
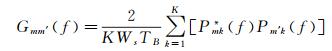 (2)
(2)
式中,K为传声器阵列数据分块数,Pm′k(f)为第m′个传声器第k段数据块的单边频域信号,Ws为频谱分析的加窗幅值恢复系数。上标*号表示复共轭。互谱矩阵G的下三角元素与上三角元素复共轭相等。对于任意空间点,传声器阵列的聚焦向量定义为g =[g1, g2, …, gN]T,其中gn(n=1, 2, …,N)为均匀流中单位强度单极子声源的格林函数,即:
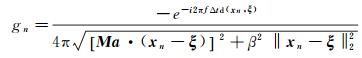 (3)
(3)
其中,‖·‖ 2为2范数符号,表示距离。f为声波的频率,Δtd为从声源到传声器的声传播延迟时间,开口风洞需要考虑剪切层引起的延迟时间变化。xn为传声器位置向量,ξ为扫描点位置向量,Ma为来流马赫数,β2=1- |Ma| 2为常数。由互矩阵和聚焦向量可以得到传声器阵列的自功率谱:
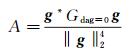 (4)
(4)
为了减小背景噪声的影响,通常将互谱矩阵的对角线元素置零。根据式(4)就可以得到试验模型的噪声源分布结果。
2 剪切层速度剖面在剪切层修正的理论模型中,通常将剪切层近似为无限薄的涡流面[6-7],即认为射流内部的流速为U,射流外部的流速为0。但实际上剪切层具有一定的厚度,并且剪切层内的射流速度呈一定规律分布。从定常旋涡粘滞模型和湍流边界层方程出发,Gortler[11]得到了2种不同速度的射流边界的流场理论解。当其中一种射流的速度为0时,这种边界即为风洞自由射流剪切层。因此,Gortler的理论解可推广到风洞剪切层速度剖面的求解。引入自相似参数:
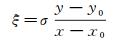 (5)
(5)
其中,x0、y0为风洞喷口端面上的参考点,σ是由风洞试验确定的常数。经过推导,可以得到剪切层内的轴向和切向速度剖面表达式:
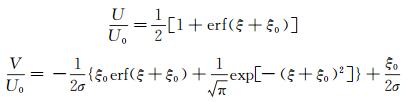 (6)
(6)
式中,U0为平均流速,U为轴向速度,V为切向速度,erf为误差函数。一般来说,自由射流剪切层的半速度剖面位置与风洞的喷口边缘线并不重合,式(6)中需设置一个偏移量ξ0。在Gortler的理论中,剪切层厚度是这样两个点之间的距离:流体的速度在其中一个点上接近0,在另一个点上接近射流速度U0。为了使剪切层厚度计算不受边界选择的影响,引入动量厚度:
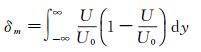 (7)
(7)
Candel[12]研究指出剪切层的厚度约等于4倍动量厚度,即δ≈4δm=0.17x。
3 剪切层修正方法风洞剪切层修正方法主要分为两类,即时域方法和频域方法。基于LEE、Lilley方程、CAA等的计算方法为时域方法,其优点是精度高且不受声波频率的限制,缺点是计算速度慢。大型声学风洞的试验段尺寸通常在10m量级,从声源位置到传声器位置的距离也达数米,时域方法受网格尺度和时间步长的限制耗时太长而不适用。Schinker[5]等人指出,当声波波长超过风洞喷口尺寸时,使用频域剪切层修正方法不会引入较大误差。因此,本文主要研究频域剪切层修正方法。
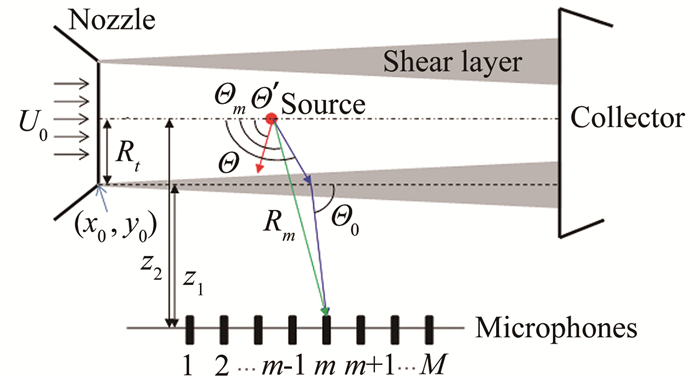
3.1 Amiet 2D方法如图 1所示,开口风洞核心射流与周围的静止空气之间存在无限薄的剪切层[6-7]。假设声源位于射流中心线上,Θ′为声波的初始发射角,Θm为测量角,Θ为对流角,Θ0为折射角。Rt表示风洞喷口的半宽,Rm为声源-传声器之间的测量距离。在风洞核心射流和剪切层的共同作用下,实际声线将按照“对流-折射”路径传播并达到传声器m处。
|
| 图 1 声波穿过剪切层的折射效应示意图 Fig.1 Schematic of the refraction of rays across shear layer |
根据对流关系和Snell定律,Amiet[6-7]得到了如下的角度修正关系:
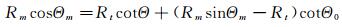 (8)
(8)
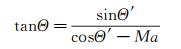 (9)
(9)
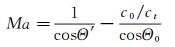 (10)
(10)
式(10)中,c0和ct分别为射流内部和外部的声速,Ma=U/c0为来流马赫数。式(8)~(10)可使用牛顿迭代法求解。根据图上的几何关系,可以计算声波从声源到传声器的传播延迟时间:
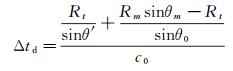 (11)
(11)
需要注意的是,Amiet 2D方法是通过圆形风洞喷口导出的,对于方形喷口(例如CARDC FL-17风洞),需要推导Amiet三维修正方法。
3.2 平均马赫数法Oerlemans[13]等人提出了一种剪切层修正的工程化近似方法:假设声源、传声器都位于平均流场内,则气流的平均马赫数为:
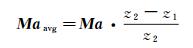 (12)
(12)
其中,z1为剪切层到传声器的距离,z2为声源到传声器的距离(见图 1)。根据对流关系确定漂移后的声源位置,进而得到修正后的声波传播延迟时间。
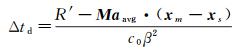 (13)
(13)
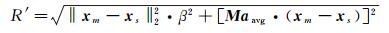 (14)
(14)
由数值模拟结果得到启发,根据声波传播的惠更斯原理和费马原理,张军[14]等人提出了有限厚度剪切层的简化射线法修正方法。基于简化射线法的延迟时间计算示意图如图 2所示。
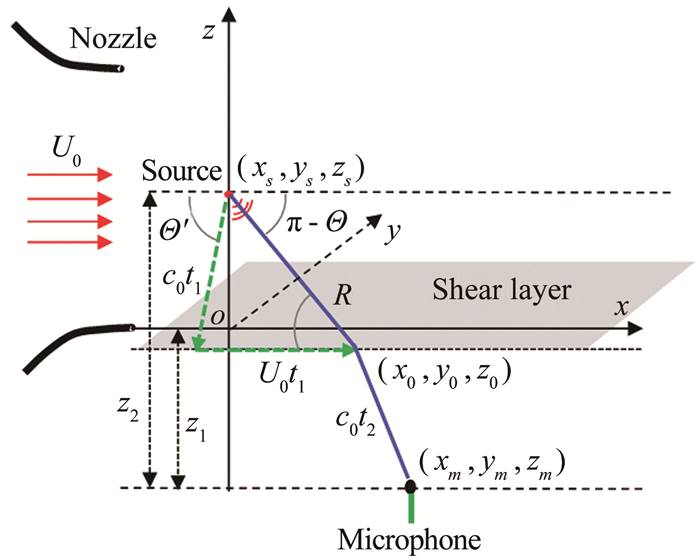
|
| 图 2 基于简化射线法的延迟时间计算示意图 Fig.2 Schematic of delay time calculation based on simplified ray method |
射流内部和外部的声波传播时间分别为:
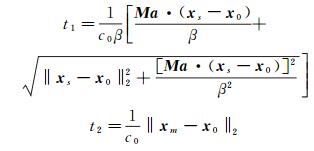 (15)
(15)
其中,x0=(x0, y0, z0), z0=σ(x0, y0)/2为剪切层半厚度点位置。因此声线从射流内的声源位置到射流外的传声器位置的总传播时间为t=t1+t2。t是声线与剪切层交点(x0, y0)为自变量的二元函数。根据费马原理,两点之间声线的传播满足最短路径原则,声源-传声器声波传播延迟时间的计算转化为求解下式的最小值:
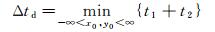 (16)
(16)
式(16)可通过最优化数值方法求解。
3.4 射线追踪法在高频条件下,声波的传播可视为声线的传播,声线是与波阵面垂直的射线。从射流内声源到射流外传声器的传播延迟时间可以通过追踪声线的轨迹进行计算。声线的传播由以下方程组控制:
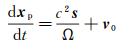 (17)
(17)
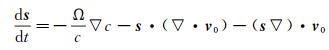 (18)
(18)
式中,xp为声线的空间位置,v0为式(6)确定的剪切层速度矢量,c表示声速,s =∇σ为慢变矢量,σ为声波的波阵面,Ω=1- v0·∇σ为自定义的中间变量。给定剪切层速度场和声波的初始方向矢量n0,上式可以通过自适应步长的Runge-Kutta法求解。
4 风洞实验为验证上述剪切层修正方法的正确性和适用范围,在中国空气动力研究与发展中心(CARDC)0.55m×0.40m声学风洞中开展了实验测量[15]。实验内容分为:剪切层速度剖面测量、声波传播延迟时间测量和噪声源定位测量。
利用总压耙进行剪切层速度剖面测量。总压耙上有30根总压管、1根静压管。总压管通过测压软管连接DSM3200扫描阀,扫描阀的量程为1Psi。通过燕尾槽连接方式将总压耙安装在可移动的导轨上。
声波传播延迟时间测量使用射流内参考声源和射流外传声器对。射流内参考声源由发声部件和整流罩组成,声源发声部件为功率5W的扬声器,带有音量控制单元,扬声器的发声频率为0.1~20kHz,信噪比大于85dB,失真度小于0.1%。整流罩一面开有5cm×3cm的窗口,表面采用穿孔金属网覆盖,在保证透声的同时也可避免气流的干扰。传声器对采用GRAS公司的1/2英寸46AE传声器,由2个相距30cm的传声器组成传声器对,距离风洞轴线0.666m。传声器对沿射流下游移测,移动间隔0.15m。对到达传声器的2个声压信号进行互相关运算可以确定延迟时间,进而确定声波的传播方向。
声源定位测量采用射流内参考声源和射流外传声器阵列。阵列传声器为GRAS公司的1/4英寸40PH传声器,阵列等效孔径为0.72m,采用8条螺旋臂,每个螺旋臂上分布5个传声器,共计分布40个传声器。阵列面到声源的距离为1.61m。剪切层修正实验测量装置如图 3所示。
4.1 剪切层速度剖面图 4给出了30、50和70m/s风速条件下,风洞剪切层速度剖面实验测量结果和理论计算结果的对比。图中带标记的彩色曲线表示测量结果,加粗的黑色实线表示理论计算结果,横坐标ξ表示归一化参数。D=0.55m,为风洞喷口宽度。x方向为射流方向,y方向在水平面内与x方向垂直。测量面为射流中心线所在的水平面。坐标原点选取如图 1所示。y=0为喷口壁面位置,y为正表示测点在靠近射流中心一侧,y为负表示测点远离射流中心。理论计算选取σ=9,ξ0=0.2。从图中可以看出,剪切层速度剖面的测量结果和理论计算结果吻合较好。在不同流向位置处,由归一化参数描述的剪切层速度剖面重合度较好,这说明剪切层的速度剖面具有“自相似”的特征,即在y/x相等的斜线上速度值大致相等。在高风速条件下,靠近风洞喷口(x/D=0.16)处的速度剖面分布在一定程度上偏离远离风洞喷口处的结果,这说明剪切层速度剖面并不是严格的自相似。出现这种情况的原因主要有2个方面:一方面可能是由测量误差导致;另一方面,出现偏差的测量剖面主要靠近喷口位置,在较高风速下风洞喷口附近的脱落涡对剪切层速度剖面可能有影响。
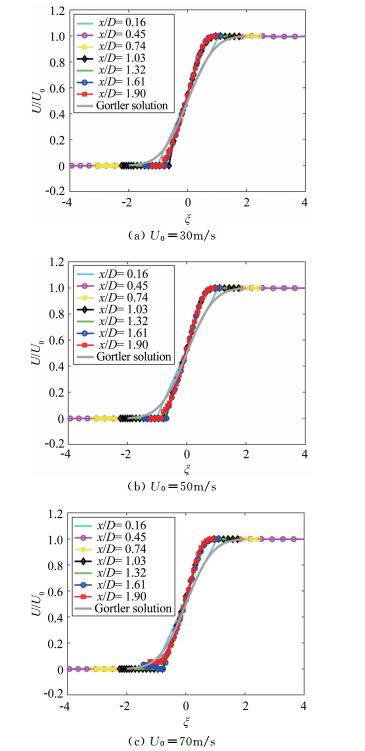
|
| 图 4 剪切层速度剖面理论值和测量值对比 Fig.4 Comparison of experimental and theoretical velocity profile |
定义剪切层的厚度为两点之间的距离,这两点分别对应流速为核心射流速度的10%和90%的位置。图 5给出了剪切层厚度随风速变化的测量结果和理论预测结果,其中灰色加粗实线是根据式(7)得出的计算结果,带标记的实线表示测量结果。从测量结果可以看出,剪切层厚度沿射流方向呈线性关系增长,射流速度对剪切层厚度的变化几乎没有影响。理论预测结果在变化趋势上与实验测量结果符合,但是在斜率上有较大差别。根据一次曲线拟合,0.55m×0.40m声学风洞剪切层厚度与流向位置之间的关系为:y=0.15x,x为距离喷口的流向距离。
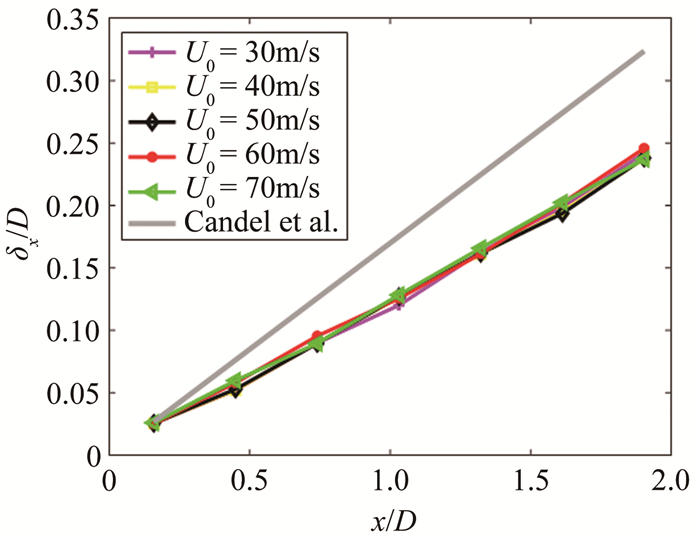
|
| 图 5 剪切层厚度的理论值和测量值对比 Fig.5 Comparison of experimental and theoretical shear layer thickness |
图 6给出了从声源到远场传声器位置的声波传播延迟时间的实验测量结果和理论计算结果对比。声波频率为8kHz,风速分别为30、50和70m/s。圆圈表示的离散点为实验测量结果(通过互相关运算求出),不同颜色和线型的曲线表示理论计算结果。可以看出,在不同风速下,理论结果和测量结果之间符合较好,不同理论方法之间的计算结果差别也很小。在不同的预测方法中,平均马赫数法的计算速度最快,Amiet 2D方法次之,简化射线法及射线追踪法的计算速度较慢(由于使用了较为复杂的迭代算法)。
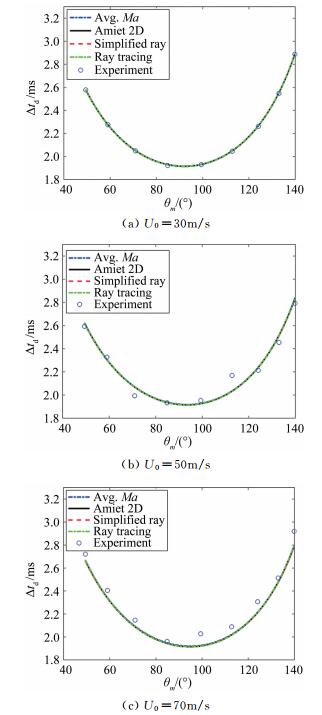
|
| 图 6 声源-传声器传播延迟时间理论值和测量值对比 Fig.6 Comparison of experimental and theoretical delay time |
根据不同方法得到的曲线几乎重合,难以直观地看出它们之间的差别。为考察不同剪切修正方法之间计算精度的差别,本文以Amiet 2D方法的计算结果为标准考察了不同修正方法给出的延迟时间相对误差:
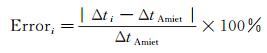 (19)
(19)
式中,ΔtAmiet表示Amiet 2D方法给出的计算结果,Δti(i=1, 2, 3)为其他修正方法的计算结果。
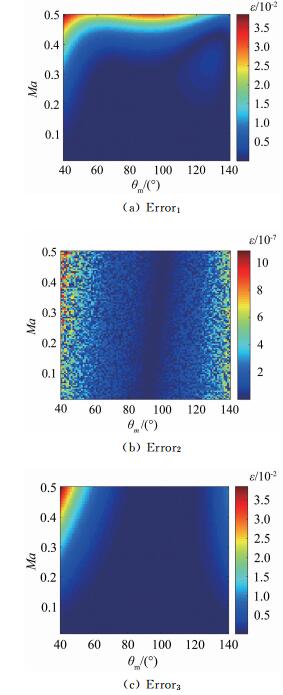
图 7给出了其他3种剪切层修正方法与Amiet 2D方法关于声源到传声器之间的传播延迟时间计算结结果的相对误差。Error1~Error3分别表示平均马赫数法、简化射线法及射线追踪法与Amiet 2D方法给出的结果之间的相对误差。其中,射线追踪法的计算没有考虑剪切层厚度。根据计算结果,随着来流马赫数的增加(Ma>0.4),平均马赫数法与Amiet 2D方法之间的相对误差增大。在测量角40°~140°范围内,Ma < 0.5的情况下,不同修正方法之间的相对误差最大不超过5%。如果将马赫数进一步限制在0.3以下(低速风洞常用马赫数范围),简化射线法、平均马赫数法及射线追踪法与Amiet 2D方法之间的相对误差可以忽略不计(< 1%)。如果仅对剪切层折射引起的相位失配进行修正,就计算速度而言平均马赫数法最快。
|
| 图 7 不同剪切层修正方法之间的相对误差 Fig.7 Relative errors of different shear layer correction methods |
表 1给出了不同风速和频率下,通过噪声源图得到的声源位置漂移量计算结果,定义声源位置漂移量在风速为0或不为0时的沿射流方向的声源位置差。计算采用本文第1节的常规波束形成算法和第3节的剪切层修正方法。当风速为0m/s时,对应2、4和8kHz的扬声器发声频率(与分析频率相同)下噪声源的空间位置为:(-0.16,0.18),坐标轴为m。上述声源位置是通过选取声源图中峰值点在扫描面上所处的位置得到的。表中N.C表示没有经过修正的噪声源x坐标位置,AMM、Amiet、SRM和RT分别表示经平均马赫数法、Amiet 2D方法、简化射线法和射线追踪法修正后得到的漂移量。
| f/kHz | U0/(m·s-1) | N.C | AMM | Amiet | SRM | RT |
| 30 | -0.15 | -0.020 | -0.020 | -0.020 | -0.020 | |
| 2 | 50 | -0.13 | -0.018 | -0.020 | -0.018 | -0.024 |
| 70 | -0.12 | -0.024 | -0.022 | -0.022 | -0.018 | |
| 30 | -0.14 | 0 | 0 | 0 | 0 | |
| 4 | 50 | -0.12 | 0 | 0 | 0 | -0.010 |
| 70 | -0.10 | 0 | 0 | 0 | -0.002 | |
| 30 | -0.14 | 0 | -0.002 | 0 | -0.020 | |
| 8 | 50 | -0.15 | 0.020 | -0.020 | -0.020 | -0.020 |
| 70 | -0.10 | 0 | 0 | 0 | 0 |
从表中可以看出,在开口风洞实验测量中如果不进行剪切层修正,那么从声源图得到的噪声源位置相对真实声源位置将出现漂移。且随着风速的增加,声源位置的漂移量增加(第3列数据)。在4kHz、8kHz分析频率、相同风速条件下得到的漂移量大致相等,显然这是符合物理实际的。2kHz条件下的修正效果比其他频率下的更差,这是由传声器阵列的低频分辨率问题导致的,采用CLEAN-SC等反卷积算法可改善这种情况。经过剪切层修正方法对延迟时间进行修正后,声源的漂移量减小,噪声源位置更接近真实声源的位置。理想条件下,经过剪切层修正后声源漂移量应当为0,但是实际上由于风洞背景噪声、支撑装置或风洞洞体结构对声波的反射、阵列面上阵元位置误差、传声器相位响应相对误差等的存在,声阵列成像得到的噪声源位置与真实声源位置总是存在一定的误差。
5 射线追踪法的快速计算方法在射线追踪法的计算过程中,要使从声源处发出的射线准确到达测量点处,需要使用迭代算法,从而使得该方法的计算速度较慢。使用个人台式电脑(4核i5-3470CPU 3.2GHz)在不开并行计算的前提下,追踪一条声线的时间约为1s。通常声学风洞测量中的阵列高达上百个通道,扫描面网格点数上万个,延迟时间计算需要追踪上百万条声线,因此传统的射线追踪法无法适用于声阵列在线测量。如果能够大幅减少追踪声线的数量并能保证计算精度,那么射线追踪法的计算速度就可以得到显著提高。显然,要减少追踪声线的数量,可以使用空间插值的方法,如图 8所示。
|
| 图 8 快速射线追踪法的空间插值方法 Fig.8 Spatial interpolation method of fast ray tracing |
理论上,声线是从扫描网格点发出并穿过剪切层后到达传声器位置处的。根据线性声学的互易原理,互换声源和传声器的位置后,声场的特性不会发生改变。让声线从传声器位置发出,穿过剪切层后到达扫描网格点位置,并根据射线轨迹计算这些网格点上的延迟时间,其余扫描网格点上的延迟时间通过空间插值方法进行计算。经过数值模拟,发现使用较少的声线数量就可以达到较高的插值精度,这种方法可以将计算速度提高至少2个数量级。
6 结论在开口声学风洞气动噪声试验中,试验模型和射流外传声器阵列之间存在剪切层。为了获得真实的噪声源位置,必须对阵列测量结果进行剪切层修正。本文首先在0.55m×0.40m声学风洞中开展了剪切层修正的实验研究,得到了不同风速下的剪切层速度剖面、声波传播延迟时间和声源定位的结果。根据实验结果,对剪切层速度剖面的Gortler理论解进行了验证,并对比分析了4种剪切层修正方法。研究结果表明:
(1) 选择自相似参数σ=9,ξ0=0.2时剪切层速度剖面测量值与理论值符合较好;剪切层厚度与轴向距离之间的关系为y=0.15x。
(2) 马赫数Ma≤0.3,测量角θm在40°~140°范围内,不同剪切层修正方法对声波延迟时间计算结果的相对误差在1%以内。不同修正方法均可以对对流-折射效应引起的声源位置漂移进行有效修正。
(3) 提出了射线追踪法的快速计算方法,该方法较常规射线追踪法的计算速度可提高2个数量级,从而使其适用于声阵列在线测量。
需要注意的是,本文所述的剪切层修正方法只考虑了由折射效应引起的声波相位失配,没有考虑阵列传声器处的幅值修正,因此,该方法主要应用于开口风洞中的噪声源定位测量。对于远场噪声测量以及通过声源图(区域积分)估计目标区域的辐射声功率等应用场合,则需要考虑剪切层的幅值修正。同时,本文也没有考虑剪切层内的湍流散射效应对声波传播的影响,对于纯音噪声(例如螺旋桨、直升机旋翼气动噪声中的纯音分量)的远场测量,剪切层内的湍流将会使噪声的频谱特性发生改变(国外文献称之为“Spectral broadening” [17])。为了得到更加准确的射流内声源信息,下一步需要继续开展这些方面的研究工作。
| [1] |
王勋年, 李征初, 陈正武, 等. 声学风洞内气动噪声源识别定位方法研究[J]. 空气动力学学报, 2012, 30(3): 284-290. Wang X N, Li Z C, Chen Z W, et al. Researching on aerodynamic noise sources identification technology in anechoic wind tunnel[J]. Acta Aerodynamica Sinica, 2012, 30(3): 284-290. DOI:10.3969/j.issn.0258-1825.2012.03.002 |
| [2] |
陈正武, 王勋年, 李征初, 等. 基于声学风洞的麦克风阵列测试技术应用研究[J]. 实验流体力学, 2012, 26(3): 84-90. Chen Z W, Wang X N, Li Z C, et al. Application investigation of microphone array measuring and testing technique in anechoic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(3): 84-90. DOI:10.3969/j.issn.1672-9897.2012.03.016 |
| [3] |
Miles J W. On the reflection of sound at an interface of relative motion[J]. Journal of the Acoustical Society of America, 1957, 29(2): 226-228. DOI:10.1121/1.1908836 |
| [4] |
Ribner H S. Reflection, transmission, and amplification of sound by a moving medium[J]. Journal of the Acoustical Society of America, 1957, 29(4): 435-441. DOI:10.1121/1.1908918 |
| [5] |
Schlinker R H, Amiet R K. Refraction and scattering of sound by a shear layer[R]. NASA-CR-3371, 1980.
|
| [6] |
Amiet R K. Correction of open jet wind tunnel measurements for shear layer refraction[C]//Proc of AIAA 2nd Aero-acoustics Conference. 1975.
|
| [7] |
Amiet R K. Refraction of sound by a shear layer[J]. Journal of Sound and Vibration, 1978, 58(4): 467-482. DOI:10.1016/0022-460X(78)90353-X |
| [8] |
Candel S M, Guedel A, Julienne A. Radiation, refraction, and scattering of acoustic waves in a free shear layer flow[R]. AIAA-1976-544, 1976.
|
| [9] |
Ahuja K K, Tanna, H K, TesterB J. An experimental study of transmission, reflection and scattering of sound in a free jet flight simulation facility and comparison with theory[J]. Journal of Sound and Vibration, 1981, 75(1): 51-85. DOI:10.1016/0022-460X(81)90235-2 |
| [10] |
Wang Y G, Yang J S, Jia Q, et al. An improved correction method for sound source drift in a jet flow and its application to a wind tunnel measurement[J]. Acta Acustica united with Acustica, 2015, 101(3): 642-649. DOI:10.3813/AAA.918859 |
| [11] |
Zana S. Effect of open jet shear layers on aeroacoustic wind tunnel measurements[D]. Mekelweg: Delft University, 2011.
|
| [12] |
Candel M, Julienne A, Guedel A. Refraction and scattering of sound in an open wind tunnel flow[C]//Proc of the 6th international congress on instrumentation in aerospace simulation faci-lities. Ottawa: Institute of Electrical and Electronics Engineers, Inc., 1975.
|
| [13] |
Oerlemans S. Detection of aeroacoustic sound sources on aircraft and wind turbines[D]. Enschede: University of Twente, 2009.
|
| [14] |
张军, 陈鹏, 张俊龙, 等. 基于简化射线模型的剪切层相位修正方法[J]. 航空动力学报, 2018, 33(10): 2459-2465. Zhang J, Chen P, Zhang J L, et al. Shear layer phase shift correction method based on a simplified ray model[J]. Journal of Aerospace Power, 2018, 33(10): 2459-2465. |
| [15] |
张俊龙, 李征初, 卢翔宇. 开口风洞剪切层对传声器及其阵列测量影响试验研究[J]. 实验流体力学, 2018, 32(1): 71-77. Zhang J L, Li Z C, Lu X Y. Experimental research on the influence of open jet shear layer on microphone and microphone array measurement[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(1): 71-77. |
| [16] |
Humphreys W M, Hunter W W, Meadows K R. Design and use of microphone directional arrays for aeroacoustic measurement[R]. AIAA-98-0471, 1998.
|
| [17] |
Sijtsma P, Oerlemans S, Tibble T G, et al. Spectral broadening by shear layers of open jet wind tunnels[R]. AIAA-2014-3178, 2014.
|




