2. 中国空气动力研究与发展中心 高超声速冲压发动机技术重点实验室, 四川 绵阳 621000;
3. 国防科技大学 高超声速冲压发动机技术重点实验室, 长沙 410073
2. Science and Technology on Scramjet Laboratory, China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China;
3. Science and Techno-logy on Scramjet Laboratory, National University of Defense Technology, Changsha 410073, China
高超声速飞行器是现代航空航天技术发展的必然趋势,超燃冲压发动机(Scramjet)[1]作为高超声速飞行器的理想动力装置和关键技术之一,已成为各国竞相研究的热点。21世纪以来,美国先后启动HyTech计划、Hyper-X计划、HyFly计划[2]和HIFIRE[1]项目验证高超声速飞行及其推进的关键技术并取得突破。国内多家单位开展超燃冲压发动机相关研究并在工程攻关上取得一定突破[3],但对一些机理性和规律性的问题认识仍不清晰,严重阻滞发动机性能的进一步提升。当前,超燃冲压发动机性能的进一步提升仍有赖于对其燃烧室内燃料雾化掺混机理的深刻认识和对燃/气混合效果的有效测量与预测。国内外研究者开展了大量超声速气流中气液燃料横向射流喷注混合研究,其中液态碳氢燃料的雾化、蒸发、混合过程尤其复杂[4-6]。
一般地,燃料在超声速空气来流中的空间分布是燃料与空气混合质量的重要衡量评断标准和控制手段。在传统的描述燃料空间分布的参数中,燃料边界分布(即理论上燃料当量比无限接近于0的位置)是定量评述燃料空间分布的常用参数,例如穿透深度和展向分布等。研究者对超声速气流中燃料穿透深度的研究最为深入,Forde[7]最早提出采用简单的理论模型预测超声速气流中液体射流的运动轨迹。Yates[8]利用直接拍照方法,研究不同马赫数、不同液气动量通量比q及不同介质物性参数等对液态燃料在超声速气流中的穿透深度和展向分布的影响,指出超声速气流中液体横向射流喷注过程具有强烈的非定常特性,空间分布主要由喷孔直径和液气动量通量比决定,并基于喷孔的有效直径对无量纲化后的穿透深度和展向宽度开展经验公式拟合。Baranovsky[9]进一步研究了喷注角度对穿透深度和破碎过程的影响,将喷注角度信息融入Yates关于穿透深度的经验公式中[8]。
Lin[10]采用激光片光照明方法、阴影拍照方法对倾斜喷注的气泡雾化喷嘴空间分布和雾化开展了系统细致的研究,认为气泡雾化喷嘴有利于穿透深度的提高,并将喷射角度和含气率等信息融入穿透深度经验公式。Ghenai[11]通过研究也得出液气动量通量比和含气率是影响穿透深度最主要因素的结论。同时Lin还采用PDA方法对Ma1.94气流中液体射流的雾化特性开展了全场测量研究[12],指出归一化后的截面粒径分布和速度分布沿纵向分别呈S型和镜像S型,这也是可见报道的为数不多的关于射流/喷雾横截面分布的研究。此外,Perurena等[13]还开展了撞击式喷嘴、射流中加入固体颗粒、异型喷孔等的穿透深度研究并取得进展。
国内关于超声速气流中液体射流喷注的研究起步较晚,中国科学技术大学徐胜利等[14]最早对超声速气流中的液体燃料非定常喷射过程开展成像研究。中国科学院力学所王东、俞刚等[15]在超声速气流中液体射流喷注的流场细致结构观测方面亦作出巨大贡献。中国科学技术大学费立森等[16]采用PLIF方法和阴影方法对冷态来流条件下煤油的扩散、混合现象进行试验研究,指出射流和来流的动压比越大,穿透深度越大,射流更容易破碎和雾化;但同时也会诱导更强的激波,造成更大的总压损失。潘余[17]采用高射摄影/纹影方法研究发现,激波入射能够扩大燃料空间分布区域,提高液体射流穿透深度。刘静[18]采用纹影法获得了射流穿透深度经验公式,并指出其纹影结果与PDA方法得到的穿透深度接近。陈亮[19]和曹娜[20]采用全息和高速摄影方法对冷态超声速来流中横向液态射流雾化过程进行更加细致的研究,分析了不同来流马赫数、来流总压、喷孔直径、喷射介质和喷注压降下的射流喷注雾化现象,发现射流穿透深度基本由液气动量通量比和喷孔直径决定。杨辉[21]、李锋[22]则采用纹影方法对不同喷注压降和喷射角度液体射流柱前弓形激波及射流穿透深度开展研究,拟合出包含喷注角度信息的穿透深度公式。此外,刘林峰[23]还对有/无凹腔的凹腔内煤油射流喷注掺混效果开展对比研究,指出凹腔存在强剪切层导致液体射流更难进入气体主流,凹腔喷注的煤油射流穿透深度略小于平板壁面喷注方式。
综上所述,国内外针对超声速气流中液体横向射流/喷雾空间分布开展研究极为广泛,重点聚焦在穿透深度影响因素和预测规律研究上,得到大量一致性认识和规律,但仍缺乏对展向宽度和横截面分布的深入研究,特别缺乏射流/喷雾三维空间分布的预测模型,并且现有的空间分布描述方法本身存在缺陷。首先,采用试验手段获取射流/喷雾边界的过程中,受光学测试方法、图像处理方法以及其他人为因素的影响较大,不同试验方法对于流场中液滴浓度的敏感性亦不同。Lin[12]曾分别采用PDA和高速相机对液体在纵向上的空间分布进行研究,结果发现,通过PDA测量得到的射流穿透深度比高速成像结果高约50%。其次,基于理论定义的穿透深度或者展向宽度所描述的射流/喷雾边界上燃料浓度无限接近于零,其附近的燃料浓度也很低,无法实现有效燃烧,这种边界在实际的燃烧边界判断中实用性不高。另外,穿透深度或者展向宽度曲线只能表征喷雾的最外围位置,会造成喷雾空间浓度信息的全部丢失,在应用中存在局限性。最后,超声速气流中液体横向射流喷注过程具有强烈的非定常性,穿透深度或者展向宽度参数是一个静态量,不能够描述射流/喷雾本身具有的这种振荡特征。
本文基于超声速气流中液体横向射流空间分布研究现状及存在的不足,从基本的光学成像原理出发,提出采用高时空分辨率的瞬态成像方法对喷雾进行“冻结”拍摄,并提出新的无量纲参数来定量化描述射流/喷雾边界上的浓度分布,以及射流/喷雾边界的振荡特性。另外,深入研究射流/喷雾的横截面分布规律,探索性地建立可以描述超声速气流中液体横向射流三维空间振荡分布的预测模型。
1 试验装置与试验方法 1.1 超声速风洞超声速气流中液体横向射流试验在一座小型二维下吹式风洞中进行,如图 1所示。高压空气作为流动介质与能量源,经气体供应系统进入稳压室,经由等截面低速段进一步整流(低速段内装有蜂窝整流装置),最后由超声速拉瓦尔喷管将均匀的低速来流加速到设计马赫数。试验段与超声速喷管出口直接连接,试验后气体排入大气环境中。风洞能够通过调节上游供气压力和供气流量控制超声速来流总压条件,能够通过更换超声速喷管实现不同来流马赫数的模拟,本文中风洞设计参数为:气流Ma=2.1,总温T0=300K,总压p0=642~1010kPa。风洞系统的详细介绍可以参考文献[4]。
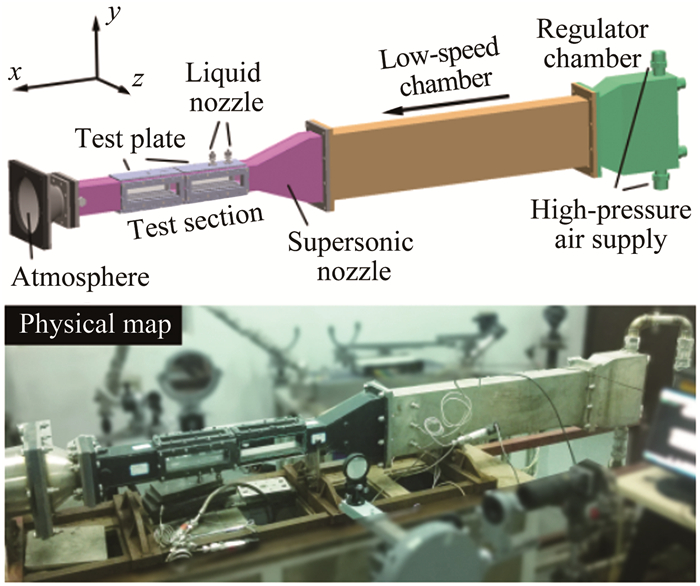
|
| 图 1 风洞结构示意图与实物图 Fig.1 The supersonic tunnel system |
风洞试验段横截面尺寸为40mm×60mm,两段试验窗长度均为200mm,试验段四面开窗,其中底面用于安装可拆卸试验件,其他三处可安装光学石英玻璃用于光学观测。液体通过试验件上的圆孔垂直进入超声速气流。试验采用左手坐标系,其中超声速气体流动方向定义为流向,称之为x+方向,液体射流初始出射方向定义为纵向,称之为y+方向,坐标原点位于喷孔出口靠近气流上游的边缘处。
试验前对风洞流场品质进行标定,主要采用PIV方法测量了试验段中心对称面上(z=0)的速度分布,图 2给出了流场速度场分布云图,结果显示该风洞主流气流速度为531m/s,主流速度分布均匀,边界层厚度约为3mm,流场品质达到设计要求,满足试验需求。
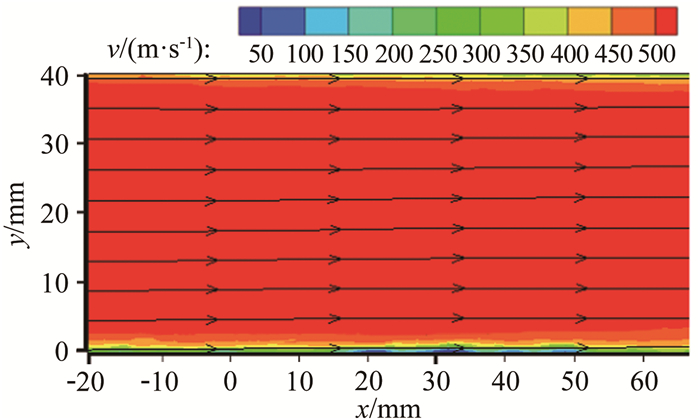
|
| 图 2 风洞试验段速度分布云图(x=0为喷射位置) Fig.2 The airflow velocity distribution in test section (PIV result), 'x=0' is the injection position |
研究中使用了两种光学成像方法,其中脉冲激光背景成像方法(后文简称PLBI)用于射流/喷雾纵向分布的瞬态结构成像。光学系统布局如图 3所示。
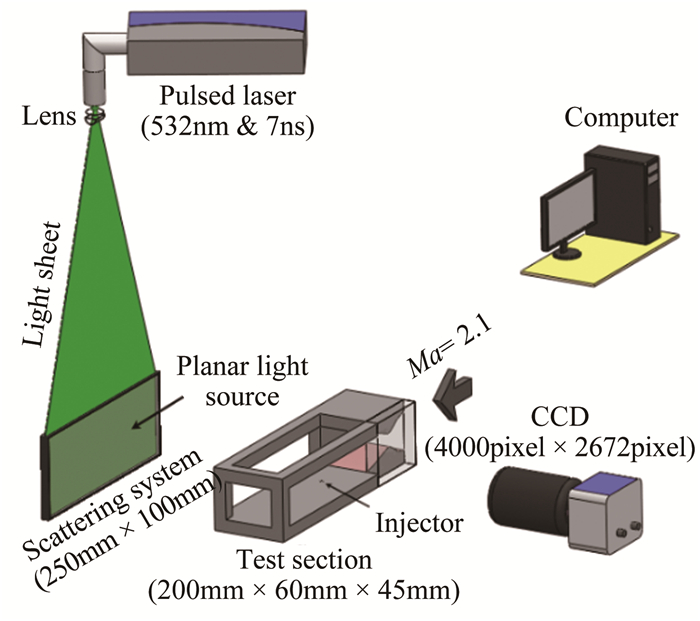
|
| 图 3 脉冲激光背景成像方法成像过程示意图 Fig.3 Sketch map of imaging process of PLBI |
高能量脉冲激光束通过凸透镜和柱面透镜转换成片光并射入装有溶胶介质的散射系,利用溶胶介质的丁达尔散射原理将激光传播方向和相位无序化,进而消除激光固有的干涉效应,同时使光强在整个出光面上分布更加均匀。面光源出光面尺寸约250mm×100mm,照明脉冲宽度约7ns,CCD相机位于面光源的正前方并且拍摄区域位于两者之间,CCD像素空间尺寸为4000pixel×2672pixel,灰度等级为256,CCD相机配合Sigma 105定焦镜头在物距100mm的拍摄距离上对物理空间96mm×64mm的区域进行成像。经验证,在本次试验参数下,成像系统景深为30mm,能够完全覆盖喷雾区域,7ns脉冲照明时间内物体运动距离不超过0.3pixel,能够确保拍摄图像无拖影和虚焦现象。
基于PIV原理的倾斜成像方法(后文简称SPIV)用于对射流/喷雾横截面分布进行“冻结”拍摄。如图 4所示,脉冲激光片光透过侧面玻璃瞬间照亮横截面喷雾区域(液体喷雾作为散光粒子),CCD相机同时对喷雾场成像。试验中相机镜头中轴线与所需拍摄的横截面夹角始终保持68°,通过调整CCD感光元件与镜头中轴线的夹角,可以对横截面上的液雾清晰成像,由于倾斜布置相机导致成像过程中产生的图形畸变可以基于Scheimpflug原理进行修正。相机和光源相对位置固定,通过电控位置平台实现前后位置的移动,进而实现不同横截面喷雾图像的拍摄。
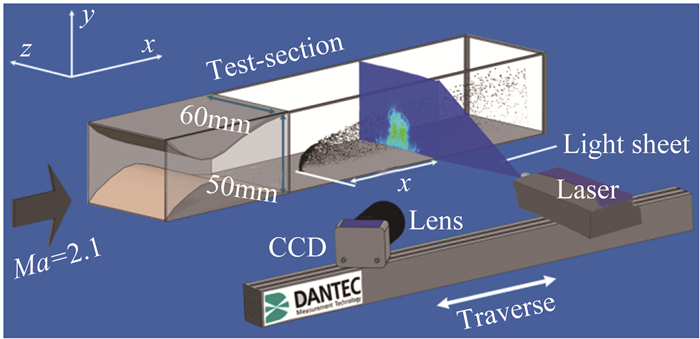
|
| 图 4 试验风洞与试验方法 Fig.4 The schematic diagram of test section and optical path |
本研究共涉及67组试验与测量工况,其中1~40组工况用于射流/喷雾纵向分布研究,详细参数列于表 1中。超声速来流总压参数可变,液体射流介质为煤油,主要研究参数包括:Ma=2.1,试验段总压范围为642~1010kPa,喷嘴流道直径范围为0.48~1.52mm,喷注压降范围为0.36~4.61MPa,液气动量比范围为0.11~7.49。工况40为单独设计的验证试验,与前39组工况不同之处在于液体射流喷注介质为纯净水。
| No. | Supersonic crossflow (Ma=2.1; T0=300K) | Kerosene jet (density: 800kg/m3; l=1.5mm) | ||||
| p0/kPa | d/mm | Δp /MPa | Vl /(m·s-1) | q | ||
| 1~8 | 920 | 1.52 | 0.48~3.93 | 23~69 | 0.68~6.16 | |
| 9/10 | 714 | 1.52 | 0.43/1.24 | 22/38 | 0.84/2.46 | |
| 11/12 | 792 | 1.52 | 0.48/1.35 | 23/40 | 0.82/2.41 | |
| 13~18 | 923 | 1.25 | 0.58~4.10 | 22~61 | 0.62~4.85 | |
| 19 | 1010 | 1.25 | 1.92 | 41 | 2.04 | |
| 20 | 820 | 1.25 | 1.87 | 41 | 2.47 | |
| 21 | 719 | 1.25 | 2.26 | 45 | 3.44 | |
| 22 | 645 | 1.25 | 2.00 | 43 | 3.40 | |
| 23~29 | 915 | 1.00 | 0.36~4.61 | 18~72 | 0.42~6.84 | |
| 30~32 | 797 | 1.00 | 2.81~4.39 | 57~71 | 4.97~7.49 | |
| 33~36 | 795 | 0.48 | 0.63~4.55 | 15~23 | 0.11~0.78 | |
| 37 | 642 | 0.48 | 4.33 | 22 | 0.92 | |
| 38 | 742 | 0.48 | 4.37 | 23 | 0.80 | |
| 39 | 947 | 0.48 | 4.37 | 23 | 0.63 | |
| 40 | 1.00 | 3.80 | ||||
工况41~67等27组横截面分布测量试验详细参数信息列于表 2中。气体主流的马赫数、总温、总压保持不变,通过改变液体射流的喷注压降实现液气动量比的变化。研究涉及的喷孔直径包括5种:0.68、0.99、1.25、1.51和2.07mm。液气动量通量比q的变化范围为1.1~10,涉及到无量纲的横截面位置x/d范围为10~100。
| No. | d/mm | x/d | q | |
| Gas crossflow | 41~44 | 0.68 | 100 | 1.6/3.4/6.1/10 |
| Ma=2.1 | 45~46 | 0.99 | 10 | 3.7/5.5 |
| T0=300K | 47~48 | 0.99 | 20 | 3.9/5.7 |
| p0=891kPa | 49 | 0.99 | 30 | 3.9 |
| 50~51 | 0.99 | 50 | 3.9/5.6 | |
| 52 | 0.99 | 70 | 3.9 | |
| Water Jet | 53~56 | 0.99 | 100 | 3.9/5.6/7.4/9 |
| ρ=1000kg/m3 | 57~60 | 1.25 | 100 | 1.1/2.4/3.7/4.9 |
| Tw=300K | 61~64 | 1.51 | 66 | 1.4/2.7/4.1/5.5 |
| 65 | 2.07 | 10 | 2.3 | |
| 66 | 2.07 | 30 | 1.1 | |
| 67 | 2.07 | 45 | 2.3 |
超声速气流中,液体射流本身湍流度、气体来流脉动以及气液强剪切作用等因素使射流分布随时间和空间发生不规则变化,液雾的空间分布形态呈现剧烈的非定常特性。图 5显示的是利用SPIV方法获得的不同随机时刻横截面上液雾的瞬态分布(亮色区域为液雾)。图中不同时刻液雾的空间分布形态完全不同,时间历程的空间分布成像结果也说明了射流/喷雾的非定常分布特性。需要说明的是,图 5中只显示了中心对称截面一侧的分布结果。
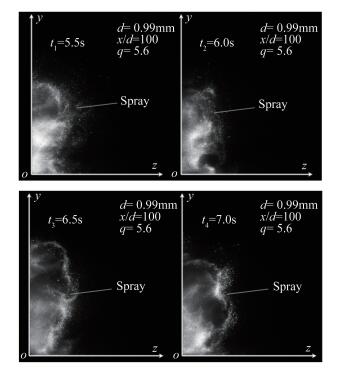
|
| 图 5 不同时刻横截面液雾瞬态分布(零时刻为开阀喷注起始时间) Fig.5 Cross-section distributions of the spray at four random moments in case 54 |
为了描述射流/喷雾振荡分布这一非定常现象,借鉴气体湍流边界层研究方法[24]提出无量纲参数γ(喷雾分数)。本文中,喷雾分数γ定义为空间某一点被液体喷雾包围或者占据的时间占总试验测量时间的比值,其数学表达式为:
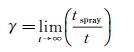 (1)
(1)
其中,tspray是空间点被液体喷雾包围或者占据的时间,t是试验测量总时间。由定义可知,始终被喷雾包围或者占据的空间点上喷雾分数γ值为1,气体主流区域喷雾分数γ值恒为0。
射流/喷雾在空间中的分布是实时变化的,基于喷雾分数的定义可知,存在一个区域,对应的喷雾分数值的范围为γ∈(0, 1),射流/喷雾边界始终在该区域内振荡分布,称该区域为“边界带”。
由于试验中无法直接获得一段试验测量时间内某一空间点被液体喷雾包围或者占据的时长,需要采用极限逼近方法对实际喷雾分数进行测量计算,基于样本统计概率逼近真实值。文献[25]详细介绍了喷雾分数的具体计算过程,并指出样本数越大,计算得到的概率值越接近喷雾分数真实值,当样本数为200时获得的喷雾分数分布可以较好地反映实际喷雾分数分布情况。
图 6是基于200幅瞬态喷雾图像计算得到的喷雾分数分布云图。γ云图由3部分组成,其中纯红色区域对应的喷雾分数γ值恒为1,说明射流/喷雾能够始终包围或覆盖该区域,定义为“恒喷雾区”;纯蓝色区域对应的喷雾分数γ值恒为0,说明液体始终不会到达该区域,定义该区域为“纯气相区”;颜色渐变区域喷雾分数γ值介于0到1,且射流/喷雾边界在该区域范围内振荡,该区域即为“边界带”区域。从等值线图可以看出,边界带实际上是由多条γ等值线组成,任意一条γ等值线均可认为是射流/喷雾的时均边界,其中γ值无限趋近于0代表的边界即为传统意义上的穿透深度。
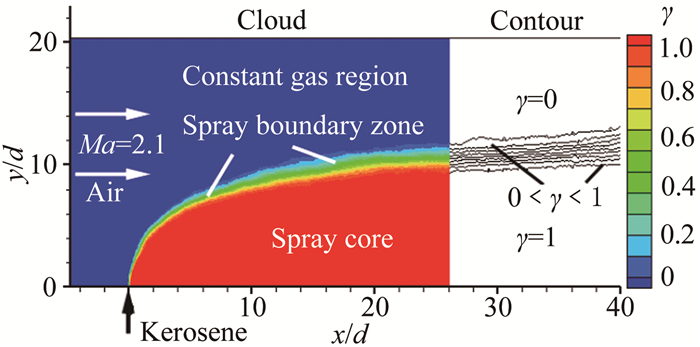
|
| 图 6 纵向喷雾分数计算结果 Fig.6 Numerical result of γ value |
图 7显示的是具有不同来流总压(p0)/射流速度(Vl)/喷嘴流道直径(d)的几个工况条件下边界带喷雾分数的分布情况。边界带宽度沿流向逐渐增加,变化趋势与穿透深度相似。在x/d较小时,边界带宽度增加较快,随着x/d的增加,边界带宽度增加速度逐渐变缓。通过对表 1中所列全部工况进行喷雾分数分布规律研究发现,不同工况参数条件下,射流边界带宽度沿流向的变化趋势相同,均表现出随着流向距离(x/d)的增加,边界带宽度不断增加,并且边界带可以以γ=0.5为界分为上下两个部分,γ越大或越小,对应的边界位置距离γ=0.5等值线越远。
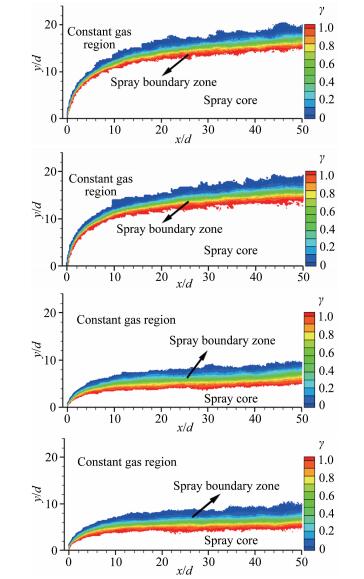
|
| 图 7 多参数协同作用对边界带的影响 Fig.7 The spray boundary zones under various operating conditions |
图 8中针对5个流向位置,对边界带内喷雾分数沿纵向的分布进行研究,固定x/d位置,将喷雾分数随纵向高度的变化以图表形式给出,从图中可以看出,在x/d=10、20、30、40和50这5个位置上,喷雾分数γ在边界带内沿纵向上几乎呈线性变化。从图中还发现,γ=0.5始终处于边界带中心位置上,以γ=0.5为中心,不同γ值对应的空间位置偏离γ=0.5对应位置的幅度几乎完全对称。喷雾分数γ在边界带内沿纵向的线性变化规律在所有试验工况条件下得到了验证。
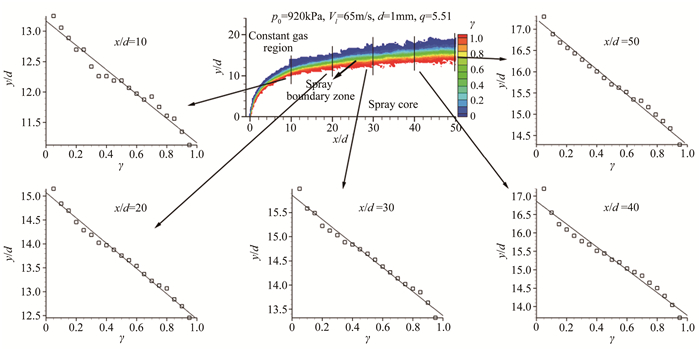
|
| 图 8 喷雾分数沿纵向分布规律 Fig.8 The γ trend in longitudinal direction |
基于以上研究结论,借鉴射流穿透深度公式的幂函数形式,构造包含喷雾分数γ的射流/喷雾边界带经验模型如下:
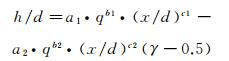 (2)
(2)
其中,等式右边第一项为γ=0.5对应的边界,第二项为不同γ值对应边界距离γ=0.5边界线的纵向距离,a1、b1、c1、a2、b2、c2为待定的常系数。当γ=0时,公式(2)退化为传统的穿透深度经验公式。
假设不同工况下边界带宽度与γ=0.5代表的射流纵向高度存在正比关系,则式(2)可以进一步简化:
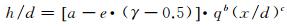 (3)
(3)
因为γ=0.5对应边界在边界带内的相对位置比较稳定,在对式(3)中常系数进行优选时,首先令γ=0.5,基于表 1所示工况下γ=0.5的全部试验数据,利用非线性拟合方法对数据进行处理,得到最优结果如式(4)所示,其中,拟合结果与试验数据的相关系数为0.9595,拟合标准差为0.7673。图 9显示的是式(4)对全部工况下γ=0.5对应边界曲线的拟合效果。
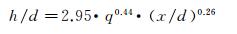 (4)
(4)
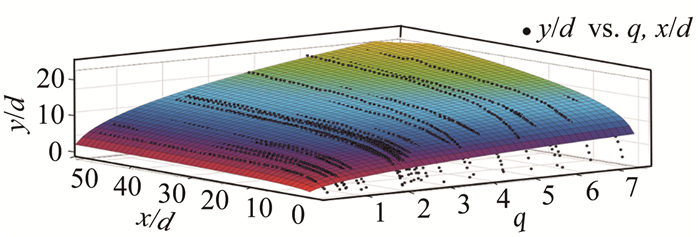
|
| 图 9 全部工况下γ=0.5对应边界曲线的拟合 Fig.9 Fitting result of the experimental results for γ=0.5 |
另外,在确定了常系数b=0.44,c=0.26后,进一步对γ=0.1、0.3、0.7、0.9等几条对应边界单独进行数据拟合,得到的拟合结果分别对应式(5)~(8),且拟合公式与试验数据吻合良好,两者之间的相关系数均大于0.95,拟合标准差分别为0.8915、0.7958、0.7608和0.7908。
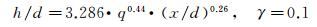 (5)
(5)
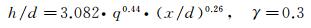 (6)
(6)
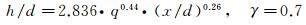 (7)
(7)
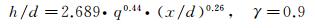 (8)
(8)
从式(5)~(8)中可以看出,随着γ的增加,对应边界的拟合公式中常系数项a的值均匀递减,通过对γ=0.1到γ=0.9之间以0.05为步进长度的所有边界数据进行提取,基于所得数据对纵向边界带模型进行最终的拟合,式(9)即为纵向边界带模型的经验公式,对应的拟合标准差为0.9825。
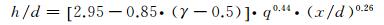 (9)
(9)
当γ=0时,纵向边界带模型退化为传统穿透深度模型;当γ=1时,纵向边界带模型代表射流振荡区域的最内边沿;当0 < γ < 1时,根据γ取值不同,纵向边界带模型按射流边界活跃频率对边界带进行分区,定量描述射流的振荡分布。
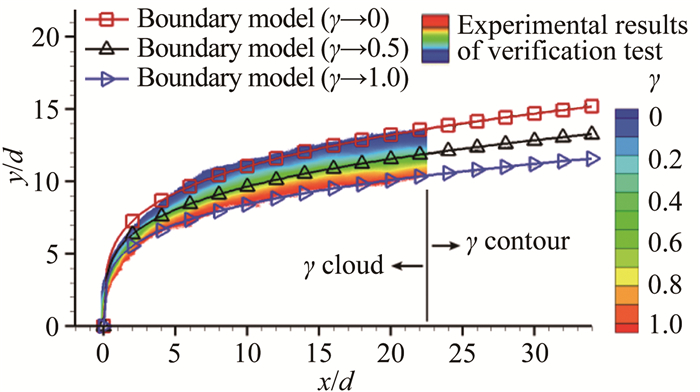
图 10所示为采用纵向边界带模型对圆柱水射流垂直喷入Ma2.1气流中的射流振荡分布进行预测的效果,验证试验喷孔直径为1.0mm,液气动量通量比为3.8。从图中可以看出,纵向边界带模型预测得到的射流边界带区域(0 < γ < 1区域)与试验结果(云图及等值线图)吻合较好。通过计算,在0 < x/d < 34区域内,边界带模型对边界带内γ=0.5边界的预测误差平方和均值为0.04,对射流穿透深度(γ=0)的预测误差平方和均值为0.08,对边界带内液核区边界(γ=1.0)的预测误差平方和均值为0.08。
|
| 图 10 边界带模型预测效果(验证试验工况参数:喷射介质为水; 喷孔直径d=1.0mm; 喷注压降pl=1.49MPa; Ma=2.1;液气动量通量比q=3.8) Fig.10 Evaluation of the accuracy of the model |
图 11给出了横截面上喷雾分数γ的典型分布计算结果,其中左半部分为γ分布云图,右半部分为γ分布的等值线图,对应γ值分别为0.1、0.3、0.5、0.7和0.9,对称分布结果由镜像方法得到。与纵向分布类似,横截面上γ分布云图亦由三部分特征组成,分别是γ=1的纯红色“恒喷雾区”、γ=0的纯蓝色“纯气相区”和γ介于0~1之间的颜色渐变“边界带”。
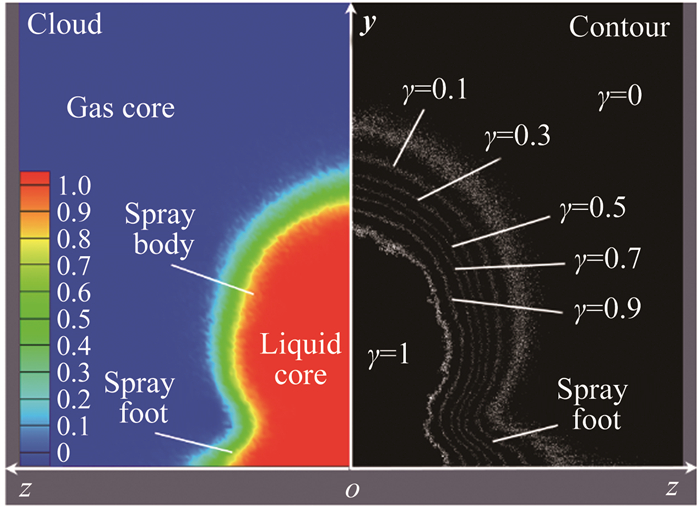
|
| 图 11 横截面喷雾分数分布计算结果 Fig.11 Numerical result of the γ-value at a cross-section |
从图中可以看出,横截面γ等值线呈“Ω”型分布,可以分为spray body和spray foot两部分,其中贴近喷注壁面并沿展向向外延伸的喷雾部分称之为spray foot。根据前期的研究,液体圆柱射流进入超声速气流中后,在气液剪切作用下有大量小液滴从射流柱上剥离,这一剥离过程在射流根部的亚声速区、表面波主导破碎区的表面波发展区以及射流柱断裂位置附近均有发生,其中边界层内的小液滴因为边界剪切层的存在不易再进入主流区域;同时大量小液滴在产生之初分布在壁面附近,在向下游的运动过程中,部分小液滴通过壁面剪切层进入边界层内,边界层内小液滴的存在和运动是spray foot产生和发展的根本原因。Spray foot内液体占据总液体体积很小一部分,大部分液体集中分布在spray body部分,spray body的扩散及其与气体的混合决定了横截面中喷雾分布的形状。
2.4.2 横截面分布的规律性图 12显示了d和q不变的条件下,横截面液雾分布随流向距离x的变化过程。从图中可以看出,随着x的增加,横截面上液雾逐渐向周围扩展,使喷雾横截面面积不断增加。而且,x < 50时,这种变化幅度相对于x>50时更大。这是因为在x=50位置处,液体的雾化和混合基本完成[5],液雾继续向下游发展,主要是在剪切作用下进一步完成与气体的混合,同时液雾缓慢向外围扩散,这种混合和扩散过程相对于近场强气液作用下的对流扩散效率低得多。另外,当流向距离越大,spray foot沿展向扩张,且距离壁面的距离有所增加。

|
| 图 12 d和q不变的条件下,液雾横截面分布随x的变化 Fig.12 Impact on the spray's cross-section distribution when x changes (d and q keep constant) |
图 13比较了在相同x和d条件下,不同q对横截面液雾分布的影响。液气动量通量比q增加时,液体流量及离开喷孔后射流轴向和周向的初始动量均有增加,导致喷雾横截面上喷雾区域的面积明显增加。同时,随q的增加, spray foot在展向上有向内收缩的趋势,这是因为射流离开喷孔后在展向和纵向上的扩散都是一个连续的过程,距离喷孔越近,展向宽度越小,此时从射流柱上剥离的液滴在气体扰动下到达下壁面,在展向上分布的宽度也会相对较小;而从距离喷孔越远位置剥离的小液滴形成的spray foot在展向宽度上会更大,但是因为流向气流的气动作用,距离喷孔越远,剥离的小液滴越不容易被吹到下壁面。

|
| 图 13 d和x不变的条件下,液雾横截面分布随q的变化 Fig.13 Impact on the spray's cross-section distribution when q changes (d and x kept constant) |
基于喷雾分数γ建立横截面喷雾分布的数学模型,采用分段函数形式描述横截面上γ等值线分布。如图 14所示,分段点s的数学意义是对应的γ等值线上的极小值点,其坐标表示为(zs,ys)。
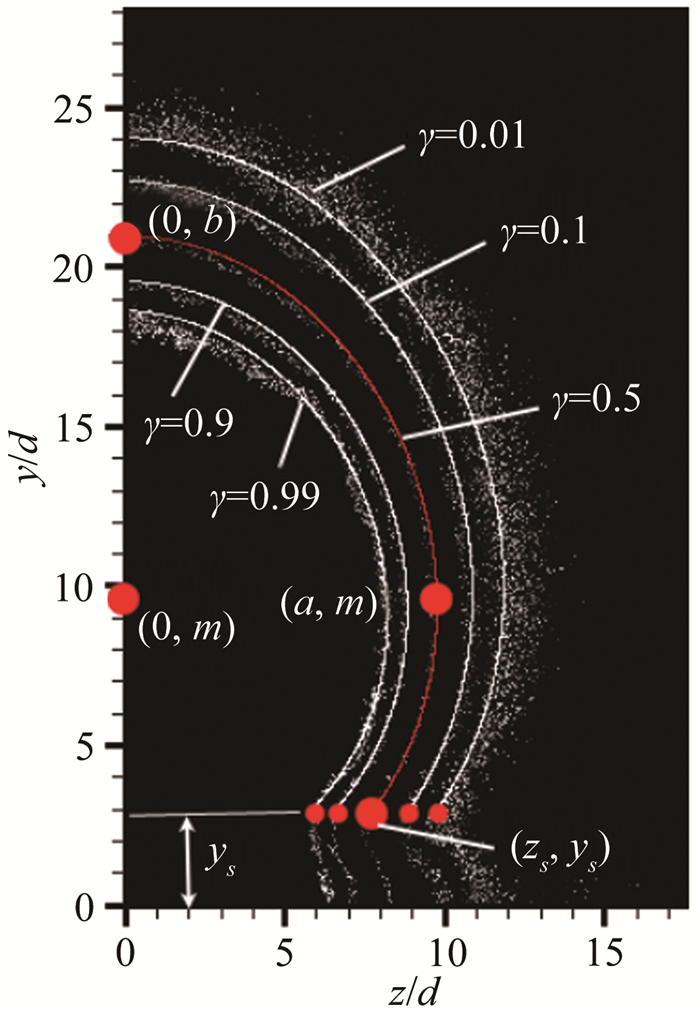
|
| 图 14 γ等值线 Fig.14 The γ contour line |
以分段点为界,分段点以上部分即为spray body,其下为spray foot。在同一横截面上,不同γ对应的ys变化较小,为简化模型,取不同γ等值线对应的ys平均值作为最终的分段点纵向坐标。通过不同工况下ys的统计分析,ys可由式(10)预测得到,从式(10)中可以看出,ys随q的增加有所减小,随x/d的增加而增加。
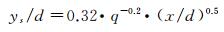 (10)
(10)
以分段点为界,采用egg-shape曲线描述spray body部分的喷雾分数等值线,采用抛物线曲线描述spray foot部分,分段点坐标(zs, ys)分别满足式(11)和(12)代表的两个函数。因为横截面内液体喷雾主要集中在spray body部分,本文主要针对spray body部分开展深入研究,基于试验数据对式(11)中的常系数进行拟合确定。
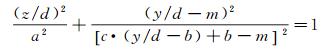 (11)
(11)
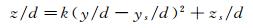 (12)
(12)
由egg-shape曲线的几何性质可知,式(11)代表的曲线以y轴为中心左右对称,其中,egg-shape曲线中心坐标为(m,0),系数a代表展向能够到达的最远距离(宽度),系数b代表纵向能够到达的最高点(高度),c是曲线的变形系数。对于γ=0的特殊情况,a即为流向位置x处的展向宽度,b即为流向位置x处的穿透深度。
对于任意一条γ等值线,均对应一组最佳的a、b、c、m值使式(11)对其空间分布的拟合结果最优。在优选拟合系数过程中,目标函数如式(13)所示,以目标函数最小为优化目标。其中(yi, zi)是基于试验结果计算得到的γ等值线上的点,N代表点的总数。
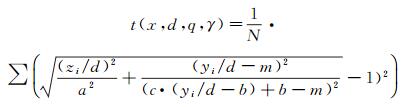 (13)
(13)
从图 14中可以看出,不同的γ值对应的模型常系数明显不同,这说明常系数a、b、c、m分别是γ的函数,从前面的分布规律还可以清晰得到,a、b、c、m至少还是x/d和q的函数。
综上所述,采用egg-shape曲线描述横截面γ等值线分布时,存在5个特征参数,分别是变形系数c,宽度a,高度b,中心点的纵向坐标m和分段点的纵坐标ys,且a、b、c、m均与γ、x/d和q相关,其中ys只受x/d和q的影响。
2.5 空间振荡分布的三维重构为了重构喷雾在超声速气流中的三维分布,需要准确确定横截面分布模型中a、b、c、m等常系数随各工况参数的变化规律,建立系数模型。
基于γ的物理意义以及前面的分析可知,γ无限趋近于零的等值线对应的最佳拟合参数a和b分别代表传统意义上的穿透深度和展向宽度。已有的大量研究表明,穿透深度和展向宽度主要由x/d和q决定,且满足幂函数关系式。从图 14中γ等值线图上还可以看出,以γ=0.5为中心,随着γ-0.5绝对值的增大,a和b变化的幅度越来越大,不妨基于幂函数关系式提出带有γ的系数模型,如式(14)所示,进而确定a、b、c、m等常系数与工况参数之间的定量关系。
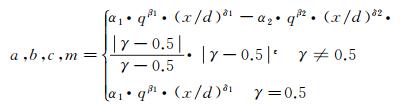 (14)
(14)
因为常系数a和b的实际物理含义是射流/喷雾不同γ值对应的展向宽度和穿透深度,所以采用幂函数形式关系式对其进行拟合可以得到较好的拟合效果。基于表 2中工况对应的试验结果,首先对a(x/d, q, γ=0.5)和b(x/d, q, γ=0.5)进行拟合,得到对应常系数值,再根据剩余试验数据对式中的其余常系数进行拟合确定,最终得到的a和b系数模型,如式(15)和(16)所示,模型与试验数据的相似度达到0.9025,拟合标准差为0.9376。采用同样方法对系数c和m表达式中的常系数进行确认,幂函数关系式对中心点纵向坐标m能够实现较好的拟合,得到m系数模型,如式(16)所示,其中,模型与试验数据的相关系数为0.8869,拟合标准差为0.9288。变形率c基于不受γ影响,最终的拟合结果如式(17)所示,c系数模型与试验数据的相关系数达到0.9125。
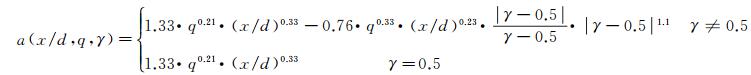 (15)
(15)
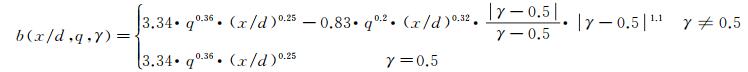 (16)
(16)
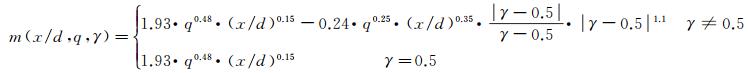 (17)
(17)
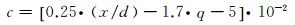 (18)
(18)
综上研究,式(10)~(11)和式(15)~(18)共同构成喷雾spray body三维空间分布模型。当γ=0时,模型描述的是喷雾的三维外边界,外边界以外区域不存在任何液体;当γ=1时,模型描述的是喷雾的三维内边界,内边界以内区域始终能够被液雾覆盖;当0 < γ < 1时,模型描述的是喷雾的非定常振荡特性,实时的瞬态喷雾边界在内边界和外边界之间的边界带区域振荡,γ值的大小能够定量描述这种非定常振荡。
3 结论超声速气流条件下的液体横向射流喷注掺混研究中,传统描述参数和预测模型不适用于具有强烈非定常特性的射流/液雾三维空间分布研究。本文主要结论如下:
提出并定义新的用于定量描述射流/喷雾空间振荡分布的无量纲参数——喷雾分数(γ),赋予γ明确的物理意义以及计算过程。在纵向分布研究中,γ无限接近于0对应的等值线,即为传统的穿透深度曲线,基于γ建立了纵向边界带模型,实现了对射流/喷雾振荡分布的准确预测,并通过试验检验了模型的准确性。
同时,基于γ对横截面上的液雾分布开展研究,发现横截面上喷雾的“Ω”型分布特征,并提出spray body和spray foot的分区概念。构造egg-shape曲线拟合spray body内的γ等值线,提炼出横截面分布数学模型中的5个重要系数,通过开展不同工况和不同截面位置的测量试验,最终建立横截面模型系数与x/d、q和γ的定量关系式,进而建立了超声速气流中液体横向射流三维空间振荡分布预测模型。
| [1] |
邓帆, 叶友达, 焦子涵, 等. HIFiRE项目中气动/推进一体化高超声速飞行器设计研究[J]. 实验流体力学, 2017, 31(2): 73-80. Deng F, Ye Y D, Jiao Z H, et al. Research on HIFiRE project's hypersonic vehicle integrated design of aerodynamic and scramjet propulsion[J]. Journal of Experiments in Fluid Mechanics, 2017, 31(2): 73-80. |
| [2] |
Boudreau A H. Status of the U.S. air force HyTech program[R]. AIAA-2003-6947, 2003.
|
| [3] |
冮强, 王辽, 郭金鑫, 等. 基于总温测量的超燃冲压发动机燃烧效率研究[J]. 实验流体力学, 2012, 26(4): 1-5. Gang Q, Wang L, Guo J X, et al. Scramjet combustion efficiency studies based on the total temperature measurement[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(4): 1-5. DOI:10.3969/j.issn.1672-9897.2012.04.001 |
| [4] |
Wang Z G, Wu L Y, Li Q L, et al. Experimental investigation on structures and velocity of liquid jets in a supersonic crossflow[J]. Applied Physics Letters, 2014, 105(13): 134102. DOI:10.1063/1.4893008 |
| [5] |
Wu L Y, Wang Z G, Li Q L, et al. Breakup and coalescence of kerosene droplet group in a Mach 1.86 supersonic crossflow[J]. Applied Physics Letters, 2014, 107(10): 104103. (WOS:000361640200066). |
| [6] |
Wu L Y, Wang Z G, Li Q L, et al. Study on transient structure characteristics of round liquid jet in supersonic crossflow[J]. Journal of Visualization, 2016, 19(3): 337-341. DOI:10.1007/s12650-015-0328-4 |
| [7] |
Forde J M, Molder S, Szpiro E J. Secondary liquid injection into a supersonic airstream[J]. Journal of Spacecraft and Rockets, 1965, 3(8): 1172-1176. |
| [8] |
Yates C. Liquid injection into supersonic airstreams[R]. AIAA-1971-724, 1971.
|
| [9] |
Baranovsky S I, Schetz J A. Effect of Injection angle on liquid injection in supersonic flow[J]. AIAA Journal, 1980, 18(6): 625-629. DOI:10.2514/3.50798 |
| [10] |
Lin K C, Kennedy P J, Jackson T A. Spray penetration heights of angle-injected aerated-liquid jets in supersonic crossflows[R]. AIAA-2000-0194, 2000.
|
| [11] |
Ghenai C, Sapmaz H, Lin C X. Penetration height correlations for non-aerated and aerated transverse liquid jets in supersonic cross flow[J]. Experiments in Fluids, 2009, 46(1): 121-129. DOI:10.1007/s00348-008-0547-8 |
| [12] |
Lin K C, Kennedy P J, Jackson T A. Structures of water jets in a Mach 1.94 supersonic crossflow[R]. AIAA-2004-971, 2004.
|
| [13] |
Perurena J B, Asma C O, Theunissen R, et al. Experimental investigation of liquid jet injection into Mach 6 hypersonic crossflow[J]. Experiments in Fluids, 2009, 46(3): 403-417. DOI:10.1007/s00348-008-0566-5 |
| [14] |
徐胜利, Archer R D, Milton B E, 等. 煤油在超声速气流中非定常横向喷射的实验观察[J]. 空气动力学学报, 2000, 18(3): 272-279. Xu S L, Archer R D, Milton B E, et al. Experimental investigation on unsteady transverse injection of kerosene into a supersonic flow[J]. Acta Aerodynamica Sinica, 2000, 18(3): 272-279. DOI:10.3969/j.issn.0258-1825.2000.03.003 |
| [15] |
王冬, 俞刚. 煤油射流在超声速燃烧室中的实验研究[J]. 实验流体力学, 2005, 19(2): 11-13. Wang D, Yu G. Investigation of kerosene jet spray in supersonic combustion[J]. Journal of Experiments in Fluid Mechanics, 2005, 19(2): 11-13. DOI:10.3969/j.issn.1672-9897.2005.02.003 |
| [16] |
费立森, 徐胜利, 王昌建, 等. 高速冷态气流中煤油雾化现象的实验研究[J]. 中国科学(E辑:技术科学), 2008, 38(1): 72-78. |
| [17] |
潘余, 王振国. 激波对超声速流中横向射流的影响[J]. 国防科技大学学报, 2007, 29(6): 6-9. Pan Y, Wang Z G. Shock impinge on supersonic cross flow injection[J]. Journal of National University of Defense Technology, 2007, 29(6): 6-9. DOI:10.3969/j.issn.1001-2486.2007.06.002 |
| [18] |
刘静, 王辽, 张佳, 等. 超声速气流中横向射流雾化实验和数值模拟[J]. 航空动力学报, 2008, 23(4): 724-729. Liu J, Wang L, Zhang J, et al. Experimental and numerical simulation of atomization of liquid jet in supersonic crossflow[J]. Journal of Aerospace Power, 2008, 23(4): 724-729. |
| [19] |
陈亮, 乐嘉陵, 宋文艳, 等. 超声速冷态流场液体射流雾化实验研究[J]. 实验流体力学, 2011, 25(2): 29-34. Chen L, Le J L, Song W Y, et al. Experimental investigation of liquid jets atomization in supersonic cold crossflow[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(2): 29-34. DOI:10.3969/j.issn.1672-9897.2011.02.006 |
| [20] |
曹娜, 徐青, 曹亮, 等. 脉冲全息技术在发动机射流雾化场测量中的应用[J]. 现代应用物理, 2013, 4(4): 323-329. Cao N, Xu Q, Cao L, et al. Measurement of spray characterization of engine nozzle by pulsed holography[J]. Modern Applied Physics, 2013, 4(4): 323-329. DOI:10.3969/j.issn.2095-6223.2013.04.004 |
| [21] |
Yang H, Li F, Sun B. Trajectory analysis of fuel injection into supersonic cross flow based on schlieren method[J]. Chinese Journal of Aeronautics, 2012, 25(1): 42-50. DOI:10.1016/S1000-9361(11)60360-9 |
| [22] |
李锋, 吕付国, 罗卫东, 等. 超声速气流中液体横向射流的破碎特性[J]. 北京航空航天大学学报, 2015, 41(12): 2356-2362. Li F, Lyu F G, Luo W D, et al. Breakup characteristics of li-quid jet in supersonic cross flow[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(12): 2356-2362. |
| [23] |
刘林峰, 徐胜利, 郑日恒, 等. 超声速气流中凹槽结构煤油喷射和掺混研究[J]. 推进技术, 2010, 31(6): 721-729. Liu L F, Xu S L, Zheng R H, et al. Studies on kerosene injection and mixing with cavity in supersonic flow[J]. Journal of Propulsion Technology, 2010, 31(6): 721-729. |
| [24] |
Humble R A, Peltier Bowersox S J R D W. Visualization of the structural response of a hypersonic turbulent boundary layer to convex curvature[J]. Physics of Fluids, 2012, 24(10): 148-154. |
| [25] |
吴里银, 王振国, 李清廉, 等. 超声速气流中液体横向射流的非定常特性与振荡边界模型[J]. 物理学报, 2016, 65(9): 178-186. Wu L Y, Wang Z G, Li Q L, et al. Unsteady oscillation distribution model of liquid jet in supersonic crossflows[J]. Acta Physica Sinica, 2016, 65(9): 178-186. |



