2. 北京电子工程总体研究所, 北京 100854;
3. 中国科学院 力学研究所, 北京 100089
2. Beijing Institute of Electronic System Engineering, Beijing 100854, China;
3. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100089, China
粒子图像测速(Particle Image Velocimetry, PIV)是基于流场显示技术发展而来的二维/三维流场测量方法,因其具有高精度、非接触等测量优势而被广泛应用于各类高速流动测量中。Scarano和Haertig (2003)[1]使用260nm粒径氧化钛粒子测量高超声速(Ma=6)球体流场;Haertig[2]采用320nm粒径氧化钛粒子实现了激波风洞测量等。PIV作为一种流场测量手段,在解决高/超声速流动问题中具有广阔的应用前景[3]。然而高速流动PIV测量技术仍面临着巨大的挑战,其实验结果与示踪粒子物化特性紧密相关,例如测量精度取决于示踪粒子的随流能力,小粒径粒子有更强的跟随特性而图像显示则要求粒子粒径足够大以保证粒子散射图像清晰。因此示踪粒子的选择成为了当前的研究重点,正如Schrijer与Fulvio Scarano[4]所述,PIV技术应用于高/超声速的主要挑战是粒子布撒与示踪粒子的选择。
粒子选择方面,国内外学者进行了大量研究。Melling[5]提出一个近似模型,认为激波法向马赫数小于1.4时,粒子松弛过程与时间呈线性关系;赵玉新[6]从粒子动力学的角度研究了纳米粒子在超声速流场中的跟随性问题;陈小虎[7]通过数值模拟方法探究PIV示踪粒子的Stokes数(St数)和布撒浓度对跟随响应特性的影响;易仕和[8]阐明了纳米示踪粒子可以在激波复杂流场高时空分辨率流动显示的同时获取流场同一区域的速度场与密度场。尽管陈方[9]提出了新的粒子松弛特性模型,并论证Ma=4高速流动PIV实验中,20~50nm粒径的示踪粒子才能更好地捕捉流场特征,然而该松弛特性模型缺少足够的实验支撑,包括不同激波角、斜激波和脱体激波的验证。
为了研究示踪粒子粒径对高速流动PIV技术测量的影响,本文首先以不同粒径粒子作为示踪粒子,利用PIV技术测量Ma4的高速流动。气流经过10°尖劈并在其头部诱导产生1道22°激波,通过测量可以得到激波边界和流场分布。经过比较分析,选择合适的示踪粒子,并验证其在不同激波结构下(30°尖劈模型产生的斜激波与45°尖劈模型产生的脱体激波)的跟随响应特性。通过理论分析、数值模拟和不同模型的实验结果对比,分析高速流动下示踪粒子的跟随响应特性。
1 实验设备和系统 1.1 多马赫数风洞系统基于上海交通大学多马赫数风洞进行高速流动PIV实验[10]。风洞系统组成部分如图 1所示,为吹气式高速流动风洞,高压气体由可存储20MPa空气的高压储罐提供;真空球可由二级真空泵实现100Pa的真空度;蓄热式加热器可最高加热至700K,以防止高速流动中气体冷凝;加热器下端为整流段与可更换喉道的Laval喷管,实现多马赫数实验;实验舱内有供粒子收集并导出的收集段,以防示踪粒子大量滞留。在压力和温度都稳定的前提下,单次PIV实验测量有效时间可达10s。

|
| 图 1 上海交通大学多马赫数风洞 Fig.1 Multi-Mach number high-speed wind tunnel of Shanghai Jiao Tong University |
图像采集系统使用SM-CCD11M05跨帧相机;Nd:YAG双脉冲激光器提供波长532nm激光,双脉冲时间间隔和频率与跨帧相机同步,单次脉冲能量约为520mJ,激光光束经导光臂与片光头后形成等腰三角形片光(焦距750mm,三角形底边长750mm);SM-MicroPulse725同步控制器实现激光器和相机等多设备的时序触发;PIV分析软件经互相关迭代、窗口变形、自动向量滤波等功能实现图像处理分析。其中双脉冲激光器连续2束激光的时间间隔取决于所测量的速度与视窗大小,若间隔太小,则会对利用互相关原理判断粒子相应关系产生影响;反之则粒子飞出视窗范围。根据常用判定公式(1),以1/4判读小区作为粒子跨帧位移上限:
 (1)
(1)
其中,FOV为视场区域,Resolution为CCD相机的分辨率,IA为判读小区, 在已知来流速度约为800m/s的条件下,估算出跨帧时间约为800ns,实验设置如图 2所示。

|
| 图 2 实验设置 Fig.2 Experimental setup |
实验采用尖劈模型,半顶角分别取10°、30°和45°,如图 3所示。

|
| 图 3 模型图片 Fig.3 Image for models |
实验工况如表 1所示,主流气体为空气。总压依照实际的飞行参数而定,总温则是保证实验段气流不冷凝。为最大限度减小粒子对流场的影响,限制流量约为50mL/s。实验持续时间设定为15s。
| Ma | Specific heat ratio γ | Total-temperature/K | Total-pressure/MPa |
| 4 | 1.39 | 400 | 0.4 |
PIV技术通过测量示踪粒子的速度,并以此近似地认为是该点的流场速度,这就要求示踪粒子有足够好的跟随特性。然而小粒径的粒子虽然可以保证强跟随性,但其有以下弱点:(1)散射光较弱,容易在图像视野中消失,造成相关计算时的误判; (2)抗噪性低易受其他光源影响; (3)经济成本昂贵。示踪粒子选择的重点就是如何实现既满足图像处理要求又满足跟随性的要求。
刘伟等[11]研究了时间和空间发展的气固两相混合层中的颗粒弥散在混合层中的浓度分布,表明St数仍是影响颗粒弥散的主要因素;樊建人等[12-13]采用拟谱法得到气固两相混合层的三维特征会影响其动量厚度发展及St数会影响粒子在混合层中的分布等结论。示踪粒子St数常用来表征粒子的松弛时间尺度与流场特征时间尺度之比,其计算公式如下:
 (2)
(2)
τf为气流的无量纲时间,τf=ΔUg/θ0,ΔUg为激波前后速度差,θ0为来流入口处的初始混合层厚度。同样来流条件和相同尖劈模型下τf为常值。公式表明,同样实验条件下St数对实验的影响和τp相同,故可研究τp对粒子跟随响应特性的影响。τp为粒子的无量纲松弛时间:
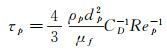 (3)
(3)
μf为空气动力粘度,dp与ρp分别为粒子粒径和密度,CD为阻力系数,Rep为粒子雷诺数,由粒子速度与流场速度之间的相对速度给出:
 (4)
(4)
ρf为流场气体密度,Up为粒子速度,U为流场速度。
粒径小于10μm的超细粉体颗粒会不可避免地出现聚团现象[14],相较于氧化钛,氧化铝更易发生聚团[15],且氧化钛有高折射率,在成本和操作上都有更大的优势[16],故本文采用氧化钛为示踪粒子。为了确定示踪粒子大小,这里采用陈方[17]提出的适用性更广的分析模型:
 (5)
(5)
xn为粒子经过松弛时间t的法向松弛距离,ξn为粒子跨越激波面的法向松弛距离,U*为无量纲滑移速度:
 (6)
(6)
Upn(t)为粒子法向速度,Un1与Un2分别为激波前后速度。则粒子松弛距离计算公式为:
 (7)
(7)
则30nm氧化钛示踪粒子的松弛距离约为0.81mm,远小于图像尺寸(0.1m×0.1m),满足实验所需。
陈方提出的粒子选择准则[17]表明, 粒径在20~50nm范围内的示踪粒子能更好地捕捉Ma4的高速流动。本研究选择30和100nm的氧化钛粉末进行对比实验。具体松弛特性参数如表 2所示。
| 30nm | 100nm | |
| Relative Reynold number | 0.03 | 0.1 |
| Particle Knudsen number | 14 | 4 |
| Relative Mach number | 0.29(t=τ) | |
| Relaxation time/μs | 1.55 | 5.24 |
| Relaxation distance/mm | 0.38 | 1.29 |
根据公式(3)计算粒子松弛时间。μf取6.4×10-6kg/(m·s),ρp取4.23×103kg/m3,ρf取0.04kg/m3,30nm氧化钛示踪粒子的松弛时间约为1.97μs。30nm粒子的松弛时间仅为100nm粒子松弛时间的1/3。此处以30nm氧化钛粒子为例,进行不同尖劈模型的相关松弛特性计算,结果如表 3所示。
| 10°wedge | 30°wedge | |
| Relative Reynold number | 0.03 | 0.08 |
| Particle Knudsen number | 14 | 14 |
| Relative Mach number | 0.27 | 0.78 |
| Shock wave angle/(°) | 22 | 44 |
| Freestream velocity U/(m·s-1) | 797.8 | 797.8 |
| Velocity Un1/(m·s-1) | 299.7 | 565.1 |
| Shockwave strength Man1 | 3.71 | 2.87 |
| Velocity Un2/(m·s-1) | 157.6 | 151.9 |
| Relaxation time/μs | 1.55 | 1.97 |
| Relaxation distance/mm | 0.38 | 0.81 |
高速流场突变明显和结构复杂导致速度梯度分布不均,这使均匀布撒示踪粒子成为高速流动PIV技术的另一个难点。本实验中,采用如下技术实现均匀布撒:
粒子装载进粒子发生器前经加热器加热烘干,减少因潮湿形成的巨型粒子团,并能有效地减少粒子对光学视窗的污染。新型粒子布撒器由上海交通大学高超创新实验室自主研发,底部喷嘴采用旋风气流设计,能将粒子均匀布撒,如图 4所示[18]。高压氮气瓶提供的气流携带示踪粒子形成旋风式流场,在发生器内经多次碰撞削弱粒子间粘结度。为防止粒子刚注入主流时形成堆积现象,在粒子注入主流之前的管路中安装流量计与限流装置,能有效地实现流量均匀注入。

|
| 图 4 粒子布撒器罐体内旋风式气流示意图 Fig.4 Visualization of cyclone flow in particle seeder |
实验方法可以直观地认识问题的物理本质,而数值模拟方法可以与实验结果进行对比、分析,有助于更深入理解粒子跟随响应特性。
PIV实验中示踪粒子跟随响应特性计算本质上属于气固两相流动的范畴,此处采用欧拉-拉格朗日方法进行研究。连续相大涡模拟耦合离散相拉格朗日颗粒轨道的模型研究作为两相湍流的重要手段,能更准确地阐述气固两相流动中连续相和离散相之间的相互联系。在相间耦合时,先对气相流场进行初始化计算;再在连续流场中喷射粒子;然后得到粒子的动量和热量交换项重新对流场计算;再校对示踪粒子的运动轨道进行矫正;最后迭代以上2步,得到收敛的双向耦合解[7]。
3 结果与分析 3.1 不同粒径10°尖劈模型实验结果基于10°尖劈模型,进行不同粒径的示踪粒子实验。实验结果处理后得到流场云图再采用MATLAB软件分析得到激波平面位置(红线处),多组实验结果中取出1张图片为例,如图 5所示。

|
| 图 5 100nm TiO2示踪粒子流场图 Fig.5 Flow field images for 100nm TiO2 |
从图中可以看出,相同实验条件下,不同粒径氧化钛粒子的跟随响应能力有明显差别。其中小粒径粒子在图像上能更清晰地显示激波结构,但是整体亮度偏暗,图像显示效果稍差;而100nm的大粒径示踪粒子图像上可以较清晰观察到流场中粒子在激波面前后的差异,但是激波结构稍微混乱;2幅图流线比较相似,在激波前后速度偏转明显。所计算出的激波角近似于解析解的激波角度,其中小粒径粒子的实验值更接近于理论值。结果表明小粒径示踪粒子能更准确地反应高速流动的实际情况。从图中显示的激波角度和流线的连续性来说,30nm粒径的氧化钛示踪粒子有更好的跟随特性。

|
| 图 6 30 nm TiO2示踪粒子流场图和数值模拟图 Fig.6 Flow field images and numerical simulation results for 30nm TiO2 |

|
| 图 7 粒径30nm和100nm的粒子图像 Fig.7 Images of 30 and 100nm diameter particles |
综合考虑30nm的氧化钛粒子具有误差小、实验成功率高且激波前后流场结构清晰等优势,故选用此种粒子进行不同角度模型实验来验证粒子跟随响应特性。
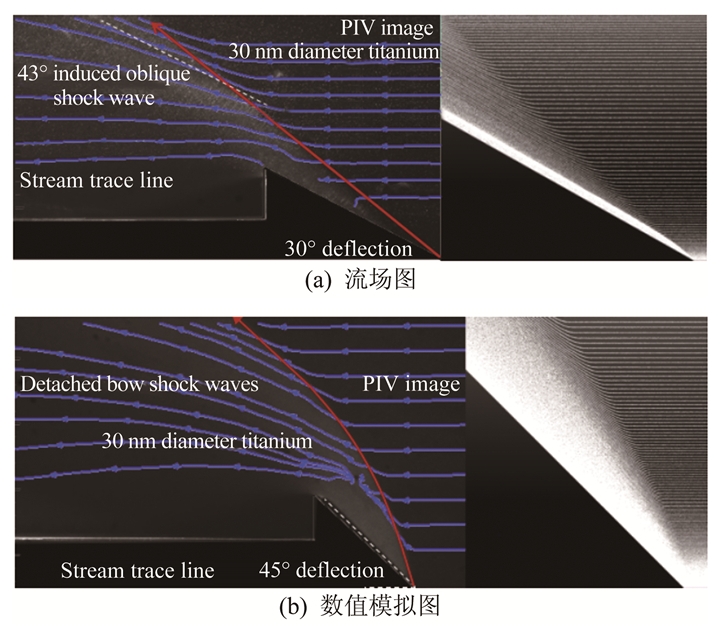
3.2 同种粒子不同模型验证结果以不同角度尖劈(半顶角分别为10°、30°和45°)为模型,30nm氧化钛颗粒为示踪粒子,Ma4条件下的高速流动PIV实验与数值模拟结果对比来探讨30nm氧化钛示踪粒子在不同角度斜激波和脱体激波的跟随响应特性。实验结果如表 5所示,实验图像和数值模拟结果如图 8所示。
| 10°模型 | 30°模型 | 45°模型 | |||
| (度数) | 误差 | (度数) | 误差 | ||
| 理论值 | 22.23 | 0 | 44.07 | 0 | 脱体激波 |
| 实验值 | 21.75 | -2.1% | 42.64 | -3.2% | |
| 数值模拟 | 23.55 | 5.9% | 44.28 | 0.5% | |
|
| 图 8 30°和45°尖劈模型的流场图和数值模拟图 Fig.8 Flow field and number simulation images for 30° and 45° models |
对于10°尖劈模型而言,实验所得激波角略低于理论值,误差约为2.1%,而数值模拟结果明显高于理论值,其误差高于实验值;实验所得的激波偏转角度与速度分布符合实际情况,与数值模拟值接近。对于30°尖劈模型而言,实验所得激波角明显低于理论值,误差为3.2%,数值模拟值却很接近于理论值;图像结果显示实验图片中的流线清晰明显,沿着激波面偏转并在激波面堆积拥簇。Ma4的高速流场经过45°尖劈模型会产生脱体激波,这是因为气流内折角过大时,超声速气流无法通过一道附体激波来满足物面边界条件,故在尖劈头部产生弓形激波,后半段为斜激波;实验所得的流场流线在激波处剧烈压缩,头部弓形激波后有1个不大的亚声速区;实验流线图所得到的激波面形态与数值模拟结果基本吻合。
综合而言,在验证不同角度尖劈模型的激波角时,实验法误差值相近,其中在测量小角度模型有更高的可信度;相比于数值模拟方法,实验法在小角度模型测量有更大优势。30nm氧化钛粒子作为示踪粒子有良好的跟随性,可以近似认为随流位移与实际值相同,更适用于高速流场显示测量。
4 结论高速流动PIV测量技术的重点是粒子的布撒与粒子选择,示踪粒子的选择是能否完成精准测量的决定性因素。本文对示踪粒子的跟随响应特性开展实验并进行探讨,得到了以下结论:
(1) 通过理论模型分析,马赫数4的高速流动经过10°尖劈模型产生22°激波,粒径为30nm的氧化钛粒子的松弛时间约为100nm的氧化钛粒子的1/3,理论上小粒径粒子的跟随响应特性强于大粒径粒子的跟随响应特性;
(2) 30和100nm氧化钛示踪粒子的高速流动实验结果在流场结构方面有着类似的结果,得到的激波角与理论值相近,但小粒径粒子实验得到的激波角度更接近理论值,更适合Ma4的高速流场示踪;
(3) 综合性能更好的30nm氧化钛示踪粒子同样适用于不同角度尖劈高速流动实验。其斜激波的实验值与理论值接近,脱体激波与数值模拟一致。验证了30nm氧化钛粒子在Ma4的高速流场具有良好的跟随响应特性。
致谢: 感谢国家自然基金(11672183、91641129和91441205)、国家973计划项目以及高温气体动力学国家重点实验室开放课题的支持。| [1] | Scarano F, Haertig J. Application of non-isotropic resolution PIV in supersonic and hypersonic flows[J]. Journal of Mechanical Design, 2009, 100(2): 208–215. |
| [2] | Haertig J, Havermann M, Rey C, et al. Particle image velocimetry in Mach 3.5 and 4.5 shock-tunnel flows[J]. AIAA Journal, 2002, 40(6): 1056–1060. DOI:10.2514/2.1787 |
| [3] | 徐惊雷. PIV技术在超及高超声速流场测量中的研究进展[J]. 力学进展, 2012, 42(1): 81–89. Xu J L. The development of the PIV experimental study of the super/hypersoinc flowfield[J]. Advances in Mechanics, 2012, 42(1): 81–89. |
| [4] | Schrijer F F J, Scarano F, Oudheusden B W V. Application of PIV in a Mach 7 double-ramp flow[J]. Experiments in Fluids, 2006, 41(2): 353–363. DOI:10.1007/s00348-006-0140-y |
| [5] | Melling A. Tracer particles and seeding for particle image velocimetry[J]. Measurement Science & Technology, 1997, 8(12): 1406–1406. |
| [6] | 赵玉新, 易仕和, 田立丰, 等. 基于纳米粒子的超声速流动成像[J]. 中国科学, 2009, 39(12): 1911–1918. |
| [7] | 陈小虎, 陈方, 刘洪, 等. 高速流动PIV示踪粒子跟随性分析[J]. 气体物理, 2017, 2(4): 36–45. Chen X H, Chen F, Liu H, et al. Tracking characteristics of PIV tracer particles in high speed flows[J]. Physics of Gases, 2017, 2(4): 36–45. |
| [8] | 易仕和, 何霖, 田立丰, 等. 纳米示踪平面激光散射技术在激波复杂流场测量中的应用[J]. 力学进展, 2012, 42(2): 197–205. Yi S H, He L, Tian L F, et al. The application of nano-tracer planar laser scattering in shock wave field measurement[J]. Advances in Mechanics, 2012, 42(2): 197–205. |
| [9] | Chen F, Liu H, Rong Z. Development and application of nanoparticle tracers for PIV in supersonic and hypersonic flows[R]. AIAA-2012-0036. |
| [10] | 张亚, 陈方, 刘洪, 等. 高速流动中PIV示踪粒子松弛特性研究[J]. 实验流体力学, 2013, 27(6): 70–75. Zhang Y, Chen F, Liu H, et al. Research on the relaxation characteristics of PIV tracer particles in supersonic flow[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(6): 70–75. DOI:10.3969/j.issn.1672-9897.2013.06.013 |
| [11] | 刘伟, 万国新, 陈景兵, 等. 可压缩气固混合层中离散相与连续相的相互作用研究[J]. 计算力学学报, 2009, 26(1): 8–14. Liu W, Wan G X, Chen J B, et al. Study on the interaction between the continuous and the dispersed phases in compressible gas-solid mixing layer[J]. Chinese Journal of Computational Mechanics, 2009, 26(1): 8–14. |
| [12] | 樊建人, 郑友取, 岑可法. 三维气固两相混合层湍流拟序结构的直接数值模拟[J]. 工程热物理学报, 2001, 22(2): 241–244. Fan J R, Zheng Y Q, Cen K F. Direct numerical simulation in turbulent coherent structures of three-dimensional gas-particle two-phase mixing layer[J]. Journal of Engineering Thermophysics, 2001, 22(2): 241–244. DOI:10.3321/j.issn:0253-231X.2001.02.031 |
| [13] | 樊建人, 罗坤, 金晗辉, 等. 直接数值模拟三维气固两相混合层中颗粒与流体的双向耦合[J]. 中国电机工程学报, 2003, 23(4): 153–157. Fan J R, Luo K, Jin H H, et al. Direct numerical simulation of the two-way coupling effects between particles and fluid in the three-dimensional particle-laden mixing layer[J]. Proceedings of the CSEE, 2003, 23(4): 153–157. DOI:10.3321/j.issn:0258-8013.2003.04.031 |
| [14] | 李召好, 李法强, 马培华, 等. 超细粉末团聚机理及其消除方法[J]. 盐湖研究, 2005, 13(1): 31–36. Li Z H, Li F Q, Ma P H, et al. Eliminetion methods and mechanism of agglomeration of ultrafine powders[J]. Journal of Salk Lake Research, 2005, 13(1): 31–36. DOI:10.3969/j.issn.1008-858X.2005.01.006 |
| [15] | Scarano F, Oudheusden B W V. Plannar velocity measurements of a two-dimensional compressible wake[J]. Experiments in Fluids, 2003, 34(3): 430–441. DOI:10.1007/s00348-002-0581-x |
| [16] | Urban W, Mungal M, Urban W, et al. Planar velocity measurements in compressible mixing layers[J]. Journal of Fluid Mechanics, 2001, 431(431): 189–222. |
| [17] | Chen F, Liu H, Yang Z, et al. Tracking characteristics of tracer particles for PIV measurements in supersonic flows[J]. Chinese Journal of Aeronautics, 2017, 30(2): 577–585. DOI:10.1016/j.cja.2016.12.033 |
| [18] | 刘洪, 陈方, 励孝杰, 等. 高速复杂流动PIV技术研究实践与挑战[J]. 实验流体力学, 2016, 30(1): 28–42. Liu H, Cheng F, Li X J, et al. Practices and challenges on PIV technology in high speed complex flows[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(1): 28–42. |



