2. 中国空气动力研究与发展中心, 四川 绵阳 621000
2. China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China
风洞实验中,来流的流动速度是最为基本的物理量,湍流度是风洞流场品质的重要参数,需要对其进行准确测量,并对其影响进行修正,以提高风洞实验数据精准度[1-2]。如果湍流度测量不准确,风洞实验得到的模型气动系数也不精确,将会在很大程度上影响飞行器气动性能的预测精度。特别是随着现代航空、航天技术以及空气动力学科的迅速发展,超声速、高超声速飞行器风洞实验中,对来流湍流度的测量需求变得十分迫切,发展先进的速度及湍流度测量技术,提供可靠的风洞实验结果,对促进国家高速飞行器及武器装备的快速发展和推动空气动力学科不断进步具有十分重要的意义。
目前能够实现风洞流场湍流度测量的技术主要有热线风速仪测速技术[3]、激光多普勒测速技术[4-5]和时间分辨粒子图像测速技术[6]。热线风速仪多用于亚声速、跨声速流动湍流度测量,并且属于接触式测量,在测量过程中对流场有一定的干扰;激光多普勒测速技术和时间分辨粒子图像测速技术在速度测量时需要添加示踪粒子,目前受粒子添加技术及示踪粒子本身跟随性的影响,其在高速非定常流动的速度测量中受到较多的限制,甚至无法测量。
为实现高速流场速度脉动测量,20世纪90年代,出现了一种干涉瑞利散射(Interferometric Rayleigh Scattering, IRS)测量技术[7-11],其通过对流场气体分子瑞利散射光谱的分析,在不需要外加示踪粒子的条件下,实现了对高速流场速度和湍流度等参数的非接触测量。现有的干涉瑞利散射测量技术多采用光电倍增管,对瑞利散射光信号形成的干涉条纹进行快速采集。NASA Glenn Research Center先后利用不同方案,将瑞利散射同一级次干涉条纹成像于不同的光电倍增管,再通过相应图像处理算法,获取了时间分辨的干涉条纹在像平面的空间位置及线型分布,实现了流场速度脉动等参数的定量测量[1-2, 12-14]。虽然光电倍增管具有较高的弱信号放大能力,但其在干涉条纹的快速采集过程中,需要利用光学器件将同一级次干涉条纹进行空间分割,使其被不同的光电倍增管采集,并通过复杂的解算分析得到干涉条纹的空间位置及线型信息,这极大增加了系统的复杂性;同时,由于该系统只能依靠少量光电倍增管探测的光强信息进行分析,空间采样率较低,在一定程度上降低了流场速度等参数的测量精度。为此,本文将高帧频的EMCCD相机应用于干涉瑞利散射测速技术中,结合大功率窄线宽连续激光器和法布里-珀罗干涉仪,在大幅简化光路系统的基础上,建立了一套干涉瑞利散射测速装置,实现了高速流场速度脉动的非接触测量,并将该装置应用于0.3m×0.3m暂冲式跨超声速风洞实验,获得了Ma3.0条件下,风洞来流速度及湍流度测量结果,实验中装置时间采样率达到4kHz。
1 基本原理当一束激光入射到流场中时,会伴随气体分子的瑞利散射,当流场气体存在一定运动速度时,瑞利散射光将相对入射激光发生多普勒频移,频移的大小与气体的宏观运动速度相关,因此可通过对散射光相对于入射激光的多普勒频移测量,实现对气流运动速度的定量测量[15]。
通常,流场气体运动速度引起的多普勒频移很小,在波长532nm的激光照射下,100m/s的流动引起的多普勒频移约为265MHz(波长频移0.00025nm),常规光谱仪已经不能将其分辨,此时,基于多光束干涉原理的Fabry-Pérot干涉仪因具有很高的光谱分辨能力成为一个不错的选择[9-17]。
Fabry-Pérot干涉仪是一种多光束干涉设备,其通过将不同波长的单色光,在像平面形成十分明锐且半径不同的干涉圆环,可实现对光谱的超高精度分辨。在干涉瑞利散射测速系统中,流场气体分子的散射激光由于多普勒效应,将相对激光器输出的参考激光产生一定的频移,在Fabry-Pérot干涉仪的像平面,同一级次散射光与参考激光将形成独立的、半径不同的干涉圆环,散射信号干涉圆环的半径与流场速度相关。因此,通过测量散射光干涉圆环的半径,即可实现对流场速度的定量测量[15]。
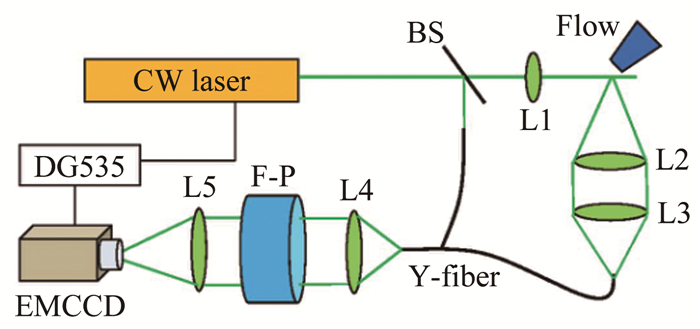
2 实验装置简介 2.1 装置光路简介设计的干涉瑞利散射测速装置主要由激光光源、散射光收集装置、Fabry-Pérot干涉仪和EMCCD相机组成,如图 1所示。激光光源为大功率、窄线宽、连续激光器,波长为532nm,功率10W,线宽约5MHz。Fabry-Pérot干涉仪的通光口径为50mm,端面反射率90%,自由光谱范围约6.6GHz。EMCCD相机的最高帧频可达到10 000 frames/s,即装置的理论采样率达到10kHz。散射光收集方向与入射激光传输方向之间的夹角可根据实验工况合理设置。激光器输出的激光经分束器BS分出很小一部分进入Y型光纤的一个输入端,作为参考信号;大部分光经焦距f=500mm的透镜L1汇聚后照射被测流场,流场的瑞利散射光经透镜组L2(f=300mm)和L3(f=200mm)耦合进入Y型光纤的另一输入端,参考激光及瑞利散射信号光经焦距f=30mm透镜L4后形成平行光照射Fabry-Pérot干涉仪,再由焦距f=1000mm透镜L5将多光束干涉形成的干涉圆环成像至EMCCD,EMCCD同步记录了同一时刻参考激光及瑞利散射信号的Fabry-Pérot干涉条纹信息,如图 2(a)所示。通过分析同一时刻同一级次流场瑞利散射信号光相对于参考光干涉圆环半径的变化,即可获得散射光波长(频率)的改变量,进而获得时间分辨的流场速度测量结果。系统的时序控制由一台DG535实现。由于Fabry-Pérot干涉仪的自由光谱范围完全由厚度确定,对于一定的多普勒频移引起的干涉圆环半径的变化量,相对于相邻两级次干涉圆环半径差的比例是固定不变的,仅由频移大小及Fabry-Pérot干涉仪的厚度决定,与成像透镜L5的焦距无关[18],因此,系统在实验前不需要速度预标定。
|
| 图 1 干涉瑞利散射测速装置示意图 Fig.1 Sketch of the time-resolved IRS speedometer |
|
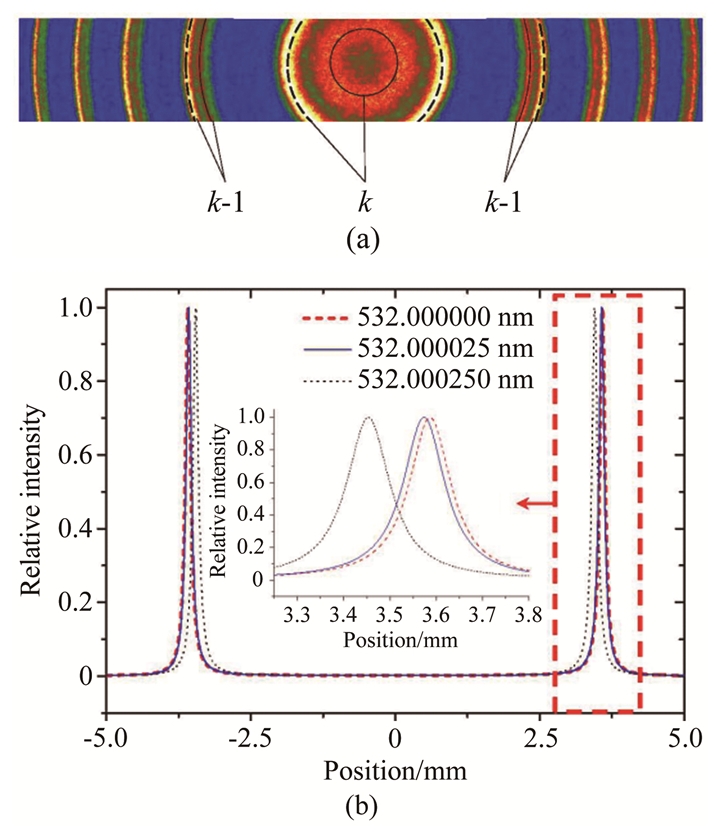
| 图 2 (a) 同一时刻不同级次(只标记出k,k-1)的参考激光(用黑色虚线标记)及瑞利散射信号(用黑色点线标记)形成的干涉圆环;(b)不同波长激光Fabry-Pérot干涉圆环一维强度分布计算结果,插图为局部放大结果 Fig.2 (a) Interference rings consist of the reference laser (black dotted lines) and the Rayleigh light (black solid lines) scattered simultaneously at different levels (k, k-1), (b) Computational 1D intensity distributions of Fabry-Pérot interference rings at different laser wavelengths. The inset shows a partially enlarged view |
目前,装置一次只能收集某一方向的散射信号,即根据光学多普勒测速原理,只能实现某一方向的速度测量[15],由某一方向N个不同时刻的速度Vi及该方向的平均速度V,即可获得该方向的湍流度ε:
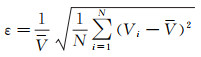 (1)
(1)
通过改变散射光收集方向,可实现不同方向速度脉动及湍流度的定量测量。
2.2 装置速度分辨率理论分析针对图 1所示的光路,模拟计算了不同波长激光经Fabry-Pérot干涉仪多光束干涉后在像平面上的一维光强分布。图 2(b)给出了不考虑气体分子热运动引起瑞利散射谱线展宽的条件下,波长为532.000000、532.000025和532.000250nm的激光经Fabry-Pérot干涉成像后,在像平面上光强的一维分布,由图可知,随着激光波长增加,同一级次干涉圆环半径变小。以532.000000和532.000025nm的2束激光为例,这2束光的波长间隔为0.000025nm(相当于Vk=10m/s速度引起的波长改变量),其中心级次干涉极大值在像平面分开的距离为13μm,干涉条纹宽度约0.2mm。为了提高数据处理精度,可采用最小二乘拟合的方法对同一干涉级次强度进行拟合处理,确定出干涉条纹中心位置,此时干涉条纹中心位置识别精度将优于0.1像素,而测试装置中相机的像元尺寸为16μm,即干涉条纹位置分辨率可达到1.6μm。在实际测试中,流场气体分子的热运动,只会使干涉条纹变宽,而不会影响干涉条纹的中心位置,因此设计的干涉瑞利散射测速装置的理论速度分辨率可达到1.23m/s。通过改变Fabry-Pérot干涉仪的参数,使用像元尺寸更小的EMCCD相机,还可进一步提高装置的速度分辨率。
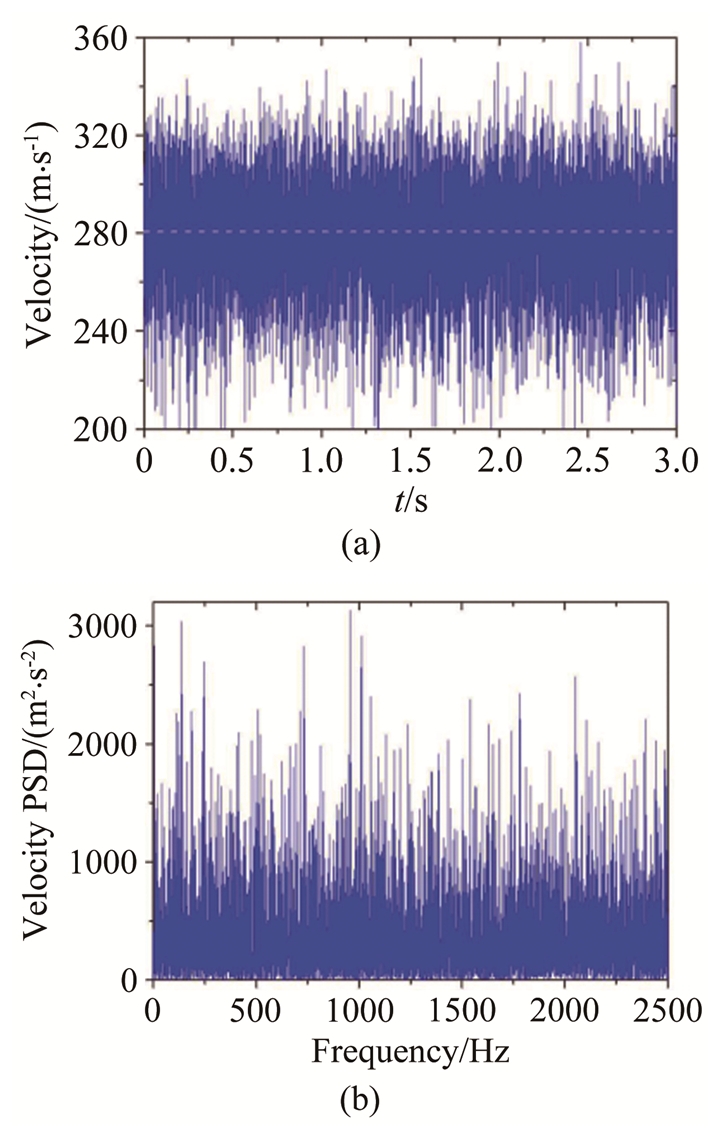
2.3 装置湍流度测量验证实验为验证干涉瑞利散射测速装置的性能,分别利用热线风速仪和本文研究的干涉瑞利散射测速装置,对设计马赫数1.8,出口直径4.7mm的拉瓦尔喷管尾流的同一位置,开展了轴向速度脉动测量对比实验(为了避免激光干扰热线测量结果,热线测量实验与干涉瑞利散射测量实验分别独立开展)。对比实验中,热线风速仪与干涉瑞利散射测速装置的采样率均设置为5kHz,即可测量的湍流度信号的最大频率值均为2.5kHz[19],采集时间为3s,拉瓦尔喷管入口压力为0.7MPa。图 3和4分别给出了利用热线风速仪和瑞利散射测速装置获得的轴向速度脉动测量结果和相应的功率谱计算结果。经过进一步的计算,热线风速仪测量的该测点平均速度为280m/s,湍流度为7.08%;而干涉瑞利散射测速装置测量该测点的平均速度为291m/s,湍流度为6.98%,实验证明,2种方法测量结果吻合较好,研究的干涉瑞利散射测速装置可应用于流场速度脉动及湍流度测量实验研究。
|
| 图 3 热线风速仪速度脉动(a)及功率谱(b)测量结果 Fig.3 The measured velocity pulsation (a) and the power spectrum (b) by the hot wire anemometry |
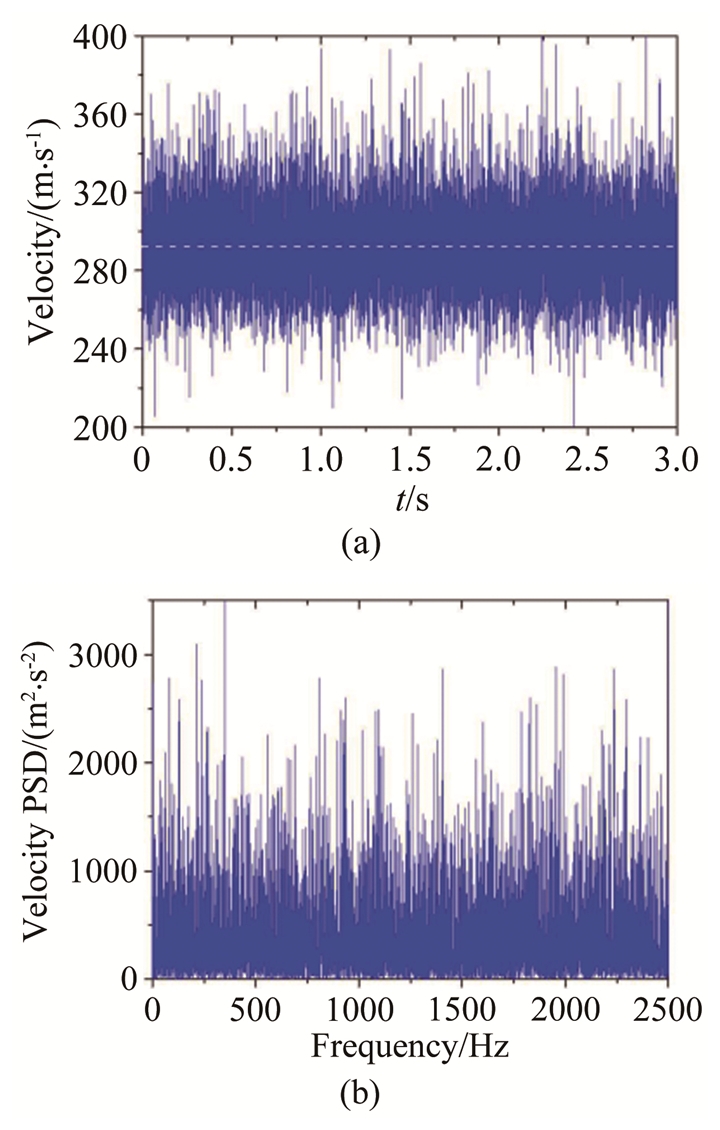
|
| 图 4 干涉瑞利散射测速装置速度脉动(a)及功率谱(b)测量结果 Fig.4 The measured velocity pulsation (a) and the power spectrum (b) by the IRS speedometer |
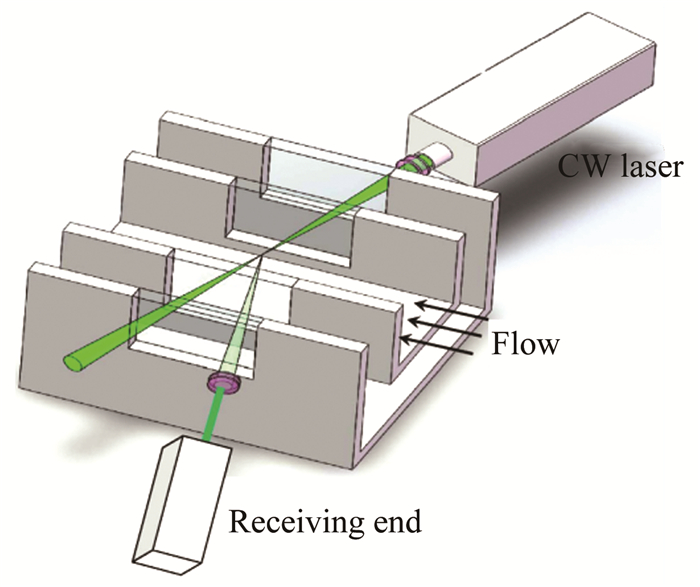
利用干涉瑞利散射测速装置,在0.3m×0.3m跨超声速风洞上,开展了超声速流动轴向速度和湍流度测量实验研究。采用如图 5所示的实验布局,实验中,超声速气流从右向左流动,连续激光器输出的激光经透镜汇聚后穿过实验段右侧观察窗玻璃,并在实验段中心聚焦,测点位于该焦点处。散射光收集及信号采集光路系统与激光传输方向成78°夹角,实验马赫数为3.0,总压458.7kPa,静压11.26kPa,总温298K,图像采样帧频4282 frame/s(可测量的湍流度信号的最大频率值为2141Hz[19]),对应理论流场速度为620m/s。
|
| 图 5 干涉瑞利散射测速装置在0.3m×0.3m跨超声速风洞上的实验布局 Fig.5 The measuring layout in 0.3m×0.3m transonic wind tunnel using the time-resolved IRS speedometer |
通过对风洞来流的瑞利散射光谱进行分析,得到Ma3.0条件下,实验段来流轴向的速度脉动测量结果和相应的功率谱计算结果,如图 6所示。经过计算,该实验条件下,来流的轴向平均速度为630m/s,与计算结果基本吻合,来流湍流度为0.73%。
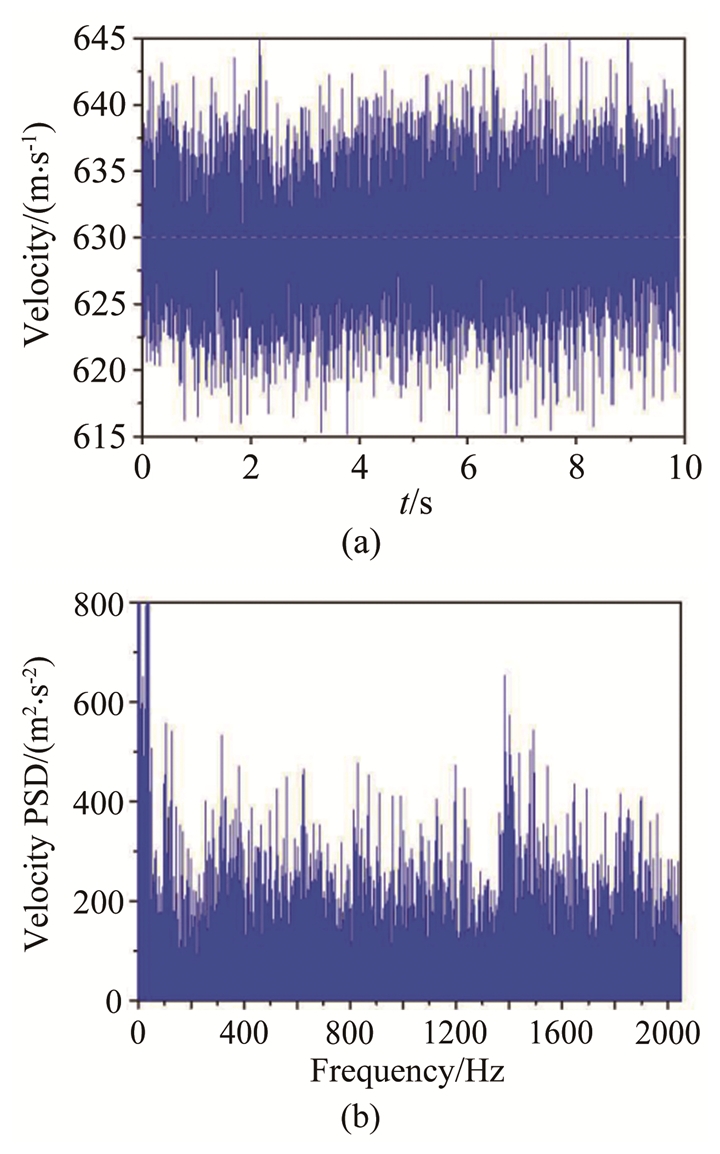
|
| 图 6 速度脉动(a)及功率谱(b)测量结果 Fig.6 Velocity pulsation (a) and the power spectrum (b) |
基于瑞利散射原理,以大功率窄线宽连续激光器为光源、Fabry-Pérot干涉仪为光谱特性分析设备、高帧频EMCCD相机为图像采集设备,设计了一套单点干涉瑞利散射速度测量装置,装置采样率达到4kHz。可得到以下结论:
(1) 经过理论分析,所研究的干涉瑞利散射测速装置的速度分辨率优于1.23m/s;
(2) 通过与热线风速仪湍流度测量对比实验,验证了干涉瑞利散射测速技术具备流场湍流度非接触测量能力;
(3) 利用设计的干涉瑞利散射速度测量装置,在0.3m×0.3m跨超声速风洞上,开展了Ma3.0条件下风洞来流的轴向速度和湍流度测量实验研究,定量得到了实验段中心处的风洞来流轴向速度和湍流度大小,测量结果和理论计算结果基本一致,下一步将开高超声速风洞湍流度测试应用研究。
| [1] | Mielke A F, Seasholtz R G, Elam K A. Time-average measurement of velocity, density, temperature, and turbulence velocity fluctuations using Rayleigh and Mie scattering[J]. Exp Fluids, 2005, 39(2): 441–454. DOI:10.1007/s00348-005-0990-8 |
| [2] | Mielke A F, Elam K A. Multiproperty measurements at high sampling rates using Rayleigh scattering[J]. AIAA Journal, 2009, 47(4): 850–862. DOI:10.2514/1.37369 |
| [3] | 朱博, 汤更生. 声学风洞流场低湍流度及频谱测量研究[J]. 实验流体力学, 2015, 29(4): 58–64. Zhu B, Tang G S. Low turbulence intensity and spectrum measurement research in aeroacoustic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(4): 58–64. |
| [4] | Dorothea I, Hollnagel M, Paul E. Laser Doppler Velocimetry (LDV) and 3D Phase-Contrast Magnetic Resonance Angiography (PC-MRA) velocity measurements:Validation in an anatomically accurate cerebral artery aneurysm model with steady flow[J]. J Magn Reson Imaging, 2007, 26(6): 1493–1505. DOI:10.1002/(ISSN)1522-2586 |
| [5] | Yeh Y, Cummins H Z. Localized fluid flow measurements with an He-Ne laser spectrometer[J]. Appl Phys Lett, 1964, 4(10): 176–178. DOI:10.1063/1.1753925 |
| [6] | Kaffelabc A, Moureha J, Harionbc J L. TR-PIV measurements and POD analysis of the plane wall jet subjected to lateral perturbation[J]. Exp Fluids, 2016, 77(4): 71–78. |
| [7] | Lock J A, Seasholtz R G, John W T. Rayleigh-brillouin scattering to determine one-dimensional temperature and number density profiles of a gas flow jet[J]. Appl Opt, 1992, 31(15): 2839–2848. DOI:10.1364/AO.31.002839 |
| [8] | Seasholtz R G, Zupanc F J, Schneider S J. Spectrally resolved Rayleigh scattering diagnostic for hydrogen-oxygen rocket plume studies[J]. J Propulsion and Power, 1992, 8(5): 935–942. DOI:10.2514/3.23575 |
| [9] | Seasholtz R G, Buggele A E, Reeder M F. Flow measurements based on Rayleigh scattering and Fabry-Perot interferometer[J]. Optics and Lasers in Engineering, 1997, 27(6): 543–570. DOI:10.1016/S0143-8166(96)00063-2 |
| [10] | Seasholtz R G, Greer L C. Rayleigh scattering diagnostic for measurement of temperature and velocity in harsh environments[R]. AIAA-1998-0206, 1998. |
| [11] | Mielke A F, Elam K A. Dynamic measurement of temperature, velocity, and density in hot jets using Rayleigh scattering[J]. Exp Fluids, 2009, 47(4): 667–673. |
| [12] | Seasholtz R G, Panda J, Elam K A. Rayleigh scattering diagnostic for dynamic measurement of velocity fluctuations in high speed jets[R]. AIAA-2001-0847, 2001. |
| [13] | Seasholtz R G, Panda J, Elam K A. Rayleigh scattering diagnostic for measurement of velocity and density fluctuation spectra[R]. AIAA-2002-0827, 2002. |
| [14] | Mielke A F, Elam K A. Rayleigh scattering diagnostic for measurement of temperature, velocity, and density fluctuation spectra[R]. AIAA-2006-837, 2006. |
| [15] | 陈力, 杨富荣, 苏铁, 等. 基于法布里-珀罗干涉仪的瑞利散射测速技术研究[J]. 光子学报, 2015, 44(1): 0112004-1–0112004-4. Chen L, Yang F R, Su T, et al. Interferometric Rayleigh scattering velocimetry using a Fabry-Perot interferometer[J]. Acta Photonic Sinica, 2015, 44(1): 0112004-1–0112004-4. |
| [16] | Mielke A F, Clem M M, Elam K A. Rayleigh scattering measurements using a tunable liquid crystal Fabry-Perot interferometer[R]. AIAA-2010-4350, 2010. http://www.researchgate.net/publication/268558358_Rayleigh_Scattering_Measurements_Using_a_Tunable_Liquid_Crystal_Fabry-Perot_Interferometer |
| [17] | Amy F F, Michelle M C, Kristie A E. Improvement in Rayleigh scattering measurement accuracy[R]. AIAA-2012-1060, 2012. https://arc.aiaa.org/doi/abs/10.2514/6.2012-1060 |
| [18] | 郭永康. 光学[M]. 北京: 高等教育出版社, 2005. Guo Y K. Optics[M]. Beijing: Higher Education Press, 2005. |
| [19] | 盛森芝. 热线热膜流速计[M]. 北京: 中国科学技术出版社, 2003. Sheng S Z. Hot wire/film anemometer[M]. Beijing: Science and technology of China press, 2003. |



