2. 中国空气动力研究与发展中心 高速空气动力研究所, 四川 绵阳 621000
2. High Speed Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang, Sichuan 621000, China
在航空航天领域,空腔构型普遍存在于各类飞行器部件中[1],例如內埋武器舱、飞机起落架舱、发动机燃烧室等,空腔结构的研究对于飞行器隐身性能提高、机身阻力降低、武器投放安全、快速混合燃烧等具有重要意义。当气流流过空腔时,腔内经常发生流激振荡现象,形成扰动反馈增长回路,导致主流能量不断向声场转化,产生空腔流致噪声,并且噪声不断向外辐射,使空腔近场和远场均处于强烈的噪声环境之中,对飞行器性能提升产生不利影响。
空腔流致噪声问题具有重要的学术研究价值和工程应用背景。空腔非定常流动及其诱导噪声的产生、演化及其控制机制涉及许多空气动力学的基础前沿问题,如湍流混合、剪切层失稳、涡-固壁相互作用、波-涡相互作用、边界层分离等,对于空气动力学和气动声学发展具有重要的学术研究意义。在工程应用方面,空腔近场噪声对于武器舱内电子仪器、仪表等极具破坏作用,噪声载荷中存在不同频率成分,容易引起武器舱结构振动增强,甚至诱发结构共振,威胁飞行安全。空腔远场噪声的增强限制了飞行器达到适航标准,如飞机起降阶段,起落架舱引起的空腔噪声是全机重要的噪声源。
从20世纪50年代开始,国内外研究机构对空腔非定常流动及其气动声学问题开展了大量研究[2]。作为一个复杂的动力学系统,空腔流致噪声具有明显的非定常和非线性特征,空腔流场中存在多种类型声源,如单极子、偶极子和四极子声源,这些声源的产生与空腔非定常流动特性密切相关。空腔前缘来流边界层分离以后,扰动在剪切层不稳定性作用下增长,并逐渐演化形成不同尺度涡结构,当涡撞击到空腔后缘时,流场中产生声波并向外辐射,腔内声波前传至边界层分离区时,会诱导产生新的扰动,进而形成扰动反馈增长回路。空腔噪声产生过程主要包括4个阶段:(1)剪切层不稳定性诱导涡扰动不断增长,形成非均匀涡流运动;(2)涡-固壁相互作用产生压力扰动,引起压力场不均匀性增强;(3)压力扰动在腔内低速区向前传播,在腔外以噪声形式向空间辐射能量;(4)在压力扰动影响下,空腔前缘流动分离区域的边界层感受性增强,初始剪切层扰动进一步增长。在空腔几何形状的约束下,空腔噪声产生和辐射过程中可能被进一步放大[3]。
空腔流致噪声产生、演化与流激振荡现象密切相关,空腔流激振荡主要受到空腔几何形态、来流参数以及结构振动等因素影响。空腔几何形状是影响流激振荡的重要因素,当空腔长深比较大时,空腔前缘边界层分离以后,形成剪切层再附于空腔底板,称为闭式空腔流动;当空腔长深比较小时,剪切层跨过空腔开口区域,再附于空腔后壁及下游区域,称为开式空腔流动,2种流动类型的临界长深比随来流参数等工况变化而不同,一般为10~13,称为过渡式空腔流动[4]。Sarohia等[5]将开式空腔流动进一步划分为深腔和浅腔流动,二者长深比临界值为1,在深腔流动中,空腔流激振荡现象包含更强的声学驻波模态,而在浅腔流动中,扰动通常通过腔内传播并与剪切层耦合,最终形成扰动反馈增长回路。基于扰动反馈机制,Rossiter等[6]建立了空腔振荡频率半经验预估模型,其预测结果与风洞试验结果一致。在Heller、Tam等[3, 7]的完善下,模型适用范围与预测精度均得到进一步提高。Arunajatesan等[8]结合数值和实验方法研究了空腔三维流动特性,发现空腔侧壁区域的流向涡影响了剪切层不稳定特性,并改变了空腔湍流特征。Bres等[9]和Crook等[10]基于三维空腔流动特性分析,发现空腔开口区域的流向涡能够引起流动不稳定性增强,进而对空腔流激振荡产生影响。Beresh等[11-13]通过高时间分辨率粒子图像测速技术,研究了空腔宽度对非定常流场结构的影响,分析了可压缩效应较强时空腔剪切层以及湍流结构的演化规律。杨党国等[14]通过高速风洞实验,发现空腔开口区域剪切层与固壁相互作用减弱时,腔内噪声能够得到有效控制。侯中喜等[15]与司海青等[16]通过数值模拟方法,研究了高速来流条件下,三维空腔流激振荡特性。李晓东等[17]通过求解非定常雷诺平均方程,分析了二维空腔流致噪声的频率特性以及空腔前缘边界层的影响规律。
随着航空航天技术的发展,空腔可压缩流致噪声问题得到人们的重视,不过在高速来流条件下,空腔流动/噪声/振动耦合机理、流致噪声产生与控制机制、工程实用的控制策略等问题的研究仍然存在较大不足。本文针对空腔可压缩流致噪声问题研究进展进行综述,重点介绍高速来流条件下,空腔可压缩流致噪声产生机制、演化规律以及控制技术的研究情况,总结其中关键问题和面临挑战,并对未来发展趋势进行展望。
1 空腔可压缩流动与气动声学特性高速来流条件下,空腔流场中呈现强非定常性,前缘边界层分离以后,形成剪切流与空腔固壁相互作用,产生强烈的压力脉动,如图 1所示。当流场可压缩性较强时,随着剪切层中涡扰动增长,腔内外波系的演化发展与流场中涡流结构相互耦合,易形成扰动反馈增长回路,并向外辐射噪声,在特定空腔几何形状约束下,腔内声波辐射能量具有放大效应,声压级高达170dB[18]。空腔可压缩流动与气动声学特性研究是突破空腔噪声产生机制与控制技术等相关问题研究的关键。
空腔可压缩流动特性研究起步较早,空腔流场结构复杂,其非定常特性是影响空腔气动声学特性以及空腔噪声产生和传播的重要因素,故受到广泛关注[20-21]。根据空腔流激振荡产生及演化过程,空腔非定常流动特性受到剪切层不稳定性、湍流发展、波系演化、流动分离及涡流运动等影响,如图 2所示。空腔剪切层与后壁的撞击是产生空腔气动噪声的重要来源,在空腔后壁与剪切层相互作用区域,腔内外存在很强的质量交换,形成强噪声源[22]。来流边界层在空腔前缘分离以后,空腔开口区域形成剪切层,剪切层的演化发展、空间涡脱落特性与前缘边界层特征参数直接相关。空腔剪切层演化特性与自由发展的湍流混合层之间存在相似之处[19],但二者之间具有本质不同,首先,在腔内强噪声环境下,空腔剪切层不稳定性受到腔内扰动波的作用更加显著;其次,在空腔固壁约束下,空腔剪切层演化发展与后期涡脱落特性存在边界效应的影响;第三,腔内回流区引起腔内涡流运动,会导致空腔剪切层形态发生改变。
空腔剪切层在流动不稳定性作用下,其尺度逐渐增长,对周围流体形成卷吸效应,并诱导产生不同尺度涡结构。伴随不同尺度涡结构合并发展以及湍流结构形成,靠近空腔后壁区域时,剪切层非定常拍动增加了腔内与腔外流体的质量交换,引起流场速度脉动增强,导致剪切层尺度增长率显著提高,如图 3所示。
在空腔后壁与剪切层相互作用区域,流体沿着壁面向腔内流动,由于腔内外流动方向不同,在腔内中心区域形成主回流区,产生大尺度涡结构[24]。针对空腔噪声与涡结构相互作用关系,Wagner等[21]利用高时间分辨率粒子图像测试技术研究了空腔流场相干结构的演化以及空腔噪声特性,空腔一阶Rossiter模态与回流区内大尺度结构的传播密切相关,而二阶和三阶模态与剪切层中涡扰动的对流运动相关。针对空腔表面流动分离特性,在空腔前壁附近,边界层分离以后,流体沿着空腔前壁向腔内流动,存在从腔前壁向后壁的流动,在空腔后壁附近,存在腔后壁向前壁的运动,两部分流体相遇以后,引起较强的流动分离,并产生旋转方向相反的Tornado涡对结构[10, 25],如图 4所示,对剪切层三维特性发展及空腔侧壁区域的流向涡演化具有重要影响。
空腔流场中扰动波的生成、传播与演化是空腔流激振荡及可压缩流致噪声产生的重要过程[3, 6-7],尤其在高速来流条件下,空腔流场中波系结构复杂。Zhang等[26]利用全息干涉和纹影技术,对超声速空腔流场中复杂波系结构进行了定性测试,不过由于测量手段限制,测试结果的时间分辨率较低,无法研究波系传播特性。为了提高流场显示的时间分辨率,Handa等[27]采用高速纹影技术,研究了波系结构传播与演化的时序过程。结果显示,剪切层撞击空腔后壁形成压缩波,压缩波向空腔内外传播的过程中,在空腔底板和前壁发生反射,进一步激发了剪切层的扰动增长,并显著增强了波系结构的复杂程度。针对超声速空腔流场波系与涡结构传播和演化特性,Zhuang等[28-29]利用脉动压力测量、阴影以及粒子图像测速技术,研究了来流马赫数为2,空腔长度与空腔深度之比为5的流动和噪声特性,如图 5所示。流场中波系的产生与边界层分离、剪切层失稳、涡结构增长等流动结构密切相关,空腔上游流场结构主要以二维流动为主,而随着扰动波、涡等结构的传播,在下游区域,湍流剪切层占据主导,流动的三维特性显著增强。近年来,随着测试技术的发展,人们对超声速空腔流场中扰动波产生传播等规律已经具有初步认识,不过,复杂波系与其它流场结构如剪切层、回流区、不同尺度涡结构的耦合机理等方面研究仍存在较大不足,空腔流场中波系结构在可压缩流致噪声中的作用机制,以及如何利用空腔波系特征对超声速空腔流致噪声进行控制仍需进一步研究。
空腔噪声的产生、传播和辐射是基本的气动声学问题,一方面空腔噪声产生与不同尺度流场结构如旋涡、湍流、波等直接相关,另一方面气动声载荷是结构振动的重要激励源,与结构动力学具有直接联系。空腔流致噪声中经常包含较强的离散和宽频噪声成分,腔内物体和腔体结构受到交变载荷的潜在威胁。目前,随着飞行器空腔类型气动布局的广泛应用,空腔气动声学问题逐渐得到关注,不过从机理上阐明空腔气动声学特性及其与非定常流动的相互关系仍然存在较大困难[30]。
空腔流致噪声的产生受到扰动反馈回路形成的重要影响,随着主流能量经空腔系统向声场转换,噪声向空腔外部辐射,空间中噪声分布范围较广。空腔近场噪声与远场噪声之间既存在较大不同,又存在较强联系。首先,空腔近场噪声是流动非定常性的直接反映,相对于远场噪声,空腔近场噪声主要受到空间和表面流场结构的影响,腔内主涡结构、湍流、壁面流动分离以及剪切层-固壁相互作用等都对近场噪声具有重要作用。其次,与近场噪声情况不同,空腔远场噪声反映了声源产生噪声的辐射与传播特性。噪声在向外辐射过程中,其频率成分不会发生本质变化,不过由于噪声能量有限而传播范围较广,噪声声压级相对于近场噪声有所降低。
在空腔气动声学试验研究方面,Krishnamurty等[20]采用纹影技术观测了高亚声速空腔的辐射声场特征,其结果与Rowley等[19]和李晓东等[17]的数值计算结果吻合,如图 1所示。Beresh等[11]通过脉动压力传感器进行空腔近场噪声测试,研究了空腔近场区域的气动声模态特性,在腔内回流区噪声以低频声模态为主,而在剪切层区域,噪声中高频声模态占主导地位。Wagner等[21]利用高频粒子图像测试技术,研究了空腔声模态与流体动力学特性的关系,发现空腔一阶Rossiter模态与回流区大尺度涡结构相关,而二阶和三阶主要受到流场中对流涡扰动传播特性影响。杨党国和刘俊等[18, 31]通过风洞试验分析了来流边界层厚度对空腔近场声学特性影响。结果发现,随着边界层厚度增加,腔内噪声声压级降低。赵小见等[32]通过相阵列与脉动压力风洞试验,研究了空腔流场的声源识别与强度评估方法,并初步分析了气动声源与脉动压力结果之间的关系。吴继飞等[33]针对开式空腔气动声学特性开展了大量研究。结果显示,由于流激振荡现象,腔内存在强烈噪声,而剪切层扰动对腔内噪声环境有重要影响,不过这种影响与来流马赫数密切相关。针对远场噪声传播特性,Yamouni等[34]通过全局稳定性分析方法,研究了腔内声共鸣模态对腔外辐射噪声场指向性的影响。Fontaine等[35]利用麦克风进行远场声学测试,研究了湍流边界层特征尺度对后期发展剪切层流场噪声的影响,随着剪切层初始厚度增加,气动噪声强度受到抑制。
在空腔气动声学计算研究方面,主要包括2类方法:直接方法与混合方法[30]。直接方法包括传统直接数值模拟、大涡模拟以及非定常雷诺平均(URANS)方法等,利用数值格式同时捕获空间流场结构和声源信息,不过要求计算域足够大以包括所有声源信息,由于与流场相比声场能量较小,在求解过程中不得不考虑高精度数值格式以及精确的声学边界条件[36],尤其当雷诺数较高时,直接方法的计算精度和资源消耗不易同时保证,因此在工程应用中的实现面临较大挑战。在混合方法中,流场计算和声场计算解耦,假定非定常流动产生了声,但声不会显著地影响流动,因此可以在流场计算基础上,基于声比拟理论,通过后处理进行声场特性求解。由于混合计算方法有效降低了远场声求解的资源消耗,更适合涉及复杂气动声学的工程应用问题,不过对于高可压缩流动问题,计算难度显著增加,并且研究问题需要满足流场与声场非全耦合的前提条件。Lai等[37]利用大涡模拟进行近场声源计算,并利用声比拟方法进行远场噪声预测,数值研究了三维可压缩空腔流动的近场和远场声学特性。Chen等[38]研究了相同尺寸的空腔气动声学特性,其中近场声源通过脱体涡模拟方法进行计算,远场噪声通过低存储消耗的FW-H方程进行预测,声辐射峰值出现在相对来流方向约60°区域,不过当来流雷诺数较低时,该角度值略有降低。杨党国等[39]基于气动声学时域理论,数值研究了空腔近场和远场噪声的产生及演化机理,并分析了空腔噪声的传播特性。
为了对空腔噪声进行预测,Rossiter等[5]基于涡扰动反馈机制,建立了噪声频率预估模型:
 (1)
(1)
其中,f为振荡频率,L为空腔长度,U∞和Ma为来流速度和马赫数,α为声波形成延迟因子,κ为涡扰动对流速度。在Rossiter模型中,腔内声波传播速度利用来流声速表述,不过根据腔内温度测量结果,二者并不相等,Heller等[6]人提出修正公式为:
 (2)
(2)
其中,r为腔内温度恢复因子,γ为比热比。Rossiter模型为典型的经验公式,其适用范围为高亚声速和跨声速范围,由于模型并未考虑剪切层与固壁相互作用、腔内复杂波系和流场非线性效应等诸多关键影响因素,导致模型对高阶模态的预测通常会引起较大误差,同时也无法给出噪声强度预测结果。尽管Rossiter和Heller模型中半经验系数存在一些改进算法[40-41],不过由于模型简单易用并取得了与实验数据一致的结果[19, 42],因此仍得到了广范应用。
1.3 空腔流致噪声产生机制空腔流致噪声的产生一般认为存在扰动反馈和声共鸣2种机制。其中,扰动反馈机制主要由流体动力学作用引起。Rossiter等[6]发现,在开尔文-亥姆霍兹不稳定性影响下,剪切层内扰动不断增长,并再附于空腔下游区域,形成反馈扰动波,当扰动波传播到空腔前缘边界层分离区时,流场中产生新的扰动,形成扰动反馈增长回路,在非线性、粘性耗散等机制的影响下,空腔系统维持流激振荡并向外辐射噪声。在Heller等[3]与Tam等[7]的发展下,扰动反馈机制逐渐得到完善,并基于此提出波涡干涉理论和声学预测模型等。Rowley等[19]通过分析剪切层与空腔边界的相互作用,研究了空腔振荡的剪切层模态与尾迹模态,2种模态的转换与来流特性和空腔几何特征直接相关,来流马赫数较高并且边界层尺度较小的工况下,流动更容易进入尾迹模态。在不同模态下,流场中形成的空腔振荡与气动声学特性显著不同。声共鸣机制主要由空腔声学特性引起,当声波与空腔尺度量级相当时,扰动波在空腔内容易形成声学驻波模态。在实际的空腔流动中,尽管扰动反馈机制与声共鸣机制不容易区分,但是二者通常共同作用于空腔流场[7]。Yamouni等[34]通过全局稳定性分析方法,研究了声共鸣机制与扰动反馈机制的作用效果,结果发现,在低马赫数空腔流场中,扰动反馈机制占据主导地位,而在高马赫数空腔流场中,声共鸣机制对于空腔辐射声场的作用效果增强。
空腔弹性边界与流场结构之间的相互作用是空腔流致噪声的重要来源,一方面,弹性边界运动对流场结构具有重要作用,也必然影响到流致噪声的产生与传播;另一方面,结构振动同样会向外辐射噪声,改变空腔气动声学特性。研究指出,当结构振动幅度较小时,其辐射噪声强度较弱,对空腔气动声学特性的影响较小[43],不过当结构振动与气动声学激励形成强耦合时,这种影响不可忽略。
近年来,国内外针对空腔流致噪声的形成原因开展了较多研究[44],对于空腔流激振荡及其诱导噪声成因存在不同角度的解释。空腔可压缩流致噪声的形成受到湍流、涡流、波系演化、结构振动等多种因素的影响,尤其在特定条件下,存在流动/噪声/振动之间的耦合作用,其产生机制和传播规律非常复杂,对空腔可压缩流致噪声的产生机制以及气动声学特性如振荡模态转换、噪声强度预测等现象的认识尚无法达成一致,仍有待于开展更加系统深入的研究。
2 空腔可压缩流致噪声参数影响规律空腔可压缩流致噪声问题的影响因素较多,主要包括来流参数、空腔形态、结构振动等,例如空腔长深比、来流马赫数、边界层尺度、空腔弹性边界。这些影响因素分析以及参数影响规律,对于空腔流致噪声的产生机理以及控制方法的研究均具有重要意义。
2.1 空腔可压缩流致噪声影响因素分析根据Navier-Stokes方程以及气动声学控制方程,空腔可压缩流致噪声受到空腔流动的作用效果显著,来流条件、空腔形态、结构振动等因素对于空腔流动及其诱导噪声的作用效果不同,有些参数通过影响空腔流动间接影响流致噪声,例如来流马赫数、边界层尺度,而有些直接影响流致噪声,例如振动辐射声。Bres等[9]通过直接数值模拟方法研究了空腔长深比、来流边界层尺度、雷诺数以及马赫数的影响。Sun等[45]通过这些参数影响规律的分析,阐述了空腔流激振荡的产生机理与触发机制,并且相关数值工作与风洞试验结果吻合[46-47]。目前,空腔流致噪声的影响因素得到广泛研究,不过这些因素对空腔流激振荡及噪声产生、传播、抑制的作用机理尚没有完全阐明,这些问题的解决对于工程实际与型号应用具有重要意义。
2.2 来流参数影响规律空腔流场及声场能量主要来源于主流,来流参数是影响空腔流动的决定性因素,包括来流马赫数、雷诺数、边界层特性等。
2.2.1 马赫数影响空腔流动和气动声学特性随着来流马赫数不同而存在显著差异,其根本原因在于高速来流条件下,流场的可压缩性和非线性效应均相应增强,空腔流致噪声中各阶模态的相互作用程度也相应提高。在高来流马赫数条件下,剪切层涡流与空腔后壁相互作用增强,空腔噪声的强度显著提高。空腔可压缩流致噪声的产生机制与不可压缩条件不同,当可压缩性较强时,空腔剪切层及其相关的涡脱落特性发生变化,尤其在超声速空腔流场中波系结构更加复杂,并且存在与剪切层、流场主涡结构之间的耦合,流动的非定常和非对称效应显著增强,从而引起空腔流致噪声特性产生差异。
在超声速来流条件下,空腔流场中波系结构对空腔流致噪声的影响增强,流场中运动波系结构与固定波系结构相互干扰,增加了超声速空腔流致噪声产生机制问题的复杂性。在空腔前缘,随着剪切层的周期性拍动,流场中交替出现压缩波和稀疏波[29],影响了空腔前缘边界层感受性以及剪切层的初始扰动增长。在空腔后缘,主流与空腔后壁撞击以后形成的扰动波无法在空腔外部向前传播,空腔后壁附近的扰动波会逐渐在空间中形成一道斜激波。针对超声速空腔流场的波系演化规律,Schmit等[48]利用高速纹影技术研究了来流马赫数为1.5, 长深比为5.67的空腔流场波系结构,如图 6所示。结果发现,空腔噪声的主频成分与剪切层内涡扰动频率密切相关,而流场中大涡结构主要对空腔噪声中宽频部分产生影响。
2.2.2 雷诺数影响随着来流条件不同,空腔雷诺数随之改变,空腔开口区域的剪切层与边界层特征发生变化,导致空腔流致噪声特性产生差异。影响空腔雷诺数的关键因素包括:来流条件、空腔尺度和边界层厚度等,基于不同的尺度参数,空腔雷诺数存在不同定义方式,例如基于空腔长度、深度以及来流边界层厚度的雷诺数,本节主要讨论基于空腔长度的雷诺数影响。
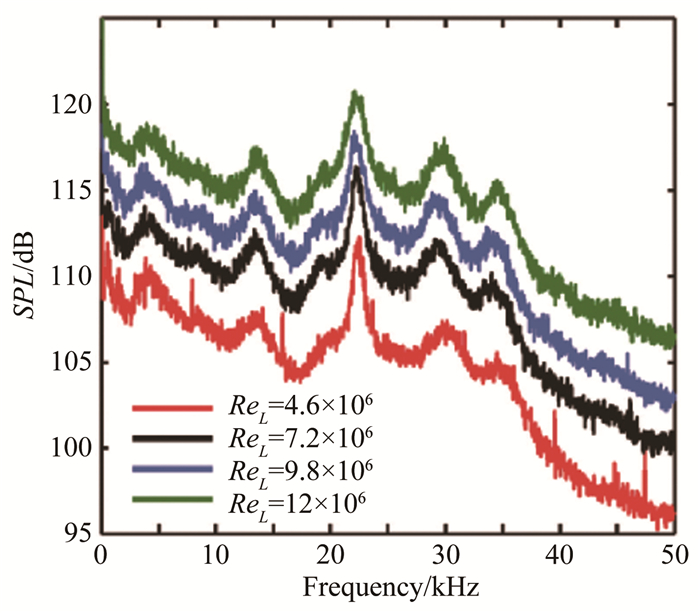
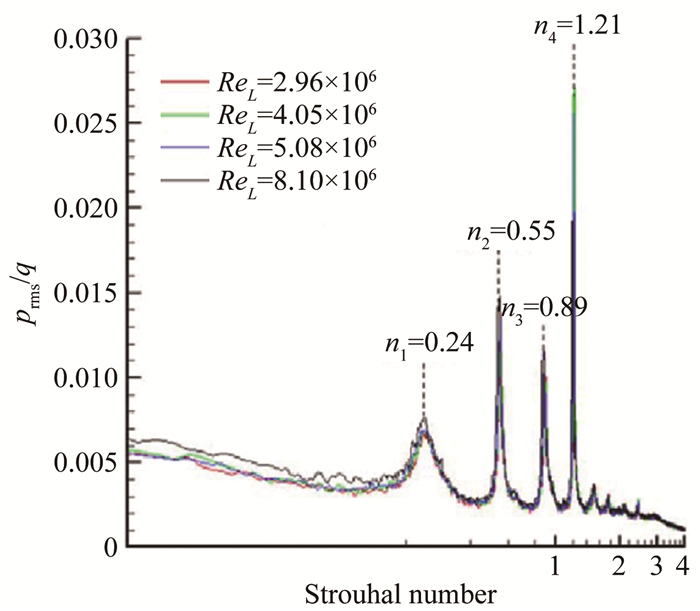
在空腔流激振荡形成的4个环节中,雷诺数对于空腔开口区域剪切层的形成与演化具有重要影响。在低雷诺数流动中,剪切层主要受到开尔文-亥姆霍兹不稳定性影响,并且逐渐形成不同尺度涡脱落与发展。当雷诺数较高时(如ReL > 106,其中ReL表示基于空腔长度的雷诺数),剪切层中不稳定性影响区域相对减小,不同尺度涡结构之间会发生严重的干扰与合并,并逐渐发展成为湍流。Bres等[9]基于稳定性分析发现,较低雷诺数范围时,空腔振荡主模态的增长率受雷诺数影响较大,振荡频率随雷诺数的增大而略有降低,当低于某个临界雷诺数范围时,空腔流动以二维不稳定性为主。与此相似,Sun等[45]也发现,当雷诺数较低时,随着雷诺数与马赫数的提高,空腔振荡主模态由低阶向高阶过渡。在高雷诺数流动条件下,Gai等[40]和Moon等[49]通过改变来流速压改变雷诺数,研究了超声速空腔噪声随来流雷诺数的演化规律,随着雷诺数增加,空腔噪声各阶模态频率变化较小,而不同频率对应的声压级以及腔内总声压级均有所升高,如图 7所示,与Zhuang等[28]关于声压级与来流速压关系的分析一致。Robertson等[50]利用来流动压对腔内脉动压力进行无量纲化,在雷诺数变化范围ReL=(2.96~8.1)×106时,经过无量纲化的空腔噪声谱趋于一致,并与雷诺数无关,如图 8所示。
2.2.3 边界层特性影响来流边界层尺度、湍流度、背景噪声等对空腔非定常流动及其诱导噪声特性具有重要影响,由于在空腔前缘位置,边界层分离后形成剪切层,边界层特性直接影响了剪切层的演化发展以及涡脱落特性,而剪切层演化规律的不同进而影响了空腔流激振荡及空腔噪声的主要性质。相比于湍流边界层,层流边界层噪声程度较低,不过当空腔前缘边界层为层流时,空腔流场中会产生更强的压力脉动。Heller等[3]发现,边界层参数是空腔噪声预测理论中必须包含的参数,一方面,来流边界层从层流转换为湍流时,空腔噪声响应受到显著影响,另一方面,当来流边界层为湍流时,压力振荡特征对于雷诺数的敏感性降低。
在低雷诺数条件下,来流边界层厚度与剪切层内涡脱落特性直接相关,对空腔噪声的模态选择具有重要影响。Tam等[7]研究中发现,边界层尺度是影响剪切层不稳定性以及空腔气动声学特性的重要因素。利用全局稳定性分析方法,Yamouni等[34]分析了较低雷诺数空腔剪切层不稳定模态的影响,随着空腔长度与来流边界层尺度之比的增加,空腔流动的不稳定性增强。Bres等[9]通过数值模拟,指出空腔长度与边界层动量厚度之比是影响空腔三维不稳定性的关键参数。Sarohia等[5]指出,当来流马赫数较低时,为保证空腔流激振荡发生,空腔长度与边界层动量厚度之比存在一个与来流条件相关的最小值,当空腔长度较低或边界层尺度相对较大时,剪切层无法卷起,流场中不存在流激振荡现象。Gharib等[51]研究了边界层形态变化对于空腔流激振荡与噪声产生机理的影响,认为边界层内TS波可能对剪切层稳定性产生影响,从而对一些噪声频率产生控制效果,并且空腔流激振荡现象发生时,空腔长度与边界层动量厚度之比最小值大约为80。Daoud等[52]针对低速空腔流动问题,分析了空腔长度和深度对空腔流激振荡的影响,并且指出最小空腔长度Lmin与前缘边界层动量厚度θ之比为:Lmin/θ≈800Reθ-0.5,其中Reθ为基于边界层动量厚度的雷诺数。不过,在高马赫数来流条件下,空腔长度与边界层尺度关系对于腔内非定常流声特性的影响机制仍需进一步完善[49]。
在高雷诺数条件下,来流边界层厚度对空腔振荡主模态选择机制影响减弱,这是因为剪切层内大尺度涡的卷起受到流动不稳定性影响减弱,其涡流特性主要表现为开尔文-亥姆霍兹涡的汇聚,导致来流边界层厚度影响降低[53]。Chung等[54]发现,对于固定空腔长深比情况,来流边界层尺度对于后壁脉动压力的影响要高于腔内,空腔尺度与边界层厚度之比在一定范围内增加时,后壁脉动压力增强,当二者比值增加到一定程度时,这种增强趋势会减弱。Rowely等[19]通过数值求解可压缩Navier-Stokes方程,研究了边界层动量厚度对空腔流动特性的影响,在可压缩流动条件下,边界层尺度是影响空腔流动剪切层模态以及尾迹模态的重要因素。Baseley[55-56]等研究发现,随着来流边界层动量厚度增加,空腔噪声频率降低。杨党国[31]和刘俊等[18]通过风洞试验和数值研究,发现随着来流边界层尺度增加时,空腔噪声谱的峰值频率受到影响较小,而相应频率成分的幅值降低,与李晓东等[17]的数值计算结果一致。
2.3 空腔形态因素影响规律空腔形态因素对空腔流激振荡及噪声具有重要影响,是空腔非定常流声问题的重要边界条件,如空腔几何尺寸、复杂外形、腔内存储物等。
2.3.1 几何尺寸影响空腔几何尺寸是影响流激振荡及其诱导噪声的重要因素。Stallings等[4]和Tracy等[4, 57]指出空腔长深比L/D是影响流激振荡的关键因素之一,其中D表示空腔深度。当L/D < 1时,空腔流动类型为深腔流动,当来流速度较低时,空腔振荡受到腔内声共鸣机制的影响为主,空腔深度方向的驻波特性作用效果显著,当来流速度较高时,空腔振荡受到扰动反馈机制的作用效果更显著[3]。随着空腔长深比增加,当L/D > 1时,空腔流动类型为浅腔流动,此时空腔扰动反馈机制作用效果增强,空腔开口区域剪切层与空腔相互作用发生明显变化,腔内压力以及脉动压力分布随长深比的变化而差异显著。当空腔长深比较小时(如L/D < 10),剪切层与空腔后壁相撞,腔内易发生流激振荡现象,气动噪声强烈,形成典型的开式流动类型;当空腔长深比较大时(如L/D > 13),剪切层与空腔底板相撞,空腔气动声学响应频带范围较宽,流激振荡现象也会相应消失,形成典型的闭式流动类型;当空腔长深比介于二者之间时,空腔流动及气动声学响应受到来流条件等参数影响,介于开式与过渡式特性之间,称之为过渡式流动类型。
在典型的矩形空腔流动及噪声问题研究中,Vikramaditya等[58]通过改变空腔深度,研究了长深比为2和3的超声速空腔流动,结果发现不同长深比的空腔噪声主频成分具有显著差异。空腔流动稳定性分析结果显示[9],二维空腔稳定性与空腔长度密切相关,这是由于流场不稳定性受到涡结构发展和辐射声波传播规律的影响。与此不同,三维空腔不稳定性与空腔深度密切相关,这是由于三维空腔不稳定性中,不稳定频率除了受到二维基本流动的影响以外,还受到腔内回流区影响。
空腔展向宽度对于空腔三维流动特性及其展向效应具有重要影响。Aradag等[59]基于数值模拟,研究了来流马赫数为1.5的三维空腔流动特性,空腔长深比为5.07,长宽比为1.9,采用相同来流条件进行二维和三维数值模拟,在三维数值模拟中,腔内声压级低于二维情况,后壁附近的声压级降低幅度达5dB,实验结果也说明三维数值模拟与实际情况更加符合。Wagner等[60]通过风洞试验,Arunajatesan等[8]通过数值模拟,研究了亚跨声速(Ma=0.5~0.9)来流条件下,长深比为5并且长宽比为1~5的3种空腔流动特性。结果显示,长宽比是影响空腔流声特性的重要参数,最宽空腔(长宽比为1)流场中剪切层与回流区湍流度最高。在超声速来流条件下,Beresh等[24, 61]研究发现,中间宽度的空腔流场中剪切层与回流区区域湍流度最小。Das等[62]研究了长深比为2、长宽比为2~4的超声速空腔流动(马赫数为1.7),结果发现,随着空腔宽度增加,空腔长宽比降低,空腔前缘湍流度基本不变,空腔后缘湍流度增强,并且最宽空腔对应湍流度和噪声强度均最大,空腔噪声频谱特性以及主频成分随着长宽比改变发生显著变化。
2.3.2 复杂构型影响目前,经常采用矩形空腔对武器舱进行模拟,然而,这个简化忽略了许多实际几何特征,而这些特征可能对空腔非定常流动与武器舱载荷特性产生重要影响。针对复杂形状空腔噪声问题,Ukeiley等[63]采用侧壁修型和倾斜底板的方法,研究了复杂三维空腔的流动特性,分析了复杂形状对空腔噪声强度以及剪切层三维不稳定性的影响。Casper[64-65]等研究了空腔噪声高频成分对于前缘突出、空腔布局改变的依赖性,与矩形空腔情况相比,前缘斜坡可以降低空腔噪声,而腔内侧壁附加物降低了腔内空间宽度,腔内噪声强度增加。针对弹舱舱门对空腔气动声学特性的影响,Shaw等[1]研究了F-111弹舱舱门对其声学特性的作用规律,在长深比为6.79和10.27,来流马赫数0.7~2.0条件下,舱门使空腔噪声各阶模态增强,不过增加幅度与来流条件相关。Tuna等[66]研究了串列空腔构型的流激振荡特性,分析了剪切层固有模态以及驻波模态之间的耦合效应。吴继飞等[67-68]通过风洞试验研究了亚声速来流条件下舱门对空腔静态和动态压力的影响,在舱门开启过程中,空腔噪声及频率成分发生显著变化,当舱门开启角度较小时,腔内噪声强度较低且变化平缓,随着舱门开启角度增大,腔内噪声强度显著提高,当舱门开启到一定角度以后,腔内噪声强度趋于稳定。
2.3.3 腔内物体影响腔内存在物体时,空腔流场会受到较大干扰,空腔噪声也会随之改变,鉴于该问题具有重要的工程应用背景,国内外学者对此进行了广泛研究。Flora[69]等研究了长深比为4.5,来流马赫数为2.94的超声速空腔流场与腔内物体相互作用,腔内物体在释放之前与释放后相比,空腔噪声强度较低。Merrick[70]等通过高速纹影技术捕获了腔内物体释放后的运动轨迹,分析了腔内物体分离特性。针对腔内物体对空腔静态压力特性的影响,吴继飞等[71]通过风洞试验研究了长深比为9的可压缩空腔流动与腔内物体之间的相互作用,发现腔内物体引起空腔内部压力梯度降低,在内埋弹舱应用中更有利于武器分离。
腔内物体对空腔气动声学特性具有重要影响,Coley[72]等采用数值模拟,研究了长深比为4.5、来流马赫数为0.95的空腔气动声学特性与腔内细长物体的相互作用,腔内物并不会显著改变空腔声学模态,不过空腔动态压力特性对于腔内细长体的力和力矩有显著影响,力和力矩频率成分与噪声频率相对应。Murry[73]等研究了来流马赫数为1.5的空腔声场与腔内物体的相互作用,在腔内物体未释放时,与干净空腔相比,空腔噪声特性受到影响较小,不过腔内物体释放以后,物体的姿态以及运动轨迹与物体释放时所处的空腔噪声相位有着重要关系,因此可以考虑利用空腔噪声脉动压力信号作为释放腔内物体的控制信号。Robertson等[50]通过开展来流马赫数为2,长深比为4.5工况下,腔内细长体对空腔气动声学问题的影响研究,腔内存在物体时,空腔噪声总声压级降低约2~3dB,噪声能量可能在不同频率成分之间发生转移。考虑到腔内物体位置对空腔噪声特性的影响,Bjorge等[74]研究了长深比为3.6,来流马赫数为1.8和2.9的超声速空腔流声特性,存在腔内物体时,空腔噪声特性不仅与腔内物体尺寸、位置等相关,还受到马赫数等来流条件影响。Shaw等[1]等研究指出,腔内物体在剪切层区域时,空腔噪声声压级降低幅度最大,这是因为腔内物体与剪切层相互作用时抑制了剪切层不稳定性增长以及涡结构发展,干扰腔内扰动反馈回路,从而降低了空腔噪声强度,在马赫数0.9~1.2范围内,噪声主频峰值降低幅度达到15dB以上。
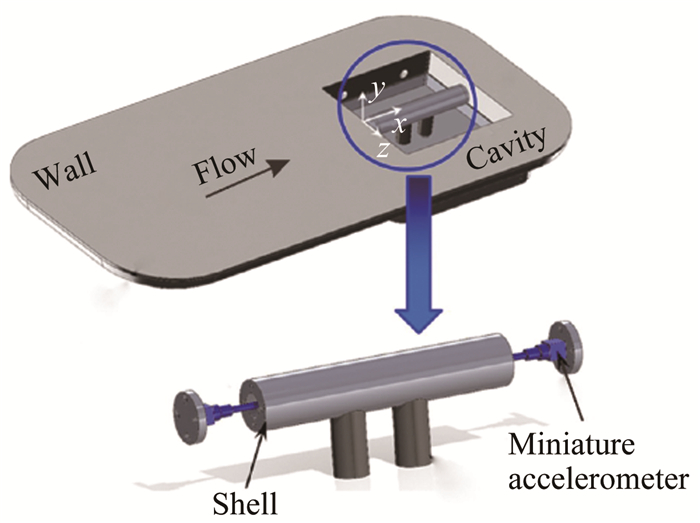
2.4 结构振动影响规律结构振动影响因素主要包括腔内物体振动以及空腔边界振动等。针对空腔复杂声场环境以及腔内物体结构振动耦合问题,Wagner[75-77]等通过风洞试验,研究了来流马赫数为0.6~2.5,长深比为3.3的可压缩空腔流致振动噪声问题,利用高精度动态压力传感器以及加速度传感器测得了腔内物体的噪声载荷以及结构振动信息,如图 9所示。尽管腔内物体占据的空腔体积较小,却显著改变了空腔气动声学特性。当腔内存在物体时,物体振动受到空腔噪声载荷影响显著,根据腔内物体振动与噪声的相关性分析结果,空腔噪声载荷主要激励腔内物体的流向和法向振动。Braone[78]等基于数值模拟方法,研究了内埋弹舱声振耦合问题,当腔内存在物体时,空腔内存在较强流激振荡以及噪声载荷,空腔压力谱峰值发生显著变化,腔内物体振动响应特性受到空腔噪声载荷以及结构固有特性的共同影响。
针对飞行器蒙皮结构与噪声载荷之间的声振耦合问题,王显圣等[79]通过改变弹性空腔结构固有频率,利用高速风洞试验模拟了空腔可压缩流致噪声/振动相互作用,如图 10所示,腔体结构振动响应与噪声载荷和结构固有属性相关,结构振动主要以低阶模态为主,并且当振动强度较弱时,空腔噪声受到结构振动辐射能量的影响较小。
3 空腔可压缩流致噪声控制技术空腔可压缩流致噪声控制机理与控制策略具有重要的学术和工程研究意义。尽管空腔可压缩流致噪声问题得到广泛关注,但空腔非定常流动及噪声控制机制的研究仍存在较大不足。空腔流致噪声载荷引起腔体结构和腔内物体等承受交变应力影响,尤其在超声速来流条件下,流场空间波系结构复杂,空腔噪声控制技术受到前所未有的挑战,工程实用的控制策略需求迫切。
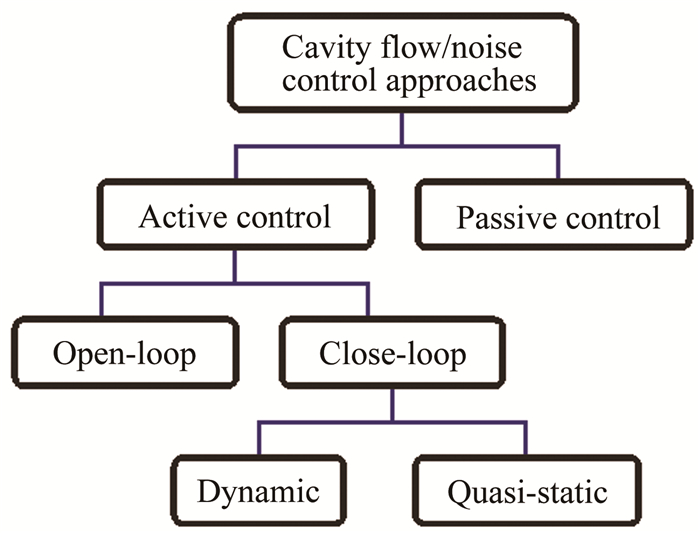
空腔流动以及流致噪声控制方法分为主动和被动2种方式[80],如图 11所示。被动控制措施主要通过改变几何外形对流场形成干扰达到降噪目的,主动控制措施主要通过向流场提供外部能量方式实现控制效果。在主动控制方法中,为了使控制效果达到最佳,通常将空间流动与噪声信号引入控制系统,以此修改控制参数,形成反馈控制回路。根据控制系统是否引入反馈信号,主动控制方法分为开环控制和闭环控制2种类型。根据反馈信号更新速度与控制参数时间尺度相比的快慢,闭环控制可以划分为准静态与动态反馈控制2种类型。
根据控制装置相对于空腔位置的不同,空腔非定常流动及噪声控制措施可以分为前缘流动控制、后缘流动控制、腔内扰流控制、腔壁阻抗控制等类型。在前缘流动控制措施中,扰动经过剪切层不稳定性放大作用后,能够有效干扰腔内反馈回路形成,流动控制效果增强,控制系统消耗能量也相应降低。在后缘流动控制措施中,空腔后缘区域结构状态改变,减弱了剪切层-空腔后壁之间相互作用,进而降低空腔噪声。腔内扰流控制措施通过改变腔内边界条件,对剪切层以及腔内流场形成干扰,进而达到控制整个空腔流场及其诱导噪声的目的。腔壁阻抗控制类型主要通过改变空腔壁面阻抗条件,干扰腔内声波传播特性,实现控制腔内噪声效果。
空腔流致噪声控制措施种类较多,Cattafesta等[80-82]对此进行了详细的综述,这些控制措施均在一定范围内具有明显的控制效果,不过不同的控制方法也表现出相应不足。被动控制措施结构简单,便于工程应用,然而其控制效果通常无法随工况变化而变化,并且控制过程中流场结构受到干扰,容易引起主流能量损失。主动控制措施依靠外界能量改变流动特征,对不同工况适应性强,不过开环控制方法受到激励器带宽与能量大小的限制,闭环控制系统复杂度显著增加,对于高马赫数条件下,控制系统适应性与可靠性仍需进一步发展和完善[2]。
3.1 被动控制技术发展近年来,空腔被动控制技术得到较大发展和进步,其面临的主要挑战在于保证结构可靠基础上,进一步增强控制参数对不同工况条件的适应性,并降低控制装置自身引起的不利影响。
针对前缘流动控制措施,Long等[83]研究了空腔前缘法向锯齿的噪声抑制效果,前缘法向锯齿能够增加空腔开口区域剪切层的厚度,减弱了剪切层-固壁相互作用强度,对空腔内脉动压力及噪声具有明显抑制效果。与此不同,Flaherty等[84]、Gai等[40]和Moon等[49]研究了空腔前缘流向锯齿对空腔非定常流动以及流致噪声的控制效果。结果发现,空腔前缘流向锯齿对于腔内噪声的影响较小。与此类似,Flaherty等[84]围绕空腔前缘法向襟板的控制效果进行研究,发现法向襟板也具有类似锯齿的降噪效果。冯强等[85]针对空腔前缘法向锯齿和法向襟板2种控制措施开展研究,发现2种控制方式均具有降噪效果并且表现出一定减阻效果,而前缘法向锯齿的减阻效果更优。针对空腔前缘法向圆柱控制技术,Thiemann等[86]采用法向圆柱阵列对空腔噪声控制效果进行研究,结果发现,法向圆柱改变了剪切层的速度、涡量分布以及流场-空腔结构的能量交换,对空腔噪声具有明显的控制效果,其控制效果不仅与圆柱的高度相关,还受到圆柱的分布类型影响。针对空腔前缘展向圆柱的控制效果,Illy等[87]开展风洞试验研究了展向圆柱对于跨声速空腔流动以及流致噪声的作用机制,如图 12所示,分析了圆柱尾迹区域的脱落涡对腔内噪声的重要影响,圆柱-壁面间距与圆柱直径之比是影响空腔噪声控制效果的关键参数,最优控制效果时该比值约为0.6~1.9。在超声速来流条件下,Dudley等[88]研究了空腔前缘展向圆柱对于超声速空腔流场及流致噪声的控制效果,圆柱位于边界层顶部40%区域时,降噪效果达到最优。Zhang等[89]通过数值方法研究了前缘可压缩斜坡与膨胀面对空腔流致噪声的影响,不同马赫数条件下,空腔前缘膨胀面均能够有效降低腔内噪声,说明抬高剪切层运动轨迹并非降低腔内噪声的唯一机制。Casper等[65]利用前缘连续斜坡技术、Long等[83]利用离散斜坡技术,通过风洞试验,验证了空腔前缘不同类型斜坡的降噪效果。Crafton等[66]利用压力敏感漆测试技术,研究了前缘流动控制措施对空腔流场非对称性的影响,空腔前缘流动控制措施能够增强空腔流场的非对称模态,而这种非对称性在超声速来流条件下更加显著。
针对后缘流动控制措施,Shaw等[1]采用空腔后壁倒角及后壁泄压孔方式进行被动流动控制,结果显示这2种控制方式均表现出明显降噪效果。Pereira等[90]通过后壁倒圆或后壁增加柱状突出物等方式减弱剪切层与空腔后壁相互作用及扰动波强度,降低了空腔噪声频谱的峰值,并且空腔噪声的各阶模态频率值受到的影响较小。杨党国等[14]采用后壁倒角方式进行腔内噪声控制,随着空腔后壁倾角增加,剪切层与空腔后壁撞击强度减弱,腔后壁区域噪声强度降低。吴继飞等[91]通过空腔后壁倒圆方式进行腔内噪声控制,后壁倒圆有利于降低腔内噪声,不过某些工况下,腔内静压梯度会有所升高,不利于武器安全分离。Gautam等[92]通过降低腔后壁高度方式进行空腔噪声控制,当腔后壁高度降低幅度较小、达到原来高度95%时,腔内噪声强度和频率成分基本不变,其中低频噪声成分甚至略有增加,当腔后壁降低幅度较大、达到原来高度90%时,空腔噪声频谱峰值显著降低,其降低幅度超过10dB。
针对腔内扰流和腔壁阻抗控制措施,Wilcox等[93]利用开孔底板方法研究超声速空腔流动控制技术,通过对腔内前后低压和高压区进行联通,降低腔内逆压梯度以及腔内压差阻力,在空腔长深比大于12的闭式空腔流动中,开孔底板作用效果明显,有效降低了空腔阻力系数。Stallings等[94]研究了亚跨声速条件下多种开孔底板方式对空腔流场的控制效果,开孔底板对于闭式空腔流场的控制效果比开式空腔更加显著,并且随着开孔面积的增加,控制效果趋于饱和。Zhang等[95]通过在空腔底部增加隔板实现流动控制,由于隔板对腔内回流特性产生影响,空腔底部隔板能够降低腔内压力梯度,并有助于改善腔内关键区域的噪声环境。吴继飞等[33]通过在空腔开口区域剪切层内增加扰流片,对剪切层发展与脱落涡演化等形成干扰,影响了空腔流动反馈回流以及流激振荡特性,降低了腔内噪声水平。
3.2 主动控制技术发展空腔主动控制技术因适应性强,能量消耗低而得到广泛关注,其面临的主要挑战在于增强控制系统可靠性以及工程实用性,并进一步扩展控制系统的适用范围。
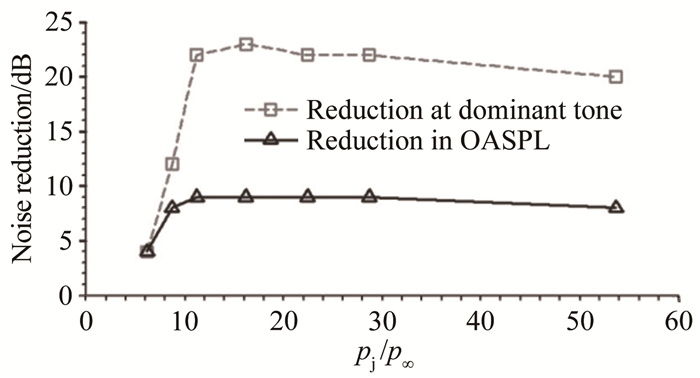
空腔前缘射流对剪切层中涡扰动增长特性以及波-涡相互作用具有较强干扰,是一种典型的空腔前缘流动控制措施,能够有效抑制空腔流激振荡的形成与气动噪声的产生,其作用机制主要包括2个方面:(1)前缘射流开启时,能够引起来流边界层厚度增加,导致边界层对空腔后壁前传声波的感受性降低,干扰了空腔扰动反馈回路的形成;(2)射流诱导的流向涡增加了剪切层厚度以及三维特性,改变了剪切层不稳定演化特性,并抬升了剪切层运动轨迹,减弱了剪切层与空腔结构的相互作用。Zhuang等[29]研究了超声速空腔前缘射流方法的控制效果,如图 13所示,降低马赫数2.0的空腔近壁噪声总声压级OASPL高达9dB,不过随着射流压力的增加,空腔噪声抑制效果趋于饱和,如图 14所示。Sahoo等[96-97]研究了空腔前缘射流对腔内噪声以及物体分离的控制效果,利用正交模态分解方法建立了低阶控制模型,研究发现,随着射流能量的增加,腔内噪声降低并趋于控制饱和状态,当射流能量超过最优参数时,腔内物体安全分离的风险增加。Bower等[98]通过高速纹影技术对此进行了试验验证,并分析了前缘射流对于腔内物体安全分离的影响机制。
针对不同射流孔配置方案对空腔噪声的控制效果,George等[99]发现,相比与单孔射流,三孔射流方案更有利于增强腔内噪声控制效果。Thangamani等[100]研究了射流孔位置对空腔噪声的控制效果,当射流孔位于空腔底板前部时,其噪声控制效果优于空腔底板中后部射流孔方案,并且与来流边界层内的射流孔方案相比,空腔底板前部射流对于空腔后部噪声的抑制效果更优,不过对于空腔前部噪声的抑制效果较差[92]。王一丁等[101]通过数值模拟研究了前缘气帘对超声速以及高超声速空腔噪声的抑制效果,施加控制措施后,空腔剪切层形态发生变化,腔内噪声强度显著降低。
针对空腔前缘的非定常射流控制措施,Ali等[102]通过风洞试验发现,与定常射流方案相比,高频脉冲射流对窄带噪声频率成分的控制效果较好,不过高频脉冲射流可能引起来流边界层内噪声强度增加。Bower等[98]采用空腔前缘高频射流方案,实现了超声速来流条件下对空腔流动反馈回路的干扰,有效抑制了腔内噪声强度。空腔前缘零质量射流能够对来流边界层与剪切层等流动结构产生干扰,进而影响空腔流动反馈回路。虽然控制系统对空腔流场不存在平均质量注入,但是对流动结构存在动量以及能量输入,在特定工况下,零质量射流方案仍然表现出较好控制效果[2]。吴继飞等[103]利用活塞式零质量射流方案,在跨声速来流条件下,有效改善了腔内噪声环境。在超声速来流条件下,活塞式零质量射流控制系统能量相对较小,不过该方法对于超声速空腔噪声控制效果较弱。罗柏华等[104]研究了空腔前缘单频声激励方法对空腔噪声的控制效果,在低亚声速来流条件下,控制措施对腔内噪声峰值频率成分的影响效果显著,不足之处在于对腔内噪声宽频成分影响较小,并且随着来流马赫数提高,前缘声激励控制效果显著降低。Chan等[105]将等离子体技术应用于空腔噪声控制,等离子激励器产生的流向涡向下游演化过程中,抑制了剪切层内脱落涡的产生,对空腔流动反馈回路形成干扰,由于等离子体激励器能量较弱,这种控制方法仅在低速来流条件下效果显著。Webb等[106]扩展了等离子体控制技术的适用范围,研究了其对于超声速空腔流动的控制效果,阐述了通过激发剪切层开尔文-亥姆霍兹不稳定性,进而控制剪切层结构演化以及空腔可压缩流致噪声的控制机制。
闭环控制措施主要通过控制器与反馈信号实现控制参数的优化选取,从而降低控制系统能量消耗,提高控制效果[107]。Williams等[108]利用空腔前缘射流激励器实现了高速空腔噪声的闭环流动控制,有效抑制腔内噪声的主频成分,不过射流激励器与噪声扰动反馈信号之间的相位差需要合理选择,否则可能使空腔噪声增强。Kim等[109]利用风洞试验,针对合成射流激励器控制效果的动态补偿效应,建立了亚声速来流条件下,激励器与反馈信号的时间延迟模型。Illingworth等[110]采用直接数值模拟,建立了低亚声速线性闭环流动控制模型,并利用数值结果,分别在时间域和频率域验证模型的有效性。Cattafesta等[111]通过压电控制器改变空腔边界阻抗特性,实现了空腔噪声闭环流动控制,由于控制能量较弱,与开环控制措施相比,压电闭环控制系统对于超声速空腔噪声的抑制效果较弱。随着自动控制技术、信息技术、机械加工技术等方面的不断进步,空腔噪声闭环控制技术得到较大发展,不过与其他控制手段相比,闭环控制系统复杂度显著提高,其工程实用性仍然存在较大发展空间,面临挑战主要在于建立适用高速来流条件的闭环流动控制模型,发展可靠性高并且实用性强的控制策略。
4 结论与展望近年来,随着航空航天技术的发展,空腔可压缩流致噪声问题得到关注,相关研究取得显著进展,不过空腔可压缩流致噪声是流体动力学、气动声学以及结构振动力学等多学科交叉问题,其产生、传播与控制机制复杂,相关问题仍需更为系统深入的研究。本文主要从空腔可压缩流致噪声的产生机制、参数影响规律以及控制技术研究成果进行总结和归纳,旨在呈现相关问题的研究水平,发现其中不足,以便进一步推动该领域研究的发展。
空腔可压缩流场结构以及气动声学特性产生机理复杂,存在边界层分离、剪切层失稳、旋涡生成与演化、涡-固壁相互作用、波/涡相互干扰等复杂流动现象,以及激波、膨胀波等复杂波系结构。流场中经常形成扰动反馈增长回路,发生流激振荡现象,诱导产生强气动噪声,这些复杂现象给空腔气动声学研究带来较大困难。目前,国际上对空腔流激振荡以及可压缩流致噪声的产生、传播机制尚未达成一致意见,相关研究面临较大挑战。在高速来流条件下,开展空腔气动声学特性、流场结构与结构振动之间耦合机理的深入研究,掌握空腔流激振荡以及流致噪声的发生机理,建立空腔流致噪声频率和强度试验模拟准则及理论预测模型,深入研究空腔流场、声场、结构振动等多场耦合机制,是解决空腔可压缩流致噪声问题的关键。
近年来,空腔实验和数值模拟技术的进步有效推动了空腔问题的研究[112],不过随着问题复杂程度提高,对相关研究手段提出了更高要求。三维空腔复杂波系与多涡结构显示、空腔多场特性同步测试、测试结果模态相关分析等,对空腔实验技术提出了挑战,而复杂空腔外形的可压缩流致噪声精准预测、空腔噪声/流动/振动多场耦合特性模拟、空腔可压缩湍流模型与高精度数值格式发展等,对空腔数值模拟技术提出了更高要求。
为了提高空腔类飞行器部件的工程实用性,空腔噪声控制技术和控制模型逐渐成为研究热点。空腔控制策略的引入通常能够改善腔内外噪声环境[113],不过国际上对于空腔噪声控制机制的研究存在分歧,并且控制策略的引入可能对飞行器整体性能产生不利影响,例如飞行器阻力增加、控制系统附加质量效应显著等。因此,亟需综合考虑空腔噪声/流动/振动的多场耦合控制模型,深入分析控制系统的多目标优化方案,建立工程实用的控制方法,使控制系统对飞行器整体性能的提高产生积极效果。
| [1] | Shaw L, Clark R, Talmadge D. F-111 generic weapons bay acoustic environment[J]. J Aircraft, 1988, 25(2): 147–153. DOI:10.2514/3.45555 |
| [2] | Rowley C W, Williams D R. Dynamics and control of high-Reynolds-number flow over open cavities[J]. Annu Rev Fluid Mech, 2006, 38(1): 251–276. DOI:10.1146/annurev.fluid.38.050304.092057 |
| [3] | Heller H H, Holmes D G, Covert E E. Flow-induced pressure oscillations in shallow cavities[J]. J Sound Vib, 1971, 18(4): 545–553. DOI:10.1016/0022-460X(71)90105-2 |
| [4] | Stallings R L, Wilcox F J. Experimental cavity pressure distributions at supersonic speeds[R]. NASA TP-2683, 1987. |
| [5] | Sarohia V. Experimental investigation of oscillations in flows over shallow cavities[J]. AIAA J, 1997, 15(7): 984–991. |
| [6] | Rossiter J E. Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds[R]. Aeronautical Research Council Reports and Memoranda, TR-3438, 1964. |
| [7] | Tam C K W, Block P J W. On the tones and pressure oscillations induced by flow over rectangular cavities[J]. J Fluid Mech, 1978, 89(2): 373–399. DOI:10.1017/S0022112078002657 |
| [8] | Arunajatesan S, Barone M F, Wagner J L, et al. Joint experimental/computational investigation into the effects of finite width on transonic cavity flow[R]. AIAA 2014-3027, 2014. |
| [9] | Bres G A, Colonius T. Three-dimensional instabilities in compressible flow over open cavities[J]. J Fluid Mech, 2008, 599: 309–339. |
| [10] | Crook S D, Lau T C W, Kelso R M. Three-dimensional flow within shallow, narrow cavities[J]. J Fluid Mech, 2013, 735: 587–612. DOI:10.1017/jfm.2013.519 |
| [11] | Beresh S J, Wagner J L, Demauro E P, et al. Resonance characteristics of transonic flow over a rectangular cavity using pulse-burst PIV[R]. AIAA 2016-1344, 2016. |
| [12] | Beresh S J, Wagner J L, Casper K M, et al. Spatial distribution of resonance in the velocity field for transonic flow over a rectangular cavity[J]. AIAA J, 2017, 55(7): 1–16. |
| [13] | Beresh S J, Wagner J L, Casper K M. Compressibility effects in the shear layer over a rectangular cavity[J]. J Fluid Mech, 2016, 808: 116–152. DOI:10.1017/jfm.2016.540 |
| [14] | 杨党国, 范召林, 李建强, 等. 后壁倒角对空腔噪声的抑制效果[J]. 实验流体力学, 2010, 24(5): 22–25. Yang D G, Fan Z L, Li J Q, et al. Suppression effects of rear-face angle of cavity on its aerodynamics noise[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(5): 22–25. DOI:10.3969/j.issn.1672-9897.2010.05.005 |
| [15] | 侯中喜, 夏刚, 秦子增. 三维超声速开式空腔振荡特性研究[J]. 国防科技大学学报, 2004, 26(6): 1–4. Hou Z X, Xia G, Qin Z Z. The numerical analysis of oscillatory characteristics in 3D supersonic open cavity[J]. Journal of National University of Defense Technology, 2004, 26(6): 1–4. DOI:10.3969/j.issn.1001-2486.2004.06.001 |
| [16] | 司海清, 马晓晖, 陈都, 等. 偏航状态下空腔流动的数值模拟[J]. 南京航空航天大学学报, 2013, 45(2): 191–195. Si H Q, Ma X H, Chen D, et al. Numerical simulation of cavity flow at different yaw angles[J]. Journal of Nanjing University of Aeronautics and Astronautic, 2013, 45(2): 191–195. DOI:10.3969/j.issn.1005-2615.2013.02.006 |
| [17] | 李晓东, 刘婧东, 高军辉. 空腔流激振荡发声的数值模拟研究[J]. 力学学报, 2006, 38(5): 599–604. Li X D, Liu J D, Gao J H. Numerical simulation of flow-induced oscillation and sound generation in a cavity[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(5): 599–604. |
| [18] | 刘俊, 杨党国, 王显圣, 等. 湍流边界层厚度对三维空腔流动的影响[J]. 航空学报, 2016, 37(2): 475–483. Liu J, Yang D G, Wang X S, et al. Effect of turbulent boundary layer thickness on a three-dimensional cavity flow[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 475–483. |
| [19] | Rowley C W, Colonius T, Basu A J. On self-sustained oscillations in two-dimensional compressible flow over rectangular cavities[J]. J Fluid Mech, 2002, 455(455): 315–346. |
| [20] | Krishnamurty K. Sound radiation from surface cutouts in high speed flow[D]. California: California Institute of Technology, 1956. http://www.researchgate.net/publication/35133550_Sound_radiation_from_surface_cutouts_in_high_speed_flow |
| [21] | Wagner J, Beresh S J, Casper K M, et al. Relationship between transonic cavity tones and flowfield dynamics using pulse-burst PIV[R]. AIAA 2016-1345, 2016. http://www.researchgate.net/publication/313844747_Relationship_between_Transonic_Cavity_Tones_and_Flowfield_Dynamics_using_Pulse-Burst_PIV |
| [22] | Zhang X. Compressible cavity flow oscillation due to shear layer instabilities and pressure feedback[J]. AIAA J, 1995, 33(8): 1404–1411. DOI:10.2514/3.12845 |
| [23] | Forestier N, Jacquin L, Geffroy P. The mixing layer over a deep cavity at high-subsonic speed[J]. J Fluid Mech, 2003, 475(475): 101–145. |
| [24] | Beresh S J, Wagner J L, M P B O, et al. Supersonic flow over a finite-width rectangular cavity[J]. AIAA J, 2015, 53(2): 296–310. DOI:10.2514/1.J053097 |
| [25] | Lada C, Kontis K. Experimental studies of open cavity configurations at transonic speeds with flow control[J]. J Aircraft, 2011, 48(2): 719–724. DOI:10.2514/1.C031174 |
| [26] | Zhang X. Experimental investigation of supersonic flow over two cavities in tandem[J]. AIAA J, 2015, 30(2): 1182–1190. |
| [27] | Handa T, Miyachi H, Kakuno H, et al. Generation and propagation of pressure waves in supersonic deep-cavity flows[J]. Exp Fluids, 2012, 53(6): 1855–1866. DOI:10.1007/s00348-012-1400-7 |
| [28] | Zhuang N. Experimental investigation of supersonic cavity flow and their control[J]. Dissertation & Theses-Gradworks, 2007, 44(9): 2118–2128. |
| [29] | Zhuang N, Alvi F S, Alkislar M B, et al. Supersonic cavity flows and their control[J]. AIAA J, 2006, 44(9): 2118–2128. DOI:10.2514/1.14879 |
| [30] | Wang M, Freund J B, Lele S K. Computational prediction of flow-generated sound[J]. Annu Rev Fluid Mech, 2006, 38(1): 483–512. DOI:10.1146/annurev.fluid.38.050304.092036 |
| [31] | 杨党国, 罗新福, 李建强, 等. 来流边界层厚度对开式空腔气动声学特性的影响分析[J]. 空气动力学学报, 2011, 29(4): 486–490. Yang D G, Luo X F, Li J Q, et al. Analysis of aeroacoustic characteristics in open cavities influenced by boundary-layer thickness[J]. Acta Aerodynamica Sinica, 2011, 29(4): 486–490. DOI:10.3969/j.issn.0258-1825.2011.04.015 |
| [32] | 赵小见, 赵磊, 冯峰, 等. 某空腔低速流动噪声风洞试验[J]. 航空学报, 2015, 36(7): 2145–2154. Zhao X J, Zhao L, Feng F, et al. Wind tunnel test into noise induced by low-speed cavity flow[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2145–2154. |
| [33] | 吴继飞, 徐来武, 范召林, 等. 开式空腔气动声学特性及其流动控制方法[J]. 航空学报, 2015, 36(7): 2155–2165. Wu J F, Xu L W, Fan Z L, et al. Aeroacoustic characteristics and flow control method of open cavity flow[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2155–2165. |
| [34] | Yamouni S, Sipp D, Jacquin L. Interaction between feedback aeroacoustic and acoustic resonance mechanisms in a cavity flow:a global stability analysis[J]. J Fluid Mech, 2013, 717(2): 134–165. |
| [35] | Fontaine R A, Elliott G S, Austin J M, et al. Very near-nozzle shear-layer turbulence and jet noise[J]. J Fluid Mech, 2015, 770: 27–51. DOI:10.1017/jfm.2015.119 |
| [36] | 司海清, 王同光. 边界条件对三维空腔流激振荡的影响[J]. 南京航空航天大学学报, 2006, 38(5): 595–599. Si H Q, Wang T G. Influence of boundary conditions on 3D cavity flow induced oscillations[J]. Nanjing University of Aeroacoustics & Astronautics, 2006, 38(5): 595–599. DOI:10.3969/j.issn.1005-2615.2006.05.013 |
| [37] | Lai H, Luo K H. Acoustic source and near field of three-dimensional compressible flow over an open cavity[R]. AIAA 2005-2805, 2005. |
| [38] | Chen X X, Sandham N D, Zhang X. Cavity flow noise predictions[R]. University of Southampton Report, AFM-07/05, 2007. |
| [39] | 杨党国, 李建强, 梁锦敏. 基于CFD和气动声学理论的空腔自激振荡发声机理[J]. 空气动力学学报, 2010, 28(6): 724–730. Yang D G, Li J Q, Liang J M, et al. Sound generation induced by self-sustained oscillations inside cavities based on CFD and aeroacoustic theory[J]. Acta Aerodynamica Sinica, 2010, 28(6): 724–730. DOI:10.3969/j.issn.0258-1825.2010.06.019 |
| [40] | Gai S L, Kleine H, Neely A J. Supersonic flow over a shallow open rectangular cavity[J]. J Aircraft, 2015, 52(2): 609–616. DOI:10.2514/1.C032781 |
| [41] | 杨党国, 祝静, 李建强, 等. 跨超声速开式空腔流激振荡模态预估分析[J]. 空气动力学学报, 2014, 32(3): 369–375. Yang D G, Zhu J, Li J Q, et al. Prediction and analysis of flow oscillation modes inside open cavities at transonic or supersonic speeds[J]. Acta Aerodynamica Sinica, 2014, 32(3): 369–375. |
| [42] | 万振华, 周林, 孙德军. 方腔流致振荡及噪声的数值研究[J]. 空气动力学学报, 2012, 30(3): 291–298. Wan Z H, Zhou L, Sun D J. Numerical investigation of flow induced oscillations and noise in a rectangular cavity[J]. Acta Aerodynamica Sinica, 2012, 30(3): 291–298. DOI:10.3969/j.issn.0258-1825.2012.03.003 |
| [43] | Rockwell D, Naudascher E. Review-self-sustaining oscillations of flow past cavities[J]. J Fluids Eng, 1978, 100(2): 152–165. DOI:10.1115/1.3448624 |
| [44] | Lawson S. Review of numerical simulations for high-speed, turbulent cavity flows[J]. Prog Aerospace Sci, 2011, 47(3): 186–216. DOI:10.1016/j.paerosci.2010.11.002 |
| [45] | Sun Y, Nair A G, Taira K, et al. Numerical simulations of subsonic and transonic open-cavity flows[R]. AIAA 2014-3092, 2014. http://www.researchgate.net/publication/269229214_numerical_simulations_of_subsonic_and_transonic_open-cavity_flows |
| [46] | 杨党国, 范召林, 李建强, 等. 弹舱流动特性数值模拟及风洞试验研究[J]. 空气动力学学报, 2009, 27(3): 378–383. Yang D G, Fan Z L, Li J Q, et al. Studies on flow characteristics of cavity by numerical simulation and wind tunnel test[J]. Acta Aerodynamica Sinica, 2009, 27(3): 378–383. DOI:10.3969/j.issn.0258-1825.2009.03.021 |
| [47] | Ahuja K. Effects of cavity dimensions, boundary layer, and temperature on cavity noise with emphasis on benchmark data to validate computational aeroacoustic codes[R]. NASA Contractor Report 4653, 1995. |
| [48] | Schmit R F, Grove J E, Semmelmayer F, et al. Nonlinear feedback mechanisms inside a rectangular cavity[J]. AIAA J, 2014, 52(10): 2127–2141. DOI:10.2514/1.J052804 |
| [49] | Moon S J, Gai S L, Kleine H, et al. Supersonic flow over straight shallow cavities including leading and trailing edge modifications[R]. AIAA 2010-4687, 2010. https://arc.aiaa.org/doi/abs/10.2514/6.2010-4687 |
| [50] | Robertson G, Kumar R, Doyle S, et al. Acoustics of a supersonic cavity with a generic store[R]. AIAA 2015-1292, 2015. https://arc.aiaa.org/doi/abs/10.2514/6.2015-1292 |
| [51] | Gharib M. Response of the cavity shear layer oscillations to external forcing[J]. AIAA J, 1987, 25(1): 43–47. DOI:10.2514/3.9576 |
| [52] | Daoud M, Naguib A M, Bassioni I, et al. Microphone-array measurements of the floor pressure in a low-speed cavity flow[J]. AIAA J, 2006, 44(9): 2018–2023. DOI:10.2514/1.18129 |
| [53] | Gloerfelt X. Cavity noise[C]. VKI Lecture: Aerodynamic noise from wall bounded flows, Brussels, 2009. |
| [54] | Chung K. Characteristics of compressible rectangular cavity flows[J]. J Aircraft, 2003, 40(1): 137–142. DOI:10.2514/2.3068 |
| [55] | Baseley J, Pastur L R, Lusseyran F, et al. On the modulating effect of three-dimensional instabilities in open cavity flows[J]. J Fluid Mech, 2014, 759: 546–578. DOI:10.1017/jfm.2014.576 |
| [56] | Baseley J, Pastur L R, Delprat N, et al. Space-time aspects of a three-dimensional multi-modulated open cavity flow[J]. Phys Fluids, 2013, 25(6): 64105. DOI:10.1063/1.4811692 |
| [57] | Tracy M B, Plentovich E B, Hemsch M J, et al. Effects of sweep on cavity flow fields at subsonic and transonic speeds[R]. NASA TM-2012-217577, 2012. https://core.ac.uk/display/10568231 |
| [58] | Vikramaditya N S, Kurian J. Nonlinear aspects of supersonic flow past a cavity[J]. Exp Fluids, 2012, 52(6): 1389–1399. DOI:10.1007/s00348-012-1261-0 |
| [59] | Kim H J, Aradag S, Knight R D. Two and three dimensional simulations of supersonic cavity flow[R]. AIAA 2006-2431, 2006. https://www.ixueshu.com/document/914fd23eb580fb6e318947a18e7f9386.html |
| [60] | Wagner J L, Beresh S J, Casper K M, et al. Experimental investigation of aspect-ratio effects in transonic and subsonic rectangular cavity flows[R]. AIAA 2014-1446, 2014. |
| [61] | Beresh S J, Wagner J L, Pruett B O M. Particle image velocimetry of a three-dimensional supersonic cavity flow[R]. AIAA 2012-0030, 2012. http://www.researchgate.net/publication/268471908_Particle_Image_Velocimetry_of_a_Three-Dimensional_Supersonic_Cavity_Flow |
| [62] | Das R, Kim H D, Kurian J. Experimental study of supersonic entrainment using a cavity[J]. J Propul Power, 2014, 30(5): 1–9. |
| [63] | Ukeiley L, Sheehan M, Coiffet F, et al. Control of pressure loads in geometrically complex cavities[J]. J Aircraft, 2008, 45(3): 1014–1024. DOI:10.2514/1.33324 |
| [64] | Casper K M, Wagner J L, Beresh S J, et al. Complex geometry effects on subsonic cavity flows[R]. AIAA 2015-1291, 2015. https://www.researchgate.net/publication/306305839_Complex_Geometry_Effects_on_Subsonic_Cavity_Flows |
| [65] | Casper K M, Wagner J L, Beresh S J, et al. Complex geometry effects on supersonic cavity flows[R]. AIAA 2014-3025, 2014. |
| [66] | Crafton J, Stanfield S, Rogoshchenkov N, et al. Investigation of Passive Flow Control of Cavity Acoustics Using Dynamic Pressure-Sensitive Paint[R]. AIAA 2017-1178, 2017. |
| [67] | 吴继飞, 徐来武, 范召林, 等. 内埋弹舱舱门气动特性研究[J]. 空气动力学学报, 2012, 30(6): 744–748. Wu J F, Xu L W, Fan Z L, et al. Investigation on aerodynamic characteristics of internal bay's door[J]. Acta Aerodynamica Sinica, 2012, 30(6): 744–748. |
| [68] | 吴继飞, 徐来武, 范召林, 等. 内埋武器舱舱门开闭动态模拟试验技术研究[J]. 实验流体力学, 2015, 29(4): 88–94. Wu J F, Xu L W, Fan Z L, et al. Investigation on dynamic simulation technology of internal weapon bay's doors opening and closing[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(4): 88–94. |
| [69] | Flora T J, Reeder M F, Lofthouse A, et al. Dynamic store release of ice models from a cavity into Mach 2. 9 Flow[J]. J Aircraft, 2014, 51(6): 1–15. |
| [70] | Merrick J D, Reeder M F. Cavity-store interaction under supersonic freestream conditions[R]. AIAA 2015-3017, 2015. http://www.researchgate.net/publication/299644306_Cavity-Store_Interaction_under_Supersonic_Freestream_Conditions |
| [71] | 吴继飞, 罗新福, 范召林. 内埋式弹舱流场特性及武器分离特性改进措施[J]. 航空学报, 2009, 30(10): 1840–1845. Wu J F, Luo X F, Fan Z L, et al. Flow control method to improve cavity flow and store separation characteristics[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(10): 1840–1845. DOI:10.3321/j.issn:1000-6893.2009.10.008 |
| [72] | Coley C J, Lofthouse A J. Correlation of weapon bay resonance and store unsteady force and moment loading[R]. AIAA 2012-0415, 2012. http://www.researchgate.net/publication/269045805_Correlation_of_Weapon_Bay_Resonance_and_Store_Unsteady_Force_and_Moment_Loading |
| [73] | Murray N E, Jansen B J, Gui L, et al. Measurements of store separation dynamics[R]. AIAA 2009-105, 2009. http://www.researchgate.net/publication/269061737_measurements_of_store_separation_dynamics |
| [74] | Bjorge S T, Reeder M F, Subramanian C, et al. Flow around an object projected from a cavity into a supersonic freestream[J]. AIAA J, 2005, 43(7): 1465–1475. DOI:10.2514/1.10943 |
| [75] | Wagner J L, Casper K M, Beresh S J, et al. Experimental investigation of fluid-structure interactions in compressible cavity flows[R]. AIAA 2013-3172, 2013. http://www.researchgate.net/publication/269049382_Experimental_Investigation_of_Fluid-Structure_Interactions_in_Compressible_Cavity_Flows |
| [76] | Wagner J L, Beresh S J, Casper K M, et al. Simultaneous vibration and acoustic measurements of a store in compressible open cavity flow[R]. AIAA 2013-0228, 2013. http://www.researchgate.net/publication/287096751_Simultaneous_vibration_and_acoustic_measurements_of_a_store_in_compressible_open_cavity_flow |
| [77] | Wagner J. Fluid-structure interactions in compressible cavity flows[J]. Phys Fluids, 2015, 27(6): 152–165. |
| [78] | Barone M, Arunajatesan S. Pressure loading within rectangular cavities with and without a captive store[R]. AIAA 2014-1406, 2014. http://www.researchgate.net/publication/269247720_Pressure_Loading_Within_Rectangular_Cavities_With_and_Without_a_Captive_Store |
| [79] | 王显圣, 杨党国, 刘俊, 等. 弹性空腔流致噪声/结构振动特性试验[J]. 航空学报, 2017, 38(7): 120873. Wang X S, Yang D G, Liu J, et al. Test on interactions between aeroacoustic noise and structural vibration in elastic cavity flow[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 120873. |
| [80] | Cattafesta L N, Song Q, Williams D R, et al. Active control of flow-induced cavity oscillations[J]. Prog. Aerospace Sci, 2008, 44: 479–502. DOI:10.1016/j.paerosci.2008.07.002 |
| [81] | Cattafesta L N, Williams D R, Rowley C W, et al. Review of active control of flow-induced cavity resonance[R]. AIAA 2003-3567, 2003. |
| [82] | Cattafesta L. Actuators for Active Flow Control[J]. Annu Rev Fluid Mech, 2011, 43(43): 247–272. |
| [83] | Long D F. Spatial structure of cavity pressure fluctuations at transonic speeds[J]. AIAA J, 2006, 44(9): 1983–1992. DOI:10.2514/1.5236 |
| [84] | Flaherty W, Reedy T M, Elliott G S, et al. Investigation of cavity flow using fast-response pressure-sensitive paint[J]. AIAA J, 2014, 52(11): 2462–2470. DOI:10.2514/1.J052864 |
| [85] | 冯强, 张洋, 崔晓春. 弹舱对飞翼布局飞机气动特性影响及其控制[J]. 实验流体力学, 2013, 27(3): 31–40. Feng Q, Zhang Y, Cui X C. Study on the effect of weapons bay on aerodynamic characteristics of flying wing aircraft and its control[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(3): 31–40. DOI:10.3969/j.issn.1672-9897.2013.03.006 |
| [86] | Thiemann C L, Milne G J, Vakili A D. An experimental investigation of supersonic cavity flow control with vertical cylinders[R]. AIAA 2013-3173, 2013. http://www.researchgate.net/publication/269049590_An_Experimental_Investigation_of_Supersonic_Cavity_Flow_Control_with_Vertical_Cylinders |
| [87] | Illy H, Jacquin L, Geffroy P. Observation on the passive control of flow oscillation over a cavity in a transonic regime by means of a spanwise cylinder[R]. AIAA 2008-3774, 2008. |
| [88] | Dudley J G, Ukeiley L. Suppression of fluctuating surface pressures in a supersonic cavity flow[R]. AIAA 2010-4974, 2010. http://www.researchgate.net/publication/268483009_Suppression_of_Fluctuating_Surface_Pressures_in_a_Supersonic_Cavity_Flow |
| [89] | Zhang X, Chen X X, Rona A, et al. Attenuation of cavity flow oscillation through leading edge flow control[J]. J Sound Vib, 1999, 221(1): 23–47. DOI:10.1006/jsvi.1998.2012 |
| [90] | Pereira J C F, Sousa J M M. Influence of impingement edge geometry on cavity flow oscillations[J]. AIAA J, 1994, 32(8): 1737–1740. DOI:10.2514/3.12168 |
| [91] | 吴继飞, 陶洋, 范召林, 等. 后缘修型对空腔流场特性影响分析[J]. 空气动力学学报, 2010, 28(2): 197–202. Wu J F, Tao Y, Fan Z L, et al. Analysis of the effect of the modification at the trailing edge on cavity flow characteristics[J]. Acta Aerodynamica Sinica, 2010, 28(2): 197–202. DOI:10.3969/j.issn.0258-1825.2010.02.012 |
| [92] | Gautam T, Lovejeet G, Vaidyanathan A. Experimental study of supersonic flow over cavity with aft Wall offset and cavity floor injection[J]. Aerosp Sci Technol, 2017, 70: 211–232. DOI:10.1016/j.ast.2017.07.024 |
| [93] | Wilcox F J. Passive venting system for modifying cavity flowfields at supersonic speeds[J]. AIAA J, 1988, 26(3): 374–376. DOI:10.2514/3.9902 |
| [94] | Stallings R. Effect of passive venting on static pressure distributions in cavities at subsonic and transonic speeds[R]. NASA Technical Memorandum 4549, 1994. |
| [95] | Zhang J, Morishita E, Okunuki T, et al. Experimental and computational investigation of supersonic cavity flows[R]. AIAA 2001-1755, 2001. http://www.researchgate.net/publication/269218849_Experimental_and_computational_investigation_of_supersonic_cavity_flows |
| [96] | Sahoo D, Annaswamy A, Alvi F. Microjets-based active control of store trajectory in a supersonic cavity using a low-order model[R]. AIAA 2005-3097, 2005. |
| [97] | Sahoo D, Annaswamy A, Zhuang N, et al. Control of cavity tones in supersonic flow[R]. AIAA 2005-793, 2005. https://arc.aiaa.org/doi/abs/10.2514/6.2005-793 |
| [98] | Bower W W, Kibens V, Cary A W, et al. High-frequency excitation active flow control for hight-speed weapon release (HIFEX)[R]. AIAA 2004-2513, 2004. http://www.researchgate.net/publication/268561111_High-Frequency_Excitation_Active_Flow_Control_for_High-Speed_Weapon_Release_HIFEX |
| [99] | George B, Ukeiley L, Cattafesta L N, et al. Control of three-dimensional cavity flow using leading-edge slot blowing[R]. AIAA 2015-1059, 2015. https://arc.aiaa.org/doi/abs/10.2514/6.2015-1059 |
| [100] | Thangamani V, Kurian J. Control of cavity oscillations in a supersonic flow by microjet injection[J]. J Aircraft, 2013, 50(4): 1305–1308. DOI:10.2514/1.C032003 |
| [101] | 王一丁, 郭亮, 童明波, 等. 高速飞行器空腔脉动压力主动控制与非线性数值模拟[J]. 航空学报, 2015, 36(1): 213–222. Wang Y D, Guo L, Tong M B, et al. Active control and nonlinear numerical simulation for oscillating pressure of high-speed aircraft cavity[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 213–222. |
| [102] | Ali M Y, Solomon J T, Gustavsson J, et al. Control of resonant flow inside a supersonic cavity using high bandwidth pulsed micro-actuators[R]. AIAA 2010-1198, 2010. http://www.researchgate.net/publication/269051079_control_of_resonant_flow_inside_a_supersonic_cavity_using_high_bandwidth_micro-actuators |
| [103] | 吴继飞, 罗新福, 徐来武, 等. 活塞式合成射流技术及其应用研究[J]. 实验流体力学, 2014, 28(6): 61–65. Wu J F, Luo X F, Xu L W, et al. Investigation on piston-typed synthetic jet technology and its application[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(6): 61–65. |
| [104] | 罗柏华, 胡章伟, 戴昌晖. 声激励抑制空腔流激振荡的实验研究[J]. 南京航空航天大学学报, 1999, 31(1): 1–5. Luo B H, Hu Z W, Dai C H. Experimental study on suppression of cavity flow oscillations by means of acoustic excitation[J]. Journal of Nanjing University of Aeronautics and Astronautics, 1999, 31(1): 1–5. DOI:10.3969/j.issn.1005-2615.1999.01.001 |
| [105] | Chan S, Zhang X, Gabriel S. The attenuation of cavity tones using plasma actuators[R]. AIAA 2005-2802, 2005. http://www.researchgate.net/publication/268582149_The_Attenuation_of_Cavity_Tones_Using_Plasma_Actuators |
| [106] | Webb N, Samimy M. Control of supersonic cavity flow using plasma actuators[J]. AIAA, 2017, 55(60): 1–10. |
| [107] | Williams D R, Rowley C W. Recent progress in closed-loop control of cavity tones[R]. AIAA 2006-712, 2006. https://arc.aiaa.org/doi/abs/10.2514/6.2006-712 |
| [108] | Williams D R, Cornelius D, Rowley C W. Closed-loop control of linear supersonic cavity tones[R]. AIAA 2007-4226, 2007. http://www.researchgate.net/publication/255583442_Closed-Loop_Control_of_Linear_Supersonic_Cavity_Tones |
| [109] | Kim K, Debiasi M, Schultz R, et al. Dynamic compensation of a syntheitic jetlike actuator for closed-loop cavity flow control[J]. AIAA J, 2008, 46(1): 232–240. DOI:10.2514/1.30095 |
| [110] | Illingworth S J, Morgans A S, Rowley C W. Feedback control of cavity flow oscillations using simple linear models[J]. J Fluid Mech, 2012, 709(4): 223–248. |
| [111] | Cattafesta L N, Shukla D, Garg S, et al. Development of an adaptive weapons-bay suppression system[R]. AIAA 1999-1901. 1999. https://arc.aiaa.org/doi/abs/10.2514/6.1999-1901 |
| [112] | 张征宇, 王显圣, 黄旭辉, 等. 高速复杂流动结构的视频测量[J]. 航空学报, 2017, 38(8): 120989. Zhang Z Y, Wang X S, Huang X H, et al. Videogrammetry measurement for high-speed complex flow structure[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(8): 120989. |
| [113] | 周方奇, 杨党国, 王显圣, 等. 前缘直板绕流对高速空腔的降噪效果分析[J]. 航空学报, 2018, 39(6): 21812. Zhou F Q, Yang D G, Wang X S, et al. The effect of leading edge plate on high speed cavity noise controlling[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(6): 21812. |