自FAR 25部修正案的140号文件发布以来,由过冷大水滴(SLD)引发的异常结冰问题引起了广泛的关注与研究。SLD撞击结冰问题不仅包括传统的铺展、飞溅和溢流等动力学问题[1-7],还包括复杂的非稳态传热相变问题[8]。已开展的冰风洞实验验证了SLD撞击结冰问题的复杂性,即使碰撞条件发生微小的改变(如撞击速度、撞击角度等的改变),SLD都会呈现完全不同的冻结特征[9]。Li用高速相机捕捉了单个SLD在冰风洞中撞击结冰的完整过程,指出SLD的大粒径效应是导致其异常结冰的重要原因[10]。Potapczuk通过实验发现SLD具有很强的冻结特性,任意单个特征参数并不能决定最终的结冰形态[11]。Yang通过SLD撞击柱状金属表面结冰实验提出瞬态结冰和非瞬态结冰2种SLD冻结模式[12]。这些实验均在一定程度上加深了对SLD异常结冰问题的理解,并为深入研究SLD撞击结冰问题打下初步理论基础。
然而,目前关于SLD间的干扰对撞击结冰过程影响的实验研究十分有限。以FAA发布的附录O[13]中所给出的冻毛毛雨环境作为典型云雾环境,做一个简单计算:平均水含量LWC为0.3g/m3, 平均水滴直径MVD为100μm。SLD的数量可达106/m3。当大量的SLD相继撞击在邻近区域内时,SLD间的干扰对结冰过程的影响不可忽略。
目前虽鲜有文献专门探讨SLD间的相互干扰对撞击结冰的影响,但在相近领域关于多液滴撞击及相变过程的实验研究早已开展。R. Ghafouri-Azar研究2个熔融的锡液滴撞击低温表面并凝固的物理过程,建立凝固形态与双液滴落点间的偏移量的关系[14]。Fujimoto设计双水滴撞击实验并揭示了撞击参数与热流量的关系[15]。这些研究表明多液滴间的干扰会改变撞击传热过程中原有的动力学和热力学行为。
为探明SLD间的干扰对撞击结冰的影响,设计双SLD相继撞击金属壁面结冰的实验。用高速相机记录整个结冰过程,找出双SLD落点间的位置偏移,相继撞击时间间隔和结冰形态,结冰速度的关系。本实验实验结果均与不存在相互干扰的双SLD撞击结冰实验结果做对比。
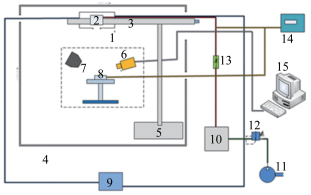
1 实验方案 1.1 实验装置实验装置主要包括SLD制备发生系统、低温撞击平台及观测系统等,实验总体布局如图 1所示。
|
| 图 1 实验的总体布局图 Fig.1 The overall layout of the experiment 1, 9循环冷却水浴箱; 2 SLD发生器; 3螺旋微调支架; 4低温环境; 5支架底座; 6高速相机; 7平行光源系统; 8撞击表面; 10~13水压调节系统; 14温度监控仪; 15 PC终端 |
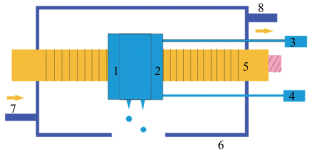
其中,SLD制备发生系统如图 2所示,过冷水是一种亚稳定的存在状态,大量过冷水难以以液体形式稳定存在。在SLD发生器内部腔体预先装有少量低温超纯水,腔体内部经过亲水处理,外界气泡不易混入,不会对后续SLD的发生造成干扰。腔体的进口管路连接水压调节系统,可在一定范围内稳定连续调节水压以控制SLD的发生速率。SLD发生器的出口为用于显微注射的毛细玻璃管,其尖端经超疏水处理,产生的过冷水滴不会粘滞在尖端出口,多个卫星液滴干扰实验结果的现象不会出现。SLD的制备过程需缓慢降温, 冷却液不断流入循环冷却水浴箱并通过PT1000温度传感器监控温度的变化。实验采用2个SLD发生器组合控制的方式实现双SLD的相继发生,并用标有刻度的微调支架实现双SLD不同的落点偏移量。
|
| 图 2 SLD制备发生系统 Fig.2 SLD preparation and generation system |
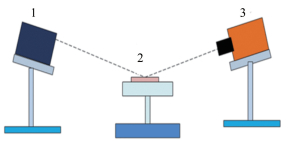
观测系统主要由双向平行LED光源、高速相机和温度测量系统构成,通过连接至高速相机的PC端可清晰观察到SLD撞击结冰过程。为尽量排除外界条件变化对SLD结冰过程的干扰,实验在密闭的温控箱中开展,温控箱内的环境温度保持恒定低温。
低温撞击平台主要由撞击实验表面和制冷芯片构成。撞击实验表面为100mm×100mm的经砂纸打磨的铝制表面。铝表面下面安装制冷芯片,通过PT1000温度传感器读取实验表面温度的相关数据。由于SLD撞壁结冰过程在短时间内放出大量热量,仅靠低温环境作为冷源难以保证撞击表面的恒定低温。对制冷芯片两极施加恒定电压以保证铝撞击表面恒定低温。图 3展示了这2个系统主要部件的示意图。
|
| 图 3 观测系统以及低温撞击实验平台 Fig.3 High-speed shooting system and test piece platform 1平行光源; 2撞击实验表面及制冷芯片; 3高速相机 |
SLD撞击结冰过程由多个因素共同决定。SLD的直径大小、撞击速度、撞击角度、壁面温度和过冷度等均会影响最终的结冰特征。实验旨在探讨双SLD间的干扰对结冰的影响,与其无关的因素,均取做常量:SLD的直径均为1050±50μm,SLD的撞击速度为2.2 m/s,SLD的温度和撞击壁面的温度均为-7℃。
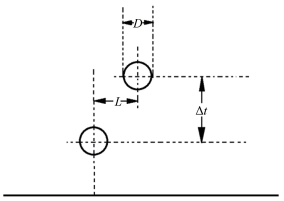
实验变量有2个:(1)双SLD落点间的相对偏移量L/D,其中L为落点位置的绝对偏移量,D代表单个SLD的直径, 对应空间上的干扰因素;(2)相继撞击壁面的时间间隔Δt,对应时间上的干扰因素,Δt反映第2滴SLD撞壁时不同的壁面换热条件,Δt越大,第1滴SLD的冻结过程进行得越彻底,壁面残余水量越少。图 4所示为双SLD相继撞击壁面的示意图。
|
| 图 4 双SLD相继撞击壁面实验示意图 Fig.4 Schematic diagram of two SLDs successively impacting on the surface |
Bathel[5]和Zhang[16]的碰撞实验中均揭示了:SLD在撞击壁面后均有一个短暂的铺展而后回缩结冰的过程,SLD最大铺展率(水滴在壁面最大铺展直径与水滴直径之比)与撞击速度、撞击粒径相关,大小介于3.2~5.5之间。Yang[12]和Zhang[16]的实验揭示了SLD冻结时间与过冷水温度和壁面温度等相关联,时间在几十微秒到数秒之间。SLD的结冰呈现一定的随机性,需在本实验条件下预先标定相关冻结参数。在本实验的所有无关变量固定的条件下,根据多次实验结果表明:SLD的铺展率介于2.7~3.0之间,完全结冰的时间约为0.7s左右(完全结冰时间的确定标准如下:(1)壁面上液滴不再流动,外形不再变化;(2)由于水和冰对光线的折射率不一样,图像中心部位的亮度不再变化)。
在本实验条件下,SLD的铺展率在2.7~3.0,当L/D>1.5时,双SLD间在壁面结冰过程中无直接接触。因此实验选取L/D的大小在0~1.5内变化,对于双SLD无直接接触的情况不予以研究。选取3组典型撞击时间间隔(Δt=0.3、0.6和0.9s)进行后续的相应实验研究。
实验采用控制变量法进行研究:固定双SLD相继撞壁的时间间隔,由小至大地改变双SLD落点位置的偏移量,记录结冰过程。改变相继撞击的时间间隔,重复上述过程。
实验中保证一个SLD发生器的发生速率稳定,调节另一个SLD发生器的供水压力使相继发生时间间隔为指定要求,待发生速率稳定后,开启水浴箱底部通道使双SLD液滴通过并相继撞击在壁面。用微调支架调节双SLD发生器的相对位置以改变双SLD落点的偏移量。
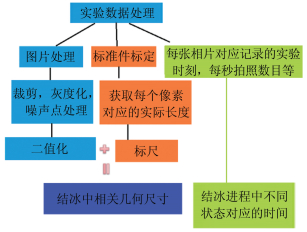
实验需对高速相机拍摄的原始图像信息进行处理,对原始数据的方法分以下2类:
一类是与结冰相关的几何尺寸,主要为撞击结冰过程中冻结形态的相关尺寸,处理流程如下:(1)在特定焦距下对已知尺寸的标准件进行标定,得到每个像素点对应的实际长度;(2)对结冰图片经进行剪裁、降噪处理后,经二值化处理获取结冰初始尺寸对应的像素点数目,与已标定尺寸对比后,得到包括最终铺展半径、冻结半径等相关几何尺寸的准确值。另一类原始数据与时间相关,为结冰进程中各状态所对应的时刻,可从高速相机的PC端窗口直接读取。数据的初步处理提取如图 5所示。
|
| 图 5 原始数据处理提取流程 Fig.5 Flow chart of initial data processing |
图 6为双SLD相继撞壁结冰的典型过程:实验工况为L/D=1.1, Δt=0.9s。第1滴SLD撞击后如常地回缩结冰,结冰过程由底部向顶部,由四周向中心推进。第2滴SLD最大铺展直径dmax2略有增加,如图 6中t=0.908s的图片所示。经标定两者相差不超过5%,可认为dmax1≈dmax2。第2滴SLD滴落在积冰部分液滴的回缩现象受到明显抑制,如t=1.35s的图片所示,dfinal2明显大于dfinal1。

|
| 图 6 双SLD相继撞击壁面结冰过程图 Fig.6 The freezing process diagram of two SLDs impacting on the substrate |
已开展的SLD撞击结冰实验通中常采用结冰回缩率β衡量结冰形态的不同[5]。
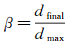 (1)
(1)
式中:dmax代表最大铺展直径;dfinal代表SLD最终冻结直径,如图 6中t=0.6s的照片所示。
该典型实验工况下,第2滴SLD的结冰回缩率β2(0.86)大于第1滴SLD的结冰回缩率β1 (0.81)。第2滴SLD完全冻结时间明显变长,以工况为L/D=10, Δt=0.9s实验作对比实验,双SLD完全结冰时间是对比实验的1.15倍。
3 结果与讨论 3.1 SLD间的干扰对结冰形态的影响及分析SLD的撞壁铺展耗时极短(约为3ms),而后的回缩过程是主要的换热相变过程。SLD最终的结冰形态是由这一过程中的热力学、动力学行为共同决定的,结冰回缩率的大小可直观反映这一变化。本实验条件下,单个SLD撞击结冰回缩率介于0.76~0.82之间。定义回缩率之比ε来衡量SLD间的干扰对结冰形态的影响,表达式如下:
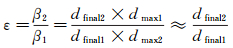 (2)
(2)
式中:dfinal1为第1滴SLD最终成冰直径;dfinal2为第2滴SLD最终成冰直径。
ε>1代表SLD间的干扰抑制回缩的进行。如图 7所示的4种不同实验工况:黄线标注的长度代表dfinal1,红线标注的长度代表dfinal2。dfinal2均明显大于dfinal1,ε普遍大于1。这表明不同的实验工况下SLD的回缩过程均受到抑制,但抑制效应的强弱有所不同。

|
| 图 7 不同实验工况对比图:(a)单SLD撞击结冰(b)、(d) L/D为0, Δt分别为0.6s和0.9s. (c)和(e) L/D分别为0.5和1.2, Δt为0.6s Fig.7 Contrast images of different experimental conditions: (a) a single SLD impacts and freezes; (b), (d) L/D=0, Δt=0.6s, 0.9s; (c), (e) L/D=0.5, 1.2, Δt= 0.6s |
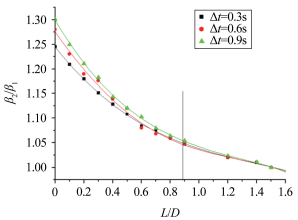
计算不同实验工况点的回缩率之比ε,绘制不同的撞击时间间隔下,不同偏移下的ε曲线如图 8所示。
|
| 图 8 SLD间的干扰和回缩率之比的关系 Fig.8 Relationships between interactions and the ratio of the shrinking rate |
为分析抑制回缩效应变化趋势,定义回缩抑制效应的衰减率η1为:
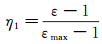 (3)
(3)
式中:εmax代表每一条ε曲线在不同偏移下的最大值。不同撞击时间间隔Δt下,ε的最大值εmax均在L/D=0时达到。
图 8表明,抑制回缩效应在L/D=0处最强,双SLD的落点重合,彼此受到干扰的面积最大,空间上的相互干扰最强烈,抑制效应随L/D的增加而迅速减少。当L/D>0.9时,抑制回缩效应已衰减80%以上,η1 < 0.2。回缩抑制效应随L/D增加而继续下降的空间相当有限,抑制效应减弱的速度也大大降低,空间上的干扰对结冰形态的影响趋于稳定(见图 8中所标直线右侧区域)。当L/D>1.5,ε趋近于1,这表明SLD间的干扰对撞击结冰形态的影响消失。图 8中不同Δt下的3条实验曲线在坐标轴内十分接近:当L/D相同时,ε随Δt的增大略有增大,但变化很小。这表明时间上的相互干扰对回缩抑制效应的影响有限。空间上的相互干扰是抑制回缩行为的主要因素,并影响最终的结冰形态。
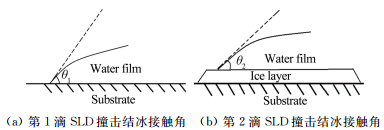
SLD的回缩受到抑制是由于当第2滴SLD撞击发生时撞击表面的性质已改变:第1滴SLD形成的冰层是一个亲水性的基底,已有实验证明[17-18],亲水性基底会使得导致固液界面的接触角变小,如图 9所示,θ2 < θ1,回缩行为受到抑制;第2滴SLD在壁面以更大的面积结冰。
|
| 图 9 接触角变化图 Fig.9 The change of contact angle |
第2滴SLD的撞击会打乱第1滴SLD的结冰进程,并与壁面上尚未结冰的水融合后继续结冰。Δt越小,当后续撞击发生时,壁面残余水量越大,融合后回缩受到的表面张力越大,回缩效应有所增强。但由于SLD结冰迅速,固液接触面的冰层在很短的时间内已形成,抑制回缩条件已经满足,ε的大小与Δt的联系并不紧密。
3.2 SLD间的干扰对结冰速度的影响及分析实验中常用SLD撞击结冰时间量化结冰速度,Zhang的实验[16]研究发现了单个粒径尺度下,SLD的过冷扩散率与冻结时间呈现反比的关系,Yang的实验[12]也用结冰时间定义瞬态结冰和非瞬态结冰这2种SLD撞击结冰模式。
不同实验工况下,双SLD的结冰速度呈现较大差异。以图 10中2个典型的实验工况为例,工况(a)和工况(b)的Δt分别为0.9和0.6s,L/D均为0, 以第1滴SLD撞壁时刻作为记时起点,经过2.1s后,工况(a)尚未完成结冰, 工况(b)已经完成结冰。

|
| 图 10 不同实验工况下完全冻结时间对比图 Fig.10 Contrast images of complete freezing time under different experimental conditions |
通过对比发现,仅比较双SLD完全冻结时间的长短,忽略相继撞击时间间隔的不同,难以准确反映结冰速度的变化。引入结冰时间变化率τ衡量SLD间的相互干扰对结冰速度的影响。
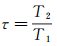 (4)
(4)
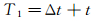 (5)
(5)
式中:T1为相距很远的双SLD相继撞击壁面的完全结冰时间,Δt为相继撞击的时间间隔,t为单SLD平均完全冻结时间。T2为实验中得到的双SLD完全结冰时间。
提取计算不同实验工况点的结冰时间变化率τ,绘制不同的撞击时间间隔下,不同偏移下的τ曲线如图 11所示。
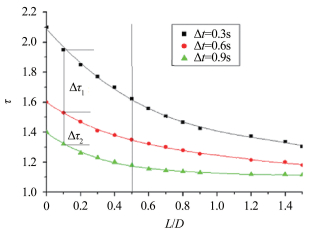
|
| 图 11 结冰时间变化率与双SLD间的干扰的关系 Fig.11 Relationship between the rate of freezing time and interactions |
同理采用η2量化反映结冰速率变化趋势:
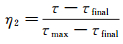 (6)
(6)
式中:τmax和τfinal分别代表每一条实验曲线的结冰时间变化率τ的最大值和最终稳定值。
图 11表明,双SLD间的干扰会降低结冰速度,延长双SLD完全结冰时间,使τ>1。在小偏移的情况下(L/D < 0.5),L/D的变化对结冰速度的影响很大,结冰速度随L/D的增大而不断加快,τ的值迅速减小。当L/D>0.5,结冰速度大幅上升,η2 < 0.2,结冰时间变化率τ随L/D增加继续变化的空间相当有限(见图 11所标注的直线右边区域),L/D的变化对结冰速度影响逐渐减弱并趋于稳定。
当相继撞击时间间隔Δt不同,结冰速率也大不相同。如图 11标注,Δτ是在相同偏移下,不同时间间隔下τ的差值。Δτ随L/D的变化如图 12所示。
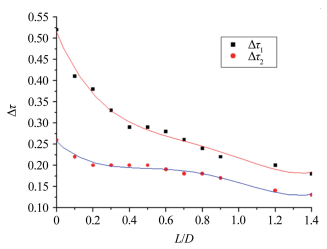
|
| 图 12 Δτ随L/D变化图 Fig.12 Relationship between Δτ and L/D |
图 11中3条不同结冰时间变化率的实验曲线随L/D变化的趋势相同,但相差较大。如图 12所示,当L/D增大时,空间上的干扰对结冰的影响逐渐减小,相继撞击的时间间隔不同对结冰速度的影响更加明显:Δτ虽有所减小,但仍保持在较大数值,这表明相继的撞击会稳定地延长双SLD的整体结冰时间。相继撞击时间间隔越短,SLD之间的相对偏移越小,双SLD撞击结冰速度越慢,结冰时间延长程度越大。
结冰时间的延长主要是由于壁面积冰的存在,固液接触界面处的换热强度被削弱。L/D越大,空间上的相互干扰越小,整个冻结过程进行的越快。Δt越大,当第2滴SLD撞击壁面时,壁面上未结冰的液体越少,壁面积冰量越大,由于冰的导热率大于水的导热率,第2滴SLD结冰时换热增强,结冰时间变短,τ随之变小。
3.3 SLD间的干扰对撞击结冰影响的综合分析SLD间的干扰(包括空间、时间上的干扰)对结冰形态和结冰速度的影响已在3.1和3.2小节详细叙述,本小节将干扰因素对结冰的影响范围进行简单的划分,以求直观地反映出在不同范围内,相继撞击的干扰对SLD结冰过程的不同影响。图 13列出本实验所有工况点,横轴和纵轴分别代表双SLD间落点偏移大小L/D和相继撞击时间间隔Δt。
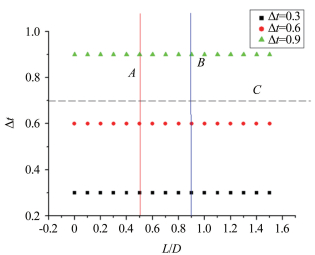
|
| 图 13 实验工况点及区域划分 Fig.13 The experimental working condition and region divisions |
直线A、B分别为结冰时间变化率τ、结冰回缩率之比ε在不同撞击时间间隔下随L/D变化区域的分界线;虚线C为当第2滴SLD撞击壁面时,第1滴SLD是否完全冻结的分界线。
直线A左侧区域内,L/D < 0.5,τ随L/D的增大而迅速减小,结冰速度迅速加快;直线A右侧区域内,L/D>0.5,τ随L/D的增大减小的速度明显减小。L/D的增大对结冰速率的减缓作用趋于稳定并逐渐消失。在L/D由小变大整个过程中,时间上的干扰对结冰速率的延缓效应稳定存在,不可忽略。
直线B左侧区域内,L/D < 0.9, 结冰回缩率之比ε随L/D的增大而迅速减小,B右侧区域内,ε随L/D的增加而减小的速度显著减小。时间上的干扰对于抑制回缩的影响不大,空间上的相互干扰是影响结冰形态的主因。
虚线C与纵轴的交点对应单个SLD的平均完全冻结时间。在C下方区域内,Δt < 0.7s时,第2滴SLD撞壁时第1滴SLD尚未完全冻结,彼此融合后继续结冰。C上方区域内,Δt>0.7s时,第2滴SLD撞击在完全冻结的冰层并完成结冰过程。实验证明,撞击时壁面性质的不同会影响SLD的冻结速度,Δt越小,SLD结冰时间变化率τ越大,结冰速度有所减慢。
4 结论本文设计双SLD相继撞击低温铝金属表面结冰实验。实验表明:双SLD间的干扰会阻碍第2滴SLD撞壁后的回缩过程进而影响结冰形态,降低结冰速度,延长双SLD结冰时间,具体影响如下:
(1) 空间上的干扰对结冰速度和结冰形态均有影响:对回缩行为的抑制效应和对结冰速率的减缓效应随着L/D的增大急剧减小,并趋于稳定逐步消失。
(2) 时间上的干扰对结冰形态的影响不大,但对结冰速率有着明显且稳定的延迟作用,结冰速率随相继撞击时间间隔的增大而加快。
本实验没有细致考虑双SLD受到彼此干扰后各点冻结顺序的变化,这也是下一步实验开展的方向。
| [1] | Chandra S, Avedisian C T. The collision of a droplet with a solid surface[J]. Proceedings Mathematical & Physical Sciences, 1991, 432(1884): 13–41. |
| [2] | Bennett T, Poulikakos D. Splat-quench solidification:estimating the maximum spreading of a droplet impacting a solid surface[J]. Journal of Materials Science, 1993, 28(4): 963–970. DOI:10.1007/BF00400880 |
| [3] | Mundo C, Sommerfeld M, Tropea C. Droplet-wall collisions:experimental studies of the deformation and breakup process[J]. International Journal of Multiphase Flow, 1995, 21(2): 151–173. DOI:10.1016/0301-9322(94)00069-V |
| [4] | Quero M, Hammond D W, Purvis R. Analysis of supercooled water droplet impact on a thin water layer and ice growth[C]. 44th AIAA Aerospace Sciences Meeting and Exhibit, 2006. https://ueaeprints.uea.ac.uk/view/divisions/MTH.default.html |
| [5] | Bathel B F, Stephen N, Johnson L. Prediction of post contact parameters of fluid droplet impact on a smooth surface[J]. AIAA Journal, 2015, 45(7): 1725–1733. |
| [6] | 王桥, 肖京平, 刘森云. 过冷大水滴变形及阻力特性的温度影响实验研究[J]. 实验流体力学, 2016, 30(3): 21–26. Wang Q, Xiao J P, Liu S Y. Experimental study on temperature effect on deformation and drag characteristics of supercooled large droplet[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(3): 21–26. |
| [7] | 桑为民, 贾韫泽, 鲁天. 水滴撞击飞溅效应对过冷大水滴结冰影响研究[J]. 西北工业大学学报, 2016, 34(5): 739–746. Sang W M, Jia Y Z, Lu T. Numerical analysis of splashing for freezing effects at supercooled large droplet impingement[J]. Journal of Northwestern Polytechnical University, 2016, 34(5): 739–746. |
| [8] | 闵现花. 结冰条件下过冷水滴撞击特性及热平衡分析[D]. 上海: 上海交通大学, 2010. Min X H. Supercooled water droplet impingement property and thermal balance analysis under the condition of icing[D]. Shanghai: Shanghai Jiao Tong University, 2010. |
| [9] | Jung S, Tiwari M K, Doan N V. Mechanism of supercooled droplet freezing on surfaces[J]. Nature Communications, 2012, 3: 615. DOI:10.1038/ncomms1630 |
| [10] | 李海星. SLD碰撞结冰机理实验研究[D]. 上海: 上海交通大学, 2013. Li H X. Experimental study of the mechanism of SLD's impacting-icing[D]. Shanghai: Shanghai Jiao Tong University, 2013. |
| [11] | Potapczuk M G. Aircraft icing research at NASA Glenn research center[J]. Journal of Aerospace Engineering, 2013, 26(2): 260–276. DOI:10.1061/(ASCE)AS.1943-5525.0000322 |
| [12] | 杨国敏, 郭开华, 李宁. 过冷水滴碰撞导线表面结冰机理的实验研究[J]. 制冷学报, 2011, 32(5): 37–41. Yang G M, Guo K H, Li N. Freezing mechanism of supercooled water droplet impacting on metal surfaces[J]. International Journal of Refrigeration, 2011, 32(5): 37–41. |
| [13] | Federal Aviation Administration. Airplane and engine certification requirements in supercooled large drop, mixed phase and ice crystal icing condition, final rule[M]. Department of Transportation, November 4th, 2014. |
| [14] | Ghafouri-Azar R, Shakeri S, Chandra S. Interactions between molten metal droplets impinging on a solid surface[J]. International Journal of Heat & Mass Transfer, 2003, 46(8): 1395–1407. |
| [15] | Fujimoto H, Tong A Y, Takuda H. Interaction phenomena of two water droplets successively impacting onto a solid surface[J]. International Journal of Thermal Sciences, 2008, 47(3): 229–236. DOI:10.1016/j.ijthermalsci.2007.02.006 |
| [16] | Zhang C, Liu H. Effect of drop size on the impact thermodynamics for supercooled large droplet in aircraft icing[J]. Physics of Fluids, 2016, 28(6): 260–283. |
| [17] | Jin Z, Zhang H, Yang Z. Experimental investigation of the impact and freezing processes of a water droplet on an ice surface[J]. International Journal of Heat & Mass Transfer, 2017, 109: 716–724. |
| [18] | 王静, 孔维梁, 王福新. 表面能对过冷水中冰生长的影响[J]. 上海交通大学学报, 2016, 50(4): 588–594. Wang J, Kong W L, Wang F X. Experimental study of surface energy on growth of icing in supercooled water[J]. Journal of Shanghai Jiao Tong University, 2016, 50(4): 588–594. |



