2. 高速高雷诺数气动力航空科技重点实验室, 沈阳 110034
2. Aeronautic Science and Technology Key Lab for High Speed and High Reynolds Number Aerodynamic Research, Shenyang 110034, China
推力矢量技术是指推进系统除为飞机提供前进推进外,尚能同时或单独地在飞机俯仰、偏航、滚转、反推力和前进推力轴线上提供发动机内部推进力,用以取代常规飞机舵面或其他装置产生的外部气动力来进行飞机控制。采用推力矢量技术的飞机,能够通过喷管偏转,利用发动机产生的推力,获得多余的控制力矩,实现飞机的姿态控制。其突出特点是控制力矩与发动机紧密相关,而不受飞机本身姿态的影响。因此,飞机在作低速、大迎角机动飞行而操纵舵面几乎失效时,可以利用矢量推力提供的额外操纵力矩来控制飞机机动[2]。
推力矢量技术的运用提高了飞机的控制效率,使飞机的气动控制面,例如垂尾和平尾可以大大缩小,从而飞机的重量可以减轻。另外,垂尾和平尾形成的反射面也因此缩小,飞机的隐身性能也得到了改善[3]。
矢量喷管对于推力矢量技术的实现至关重要。美国的F22和F35采用了机械偏转式的矢量喷管,但由于需要作动系统驱动,因此质量和复杂性大大提高。从20世纪90年代开始,推力矢量喷管的研究重心从机械式矢量喷管向射流控制矢量喷管转移[4]。美国的IHPTET计划、FLINT计划以及美国空军的IFC计划均大量开展了射流控制矢量喷管技术的研究。几何形状固定的射流控制矢量喷管,相比于传统的机械式矢量喷管,其结构更简单,质量更少,成本更低,可靠性更高。射流控制矢量喷管可以使质量减少24%~80%,发动机推质比提高7%~12%,成本维护费用降低37%~53%[5-8]。
而随着涡轮基组合循环发动机(TBCC)和超燃冲压发动机等高速喷气推进系统研究领域的兴起,许多航空大国都对单边膨胀喷管(SERN)进行了大量的试验和数值模拟研究[9]。
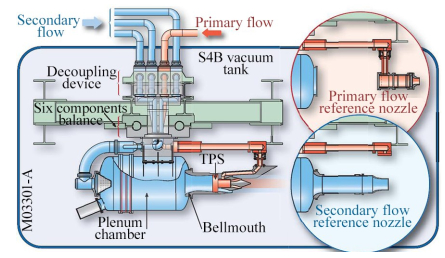
随着喷管技术的发展,喷管流场和性能试验测量技术也在不断发展和提高,并为此建造了许多试验平台。具有代表性的是法国ONERA的S4B推力测量平台,其中4″平台最大轴向推力为3300N,9″平台最大轴向推力为5000N,流量系数测量精度±0.1%,推力系数测量精度±0.15%,平台结构如图 1所示[10]:
|
| 图 1 S4B平台结构示意图 Fig.1 Sketch map of S4B test bench's construction |
其他类似的试验设备还包括英国ARA的MST推力测量平台、德国DLR的静推力平台、荷兰NLR的发动机模型校准设备ECF等[11]。国内一些高等院校和研究机构针对矢量喷管静推力精确测量试验,开展了大量的研究工作,但总体试验技术水平远未有国外成熟,大多数处于起步阶段,或刚刚具备承接型号试验的能力。其中中国航空工业空气动力研究院于“十二五”期间,以S4B为原型,新建了推力测量平台,并已完成调试,达到工程应用水平。
本文详细介绍在推力测量平台上进行矢量喷管静推力精确测量的试验技术,重点研究流量修正、模型安装姿态修正以及空气桥对于天平系统影响量的修正问题。
1 试验相似参数及原理 1.1 试验相似参数一般来说,对于喷管性能试验有4个相似参数:
(1) 模型与飞行器喷流落压比相等:
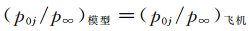 (1)
(1)
(2) 模型与飞行器喷管出口马赫数相等:
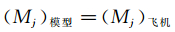 (2)
(2)
(3) 喷流介质比热比相等:
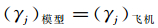 (3)
(3)
(4) 喷流气体常数与温度乘积相等:
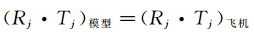 (4)
(4)
但在具体试验过程中,同时模拟4个参数十分困难,只能依据所研究问题的性质,选择主要参数保持相似。有资料表明,利用冷空气作为模型喷流介质,所导致的模型与飞行器涡轮喷气发动机的γ和RT的差别,对喷流特性的影响尚不严重[12],国外也常采用冷喷流进行喷管以及涡轮动力模拟器(TPS)的静推力测量试验。本文的矢量喷管性能试验采用冷喷流,完全模拟相似参数(1)、(2),而忽略相似参数(3)和相似参数(4)的影响。
1.2 试验原理喷管性能试验模型内部必须引入高压气体,为了实现较高的喷流落压比,试验需要在真空背压环境中进行,从而大幅降低喷流总压、喷流流量以及喷管载荷等参数;另外,必须借助于高精度的天平测量系统实现喷管载荷的精确测量。
在实际的试验过程中,喷管模型同时与高压供气管路以及天平测量系统相连接,这就使得高压供气管路和天平测量系统形成了结构上的并联关系,喷管产生的推力会同时传到天平和高压供气管路上,因此必须在高压供气管路中设置一个软性连接。该软性连接刚度相对于天平刚度极小,受到力后,产生相对较大变形,从而使得天平测量到绝大部分气动力;而软性连接传导的喷管模型的气动力极小,而且这种影响量是可以通过技术手段精确检测出来并具有较高的重复性精度,即空气桥系统,以消除高压供气管路对天平测量系统产生的大部分干扰量。因此,试验必须在专用设备上进行,例如S4B等推力测量平台设备。
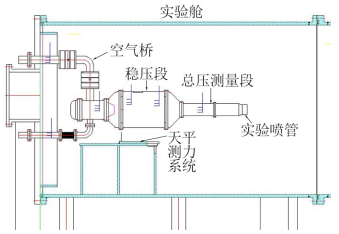
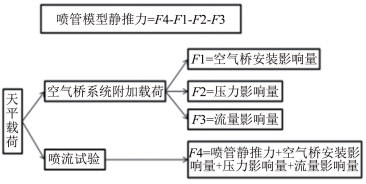
喷管模型采用垂直于轴线方向两侧进气方式,可以保证被测量系统入口冲量在X方向以及Y方向为0,在Z方向相互抵消(见图 2),从而使得天平测量的结果仅仅包括喷管静推力、空气桥系统对天平的附加力和力矩,而不需要进行入口冲量修正,在一定程度上减少了二次修正量,提高了测力数据的精准度,实验原理如图 3所示。
|
| 图 2 喷管性能试验结构示意图 Fig.2 Construction of nozzle characteristics testing |
|
| 图 3 喷管性能试验原理图 Fig.3 Principle of nozzle characteristics testing |
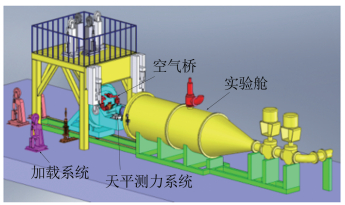
中国航空工业空气动力研究院的推力测量平台以ONERA的S4B为原型,由高压供气管路系统、基于橡胶膜片的空气桥系统、稳压段、六分量天平测量系统、真空试验舱以及配套的压力测量系统组成,总体结构如图 4所示。
|
| 图 4 推力测量平台总体结构 Fig.4 Construction of thrust testing bench |
推力测量平台六分量天平测量系统轴向载荷能力分为0~2500N和2500~5000N 2档,经过校准,各元测力精准度均满足国军标要求;高压供气管路系统流量控制精度为1g/s,最大质量流量10kg/s;稳压段最高承压2.5MPa,喷管模型喉道直径最大可达100mm;真空试验舱最低真空度10kPa(绝压),最大喷流落压比80,可以满足设计马赫数3.0、最大喷流落压比80左右矢量喷管性能试验的需求。

|
| 图 5 推力测量平台实物照片 Fig.5 Photograph of thrust testing bench |
由于喷管性能试验数据处理的需要,流经喷管模型的质量流量必须精确测量。为此,引进了一套临界流文氏管系统来对高压供气管路系统中的流量计进行进一步的校准。美国阿诺德工程发展中心(AEDC)的16T风洞、NASA兰利研究中心的NTF风洞、德荷风洞联合体(DNW)的TPS校准平台、英国飞机研究协会有限公司(ARA)的MST1平台和法宇航(ONERA)的TPS校准平台等诸多世界先进风洞和设备,均采用临界流文氏管,作为高精度流量测量的手段。经校准,临界流文氏管的流量精度可达0.15%[13]。

|
| 图 6 临界流文氏管在平台内的安装照片 Fig.6 Photograph of critical Venturi nozzle installed in thrust testing bench |
在推力测量平台上,进行矢量喷管静推力测量试验研究,研究内容包括:流量计的精确校准实验、模型姿态精确测量、空气桥-天平系统校准试验以及喷流测力试验。
3.1 流量计的精确校准实验将临界流文氏管安装在推力测量平台稳压段之后,与高压供气管路系统中的CLJ槽道流量计形成串联关系,在大气压环境中,利用高精度数字阀控制流入临界流文氏管气流的总压参数。稳定之后,同时记录气流的总压、温度、落压比和流量计输出的流量值等参数。
临界流文氏管流量的工程计算公式为:
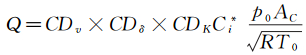 (5)
(5)
式中:Q为质量流量;CDv为真实气体影响系数;CDδ为粘性影响系数;CDK为音速面弯曲效应影响系数;Ci*为理想气体临界流动系数;p0为临界流文氏管喉道处的气流总压;AC为临界流文氏管的喉道面积。
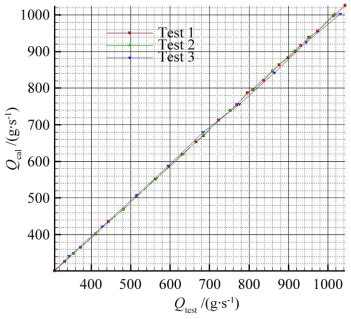
由此计算得到临界流文氏管的理论质量流量值,以CLJ槽道流量计输出的质量流量为横坐标,以理论质量流量为纵坐标,可以得到流量计的修正结果以及重复性如图 7所示。
|
| 图 7 CLJ流量计修正曲线及重复性数据 Fig.7 Repetition and modified curve of CLJ flow meter |
由图可见,重复性相对误差在0.2%以内,且修正曲线几为线性,流量修正量在2%左右。经过校准之后的质量流量值可以用于试验。
3.2 模型姿态精确测量在推力测量平台上,外式六分量天平系统、加载系统等设备已经经过了定位,能确保其位于同一个平面(理想情况是一个水平面),即校准中心所处的平面。但在进行流量影响校准试验以及喷管静推力试验时,由于加工、安装等各种不可控误差,有可能导致喷管的中心平面与天平校心平面不重合,即喷管的坐标系和推力测量平台天平的坐标系存在一个位移和夹角偏差,在一定程度上影响数据的修正以及测量,需要在测力试验前进行模型安装姿态的精确测量,得到模型与天平系统之间的相对位置偏差。
本文在进行流量影响校准试验以及喷管静推力试验时,均采用测量精度为10μm的RADIAN-80型激光跟踪仪对模型与天平系统之间的相对位置偏差进行了精确测量,得到了其相对于天平系统的偏差结果,如表 1所示。
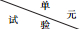 |
Y/mm | Z/mm | α/(°) | β/(°) | γ/(°) |
| 流量校准试验 | 0 | 0 | 0.12 | 0.16 | 0.19 |
| 喷管静推力试验 | 0 | 0 | 0.12 | 0.17 | 0.19 |
天平测力结果得到之后,需要根据上述的相对位置偏差结果,对天平力进行坐标系偏差修正,换算到喷管模型坐标系下,得到模型实际的六元气动力。
3.3 空气桥-天平系统校准试验空气桥-天平校准试验分5步进行:(1)光天平的静态校准;(2)带空气桥天平系统的静态校准;(3) 2次校准天平主系数差异分析;(4)空气桥的压力影响校准;(5)空气桥的流量影响校准。
表 2为光天平及带空气桥天平系统的校准结果,本文仅分析了纵向三元(如无特殊标注,本文力矩参考点均相对于推力测量平台外式天平的校心),可以看出光天平及带空气桥天平的纵向三元精准度均满足国军标合格指标,部分接近先进指标。
 |
Y | MZ | X | |
| 设计载荷加载 载荷/(N, N·m) |
1250 875 |
1750 1400 |
2500 1750 |
|
| 综合加载 重复性误差/% |
合格指标 | 0.20 | 0.20 | 0.30 |
| 先进指标 | 0.06 | 0.06 | 0.10 | |
| 光天平 | 0.03 | 0.01 | 0.03 | |
| 空气桥天平 | 0.027 | 0.01 | 0.032 | |
| 综合加载 准度误差/% |
合格指标 | 0.40 | 0.40 | 0.50 |
| 先进指标 | 0.10 | 0.10 | 0.20 | |
| 光天平 | 0.35 | 0.10 | 0.20 | |
| 空气桥天平 | 0.39 | 0.21 | 0.16 | |
一般情况下光天平和带空气桥天平系统的公式存在一定的差异,差异越小,则空气桥对天平的静态影响越小,性能优异的空气桥2次校准主系数的相对差异约为0.1%~0.5%[14-15](见表 3),本文2次校准纵向三元主系数相对差异最大值为0.94%,与国外先进水平相比,有一定的差距,但也在可接受的范围内,后续的测力试验都将采用带空气桥天平系统的静校公式。
 |
Y | MZ | X |
| 光天平 | 10.199 | 1.477 | 10.254 |
| 带空气桥天平 | 10.217 | 1.491 | 10.303 |
| 绝对差异 | -0.018 | -0.014 | -0.049 |
| 相对差异/% | -0.18 | -0.94 | -0.48 |
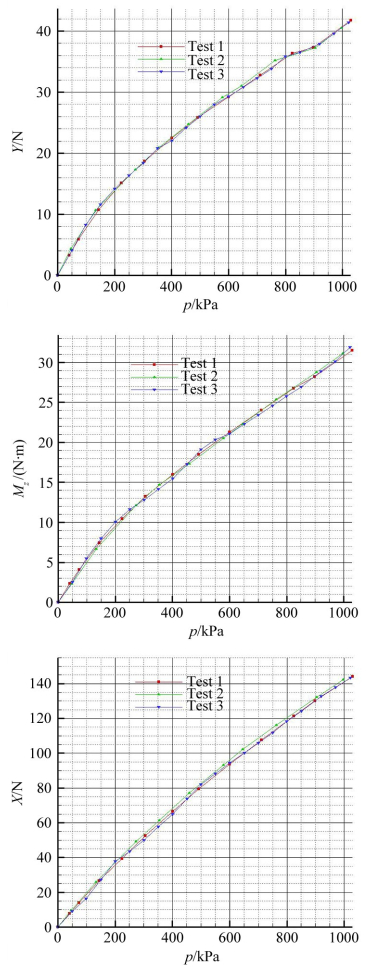
由于空气桥的膜片同时连接了天平的固定端和测量端,空气桥内部气流压力会对天平产生一个随压力变化的附加载荷,该载荷可以通过气体无流动状态的充压试验,找出零点随压力的变化规律,消除附加载荷的影响。本文在不同时间进行了3次充压试验,得到了天平纵向三元的压力影响修正曲线及重复性,如图 8所示。
|
| 图 8 无流动状态下纵向三元的压力修正曲线 Fig.8 Modified curve of pressure affection of bellows system |
可以看到,压力影响重复性良好,相对误差在0.2%以内。空气桥系统对天平的压力影响规律较为明显,本文采用二次函数F=f(p)拟合后,其拟合优度可决系数R2均大于0.99。
为检验压力影响修正的合理性,对不同压力下的空气桥-天平测量系统施加若干组不同载荷,以压力修正后的测力计算值与加载砝码真实载荷相比较,其准度结果均在0.5%以内。
最后安装临界流文氏管,进行空气桥的流量影响校准试验,同时采集流量计流量、喷管落压比、空气桥内外压差和天平力等参数。以未充气时天平的输出为初读数,利用空气桥内外压差,进行空气桥压力影响修正,可得到压力影响修正后的值。
以临界流文氏管的推力值为真值,与压力修正值的差即为流量影响修正值。
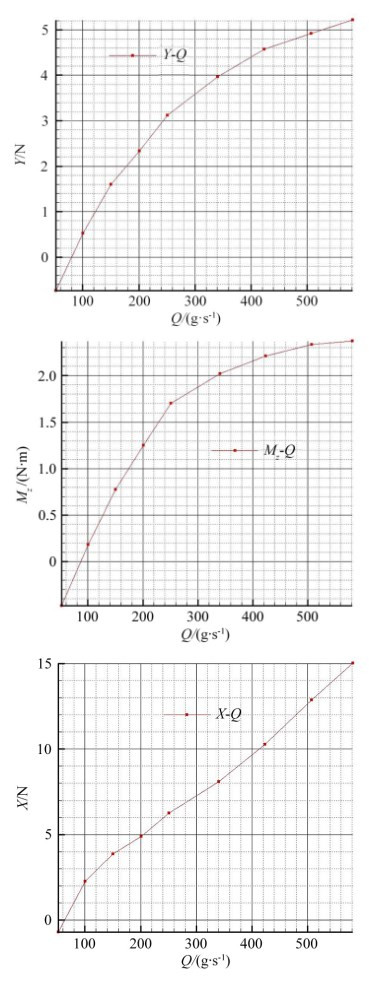
改变流量,可得到不同流量(流量已经过修正)下空气桥的修正量,即随流量变化的修正量曲线。本文在验证重复性相对误差满足0.2%的基础上,最终得到的空气桥的流量影响修正曲线如图 9所示。
|
| 图 9 流动状态下纵向三元的流量影响修正曲线 Fig.9 Modified curve of mass-flow affection of bellows system |
空气桥系统对天平的流量影响规律较为明显,本文采用三次函数F=f(p)拟合后,其拟合优度可决系数R2均大于0.99。流量影响量值较压力影响小了很多,大约只有压力影响修正数据的10%左右,可见,对于本套空气桥-天平系统来说,压力影响起决定性的作用。
4 数据处理过程本文采用某型单边膨胀矢量喷管,在设计喷流落压比附近进行喷管静推力测量试验。利用高精度气动数字阀精确控制喷管入口总压值(本文喷管入口总压控制精度在±300Pa左右),利用真空试验舱控制系统精确控制试验舱真空压力(本文真空舱压控制精度在±50Pa左右),并同时记录试验过程中稳定的喷管入口总压、气流温度、空气桥橡胶膜片内外侧静压值、流量计输出的流量和真空试验舱静压值等。
首先进行流量计输出流量的修正,得到喷管模型准确的流量值,并利用公式(6)得到喷管的等熵推力值。然后进行天平测量数据的模型姿态修正,得到的结果再进行压力影响修正和流量影响修正,就可以得到喷管模型的静推力。利用公式(7)、(8)和(9),计算得到喷管模型的轴向推力系数、法向推力系数以及矢量角等参数。
喷管等熵推力的计算。计算公式为:
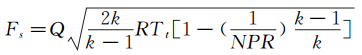 (6)
(6)
喷管轴向推力系数:
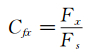 (7)
(7)
喷管法向推力系数:
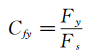 (8)
(8)
矢量角:
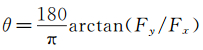 (9)
(9)
式中:Fs为喷管的等熵推力,单位为N;Q为经过校准之后的质量流量,单位为kg/s;Tt为气流温度,单位为K;NPR为喷管喷流落压比;Fx为喷管轴向静推力,Fy为喷管法向静推力,单位为N。
5 试验结果 5.1 重复性试验结果试验数据重复性精度是考察数据可靠性的重要依据,因此选定一部分状态,进行了7次重复性验证试验。其中落压比状态25的重复性试验结果如表 4所示。
| 车次 | NPR | Cfx | Cfy | θ/(°) |
| 1 | 25.26 | 0.9493 | -0.1886 | -11.23 |
| 2 | 25.32 | 0.9502 | -0.1880 | -11.19 |
| 3 | 25.30 | 0.9498 | -0.1886 | -11.23 |
| 4 | 25.27 | 0.9492 | -0.1884 | -11.23 |
| 5 | 25.29 | 0.9497 | -0.1884 | -11.22 |
| 6 | 25.30 | 0.9500 | -0.1888 | -11.24 |
| 7 | 25.28 | 0.9494 | -0.1882 | -11.21 |
| aver | 25.29 | 0.9497 | -0.1884 | -11.22 |
| σ | 0.0188 | 0.0003 | 0.0002 | 0.0154 |
可以看到,本次重复性试验喷流落压比标准差为0.0188,轴向推力系数标准差为0.0003,法向推力系数标准差为0.0002,矢量角标准差为0.0154。对照常规测力,可以看到推力系数的重复性结果达到国军标要求,证明本文试验数据具有较高的可靠性,试验技术可以用于喷管静推力的精确测量。
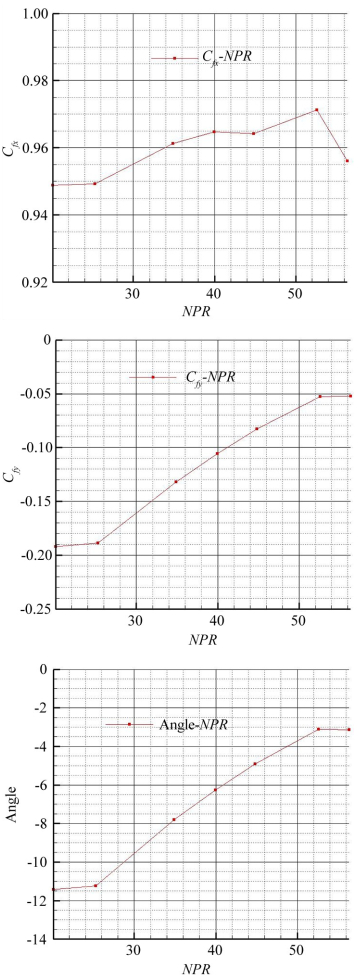
5.2 随喷流落压比的变化规律进行了不同喷流落压比条件下的矢量喷管性能试验,喷流落压比状态分别为20.09、25.26、34.91、39.97、44.81、52.60和56.36,试验结果如图 10所示。
|
| 图 10 推力系数随落压比的变化规律 Fig.10 Thrust coefficients from the change of NPR |
可以看出,本矢量喷管各参数随着喷流落压比的变化规律与文献[9]叙述一致。在低落压比状态,由于矢量喷管内部出现了自由激波、分离激波、2种激波相交及相互影响、自由激波分离和诱导激波分离等复杂现象,上膨胀面大面积的气流分离而形成的低压区使喷管轴向推力系数相对较小; 随着落压比的增大,呈现出快速增大的趋势,在设计落压比附近达到最大值0.972;继续增大喷流落压比,由于膨胀不足,轴向推力系数反而有一定程度的下降;而由于该矢量喷管具有向上的偏度,法向推力系数和矢量角在各落压比条件下均为负值,产生负向升力。和轴向推力系数变化规律一致,随着落压比的增加,法向推力系数逐渐增大,在设计落压比附近法向推力系数达到最大,之后继续增大喷流落压比,法向推力系数和矢量角均有所减小。
6 结论本文模拟喷管模型的喷流落压比和出口马赫数参数,在推力测量平台上进行某型矢量喷管静推力试验,采取了保证模型入口冲量为零、流量计校准、模型姿态精确测量和空气桥-天平测量系统精确校准等提高数据精准度的方法,最终获得了可靠的试验数据以及正确的轴向推力系数、法向推力系数以及矢量角随落压比的变化规律,该试验技术具有以下特点:
(1) 推力测量平台采用垂直于轴线方向两侧进气方式,不需要修正入口冲量,减少了二次修正量,可以提高测力试验数据的精准度;
(2) 试验过程中利用临界流文氏管对流量进行校准,采用激光跟踪仪对模型状态进行精确测量,进一步提高了测力试验数据的精准度;
(3) 推力测量平台的空气桥-天平系统性能优异,能准确得到试验过程中高压供气系统对天平的影响量,且规律明显,修正曲线便于数据拟合;
(4) 试验数据表明,试验结果重复性良好,规律正确,该试验技术达到工程应用水平,可以用于型号试验。
| [1] | 王如根, 高坤华. 航空发动机新技术[M]. 北京: 航空工业出版社, 2003. Wang R G, Gao K H. The new technology of aero engine[M]. Beijing: Aviation Industry Press, 2003. |
| [2] | Steven A. Thrust vectoring:a new angle to air superiority[J]. Mechanical Engineering, 1995: 58–64. |
| [3] | Thomas M B, Norbert C B. Thrust vector behaviorof highly integrated asymmetric nozzle for advanced fighter aircraft[R]. AIAA-98-0948, 1998. |
| [4] | 王猛杰, 额日其太, 王强, 等. 激波矢量控制喷管落压比影响矢量性能及分离区控制数值模拟[J]. 航空动力学报, 2015, 30(2): 526–536. Wang M J, Eriqitai, Wang Q, et al. Numerical simulation of nozzle pressure ratio effect on vector performance and separation control for shock vector control nozzle[J]. Journal of Aerospace Power, 2015, 30(2): 526–536. |
| [5] | Karen A D. Summary of fluidic thrust vectoring research conducted at NASA Langley research center[R]. AIAA-2003-3800, 2003. http://www.cs.odu.edu/~mln/ltrs-pdfs/NASA-aiaa-2003-3800.pdf |
| [6] | Wing D J. Static investigation of two fluidic thrust-vectoring concepts on a two-dimensional convergent-divergent nozzle[R]. NASA TM-4574, 1994. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19950012627.pdf |
| [7] | Deere K A. Computational investigation of the aerodynamic effects on fluidic thrust vectoring[R]. AIAA-2000-3598, 2000. https://www.scientific.net/amr.998-999.613.pdf |
| [8] | Andrew J N, Fernando N G, John Y. Performance studies of shock vector control fluidic thrust vectoring[R]. AIAA-2007-5086, 2007. |
| [9] | 谭杰, 金捷. 单边膨胀喷管几何参数对内特性和流场的影响[J]. 推进技术, 2013, 34(2): 152–160. Tan J, Jin J. Effect of geometric parameters on internalperformance and flow field on single expansion ramp nozzles[J]. Journal of Propulsion Technology, 2013, 34(2): 152–160. |
| [10] | Bousquet J M. Survey of engine integration testing in ONERA wind tunnels[C]. 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, 2005. http://mams.rmit.edu.au/42tca1i3stiy.doc |
| [11] | Fluidic Dynamics Panel Working Group 19. Sonic nozzles for mass flow measurement and reference nozzles for thrust verification[R]. AGARD-AR-321, 1997. http://dtic.mil/cgi-bin/GetTRDoc?AD=ADA326995 |
| [12] | 范洁川. 风洞试验手册[M]. 北京: 航空工业出版社, 2002. Fan J C. Handbook of wind tunnel test[M]. Beijing: Aviation Industry Press, 2002. |
| [13] | Beale D K. Experimental measurement of venturi discharge coefficient including sensitivity to geometric and flow quality variables[R]. AIAA-99-0304, 1999. |
| [14] | 章荣平, 王勋年, 黄勇, 等. 低速风洞全模TPS试验空气桥的设计与优化[J]. 试验流体力学, 2012, 26(6): 48–52. Zhang R P, Wang X N, Huang Y, et al. Design and optimization of the air bridge for low speed full-span TPS test[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(6): 48–52. |
| [15] | Becle J P, Girard D. Development of strain gage balances with air flow-through system for ONERA wind tunnels[C]. Seventy-first Simi-annual S T A Meeting, 1989. |



