湍流火焰广泛存在于燃气轮机、航空发动机、内燃机、工业燃烧器等各种燃烧设备中,是宽广时间空间尺度上湍流与火焰耦合作用的复杂物理化学问题,其研究具有重要的工程和科学意义。根据Borghi[1]等人的湍流火焰模式分区理论,实际燃烧室湍流火焰主要位于火焰片模式及薄反应区模式下,此时,湍流火焰的研究主要集中在湍流与局部层流火焰的相互作用。目前主要是从2个方面对此开展实验研究:一是从实验出发,研究湍流特性,包括湍流强度、积分尺度等对火焰的影响[2-4],以及火焰化学反应和热释放对湍流场的影响[5-6]。二是在数据处理方面,通过一定的数学统计分析方法对湍流火焰数据进行提取和挖掘,找到湍流火焰中的特征参数,比如湍流火焰速度[7]、湍流火焰分形维数[8-9]等。湍流火焰的数据处理一般分为2种,一种是基于欧拉思想的火焰面平均,研究火焰面整体的变化,包括火焰面密度、火焰面曲率的PDF分布[3, 10]、火焰面分形维数等。二是基于拉格朗日思想,把火焰面看做一系列包含温度、速度等信息的点,研究离散点随时间空间的变化[11-13]。
在湍流火焰中,火焰自身特性与不同湍流尺度复杂的耦合作用使得湍流火焰面发生褶皱,其中有一部分褶皱结构很深入火焰已燃区或未燃区,这部分褶皱区域被称作湍流火焰面上的关键褶皱结构。它们是湍流火焰刷厚度增加的主要原因,也控制着湍流火焰速度等关键参数,是湍流与火焰相互作用的具体体现。根据Chen[14]等人的模拟结果,湍流火焰面“孤岛”结构的形成机理也与这些结构相关。但是,传统的曲率PDF分析方法并不能区分出火焰上这些关键褶皱区域。这是因为,这些结构很深入火焰的已燃区或未燃区,但由于其面积较大,导致单位长度内的弧度增量较小,故曲率并不一定大。另外,在前述2种思想的湍流火焰数据处理过程中,湍流火焰面上的空间相关信息也无法体现出来。
近几年来,网络拓扑结构已经成功运用于生物、物理等领域,分析复杂系统中节点的联系规律和机理,其优点是可以标记出系统中具有某些特征的关键节点或结构。在湍流方面,Liu[15]等人利用时间信息构建的网络拓扑结构揭示了充分发展的三维湍流中存在的幂指规律,M. Meenatchidevi[16]等人利用时间网络拓扑结构研究了热声震荡的机理,分析了火焰由不震荡到震荡的关键临界状态,找到了热声震荡的临界点。
本文利用网络结构方法构建湍流火焰面的拓扑结构,标记对湍流火焰面有较大影响的关键褶皱结构,分析湍流与火焰的相互作用规律。
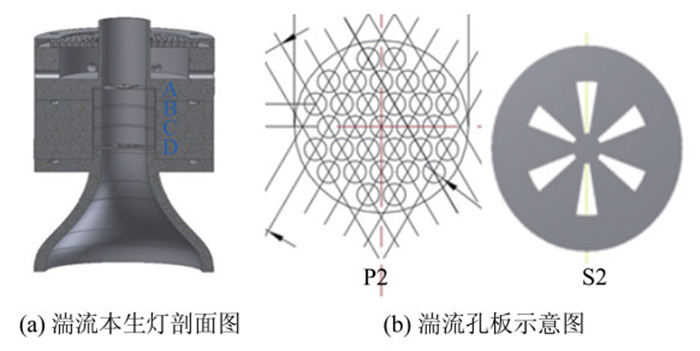
1 实验装置和方法 1.1 湍流实验装置实验装置由供气系统,OH-PLIF系统以及湍流本生灯系统组成。OH-PLIF系统包括Nd:YAG激光器(型号为Quanta-Ray Pro 190,频率为10Hz,脉冲时间10ns,脉冲能量300mJ)、染料激光器以及片光透镜组组成。供气系统由气瓶、混合室以及MKS质量流量计(1179A,量程:0~50 SLM和1159A,量程:0~5 SLM)组成。关于OH-PLIF系统的详细信息见文献[17-18]。湍流本生灯剖面图如图 1(a)所示,出口直径D=20mm。A、B、C、D代表孔板与本生灯出口间的不同距离。湍流产生板的形状如图 1(b)所示,S和P分别代表不同形状的湍流产生板,利用不同的孔板放置位置及形状,可以产生不同强度的湍流。
|
| 图 1 湍流燃烧实验装置 Fig.1 Schematic of turbulent Bunsen burner and perforated plate |
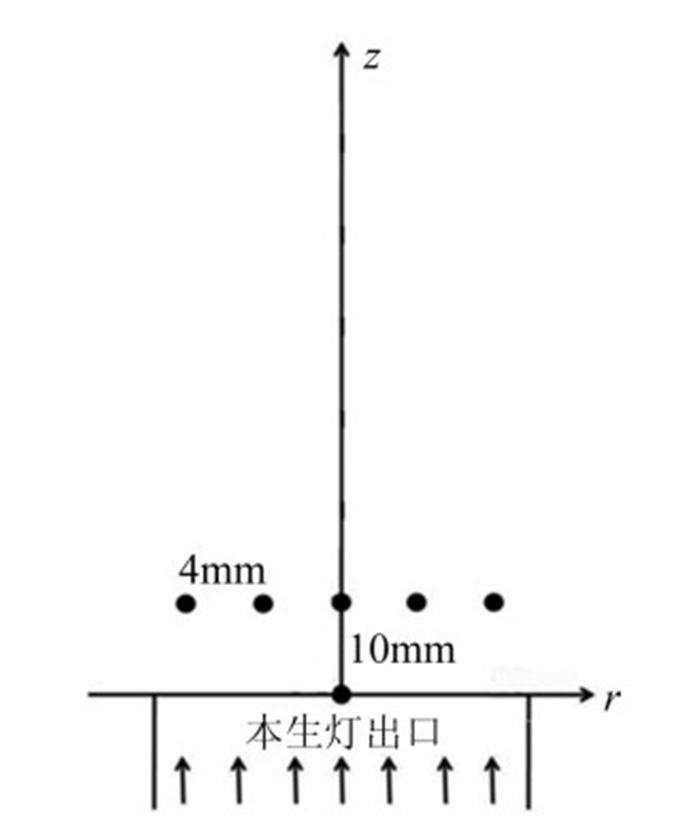
湍流流场特征参数利用热线风速仪(Dantec,Streamline 90N)测量,并采用各向同性湍流假设计算获得。在本生灯出口10mm处,沿着本生灯中心线各取4和8mm为测量点,分别测量这5个点当地的湍流强度、积分尺度、泰勒尺度以及柯氏尺度。然后进行平均,从而得到冷态下整个流场的信息,如图 2所示。
|
| 图 2 本生灯湍流场测量示意图 Fig.2 Schematic of measurement of flow field |
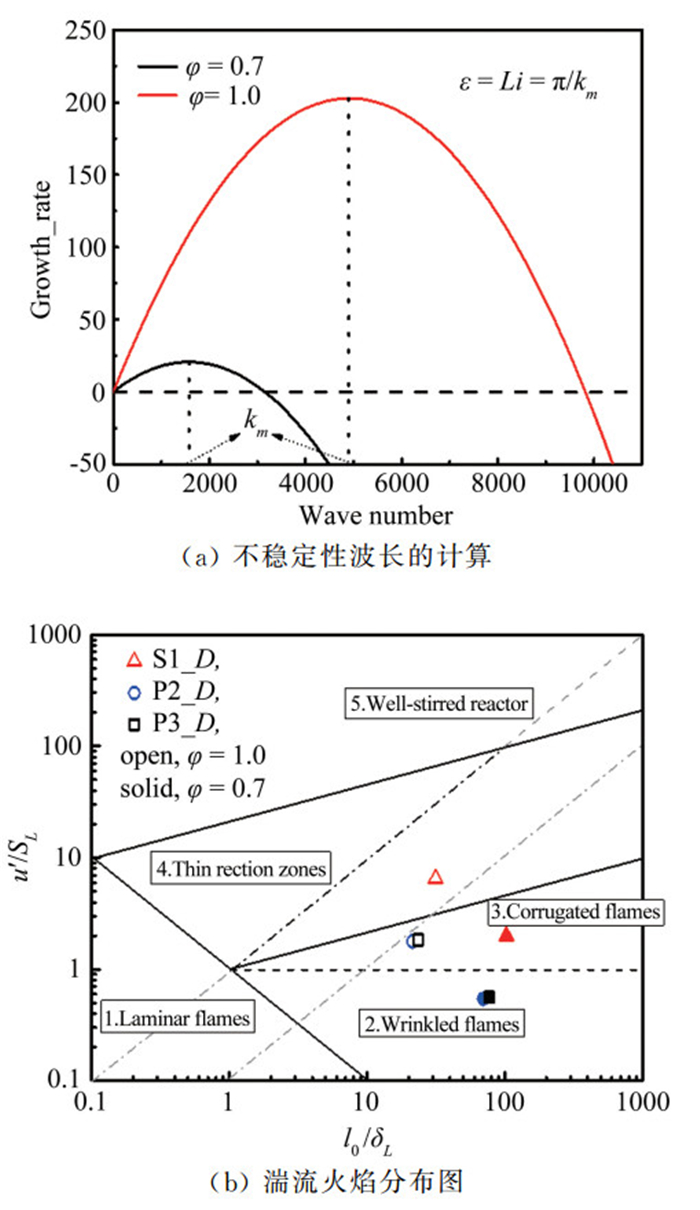
本文实验中,采用甲烷作为燃料,这是因为甲烷的有效Lewis数接近于1,可以排除热扩散不稳定性的影响。表 1所示为不同工况下实验参数。实验中采用3种不同的孔板,S1、P2、P3,D表示孔板放置高度距离本生灯出口73.6mm,φ为当量比,Uave为本生灯出口速度,m/s; u′为湍流强度,m/s;l0、l、h分别为积分尺度、泰勒尺度和柯氏尺度, mm。Li表示火焰自身不稳定性引起的空间波长[19],计算过程如图 3(a)所示。
| 孔板 | φ | Uave | u′ | SL0 | l0 | l | h | Li |
| S1_D | 0.7 | 3 | 0.74 | 19.0 | 5.57 | 0.34 | 0.08 | 2 |
| S1_D | 1.0 | 3 | 0.74 | 37.1 | 5.57 | 0.34 | 0.08 | 0.64 |
| P3_D | 0.7 | 3 | 0.21 | 19.0 | 4.18 | 0.55 | 0.19 | 2 |
| P3_D | 1.0 | 3 | 0.21 | 37.1 | 4.18 | 0.55 | 0.19 | 0.64 |
| P2_D | 0.7 | 3 | 0.17 | 19.0 | 4.59 | 0.66 | 0.24 | 2 |
| P2_D | 1.0 | 3 | 0.17 | 37.1 | 4.59 | 0.66 | 0.24 | 0.64 |
图 3(b)给出了实验工况在湍流火焰模式分区中的位置,可以看到,设计工况处于3个湍流火焰模式中:褶皱层流火焰面模式、波纹板式火焰面模式和薄反应区。
|
| 图 3 不稳定性波长计算及湍流分布图 Fig.3 Calculation of DL instability wavelength and experimental conditions in the combustion diagram |
图 4所示为火焰面边界提取过程。利用OH-PLIF装置可以得到湍流火焰OH基的分布,其边界为未燃区与已燃区边界,被看做为湍流火焰面。把ICCD相机得到的原始OH-PLIF图片剪裁后灰度化,再利用本课题组发展的自适应阈值法可以精确地得到火焰面的位置信息[20]。经过剪裁后的OH图片大小为21.44mm×70.02mm,像素点为120×490。

|
| 图 4 火焰前锋面结构提取过程 Fig.4 Procedure of image process |
对湍流火焰的关键褶皱结构进行仔细分析可以发现,相比湍流火焰面的非褶皱部分,它们可以看到更多的火焰面。因此,我们利用“visible[21]”方法构建湍流火焰的网络拓扑结构。
要得到1个系统的拓扑图,需要有节点、链路及映射函数3个信息。其中,湍流火焰拓扑结构的节点就是提取的火焰前锋面上所有像素点。有了节点之后,对于1个节点,可以和其它节点之间连成直线。由于计算机中直线的计算是通过像素来表示的,因此,我们采用Bresenham算法[22]来计算2个节点之间的连线。
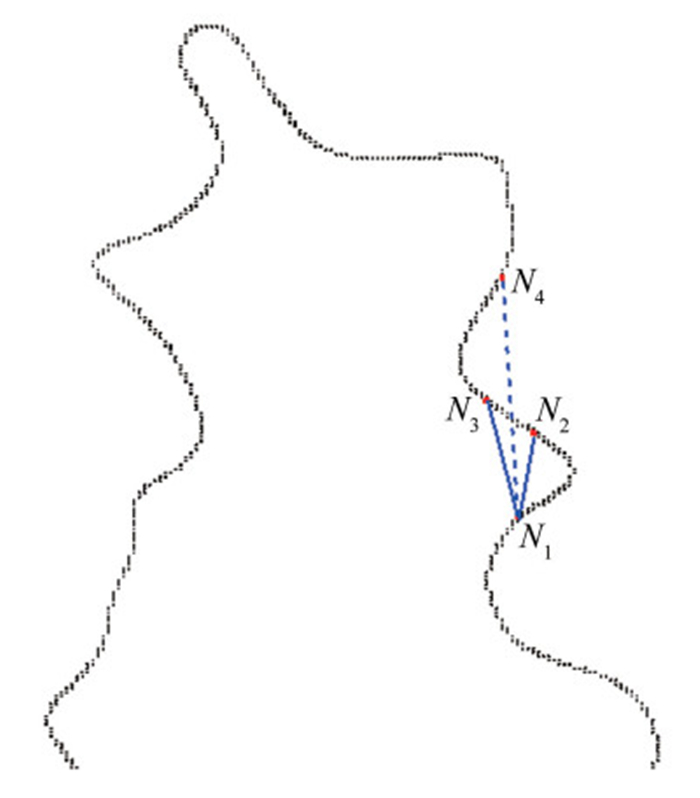
在湍流火焰中,湍流穿过高温火焰面之后,湍流强度以及湍流涡会发生较大的变化。因此,为了表征不同空间尺寸的涡对临近火焰面的影响,我们定义节点的关联如下。同一个空间尺度下,在火焰面的未燃区内,如果2个节点之间的连线和火焰面不相交,则这2个节点是“可见”的,在物理上,说明未燃区内这2个节点可能受到同一湍流涡的影响,如果2个节点之间是“可见”的,那么这2个节点存在空间上的联系,这个就是火焰的映射函数。如图 5所示的节点N1、N2、N3、N4,在规定的空间尺度下,我们认为N1和N4是“不可见”的,N1和N2、N3是“可见”的。
|
| 图 5 湍流火焰拓扑构建示意图 Fig.5 The schematic network structure |
定义了湍流火焰拓扑结构的关系之后,对于任意湍流火焰面,可以得到其拓扑结构信息。此时,就可以得到整个湍流火焰节点的邻接矩阵。拓扑结构的邻接矩阵定义如下:
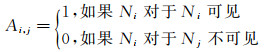 (1)
(1)
为了对得到的网络拓扑结构进行分析,计算出每个节点的节点度[23]k:
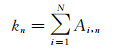 (2)
(2)
其中kn表示第n个节点的节点度。节点度的概率密度为P(k),其变化描述出网络拓扑结构的动态特性。由于Bresenham算法在相邻节点上算法的不确定性,在后续分析中,节点度小于5的节点被舍去。
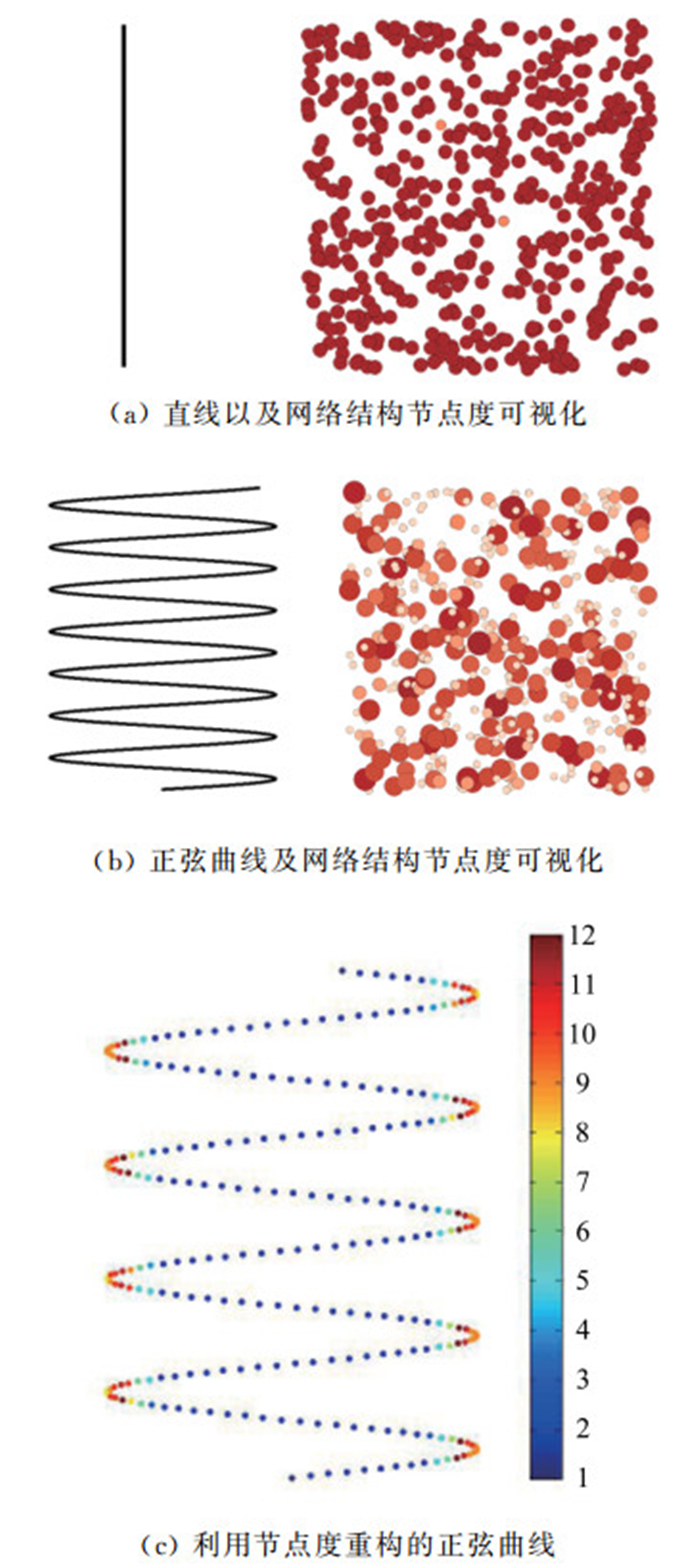
2.2 一般曲线网络拓扑结构为了验证构建方法的正确性,我们首先对一般的正弦曲线和直线进行了网络拓扑结构构建。其中,直线和正弦曲线的像素点及图片大小和剪裁后的OH-PLIF图片大小一致。图 6所示为一般曲线及其网络拓扑结构在Gephi软件中可视化结果。在Gephi可视化图中,每个圆点对应曲线中每个节点,其中圆的大小和颜色深度反应原图上每个像素节点度的大小。可以看出,在图 6(a)中,只有直线2个端点的节点度比较小,其它节点度一样。根据图 6(b)和(c)可以看到,利用前述方法对曲线进行网络拓扑构建,节点度大的点可以标记出曲线褶皱部分。
|
| 图 6 一般曲线及其网络结构可视化 Fig.6 Nerwork structure of straight and sinusoidal line |
在湍流火焰中,湍流与火焰的相互作用使得湍流火焰面有很多褶皱结构。它们主要可以分为以下2种:第一种褶皱结构具有较大的面积,很深入已燃气或未燃气,如图 7(a)中红色实线方框所示,第二种褶皱结构是湍流火焰面上微小突起,如图 7(b)中红色虚线方框所示。但是,这2种褶皱结构对整个湍流火焰的整体贡献是不一样的,第一种褶皱结构对湍流火焰具有较大的影响,控制着湍流火焰刷厚度、湍流火焰体积、湍流火焰速度等参数,是湍流与火焰相互作用的具体体现[24-25],是湍流火焰面上的关键褶皱区域。利用传统的曲率PDF(Probability density function)方法无法准确表征出不同工况湍流火焰面上这种关键褶皱区域的不同。这是因为,这些关键的褶皱区域虽然很深入已燃气体,但是,由于面积较大,导致单位长度内的弧度增量较小,曲率较小,比如图 7(b)中红色虚线内火焰褶皱结构的曲率比图 7(a)中红色实线的大。因此,利用曲率PDF分布无法区分出来图 7(a),(b)所示不同工况下湍流火焰结构的不同。

|
| 图 7 不同工况下湍流火焰OH-PLIF图片 Fig.7 OH-PLIF images under different conditions |
图 8所示为不同工况下湍流火焰曲率PDF分布。

|
| 图 8 不同工况下湍流火焰曲率PDF分布 Fig.8 PDF of curvature under different conditions |
对比图 7(a)~(f)的3组图片,可以看出在不同的当量比下,湍流火焰结构有比较明显的变化,但是曲率的PDF分布却不能表征出这种变化。
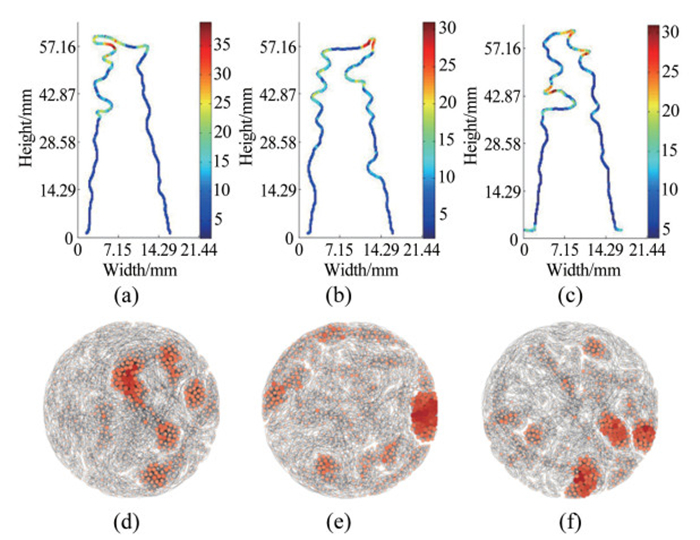
由于曲率PDF无法反映不同火焰关键褶皱区域,因此,我们利用网络拓扑结构来标记湍流火焰面的关键褶皱区域。采用2.1节所述方法,可以对湍流火焰前锋面进行网络拓扑结构构建。图 9所示为P2_D工况下,对不同时刻3张OH-PLIF图片进行网络拓扑构建后的结果。图 9(a)~(c)为利用每个节点的节点度重构的湍流火焰面,(d)~(f)为对应的网络结构在Gephi软件中利用Fruchterman reingold[26]算法可视化结果。由图 9(a)~(c)可知,利用网络结构可以对湍流火焰每个区域内节点进行标记,其中标记出来具有较大节点度的节点位于湍流火焰前锋面的褶皱区域,即图中颜色较深区域的火焰结构。仔细观察可知,这些褶皱区域很深入地进入到火焰的已燃区或者未燃区,也就是湍流火焰面的关键褶皱区域。图 9(d)~(f)中,每个圆圈代表其对应火焰面图片上的1个像素点,其中颜色较深、半径较大的节点,对应了(a)~(c)中颜色较深火焰结构处的像素点,图中的黑色细实线代表了各个像素点在网络结构间的联系,即2个节点是“可见”的。
|
| 图 9 湍流火焰拓扑结构及可视化 Fig.9 Network structure of turbulent Bunsen flames |
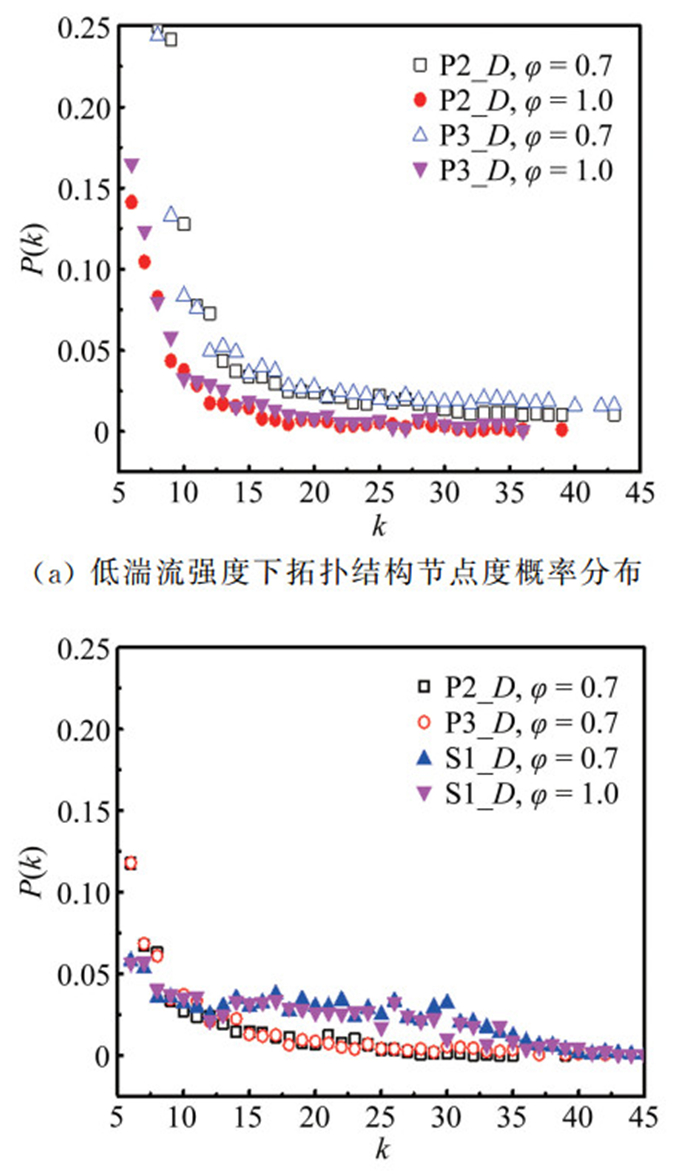
在网络拓扑结构中,每个节点节点度的分布可以反映出系统的关键特性[27],相似系统节点度的分布会展现出一定的相似性。湍流火焰的每1张OH-PLIF图片都可以得到其对应的网络拓扑结构及图片上每个节点的节点度,然后对50张OH-PLIF图片进行统计,得到所有节点度的概率分布,如图 10所示。可以看到,低湍流强度下,不同当量比湍流火焰拓扑结构节点度的概率分布不同,当量比f=0.7的湍流火焰大节点度的概率比f=1.0的高。这是因为节点度大的点属于湍流火焰面中关键的褶皱区域,而根据图 7的OH-PLIF图片可以看到,低湍流强度下,相同湍流强度时,f=0.7的湍流火焰面上关键褶皱区域更多。对比同一当量比下,P2_D和P3_D这2种不同湍流强度的湍流火焰,可以发现,其网络拓扑结构节点度的分布基本相同。这说明了在低湍流强度下,湍流火焰的关键褶皱区域是由于火焰的自身特性引起的,由于实验燃料甲烷的热扩散不稳定性很小,那么此时引起湍流火焰面褶皱的主要因素是火焰自身的DL不稳定性。
|
| 图 10 不同工况湍流火焰网络结构节点度概率分布 Fig.10 Degree distribution under different conditions |
当湍流强度增大到S1_D孔板时,可以看到,其网络拓扑结构大节点度的概率更大,表明此时湍流火焰面关键褶皱区域更多,这个现象也可以从图 7中看出。在S1_D孔板产生的湍流中可以看到,当量比为0.7和1.0的湍流火焰网络结构节点度概率分布基本一致。说明在高湍流强度下,湍流火焰前锋面关键褶皱区域的形成跟火焰自身特性无关,主要是受到湍流强度增加从而湍流涡尺度减小的影响,此时火焰自身不稳定性对火焰褶皱影响较小。
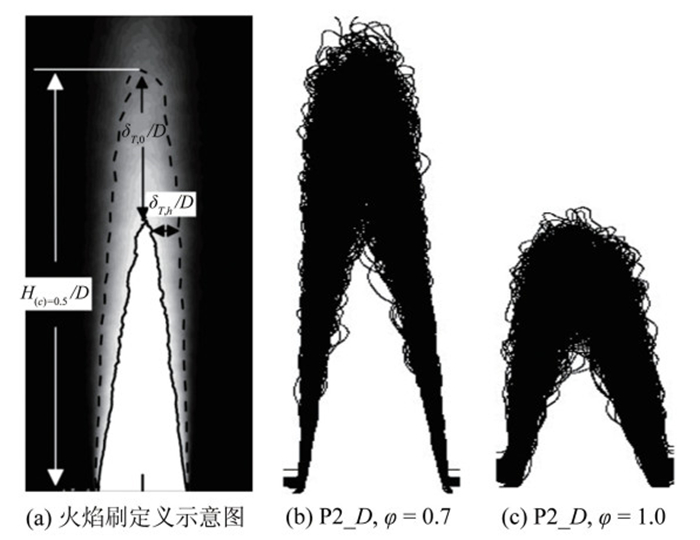
3.3 火焰自身不稳定性在湍流火焰空间发展本生灯湍流火焰属于附着在燃烧器出口的湍流火焰,其与球形火焰等自由传播火焰最大的区别就是来流气体在火焰刷的切向有分量[28],从而使火焰面的褶皱部分向下游传播。也就是说,由于来流气体的作用,下游火焰的火焰刷以及火焰面密度会受到上游火焰褶皱结构影响,从而影响湍流局部消耗速率[7],这也是湍流火焰的非局部效应[29]。现阶段,对于湍流燃烧局部消耗速率的大部分模型都是基于自由传播的湍流火焰[30-31],很少关注湍流在本生灯火焰的非局部效应。对于DL不稳定性在本生灯湍流火焰中发展的研究则更少。本文在低湍流强度下,利用标记出来的关键褶皱区域可以对DL不稳定性在本生灯湍流火焰中的发展规律进行研究。由图 9(a)~(c)可以看到,利用网络拓扑结构标记出来的关键褶皱区域位于靠近本生灯的顶端处,而在底部,这种关键褶皱区域很少。对P3_D湍流下的湍流火焰进行分析,我们可以得到类似的结论。这说明在本生灯湍流火焰中,火焰由于自身不稳定性因素引起的火焰面褶皱以及火焰刷厚度的增加是随着空间发展的,越靠近本生灯火焰的顶端,这种影响越明显。在本生灯湍流火焰中,对500张得到的OH-PLIF图片进行提取火焰前锋面后叠加,可以得到火焰面进展变量<c>的分布,为了得到火焰前锋面上关键褶皱区域对湍流火焰的影响,我们定义2个火焰刷厚度:水平火焰刷厚度dT, h以及中心线火焰刷厚度dT, 0。根据不同的定义方法可以得到不同的火焰刷厚度,但是在相同的定义方式下,其变化规律相同[32]。本文定义中心线火焰刷厚度dT, 0为本生灯中心线上进展变量<c>=0.1和0.5之间的厚度,水平火焰刷厚度dT, h为在本生灯出口高度一定距离h处,进展变量<c>=0.1和0.5火焰面之间水平方向的距离,如图 11(a)所示,图 11(b)和(c)所示为P2_D湍流强度下,f=0.7和1.0的湍流火焰刷,其中心线火焰刷厚度dT, 0分别为20.50和13.63mm。这是因为,该湍流强度下,当量比f=0.7的湍流火焰的不稳定性比1.0大,湍流火焰面上关键褶皱区域多,所以其顶端处中心线火焰刷厚度大。
|
| 图 11 不同工况下火焰刷厚度及定义 Fig.11 Schematic of definition of flame brush thickness and two flame brush under different conditions |
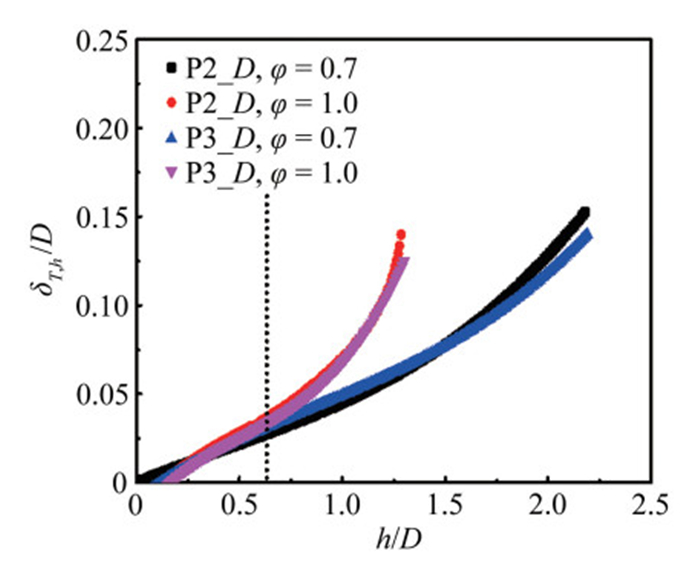
图 12所示为低湍流强度下,不同当量比湍流火焰水平火焰刷厚度(dT, 0/D)随本生灯出口高度(h/D)无量纲后的变化。可以看到,在距离本生灯出口高度一定范围内,不同当量比湍流火焰的水平火焰刷厚度基本一致,在无量纲出口距离达到一定高度处才表现出不同。说明在本生灯湍流火焰中,火焰自身不稳定性对湍流火焰的影响跟火焰自身的发展时间有关,在距离出口一定距离内,火焰自身不稳定对湍流火焰的影响体现不出。
|
| 图 12 水平火焰刷厚度随出口高度的变化 Fig.12 The normalised horizotal flame brush thickness with respect to the normalised axial distance from Bunsen burner exit |
(1) 利用网络拓扑结构方法可以标记出本生灯湍流火焰面的关键褶皱结构。
(2) 在低湍流强度下,湍流火焰关键褶皱结构主要由自身不稳定性引起,在高湍流强度下,火焰关键褶皱结构主要受湍流尺度影响。
(3) 在本生灯湍流火焰这种附着火焰中,火焰自身不稳定性引起的火焰褶皱与火焰发展距离有关,在距本生灯出口一定距离处,火焰自身不稳定性对火焰褶皱影响较小。随着火焰向下游发展,其对火焰面影响逐渐增大,火焰褶皱程度增加。
| [1] | Peters N. Turbulent combustion[M]. Cambridge University Press, 2000. |
| [2] | Tamadonfar Parsa, Gülder ömer L. Flame brush characteristics and burning velocities of premixed turbulent methane/air Bunsen flames[J]. Combustion and Flame, 2014, 161(12): 3154–3165. DOI:10.1016/j.combustflame.2014.06.014 |
| [3] | Fragner R, Halter F, Mazellier N, et al. Investigation of pressure effects on the small scale wrinkling of turbulent premixed Bunsen flames[J]. Proceedings of the Combustion Institute, 2015, 35(2): 1527–1535. DOI:10.1016/j.proci.2014.06.036 |
| [4] | Poludnenko A Y, Oran E S. The interaction of high-speed turbulence with flames:Global properties and internal flame structure[J]. Combustion and Flame, 2010, 157(5): 995–1011. DOI:10.1016/j.combustflame.2009.11.018 |
| [5] | Lipatnikov A N, Chomiak J. Effects of premixed flames on turbulence and turbulent scalar transport[J]. Progress in Energy and Combustion Science, 2010, 36(1): 1–102. DOI:10.1016/j.pecs.2009.07.001 |
| [6] | Nishiki S. Modeling of flame-generated turbulence based on direct numerical simulation databases[J]. Proceedings of the Combustion Institute, 2002, 29: 2017–2022. DOI:10.1016/S1540-7489(02)80246-2 |
| [7] | Lipatnikov A N, Chomiak J. Turbulent flame speed and thickness:phennomenology, evaluation, and application in multi-dimensional simulations[J]. Progress in Energy & Combustion Science, 2002, 28: 1–74. |
| [8] | Fureby C. A fractal flame-wrinkling large eddy simulation model for premixed turbulent combustion[J]. Proceedings of the Combustion Institute, 2005, 30(1): 593–601. DOI:10.1016/j.proci.2004.08.068 |
| [9] | Cintosun Esen, Smallwood Gregory J, Gülder ömer L. Flame surface fractal characteristics in premixed turbulent combustion at high turbulence intensities[J]. AIAA Journal, 2007, 45(11): 2785–2789. DOI:10.2514/1.29533 |
| [10] | Bradley D. Application of a reynolds stress, stretched flamelet, mathematical model to computations of turbulent burning velocities andcomparison with experiments[J]. Combustion & Flame, 1994, 96: 221–248. |
| [11] | Yeung P K. Lagrangian statistics from direct numerical simulations of isotropic turbulence[J]. Journal of Fluid Mechanics, 1989, 207: 531–586. DOI:10.1017/S0022112089002697 |
| [12] | Pope S. Lagrangian PDF methods for turbulent flows[J]. Annu Rev Fluid Mech, 1994, 26: 23–63. DOI:10.1146/annurev.fl.26.010194.000323 |
| [13] | Chaudhuri S. Life of flame particles embedded in premixed flames interacting with near isotropic turbulence[J]. Proceedings of the Combustion Institute, 2015, 35(2): 1305–1312. DOI:10.1016/j.proci.2014.08.007 |
| [14] | Chen H J. The mechanism of two-dimensional pocket formation in lean premixed methane-air flames with implications to turbulent combustion[J]. Combustion & Flame, 1999: 15–48. |
| [15] | Liu C, Zhou W X, Yuan W K. Statistical properties of visibility graph of energy dissipation rates in three-dimensional fully developed turbulence[J]. Physica A:Statistical Mechanics and its Applications, 2010, 389(13): 2675–2681. DOI:10.1016/j.physa.2010.02.043 |
| [16] | Murugesan Meenatchidevi, Sujith R I. Combustion noise is scale-free:transition from scale-free to order at the onset of thermoacoustic instability[J]. Journal of Fluid Mechanics, 2015, 772: 225–245. DOI:10.1017/jfm.2015.215 |
| [17] | 张猛, 王金华, 谢永亮, 等. 利用OH_PLIF测量CH4/H2/空气混合气湍流燃烧速率[J]. 燃烧科学与技术, 2013, 19(6): 512–516. Zhang M, Wang J H, Xie Y L, et al. Measurement of turbulent burning velocity of CH4/H2/Air mixtures using OH-PLIF[J]. Journal of Combustion Science and Technology, 2013, 19(6): 512–516. |
| [18] | Zhang M, Wang J H, Wu J, et al. Flame front structure of turbulent premixed flames of syngas oxyfuel mixtures[J]. International Journal of Hydrogen Energy, 2014, 39(10): 5176–5185. DOI:10.1016/j.ijhydene.2014.01.038 |
| [19] | Kobayashi H, Tamura T, Maruto K, et al. Burning velocity of turbulent premixed flames in a high pressure environment[J]. Proceedings of the Combustion Institute, 1996, 26(1): 389–396. DOI:10.1016/S0082-0784(96)80240-2 |
| [20] | 张猛, 王金华, 俞森彬, 等. 自适应阈值二值法提取湍流火焰前锋面结构[J]. 燃烧科学与技术, 2016, 22(3): 212–217. Zhang M, Wang J H, Yu S B, et al. Flame front tracking of turbulent premixed flames using adaptive threshold binarization[J]. Journal of Combustion Science and Technology, 2016, 22(3): 212–217. |
| [21] | Luque B, Lacasa L, Ballesteros F, et al. Horizontal visibility graphs:Exact results for random time series[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2009, 80(2): 046103. |
| [22] | Bresenham J E. Algorithm for computer control of a digital plotter[J]. IBM Systems Journal, 1965, 4(1): 25–30. DOI:10.1147/sj.41.0025 |
| [23] | Barabasi A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509. DOI:10.1126/science.286.5439.509 |
| [24] | Hamlington P E, Poludnenko A Y, Oran E S. Interactions between turbulence and flames in premixed reacting flows[J]. Physics of Fluids, 2011, 23(12): 125111. DOI:10.1063/1.3671736 |
| [25] | Chakraborty N, Klein M, Swaminathan N. Effects of lewis number on the reactive scalar gradient alignment with local strain rate in turbulent premixed flames[J]. Proceedings of the Combustion Institute, 2009, 32(1): 1409–1417. DOI:10.1016/j.proci.2008.06.021 |
| [26] | Fruchterman T M J, Reingold E M. Graph drawing by force-directed placement[J]. Software Practice & Experience, 2010, 21(11): 1129–1164. |
| [27] | Scholz M. Node similarity as a basic principle behind connectivity in complex networks[J]. Computer Science, 2015: 1–7. |
| [28] | Boyer L, Quinard J. On the dynamics of anchored flames[J]. Combustion & Flame, 1990, 82(1): 51–65. |
| [29] | Lieuwen T. Local consumption speed of turbulent premixed flames-An analysis of "memory effect"[J]. Combustion & Flame, 2010, 157: 955–965. |
| [30] | Clavin P, Williams F A. Theory of premixed-flame propagation in large-scale turbulence[J]. Journal of Fluid Mechanics, 2006, 90(3): 589–604. |
| [31] | Aldredge R C, Williams F A. Influence of wrinkled premixed-flame dynamics on large-scale, low-intensity turbulent flow[J]. Journal of Fluid Mechanics, 2006, 228(228): 487–511. |
| [32] | Tamadonfar Parsa, Gülder ömer L. Effects of mixture composition and turbulence intensity on flame front structure and burning velocities of premixed turbulent hydrocarbon/air Bunsen flames[J]. Combustion and Flame, 2015, 162(12): 4417–4441. DOI:10.1016/j.combustflame.2015.08.009 |



