2. 高超声速冲压发动机技术国防科技重点实验室, 四川 绵阳 621000
2. Science and Technology on Scramjet Laboratory, China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China
高超声速飞行技术是21世纪航空航天领域的研究热点之一,高超声速飞行器具有重要的战略意义和极高的应用价值[1-3]。获得优化的气动布局,从而提高飞行器的气动性能,是高超声速吸气式飞行器研制中必须解决的一个重要问题。在飞行器气动布局的研究和设计中,如何准确获得飞行器的内流道气动特性,是需要重点关注的问题之一[4-5]。
准确测量高超声速通气模型内流道出口参数是获得内流道气动特性的基础。目前,使用测压耙进行出口压力测量仍然是主要的技术手段[6]。通常是采用固定位置的单排测压耙(见图 1),静压和皮托压力探针只能测量固定位置的气流参数,不能在出口截面内移动。由于出口气流极不均匀,单排测压耙固定测点获得的测量结果不能全面而准确地反映出口流动的实际情况。

|
| 图 1 单排测压耙 Fig.1 Single-row pressure harrow |
为克服单排测压耙的不足,设计过一种固定位置的多排测压耙(见图 2),在一次试验中同时获得出口截面上不同水平位置的气流参数。为避免相邻2根静压管头部激波相互干扰并保证内流道流通面积,测点不能布置得太密。因此,这种方法也不能全面反映出口流动的实际情况。

|
| 图 2 多排测压耙 Fig.2 Pressure harrow |
中国航天空气动力技术研究院黄湛等人应用DPIV技术测量了Ma5条件下的吸气式飞行器尾喷管出口气流速度,并用皮托压力探针测量出口皮托压力。通过气流速度、总温与皮托压力换算得到喷管出口的静压[7]。此方法的优点是对喷管出口流场的干扰很小,可以忽略不计,理论上能够获得整个喷管出口的流场分布;缺点是技术难度较大,设备复杂,出口气流的总温很难准确获得。
本研究的目的是通过研究探针布置方式对测量结果的影响,改进现有的测量技术,达到尽可能全面地了解吸气式飞行器模型尾喷管出口气流参数分布的目的,并在Φ1m高超声速风洞上建立更加准确的喷管出口气流参数测量技术,为飞行器设计提供更丰富、可靠的试验数据。
1 气流参数测量试验方法研究 1.1 静压探针布置对测量结果影响研究若尾喷管出口处是超声速气流,在静压探针的头部会产生激波,如果相邻2个静压探针之间的距离太近,头部激波的相互干扰会对测量结果造成影响;同时出口气流是有一定流向角的,若静压探针与气流流向之间夹角过大,同样也会对测量结果产生影响。因此,需要开展CFD计算,研究相邻静压探针之间的距离以及静压探针与气流流向之间的偏角对测量结果的影响。
1.1.1 计算模型计算模拟的静压探针是由1个半锥角为1.91°、底部直径为4mm的尖锥与外直径为4mm、内直径为2mm、长度为80mm的圆筒组合而成的。在距离圆筒与尖锥贴合面19.8mm处等间隔开4个直径为0.4mm的小孔,小孔贯穿圆筒壁面,使内外流场相通。
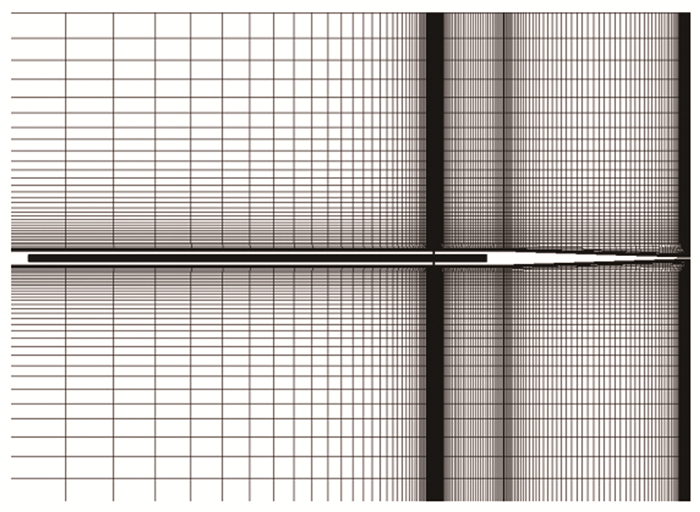
1.1.2 计算网格及边界条件进行了三维数值计算。网格采用六面体结构网格,壁面第一层网格间距为0.001mm,外流场采用C-H型网格包裹,最终生成网格总数约200万。图 3为对称面网格示意图。
|
| 图 3 计算网格 Fig.3 Mesh of symmetry plane |
计算的来流状态如表 1所示:
| Ma | p /Pa | T/K | V/(m·s-1) |
| 6 | 1520 | 60 | 929 |
计算中流场外边界条件由来流状态给出,壁面采用无滑移绝热壁,并采用壁面差值函数,静压管外流场出口采用外插,内腔出口在试验中与扫描阀连接,采用壁面边界条件。采用CFD++商业软件,选用k-ε湍流模型。
1.1.3 计算结果分析(1) 探针间距的影响
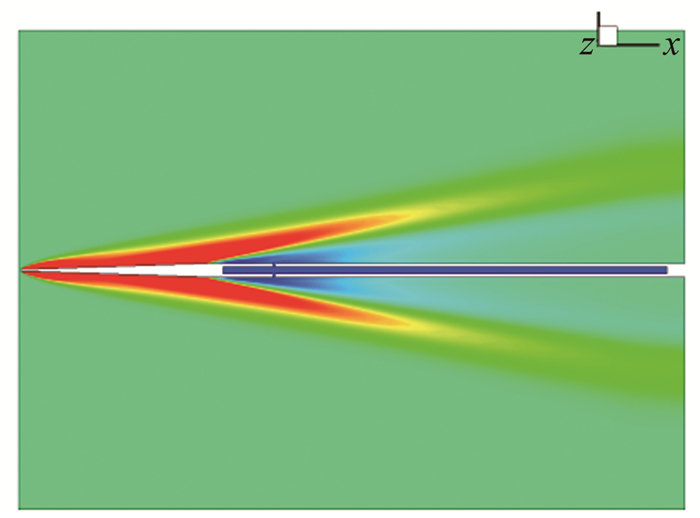
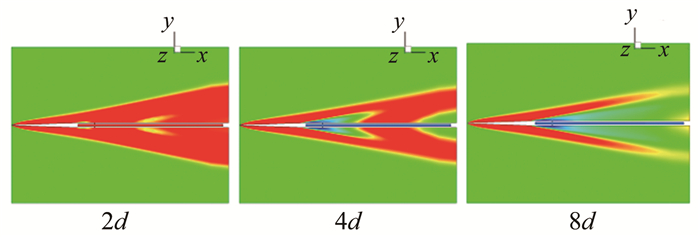
图 4给出了1根探针、迎角为0°时的压力分布云图;图 5给出了2根相邻探针、迎角0°、不同间距时的压力分布云图,计算数据如表 2所示。
|
| 图 4 α=0°单根静压管计算结果 Fig.4 Pressure contour of one static tube at α=0° |
|
| 图 5 两根静压管不同距离计算结果 Fig.5 Pressure contour of two static tubes |
| Distance | Single | 2d | 4d | 8d |
| p /Pa | 1463 | 1629 | 1468 | 1470 |
1根探针、0°迎角时,计算得到的静压为1463Pa。根据表 2的结果,相邻两根探针距离不小于4倍管径时相互之间基本无干扰。
综合上述计算结果,并考虑到喷管出口实际马赫数可能低于6,静压探针的最小距离应不小于6倍管径。
(2) 探针与气流夹角的影响
在试验时,探针与气流之间的纵向夹角可以通过三自由度压力测量装置的俯仰角进行调整;而横向夹角则只能通过在测压耙上预设角度实现。由此造成的测量误差是需要评估的。
CFD计算结果表明(见表 3),探针与气流夹角在2°以内时静压的测量误差1%左右(相对0°夹角),4°时为15%左右。
| Angel/(°) | 0 | 1 | 2 | 4 |
| p /Pa | 1463 | 1460 | 1448 | 1239 |
本项研究选取1个去除了所有安定面和舵面的带进气道升力体布局飞行器模型作为研究对象。
为模拟飞行的外流条件及内流道通气状态,在试验中采取的模拟方法如下[8]:
(1) 外形相似模拟。严格按照理论尺寸缩尺模拟飞行器前体、压缩面、进气道和尾喷管型面。
(2) 外流模拟:外流马赫数、雷诺数模拟。
(3) 内流道流动。由于内流道的流动由外流参数、入口参数和内流道及喷管型面所确定,因此内流道流动由外形相似和外流参数模拟即可保证。
1.3 测压点布置为准确了解喷管出口压力分布,应当测量出口截面每一个位置的压力值,从而得到完整的出口压力云图。但由于受模型强度等因素的限制,这是不可能实现的。因此,在模型壁面和喷管出口布置压力测点时相互之间是有一定间距的,具体布置如下:
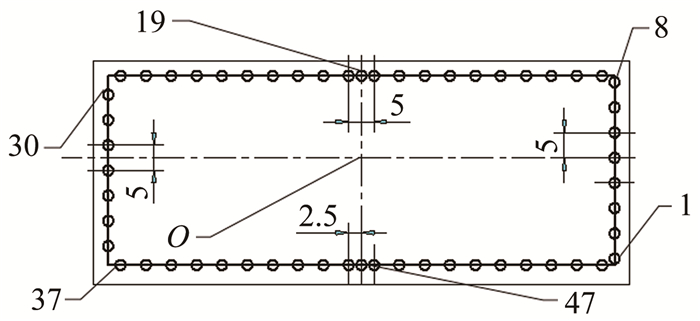
(1) 壁面测点布置。为测量近壁面气流静压,在与尾喷管出口截面平行、距离2mm的截面处,沿喷管四周布置了57个静压测点,测点轴线严格垂直于当地喷管切面。图 6为壁面静压测点的位置及编号示意图(模型反装)。中间测点与两侧测点的距离为2.5mm,其余相邻测点之间距离5mm。
|
| 图 6 壁面静压点布置 Fig.6 Measuring points of wall static pressure |
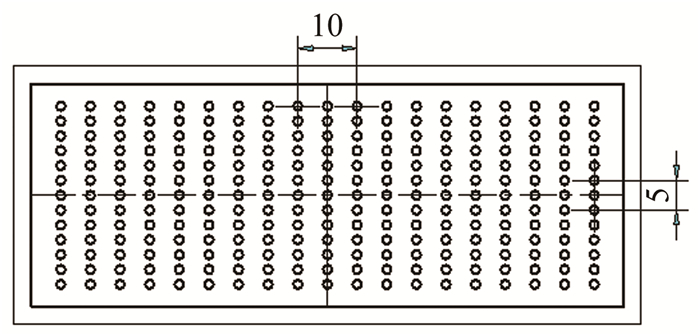
(2) 空间测点布置。空间测点是测压耙上的静压和皮托压力探针在喷管出口处的空间位置。选定的空间测点位置如图 7所示(模型反装),13行、19列,共计247个点位,各列之间间距均为5mm,行间距为2.5mm。最外侧到喷管上下和左右壁面的距离分别为3.76和4.96mm。按照从喷管下表面到上表面、从左侧到右侧的顺序将测点依次划分为第1~13行和第1~19列。
|
| 图 7 喷管出口测点位置 Fig.7 Measuring points of pitot pressure and static pressure |
出口截面坐标系定义为:以出口截面几何中心O点(见图 6)为坐标原点,OY轴指向出口底面为正,OX轴指向右为正。
各压力测点的坐标可根据坐标系定义及测点位置图(见图 6和7)一一确定,在此不再赘述。
1.5 测压耙设计测压耙设计要考虑每个测压点位测压管与气流的横向夹角。由于喷管出口流场不均匀,很难准确预测每个测点处的气流流向角,只能大致估计。研究选取的试验模型喷管出口处两侧型面膨胀角约为1.35°。设左侧角度为1.35°,右侧为-1.35°,则测压耙1号点(测压耙最左侧)的预置偏角为1.35°,19号点(测压耙最右侧)为-1.35°,从1号点到19号点依次等比例递减。
1.6 三自由度压力测量装置研制了1台三自由度压力测量装置,使压力探针能够上下左右移动和绕固定点转动,以尽可能正对出口气流的流向,提高测量准度。各自由度运动均由电机带动传动机构实现,用编码器进行测量。运动精度为:角位移误差小于3′,重复性定位精度优于30″;线位移误差小于0.3mm/100mm,重复性定位精度小于0.3mm。
1.7 压力测量方法 1.7.1 皮托压力和壁面静压测量与静压管不同,相邻皮托压力管的间距不需要满足大于6倍管径的要求。因此,在测压耙上同时布置19个皮托压力管(相邻管子间距5mm),在同一个试验车次中通过三自由度压力测量装置的上下移动将247个点位的皮托压力全部测完。装置移动到每个位置停留1.5s,以保证压力达到平衡(静压测量时亦如此)。
迎角0°条件下,重复7次,分3个试验车次完成。其中前2次车,三自由度压力测量装置上下运动各3次,完成6次压力测量;最后1个车次,测量装置上下运动1次,完成第7次压力测量。
在测量出口皮托压力的同时测量喷管出口附近的壁面静压。
1.7.2 出口静压测量试验最初拟采用与计算相同的外径为4mm、半锥角1.91°的静压管进行静压测量。但考虑到外径越大静压管头部激波的影响范围越大,相邻静压管之间以及静压管与喷管壁面之间的干扰越严重,获得的有效试验数据较少。保持半锥角不变、减小外径,可以保证头部激波的激波角不变而影响范围大大减小,计算得到的结论依然成立。相邻静压管之间的距离相应减小,测点相应增加。因此,试验选用了半锥角1.91°、外径2mm的静压管,测量孔距静压管头锥尖点35mm。分3次试验完成全部(247个)点位的静压测量,3次试验分别测量第1/4/7/10/13/16/19列(即安装7支静压探针)、第2/5/8/11/14/17列(安装6支静压探针)和第3/6/9/12/15/18列(安装6支静压探针)的出口静压,相邻探针间距约为15mm(7.5倍静压管直径)。每个试验车次三自由度压力测量装置上下运动1~3次,完成全部点位的重复性测量。
2 风洞试验与试验结果分析 2.1 试验设备及来流条件试验在中国空气动力研究与发展中心(CARDC)的Φ1m高超声速风洞(Ma3~8支路)上进行。该风洞为一座高压下吹-真空抽吸、暂冲式运行的常规高超声速风洞,配备了出口直径为1m、名义马赫数为3、3.5、4、4.5、5、5.5、6、6.5、7和8的型面喷管,模拟高度20~60km(随马赫数的不同而模拟范围有所不同),试验时间30s。风洞配备了较完善的测控系统,可以满足试验中的各种参数测量和处理、流场显示与记录的需要。
试验来流条件如表 4所示。
| Ma | p0 /MPa |
T0 /K |
p∞ /kPa |
T∞ /K |
q∞ /kPa |
Re /m-1 |
| 6 | 2.0 | 470 | 1.267 | 57.3 | 31.92 | 1.86×107 |
模型压力测量采用DTC initium电子扫描阀压力测量系统,量程为17和103kPa,分别用于测量出口静压/壁面压力(量程17kPa)和出口皮托压力(量程103kPa),测压精度优于0.2%。
2.2 试验装置图 8是安装在风洞试验段内的试验装置照片。模型通过背支撑反装在风洞迎角机构上;皮托压力管前端以及静压管的测量孔与模型喷管出口平齐,安装角度由测压耙的预置角度确定,测压管后端与电子扫描阀相连,电子扫描阀放置在保护盒内;测压耙和扫描阀保护盒通过转接支杆安装在三自由度压力测量装置上;三自由度压力测量装置安装在风洞迎角机构上,能够与模型同步改变迎角,试验时测量装置从上向下运动(即从喷管出口下表面向上表面运动)。

|
| 图 8 试验装置照片 Fig.8 Test devices in wind tunnel |
图 9给出了壁面静压系数曲线(以来流动压为参考压力,下同)。

|
| 图 9 壁面静压曲线 Fig.9 Coefficient curves of wall static pressure |
纵坐标为压力系数,横坐标为壁面静压测点的坐标。
在喷管出口的左右两侧和底面,壁面压力总体上呈从上到下、从两侧到中央逐渐降低的趋势。
喷管上表面大部分区域压力分布也是呈从两侧到中间逐渐降低的趋势,但在接近喷管出口中央时,压力总体上呈先增后减的趋势,中央测点压力略高于临近测点。
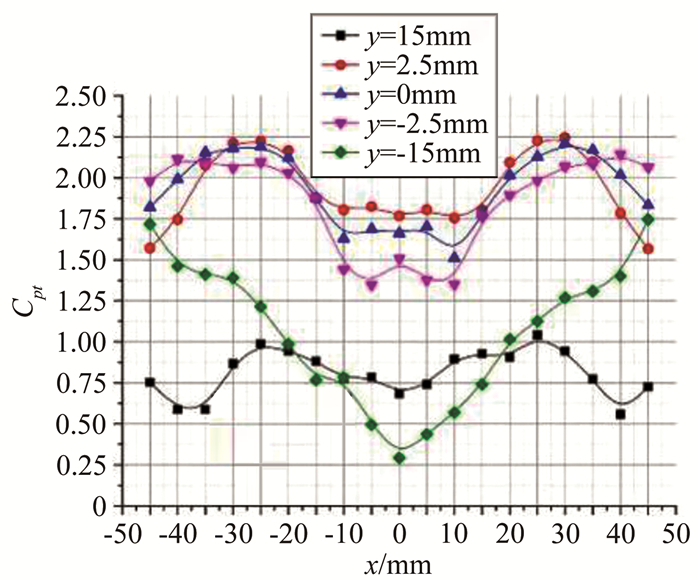
2.3.2 皮托压力分布图 10给出了喷管出口皮托压力部分测量结果,分别位于喷管下表面附近、中心及其附近、上表面附近。从测量结果看,在喷管出口上表面附近皮托压力呈“V”字形分布,即中间最低两边最高。在逐渐远离上表面的位置,皮托压力分布逐渐向“M”字形变化,最大值出现在介于喷管对称面和左右两侧壁之间的某一位置;对称面附近压力变化相对比较平缓,且越接近喷管下表面变化平缓的区域越大;喷管对称面上的皮托压力最大值出现在出口几何中心以下的某一位置。
|
| 图 10 皮托压力曲线 Fig.10 Coefficient curves of pitot pressure |
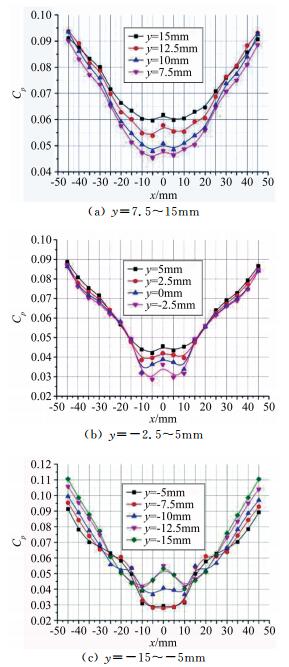
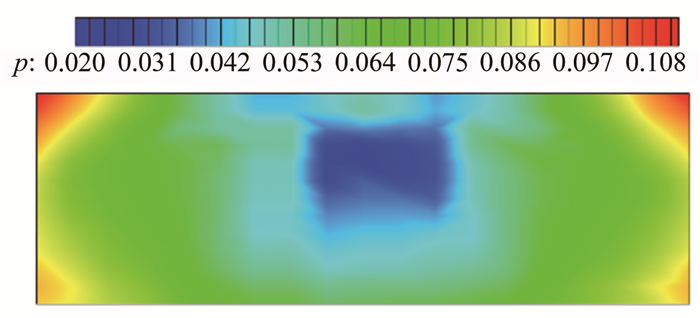
图 11为喷管出口静压的测量结果,图 12为出口静压分布云图;图 13为出口部分区域马赫数分布,图 14为出口马赫数分布云图。
|
| 图 11 静压曲线 Fig.11 Coefficient curves of static pressure |
|
| 图 12 静压云图 Fig.12 Static pressure contours |

|
| 图 13 马赫数分布 Fig.13 Mach number curves |

|
| 图 14 马赫数云图 Fig.14 Mach number contours |
出口静压总体呈两侧高、中间低的趋势。在喷管核心区附近,马赫数呈中间高、两侧低的趋势;在上下壁面附近,喷管对称面上的马赫数低于两侧。
2.3.4 α≠0°时的出口压力分布除开展了α=0°时的出口压力测量之外,本研究还进行了α=-4°和6°时的出口压力测量,测量方法与α=0°时完全相同。由于模型和三自由度压力测量装置都装在风洞迎角机构上,因此,只需要将迎角机构运动到所需迎角即可。得到的数据变化规律也与α=0°时相似。
图 15为α=-4°时出口皮托压力部分测量结果,图 16为α=-4°时出口静压测量结果,图 17为α=-4°时出口部分区域马赫数分布。图 18为α=6°时出口皮托压力部分测量结果,图 19为α=6°时出口静压测量结果,图 20为α=6°时出口部分区域马赫数分布。

|
| 图 15 α=-4°皮托压力曲线 Fig.15 Coefficient curves of pitot pressure at α=-4° |

|
| 图 16 α=-4°静压曲线 Fig.16 Coefficient curves of static pressure at α=-4° |
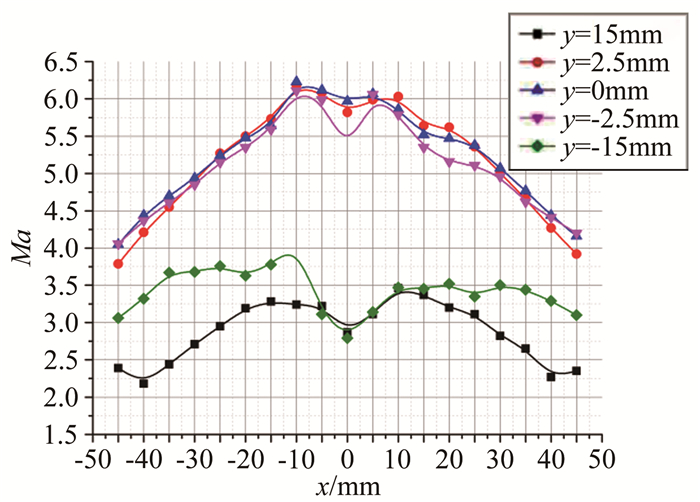
|
| 图 17 α=-4°马赫数分布 Fig.17 Mach number curve at α=-4° |

|
| 图 18 α=6°皮托压力曲线 Fig.18 Coefficient curves of pitot pressure at α=6° |
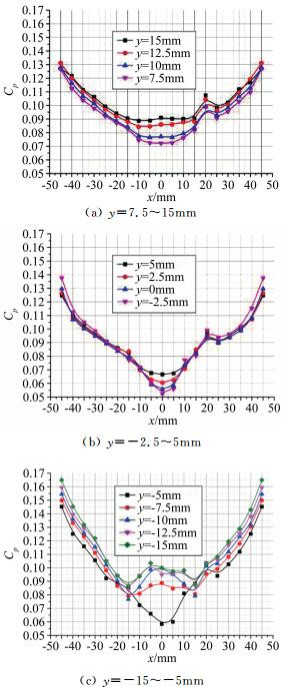
|
| 图 19 α=6°静压曲线 Fig.19 Coefficient curves of static pressure at α=6° |

|
| 图 20 α=6°马赫数分布 Fig.20 Mach number curves at α=6° |
传统的出口参数是采用固定的单排测压耙进行测量,用测量位置的相关参数作为整个出口截面的气流参数。而实际情况是,出口处的皮托压力和静压的最大值与最小值之间均有几倍的差别。因此,以某一特定位置的参数代替整个出口参数计算内流道的气动特性会产生较大偏差。新的测量方法由于测点位置布置得较为密集,能够反映整个出口截面的气流参数分布规律。
3 结束语本项研究选取典型外形,开展了高超声速通气模型喷管出口气流参数测量试验技术研究。分析了以往使用的压力测量装置存在的不足;用CFD方法研究了静压管距离和安装角度对静压测量结果的影响;研制了能够满足测量要求的三自由度压力测量装置;在CARDC的Φ1m高超声速风洞上开展了试验,获得了某飞行器喷管出口气流的静压、皮托压力和马赫数分布,试验数据规律合理。研究表明,采用三自由度压力测量装置加装带预置偏角的单排测压耙,解决了以往只能采用特定位置测量结果代替整个出口截面气流特性从而导致存在较大偏差的问题。可以为研究高超声速通气模型进气道的气动特性提供更加全面可靠的试验数据。
| [1] | McClinton C R, Hunt J L. Air breathing hypersonic technology vision vehicles and development dreams[R]. AIAA-99-4987, 1999. http://dl.acm.org/citation.cfm?id=887857 |
| [2] | 乐嘉陵. 吸气式高超声速技术研究进展[J]. 推进技术, 2010, 31(6): 641–649. Le J L. Progress in air-breathing hypersonic technology[J]. Journal of Propulsion Technology, 2010, 31(6): 641–649. |
| [3] | 白菡尘, 王泽江. 高超声速冲压发动机-飞行器计力体系讨论[J]. 推进技术, 2012, 33(1): 1–6. Bai H C, Wang Z J. Discussion on force-accounting system for airbreathing hypersonic vehicle[J]. Journal of Propulsion Technology, 2012, 33(1): 1–6. |
| [4] | 张红英, 程克明, 伍贻兆. 某高超飞行器流道冷流特征及气动力特性研究[J]. 空气动力学学报, 2009, 27(1): 119–123. Zhang H Y, Cheng K M, Wu Y Z. A study on the flowpath and the aerodynamic characteristic of a hypersonic vehicle[J]. Acta Aerodynamic Sinca, 2009, 27(1): 119–123. |
| [5] | 骆晓臣, 张堃元. 侧压式进气道内部阻力分析[J]. 推进技术, 2007, 28(2): 204–207. Luo X C, Zhang K Y. Analysis for internal drag in sidewall-compression inlet[J]. Journal of Propulsion Technology, 2007, 28(2): 204–207. |
| [6] | 范洁川. 风洞试验手册[M]. 北京: 航空工业出版社, 2002. Fan J C. Handbook of wind tunnel test[M]. Beijing: Aviation Industry Press, 2002. |
| [7] | 黄湛, 王宏伟, 张妍, 等. 高超声速飞行器DPIV内流阻力测量技术研究[J]. 推进技术, 2014, 35(4): 456–462. Huang Z, Wang H W, Zhang Y, et al. Research of internal drag DPIV measurement for hypersonic Vehicle[J]. Journal of Propulsion Technology, 2014, 35(4): 456–462. |
| [8] | 许晓斌, 舒海峰, 谢飞, 等. 通气模型内流道阻力直接测量技术研究[J]. 推进技术, 2013, 34(3): 311–315. Xu X B, Shu H F, Xie F, et al. Technique investigation on flow-through model inner-flow drag straightway measured by strain-gauge balance[J]. Journal of Propulsion Technology, 2013, 34(3): 311–315. |



