2. 中国计量大学, 杭州 310018
2. China Jiliang University, Hangzhou 310018, China
微流体(尺度约为10-4~10-3m量级)技术是在微观尺度下操作、控制及检测复杂流体的技术,近年来已经在生物、化学、医学以及生命科学等领域内产生了重要影响。流场与压力分布是开展微小流体元件优化设计的2个重要流体动力学参数。到目前为止,流场结构的研究已经有了较为完善的测量技术,但微流体压力分布测量仍然存在诸多难点需要进行解决。
微流体压力的测量之所以受到关注,一个重要的原因在于微流体条件下的结构受力与流动压力密不可分。特别地,对于生物、医学、人体生理学、微流控芯片和动力器件所涉及的流体输运都需要清楚了解流场中的压力分布。例如红细胞在血管中的运动,气泡、液滴的运动等典型微小尺度流动的受力和复杂三维运动都必须首先清楚流场中的压力分布状况,才能通过计算分析获得。此外,针对微流体动力装置的设计与动力性能研究也与流体压力的分布密切相关。因此,压力分布的测量在微流体动力学分析以及微小动力机械优化设计中具有重要应用。
遗憾的是,目前有关微流体压力分布的精确测量还存在诸多困难。近年来国内外针对这一问题开展了研究以发展可靠性的压力传感器技术为主。国内方面,杨梅和于炜等[1]设计研制了基于梁膜结构的微压传感器,能够实现0~100Pa量级的压力测量。常莹和马炳和等[2]研发了以柔性衬底基阵列的微型压力传感器,安装于翼型外表面实现压力分布测量。国外不少学者对微尺度下压力传感器阵列作了深入的研究和开发。1994年,Pong等[3]开发了微通道沿程压力测量的芯片,针对氮气和氦气进行了测量,结果表明沿程压力分布和距离呈非线性关系,受努森数(Kn)的影响显著。Ko和Liu等[4]在复杂的微通道中集成了利用一种高分子聚合物材料制作的微压传感器阵列来研究流体的流动特性。Wang等[5]将成熟的硅体微加工技术和低温PDMS工艺方法结合起来制成柔性测压元件。Li和Luo等[6]提出了利用导电性的PDMS制作微压传感器的微流体应用研究。Foland和Liu等[7]设计和制作了一种基于导模共振的压力传感器,能够检测出PDMS微通道中的微压力的变化。Jung和Yang[8]提出了一种基于液态金属的薄膜压力传感器,能够通过软光刻技术集成到微流控系统中。Tsai和Nakamura等[9]设计了一种新的用于检测微流体装置内局部压力的方法,其原理是利用聚合物PDMS薄膜材料的变形,由于变形室中的变形使得感应区颜色强度发生变化,通过亮度和压力之间的对应关系来测量微流体装置中局部压力。Yeo和Yu等[10]提出了一种基于液体的薄膜微流体压力触觉传感器,并且具有很高的灵敏度、稳定性和灵活性。Song和Gillies等[11]开发了一种基于电感耦合的微流体压力传感器。Wu和Liao等[12]研发了一种基于离子液体电读出压力传感器,通过测量微流控装置内压力引起的电路特性的变化来实现压力测量。
本文对微小通道内压力分布测量方法开展研究。制作了以微应变片为压力传感元件的微压芯片,利用高精度二次测量仪表采集通道微应变片阵列受到流体压力产生的应变信号,在开展压力-应变标定实验的基础上获得微通道沿程压力分布。
1 流体分布式压力测量系统 1.1 测量系统设计并搭建了一套基于变形传感原理的微压测量装置系统,如图 1所示。其组成部分包括,微量注射泵、微压芯片、无线AP、多通道应变仪及计算机等。采用的应变仪型号为DH3818N-2,其最高分辨率可达0.5με(微应变),主要技术指标由表 1给出。系统设计原理和工作流程如下:在被测微通道两侧均匀分布应变式微压力传感元件(本文采用应变片作为测压元件,参数等详见下文),其引线分别接入多通道应变仪的对应测量端口。流体介质(气体或液体)在微通道中流动产生的压力使应变片产生变形,其微应变值通过应变仪测量获得,利用压力-应变标定函数实现压力测量。工作时,利用微量注射泵作为动力,以精确、均匀、恒定的速度推动其上固定的注射器向微通道注入流体介质。改变微量注射泵流量,应变片在不同流量下受到流体静压而产生变形,应变值由多通道应变仪采集并通过无线AP与计算机进行数据传输。由于应变值并非压力测量的目标数据,因此,需要通过标定实验建立应变与压力之间的函数关系。

|
| 图 1 测压系统 Fig.1 Pressure measurement system |
| 参数 | 技术指标 |
| 测量通道数 | 20 |
| 适用应变片电阻值 | 50~10000Ω |
| 应变片灵敏度系数 | 1.0~3.0自动修正 |
| 采样速率 | 2Hz/通道 |
| 测量应变范围 | ±30000με |
| 系统示值误差 | 不大于0.5% |
| 最高分辨率 | 0.5με |
采用聚甲基丙烯酸甲酯(PMMA)材料加工尺度为毫米到亚毫米量级的微细通道,利用热压成型工艺制成。在通道两侧具有一定间隔的位置处加工与通道联通的方腔,其开口面覆盖微应变片,制成微压芯片。在方腔处采集与其连接点的压力信号,从而获得通道沿程各点处的压力。
设计了3组不同尺寸的微压芯片,芯片结构与制作完成的实物图如图 2所示,尺寸参数由表 2给出。芯片由上下2层PMMA板高温热压键合而成,每组微压芯片上层板加工长直通道,通道两侧分别加工若干形状大小相同且均匀分布的方腔,相邻2个腔体之间的间距为5mm。矩形腔体覆盖微应变片,所测压力为流体压力与大气压之间的压差,即表压。
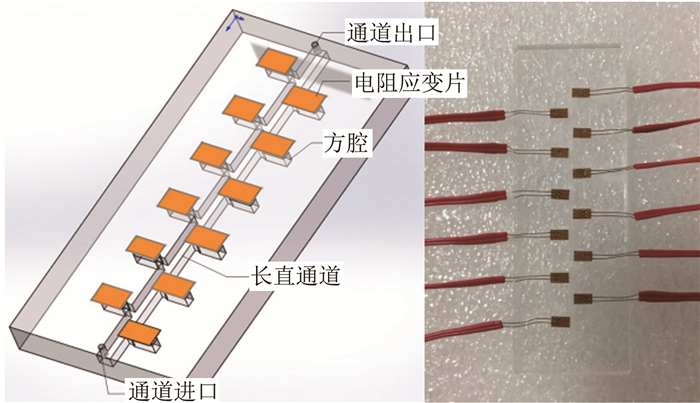
|
| 图 2 微压芯片 Fig.2 Pressure chip |
| 芯片 | 芯片尺寸/mm | 通道尺寸/mm | 方腔尺寸/mm |
| Type1 | 80×30×4 | 68×2.5×1 | 4×1.5×1 |
| Type2 | 80×30×4 | 68×1.5×1 | 3×1.5×1 |
| Type3 | 80×30×4 | 58×1×0.5 | 2×1×0.5 |
采用应变片作为压力传感元件,有如下诸多优点,包括:测量应变的灵敏度和精确度高,性能稳定、可靠,误差小于1%;应变片尺寸小,质量轻,结构简单,响应速度快;测量范围大,可测量弹性变形,也可测量塑性变形,变形范围可从1%~20%;适应性强;可在高温、超低温、高压、强磁场等恶劣环境下使用;便于多点测量、远距离测量和控制等。利用应变片感受流体静压作用产生变形,输出应变信号,通过标定后转化为流体压力值。本文选用日本生产的金属箔式应变片,根据被测对象的尺寸要求,定制了KFG-1和KFG-5这2种型号,主要参数如表 3所示。
| 参数 | KFG-1 | KFG-5 |
| 基底尺寸/mm | 4.8×2.4 | 9.4×2.8 |
| 敏感栅长/mm | 1 | 5 |
| 电阻值/Ω | 120.4±0.4 | 119.6±0.4 |
| 灵敏度系数/% | 2.13±1 | 2.09±1 |
根据应变测压原理,需建立压力与应变之间的函数关系,因此在进行测量之前,先要开展标定实验。标定系统由微注射泵、高精度微差压计、多通道应变仪以及计算机等组成,如图 3所示。其中图 3(a)为标定系统示意图,图 3(b)为该系统的实物图。
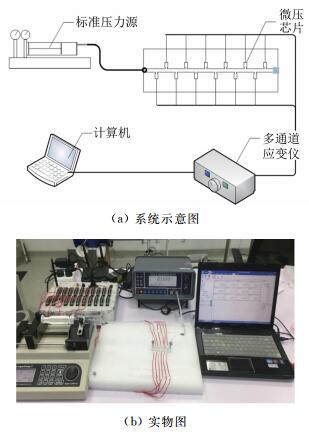
|
| 图 3 标定系统 Fig.3 Calibration system |
为了获得稳定的标定压力,将注射泵与微压芯片通道的进口端连接,对通道出口端进行密封。由于通道中的压力为数十到百帕量级,相应的标准压力源很难找到。因此本文采用将注射泵施加推力产生的静压作为标准压力,解决了标准压力源问题。由于出口端密封,通道内压力与注射泵推力容易实现平衡,测量平衡稳定状态下的压力值作为当前标准压力。与此同时,利用多通道应变仪测量各分布点应变片在该压力时的应变值。标定中,通过改变注射泵推进参数来改变标准压力值,则基于一组标准压力值与应变值之间的对应关系即可以确定,最后通过数据拟合的方法获得压力-应变函数关系。
为了获得标准压力值,高精度微压差计的使用是关键。本文采用英国Furness Controls公司生产的FCO510型高精度微差压计, 其压力测量范围为0~2000Pa,分辨率高达0.01Pa。
2.2 标定曲线和函数依次对3种通道的微压芯片开展标定实验。前2组芯片标定的最大压强是50Pa,每间隔5Pa作为1个标定区间,得到了10组标定结果。第3组微压芯片标定的最大压强为130Pa,每组标定之间的间隔为10Pa。最后得到全部35组应变值对应压强值的标定结果。标定曲线如图 4所示,其中图 4(a)和(b)分别有11个标定点,图 4(c)共13个标定点。
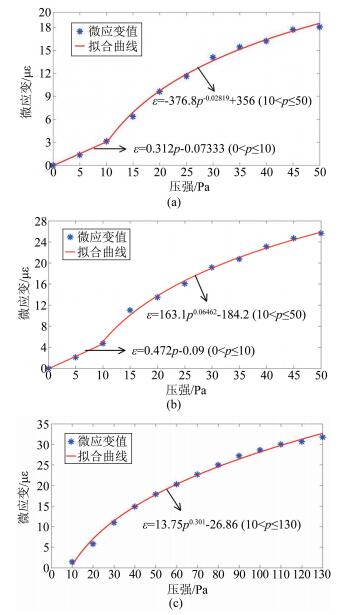
|
| 图 4 标定曲线和函数.(a)~(c)对应3种通道的情况 Fig.4 Calibration curves and functions. (a)~(c) for three kinds of channels, respectively |
在完成标定实验的基础上,利用微压测量系统,开展了微压芯片沿程压力的测量。本文采用气体作为流动介质,相应的实验方法同样适用于液体流动。实验时,分别取80、70、60及50mL/min等4种流量,利用注射泵进行输入。在不同流量下,测量应变片的应变值,利用图 4的标定函数,将应变值转化为压力值。对各点所获压力通过最小二乘拟合,获得沿程压力分布曲线,并和理论结果进行比对。
由于输入流量较小,属于低速流,因此采用不可压缩管流理论进行推导,得到沿程压力分布为,
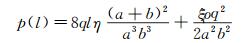 (1)
(1)
式中:p为距离通道出口位置为l(mm)的压强(Pa);q为气体流量(mL/min);η是空气的动力粘度(Pa·s);a和b分别是通道的宽度和深度(mm);ξ为局部阻力系数;ρ为密度(kg/m3)。
式(1)给出了距离通道出口位置压强的函数关系。由于通道沿程存在周期性测压腔体的分布,与完全封闭的长直通道结构有较大差别。为了简化分析,本文将这些腔体结构对流动的影响计入局部阻力损失,加上通道进出口的局部损失,成为通道阻力损失的重要组成部分。结合实测结果,对局部阻力系数进行调整,以修正长直通道的理论解。
对3个通道进行理论分析,分别取局部阻力损失占沿程阻力损失的60%、51%及32%。实验结果、拟合直线与理论直线由图 5给出。可以看到,测量点的压力呈现良好的线性分布,修正后的理论压力分布与之相吻合,平均偏差在5%以内。实验表明应变片的安装、应变测量以及标定等实验关键环节达到了预期结果。由此说明采用应变片方法测量微小尺度流动的压力具有可行性。此外,利用实验结果修正理论压力分布,也为实验确定局部损失提供了一种新思路。
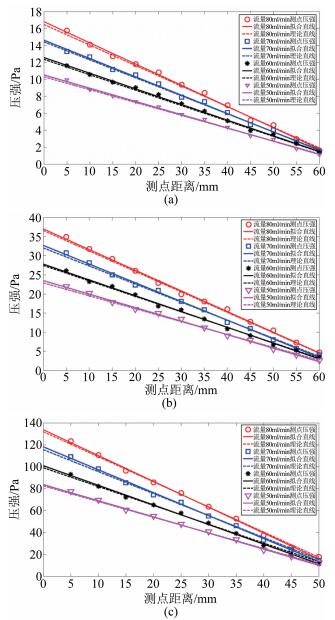
|
| 图 5 沿程压力测量值结果.(a)~(c)对应3种通道的情况 Fig.5 Measurement results of pressures along the channels.(a)~(c) for three kinds of channels, respectively |
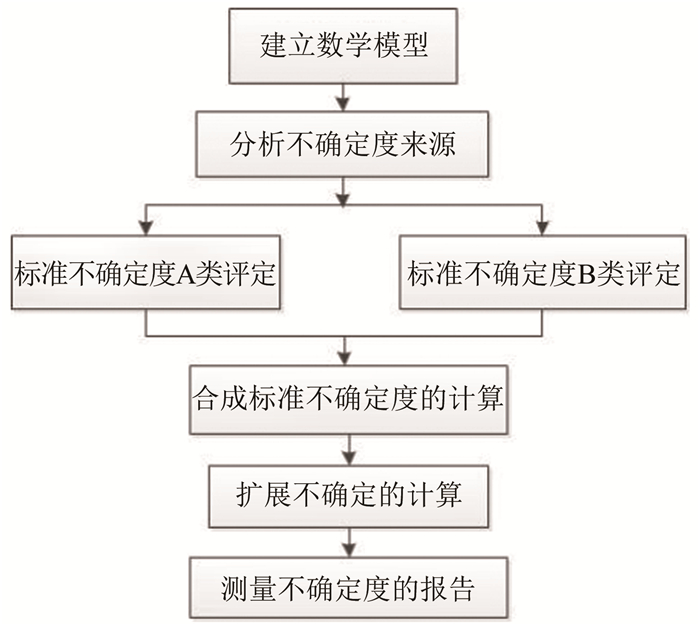
为进一步开展定量分析,对测量结果进行了不确定度的评定。不确定度评定过程如图 6所示[13]。
采用压力误差Δp作为被测量建立测量模型,即:
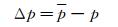 (2)
(2)
式中:p为压力值p的算术平均值,由下式确定。
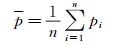 (3)
(3)
式中:n为应变信号采样数;pi为对应的第i次采样的压力测量值。
单次实验标准偏差为:
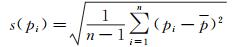 (4)
(4)
则输入量p的标准不确定度u(p)由下式计算:
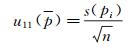 (5)
(5)
由多通道应变仪示值误差引入的标准不确定度记为u12(p),此不确定度分量采用B类方法进行评定。多通道应变仪使用说明书上提供的系统示值误差为不大于0.5%,按线性规律计算在测量点的此项标准不确定度值,为均匀分布,由下式计算:
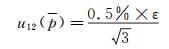 (6)
(6)
式中:ε是该点的应变测量值。
由多通道应变仪分辨率引入的标准不确定度u13(p),其分辨率为0.5,则区间半宽为0.25,属于均匀分布,计算公式为:
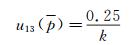 (7)
(7)
式中:k为包含因子,取值为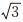
因多通道应变仪重复性引入的标准不确定度已经包含了多通道应变仪系统示值误差和分辨率引入的标准不确定度,所以最后只要取三者之中的最大值即可,即u1(p)=max(u11, u12, u13)。输入量p引入的标准不确定度分量为u2(p)。
由u1和u2进行合成获得合成不确定度。首先对式(1)求各变量的偏导数值获得灵敏系数C,
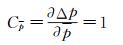 (8)
(8)
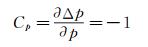 (9)
(9)
则合成标准不确定度按下式计算:
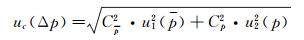 (10)
(10)
扩展不确定度是求测量结果区间的量,由合成标准不确定度的倍数进行表示,两者的乘积称为总不确定度,计算如下:
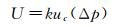 (11)
(11)
这里的倍数即为包含因子k,本文取为k=2。
由于实验共涉及3组不同微通道尺寸的压力测量,而且每组微通中距离流道进口不同距离的压力测量结果也不相同,因此需要对每组测压芯片的所有测量点进行不确定度的评定。根据以上公式,计算了所有测量点压力误差的不确定度,结果列入表 4~6中。从表中可以看到,第1组通道的相对扩展不确定度在0.26%~6.53%之间,第2组和第3组的相对扩展不确定度区间分别为0.29%~6.82%及0.15%~ 6.12%。可见测量误差不确定度分布区间较为集中,均未高于7%,体现了各压力测量点总体的一致性,测量结果具有较高的可信度。
| 测点距离 /mm |
测量不确定度/% | |||
| 流量 80mL/min |
流量 70mL/min |
流量 60mL/min |
流量 50mL/min |
|
| 5 | 2.16 | 0.45 | 0.96 | 2.71 |
| 10 | 0.68 | 1.87 | 1.03 | 0.83 |
| 15 | 1.32 | 0.52 | 0.26 | 0.75 |
| 20 | 1.51 | 2.98 | 2.57 | 1.24 |
| 25 | 2.94 | 3.01 | 3.81 | 3.08 |
| 30 | 1.27 | 1.34 | 1.89 | 1.39 |
| 35 | 3.84 | 3.73 | 2.75 | 3.79 |
| 40 | 2.11 | 1.29 | 0.94 | 2.13 |
| 45 | 3.76 | 2.84 | 3.76 | 3.88 |
| 50 | 4.18 | 5.17 | 6.13 | 1.91 |
| 55 | 3.97 | 3.26 | 2.32 | 5.46 |
| 60 | 6.53 | 6.02 | 4.75 | 5.73 |
| 测点距离 /mm |
测量不确定度/% | |||
| 流量 80mL/min |
流量 70mL/min |
流量 60mL/min |
流量 50mL/min |
|
| 5 | 2.05 | 2.49 | 2.08 | 2.17 |
| 10 | 1.62 | 1.86 | 1.07 | 2.38 |
| 15 | 1.96 | 0.36 | 2.43 | 0.29 |
| 20 | 0.77 | 1.03 | 1.75 | 1.04 |
| 25 | 0.84 | 2.68 | 2.16 | 3.18 |
| 35 | 1.04 | 1.39 | 1.18 | 0.36 |
| 40 | 3.27 | 3.12 | 2.94 | 3.77 |
| 45 | 2.83 | 1.18 | 1.36 | 1.64 |
| 50 | 4.65 | 3.42 | 6.76 | 6.73 |
| 55 | 3.29 | 2.07 | 1.61 | 5.41 |
| 60 | 6.73 | 5.26 | 6.82 | 4.95 |
| 测点距离/mm | 测量不确定度/% | |||
| 流量 80mL/min |
流量 70mL/min |
流量 60mL/min |
流量 50mL/min |
|
| 5 | 1.84 | 2.67 | 1.06 | 1.05 |
| 10 | 1.03 | 1.85 | 0.15 | 1.13 |
| 15 | 0.96 | 0.33 | 1.04 | 0.98 |
| 20 | 0.31 | 1.27 | 0.51 | 1.02 |
| 25 | 1.26 | 2.64 | 1.46 | 1.39 |
| 30 | 0.28 | 0.58 | 1.52 | 2.04 |
| 35 | 1.13 | 1.35 | 0.27 | 2.18 |
| 40 | 4.84 | 5.62 | 4.89 | 4.96 |
| 45 | 5.16 | 4.17 | 5.63 | 0.83 |
| 50 | 0.72 | 3.43 | 6.12 | 4.64 |
本文针对微流体分布式压力方法展开研究,自主设计并搭建了一套分布式微压测量系统。利用PMMA材料设计并制作了3组不同尺寸微通道芯片。采用高精度微压计对该微压芯片测量系统进行了标定,获得了压力和应变之间的标定曲线与标定函数。分别对3种微压芯片开展了4种不同流量的测量实验,将理论值与实验结果进行比对分析,结果表明3种微压芯片不同流量的实验点所获压力呈线性函数关系,与经过局部阻力修正的理论直线基本吻合。不确定度评定结果表明,压力误差的相对扩展不确定度在0.15%~6.82%之间,测量结果具有较高的有效性和可信度。本文的实验方法可用于毫米及亚毫米尺度通道的气体和液体以及多相流动的压力分布测量。
| [1] | 杨梅, 于炜, 张莹, 等. 梁-膜结构微压传感器研制[J]. 实验流体力学, 2010, 24(2): 74–76. Yang M, Yu W, Zhang Y, et al. Development of a beam-membrane structure micro-pressure sensor[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(2): 74–76. |
| [2] | 常莹, 马炳和, 邓进军, 等. 基于微型压力传感器阵列的翼面压力分布直接测量系统[J]. 实验流体力学, 2008, 22(3): 89–93. Chang Y, Ma B H, Deng J J, et al. Direct measurement system of pressure distribution on airfoil surface using micro pressure sensor array[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(3): 89–93. |
| [3] | Pong K C, Ho C M, Liu J Q, et al. Non-linear pressure distribution in uniform microchannels[C]. American Society of Mechanical Engineers, Fluids Engineering Division (Publication) FED, 1994, 197:51-56. https://www.researchgate.net/publication/284035378_Non-linear_pressure_distribution_in_uniform_microchannels |
| [4] | Ko H S, Liu C W, Gau C, et al. Flow characteristics in a microchannel system integrated with arrays of micro-pressure sensors using a polymer material[J]. Journal of Micromechanics and Microengineering, 2008, 18(7): 75016. DOI:10.1088/0960-1317/18/7/075016 |
| [5] | Wang L, Ding T, Wang P. Thin flexible pressure sensor array based on carbon black/silicone rubber nanocomposite[J]. IEEE Sensors Journal, 2009, 9(9): 1130–1135. DOI:10.1109/JSEN.2009.2026467 |
| [6] | Li H, Luo C X, Ji H, et al. Micro-pressure sensor made of conductive PDMS for microfluidic applications[J]. Microelectronic Engineering, 2010, 87(5-8): 1266–1269. DOI:10.1016/j.mee.2009.11.005 |
| [7] | Foland S, Liu K, Macfarlane D, et al. High-sensitivity microfluidic pressure sensor using a membrane-embedded resonant optical grating[J]. Sensor, 2011: 101–104. |
| [8] | Jung T, Yang S. Highly stable liquid metal-based pressure sensor integrated with a microfluidic channel[J]. Sensors, 2014, 15(5): 11823–11829. |
| [9] | Tsai C H D, Nakamura T, Kaneko M. An on-chip, electricity-free and single-layer pressure sensor for microfluidic applications[C]. International Conference on Intelligent Robots and Systems, IEEE, 2015. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=7353369 |
| [10] | Yeo J C, Yu J, Zhao M K, et al. Wearable pressure sensors based on flexible microfluidics[J]. Lab on a Chip, 2016, 16(17): 3244–3250. DOI:10.1039/C6LC00579A |
| [11] | Song S H, Gillies G T, Begley M R, et al. Inductively coupled microfluidic pressure meter for monitoring of cerebrospinal fluid shunt function[J]. Journal of Medical Engineering and Technology, 2012, 36(3): 156–162. DOI:10.3109/03091902.2011.645943 |
| [12] | Wu C Y, Liao W H, Tung Y C. A seamlessly integrated microfluidic pressure sensor based on an ionic liquid electrofluidic circuit[C]. International Conference on Micro Electro Mechanical Systems. 2011:1087-1090. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5734618 |
| [13] | 张有康, 甘蓉. 压力传感器测量中不确定度的评定[J]. 中国测试技术, 2005, 31(6): 25–26. Zhang Y K, Gan R. Evaluation of strain gauge measurement uncertainty of pressure transducer[J]. China Measurement Technology, 2005, 31(6): 25–26. |