2. 中国空气动力研究与发展中心 设备设计与测试技术研究所, 四川 绵阳 621000
2. Facility Design and Instrumentation Institute, China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China
激光通过流场产生的瑞利散射光包含气体的密度、温度和速度信息,其中散射光的信号强度与密度有关、谱线宽度与温度有关、频率的移动与速度有关,因此可用于测量流场密度、温度和速度,如图 1所示。1999年以来,该技术在NASA刘易斯研究中心和格林研究中心发展并应用,在速度及湍流度测量方面开展的试验与温度和密度测量相比较要多一些[1-9],并主要针对马赫数小于3的流场诊断。

|
| 图 1 瑞利散射测量参数原理示意图 Fig.1 Rayleigh scattering measurement principle |
中国空气动力研究与发展中心设备设计与测试技术研究所2014年成功研制了瑞利散射速度及湍流度测量系统,测量了马赫数1.8喷管(总压0.8MPa)自由射流远场(离喷管出口0.2m)的速度及湍流度[10],湍流度为6.98%,与热线风速仪测量结果7.08%较为一致;2015年测量了0.3m×0.3m跨超声速风洞马赫数3和总压0.46MPa的流场速度及湍流度,湍流度为0.7%。
高超声速流场也希望利用该技术对流场速度和湍流度进行测量,但对该技术在高超声速流场进行速度和湍流度测量的适用性缺乏了解。于是预先在Φ0.3m高超声速低密度风洞中采用该系统进行了Ma5、Ma6、Ma12流场速度和湍流度测量的初步探索。
1 原理和实验设备 1.1 原理根据光学多普勒效应,激光光源和气体分子发生相对运动时,经运动气体分子散射后的激光相对于入射激光将产生多普勒频移ΔνD,其大小与运动气体的速度V、散射光与入射光的夹角θ有关(见图 2),相互关系表示为:[10]

|
| 图 2 多普勒频移几何示意图 Fig.2 Geometric sketch of Doppler frequency-shift |
 (1)
(1)
式中:λ为入射激光波长;L为激光入射方向单位矢量;S为散射方向单位矢量;Vk为流场速度V在(S-L)方向的分量。
文中提到的湍流度是指速度脉动,即单位时间内样本速度与平均速度的均方根偏差,湍流度I的计算如下式:
 (2)
(2)
实验在中国空气动力研究与发展中心(CARDC)的Φ0.3m高超声速低密度风洞(风洞代号FD-17)上进行,该风洞是一座典型的高压下吹、真空抽吸的暂冲运行风洞。该风洞目前配备有型面喷管8套,喷管出口马赫数为5~12;锥形喷管3套,喷管出口马赫数为12、16和24,所有喷管出口直径均为Φ300mm。介质为氮气或空气,实验根据不同的状态可分别选用石墨电阻加热器或储热式加热器进行加热或不加热。本次实验的马赫数为Ma5、Ma6和Ma12, 介质为氮气和空气。测量参数包括来流总压、总温,试验段内的静压、流场速度和湍流度。风洞和测试系统如图 3所示。

|
| 图 3 风洞主体和测试设备图 Fig.3 Wind tunnel and measurement facilities |
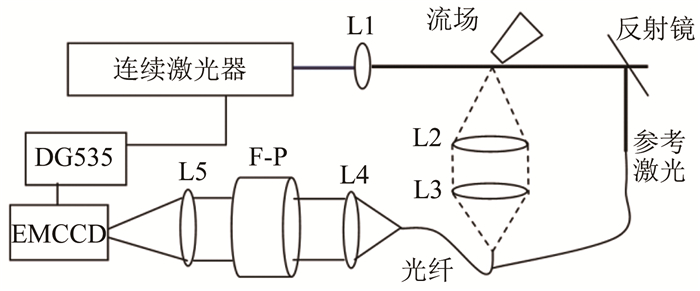
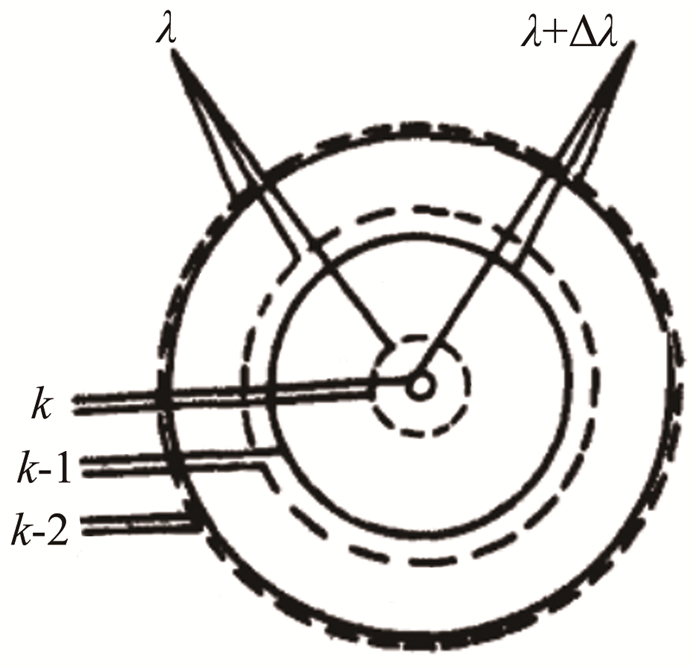
总压采用CYG105型压阻传感器测量,量程分别0~4MPa和0~10MPa,根据总压范围选用;皮托压力采用CYG219(量程0~10kPa)和CYG222(量程0~2500Pa)型压阻传感器测量;试验段内的静压用MKS电阻真空计测量;流场速度和湍流度用瑞利散射测速系统测量。该系统主要由激光光源、散射光收集传输光路、F-P干涉仪、同步时序控制器及ICCD相机组成,系统如图 4所示,光路示意图如图 5所示。激光器为大功率连续激光器,提供波长为532nm的光源,激光器输出的激光经透镜L1会聚后照射被测流场,流场中空间测点的散射光经透镜组L2和L3耦合进入一Y型光纤,经光纤传输后的散射光通过透镜L4形成平行光后照射F-P干涉仪,由透镜L5将多光束干涉形成的干涉圆环成像至EMCCD相机,整个速度测量系统的同步时序控制由一台DG535实现。当流场速度为0时,进入F-P干涉仪的散射光的波长与激光器输出的激光波长均为λ,其在F-P干涉仪像平面将形成一系列同心干涉圆环;当流场存在一定速度时,由于多普勒效应,进入F-P干涉仪的散射光波长将变为λ+Δλ,其在F-P干涉仪像平面形成的同心干涉圆环半径将随之改变(见图 6),实验中,通过ICCD采集分析不同时刻同一级次干涉圆环半径的变化,即可获得流场速度引起散射光波长(频率)的改变量,进而获得时间分辨的流场速度及湍流度测量结果。

|
| 图 4 瑞利散射干涉测速系统组成图 Fig.4 Rayleigh scattering interferometer velocity measurement system |
|
| 图 5 瑞利散射干涉测速系统光路示意图 Fig.5 Optical path sketch of Rayleigh scattering interferometer velocity measurement system |
|
| 图 6 原波长干涉环与频移干涉环示意图 Fig.6 Interferometer rings sketch of original wavelength and shift |
本次实验来流状态共5个,如表 1所示。
| 序号 | 喷管名义Ma | 介质 | 总压/MPa | 总温/K |
| 1 | 5 | 氮气 | 0.2 | 288 |
| 2 | 5 | 氮气 | 0.2 | 533 |
| 3 | 6 | 氮气 | 0.31 | 288 |
| 4 | 6 | 空气 | 0.34 | 441 |
| 5 | 12 | 氮气 | 5.53 | 628 |
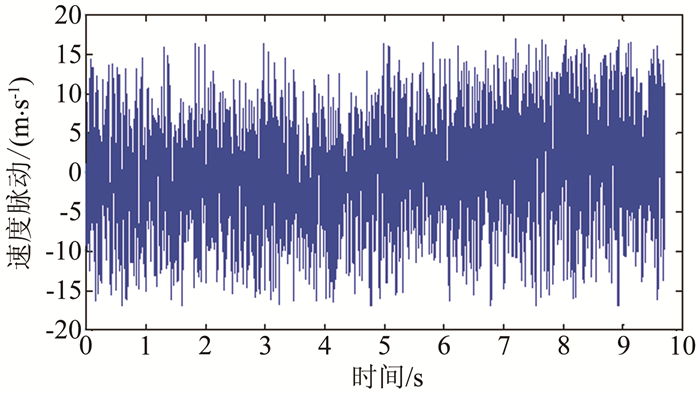
状态1流场中散射光信号较强,如图 7所示,测点位置距喷管出口端面中心点x=206mm(轴向),y=40mm(侧向),z=0mm(纵向),速度结果为698m/s。查询该状态采用皮托压力探针流场校测结果,该点Ma为5.064,速度为707m/s,瑞利散射测量结果与之偏差为1.3%。测量的速度脉动如图 8所示,湍流度为0.93%。

|
| 图 7 状态1流场散射光照片 Fig.7 Rayleigh scattering photo in flow field (case 1) |
|
| 图 8 状态1流场速度脉动测量结果 Fig.8 Velocity fluctuation measurement result (case 1) |
状态2流场中散射光信号很弱,通过延长ICCD相机的曝光时间,降低帧频,关闭分光镜来的参考光,采用风洞内的壁面反射光为参考,测点位置同状态1,测量的速度为961m/s。由于状态2无流场校测数据,采用状态1的校测Ma为5.064,该状态速度为963m/s,瑞利散射测量结果与之偏差为0.2%。
通过状态1和2的比较,差别是状态2提高了总温,可分析出状态1流场中有冷凝液滴导致散射光增强。结合原NPLS实验结果,状态1条件下在NPLS实验中没注入粒子时看不到散射光,原因可能是本次实验所用的氮气管路中混入了微量的空气才导致的冷凝,氮气介质未出现冷凝,从速度测量结果对比分析,该状态下出现的冷凝影响不大。
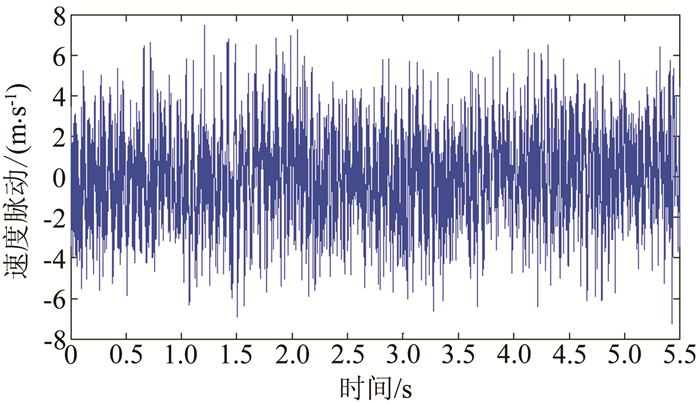
状态3流场中散射光信号较强,测点位置同状态1,测量的速度为746m/s。查询该状态采用皮托压力探针流场校测结果,该点Ma为6.035,速度为738m/s,瑞利散射测量结果与之偏差为1.07%。测量的速度脉动如图 9所示,湍流度为0.3%。
|
| 图 9 状态3流场速度脉动测量结果 Fig.9 Velocity fluctuation measurement result (case 3) |
在状态3下,测量了返回舱模型绕流流场中一个点的速度。模型由973项目组提供,模型大底直径为Φ55mm,模型实验时为0°迎角。实验过程中通过流场和模型绕流流场的散射光照片如图 10所示,在喷管出口流场中散射光较强,与图 6相似,而在模型绕流区散射光很弱,原因是大钝头产生的弓形激波加热作用,导致气体中冷凝的液滴气化。测点位于波后,测点位置距离模型大底拐点轴向40mm,纵向4mm,侧向0mm,如图 10中的“+”所示。由于测点信号非常弱,即使延长EMCCD相机的曝光时间效果也不明显,在主气流中加入些许的TiO2纳米粒子,模型绕流场中的散射光会有偶尔的强信号,通过EMCCD相机捕捉实验过程中不连续的强信号,可测量出速度,测点在状态3下的速度为637m/s。图 11为状态3来流返回舱模型绕流流场数值模拟结果,测点位置的速度计算结果为628m/s,瑞利散射测量结果与之偏差为1.4%。

|
| 图 10 返回舱模型在状态3流场中散射光照片 Fig.10 Rayleigh scattering photo in flow field around re-entry module (case 3) |
|
| 图 11 返回舱模型绕流流场数值模拟结果(状态3) Fig.11 Numerical simulation result of flow field around re-entry module (case 3) |
状态4流场中散射光信号弱,测点位置同状态1,采用和状态2下相同的措施,测量的速度为886m/s。采用状态3的校测Ma为6.035,该状态速度为898m/s,瑞利散射测量结果与之偏差为1.3%。
状态5流场中散射光信号较强,测点位置距喷管出口端面中心点x=117mm(轴向),y=30mm(侧向),z=0mm(纵向),速度结果为1204m/s,湍流度为0.52%。采用状态5的校测Ma为12.718,测点在该状态速度为1125m/s,瑞利散射测量结果与之偏差为6.5%。在喷管出口流场中散射光较强,与图 7相似,而在模型绕流区散射光很弱,原因是大钝头产生的弓形激波加热作用,导致气体中冷凝的液滴气化。
在状态5下,同样测量了返回舱模型绕流流场中一个点的速度,情况与做法和状态3下的类似;测点位置位于模型上方,距离模型大底拐点轴向20mm,纵向10mm,侧向0mm,如图 12所示;测点在状态5下的速度为520m/s,采用数值模拟方法得到测点位置的速度计算结果为880m/s,瑞利散射测量结果与之偏差较大,为69%。原因可能是TiO2纳米粒子在Ma12流场中的粒子跟随性不够。采用基于DSMC的稀薄两相流数值方法分别仿真了10、50和100nmTiO2粒子在Ma12来流时的返回舱模型绕流流场的情况,气相和固相的速度云图如图 12所示,沿测点轴线的速度分布和实验结果如图 13所示,表明10nm粒径的跟随性优于50和100nm粒径的粒子,气体实验中采用的是标称50nm的粒子,实际使用中出现会出现团聚效应,导致实际粒径更大,偏离实际的气流速度更大。

|
| 图 12 返回舱模型绕流气固两相流数值模拟结果(状态5) Fig.12 Numerical simulation result of gas-particle two-phase flow field around re-entry module (case 5) |
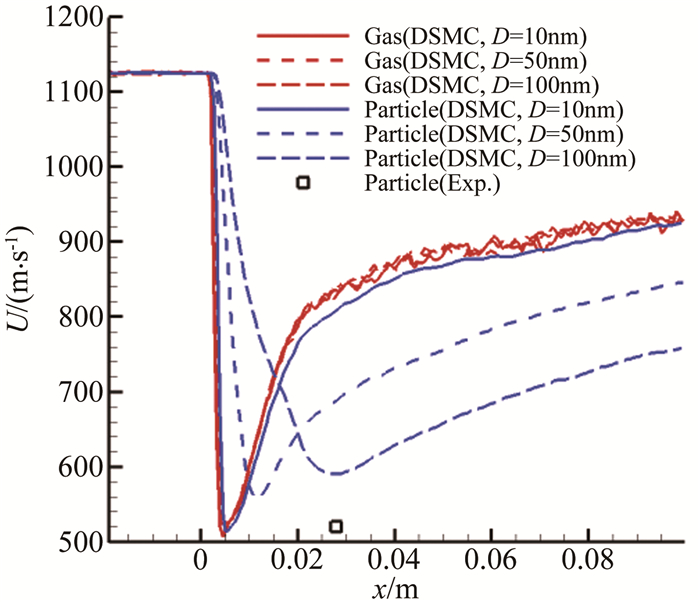
|
| 图 13 不同粒径的流场速度分布结果(状态5) Fig.13 Velocity distribution of particles and gas with different diameters(case 5) |
(1) 通过实验验证了瑞利散射速度和湍流度测量系统在高超声速流场中应用的可行性,发现了存在的问题,提出了相应的解决措施。主要是高超声速流场中激光散射光弱,需要加入部分容易液化的气体或小尺度固体粒子,在增强散射光信号情况下保持好的跟随性。
(2) 采用瑞利散射测量系统测量了Φ0.3m高超声速低密度风洞速度和湍流度,湍流度在1%以内,速度测量结果与流场校测偏差最大1.3%。
(3) 采用瑞利散射测量系统测量了返回舱模型绕流流场中的速度,Ma6时实验结果与数值模拟一致,Ma12时由于粒子跟随性不够导致结果偏差较大。
(4) 实验中发现型面喷管Ma5~12流场存在一定程度的冷凝现象,这也说明瑞利散射测量系统是用于判断流场冷凝的一种手段,初步分析原因是氮气介质中混入了空气所致,后续实验中有待进一步证实。
| [1] | Seasholtz R G, Panda J. Rayleigh scattering diagnostic for dynamic measurement of velocity and temperature[R]. AIAA-99-0641, 1999. http://arc.aiaa.org/doi/abs/10.2514/6.1999-641 |
| [2] | Panda J, Seasholtz R G. Velocity and temperature measurement in supersonic free jets using spectrally resolved rayleigh scattering[R]. AIAA-99-0296, 1999. http://arc.aiaa.org/doi/abs/10.2514/6.1999-296 |
| [3] | Seasholtz R G, Panda J. Rayleigh scattering diagnostic for simultaneous measurements of dynamic density and velocity[R]. AIAA-2000-0642, 2000. |
| [4] | Seasholtz R G, Panda J, Elam K A. Rayleigh scattering diagnostic for dynamic measurement of velocity fluctuations in high speed jets[R]. AIAA-2002-0827, 2002. http://arc.aiaa.org/doi/abs/10.2514/6.2001-847 |
| [5] | Seasholtz R G, Panda J, Elam K A. Rayleigh scattering diagnostic for measurement of velocity and density fluctuation spectra[R]. AIAA-2002-0827, 2002. https://arc.aiaa.org/doi/abs/10.2514/6.2002-827 |
| [6] | Bivolaru D, Danehy P M, Gaffney R L, et al. Direct-view multi-point two-component interferometric Rayleigh scattering velocimeter[R]. AIAA-2008-236, 2008. https://arc.aiaa.org/doi/abs/10.2514/6.2008-236 |
| [7] | Mielke A F, Elam K A, Sung C J. Multiproperty measurements at high sampling rates using rayleigh scattering[J]. AIAA Journal, 2009, 47(4): 2009, 850–862. |
| [8] | Mielke-Fagan A F, Elam K A, Clem M M. Multiple point mass flux measurement system using rayleigh scattering[R]. AIAA-2009-528, 2009. http://arc.aiaa.org/doi/abs/10.2514/6.2009-528 |
| [9] | Mielke-Fagan A F, Clem M M, Elam K A, et al. Progress on a rayleigh scattering mass flux measurement technique[R]. AIAA-2010-856, 2010. http://arc.aiaa.org/doi/abs/10.2514/6.2010-856 |
| [10] | 陈力, 杨富荣, 苏铁, 等. 基于法布里-珀罗干涉仪的瑞利散射测速技术研究[J]. 光子学报, 2015, 44(1): 207–210. Chen L, Yang F R, Su T, et al. Interferometric rayleigh scattering velocimetry using a fabry-perot interferometer[J]. Acta Photonica Sinica, 2015, 44(1): 207–210. |



