高超声速颤振试验是高超声速飞行器防颤振设计和高超声速颤振及非定常气动力问题研究的重要手段。20世纪50~60年代,美国NASA、美国空军实验室等科研机构建立了高超声速风洞颤振试验技术,并开展了一系列高超声速风洞颤振试验研究,有报道的最高试验马赫数达15.4。研究人员通过试验研究了舵翼面翼型形状、翼型厚度、迎角、前缘钝度以及翼身干扰等对舵翼面气动弹性特性的影响[1-7]。这一时期的大量试验数据支撑了高超声速飞行器的研制,如X-15高超声速试验机和航天飞机等;此外试验数据也对高超声速非定常气动力计算技术和商业软件的发展提供了支撑。20世纪60年代,国内航空航天研究单位也开展了诸多颤振试验研究,但试验马赫数最高为4.0,未及高超声速范围,相关研究也多见诸各研究院所的内部技术报告。
近年来在型号需求牵引和基础研究项目资助下,高速风洞颤振试验技术得到了进一步发展。中国航天空气动力技术研究院一直致力于航天飞行器及导弹等舵翼面结构高速风洞颤振试验及技术研究。1996年[8]冯明溪等在中国航天空气动力技术研究院FD-06风洞中利用颤振试验投放装置开展了舵面颤振试验研究,试验马赫数为1.5、2.0、2.5和3.0。2001年白葵等[9]在FD-06风洞开展了有迎角超声速舵面颤振试验,试验迎角达到10°~12°,试验验证了亚临界试验技术;杨炳渊等[10]研究了基于阻尼外推法和稳定参数法的颤振试验亚临界技术。2009年冉景洪等[11]对颤振试验中常用的激励方法和模态参数辨识方法进行了研究,季辰等设计了亚跨超风洞舵面颤振试验装置,在CG-01亚跨声速风洞中研究了NACA0012矩形舵的亚跨声速颤振特性,采用ARMA的参数辨识方式进行颤振边界的预测,试验马赫数0.3~0.75[12]。
在飞机高速风洞颤振试验研究方面:1998年钱卫等[13]在中国航空工业空气动力研究院FL-2风洞中以某小展弦比三角翼带外挂导弹和某大展弦比长直翼的跨声速颤振模型风洞试验为依托,对包括模型设计、风洞运行、模型亚临界响应测量与数据处理等试验各技术环节的特点进行了研究。2009年路波等[14]与俄罗斯中央流体研究院(TsAGI)合作建立了基于中国空气动力研究与发展中心FL-26跨声速风洞的飞机全模颤振试验悬浮支撑系统。2012年郭洪涛等[15]在FL-26风洞中研究了某战斗机的全模颤振特性,验证了全模试验技术,试验马赫数0.7~1.1;2015年,其又研究了连续变动压颤振试验技术和基于Pick-Hold法的亚临界颤振边界预测技术[16]。2016年闫昱等[17]研制了基于中国空气动力研究与发展中心FL-23亚跨超风洞的颤振投放系统,开展了跨声速和超声速颤振试验研究,试验马赫数0.8~2.0。
为了将颤振试验的马赫数进一步拓展到高超声速范围,并通过高超声速风洞研究舵、翼面颤振及非定常气动力问题,2015年,季辰等[18]提出利用现有高超声速风洞开展高超声速颤振试验的研究方案,设计了基于中国航天空气动力技术研究院FD-07高超声速风洞的颤振试验装置,建立了高超声速风洞阶梯变动压亚临界颤振试验技术,采用薄翼模型首次开展了高超声速颤振试验研究,试验马赫数5和6;陈丁等[19]应用双目视觉技术,对试验中的模型变形进行了测量和研究。本文在此试验技术和研究的基础上,建立了基于连续变动压开车方式的高超声速颤振试验方法,采用一组具有相同结构动力学特性的模型对高超声速颤振试验中的亚临界颤振边界预测方法、颤振边界预测精度以及风洞变动压速率对颤振结果的影响进行了研究。此外,由于连续变动压吹风时间较长,本文还对试验中模型的气动加热问题进行了测量研究。
1 试验设备和模型 1.1 风洞中国航天空气动力技术研究院FD-07风洞为暂冲式高超声速风洞,试验段喷口直径500mm。风洞以空气作为试验介质,通过更换喷管可实现马赫数为4.5至8.0的试验能力。试验总压变化范围约在1.0~8.0MPa之间。试验动压可以在固定马赫数下实现阶梯变化或连续变化。风洞动压可通过改变来流总压实现调节,如公式(1)所示:
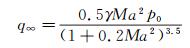 (1)
(1)
式中:q∞表示来流动压;γ表示气体比热比;Ma表示马赫数;p0表示试验总压。
1.2 数据采集和测量系统 1.2.1 振动测量试验采用东方所Coinv INV3060A数据采集仪(见图 1),可实现16通道的数据并行采集,采样精度最高达51.2kHz。地面振动试验采用加速度计测量模型模态振型及频率;风洞试验中采用应变电桥测量模型振动参数。

|
| 图 1 数据采集系统 Fig.1 Data acquisition system |
采用InfraTec Image IR8325红外热像仪对试验中的舵面模型温度分布进行测量。红外热像仪采用制冷型碲镉汞焦平面探测器,探测器为640pixel×512pixel,热灵敏度25mK@25℃,测温范围10~1200℃,测温精度±1%。红外热像仪安装在风洞试验段驻室外壁平台上,如图 2所示。

|
| 图 2 红外热像仪 Fig.2 Infrared thermal imager |
此外,试验中还采用纹影仪观察试验段模型的流场情况。
1.3 试验装置此次试验采用文献[18]所示的高超声速风洞颤振试验装置。该试验装置安装于风洞试验段驻室内,由模型支撑系统和保护系统组成。模型支撑系统具有较高刚度,能够满足弹性翼面模型和舵面模型支撑需求;保护系统采用保护罩实现模型保护,使用时能够将翼面模型隔离于流场之外以保护模型免受风洞起动/关车的流场冲击以及颤振的破坏。
1.4 试验模型试验模型为一组具有相同结构动力特性和气动特性设计的非对称钝前缘模型,由根部合金钢矩形梁悬臂支撑。模型采用隔热设计,分为2部分:一部分为等厚弹性芯板,其平面形状包括矩形支撑梁和梯形翼面部分,材料为合金钢,主要提供模型的刚度和质量特性;另一部分为泡沫舵面,将梯形翼面芯板包围以防止气动加热过快传递至金属芯板,并同时达到维形作用。
有限元计算(FEM)得到模型低阶频率如表 1所示,一阶频率32.3Hz,二阶频率55.8Hz,二阶和一阶频率比为1.73;振型如图 3所示,一阶振型主要为翼面弯曲,二阶振型主要为翼面扭转。
| Frequency/Hz | Frequency ratio | Damping ratio/(%) | |||
| f1 | f2 | f2/f1 | ξ1 | ξ2 | |
| FEM | 32.3 | 55.8 | 1.73 | -- | -- |
| GVT F5 | 33.5 | 55.7 | 1.66 | 0.31 | 0.41 |
| GVT F6 | 32.1 | 54.2 | 1.69 | 0.33 | 0.32 |

|
| 图 3 计算模态振型 Fig.3 Calculation mode shapes |
风洞试验前,将模型安装于试验装置上并进行地面振动试验(GVT),以检验模型是否安装正确同时测量安装状态下模型的频率、振型和阻尼特性。表 1列出了本试验采用的F5模型和F6模型在安装状态的地面振动试验结果,对比发现由于加工误差等诸多因素的影响,模型的结构频率和阻尼比略有偏差。
2.2 风洞颤振试验试验采用连续变动压的开车方式,将流场测量与模型振动测量同步,试验中保持马赫数不变,通过持续增加总压实现动压的增加,直到模型发生颤振。试验采用粘贴于模型根部的应变片测量模型振动,纹影仪观测模型附近流场,红外热像仪测量模型表面温度分布。
试验过程由如下步骤组成:(1)弹出模型保护罩,以低动压起动风洞并开始数据采集;(2)控制风洞并使之到达试验马赫数;(3)流场稳定后撤出保护罩;(4)缓慢增加动压直至模型发生颤振;(5)颤振发生或即将发生时弹出保护罩;(6)风洞关车,停止试验。
本期试验研究中,模型F5的试验马赫数为4.95;模型F6的试验马赫数为5.95。
3 试验结果与分析试验条件下模型的纹影图如图 4所示,由图可见激波的位置,并且模型周围流场良好,未受到其他部件干扰;舵面与反射板之间的间隙能够使得舵面根部流场远离反射板边界层的干扰。

|
| 图 4 模型纹影图 Fig.4 Schlieren photograph of the model |
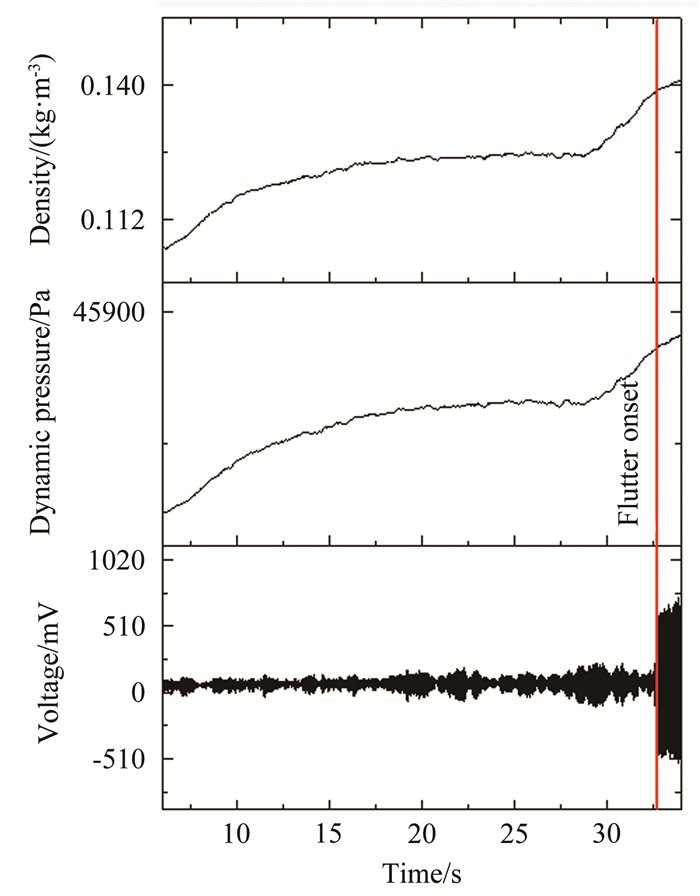
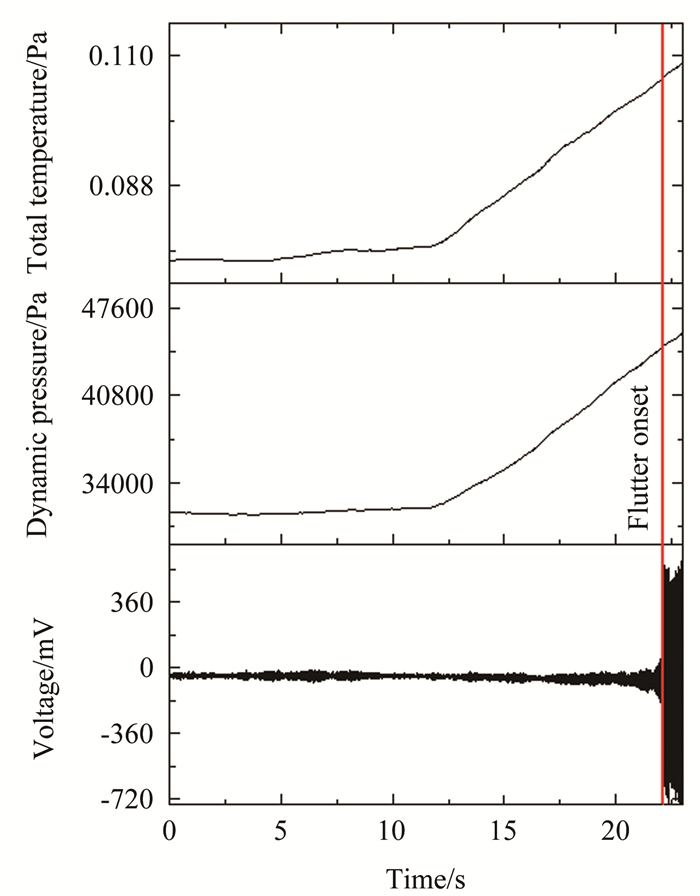
试验中测量的模型振动响应以及流场动压、密度和总压如图 5和6所示。图中可以看到,随着动压增加,模型振幅趋于增大,并最终振动发散。由试验数据可以直观判读得到模型的颤振动压qfm、试验密度ρ以及试验总温Tt等参数。颤振频率ff可由颤振发生时的时域数据经过快速傅里叶变换得到。
|
| 图 5 F5模型高超颤振试验(Ma=4.95) Fig.5 F5 hypersonic flutter test (Ma=4.95) |
|
| 图 6 F6模型高超颤振试验(Ma=5.95) Fig.6 F6 hypersonic flutter test (Ma=5.95) |
各个模型的颤振参数如表 2所示。
| Model | Mach number | qfm /(104Pa) |
ρ /(kg·m-3) |
ff/Hz | Tt/K |
| F5 | 4.95 | 4.372 | 0.1392 | 40.2 | 378.2 |
| F6 | 5.95 | 4.412 | 0.1059 | 39.1 | 477.3 |
模型在马赫数4.95时的颤振动压qfm为4.372×104Pa,颤振频率ff为40.2Hz,颤振时的密度ρ为0.1392kg/m3,总温Tt为378.2K。
马赫数5.95时的颤振动压qfm为4.412×104Pa,颤振频率ff为39.1Hz,颤振时的密度ρ为0.1059kg/m3,总温Tt为477.3K。
在试验马赫数范围内,该模型的颤振动压随着马赫数的增加而增加。
3.2 频谱特性分析颤振试验中,为了研究颤振模型的频率耦合特性,既希望从频域分析其频谱特性,辨别信号的频率成分,又希望从时域角度去辨别各个频率分量随着时间的变化趋势,即各阶频率随着动压增加的耦合趋势。
本文采用了短时傅里叶变换分布时频域分析方法[20-21]对模型振动响应信号进行了时频谱分析,研究试验中模型各阶模态频率随时间或动压增加的变化情况。
对于离散信号x(n),其离散短时傅里叶变换可以表示为:
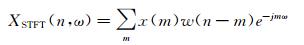 (2)
(2)
式中:w(n)为窗函数,本文采用Hamming窗。
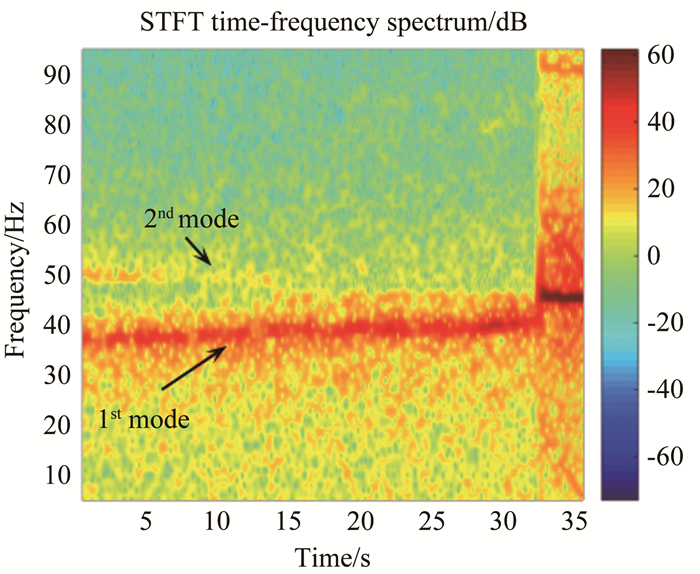
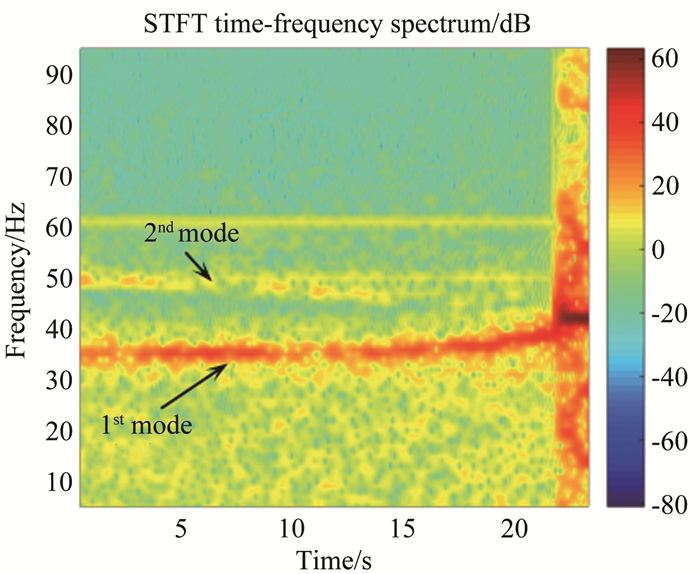
图 7和8为模型颤振试验全程的短时傅里叶时频谱,结合图 5和6可以看出,随着动压的增加,模型一阶频率上升,二阶频率下降,并最终两阶频率发生聚合且振动能量越来越大。由此可以判断,试验模型在马赫数4.95和5.95情况下发生的是由于一、二阶模态(弯扭)耦合引起的经典颤振。由频谱图色温可以看出,随着动压增加最终一阶振动发散。
|
| 图 7 时频谱图(F5, Ma=4.95) Fig.7 Time-frequency spectrum (F5, Ma=4.95) |
|
| 图 8 时频谱图(F6, Ma=5.95) Fig.8 Time-frequency spectrum (F6, Ma=5.95) |
采用试验中的亚临界振动数据,对亚临界颤振边界预测方法在高超声速颤振试验中的应用进行了研究。首先对试验数据进行了分段截取,并对每段数据采用模态参数识别方法辨识阻尼和频率。文献[8]介绍了多种常用的模态参数辨识方法。为了尽量增加数据点,本文在截取数据时每段截取512个数据点,相邻数据段有75%的数据量重复。
在辨识模态参数的基础上,本文采用颤振余度法和阻尼比外推法对颤振边界进行了预测。
3.3.1 颤振余度法颤振余度法的概念最先由Zimmerman和Weissenburger提出,该方法将由质量、刚度和阻尼组成的气动弹性力学系统视为一个控制系统,采用控制系统中的Routh稳定性判据评估这个动力学系统的稳定性。对于两自由度系统,其特征方程为一个四次多项式:
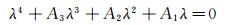 (3)
(3)
Routh稳定性判据可表示为:
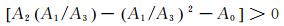 (4)
(4)
对于两自由度系统,用于评估稳定性的颤振余度F为与颤振相关的两阶模态频率ω1、ω2和模态阻尼系数β1、β2的函数:
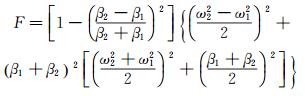 (5)
(5)
颤振余度由正变为0时,即表示系统开始不稳定,即颤振发生。
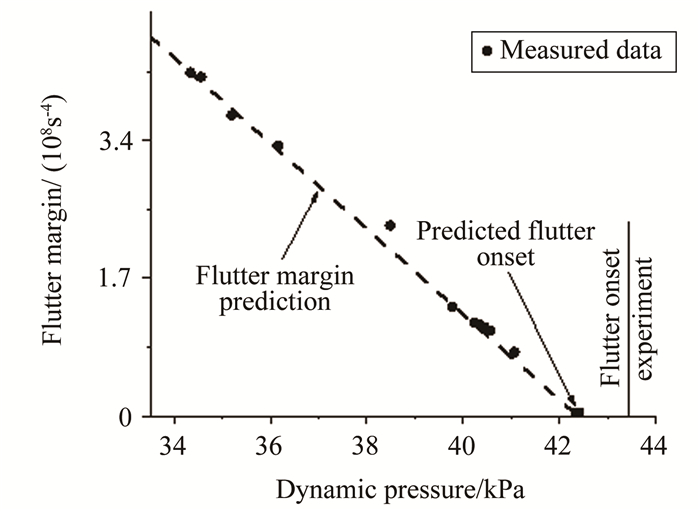
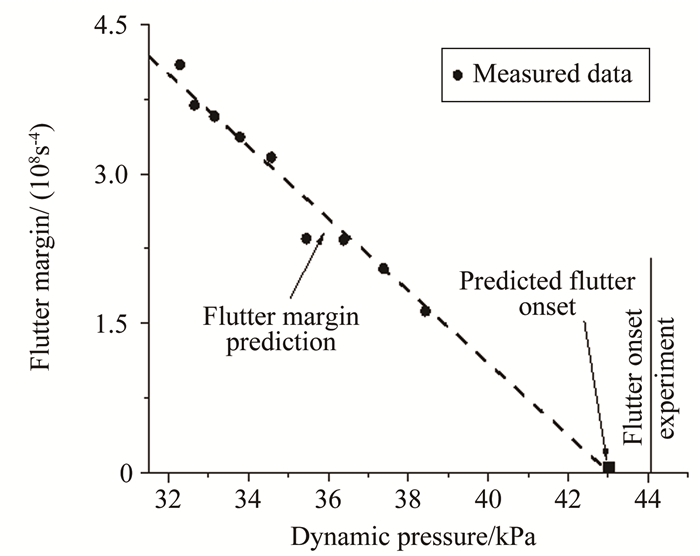
图 9~10为试验模型颤振余度随动压变化的曲线,由此外推得到模型在马赫数4.95时的颤振动压qff为4.241×104Pa,马赫数4.95时的颤振动压qff为4.305×104Pa。
|
| 图 9 颤振余度法(F5模型,Ma=4.95) Fig.9 Flutter margin method (F5, Ma=4.95) |
|
| 图 10 颤振余度法(F6模型,Ma=5.95) Fig.10 Flutter margin method (F6, Ma=5.95) |
表 3列出了颤振余度法预测的颤振动压和直接观测法的实测值,可见采用颤振余度法预测的颤振动压离实测颤振点很近。模型F5的颤振动压预测误差为-3%,模型F6的颤振动压预测误差为-2.4%。
| Model | Measured | Flutter marginfunction | Damping ratio extrapolation | ||
| qfm/(104Pa) | qff/(104Pa) | δ/% | qfd/(104Pa) | δ/% | |
| F5 | 4.372 | 4.241 | -3.0 | 4.261 | -2.5 |
| F6 | 4.412 | 4.305 | -2.4 | 4.352 | -1.4 |
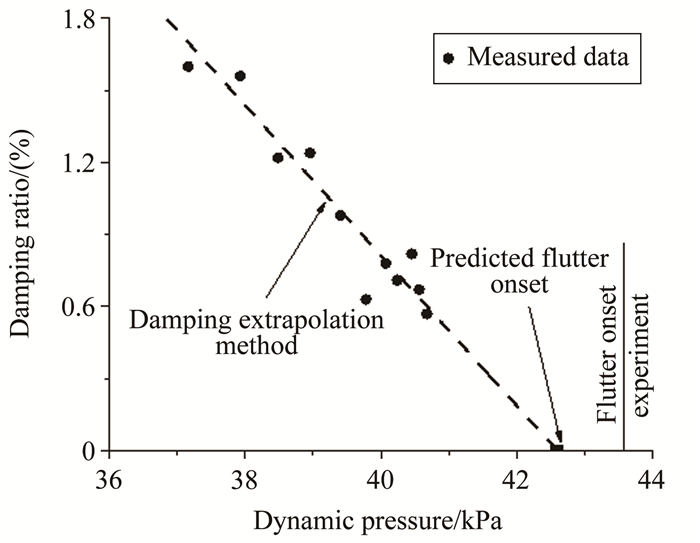
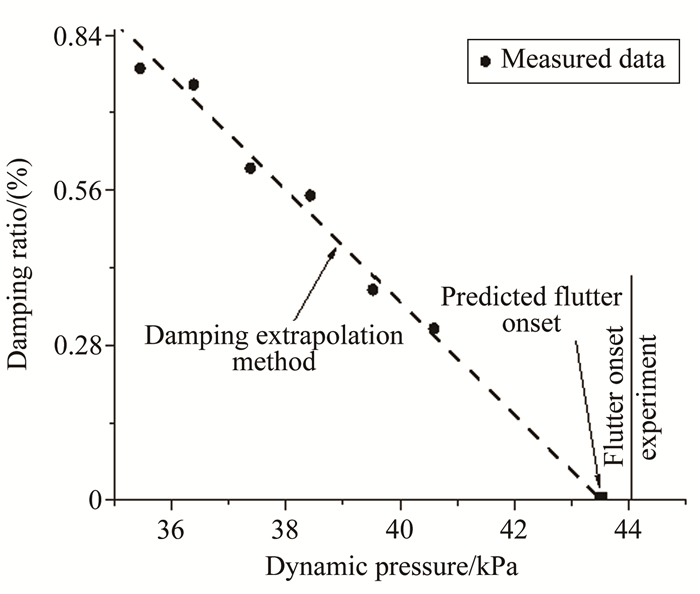
阻尼比外推是最为经典的颤振边界预测方法,其原理最为直接,即颤振发生的时候结构的阻尼比为0。图 11和12为试验模型阻尼比随动压的变化曲线。
|
| 图 11 阻尼比外插颤振边界(F5模型,Ma=4.95) Fig.11 Damping ratio extrapolation (F5, Ma=4.95) |
|
| 图 12 阻尼比外插颤振边界(F6模型,Ma=5.95) Fig.12 Damping ratio extrapolation (F6, Ma=5.95) |
通过阻尼比外推可以得到模型在马赫数4.95时的颤振动压qfd为4.261×104Pa,马赫数4.95时的颤振动压qfd为4.352×104Pa。
表 3列出了阻尼比外推法预测的颤振动压与实测颤振动压,对比可见,采用阻尼比法预测的颤振动压与实测颤振点很接近。模型F5的颤振动压预测误差为-2.5%,模型F6的颤振动压预测误差为-1.4%。
由3.3.1和3.3.2节的研究可知,采用直接观测法、颤振余度法和阻尼比外推法均可得到较为一致的颤振动压参数,这也验证了2种亚临界颤振边界预测方法是可靠的,可以用于高超声速风洞颤振试验。
3.4 动压增速影响对于固定马赫数下的两自由度气动弹性系统,其在一定动压条件下的振动方程为:
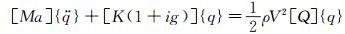 (6)
(6)
特征值分解可得到各阶频率ω和阻尼系数β,由时频域分析可知颤振相关的主要模态,如本次试验为模型一阶和二阶模态,结合关系式(5)和上式可知,给定流场条件下相同结构模型的颤振余度为定值。
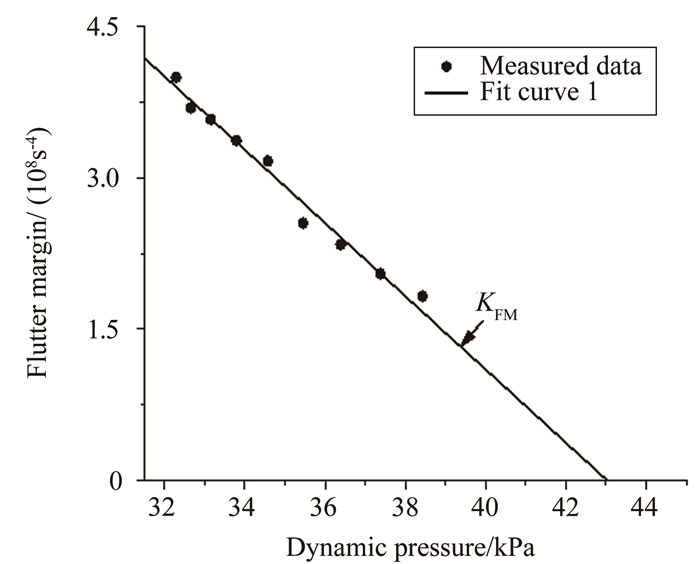
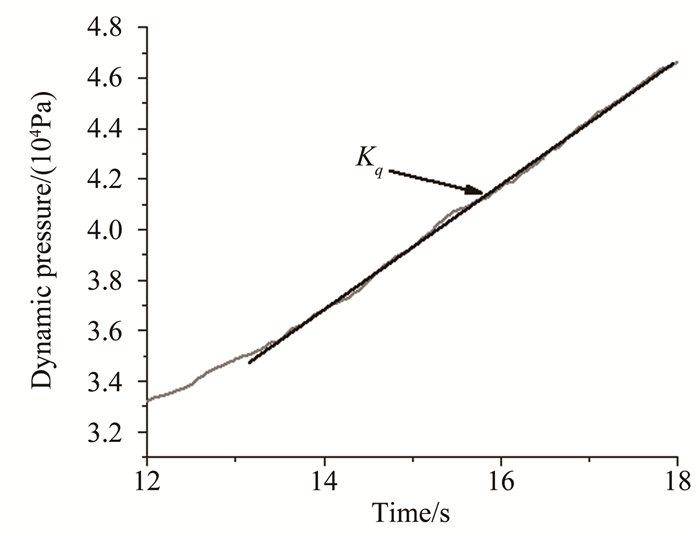
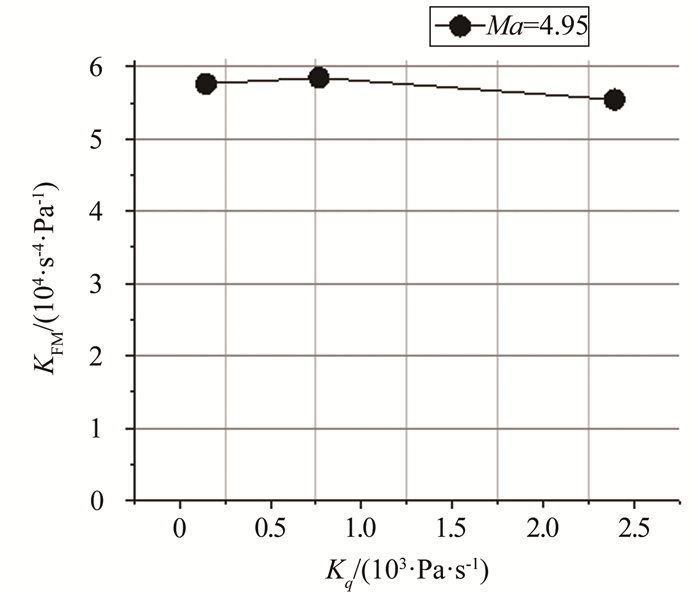
图 13为临近颤振临界点的颤振余度曲线,令KFM为线性插值斜率的绝对值,其反应了试验中颤振发展的速率。图 14为动压增加变化曲线,其增压速率由Kq表示。
|
| 图 13 颤振发展速率 Fig.13 Rate of flutter development |
|
| 图 14 动压增加速率 Fig.14 Rate of dynamic pressure increase |
这里对模型在马赫数4.95下的颤振发展速率和动压增速的关系进行研究,采用另2个结构动力学特性类似的模型F5-1和F5-2进行不同动压增速的试验,F5-1模型试验时动压增速较之F5模型放缓,增压速率约145Pa/s,F5模型试验的动压增速为767Pa/s,F5-2模型试验时动压增速提高到2393Pa/s。
各模型临近颤振时的颤振发展速率和动压增压速率如表 4和图 15所示。当动压增速降低了81.1%时,颤振发展速率降低了1.4%;当动压增速增加了212%时,颤振发展速率降低了5.2%。
| Ma | Kq /(Pa·s-1) |
KFM /(s-4·Pa-1) |
Model |
| 4.95 | 145 | 57617 | F5-1 |
| 4.95 | 767 | 58442 | F5 |
| 4.95 | 2393 | 55428 | F5-2 |
|
| 图 15 动压增速与颤振发展速率 Fig.15 KFM vs Kq plot |
对比可知同一个马赫数下临近颤振临界点附近的颤振发展速率与动压增压速率的变化关系较小,基本不随之变化且无明显规律性。可见试验中动压增速对颤振边界的影响较小,但是过快的动压增速会影响到阻尼外推法的使用,因此,建议试验中可采用渐进逼近方法,即开始试验时动压变化速率较高,在临界颤振动压时降低动压增速。
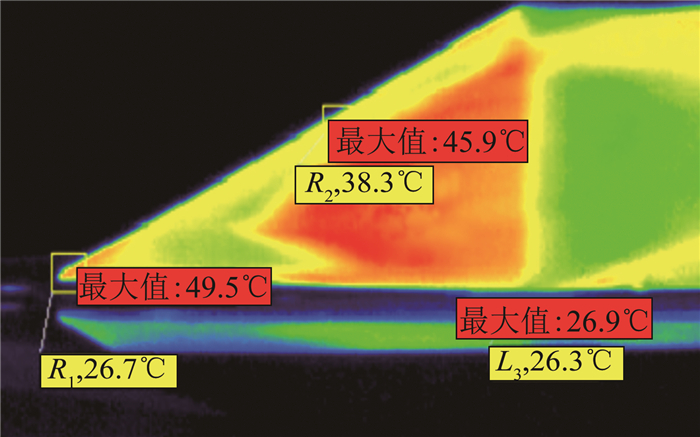
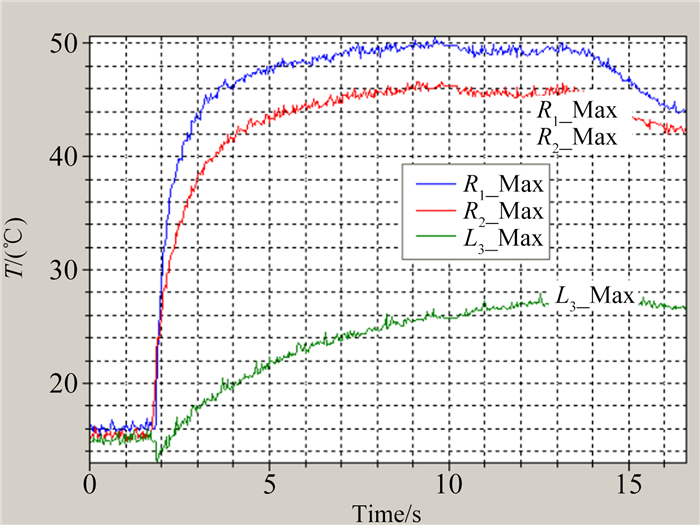
3.5 试验中的气动加热试验中采用如图 2所示的红外热像仪对模型表面气动加热的情况进行测量,并对模型舵尖前缘、前缘展向距离根部2/3位置和舵轴裸露在流场间隙部位的前缘这3点进行温度跟踪测量。该外形的舵面在马赫数4.95和5.95下的红外热成像温度分布如图 16和17所示。
|
| 图 16 F5模型表面温度分布(Ma=4.95) Fig.16 Temperature distribution of model F5 (Ma=4.95) |
|
| 图 17 F6模型表面温度分布(Ma=5.95) Fig.17 Temperature distribution of model F6 (Ma=5.95) |
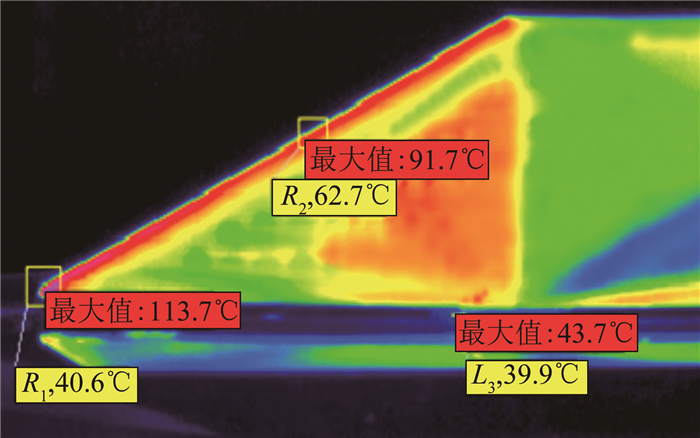
马赫数4.95时,试验总温为377.8K。舵尖前缘和前缘展向距离根部2/3位置在吹风约6s后达到温度平衡,并达到最高温度49.5和45.9℃,舵轴裸露部位前缘温度一直缓慢增加中,试验中最高为26.9℃ (见图 18)。
|
| 图 18 F5模型表面温度随时间变化曲线 Fig.18 The surface temperature of model F5 versus time |
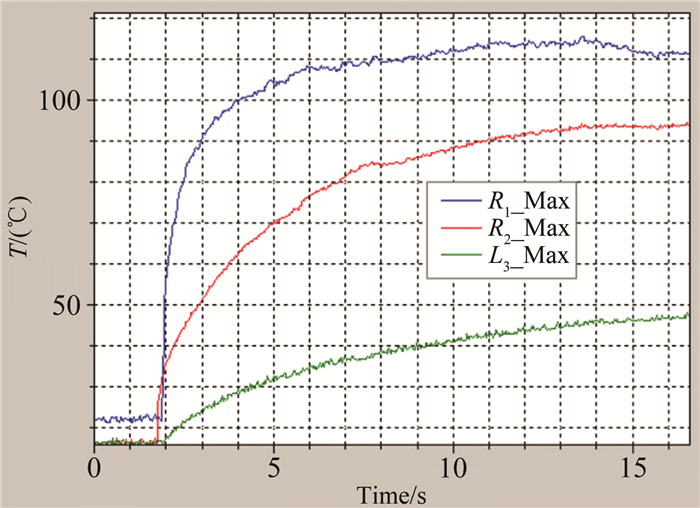
马赫数5.95时,试验总温为476.4K。舵尖前缘和前缘展向距离根部2/3位置在吹风约12s后达到温度平衡,且分别保持113.7和91.7℃的最高温度,舵轴裸露部位前缘温度在试验中一直缓慢增加,试验过程中最高温度43.7℃(见图 19)。
|
| 图 19 F5模型表面温度随时间变化曲线 Fig.19 The surface temperature of model F5 versus time |
由上述研究可知,试验中舵面最高温度出现在舵尖前缘位置,舵面前缘和舵面斜面中后部温度也较高;舵面温度在试验中经过一段时间达到温度平衡并不再增加,舵轴温度则一直缓慢增加;作为主要弹性元件的金属矩形舵轴,其裸露在流场中的部分受到的气动加热影响没有想象中的严重,可能是由于反射板附面层的作用。
4 结论建立并验证了基于连续变动压开车方法的高超声速风洞颤振试验技术,试验马赫数为4.95和5.95。试验通过直接观测法得到了模型的颤振动压,并通过时频域分析技术确认该模型高超声速颤振模态为一阶和二阶的耦合经典颤振。通过本文研究可以得到如下结论:
(1) 在高超声速风洞中采用连续变动压的试验方法可以得到可靠的颤振边界参数,颤振动压增加速率对颤振边界的影响较小;
(2) 颤振余度法和阻尼比外推法在高超声速风洞颤振试验中均具有较高的颤振边界预测精度,可以应用在高超声速风洞颤振试验中;
(3) 试验中模型前缘部位的气动加热较为严重,高马赫数情况下的模型设计需要考虑气动加热对结构动力学特性的影响;合理的控制舵面模型和反射板之间的间隙可以大幅降低气动加热带来的舵轴前缘温升。
| [1] | Garrick I E, Cunningham H J. Problems and developments inaerothermoelasticity[C]//Proceeding of Symposium on Aerothermoelasticity, ASD-TR-61-645, 1962. |
| [2] | Doggett R V Jr. An observation on the pictorial representation of aeroservothermoelasticity[R]. NASA-TM-104058, 1991. |
| [3] | Terry M H. Aeroelasticity research at wright-patterson air force base (Wright Field) from 1953-1993[J]. Journal of Aircraft, 2003, 40(5): 813–819. DOI:10.2514/2.6872 |
| [4] | Frederick W G. Flutter investigation of models having the planform of the northamerican X-15 airplane wing over a range of Mach number from 0.56 to 7.3[R]. NASA-TM-X-460, 1961. |
| [5] | Homer G M, Robert W M. Flutter tests of some simple models at a Mach number of 7.2 in helium flow[R]. NASA MEMO 4-8-59L, 1959. http://www.researchgate.net/publication/23912163_Flutter_Tests_of_Some_Simple_Models_at_a_Mach_Number_of_7.2_in_Helium_Flow |
| [6] | Robert C G. Effects of leading-edge bluntness on flutter characteristics of some square-planform double-wedge airfoils at a Mach number of 15.4[R]. NASA-TN-D-1487, 1962. |
| [7] | Robert C G. Effects of leading-edge sweep on flutter characteristics of some delta-planform surfaces at a Mach number of 15.4[R]. NASA-TN-D-2360, 1964. |
| [8] | 冯明溪, 白葵. 舵面颤振试验[C]//第五届全国流体弹性力学学术会议论文集. 1996. Feng M X, Bai K. Rudder flutter test[C]//Proceedings of the 5th National Symposium on Aeroelasticity. 1996. |
| [9] | 白葵, 冯明溪, 付光明. 超音速有迎角舵面颤振实验[C]//第七届全国空气弹性学术交流会论文集, 2001. Bai K, Feng M X, Fu G M. Experimental study of rudder flutter with angle of attack at supersonic speed[C]//Proceedings of the 7th National Symposium on Aeroelasticity, 2001. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGKQ200110003006.htm |
| [10] | 杨炳渊, 宋伟力. 舵模型风洞颤振试验中亚临界技术的应用研究[J]. 上海航天, 2003, 20(2): 18–21. Yang B Y, Song W L. Application of subcritical technology in wind tunnel flutter experiment for rudder model[J]. Aerospace Shanghai, 2003, 20(2): 18–21. |
| [11] | 冉景洪, 季辰, 刘子强, 等. 跨声速风洞颤振试验模型激振与数据处理方法研究[J]. 实验流体力学, 2009, 23(4): 87–91, 97. Ran J H, Ji C, Liu Z Q, et al. Research of data process methods and model excitation for transonic flutter experiments in wind tunnel[J]. J Exp Fluid Mech, 2009, 23(4): 87–91, 97. |
| [12] | 季辰, 冉景洪, 刘子强. 亚跨风洞中舵面亚临界颤振试验[J]. 实验流体力学, 2011, 25(3): 37–40. Ji C, Ran J H, Liu Z Q. Flutter test of rudder in sub-tran-supersonic wind tunnel using subcritical response methods[J]. J Exp Fluid Mech, 2011, 25(3): 37–40. |
| [13] | 钱卫, 何林祥, 王文卓, 等. 1. 2×1. 2m跨音速风洞模型颤振试验技术研究[C]//第六届全国流体弹性力学会议文集, 珠海, 1998. Qian W, He L X, Wang W Z, et al. 1.2×1.2m transonic wind tunnel model flutter test technology research[C]//Proceedings of the 6th National Symposium on Aeroelasticity, Zhuhai, 1998. http://d.wanfangdata.com.cn/Conference_185643.aspx |
| [14] | 路波, 杨兴华, 罗建国, 等. 跨声速风洞全模颤振试验悬浮支撑系统[J]. 实验流体力学, 2009, 23(3): 90–94, 103. Lu B, Yang X H, Luo J G, et al. Floating suspension system for full model flutter test in transonic wind tunnel[J]. J Exp Fluid Mech, 2009, 23(3): 90–94, 103. |
| [15] | 郭洪涛, 路波, 余立, 等. 某战斗机高速全模颤振风洞试验研究[J]. 航空学报, 2012, 33(10): 1765–1771. Guo H T, Lu B, Yu L, et al. Investigation on full-model flutter test of a fighter plane in high-speed wind tunnel[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(10): 1765–1771. |
| [16] | 郭洪涛, 闫昱, 余立, 等. 高速风洞连续变速压颤振试验技术研究[J]. 实验流体力学, 2015, 29(5): 72–77. Guo H T, Yan Y, Yu L, et al. Research on flutter test technology of continuously adjusting dynamical pressure in high-speed wind tunnel[J]. J Exp Fluid Mech, 2015, 29(5): 72–77. |
| [17] | 闫昱, 余立, 吕彬彬, 等. 超声速颤振风洞试验技术研究[J]. 实验流体力学, 2016, 30(6): 76–80. Yan Y, Yu L, Lyu B B, et al. Research on flutter test technique in supersonic wind tunnel[J]. J Exp Fluid Mech, 2016, 30(6): 76–80. |
| [18] | 季辰, 李锋, 刘子强. 高超声速风洞颤振试验技术研究[J]. 实验流体力学, 2015, 29(4): 75–80. Ji C, Li F, Liu Z Q. Research on flutter test technique in hypersonic wind tunnel[J]. J Exp Fluid Mech, 2015, 29(4): 75–80. |
| [19] | 陈丁, 吕计男, 季辰, 等. 双目视觉技术在高超声速颤振风洞试验中的应用[J]. 实验力学, 2015, 30(3): 381–387. Chen D, Lyu J N, Ji C, et al. Application of binocular vision measurement in hypersonic flutter wind tunnel experiment[J]. Journal of Experimental Mechanics, 2015, 30(3): 381–387. DOI:10.7520/1001-4888-14-192 |
| [20] | Oppenheim A V, Shafer R W. Digital signal processing[M]. Upper Saddle River, NJ: Prentice-Hall, Inc, 1975. |
| [21] | Cooper J E. Parameter estimation methods for flight flutter testing[R]. CP-566, AGARD, 1995. https://www.researchgate.net/publication/292241846_Parameter_estimation_methods_for_flight_flutter_testing |



