2. 河北工业大学 工程流动与过程强化研究中心, 天津 300130;
3. 天津大学 机械学院工程力学系, 天津 300350
2. Research Center of Engineering Fluid and Process Equipment, Hebei University of Technology, Tianjin 300130, China;
3. Department of Mechanics, School of Mechanical Engineering, Tianjin University, Tianjin 300350, China
液固两相流广泛存在于自然界、能源以及化工等各个领域[1]。从河流泥沙输运,到海洋流中固体颗粒的沉积,再到化工反应设备中搅拌、过滤等单元操作,颗粒对于湍流的作用机理一直是人们重点关注的研究领域。
相干结构在湍流边界层中扮演着十分重要的角色,对于湍流的产生和维持机制起着关键作用[2]。随着边界层相干结构的研究发展,颗粒相的存在对近壁湍流影响机理的研究也越来越多。以往的研究表明,湍流场中加入颗粒后,湍流强度会受到显著影响。Gore等[3]整理实验数据,发现流体湍流度与加入的颗粒直径有关,小粒径颗粒会抑制流体的湍流强度,大粒径颗粒会增强流体湍流强度。Rashidi等[4]首先在水平明渠流中研究了近壁区颗粒对湍流结构的影响作用。研究结果发现大颗粒会增加近壁区相干结构的猝发频率,从而增强流体的湍动强度,而小尺寸颗粒则减少壁面附近的猝发频率,降低流体的湍动强度。Kaftori等[5]对低浓度悬浮颗粒水平槽道壁湍流的研究发现,颗粒加快了促发事件的猝发周期,并使近壁雷诺应力增加,粘性底层的法向速度也随之增大。Kulick[6]等利用激光多普勒(LDV)研究垂直湍槽流,结果表明当加入的颗粒粒径小于1个柯尔莫哥洛夫尺度时,流体的湍流度会有所下降。Sato和Hishida[7]借助数字粒子图像测速技术(DPIV)发现,当颗粒直径大于3倍的柯尔莫哥洛夫尺度时,缓冲层和对数律层的湍流度都会有不同程度的增强。Li等人[8]对水平近壁边界层内聚苯乙烯颗粒对于湍流结构的影响进行研究,结果发现颗粒使得湍流粘性底层更薄,流向速度梯度增大。Taniere等[9],Kigerd等[10]和Guo等[11]的实验也均表明颗粒的存在引起了平均流动的减弱和湍流强度的增大。余钊圣等[12]对含有中性悬浮大颗粒的槽道流进行双重数值模拟,结果表明颗粒的存在削弱了大尺度准流向涡结构,从而削弱了近壁区流向的脉动强度;由颗粒诱导出的小尺度涡结构导致横向和展向脉动强度增大。Pan[13-14]等人利用直接数值模拟(DNS)研究了不同尺寸颗粒对于壁湍流的影响,结果显示颗粒的存在会增强流体的脉动强度和雷诺应力,较大直径颗粒时这种变化会更为明显。
综上所述,液固两相流中颗粒的存在可以改变流体的各种湍流统计量,但是对于该结果的边界层区域实验数据相对较少,因此无法从机理上充分解释颗粒对于流体的影响机理。本文利用PIV测量技术,突破以往湍流空间单点测量的局限性,针对加入颗粒前后边界层的平均速度剖面,湍流度及雷诺应力等湍流特性进行研究,同时将统计量与湍流边界层的相干结构猝发事件的运动规律结合起来,分析颗粒对于边界层猝发事件相干结构的影响。
1 实验装置及参数实验在河北工业大学PIV流体力学实验室的中型低速循环水槽中进行,其背景湍流度小于0.8%,实验段尺寸为2500mm×500mm×600mm,水流流速在0~0.5m/s内连续可调。实验所用有机玻璃平板尺寸为2000mm×500mm×15mm(长×宽×厚),平板前缘按8:1的半椭圆进行修形,为得到充分发展的湍流边界层,在距平板前段100mm处安置直径为5mm的拌线,并通过调节后缘板将平板表面沿流向的静压力梯度调节至接近于零。实验平板利用支架使其在距水槽底部250mm处水平放置。
实验过程中激光片光源、CCD相机和平板的相对位置示意图如图 1所示。激光片光源位于水槽展向中心线处,并平行于水槽两侧壁、垂直于平板。CCD相机位于水槽一侧,镜头与片光保持平行,相机拍摄区域距位于距平板前缘1200mm处。

|
| 图 1 实验装置示意图 Fig.1 Schematic diagram of the experimental facility |
实验选用PMMA-RhB荧光粒子作为流场示踪剂,荧光粒子的平均直径为20μm,密度为1200kg/m3,其在532nm激光照射下所激发的波长大于540nm,CCD相机镜头前配置540nm高通滤波片,如此,采集图像时,滤波片会滤除波长540nm以下的散射光,使相机仅能捕捉到荧光粒子的散射光并成像,即相机采集到的始终为流场信息。直径d=140μm,密度为1050kg/m3的聚苯乙烯颗粒作为固相颗粒。定义颗粒的Stokes数[15]St=τp/τf,其中τp=ρpdp2/18μ为颗粒对流体的响应时间,τf=ν/u2*为流体流动的特征流动时间,根据牛顿迭代法求得的摩擦速度u*=0.0104m/s。则颗粒的Stokes数为St=0.122。
实验时水槽自由来流速度保持在0.26m/s,环境温度为20℃,此时水的密度为998kg/m3,运动粘度为1.006×10-6 m2/s。利用双帧双曝图像采集模式,此时相机采样频率为60Hz,曝光时间为1000μs,2帧之间时间间隔为800μs,每次采集样本量为8000对。图像分辨率为2048pixel×2048pixel,拍摄区域大小为100mm×100mm,利用互相关算法对原始图像进行处理,查询窗口大小为32pixel×32pixel,窗口重叠率为75%,因此可得到具有256×256个速度矢量的瞬时速度场。
2 实验结果分析 2.1 平均速度分布将实验结果按经验公式u+=2.5lny++5.5进行拟合得到流场中分别加入颗粒和清水2种工况下平板表面同一位置处无量纲平均速度沿法向位置的分布剖面曲线,如图 2所示。横轴y+=yu*/v,纵轴u+=u/u*,其中u*为对应壁面摩擦速度,v为流体运动黏度。从图中可以看出,壁湍流平均速度剖面的缓冲层变薄,对数律区下移,即在近壁区域(y+ < 200),相同的法向y+位置处,加入颗粒后的无量纲速度u+相比于清水的无量纲速度有明显减小。y+>200区域,两者的无量纲速度逐渐趋于一致。经过分析得知,颗粒由于自身重力会在近壁区聚集,对液相存在曳力作用,导致流场速度有所下降;而在外区,颗粒聚集较少,对于液相的作用逐渐减小,从而液相的速度值趋近于清水。这与Pang[17]和余钊圣[12]的数值模拟结果相吻合。

|
| 图 2 流向平均速度剖面图 Fig.2 Profile of the streamwise mean velocity |
2种工况下壁面湍流边界层中湍流度分量的分布曲线如图 3(a)和(b)所示,从图中可以看出与清水时相比,颗粒的存在使得湍流强度沿法向位置y+发生了一些变化,但两者的变化趋势大体一致。对于流向湍流度,当y+ < 30,湍流度沿y+逐渐增大,在y+=30左右达到最大值;30 < y+ < 200时,湍流度沿y+逐渐减小,并逐渐趋于平缓。对于法向湍流度,y+ < 100时,湍流度逐渐增大并在y+=100左右达到最大值;然后湍流度随着y+的增大又逐渐下降。颗粒的加入使得内区的流向湍流度均有所增强,而法向湍流度在过渡层以前有所减小,对数律区得到增强。雷诺切应力的分布曲线如图 3(c)所示,与清水时相比,相同法向位置y+处,颗粒的存在使缓冲层的雷诺切应力下降,对数律层得到增强,而在外区时两者趋于一致。由于壁湍流猝发事件主要发生在近壁区,而此处湍流度和雷诺切应力值均增大,因此颗粒的加入促进了近壁区湍流猝发事件的发生,湍流强度被增强。

|
| 图 3 湍流度以及雷诺切应力沿法向位置y+的分布 Fig.3 Turbulent intensity and Reynolds shear stress distributions in the wall-normal direction |
相干结构维持着湍流的能量和动量的运输,是湍流产生的重要机制,本文对流向速度沿流向空间的分布进行多尺度分析[18],流向脉动速度沿流向空间的局部平均结构函数为:
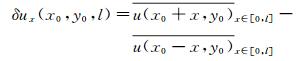 (1)
(1)
式中:u(x, y)表示流向脉动速度在(x, y)平面内的分布;x0为沿流向多尺度变形的中间位置;l为空间流向尺度;,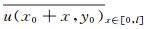
在检测湍流多尺度相干结构时,在低速流体从近壁区向外喷射阶段,当地流向脉动速度u′ < 0且达到局部极小值,δux(x0, y0, l)从负的方向向正的方向变化并经过0点,流动结构流向上上游在压缩,下游在拉伸;与此同时低速流体抬升远离壁面,法向脉动速度v′>0且达到局部极大值,δvy(x0, y0, l)从正的方向向负的方向变化并经过0点,流动结构法向上上游在拉伸,下游在压缩。
高速流体由外区冲向壁面的扫掠阶段,当地流向脉动速度u′>0且达到局部极大值,δux(x0, y0, l)从正的方向向负的方向变化并经过0点,流动结构流向上上游在拉伸,下游在压缩;与此同时高速流体向下冲向壁面,法向脉动速度v′ < 0且达到局部极小值,δvy(x0, y0, l)从负的方向向正的方向变化并经过0点,流动结构法向上上游在压缩,下游在拉伸。因此,湍流结构的检测函数——新象限分裂法[19]定义如下:
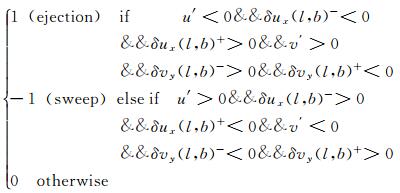 (2)
(2)
基于新象限分裂法检测多尺度相干结构猝发事件,运用空间相位平均方法[20],提取“喷射”和“扫掠”事件脉动速度分量、雷诺切应力、展向涡量等物理量的二维平均拓扑形态。如果“喷射”和“扫掠”事件中心位置被检测到,各物理量在一定尺度范围内的空间相位平均拓扑计算公式为:
 (3)
(3)
式中:(x0(k), y0(k))是第k次检测到“喷射”或“扫掠”发生的中心空间位置; lx、ly分别是拓扑结构空间的流向和法向尺度;N和M分别代表检测到“喷射”和“扫掠”发生的次数。
3.1 “喷射”事件根据前文所述的提取湍流相干结构的方法,本文主要以对数律区y+=100为检测中心,对加入颗粒和清水时水平板湍流边界层相干结构在“喷射”阶段的二维相关物理量的空间拓扑结构进行分析讨论,如图 4所示。从图中可以看出,本文采用的检测方法很好地检测到了2种实验工况下“喷射”阶段的相干结构,即上方的低速流体向下运动时,下方高速运动的流体被迫减速并向上运动。加入颗粒后湍流相干结构的二维拓扑形态与清水时相似,这说明脉动速度沿流向和法向方向上,雷诺切应力和展向涡量在流向方向上皆具有准周期性,相干结构表现出很强的拟序特性。

|
| 图 4 相干结构喷射事件物理量分布云图 Fig.4 Contours of physical quantities during ejection events |
相干结构“喷射”事件流向脉动速度的分布云图如图 4(a)所示,通过对比发现,加入颗粒后脉动速度值较大的区域相对于清水有所增大,使流场流动的脉动速度梯度增大,这说明颗粒的存在增强了壁湍流相干结构的脉动,使相干结构的“喷射”强度增大,从而加大了流体猝发的几率。相干结构“喷射”事件法向脉动速度分布云图如图 4(b)所示,加入颗粒后,“喷射”中心法向脉动速度幅值较大的区域范围虽没有明显变化,但其所对应的脉动值要大于清水的脉动速度,这表明颗粒的存在,促使流体的法向脉动增强,从而增大了湍流传输强度。在湍流运动中,雷诺切应力是流体脉动引质点间动量交换而产生的附加应力,其值愈大表示流体质点的动量交换愈大,脉动愈剧烈。相干结构“喷射”事件雷诺切应力的二维拓扑形态如图 4(c)所示,加入颗粒相后流场的雷诺切应力明显大于清水相,这是由于颗粒的存在带动了周围流体的运动,并与之产生动量交换,从而使雷诺切应力有所增大。从相干结构“喷射”事件展向涡量的云图如图 4(d)所示,加入颗粒后涡量正负幅值较高的范围相对于清水时有所增大,即“喷射”事件的展向涡量在一定程度上得到了增强,这说明颗粒的存在促使展向涡旋运动,加速低速条带的形成和发展,从而增强了湍流猝发强度。
3.2 “扫掠”事件加有固体颗粒和清水的壁湍流相干结构,在“扫掠”事件中二维拓扑形态如图 5所示。从图中可以看出,本文很好地检测到了壁湍流相干结构的“扫掠”事件,即上方为高速流体,下方为低速流体,高速流体向下方俯冲从而导致下方低速流体加速运动。与“喷射”阶段湍流相干结构类似,加入颗粒后,湍流相干结构的二维平均拓扑形态在“扫掠”阶段并没有发生改变,高速流体和低速流体交替分布,进而表现出了很强的拟序特性。

|
| 图 5 相干结构扫掠事件物理量分布云图 Fig.5 Contours of physical quantities during sweep events |
由相干结构扫掠事件流向脉动速度云图(见图 5(a))可以看出,相比于清水时,加入颗粒后“扫掠”事件低速流体区域有明显减少,高速流体区域增加,颗粒的加入使上游下扫的高速流体与周围的流体之间的速度梯度增大,促进了相干结构的猝发过程。对比加入颗粒和清水的壁湍流相干结构的法向脉动速度分布,如图 5(b)所示,加有颗粒后对法向脉动速度的影响与“喷射”时的影响不同,即与清水的法向脉动速度相比,加入颗粒相后相同位置处法向脉动速度减小,湍流的输运能力有所减弱。从相干结构“扫掠”事件的雷诺切应力的二维平均拓扑形态(见图 5(c))可以看出,颗粒的存在使相干结构“扫掠”阶段的雷诺应力变化与“喷射”阶段相似,与清水时相比,强度有所增强,这说明湍流动量交换增强,湍流的脉动受到促进。此外,由相干结构“扫掠”事件的展向涡量云图(见图 5(d))也可以看出,加有颗粒的相干结构展向涡量相比于清水时有一定程度的增强,并且正的展向涡量以及涡量正值较高的范围有所增大,这表明该位置处展向涡的发展得到促进,涡强增大,即诱导外区高速流体冲向壁面的能力增大,加剧近壁区内流动不稳定性。
4 结论本文通过运用PIV测量技术对液固两相和清水相2种不同工况下水平板湍流边界层进行研究分析,得到如下结论:
(1) 与清水时相比,颗粒的存在使边界层缓冲层厚度减小,对数律区下移,相同法向位置处的流向平均速度有所下降。边界层湍流强度以及雷诺切应力的幅值整体变大。说明颗粒的存在使得湍流边界层中流体的脉动增强,促使流体运动过程中的能量和动量的输运能力增强。
(2) 加入颗粒后的流体在近壁区存在湍流相干结构,猝发事件的二维平均拓扑形态结构与清水时相似。颗粒的存在对猝发事件产生了一定的影响:2种猝发事件中雷诺切应力的增大表明近壁区内湍流动量和能量的输运能力增强。颗粒的存在使得展向涡量增大,促进了涡对诱导流体的能力,导致近壁区湍流猝发加剧,湍流不稳定性得到增强。
| [1] | 岳湘安. 液-固两相流基础[M]. 北京: 石油工业出版社, 1996. |
| [2] | Smith C R, Walker J D A, Haidari A H, et al. On the dynamics of near-wall turbulence[J]. Philosophical Transactions of the Royal Society B Biological Sciences, 1991, 336(1641): 131–175. DOI:10.1098/rsta.1991.0070 |
| [3] | Gore R A, Crowe C T. Effect of particle size on modulating turbulent intensity[J]. International Journal of Multiphase Flow, 1989, 15(2): 279–285. DOI:10.1016/0301-9322(89)90076-1 |
| [4] | Rashidi M, Hetsroni G, Banerjee S. Particle-turbulence interaction in a boundary layer[J]. International Journal of Multiphase Flow, 1990, 16(6): 935–949. DOI:10.1016/0301-9322(90)90099-5 |
| [5] | Kaftori D, Hetsroni G, Banerjee S. The effect of particles on wall turbulence[J]. International Journal of Multiphase Flow, 1998, 24(3): 359–386. DOI:10.1016/S0301-9322(97)00054-2 |
| [6] | Kulick J D, Fessler J R, Eaton J K. Particle response and turbulence modification in fully developed channel flow[J]. Journal of Fluid Mechanics, 1994, 277: 109–134. DOI:10.1017/S0022112094002703 |
| [7] | Sato Y, Hishida K. Transport process of turbulence energy in particle-laden turbulent flow[J]. International Journal of Heat & Fluid Flow, 1996, 17(3): 202–210. |
| [8] | Li J, Wang H, Liu Z, et al. An experimental study on turbulence modification in the near-wall boundary layer of a dilute gas-particle channel flow[J]. Experiments in Fluids, 2012, 53(5): 1385–1403. DOI:10.1007/s00348-012-1364-7 |
| [9] | Tanière A, Oesterlé B, Monnier J C. On the behaviour of solid particles in a horizontal boundary layer with turbulence and saltation effects[J]. Experiments in Fluids, 1997, 23(6): 463–471. DOI:10.1007/s003480050136 |
| [10] | Kiger K T, Pan C. Suspension and turbulence modification effects of solid particulates on a horizontal turbulent channel flow[J]. Journal of Turbulence, 2002, 3(10): 27–29. |
| [11] | 郭福水, 王汉封, 柳朝晖, 等. 水平槽道内湍流变动的PTV实验研究[J]. 工程热物理学报, 2004, 25(4): 622–624. Guo F S, Wang H F, Liu Z H, et al. Experimental investigations on turbulence modulation in a horizontal channel flow using PTV[J]. Journal of Engineering Thermophysics, 2004, 25(4): 622–624. |
| [12] | 余钊圣, 王宇, 邵雪明, 等. 中性悬浮大颗粒对湍槽流影响的数值研究[J]. 浙江大学学报(工学版), 2013, 47(1): 109–115. Yu Z S, Wang Y, Shao X M, et al. Numerical studies on effects of neutrally buoyant large particles on turbulent channel flow[J]. Journal of Zhejiang University (Engineering Science), 2013, 47(1): 109–115. |
| [13] | Pan Y, Banerjee S. Numerical simulation of particle interactions with wall turbulence[J]. Physics of Fluids (1994-present), 1996, 8(8): 2733–2755. |
| [14] | Pan Y, Banerjee S. Numerical investigation of the effects of large particles on wall-turbulence[J]. Physics of Fluids, 1997, 9(12): 3786–3807. DOI:10.1063/1.869514 |
| [15] | Crowe C T, Gore R A, Troutt T R. Particle dispersion by coherent structures in free shear flows[J]. Particulate Science & Technology, 1985, 3(3): 149–158. |
| [16] | Vinkovic I, Doppler D, Lelouvetel J, et al. Direct numerical simulation of particle interaction with ejections in turbulent channel flows[J]. International Journal of Multiphase Flow, 2011, 37(2): 187–197. DOI:10.1016/j.ijmultiphaseflow.2010.09.008 |
| [17] | Pang M J, Wei J J, Yu B. Numerical investigation of phase distribution and liquid turbulence modulation in dilute particle-laden flow[J]. Particulate Science & Technology, 2011, 29(6): 554–576. |
| [18] | 姜楠, 管新蕾, 于培宁. 雷诺应力各向异性涡黏模型的层析TRPIV测量[J]. 力学学报, 2012, 44(2): 1037–1042. Jiang N, Guan X L, Yu P N. Tomographic TRPIV measurement of anisotropic eddy-viscosity model for coherent structure Reynolds Stress[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(2): 1037–1042. |
| [19] | Yang S Q, Nan J. Tomographic TR-PIV measurement of coherent structure spatial topology utilizing an improved quadrant splitting method[J]. Science China Physics, Mechanics & Astronomy, 2012, 55(10): 1863–1872. |
| [20] | 姜楠, 于培宁, 管新蕾. 湍流边界层相干结构空间拓扑形态的层析TRPIV测量[J]. 航空动力学报, 2012, 27(5): 1113–1121. Jiang N, Yu P N, Guan X L. Tomo-TRPIV measurement of coherent structure spatial topology in turbulent boundary layer[J]. Journal of Aerospace Power, 2012, 27(5): 1113–1121. |



